1 Introduction

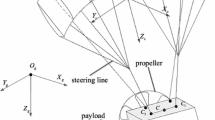
In recent years, the powered parafoil (PPF), as shown in Fig. 1, has been widely accepted for precise payload delivery and field investigation [1,2,3,4,5,6]. The steerable parafoil makes the PPF different from the traditional parachute systems. Due to the outstanding aerodynamic characteristics of the parafoil, the PPF is suitable for long distance delivery of heavy payloads with the advantages of high energy-efficiency, low costs, soft-landing capability, and inherent stability. The compact structure and foldable parafoil make the PPF easy to transport before the deployment. Moreover, the gliding characteristic of the parafoil ensures that the PPF has no risk for crash.

Fig. 1
figure 1

Powered parafoil

Full size image

The PPF is composed of the parafoil and payload, and the payload is suspended strictly under the parafoil via suspension lines. Compared with the traditional parafoil airdrop systems [7,8,9,10], the PPF is more applicable with the altitude control capability. The control inputs for the PPF involve brake deflection and thrust, which are used to control lateral direction and longitudinal altitude, respectively. The asymmetric deflection of the brake causes the yaw motion of the PPF, and the thrust effects the angle of attack of the parafoil and thus controls the altitude. Accordingly, the trajectory tracking problem can be decomposed into lateral and longitudinal control problems for simplicity. However, the PPF has strong nonlinearity and is susceptible to wind disturbances due to the low flight speed and lightweight parafoil [11]. Moreover, the payload of the PPF swings during the flight since it is suspended under the canopy. This structure makes PPF unable to use the real-time state information measured by high-precision inertial navigation system for control. The cross-coupling effect between the lateral and longitudinal control channels also makes the control problem more complicated. Therefore, the PPF has attracted considerable attention in academia, and many novel results about the application of the parafoil have been reported in the literature.

In the past decades, several control methods have been applied to the trajectory tracking of the PPF [12,13,14,15]. Garcia-Beltran [16] presented the development of passivity-based control (PBC) algorithms to stabilize an unmanned powered parachute aerial vehicle. Slegers [17] proposed a model predictive control (MPC) strategy for lateral heading control of the PPF, and a simplified linear dynamic model of six degrees of freedom (DOF) was applied as the predictive model. Ochi [18] and Li [19] employed a three-term PID controller, including the asymmetric brake deflection, symmetric brake, and thrust. These methods were developed and validated based on the linearized dynamic model, while the nonlinear dynamics were not considered. By introducing the neural network to approximate the dynamic error, Liu [20] and Qian [21] proposed the nonlinear flight control methods for the lateral-directional relative yaw angle control and the trajectory tracking control of the PPF, respectively. In recent studies, the robust backstepping tracking control [22] and all-coefficient adaptive control (ACAC) [23] methods were also presented. Considering the complexity features of PPF, Xie [24, 25] proposed an online subspace prediction method to overcome the uncertainties and disturbances and Sun [26] implemented the sliding mode control (SMC) to the PPF. Aoustin [27] designed a nonlinear control law for longitudinal motion control based on a new mathematical model, which was constructed as the system of two rigid bodies connected by an elastic joint with four DOF. However, most of the aforementioned methods depend on the linearized or precise models, which may reduce their robustness and lead weak capability to attenuate external disturbances. Moreover, it is easy to get accurate translational and angular velocity, while that is not available or expensive in practice.

Since the PPF is a complex nonlinear system and is susceptible to external wind disturbances, researchers turned to active disturbance rejection control (ADRC) methodology to enhance the robustness of the system [28,29,30,31,32,33,34,35]. The proposed method has demonstrated significant advantages in the control of nonlinear systems, including but not limited to aircraft control. Tao [36, 37] applied the ADRC in the trajectory tracking control by regarding the uncertainties and external disturbances as the total disturbance witch can be estimated and compensated actively. In the following studies, different conditions such as insufficient initial altitude [38] and various wind disturbances [39, 40] are considered by Tao. Tan [41, 42] designed the lateral and longitudinal controllers based on the ADRC separately and achieved satisfying performance based on simulations. Sun [43] proposed a hybrid control approach for PPF based on ADRC by considering that the wind interference and the unbalanced load on the actuators of its horizontal controller can extremely reduce the control effect. Luo proposed a lateral ADRC controller for the PPF based on the wind compensation to reduce the impact of the wind disturbance [44], and then the proposed method was applied to trajectory tracking control of the PPF based on wind identification [45]. The decoupling trajectory tracking control was also proposed to reduce the burden of ADRC by Luo [46, 47]. However, when the non-diminishing disturbances are introduced to the PPF, the estimation error of the total disturbance cannot be attenuated to zero, resulting in the limitation of the controller to achieve better performance. The asymptotic stability of the PPF was also not guaranteed.

In this paper, only GPS is selected to acquire the position of the PPF for cost saving, and the sliding mode control [48,49,50,51], which has shown strong robustness to the nonlinear systems, is introduced to handle the residual estimation error of the total disturbance of LESO, and a novel control scheme is proposed to ensure the asymptotic stability of the PPF. Considering the practice that the altitude and direction are the only states that can be controlled, the trajectory tracking problem is decomposed into the lateral and longitudinal control channels and the tracking controllers for each channel are designed. The 3D trajectory can be decomposed into horizontal and height targets according to the characteristics of PPF. With the elaborately designed sliding manifold, the proposed method guarantees the asymptotic stability of the desired equilibrium point even in the presence of unknown non-diminishing disturbances. The asymptotic stability of the PPF is proved by rigorous mathematical analysis based on Lyapunov method. Specifically, the heading angles for the lateral channel and the altitude for the longitudinal channel are the only required state feedback, which can enhance the robustness of the proposed method. That is, the PPF can be stabilized to the desired trajectory without velocity feedback. Moreover, the proposed method is validated by simulations and semi-physical experiments.

The remaining parts of the paper are organized as follows. Section 2 presents the eight DOF dynamic model of the PPF. Then, a complete analysis for the proposed method is provided in Sect. 3. In Sects. 4 and 5, simulation and experimental results are provided to evaluate the performance of PPF, respectively. The concluding remarks are presented in Sect. 6.

2 Modeling of the powered parafoil

A practical PPF is shown in Fig. 1. Due to the aerodynamic characteristics of parafoil and the non-rigid internal connections, the PPF has complex dynamic characteristics. Therefore, the modeling problem of the PPF is addressed firstly in this section.

Considering the relative motion between the canopy and payload, a model with eight DOF is proposed. Figure 2 shows the configuration of the PPF and three main coordinate systems are presented, including geodetic coordinate system (inertial coordinate system) \({\Sigma _{_I}}\), parafoil-fixed coordinate system \({\Sigma _c}\) and payload-fixed coordinate system \({\Sigma _p}\). These coordinate systems are fixed to a fixed point at the ground, the center of gravity (CG) of the parafoil and the CG of the payload, respectively. Specifically, to facilitate the lift and drag calculation of the parafoil, the rigging coordinate system \({\Sigma _r}\) and wind coordinate system \({\Sigma _w}\) are established as auxiliary coordinate systems. In Fig. 2, O, X,Y, and Z are origin, x-axis, y-axis and z-axis of the corresponding coordination, respectively, and the sub-script represents the corresponding coordination. \(C_R\), \(C_L\) and \(C_m\) are the right suspension point, the left suspension point, and the center of the two suspension points, respectively. Note that all the coordinate systems are right-handed.

Fig. 2
figure 2

Coordinate systems

Full size image

By using the Lagrange approach, the basic equations of motion for the payload in \({\Sigma _p}\) are given by

$$\begin{aligned} \begin{array}{l} \frac{{\partial {\textbf{P}_p}}}{{\partial t}} + {\mathbf {\omega } _p} \times {\textbf{M}_p} = \textbf{F}_p^a + \textbf{F}_p^G + \textbf{F}_p^{th} + \textbf{F}_p^{te}\\ \\ \frac{{\partial {\textbf{H}_p}}}{{\partial t}} + {\textbf{V}_p} \times {\textbf{P}_p} + {\omega _p} \times {\textbf{H}_p} = \textbf{M}_p^{te} \end{array} \end{aligned}$$
(1)

where \({\textbf{P}_p}\), \({\textbf{H}_p}\), \({\textbf{F}_p^G}\), \({\textbf{F}_p^a}\), \({\textbf{F}_p^{te}}\) and \({\textbf{F}_p^{th}} \in \textbf{R}^{3\times 1}\) are momentum, moment of momentum, gravity, aerodynamic force, tension of suspension line and the thrust provided by the propeller, respectively. \(\textbf{M}_p^{te}\in \textbf{R}^{3\times 1}\) is the moment of the tension of suspension lines. The payload is assumed to be in a regular shape and the moments of the gravity, thrust and aerodynamic drag are neglected. The forces acting on the payload are described in \({\Sigma _p}\) with the subscript p. The superscripts a, G, te and th indicate different type of forces, respectively. \({\textbf{V}_p} = {\left[ {\begin{array}{*{20}{c}} {{u_p}}&{{v_p}}&{{w_p}} \end{array}} \right] ^T}\) and \({\omega _p} = {\left[ {\begin{array}{*{20}{c}} {{p_p}}&{{q_q}}&{{r_p}} \end{array}} \right] ^T}\) are the velocity and angular rate of the payload, and the superscript T here is the transpose symbol.

The basic equations of motion for the parafoil in \({\Sigma _c}\) are

$$\begin{aligned} \begin{array}{l} \frac{{\partial {\textbf{P}_c}}}{{\partial t}} + {\omega _c} \times {\textbf{P}_c} = \textbf{F}_c^a + \textbf{F}_c^G + \textbf{F}_c^{te}\\ \\ \frac{{\partial {\textbf{H}_c}}}{{\partial t}} + {\textbf{V}_c} \times {\textbf{P}_c} + {\mathbf {\omega } _c} \times {\textbf{H}_c} = \textbf{M}_c^a + \textbf{M}_c^{te} \end{array} \end{aligned}$$
(2)

where \({\textbf{P}_c}\), \({\textbf{H}_c}\), \({\textbf{F}_c^G}\), \({\textbf{F}_c^a}\) and \({\textbf{F}_c^{te}}\) are momentum, moment of momentum, gravity, aerodynamic force and tension of suspension lines, which are represented in \({\Sigma _c}\), respectively. \(\textbf{M}_c^{te}\in \textbf{R}^{3\times 1}\) is moment of the tension of suspension lines in \({\Sigma _c}\) and \(\textbf{M}_c^{a}\in \textbf{R}^{3\times 1}\) is the moment caused by aerodynamic force. \({\textbf{V}_c} = {\left[ {\begin{array}{*{20}{c}} {{u_c}}&{{v_c}}&{{w_c}} \end{array}} \right] ^T}\) and \({\omega _c} = {\left[ {\begin{array}{*{20}{c}} {{p_c}}&{{q_c}}&{{r_c}} \end{array}} \right] ^T}\) denote the velocity and angular rate of the parafoil, where the subscript c denotes the parafoil-fixed coordinate system \(\Sigma _c\).

Applying the velocity and force constraints between the parafoil and payload, the dynamic model of the PPF can be proposed. Let \(\dot{x} = {\left[ {\begin{array}{*{20}{l}} {{\varvec{{\dot{V}}}_p}}&{{{{\dot{\omega }} }_p}}&{{\varvec{{\dot{V}}}_c}}&{{{{\dot{\omega }} }_c}}&{\textbf{F}_c^{te}}&{m_x^{te}}&{m_z^{te}} \end{array}} \right] ^T}\) be the time derivative of the state vectors, then 17 equations are obtained. Hereto, the motion of equations of the PPF is described as

$$\begin{aligned} \dot{x} = {M^{ - 1}}F \end{aligned}$$
(3)

where M and F derived from the dynamic and constraint equations. Specifically, the \(\textbf{F}_c^{te}\), \(m_x^{te}\) and \(m_z^{te}\) are calculated as auxiliary states, which are useful in mechanical analysis. The detailed descriptions of the proposed model refer to Ref. [52].

3 Problem formulation and main results

The control inputs for the PPF involve lateral brake deflection of the canopy trailing edge and thrust provided by the propeller, which are utilized to control lateral direction and altitude of the PPF, respectively. The main objective of this paper is to maintain trajectory tracking control of the PPF. To this end, the control laws of two inputs are designed.

3.1 Problem formulation

According to the structure of the PPF, the trajectory tracking problem of the PPF can be solved by designing the lateral and longitudinal control channels. Let \(\psi _l\) and h, respectively, be the lateral direction angle and longitudinal altitude, then the lateral and longitudinal control channels can be described as

$$\begin{aligned} \left\{ \begin{array}{l} {{\ddot{\psi }}_l} = {b_\psi }\left( x \right) {\delta _a} + {f_\psi }\left( x \right) \\ \ddot{h} = {b_h}\left( x \right) {F_{th}} + {f_h}\left( x \right) \end{array} \right. \end{aligned}$$
(4)

where \(b_\psi \left( x\right) \), \(b_h \left( x\right) \), \(f_\psi \left( x\right) \) and \(f_h \left( x\right) \) are lateral control gain, longitudinal control gain, lateral nonlinear dynamics and longitudinal nonlinear dynamics, respectively. \(\delta _a = \delta _R - \delta _L\) is the asymmetric deflection and \({\delta _R}\) and \({\delta _L}\) are the deflection control of the right and left trailing edge, respectively. \(F_{th}\) denotes the first term of \(\textbf{F}_p^{th}\). Then the control objective is decomposed into tracking the desired altitude \(h_d\) and tracking the reference heading angle \(\psi _d\). According to the practical constraints of the PPF, the horizontal tracking errors can only be eliminated by control the course of the PPF. Therefore, the reference of the lateral control channel is designed as \(\psi _d = \psi _r + { \mathrm atan}(e_p/k_e)\), where \(\psi _r\) is the heading angle of the reference trajectory, \(e_p\) is the horizontal position error, and \(k_e\) is a positive constant.

3.2 Controller design

To facilitate the analysis, the lateral and longitudinal control channels are designed to share the control schemes. The model of both channels can be simplified as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\xi }}_1 = \xi _2 \\ {\dot{\xi }}_2 = {b_\xi }u + {f_\xi } \end{array} \right. \end{aligned}$$
(5)

where \(\xi _1=\psi _l\), \(\xi _2={\dot{\psi }}_l\), \({b_\xi }=b_\psi \), \({f_\xi } = f_\psi \) and \(u=\delta _a\) for the lateral channel and \(\xi _1=h\), \(\xi _2=\dot{h}\), \({b_\xi }=b_h\), \({f_\xi } = f_h\) and \(u=F_{th}\) for the longitudinal channel. In order to estimate the total disturbance of each channel with LESO, the system Eq. (5) can be augmented as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\xi }}_1 = \xi _2 \\ {\dot{\xi }}_2 = {b_0}u + \xi _3 \\ \dot{\xi }_3 = w \end{array} \right. \end{aligned}$$
(6)

where \(\xi _3 = f_\xi + \left( b_\xi - b_0\right) \) is the augmented state, which is called the total disturbance, and w is the derivative of total disturbance. Then, the LESO can be designed as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}_1 = z_2 + \beta _1 \varepsilon _1 \\ \dot{z}_2 = {b_0}u + z_3 + \beta _2 \varepsilon _1\\ \dot{z}_3 = \beta _3 \varepsilon _1 \end{array} \right. \end{aligned}$$
(7)

where \(\varepsilon _1=\xi _1 - z_1\) is the estimation error and \(z_i\left( i=1,2,3\right) \) is the estimated value of \(\xi _i \left( i=1,2,3\right) \). The estimation error of LESO can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {{{\dot{\varepsilon }}}_1} = {\varepsilon _2} - {3}{\varepsilon _1}\\ {{{\dot{\varepsilon }}}_2} = {\varepsilon _3} - {3}{\varepsilon _1}\\ {{{\dot{\varepsilon }}}_3} = w - {\varepsilon _1} \end{array} \right. \end{aligned}$$
(8)

where \(\varepsilon _2=\xi _2 - z_2\) and \(\varepsilon _3=\xi _3 - z_3\). In particular, the observer gains can be selected as

$$\begin{aligned} \left[ {{\beta _1},{\beta _2},{\beta _3}} \right] ^T = \left[ {3{\omega _o},3\omega _o^2,\omega _o^3} \right] ^T \end{aligned}$$
(9)

with \({\omega _o} > 0\) for simplicity. If \(\xi _1\) (i.e., \(\psi _l\) or h) is the only feedback state and to achieve the trajectory tracking of the PPF via SMC methodology, the sliding manifold can be elaborately designed as

$$\begin{aligned} \sigma = c_0 e_1 + \epsilon _2 + \int _{0}^{t}k_s \textrm{sgn} \left( e_1\right) \text {d}s \end{aligned}$$
(10)

where \(e_1 = \xi - \xi _d\) and \(\epsilon _2 = z_2 - {\dot{\xi }}_d\). \(\xi _d\) is the reference second order differentiable and \(\dot{\xi }_d\) is the derivative of \(\xi _d\), respectively. \(\textrm{sgn}(z)\) denotes the standard sign function, which is defined as

$$\begin{aligned} {\mathop {\textrm{sgn}}} \left( z \right) = \left\{ \begin{array}{l} 1,~~~~~~z > 0\\ 0,~~~~~~z = 0\\ - 1,~~~~z < 0 \end{array} \right. \end{aligned}$$
(11)

To ensure that \(\varepsilon _1\) converges to zero asymptotically, the control law of system (5) can be designed as

$$\begin{aligned} \begin{aligned} u&=\frac{1}{b_0}\left( - c_0 \epsilon _2 - k_1 \sigma - k_2 \mathrm{{sgn}}\left( \sigma \right) - k_s \mathrm{{sgn}} \left( e_1\right) \right. \\&\quad \left. - z_3 - \beta _2\varepsilon _1\right) \end{aligned} \end{aligned}$$
(12)

where \(c_0\), \(k_1\), \(k_2\), \(k_s\) are positive parameters.

3.3 Stability analysis

Due to practical constraints, the PPF works in a domain of interest of \(D = \left\{ {\xi |{{\left\| \xi \right\| }} \le \delta } \right\} \), where \(\xi = {\left[ {{\xi _1},{{ \xi }_2}} \right] ^T}\) and \(\delta \) is positive constant. The stability of the proposed control strategy will be analyzed within D. Before proceeding with the subsequent analysis, the following assumption is made.

Assumption 1

The derivative of \(\xi _{3}\) is bounded within D and

$$\begin{aligned} \left| w\right| \le L_w \end{aligned}$$
(13)

where \(L_w\) is a positive constant.

To facilitate the subsequent stability analysis, a compact set \(B_\varepsilon \) is defined as

$$\begin{aligned} B_\varepsilon = \left\{ {\varepsilon |{{\left\| \varepsilon \right\| }} \le \delta _\varepsilon } \right\} \end{aligned}$$

where \(\varepsilon = {\left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}}&{{\varepsilon _2}}&{{\varepsilon _3}} \end{array}} \right] ^T}\) and \(\delta _\varepsilon \) is a positive constant. The LESO states are initialized to ensure that \(\left\| \varepsilon \left( 0\right) \right\| \) is within \(B_\varepsilon \).

Theorem 1

The estimation error of the observer presented in Eq. (8) is bounded and

$$\begin{aligned} \mathop {\lim }\limits _{{\omega _o} \rightarrow \infty , {t} \rightarrow \infty } \left\| \varepsilon \right\| = 0. \end{aligned}$$
(14)

Proof

Let \(\eta _i = \frac{\varepsilon _i}{\omega _o^i}\left( i=1,2,3 \right) \), then Eq. (8) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} {{{\dot{\eta }} }_1} = {\eta _2} - {\beta _1}{\eta _1}\\ {{{\dot{\eta }} }_2} = {\eta _3} - {\beta _2}{\eta _1}\\ {{{\dot{\eta }} }_3} = \frac{w}{{\omega _o^3}} - {\beta _3}{\eta _1} \end{array} \right. \end{aligned}$$
(15)

And Eq. (15) can be reformulated as

$$\begin{aligned} \dot{\eta } = A_\eta \eta + B_\eta \frac{w}{\omega ^3_o} \end{aligned}$$
(16)

for simplicity, where \(\eta = \left[ {{\eta _1},{\eta _2},{\eta _3}} \right] ^T\) and

$$\begin{aligned} {A_\eta } = \left[ {\begin{array}{*{20}{c}} { - 3}&{}1&{}0\\ { - 3}&{}0&{}1\\ { - 1}&{}0&{}0 \end{array}} \right] ,B_\eta = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}}\right] \end{aligned}$$
(17)

It is clear that \(A_\eta \) is Hurwitz. Then, there exists a unique positive definite matrix \(P_\eta \) which satisfies a Lyapunov equation \(A_\eta ^T P_\eta + P_\eta A_\eta =-Q_\eta \). By choosing the Lyapunov function candidate as \(V(\eta )=\eta ^T P_\eta \eta \), the derivative of \(V(\eta )\) can be written as

$$\begin{aligned} \begin{aligned} \dot{V}\left( \eta \right)&= - {\omega _o}{\eta ^T}{Q_\eta }\eta + 2{\eta ^T}P_\eta B_\eta \frac{w}{{\omega _o^3}}\\&\quad \le - {\omega _o}{\lambda _{\min }}\left( {{Q_\eta }} \right) {\left\| \eta \right\| ^2} + \frac{{2{L_w}\lambda _{max} \left( P_\eta \right) \left\| \eta \right\| }}{{\omega _o^3}} \end{aligned}\nonumber \\ \end{aligned}$$
(18)

Considering \(\frac{{V\left( \eta \right) }}{{{\lambda _{\max }\left( P _\eta \right) }}} \le \left\| \eta \right\| ^2 \le \frac{{V\left( \eta \right) }}{{{\lambda _{\min }\left( P _\eta \right) }}}\), inequality (18) can be rearranged as

$$\begin{aligned}{} & {} \dot{V}\left( \eta \right) \le - \frac{{{\omega _o\lambda _{\min }}\left( {{Q_\eta }} \right) }}{{{\lambda _{\max }}\left( {{P_\eta }} \right) }}V\left( \eta \right) \nonumber \\{} & {} \quad + \frac{{2{L_w}{{{\lambda _{\max }}\left( {{P_\eta }} \right) }}}}{{\omega _o^3\sqrt{{\lambda _{\min }}\left( {{P_\eta }} \right) } }}\sqrt{V\left( \eta \right) } \end{aligned}$$
(19)

Let \(W = \sqrt{V\left( \eta \right) }\), then \(\dot{W} = \frac{{\dot{V\left( \eta \right) }}}{{2\sqrt{V}\left( \eta \right) }}\) can be derived. Inequality (19) can be rewritten as

$$\begin{aligned} \dot{W} \le - \frac{{{\omega _o\lambda _{\min }}\left( {{Q_\eta }} \right) }}{{2{\lambda _{\max }}\left( {{P_\eta }} \right) }}W + \frac{{2{L_w}{{{\lambda _{\max }}\left( {{P_\eta }} \right) }}}}{{\omega _o^3\sqrt{{\lambda _{\min }}\left( {{P_\eta }} \right) } }} \end{aligned}$$
(20)

Applying the Gronwall–Bellman inequality, one obtains

$$\begin{aligned} \begin{aligned} W \le&- \left( {\frac{{2{L_w}{\lambda ^2}_{\max }\left( {{P_\eta }} \right) }}{{\omega _o^4\sqrt{{\lambda _{\min }}\left( {{P_\eta }} \right) } {\lambda _{\min }}\left( {{Q_\eta }} \right) }} - W\left( {{t_0}} \right) } \right) \\&{e^{-\frac{{{\lambda _{\min }}\left( {{Q_\eta }} \right) }}{{2{\lambda _{\max }}\left( {{P_\eta }} \right) }}\left( {t - {t_0}} \right) }}+ \frac{{2{L_w}{\lambda ^2}_{\max }\left( {{P_\eta }} \right) }}{{\omega _o^4\sqrt{{\lambda _{\min }}\left( {{P_\eta }} \right) } {\lambda _{\min }}\left( {{Q_\eta }} \right) }} \end{aligned} \end{aligned}$$
(21)

which indicates that when \(t \rightarrow \infty \), one gets

$$\begin{aligned} \begin{aligned} \left\| \eta \right\|&\le \frac{{\sqrt{V} }}{{\sqrt{{\lambda _{\min }}\left( {{P_\eta }} \right) } }} \\&\quad \le \frac{{2{L_w}{\lambda ^2 _ {\max }} \left( {{P_\eta }} \right) }}{{\omega _o^4{\lambda _{\min }}\left( {{P_\eta }} \right) {\lambda _{\min }}\left( {{Q_\eta }} \right) }}\\&\quad = \frac{M_e}{\omega _o^4} \end{aligned} \end{aligned}$$
(22)

Since \(P_\eta \) and \(Q_\eta \) are independent from \(\omega _o\), Eq. (22) indicates that

$$\begin{aligned} \mathop {\lim }\limits _{{\omega _o} \rightarrow \infty ,{t} \rightarrow \infty } \left\| \eta \right\| = 0 \end{aligned}$$
(23)

which together with \(\eta _i = \frac{e_i}{\omega _o^i}\left( i=1,2,3 \right) \) yields

$$\begin{aligned} \begin{aligned} \mathop {\lim }\limits _{{\omega _o} \rightarrow \infty ,{t} \rightarrow \infty } \left\| \varepsilon \right\| \le \mathop {\lim }\limits _{{\omega _o} \rightarrow \infty ,{t} \rightarrow \infty } \omega _o^3\left\| \eta \right\| = 0 \end{aligned} \end{aligned}$$
(24)

Furthermore, if \(\omega _o\) is tuned to ensure that \(\frac{M_e}{\omega _o}\le \delta _\varepsilon \), the estimation error of the LESO can always be limited within the compact set \(B_\varepsilon \). This completes the proof. \(\square \)

Theorem 2

Regarding the system (5), the proposed control law (12) guarantees that the tracking error converges to zero asymptotically.

Proof

For clarity, the proof of Theorem 2 is completed within two steps. It is first demonstrated that the designed control law can drive the error state to the desired manifold. And then, the convergence of the error state is proved.

Step 1: To analysis the convergence of \(\sigma \), a Lyapunov function candidate can be designed as \(V_1 = \frac{1}{2}\sigma ^2\). Then, by substituting the proposed control law (12), the time derivative of \(V_1\) can be written as

$$\begin{aligned} \begin{aligned} {\dot{V}_1}&= {\sigma }{{{\dot{\sigma }} }}\\&= {\sigma }\left( c_0 e_2 + b_0 u + z_3 + \beta _2\varepsilon _1 + k_s \mathrm{{sgn}}(e_1)\right) \\&={\sigma }\left( c_0 \epsilon _2 + c_0\varepsilon _2 + b_0 u + z_3 + \beta _2\varepsilon _1 + k_s \mathrm{{sgn}}(e_1)\right) \\&=\sigma \left( -k_1\sigma - k_2 \mathrm{{sgn}}(\sigma ) + c_0 \varepsilon _2\right) \\&=-k_1 \sigma ^2 -k_2|\sigma | + \sigma c_0 \varepsilon _2 \end{aligned}\nonumber \\ \end{aligned}$$
(25)

With \(k_2 \ge c_0\delta _\varepsilon \), Eq. (25) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{V}_1&\le -k_1 \sigma ^2 -k_2|\sigma | + \sigma c_0 \varepsilon _2\\&\le -(k_2 - c_0 \delta _\varepsilon )|\sigma |\\&=-k_\sigma |\sigma |\\&= -k_\sigma V_1^{\frac{1}{2}}\\&\le 0 \end{aligned} \end{aligned}$$
(26)

where \(k_\sigma = (k_2 - c_0 \delta _\varepsilon )\) is a positive constant. Equation (26) indicates that \(\sigma \) is asymptotically convergent. Moreover, Eq. (26) also shows that \(\sigma \) converges to zero in finite time.

Step 2: When the sliding manifold is reached and \(\sigma = 0\) is maintained, it can be inferred from Eq. (10) that

$$\begin{aligned} e_2 = \epsilon _2 + \varepsilon _2 = -c_0 e_1 - \int _{0}^{t}k_s \textrm{sgn} \left( e_1\right) \text {d}s + \varepsilon _2 \end{aligned}$$
(27)

where \(e_2\) is the derivative of \(e_1\). Substituting Eq. (27) into the equation of \(\dot{e}_1 = e_2\), one gets

$$\begin{aligned} \dot{e}_1 = -c_0 e_1 - \int _{0}^{t}k_s \textrm{sgn} \left( e_1\right) \text {d}s + \varepsilon _2 \end{aligned}$$
(28)

and it can be reorganized as

$$\begin{aligned} \left\{ \begin{aligned} {{\dot{e}}_1}&= - {c_0}{e_1} + {z_\gamma }\\ {{\dot{z}}_\gamma }&= - {k_s}{\mathop {\textrm{sgn}}} \left( {{e_1}} \right) + {{{\dot{\varepsilon }} }_2} \\&= - {k_s}{\mathop {\textrm{sgn}}} \left( {{e_1}} \right) + {\varepsilon _3} - {\beta _2}{\varepsilon _2} \end{aligned} \right. \end{aligned}$$
(29)

To proceed the analysis, the Lyapunov function candidate can be designed as

$$\begin{aligned} V_2 = \frac{1}{2}\left( c_0 e_1 - z_\gamma \right) ^2 + \left( 1 + \alpha \right) \int _{0}^{e_1} { h} \left( s\right) \text {d}s + \alpha \frac{1}{2} z_\gamma ^2 \nonumber \\ \end{aligned}$$
(30)

where \(\alpha \) is a positive constant and \(h\left( e_1\right) = k_s \textrm{sgn}\left( e_1\right) - {\varepsilon _3} + {\beta _2}{\varepsilon _2}\). Note that \(e_1h\left( e_1\right) \ge 0 \) is ensured with \(k_s \ge \left( 1 + \beta _2\right) \delta _\varepsilon \). Then, \(V_2\) is positive definite. Differentiating \(V_2\) gets

$$\begin{aligned} \begin{aligned} \dot{V}_2&= \left( c_0 e_1 - z_\gamma \right) \left( c_0 \dot{e}_1 - \dot{z}_\gamma \right) + \left( 1 + \alpha \right) { h} \left( e_1\right) \dot{e}_1 \\&\quad + \alpha z_\gamma \dot{z}_\gamma = -c_0\left( c_0 e_1 - z_\gamma \right) ^2 - \alpha e_1h\left( e_1\right) \\&\quad \le 0. \end{aligned} \end{aligned}$$
(31)

Therefore, it is proved in Eq. (31) that \(e_1\) converges to zero asymptotically. Moreover, further analysis yields that \(e_2 = 0\) when \(e_1\) is kept at zero. The proof is completed. \(\square \)

Table 1 Characteristic parameters of the PPF
Full size table

4 Simulations analysis

To evaluate the performance of the proposed method, numerical simulation analysis is presented in this section. The dynamic model of the PPF is formulated as aforementioned in Sect. 2, and the physical characteristics of a certain type of the PPF are listed in Table 1.

The proposed dynamic model of the PPF is validated by experiment, and the analysis is presented in [52]. The control parameters of the proposed controller are listed in Table 2.

As a comparison, the conventional LADRC is applied in the analysis. The control law is given by

$$\begin{aligned} u=\frac{k_p e_1 + k_d \epsilon _2 - z_3}{b_0} \end{aligned}$$
(32)

and the control parameters of the two control channels are shown in Table 3. Note that the control parameters of the conventional LADRC are quite different with the equivalent parameters of the proposed method. It is tested that the conventional LADRC controller with similar parameters as the proposed method revealed unstable control performance.

Table 2 Control parameters of the proposed controller
Full size table
Table 3 Control parameters of the comparative controller
Full size table
Fig. 3
figure 3

Circular trajectory—trajectories in the horizontal plane (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image

4.1 Circular trajectory

The PPF is controlled to track a circular trajectory with a fixed altitude in this case. The reference trajectory is a circle with a radius of 120 m and the reference altitude is 160 m. In the simulation settings, the initial velocities are set as \(V_c = V_p = \left[ 8\ 0\ 1.5\right] ^T\) m/s and the initial position of the CG of \(\Sigma _c\) is set as \(L_p = \left[ 0\ 0\ 230\right] ^T\)m. The other states are set to be zero for simplicity. Considering that the wind has severe impact on the control performance of the PPF, the wind \(V_w = \left[ 1\ 2\ 0\right] \)  m/s is added to the simulation at 200 s to evaluate the robustness of the controllers. The simulation time is set as 400 s, and the results are shown in Figs. 3, 4, 5, 6. Note that the control inputs are zero in the first 20 s to make sure that the PPF has maintained steady state.

Fig. 4
figure 4

Circular trajectory—lateral tracking errors and deflections (solid line: the proposed method, dashed line: LADRC)

Full size image

The controlled horizontal trajectories of the PPF are shown in Fig. 3. And Fig. 4 shows the horizontal tracking errors and the corresponding control inputs. It can be seen that both the proposed and the comparative controllers can achieve the control objective with the position errors less than 1 m. The performance of the proposed controller is similar with the LADRC during the first 200 s. When the wind disturbance is added to simulation at 200 s, Fig. 4 shows that the maximum horizontal position error of the proposed controller in wind environment is 0.65 m and that of the LADRC controller is 0.97 m, which indicates that the proposed method can achieve better performance than the LADRC. According to Fig. 5, the PPF is stabilized at the reference altitude under the control of both proposed and LADRC controllers. The simulation results in the first figure of Fig. 5 indicate that the proposed controller can maintain the altitude of 160 m with a settling time of 76.32 s, while that of the LADRC is 89.47 s. When the wind is added to the simulation, both controllers can compensate the disturbance actively and keep the altitude unaffected. Therefore, the control performance of the proposed method is validated.

Fig. 5
figure 5

Circular trajectory—altitude and thrust (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image
Fig. 6
figure 6

S-path trajectory—trajectories in the horizontal plane (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image

4.2 S-path trajectory

To facilitate mathematical description, the reference trajectory of the PPF is usually composed of lines and arcs. In this case, the trajectory tracking simulation of the S-path with three line segments is provided. With the aim to evaluate the performance of controllers under strict conditions, the line segments in S-path are connected directly and the arcs are not used. The simulation settings are the same with circular trajectory except the wind. After completing the simulation, the results are recorded in Figs. 6, 7 and 8.

Fig. 7
figure 7

S-path trajectory—lateral tracking errors and deflections (solid line: the proposed method, dashed line: LADRC)

Full size image

The reference and controlled horizontal trajectories are shown in Fig. 6, and the comparative results of the lateral channel are illustrated in Fig. 7. Unlike the quadrotors, the PPF cannot track the trajectories with sharp corners due to the limited control inputs. Therefore, as shown in the subplot 2 of Fig. 7, the lateral position errors occur at every corner of the reference. It is also seen that the lateral position errors can converge to zero. Comparing the proposed controller and LADRC, it can be seen that the position errors of the proposed controller is stabilized to zero from 20 m with a settling time of 54.38 s, while that of the LADRC is 84.56 s. The comparison of Fig. 7 indicates that the proposed method is superior to LADRC in the lateral channel. In the longitudinal channel, the altitude is well controlled even at the reference corners. The thrust output of both the proposed and comparative controllers yields oscillations due to the coupling effect between the lateral and longitudinal control channels when the reference is changed to another line segment at corners. Figure 8 indicates that both controllers show good control effect in steady state, while the proposed controller achieves better transient performance than the comparative one with less settling time. More precisely, the settling time of the proposed method is 79.45 s, while that of the LADRC is 91.27 s.

Fig. 8
figure 8

S-path trajectory—altitude and thrust (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image

4.3 Robustness verification

The robustness is an important objective of controller development. In order to verify the robustness of the PPF with the proposed controller, the Monte-Carlo simulation technique is applied in this paper. Considering the practice that the PPF is applied to take various loads, the mass of the payload is set to vary uniformly with \(\pm 30\%\). The MC simulation results with 50 sets of stochastic payloads are investigated and the results are shown in Figs. 9 and 10. The circular reference is applied, and the wind is also added as external disturbances. It can be found in the figures that the lateral position errors and longitudinal altitude errors are influenced by the changing of payload. Compared with Fig. 4, Fig. 10 shows that the maximum lateral position error is expanded from 1 m to 6 m. It is also seen that the settling time of the longitudinal channel is varied from 73.52 to 82.39 s with the payload. However, all the simulation results show that the lateral and longitudinal tracking errors are driven to zero by the proposed controller. Then, the robustness of the proposed method is verified by the Monte-Carlo simulations.

Fig. 9
figure 9

Monte-Carlo test—trajectories in the horizontal plane

Full size image
Fig. 10
figure 10

Monte-Carlo test—lateral and longitudinal tracking errors

Full size image

5 Semi-physical experimental analysis

5.1 Experimental setup

Due to the GPS positioning accuracy and measurement noise, the trajectory tracking performance of the PPF will be influenced in practical applications. To further investigate the effectiveness of the proposed method, the semi-physical platform with the self-designed flight controller unit and the proposed dynamic model is designed and the experiment is performed on it. The dynamic model is applied to simulate the PPF and to generate the GPS data encoded by GPGGA format. In the flight controller unit, the ARM microprocessors STM32F407 and STM32F103 are used as the main and auxiliary processor, respectively. The proposed method is programmed and implemented in the main processor, and the rudders and the thrust motor are controlled by the auxiliary processor for safety. This structure ensures the computing capacity as well as reliability of the PPF. Figure 11 shows the control system of the PPF. The positions and heading angles are measured with a sample frequency of 1 Hz from the dynamic model and transmitted to the flight controller via serial port. Then, the control inputs are calculated in the main processor and send to the dynamic model.

Fig. 11
figure 11

Rudders and flight controller unit

Full size image

5.2 Experimental results

The initial conditions of this experiment are configured as the simulation of the circular trajectory, and the corresponding experimental results are recorded in Figs. 12, 14. Figures 12 and 13 show that the proposed method and LADRC can attenuate the lateral position errors and maintain the trajectory tracking objective. Compared with Fig. 4, it is seen from the subplot 2 of Fig. 13 that lateral position errors of the proposed method and LADRC are larger than that of the simulation due to the discretization of the controller. It also can be found that the proposed method can achieve faster convergence of the lateral errors than LADRC before the wind is added. During 200–400 s, it is shown in Fig. 13 that the proposed method can achieve smaller lateral position errors than the LADRC. The same conclusion can be drawn from the comparison in Fig. 14. Specifically, it can be found that the proposed method has a overshoot of 5.62 m and a settling time of 154.33 s, which are much lower than that of the LADRC. The experiment and comparative analyses show that the proposed method can achieve better transient and stable performance than LADRC in wind environment.

Fig. 12
figure 12

Experiment—trajectories in the horizontal plane (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image
Fig. 13
figure 13

Experiment—lateral tracking errors and deflections (solid line: the proposed method, dashed line: LADRC)

Full size image
Fig. 14
figure 14

Experiment—altitude and thrust (solid line: reference, dashed line: the proposed method, dotted line: LADRC)

Full size image

6 Conclusion

In this paper, a novel SMC method for the PPF was proposed based on the disturbance compensation. By deriving the dynamic model of the PPF, the trajectory tracking problem was decomposed into the lateral and longitudinal control channels. The nonlinear dynamics of each channel and the coupling effect between the two channels were considered as the total disturbances, which were estimated and compensated actively. With the elaborately designed sliding manifold, the proposed control law ensured the asymptotic convergence of the PPF. Specifically, the heading angle and the altitude were the only required feedback states in the proposed control scheme. The closed-loop stability of the PPF was proved by rigorous mathematical analysis based on Lyapunov techniques. Finally, the numerical simulations of different reference trajectories, Monte-Carlo test, and experiment were performed to evaluate the performance of the proposed method. Through comparative analysis, it is shown that the proposed method achieved better tracking performance than the LADRC. In the future, we will seek to implement the proposed method to the practical PPF platform with better control performance. In the meanwhile, wind resistance and steerability performance need to be further studied.