Keywords

1 Introduction

Modern spacecrafts are typical Cyber-Physical Systems (CPSs) which are tight integrations between onboard cyber systems (e.g. processing, communication) and physical elements (e.g. platform structure, sensing, actuation, and environment) [1, 2]. Tasks implement on the onboard cyber systems of spacecrafts include attitudes and orbit control, onboard planning and scheduling, onboard data acquiring and analyzing et al. For the limit of onboard digital resource, saving communication bandwidth and power from the basic function like control tasks mean providing more resource to payloads onboard, which may implement a sufficient use of spacecrafts.

Classic spacecraft attitude control problem is always developed in continuous framework [3,4,5], and their implementation on the digital platform is traditionally in a periodic fashion due to the ease of design and analysis. However, periodic sampling is sometimes less preferable from a resource utilization point of view. When the system states almost keep constant and no disturbances are acting, the systems are operating desirably is a waste of digital resources. To overcome these limitations, some resource-aware control laws like anytime control [6] event-triggered control (ETC) [7,8,9] self-triggered control (STC) [10, 11] and so on are developed. In anytime control, consisting in a hierarchy of controllers for the same plant, will switch between different order control algorithms to adopt the cyber resource of the onboard system. In ETC, the classic event triggered mechanisms are detecting the system output or states varying. The main idea of STC is to select the next controller update instant based on the knowledge of the dynamics and the latest measurements of the plant state. While the ETC depending on the continuous supervision of the plant, the STC will reduce more cyber resource than ETC theoretically.

In recent years, many work addressed on STC and its applications in CPSs. In [9], the theoretical foundation rendering control system Input-to-State Stable (ISS) is introduced. Based on this framework, many STC mechanisms are proposed for linear and nonlinear systems. In [10,11,12,13,14,15], the basic self-triggered strategies for linear system are presented and a trade-off between performance and cyber resource utilization is making. However, the most expensive part of the realization of STC is the derivation of the trigger function. The above work is extremely complex so that the calculating of the trigger functions requires a lot of computing resources. From this point of view, the use of NN as a model of trigger behavior is presented in this paper.

The Neural Network is usually performed to estimate the system that transforms inputs into outputs, where a set of examples of input-output pairs are given in [16]. Furthermore, the NN was demonstrated as a universal smooth function approximator, extensive studies have been conducted for diverse applications, especially pattern recognition, identification, estimation, and time series prediction [17]. In [18], the NN is designed to predict the time delay induced in the networked control systems, which shows that the NN can alleviate the influence of time delay and improve the performance of the networked control system.

The main contribution of this paper is the design of a neural network based self-triggered control (NN-STC) strategy for the spacecraft attitude stabilization problem. The attitude motion dynamics equations are derived and a STC algorithm is proposed to ensure attitude stability. Furthermore, simulation results demonstrate the proposed approach guarantees a high control performance and a large reduction of sampling times.

2 Space Attitude Dynamics

The dynamics equations of motion of a rigid spacecraft are given by [4]

$${\mathbf{J}}\dot{\varvec{\omega }} = -\varvec{\omega}^{ \times } {\mathbf{J}}\varvec{\omega}+ \varvec{u}\mathcal{ + }\varvec{T}$$
(1)

where \({\mathbf{J}} = {\mathbf{J}}^{T} \in {\mathbb{R}}^{3 \times 3}\) is the inertia matrix, \(\varvec{\omega}=\varvec{\omega}(t) \in {\mathbb{R}}^{3}\) denotes the body angular velocity of the spacecraft body-fixed frame \(B\) with respect to the inertial frame \(I\). \(\varvec{u} \in {\mathbb{R}}^{3}\) is the actuator torque calculated by the onboard computer and \(\varvec{T} \in {\mathbb{R}}^{3}\) is the external disturbance torques.

To describe the orientation of \(B\) respect to the inertial frame \(I\) in terms of three Euler angles: roll angle \(\varphi\), pitch angle \(\theta\), and yaw angle \(\psi\). In the rigid body three-axis stability control problem, the Euler angles are all small. Therefore, the linearized kinematic differential equations can be found as

$$\omega_{1} = \dot{\varphi } - \omega_{o} \psi ,\quad \omega_{2} = \dot{\theta } - \omega_{o} ,\quad \omega_{3} = \dot{\psi } + \omega_{o} \varphi$$
(2)

We consider the attitude motion about its pitch axis, assume the effect of the attitude motion on the orbital motion with a constant angular velocity \(\omega_{o}\).

In such case, the dynamics equations (1) with small attitude errors and small products of inertial become [19]

$$\begin{aligned} & J_{x} \ddot{\varphi } + (J_{y} - J_{z} )\omega_{o}^{2} \varphi + (J_{y} - J_{z} - J_{x} )\omega_{o} \dot{\psi } = u_{x} + T_{x} ,\quad J_{y} \ddot{\theta } = u_{y} + T_{y} \\ & J_{z} \ddot{\psi } + (J_{y} - J_{z} )\omega_{o}^{2} \psi - (J_{y} - J_{z} - J_{x} )\omega_{o} \dot{\varphi } = u_{z} - \omega_{o} h_{x} + T_{z} \\ \end{aligned}$$
(3)

Also, the external disturbance torques include the gravity gradient torque, and it can be expressed in the body frame \(B\) as

$$T_{gx} \approx - 3\omega_{o}^{2} (J_{y} - J_{z} )\varphi ,\quad T_{gy} \approx - 3\omega_{o}^{2} (J_{x} - J_{z} )\theta ,\;T_{gz} \approx 0$$
(4)

Generally, from the equations above, we can see that the pitch equation is uncoupled from the roll/yaw equations. It is a Single Input & Single Output system (SISOs), which is easy to design a classical PD controller. However, if we take three dynamics equations into consideration with the self-triggered control design, the size of the state space is large, which will provide more pressure on the real time calculation on the embedded system. Therefore, we only consider roll & yaw coupled system in this paper.

The dynamics and kinematic equations can be realized in state space form as

$$\dot{\varvec{x}} = {\mathbf{A}}\varvec{x} + {\mathbf{B}}\varvec{u},\quad \varvec{x} = \left( {\begin{array}{*{20}c} \varphi & \psi & {\dot{\varphi }} & {\dot{\psi }} \\ \end{array} } \right)^{T}$$
(5)
$${\mathbf{A}} = \left( {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ { - \frac{1}{{J_{11} }}a} & 0 & 0 & {\frac{1}{{J_{11} }}b} \\ 0 & { - \frac{1}{{J_{33} }}c} & {\frac{1}{{J_{33} }}b} & 0 \\ \end{array} } \right),\quad {\mathbf{B}} = \left( {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ {\frac{1}{{J_{11} }}} & 0 \\ 0 & {\frac{1}{{J_{33} }}} \\ \end{array} } \right)$$

3 Neural Network Based Self-triggered Control Strategy Design

3.1 Problem Formulation

The attitude control system on the spacecraft is shown in Fig. 1. The control signal \(\varvec{u}\) and states signal \(\left( {\varvec{x},\dot{\varvec{x}}} \right)\) is transferred over the network. In a periodic implementation, this system is usually in the following form

$$\begin{aligned} & \dot{\varvec{x}} = {\mathbf{A}}\varvec{x}(t) + {\mathbf{B}}\varvec{u}(t) \\ & y(t) = {\mathbf{C}}\varvec{x}(t) \\ \end{aligned}$$
(6)

where \({\mathbf{A}} \in {\mathbb{R}}^{n \times n}\), \({\mathbf{B}} \in {\mathbb{R}}^{n \times r}\), \({\mathbf{C}} \in {\mathbb{R}}^{m \times n}\) are the characteristic matrices and \(x(t) \in {\mathbb{R}}^{n}\), \(u(t) \in {\mathbb{R}}^{r}\) and \(y(t) \in {\mathbb{R}}^{m}\) the state, input and output vectors respectively. If the pair \(({\mathbf{A}},{\mathbf{B}})\) is stabilizable, then a linear feedback controller \(\varvec{K}:{\mathbb{R}}^{n} \to {\mathbb{R}}^{m}\) rendering the closed-loop asymptotically stable can be found:

$$\varvec{u}(t) = \varvec{K}(\varvec{x}(t))$$
(7)

where \({\mathbf{A}} + {\mathbf{BK}}\) is Hurwitz.

Fig. 1
figure 1

CPSs on the spacecrafts

Full size image

The controller will implement on the embedded system, and a sampled-data system implementation is in a classical periodic time-triggered way:

$$\begin{aligned} & \dot{\varvec{x}} = {\mathbf{A}}\varvec{x}(t) + {\mathbf{B}}\varvec{u}(t_{k} )\quad t \in [t_{k} ,t_{k + 1} ) \\ & y(t) = {\mathbf{C}}\varvec{x}(t) \\ & \varvec{u}(t) = \varvec{K}(\varvec{x}(t_{k} )),\quad t \in [t_{k} ,t_{k + 1} ),\;k \in {\mathbb{Z}}_{ + } \\ \end{aligned}$$
(8)

where \(t_{k}\) represents the sampling time satisfying \(t_{k + 1} - t_{k} = T\). For some specified period \(T > 0\), it means \(h(\varvec{x}_{k} ,T)\) in Fig. 1 equals a constant \(T\). In discrete control aspect, \(T\) is generally chosen as small as technology and network load permit to achieve a desired performance. This strategy is easy to implemented, however, it may produce unnecessary overload on the network and power consumption.

We design the Performance Index (PI) \(\Delta J\)

$$\Delta J = 100\left[ {\int\limits_{0}^{\infty } {\left( {\varvec{x}^{T} {\mathbf{Q}}_{lqr} \varvec{x}\mathcal{ + }\varvec{u}^{T} {\mathbf{R}}_{lqr} \varvec{u}} \right)dt - J^{*} } } \right]$$
(9)

when any control \(\varvec{u}(t)\) is implemented digitally, the system performance will depend on the sampling period. As the sampling period increasing, the PI will increase and the system tends to unstable.

To extend the sampling periods without sacrificing performance, we apply self-triggered control to the system. Moreover, the longer mean sampling period means the lower network loaded.

The STC scheme can be defined in following form

$$\begin{aligned} & \dot{\varvec{x}} = {\mathbf{A}}\varvec{x}(t) + {\mathbf{B}}\varvec{u}(t_{k} )\quad t \in [t_{k} ,t_{k + 1} ) \\ & \varvec{y}(t) = {\mathbf{C}}\varvec{x}(t) \\ & \varvec{u}(t_{k} ) = \varvec{K}(\varvec{x}(t_{k} )),\quad t \in [t_{k} ,t_{k + 1} ),\,k \in {\mathbb{Z}}_{ + } \\ & t_{k + 1} = t_{k} + h(\varvec{x}_{k} ) \\ \end{aligned}$$
(10)

A general STC scheme usually means two functions: A feedback control \(\varvec{u}(t_{k} )\) is used as in the classical frame and the triggered function \(h(\varvec{x}(t_{k} ),T):{\mathbb{R}}^{m} \times {\mathbb{R}}_{0}^{ + } \to {\mathbb{R}}_{0}^{ + }\), determining the sampling time \(t_{k + 1}\) as a function of the state \(\varvec{x}(t_{k} )\) at the time \(t_{k}\). The design of these two functions is the main problem in the STC study. Moreover, a positive minimal inter-sample time is also required to fulfill, to avoid the Zeno phenomenon.

3.2 Feedback Controller Design

An LQR design technique is usually applied to the spacecraft attitude control problem. The cost function and weighting matrices used in the LQR design are

$$\begin{aligned} & J^{*} = \hbox{min} (J(\varvec{u})) = \int\limits_{0}^{\infty } {\left( {\varvec{x}^{T} {\mathbf{Q}}_{lqr} \varvec{x} + \varvec{u}^{T} {\mathbf{R}}_{lqr} \varvec{u}} \right)} dt \\ & {\mathbf{Q}}_{lqr} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{2 \times 2} } & {} \\ {} & {5{\mathbf{I}}_{2 \times 2} } \\ \end{array} } \right]\quad {\mathbf{R}}_{lqr} = 10{\mathbf{I}}_{2 \times 2} \\ \end{aligned}$$
(11)

The consideration of selecting weighting matrices in this paper is increasing system dumpling and preventing the actuators saturation.

we can solve the Riccati equation to get the unique positive definite solution \({\mathbf{P}}\)

$${\mathbf{A}}^{T} {\mathbf{P}} + {\mathbf{PA}} - {\mathbf{PB}}^{ - 1} {\mathbf{R}}_{lqr} {\mathbf{B}}^{T} {\mathbf{P}} + {\mathbf{Q}}_{lqr} = {\mathbf{0}}$$
(12)

The optimal feedback policy \(\varvec{K}\) is given by

$$\varvec{K}\mathcal{ = } - \varvec{R}_{lqr}^{ - 1} {\mathbf{B}}^{T} {\mathbf{P}}$$
(13)

The true cost of continuous LQR is

$$J^{*} = \varvec{x}_{0}^{T} {\mathbf{P}}\varvec{x}_{0}$$
(14)

3.3 NN Based Triggered Condition Design

Under certain conditions, it has been proved that the neural networks have function approximation abilities and have been frequently used as function approximators. In this section, the NN is used to approximate the function \(h(\varvec{x}_{k} ,T)\) in Fig. 1, \(h(\varvec{x}_{k} ,T)\) determines the next sampling time based on the states sampled before, so it is a mapping between state space and time space. And a neural network model can be derived from measured input/output data of the original triggered conditions.

As one of the classical neural networks, BP feedforward neural network has a simple topology and strong generalization ability. We use a four-layered feedforward neural network and adopt the BP learning algorithm to determine the sampling time.

Figure 2 shows the specific configuration of the BP feedforward network for approximating the triggered function. The BP network consists of four layers: input layer with four neurons presenting the four input states of dynamics systems (5). The neuron numbers of the two hidden layers are 12 and 4, which greatly improve the accuracy of the network. The output layer which has only one neuron for the triggered time is one dimension. The number of hidden layers and neurons are varied, but in this problem the above choice is enough.

Fig. 2
figure 2

BP network configuration for triggered time prediction

Full size image

In order to make the NN perform the desired mapping performance, the connection weights will be trained by so-called training algorithms. The detail of this algorithm is given in [20] which is no longer mentioned here. Moreover, the training data generation is another important issue.

We acquire a training set which is generated by the system under closed-loop and the specified triggered condition. The input sets with four states \((\varphi ,\psi ,\dot{\varphi },\dot{\psi })\) are generated randomly within \(( - 5,5)\,\text{deg}\) and \(( - 5,5)\,{\text{deg/s}}\) which ensure the linearized model is effective. And a triggered time is calculated from a input sets by the original triggered function. Finally, a training sample with five elements \((\varphi ,\psi ,\dot{\varphi },\dot{\psi },t_{k} )\) is acquired.

4 Simulation

In this section, an example is presented to validate the proposed STC strategy for spacecraft attitude control problem. The inertia matrix of spacecraft \({\mathbf{J}}\) is assumed to be as follows

$${\mathbf{J}} = \left[ {\begin{array}{*{20}c} {10.5} & {} & {} \\ {} & 8 & {} \\ {} & {} & {6.75} \\ \end{array} } \right]\,{\text{kg}}\,{\text{m}}^{2}$$

The control authority is limited by the maximum torque provided by the actuators is \(\pm 0.15\,{\text{N}}\,{\text{m}}\), orbit angle velocity is \(\omega_{o} = 0.0612\,{\text{deg/s}}\).

The time of simulation is 80 s, the initial attitude and angular velocity is

$$\left[ {\begin{array}{*{20}c} {\varphi_{0} } & {\psi_{0} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 5 & { - 3} \\ \end{array} } \right]^{T} \,\text{deg} ,\quad \left[ {\begin{array}{*{20}c} {\dot{\varphi }_{0} } & {\dot{\psi }_{0} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 2 & 1 \\ \end{array} } \right]^{T} \,{\text{deg/s}}$$

The disturbance is given by:

$$\left( {\begin{array}{*{20}c} {d_{ex} } \\ {d_{ez} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.0015 + 0.0012\sin (0.263t)} \\ {0.0015 + 0.0012\sin (0.245t)} \\ \end{array} } \right)$$

The triggered function is given by

$$\begin{aligned} & t_{k + 1} = \sup \left\{ {t < t_{\hbox{max} } \left| {h(\varvec{x}(t_{k} ),t) < 0} \right.} \right\} \\ & h(\varvec{x}(t_{k} ),t): = \varvec{x}(t_{k} + t)^{T} {\mathbf{P}}\varvec{x}(t_{k} + t) - \varvec{x}(t_{k} )^{T} {\mathbf{P}}\varvec{x}(t_{k} )^{T} \exp ( - \lambda t) \\ \end{aligned}$$

\({\mathbf{P}}\) is calculated by (14), \(\lambda = 1.0524\), the detail is given in [9,10,11].

From Table 1, we have compared the performance between the NN with one and two hidden layers. The results show the two hidden layers of NN has better performance. Figure 3 is the training curve of the NN, it shows that the training progress becomes very slow after 10 iterations.

Table 1 Performance of the NN
Full size table
Fig. 3
figure 3

Training curve of the NN

Full size image

From Fig. 4, we can see the Performance Index (PI) \(\Delta J\) is increasing with the sampling period increases in the scheme of periodic time triggered LQR. Moreover, with the performance of NN increasing, the mean sampling times increases in the scheme of the NN-STC. But the PI is much lower than periodic time triggered control with the same mean sampling period. It means the control performance of NN-STC is better than the periodic time triggered control using the same use of network resource.

Fig. 4
figure 4

Performance comparison between PTTC and NN-STC

Full size image

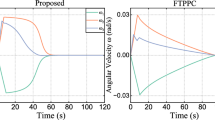
The attitude angle and angular velocity errors, by using STC and classical nonlinear controller are shown in a, b of Fig. 5. Roughly speaking, the errors converge to a small level. From c of Fig. 5, it can be seen that the sampling interval continuous increases and it keeps constant after 30 s. It means when the states convince to the steady equilibrium, the controller will entry a salient periods, which is advantageous to save the cyber resources onboard. During 0–10 s, sampling intervals changes with the states overshoot. It means the NN-STC scheme works when the system quits steady process immediately.

Fig. 5
figure 5

States responses and triggered intervals using NN-STC

Full size image

5 Conclusion

The main contribution of this paper is the development and implementation of a neural network based self-triggered control for the attitude stabilization of a rigid spacecraft. The control law ensures the system stability of the closed-loop system to the desired attitude. The approach is validated in the simulation and it shows the proposed NN-STC strategy reduces sampling times without degrading the control system performance. The overall performance of the spacecraft is improved by this CPS aspect design.