1 Introduction

The attitude control for a high nonlinear rigid spacecraft is a classical nonlinear control problem [1,2,3]. Attitude control mainly includes attitude stabilization control and attitude tracking control. Here, this note focuses on the problem of attitude stabilization control. In recent decades, in order to solve attitude stabilization control problem more effectively, a variety of control methods have been proposed, such as optimal control [4, 5], adaptive control [6, 7], backstepping control [8,9,10], and sliding mode control [11,12,13,14,15,16,17,18]. In [4], the inverse optimal control method was employed, and bypassing the task of solving the Hamilton-Jacobi equation obtains a meaningful cost functional optimal controller. The work [7] developed an adaptive controller for attitude stabilization of a rigid spacecraft with model uncertainties, external disturbances. In [11], a discrete-time super-twisting-like control scheme based on the sliding-mode control technique for robotic fishes was proposed, aiming at improving steering performance.

However, note that all above control schemes can only produce exponential convergence with infinite convergence time at most. Obviously, it would make sense if we could achieve a faster convergence speed in the control process [19, 20]. The control problem of attitude stabilization with finite convergence time has aroused wide attention [21,22,23]. Besides faster convergence rate, the control method has better robustness and disturbance rejection performance [24,25,26,27,28,29]. As a consequence, the results of finite-time control were applied to spacecraft attitude stabilization. In [30], two sliding mode controllers were employed to force that the state variables of the closed-loop system will converge to the origin in a finite time. Based on homogeneous method and switching method, a global saturated finite-time control method was developed in this work [31].

It is worth mentioning that angular velocity is necessary for attitude stabilization control of spacecraft. In practice, the value of angular velocity cannot be arbitrarily changed. Saturation limits for low rate gyro and task specifications requirement are usually caused angular rate constraint. An example is the X-ray timing probe spacecraft, which needs to maneuver within the saturation limit of the rate gyro [32]. In industrial applications, the performance of airborne equipment is seriously affected by the excessive angular velocity. Therefore, it is valuable to study the attitude control algorithm under the constrained angular velocity of spacecraft.

In recent years, some control strategies have been presented to discuss the problem of angular velocity constraint in control domain. In the work [33], on the basis of parameterized attitude constraint region of unit quaternion, a global minimum quadratic potential function was established. And another logarithmic potential function was designed to limit the angular velocity. By using these two potential functions and sliding mode control technique, a nonlinear attitude control law was obtained to ensure the stability of closed-loop system with external disturbance and attitude and angular velocity constraints. In [34], a smooth adaptive fault-tolerant constrained controller was given which can guarantee the uniformly bounded stability of the closed-loop system. This paper [35] utilizes the barrier Lyapunov function in the analysis of the Lyapunov direct method, and the constrained behavior of the system is provided in which the rotor speed, its variation, and generated power remain in the desired bounds. The work [36] is based on the direct Lyapunov method, which by use of the Nussbaum-type function provides an adaptive control scheme that can handle the effect of unknown control direction.

Different from the existing results of [33,34,35,36], this paper considers not only attitude stabilization control of spacecraft under angular velocity constraint but also disturbance rejection control. The main difficulties lie in two aspects: (1) How to employ the model structure feature to design a state-constrained finite-time attitude control scheme. (2) How to employ RBF neural network and design a finite-time attitude controller for the attitude loop dynamics subsystem with external disturbances.

The main contributions of this paper are three aspects. (1) Compared with the existing control methods for quad-rotor aircraft, the proposed control algorithm in this paper not only guarantees that the attitude stabilization in a finite time but also in the design process the angular velocity constraint is under consideration. (2) Compared with the other finite-time control algorithms, the proposed finite-time control algorithm in this paper is mainly based on the homogeneous system theory rather than the back-stepping design. As a result, the new control algorithm has a simpler structure, which implies that it is easy to design and adjust the control parameters. (3) In addition, compared with other finite-time control algorithms, the finite-time control algorithm proposed in this paper proposes an integral terminal sliding mode controller based on RBF neural network for attitude loop dynamics subsystem with external disturbance, which effectively improves the ability of disturbance rejection.

In this paper, a finite-time stability control algorithm based on quaternion is proposed for the rigid spacecraft attitude system with angular velocity constraint. The new idea is to employ the state-dependent time-varying gain by replacing the constant gain in the traditional finite-time attitude controller. However, the resulting closed-loop system is a time-varying system that makes finite-time stability analysis challenging. In order to overcome the technical problem of finite-time stability of time-varying nonlinear closed-loop system, the whole closed-loop system is proved to be stable in a finite time by employing the idea of homogeneous domination. Based on the proposed control strategy, the spacecraft attitude can converge to the equilibrium point in a finite time and the angular velocity cannot exceed the constraint region. In order to investigate the finite-time attitude stabilization control in the presence of external disturbances, the RBF neural network algorithm is used to estimate the uncertainties of the system and an integral terminal sliding mode controller is designed. At the end, some simulation results are shown to verify the effectiveness and availability of the theoretical results.

2 Problem description

2.1 Notations

Making the equation clear in concept, denote \(\mathrm{sig}^\alpha (x)=\mathrm{sign}(x)|x|^\alpha \), where \(\alpha \ge 0, x \in {\mathbb {R}}\), \(\mathrm{sign}(\cdot )\) is the standard sign function.

2.2 Spacecraft attitude kinematics and dynamics

To describe the space rotation orientation of the spacecraft, the unit quaternion is employed in this paper. Specifically speaking, define \(\Phi \) as the principal angle and

$$\begin{aligned} e=[e_{1},e_{2},e_{3}]^T \end{aligned}$$

represents the principal axis associated with Euler’s theorem, where \(e^Te=1\). The quaternion representation can be described as

$$\begin{aligned} q_{0}=\mathrm{cos}\frac{\Phi }{2},~~ q_\mathrm{v}=[q_\mathrm{{v,1}},q_\mathrm{{v,2}},q_\mathrm{{v,3}}]^T=e\mathrm{sin}\frac{\Phi }{2}, \end{aligned}$$
(1)

which satisfies that

$$\begin{aligned} q_{0}^2+q_{v}^Tq_{v}=1. \end{aligned}$$
(2)

By [37], we know the kinematic equation of spacecraft attitude is

$$\begin{aligned} \dot{q}=\frac{1}{2}E(q)\omega , \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{array}{l}E(q)=\left( \begin{array}{ll}-q_{v}^T\\ q_v^\times +q_{0}I_{3}\end{array}\right) \end{array}, \end{aligned}$$

and \(I_3\) denotes the \(3\times 3\) identity matrix. Here, the notation \(q_v^\times \) denotes the skew symmetry matrix, i.e.,

$$\begin{aligned} \begin{array}{l}x^\times =\left[ \begin{array}{ccc}0&{}-x_{3}&{}x_{2}\\ x_{3}&{}0&{}-x_{1}\\ -x_{2}&{}x_{1}&{}0\end{array}\right] \end{array}, \ \ \forall x\in {\mathbb {R}}^3. \end{aligned}$$

In addition, the dynamic equation of spacecraft attitude is given by

$$\begin{aligned} J\dot{\omega }=-\omega ^\times J\omega +\tau +d(t), \end{aligned}$$
(4)

where

  • \(J=J^T \) is the positive definite inertia matrix,

  • \(\omega =[\omega _{1},\omega _{2},\omega _{3}]^T\) is the angular velocity vector,

  • \(\tau =[\tau _{1},\tau _{2},\tau _{3}]^T\) is the control torque vector,

  • d(t) denotes the unknown time-varying external disturbances.

Furthermore, we have \(E^T(q_\mathrm{i})E(q_\mathrm{i})=I_{3}.\)

2.3 Control objectives

Different from the existing finite-time attitude control algorithm, not only the finite-time attitude stabilization can be achieved but also the angular velocity constraint is guaranteed.

Definition 2.1

(Finite-time stability [38]) For a continuous nonlinear system

$$\begin{aligned} \dot{u}=u(p),\quad u(0)=0,\quad u\in {\mathbb {R}}^n, \end{aligned}$$
(5)

where \(u(\cdot ): {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) is a continuous vector function, if system (5) satisfies the conditions Lyapunov stable and finite time convergent, then we can say it is finite-time stable. It means that there exists a function T(p(0)) such that \(\lim _{t\rightarrow T(p(0))}u(t)=0\) with \(u(t)\equiv 0,~\forall t\ge T(p(0))\).

Definition 2.2

(Homogeneity [39]) Define dilation \((g_1,\ldots ,g_n) \in {\mathbb {R}}^n\) with \(g_i > 0, i= 1,\ldots , n\). The function u(p) defined in (5) can be said to be homogeneous with degree \(\varrho \in {\mathbb {R}}\) with respect to \((g_1,\ldots ,g_n)\) provided that for any given \(\varepsilon > 0\),

$$\begin{aligned} u_i(\varepsilon ^{g_1}p_1,\ldots ,\varepsilon ^{g_n}p_n) = \varepsilon ^{\varrho +g_i}u_i(p), i= 1,\ldots , n, \forall p\in {\mathbb {R}}^n,\end{aligned}$$
(6)

where \(\varrho >-\min \{g_i,i=1,\ldots ,n\}.\)

2.4 Related lemmas

Lemma 2.1

[40, 41] If homogeneous system (5) is globally asymptotically stable and

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0}{\frac{\widehat{u}_i (\varepsilon ^{g_1}p_1,\ldots ,\varrho ^{g_n}p_n)}{\varepsilon ^{\varrho + g_i}}} =0,i=1,2,\ldots ,n,\forall p\ne 0, \end{aligned}$$
(7)

following system (8)

$$\begin{aligned} \dot{u}=u(p)+\widehat{u}(p),~~ u(0)=\widehat{u}(0)=0,~~p\in {\mathbb {R}}^n, \end{aligned}$$
(8)

is also globally finite-time stable.

Lemma 2.2

[42] For any \(\varsigma >0, p\in {\mathbb {R}}\), \({d|p|^{\varsigma +1}}/{d p}=(\varsigma +1)\mathrm{sig}^{\varsigma }(p)\), \({d[\mathrm{sig}^{\varsigma +1}(p)]}/{d p}=(\varsigma +1){}|p|^{\varsigma }\).

3 Main results

4 Design of constrained finite-time attitude controller

4.1 Case 1: case of no external disturbance

Define matrix

$$\begin{aligned} G(q_v)=(q_v^\times +q_0 I_3), \end{aligned}$$
(9)

substituting (9) into (3), it can be obtained the following relation

$$\begin{aligned} \dot{q}_v=\frac{1}{2}(q_v^\times +q_0 I_3)w=\frac{1}{2}G(q_v)w. \end{aligned}$$
(10)

Theorem 4.1

For attitude control systems (4) and (10), if the controller \(\tau \) is designed as

$$\begin{aligned} \tau&=-\, k_1 G^T(q_\mathrm{v})\mathrm{sig}^{\alpha _1}(q_\mathrm{v})-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}({\omega }), \end{aligned}$$
(11)

where \(k_1>0\), \(k_2>0\), \(0<\alpha _1<1\), \(\alpha _2=2\alpha _1/(1+\alpha _1)\), \(\chi (\omega )=|\omega _1|^{1+\alpha _2}+|\omega _2|^{1+\alpha _2}+|\omega _3|^{1+\alpha _2}\), then

  • \(|\omega _i(t)|< M\) for all time,

  • \((q_v,\omega )\rightarrow 0\) in a finite time,

Proof

The proof contains three parts. \(\square \)

4.1.1 First part: state boundedness

Choose the Lyapunov function:

$$\begin{aligned} W=&\,\frac{2k_1}{1+\alpha _1}\Big (\sum _{j=1}^3|q_{v,j}|^{1+\alpha _1}\Big )+\frac{1}{2}\omega ^TJ\omega . \end{aligned}$$
(12)

It follows from Lemma 2.2 that

$$\begin{aligned} \dot{W}=&\,{2k_1\sum _{j=1}^3\mathrm{sig}^{\alpha _1}(q_{v,j})\dot{q}_{v,j}} +\omega ^TJ\dot{\omega }\nonumber \\ =&\,k_1\omega ^T G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v) +\omega ^T\Big (-\omega ^\times J\omega +\tau \Big ). \end{aligned}$$
(13)

Here, the term \(\omega ^\times J\omega \) can be cancelled based on the model structure feature. Based on the skew symmetry, one obtains that

$$\begin{aligned} \omega ^T\omega ^\times J\omega =0, \end{aligned}$$
(14)

which leads to

$$\begin{aligned} \dot{W}=&\,k_1\omega ^T G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v) +\omega ^T\tau \nonumber \\ =&-k_2\frac{M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\omega ^T\mathrm{sig}^{\alpha _2}(\omega ) \nonumber \\ \le&\,0. \end{aligned}$$
(15)

Hence, the system state \((q_v,\omega )\) is always bounded.

4.1.2 Second part: velocity constraint

In this part, we will show that \(|\omega _i(t)|<M,i=1,2,3,\) for all time. Construct the function:

$$\begin{aligned} U=&\,\frac{1}{1+\alpha _2}\sum _{j=1}^3|\omega _{j}|^{1+\alpha _2}=\frac{1}{1+\alpha _2}\chi (\omega ), \end{aligned}$$
(16)

whose derivative is

$$\begin{aligned} \dot{U}=&\sum _{j=1}^3\mathrm{sig}^{\alpha _2}(\omega _j)\dot{\omega }_j\nonumber \\ =&\,\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega +\tau \Big ). \end{aligned}$$
(17)

Under the proposed controller, one obtains that

$$\begin{aligned} \dot{U} =&\,\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega - k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)\Big )\nonumber \\&-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\mathrm{sig}^{\alpha _2}(\omega ). \end{aligned}$$
(18)

Based on the first part’s proof, the first term in (18) is bounded, i.e., there is a constant \(C_1\) that makes

$$\begin{aligned} \Big | \mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega - k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)\Big )\Big |\le C_1. \end{aligned}$$
(19)

However, for the second term in (18), if \(\chi (\omega (t))\rightarrow M^{1+\alpha _2}\) then

$$\begin{aligned}&-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\mathrm{sig}^{\alpha _2}(\omega )\rightarrow -\infty . \end{aligned}$$
(20)

Next, a contradiction proof can be used to show that \(\chi (\omega )=M^{1+\alpha _2}\) is impossible. Suppose there exists a time \(T^*\) such that \(\chi (\omega (T^*))=M^{1+\alpha _2}\). As a result, based on (19) and (20), before the time \(T^*\), there exists a time interval \([T^{**},T^*)\) such that

$$\begin{aligned} \chi (\omega (t))<M^{1+\alpha _2}\ \ \mathrm{and}\ \ \dot{U}(t)\le 0,\ \ \forall t\in [T^{**}, T^*). \end{aligned}$$
(21)

In other words,

$$\begin{aligned} U(T^*)\le U(T^{**}). \end{aligned}$$
(22)

By the definition of U in (16), one further gets that

$$\begin{aligned} \chi (\omega (T^*))\le \chi (\omega (T^{**}))<M^{1+\alpha _2}, \end{aligned}$$
(23)

which conflicts the previous assumption that \(\chi (\omega (T^*))=M^{1+\alpha _2}\).

Hence, the conclusion can be made that \(\chi (\omega (t))<M^{1+\alpha _2}\) and \(|\omega _i(t)|<M,i=1,2,3\) for any time t.

4.1.3 Third Part: finite-time stability

Substituting proposed controller (11) into (4) to obtain the closed-loop system which can be described as:

$$\begin{aligned} \dot{q}_v&=\frac{1}{2}(q_v^\times +q_0 I_3)w=\frac{1}{2}G(q_v)w,\nonumber \\ J\dot{\omega }&=-\,\omega ^\times J\omega - k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)\nonumber \\&\quad -\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}({\omega }). \end{aligned}$$
(24)

The finite-time stability of system (24) is proved in two steps.

  • Step 1 Asymptotically stable

    Based on the proof procedure in first part, it can be concluded which \((q_v,\omega )\rightarrow 0\) as \(t\rightarrow \infty \) follows from LaSalle’s invariant principle [43].

  • Step2 Locally finite-time stable

    System (24) can be reformed as

    $$\begin{aligned} \dot{q_v}=&\,\frac{1}{2}G(0)\omega +\phi _1(q_v,\omega ), ~~~\nonumber \\ J\dot{\omega }=&- k_1 G^T(0)\mathrm{sig}^{\alpha _1}(q_v)-k_2\mathrm{sig}^{\alpha _2}({\omega })+\phi _2(q_v,\omega ), \end{aligned}$$
    (25)

    where

    $$\begin{aligned}&\phi _1(q_v,\omega )=\frac{1}{2}\Big (G(q_v)-G(0)\Big )\omega ,\nonumber \\ \phi _2(q_v,\omega )&=-\omega ^\times J\omega - k_1 \Big (G^T(q_v)- G^T(0)\Big )\mathrm{sig}^{\alpha _1}(q_v)\nonumber \\&\quad -\Big (\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}-k_2\Big )\mathrm{sig}^{\alpha _2}({\omega }). \end{aligned}$$
    (26)

    First, consider the nominal part of (25), i.e.,

    $$\begin{aligned} \dot{q_v}=&\,\frac{1}{2}G(0)\omega ,\nonumber \\ J\dot{\omega }=&- k_1 G^T(0)\mathrm{sig}^{\alpha _1}(q_v)-k_2\mathrm{sig}^{\alpha _2}({\omega }). \end{aligned}$$
    (27)

    Construct Lyapunov function as

    $$\begin{aligned} V=\frac{2k_1}{1+\alpha _1}\Big (\sum _{j=1}^3|{q}_{v,j}|^{1+\alpha _1}\Big )+\frac{1}{2}{\omega }^TJ{\omega }. \end{aligned}$$
    (28)

    By a calculation, we have

    $$\begin{aligned} \dot{V} =&\,{2k_1\sum _{j=1}^3\mathrm{sig}^{\alpha _1}(q_{v,j})\dot{q}_{v,j}}+\omega ^TJ\dot{\omega }\nonumber \\ =&-k_2\omega ^T\mathrm{sig}^{\alpha _2}({\omega })\nonumber \\ \le&\,0. \end{aligned}$$
    (29)

    As with the above proof, system (27) can be proved to be asymptotically stable. And by Definition 2.2, it can be proved that system (27) has a homogeneous of degree \(k=(\alpha _1-1)/2<0\) with respect to the dilation \((\lambda _1,\lambda _1,\lambda _1,\lambda _2,\lambda _2,\lambda _2)\), where \(\lambda _1=1,\lambda _2=(1+\alpha _1)/2\).

Based on the definition of \(G(q_v)\), we know it is a continuously differentiable function. It can be obtained via the mean inequality that

$$\begin{aligned} G(\varepsilon ^{\lambda _1}q_v)-G(0)=O(\varepsilon ^{\lambda _1}q_v), \end{aligned}$$
(30)

and

$$\begin{aligned} G^T(\varepsilon ^{\lambda _1}q_v)-G^T(0)=O(\varepsilon ^{\lambda _1}q_v). \end{aligned}$$
(31)

Next, we prove that \(\lim \nolimits _{\varepsilon \rightarrow 0}\frac{\phi _i(\varepsilon ^{\lambda _1}q_v,\varepsilon ^{\lambda _2}\omega )}{\varepsilon ^{\lambda _i+k}}=0\), \(i=1,2\), for all \((q_v,\omega )\ne 0\). According to the definition of function \(\phi _1(q_v,\omega )\), we have

$$\begin{aligned}&\lim \limits _{\varepsilon \rightarrow 0}{\frac{\phi _1 (\varepsilon ^{\lambda _1}q_v,\varepsilon ^{\lambda _2}{\omega })}{\varepsilon ^{\lambda _1+k}}}\nonumber \\&=\lim \limits _{\varepsilon \rightarrow 0}\frac{\frac{1}{2}\Big ( G(\varepsilon ^{\lambda _1}q_v)-G(0)\Big )\varepsilon ^{\lambda _2}{\omega }}{\varepsilon ^{\lambda _1+k}}\nonumber \\&=\,O(\varepsilon ^{\lambda _1}{ {q_v}})\varepsilon ^{\lambda _2-\lambda _1-k}{\omega }. \end{aligned}$$
(32)

Because \(r_2-r_1-k=0\), then

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0}{\frac{\phi _1 (\varepsilon ^{\lambda _1}{\dot{q_v}},\varepsilon ^{\lambda _2}{\omega })}{\varepsilon ^{\lambda _1+k}}}=O(\varepsilon ^{\lambda _1}{ {q_v}}){\omega } =0 \end{aligned}$$
(33)

Similarly, based on the definition of function \(\phi _2(q_v,\omega )\), we have

$$\begin{aligned}&\lim \limits _{\varepsilon \rightarrow 0}{\frac{\phi _2 (\varepsilon ^{\lambda _1}{ q_v},\varepsilon ^{\lambda _2}{\omega })}{\varepsilon ^{\lambda _2+k}}}\nonumber \\&=\lim \limits _{\varepsilon \rightarrow 0}-\varepsilon ^{-\lambda _2-k}\Big [\omega ^\times J\omega + k_1 \Big (G^T(\varepsilon ^{\lambda _1}{q_v})- G^T(0)\Big )\mathrm{sig}^{\alpha _1}(\varepsilon ^{\lambda _1}{q_v})\nonumber \\&\quad +\Big (\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}-k_2\Big )\mathrm{sig}^{\alpha _2}(\varepsilon ^{\lambda _2}{\omega })\Big ]\nonumber \\&=-\lim \limits _{\varepsilon \rightarrow 0}\Big (k_1O(\varepsilon ^{\lambda _1}{ {q_v}})\varepsilon ^{\lambda _1\alpha _1-\lambda _2-k}\mathrm{sig}^{\alpha _1}(q_v)+\varepsilon ^{-\lambda _2-k}\omega ^\times J\omega \nonumber \\&\quad +\Big (\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}-k_2\Big )\varepsilon ^{\lambda _2\alpha _2-\lambda _2-k}\mathrm{sig}^{\alpha _2}({\omega })\Big ). \end{aligned}$$
(34)

Obviously, \(\lambda _1\alpha _1-\lambda _2-k=0\), \(\lambda _2\alpha _2-\lambda _2-k=0\), then

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0}{\frac{\phi _2 (\varepsilon ^{\lambda _1}q_v,\varepsilon ^{\lambda _2}{\omega })}{\varepsilon ^{r_1+k}}} =&0 \end{aligned}$$
(35)

Therefore, by Lemma 2.1, the local finite-time stability and the global finite-time stability of the closed-loop system can be guaranteed, i.e., \((q_v,\omega )\rightarrow 0\) in a finite time. \(\square \)

Remark 4.1

Note that in Theorem 4.1, if the fractional powers in novel finite-time controller (11) are chosen to be 1, i.e., \(\alpha _{1}=\alpha _{2}=1\), then the control torque will reduce to PD with the angular velocity constrained, i.e.,

$$\begin{aligned} \tau&=- k_1 G^T(q_\mathrm{v})q_v-\frac{k_2M^{2}}{|M^{2}-\chi (\omega )|}\omega . \end{aligned}$$
(36)

In the simulation section, the dynamic performance of the proposed control strategy can be shown by comparison with traditional PD controller as well as improved PD controller.

4.2 Case 2: case of exist external disturbances

The external disturbance in system (4) \(\mathrm{d}(t)\) is bounded. To deal with lump disturbance \(\mathrm{d}(t)\), an RBF neural network is employed to estimate \(\mathrm{d}(t)\) [44]. Assume that an optimal weight \(W^{*}\) satisfies

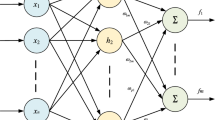
$$\begin{aligned} \mathrm{d}(\cdot )&=W^{*T}h_{d}(x)+\varepsilon _\mathrm{d}, \end{aligned}$$
(37)

where \(x=[q_\mathrm{v},\omega ]^T\) is the input, \(h_\mathrm{d}(x)\) is the radial basis function of the neural network, \(\varepsilon _\mathrm{d}\) is the network approximation error, and \(|\varepsilon _\mathrm{d}|\le \varepsilon _\mathrm{{Md}}\) with a constant \(\varepsilon _\mathrm{{Md}}\). According to the model, the output of the neural network is

$$\begin{aligned} {\hat{\mathrm{d}}}(x)=&\,{\hat{W}}^{T}h_\mathrm{d}(x), \end{aligned}$$
(38)

where \({\hat{W}}\) is an estimate value of the ideal weight \(W^{*}\). The disturbance estimation error is

$$\begin{aligned} d(\cdot )-{\hat{\mathrm{d}}}(x)=&\,W^{*T}h_\mathrm{d}(x)+\varepsilon _\mathrm{d}-{\hat{W}}^{T}h_\mathrm{d}(x)\nonumber \\ =&\,(W^{*T}-{\hat{W}}^{T})h_\mathrm{d}(x)+\varepsilon _\mathrm{d}\nonumber \\ =&\,W^Th_\mathrm{d}(x)+\varepsilon _\mathrm{d}, \end{aligned}$$
(39)

where

$$\begin{aligned} W^T=W^{*T}-{\hat{W}}^{T}. \end{aligned}$$
(40)

The radial basis function can be expressed as:

$$\begin{aligned} h_{d}(x)&=\mathrm{exp}\Big (-\frac{\parallel x-c_{j}\parallel ^{2}}{2b^{2}_{j}}\Big ),\quad j=1,2,\ldots ,n, \end{aligned}$$
(41)

where \(c_j\) is the data center of radial basis function in the j-th neuron of the hidden layer, and \(b_{j}\) is the width of radial basis function in the j-th neuron of the hidden layer.

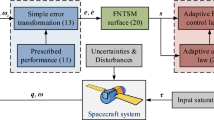
As a result, the finite-time controller based on RBF neural network is designed as follows.

Theorem 4.2

For attitude control subsystem (4) of quad-rotor aircraft in the presence of external disturbances, if the controller is designed as

$$\begin{aligned} \tau&=-\, k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}({\omega })\nonumber \\&\quad -{{\hat{d}}}-k_3\mathrm{sign}(J^Ts), \end{aligned}$$
(42)

where

$$\begin{aligned} s&=J\omega +\int _{0}^{\mu }f(q_v,\omega )\mathrm{d}\mu , \end{aligned}$$
(43)
$$\begin{aligned} f(q_v,\omega )&=k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)+\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}({\omega }), \end{aligned}$$
(44)

where the \({{\hat{d}}}\) is the output of RBF neural network given by (38), \(k_3\) is an appropriate positive constant, the parameters \(\alpha _{i},k_i,i=1,2\) are the same as that of Theorem 4.1, then the attitude of aircraft can converge to the desired state in a finite time. \(\square \)

Proof

First, it needs to be proven that system (4) can reach the sliding surface in a finite time. Then, we prove that \(|\omega _i(t)|< M\).

Choose the Lyapunov function:

$$\begin{aligned} U=\frac{1}{2}s^TJs, \end{aligned}$$
(45)

whose derivative is:

$$\begin{aligned} \dot{U}=&\,s^TJ\dot{s} \nonumber \\ =&\,s^TJ\Big (J\dot{\omega }+f(q_v,\omega )\Big ) \nonumber \\ =&\,s^TJ\Big (-\omega ^\times J\omega +\tau +\mathrm{d}(t)+f(q_v,\omega )\Big )\nonumber \\ \le&\,s^TJ\Big (d(t)-{{\hat{d}}}_\Phi -k_3sign(J^Ts)\Big )\nonumber \\ =&-s^TJ\Big (k_3\mathrm{sign}(J^Ts)-W^Th_{d}(x)-\varepsilon _{d}\Big )\nonumber \\ \le&-|s^TJ|\Big (k_3-W^Th_{d}(x)-\varepsilon _{d})\Big ). \end{aligned}$$
(46)

Since the Gaussian function \(h_{d}(x)\) and the function \(W^T\) are bounded, the \(W^Th_{d}(x)+\varepsilon _{d}\) is bounded. As a result, if the gain satisfies \(k_3\ge W^Th_{d}(x)-\varepsilon _{d}\), then

$$\begin{aligned} \dot{U}\le -|s^TJ|\gamma =&-\sqrt{s^TJJ^Ts}\gamma \nonumber \\ \le&-\sqrt{\min {\{J_{11},J_{22},J_{33}\}}s^TJs}\gamma \nonumber \\ =&-\sqrt{2U}\varrho , \end{aligned}$$
(47)

where

$$\begin{aligned} \varrho =\sqrt{\min {\{J_{11},J_{22},J_{33}\}}}\gamma . \end{aligned}$$
(48)

Clearly, the sliding mode state s will converge to 0 in a finite time and always stay there.

Once \(s\equiv 0,\) then \(\dot{s}\equiv 0.\) As a result, it follows from (59) that

$$\begin{aligned} J\dot{\omega }=-k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}({\omega }). \end{aligned}$$
(49)

Using an almost same proof as that of Case 1, it can be proven that the attitude will be stabilized in a finite time.

For \(|\omega _i(t)|< M\), we construct the function:

$$\begin{aligned} P=&\,\frac{1}{1+\alpha _2}\sum _{j=1}^3|\omega _{j}|^{1+\alpha _2}=\frac{1}{1+\alpha _2}\chi (\omega ), \end{aligned}$$
(50)

whose derivative is

$$\begin{aligned} \dot{P}=&\sum _{j=1}^3\mathrm{sig}^{\alpha _2}(\omega _j)\dot{\omega }_j\nonumber \\ =&\,\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega +\tau +d(t)\Big ). \end{aligned}$$
(51)

Under the proposed controller, one obtains that

$$\begin{aligned} \dot{P} =&\, \mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega - k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)\nonumber \\&+W^Th_{d}(x)+\varepsilon _{d}-k_3\mathrm{sign}(J^Ts)\Big )\nonumber \\&-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\mathrm{sig}^{\alpha _2}(\omega ). \end{aligned}$$
(52)

Since s is always bounded, then the first term in (52) is bounded, i.e., there is a constant \(C_1\) that makes

$$\begin{aligned}&\Big | \mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\Big (-\omega ^\times J\omega - k_1 G^T(q_v)\mathrm{sig}^{\alpha _1}(q_v)\nonumber \\&+W^Th_{d}(x)+\varepsilon _{d}-k_3\mathrm{sign}(J^Ts)\Big )\Big |\le C_1. \end{aligned}$$
(53)

However, for the second term, if \(\chi (\omega (t))\rightarrow M^{1+\alpha _2}\) then

$$\begin{aligned}&-\frac{k_2M^{1+\alpha _2}}{|M^{1+\alpha _2}-\chi (\omega )|}\mathrm{sig}^{\alpha _2}(\omega )^TJ^{-1}\mathrm{sig}^{\alpha _2}(\omega )\rightarrow -\infty . \end{aligned}$$
(54)

Next, a contradiction proof can be used to show that \(\chi (\omega )=M^{1+\alpha _2}\) is impossible. Suppose there exists a time \(T^*\) such that \(\chi (\omega (T^*))=M^{1+\alpha _2}\). As a result, based on (53) and (54), before the time \(T^*\), there exists a time interval \((T^{**}, T^*)\) such that

$$\begin{aligned} \chi (\omega (t))<M^{1+\alpha _2}\ \ \mathrm{and}\ \ \dot{P}(t)\le 0,\ \ \forall t\in (T^{**}, T^*). \end{aligned}$$
(55)

In other words,

$$\begin{aligned} P(T^*)\le P(T^{**}). \end{aligned}$$
(56)

By the definition of P in (50), one further gets that

$$\begin{aligned} \chi (\omega (T^*))\le \chi (\omega (T^{**}))<M^{1+\alpha _2}, \end{aligned}$$
(57)

which conflicts the previous assumption that \(\chi (\omega (T^*))=M^{1+\alpha _2}\).

Hence, the conclusion can be made that \(\chi (\omega (t))<M^{1+\alpha _2}\) and \(|\omega _i(t)|<M,i=1,2,3\) for any time t.

The proof is completed. \(\square \)

Remark 4.2

Note that in Theorem 4.2, if the fractional powers in novel finite-time controller (42) are chosen to be 1, i.e., \(\alpha _{1}=\alpha _{2}=1\), then the control torque will reduce to PD control with the angular velocity constrained that can deal with external disturbance, i.e.,

$$\begin{aligned} \tau&=-\, k_1 G^T(q_v)q_v-\frac{k_2M^{2}}{|M^{2}-\chi (\omega )|}{\omega }-{{\hat{d}}}-k_3\mathrm{sign}(J^Ts), \end{aligned}$$
(58)

where

$$\begin{aligned} s=J\omega +\int _{0}^{\mu }f(q_v,\omega )\mathrm{d}\mu , \end{aligned}$$
(59)
$$\begin{aligned} f(q_v,\omega )=k_1 G^T(q_v)q_v+\frac{k_2M^{2}}{|M^{2}-\chi (\omega )|}\omega , \end{aligned}$$
(60)

where the \({{\hat{d}}}\) is the output of RBF neural network given by (38), \(k_3\) is an appropriate positive constant, the parameters \(\alpha _{i},k_i,i=1,2\) are the same as that of Theorem 4.1, then the attitude of aircraft can converge asymptotically to the desired state. Compared with (58), the dynamic performance of the proposed control strategy is better, which can make the system stable in a finite time.

5 Simulation results

To verify the proposed theoretical results in Theorems 4.1 and 4.2, some numerical simulations are given. Two cases will be considered in this section.

For the first case, it is assumed that there are no external disturbances. To demonstrate the advantages of the proposed controller, two control strategies will be used for comparison, i.e., PD controller, PD controller with angular velocity constraint. In the second case, we consider the existence of external disturbances, a finite-time controller based on the integral terminal sliding mode control theory and the RBF neural network is employed.

The main parameters for the spacecraft are presented as Table 1 [45].

Table 1 The moment of inertia for aircraft
Full size table

For the simulation part, the initial state is selected as

$$\begin{aligned}&(q_1(0),q_2(0),q_3(0),q_4(0),\omega _1(0),\omega _2(0),\omega _3(0))^T \nonumber \\&=(0.7683 , 0.371, 0.384 ,0.353, -0.21, -0.23, -0.25)^T. \end{aligned}$$
(61)

5.1 Case 1: case of no external disturbance

Fig. 1
figure 1

The quaternion response curves for case 1

Full size image

Table 2 lists the parameters of the controller.

Table 2 Controllers’ parameters
Full size table

As for the choose of controllers gains \(k_1\) and \(k_2\), by using the trial and error method, we do a number of simulations and then choose the better parameters for a satisfactory performance. Although the proposed finite-time algorithm contains the fractional power, it is not difficult to implement it based on a microcontroller (Pixhawk) with the C program. In order to compare the three controllers conveniently, the response curves of the three controllers are shown in the same figure. The quaternion response curve is shown in Fig. 1.

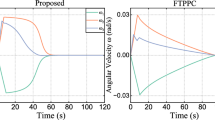
The angular velocity curves under three controller are shown in Fig. 2. In addition, in order to further illustrate that the proposed controller has better convergence speed, Table 3 is given, which compares the convergence time of the three control methods. The symbol [bold] is used for less time to highlight the effect. The convergence time is defined as the time after which \(|\omega _{i}|<10^{-3}, i=1,2,3.\)

Table 3 The convergence time of the angular velocity under employed controllers
Full size table

As shown in Fig. 2 and Table 3, PD control has a slower convergence rate than the proposed method, and the angular velocity exceeds the constraint scope. Although under the PD control with angular velocity constraint, angular velocity can be strictly constrained, its convergence rate is very slow. Compared with the first two control methods, finite-time control method with angular velocity constraint not only keeps the angular velocity strictly constrained, but also has the best convergence speed.

Fig. 2
figure 2

The angular velocity response curves for case 1

Full size image

5.2 Case 2: case of exist external disturbances

In order to verify the above theoretical results, it is shown that the proposed controller has good robustness to external disturbances, and the external disturbances are selected as [46,47,48]

$$\begin{aligned}&d_1(t)=0.002\sin (t+5),\nonumber \\&d_2(t)=0.002\cos (2t+3),\nonumber \\&d_3(t)=0.003\sin (3t+2). \end{aligned}$$
(62)

The structure diagram of RBF neural network is shown in Fig. 3. The parameters for radial basis function (41) are selected as \(c_j=[-1,-0.5, 0, 0.5, 1], bj=1, j=1, 2, 3, 4, 5,\) the parameter for finite-time controller (42) is chosen as: \(k_1 = 40, \alpha _1 = 0.5, k_2 = 55, \alpha _2 = 2/3, k_3 =30.\)

Fig. 3
figure 3

The structure diagram of RBF neural network

Full size image

As shown in Fig. 4, it can be seen that the proposed finite-time controller based on RBF neural network is effective and has the capability to capture the disturbance \(d(\cdot )\). Furthermore, from Fig. 5, it can be derived that by employing the proposed RBF-based neural network and terminal sliding mode control, the attitude stability control performance of aircraft with the angular velocity constraint and external disturbances can be further improved.

Fig. 4
figure 4

The quaternion response curves for case 2

Full size image
Fig. 5
figure 5

The angular velocity response curves for case 2

Full size image

6 Conclusion

This paper has developed a finite-time attitude stabilization control method for a angular velocity constrained quad-rotor aircraft in the presence of external disturbances. Firstly, a finite-time controller with angular velocity has been proposed to ensure the constrained angular velocity can be stabilized to the origin in a finite time. Then, a finite-time controller based on sliding mode control theory and RBF neural network is proposed to solve the problem of exit external disturbances. At the end, simulation results have been given to verify the advantages of proposed control strategies.