Environmental Policy and the Excess Entry Theorem

Abstract

This paper develops a model of Cournot oligopoly with pollution and free entry. We show that the deviation of the optimal emission tax rate from the marginal environmental damage depends crucially on the curvature of demand as well as the output elasticity of remission. Implementing the right environmental policy is therefore subject to an informational problem. We further show that under the traditional Pigouvian tax rule, the business- stealing effect is more likely to be observed than under the exogenously given tax rate. Hence, the Pigouvian tax is recommended from the informational viewpoint and it should be accompanied by entry regulation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

During the past decades, market liberalization and environmental protection have been salient features of economic policy trend in the industrialized countries. However, relatively few economic analyses have focused on how an environmental policy interacts with an antitrust or a competition policy.¹ This paper is aimed at examining the effects of these two policies on pollution control and social welfare.

Various studies have explored the optimal pollution taxation in imperfectly competitive markets. The literature is concerned about whether the optimal emission tax rate exceeds the marginal environmental damage. In a perfectly competitive market, the traditional Pigouvian tax rule suggests that the optimal rate is equal to the marginal environmental damage. In a monopolistic market, which is the other polar case, the polluting firm supplies less and thus the optimal rate falls short of the marginal damage.²

As we have seen in the aforementioned argument, when the firm exerts monopoly power in the product market, the environmental damage to a society tends to be under-internalized. In an oligopolistic industry, which has a more realistic market structure, this assertion may not be true.³ Allowing free entry in a symmetric Cournot model with a linear demand, Katsoulacos and Xepapadeas (1995) showed that the optimal pollution tax can be greater than the marginal environmental damage if the marginal abatement costs are independent of the level of output. Lee (1999) abstracted firms’ abatement activities and assumed a general inverse demand function in a free-entry Cournot oligopoly to establish the same result for the concave demand. Simpson (1995) set up a model of heterogenous Cournot duopoly to show that the optimal rate is greater than the marginal environmental damage when the two firms have sufficiently different costs. These contributions were summarized in a survey by Requate (2007) under a unified framework.

This paper uses a symmetric Cournot oligopoly model with free entry and derives the conditions for the optimal pollution tax to exceed the marginal environmental damage. The policy direction, that is, whether the optimal tax rate is greater or smaller than the marginal damage depends, especially, on the curvature of the inverse demand curve⁴ and the output elasticity of emissions. Previous models studied by Lee (1999) and Requate (2007) rely on the assumption that pollution emissions are proportional to output. This assumption implies that the elasticity of emissions with respect to output becomes unity.⁵ We generalize it to the case in which the elasticity of emission can be either greater or smaller than unity. Such generalization leads to the emergence of the perverse comparative static effects on environment: Entry of a new firm may reduce total emission, while an increase in the emission tax may expand it at the long-run free-entry equilibrium. We then show that the policy direction is reversed according to whether the elasticity of emissions is greater or smaller than unity and that the optimal tax rate can be greater than the marginal damage even in the case of convex demand.

In the antitrust literature, it is well-established that there may exist too many firms at the free-entry Cournot equilibrium from the viewpoint of social welfare. This is called the excess entry theorem, whose pioneering works include von Weizsäcker (1980), Mankiw and Whinston (1986), and Suzumura and Kiyono (1987). The last two specifically show that if the business-stealing effect is present, that is, entry of a new firm reduces output of an incumbent firm, then the social welfare is improved by reducing the number of firms from the long-run free-entry equilibrium level. The second purpose of the paper is to see how the environmental taxation affects the theorem.

We propose the traditional Pigouvian tax rule, rather than the optimal tax formula, which is complex and thus causes the informational problem. It is shown that under the traditional Pigouvian tax rule, the business-stealing effect is more likely to be realized than under the exogenously given tax rate. This implies that even though the regulator does not have full information about the curvature of demand and the output elasticity of emissions, holding the tax rate at the marginal damage level and reducing the number of firms from the free-entry equilibrium level enhance the social welfare. Hence, the joint use of the Pigouvian tax and the entry regulation resolves the informational problem.

The rest of the paper is organized as follows. Section 17.2 sets up a model of symmetric Cournot oligopoly. Section 17.3 derives the optimal pollution taxation both in the short-run and long-run equilibria, respectively. The traditional Pigouvian tax rule is proposed and the validity of the Excess Entry Theorem is explored under this tax rule.

2 The Model

Consider an oligopolistic industry in which n identical firms produce a homogenous good and emit pollution. Let q ⁱ be the output of firm $i \in \left \{1,\cdots \,,n\right \}$. The price of the good, p, is given by the inverse demand function, $p = p\left (Q\right )$, where Q ≡ ∑ _{i = 1} ⁿq ⁱ is the aggregate output. We assume p ^′ ≡ dp∕dQ < 0. However, p ^′′ ≡ d ²p∕dQ ² is allowed to be either positive or negative.⁶ Let ε denote the curvature of the inverse demand function, which is defined as ε ≡ −Qp ^′′∕p ^′. ε measures the convexity of the market demand. This is also interpreted as the output elasticity of the slope of the demand curve.

Let e ⁱ be firm i’s emission level. It is given by the emission generating function, $e^{i} = e\left (q^{i}\right )$, with $e\left (0\right ) = 0$, e ^′ > 0, and $e^{{\prime\prime}}\lesseqgtr 0$. In the literature, the function e is frequently assumed to take the linear form, for example, e ⁱ = γq ⁱ for a constant γ > 0. However, we relax this common assumption. We define the output elasticity of emission level as μ ≡ qe ^′∕e > 0. The aforementioned linear form possesses the property of μ = 1. We deal with more general cases, that is, $\mu \lesseqgtr 1$.

The regulator sets an emission tax rate, τ, per unit of pollutant prior to the firms’ output decision. Firm i’s tax payments are thus $\tau e\left (q^{i}\right )$. Let $c\left (q^{i}\right )$ be firm i’s production costs with $c\left (0\right ) > 0$, c ^′ > 0, and $c^{{\prime\prime}}\lesseqgtr 0$.⁷ Firm i’s profits are therefore given by $\pi ^{i}\left (q^{i},Q^{-i},\tau \right ) \equiv p\left (q^{i} + Q^{-i}\right )q^{i} - c\left (q^{i}\right ) -\tau e\left (q^{i}\right )$, where Q ⁻ⁱ ≡ ∑ _{j ≠ i}q ^j is the total output of firm i’s rivals. Firm i decides its own output so as to maximize π ⁱ, taking the others’ output and the emission tax rate as given. The first-order condition for profit maximization is therefore $\pi _{q^{i}}^{i} \equiv \partial \pi ^{i}/\partial q^{i} = p^{{\prime}}q^{i} + p - c^{{\prime}}-\tau e^{{\prime}} = 0$. The second-order condition is assumed to be satisfied⁸: $\pi _{q^{i}q^{i}}^{i} \equiv \partial ^{2}\pi ^{i}/\partial \left (q^{i}\right )^{2} = p^{{\prime\prime}}q^{i} + 2p^{{\prime}}- c^{{\prime\prime}}-\tau e^{{\prime\prime}} < 0$.

We assume the existence and uniqueness of a Cournot-Nash equilibrium. Focusing on the symmetric equilibrium, q ⁱ ≡ q for all i and dropping the superscripts that indicate the firm index, we write the first-order condition as

$$\displaystyle{ \pi _{q} = p^{{\prime}}\left (nq\right )q + p\left (nq\right ) - c^{{\prime}}\left (q\right ) -\tau e^{{\prime}}\left (q\right ) = 0. }$$

(17.1)

Following Seade (1980) and Mankiw and Whinston (1986), we treat the number of firms as a continuous variable. In the long-run equilibrium, the profits must be driven to zero owing to free entry and exit. Thus, the number of firms, n, is endogenously determined by the zero-profit condition:

$$\displaystyle{ \pi = p\left (nq\right )q - c\left (q\right ) -\tau e\left (q\right ) = 0. }$$

(17.2)

This implies that $p = \frac{c+\tau e} {q}$, which can be substituted into (17.1). After some manipulations, we have

$$\displaystyle{ q = \frac{\left (c^{{\prime}} +\tau e^{{\prime}}\right ) -\frac{c+\tau e} {q} } {p^{{\prime}}}. }$$

(17.3)

It should be noted that $\left (c^{{\prime}} +\tau e^{{\prime}}\right ) < \left (c +\tau e\right )/q$ is required for the long-run free-entry equilibrium to exist, that is, for the right-hand side of (17.3) to be positive. This inequality means that overall costs must exhibit scale economies, that is, average costs exceed marginal costs. Define the output elasticity of production cost as $\lambda \equiv qc^{{\prime}}/c \in \left (0,1\right )$. Then the above existence condition places the upper bound for μ, that is, $\mu < \frac{c} {\tau e}\left (1-\lambda \right ) + 1 \equiv \bar{\mu }$. Since we allow μ > 1, it is necessary for at least one of the both elasticity λ and tax payment τe or both to be sufficiently small.

In what follows, we perform comparative statics for the short-run and long-run equilibria. For that purpose, it is necessary to assume the stability of each equilibrium. First, we present the short-run stability conditions with regard to Eq. (17.1). As in Seade (1980) and Dixit (1986), π _qq ≡ ∂π _q∕∂q < 0 and $\kappa \equiv 1 -\left (c^{{\prime\prime}} +\tau e^{{\prime\prime}}\right )/p^{{\prime}} > 0$ are assumed to be satisfied. Note that κ measures the relative slope of the marginal cost curve and the demand curve. We now utilize ε and κ to express the former condition as⁹

$$\displaystyle{ \pi _{qq} = \left (-p^{{\prime}}\right )\left (\epsilon -n-\kappa \right ) < 0\quad \Leftrightarrow \quad \epsilon < n+\kappa \equiv \bar{\epsilon }. }$$

This places the upper bound for ε, which is denoted by $\bar{\epsilon }$.

Next, the long-run stability condition is introduced. The long-run equilibrium is then characterized by Eqs. (17.1) and (17.2). Appendix shows that the stability condition can be expressed as

$$\displaystyle{ H \equiv \pi _{qq}\pi _{n} -\pi _{qn}\pi _{q} = \frac{1} {n}\left (p^{{\prime}}q\right )^{2}\left (n + n\kappa -\epsilon \right ) > 0. }$$

It is also shown in Appendix that H > 0 is automatically implied by the short-run stability conditions.

2.1 Short-Run Equilibrium

The number of firms, n, is exogenously given in the short-run equilibrium. Then, in view of Eq. (17.1), we write the Cournot-Nash equilibrium output as $\tilde{q} =\tilde{ q}(\tau,n)$. Accordingly, from Appendix, the effects of an increase in the emission tax and entry of a new firm are

$$\displaystyle{ \frac{\partial \tilde{q}} {\partial \tau } = \frac{e^{{\prime}}} {\pi _{qq}} < 0,\qquad \frac{\partial \tilde{q}} {\partial n} = \frac{\epsilon -n} {\bar{\epsilon }-\epsilon } \frac{\tilde{q}} {n} \gtreqless 0\quad \Leftrightarrow \quad \epsilon \gtreqless n. }$$

(17.4)

The effect of entry is worth mentioning. In the antitrust literature, $\partial \tilde{q}/\partial n < 0$ is named as the business-stealing effect (see Mankiw and Whinston 1986). It is related with the concept of strategic substitutes (see Bulow et al. 1985). This means $\pi _{q^{i}Q^{-i}}^{i} \equiv \partial \pi _{q^{i}}^{i}/\partial Q^{-i} = p^{{\prime\prime}}q^{i} + p^{{\prime}} < 0$, that is, firm i’s marginal profits decrease with its rivals’ output. The entry of a new rival firm reduces the marginal profits, and thus the existing firms cut back their own output. In the symmetric equilibrium, we have $\pi _{q^{i}Q^{-i}}^{i} = \left (-p^{{\prime}}\right )\left (\epsilon /n - 1\right ) < 0 \Leftrightarrow \epsilon < n$. If the demand is too convex (i.e., $\epsilon \in \left (n,\bar{\epsilon }\right )$), the outputs become strategic complements, and thus the entry of a new firm expands the individual output.

The effects on total output $\tilde{Q} \equiv n\tilde{q}$ are found immediately by

$$\displaystyle{ \frac{\partial \tilde{Q}} {\partial \tau } = \frac{ne^{{\prime}}} {\pi _{qq}} < 0,\qquad \frac{\partial \tilde{Q}} {\partial n} = \frac{\kappa } {\bar{\epsilon }-\epsilon }\tilde{q} > 0. }$$

(17.5)

The short-run equilibrium price is defined as $\tilde{p} \equiv p(\tilde{Q})$, and the short-run equilibrium emission level is denoted by $\tilde{e} \equiv e\left (\tilde{q}\right )$. Clearly, $\partial \tilde{p}/\partial \tau > 0$ and $\partial \tilde{e}/\partial \tau < 0$, that is, an increase in emission tax rate, raise the price, while it reduces the emission level.

We next examine whether the net price of the product given by $\tilde{p} -\tau \tilde{ e}/\tilde{q}$ would increase. Seade (1985) was the first to point out that the net price may be raised by an increase in the output or commodity tax. We confirm his price over-shifting argument in our emission tax framework. For this, we differentiate the net price and evaluate its derivative at τ = 0, which yields the following relationship¹⁰:

$$\displaystyle{ \frac{\partial \left (\tilde{p} -\tau \tilde{ e}/\tilde{q}\right )} {\partial \tau } = \frac{\epsilon -\epsilon _{2}} {\bar{\epsilon }-\epsilon } \frac{\tilde{e}} {\tilde{q}} \lesseqgtr 0\quad \Leftrightarrow \quad \epsilon \lesseqgtr \epsilon _{2} \equiv \kappa -n\left (\mu -1\right ). }$$

(17.6)

If ε > ε ₂, then an increase in the tax would be over-shifted into the price (so-called price over-shifting). When the emission is output-elastic (or inelastic), that is, μ > (or < ) 1, the emission tax is more (less) likely to induce the price over-shifting than the output tax, whose result is generated by setting μ = 1. Moreover, when μ > (or < ) 1, more (fewer) firms in the industry are more (less) likely to cause the price over-shifting.

We find the effects on the short-run equilibrium profits denoted by $\tilde{\pi }\equiv p\left (n\tilde{q}\right )\tilde{q} - c\left (\tilde{q}\right ) -\tau e\left (\tilde{q}\right )$. Straightforward differentiations give¹¹

$$\displaystyle\begin{array}{rcl} \frac{\partial \tilde{\pi }} {\partial \tau }& =& \frac{\epsilon -\epsilon _{3}} {\bar{\epsilon }-\epsilon } \tilde{e} \gtreqless 0\quad \Leftrightarrow \quad \epsilon \gtreqless \epsilon _{3} \equiv \kappa +1 -\left (n - 1\right )\left (\mu -1\right ),{}\end{array}$$

(17.7a)

$$\displaystyle\begin{array}{rcl} \frac{\partial \tilde{\pi }} {\partial n}& =& \frac{n + n\kappa -\epsilon } {n\left (\bar{\epsilon }-\epsilon \right )} p^{{\prime}}\tilde{q}^{2} < 0,{}\end{array}$$

(17.7b)

where the last inequality is due to the stability conditions: κ > 0 and $\epsilon <\bar{\epsilon }\equiv n+\kappa < n + n\kappa$. Therefore, we conclude that the profit would be over-shifted by an increase in the emission tax for the sufficiently convex demand with $\epsilon \in \left (\epsilon _{3},\bar{\epsilon }\right )$. Furthermore, from ε ₃ −ε ₂ = μ > 0, we establish that the profit over-shifting is less likely than the price over-shifting. This is because as shown by Seade (1985), the price over-shifting is necessary for the profit over-shifting to occur.

The effects on total emission $\tilde{E} \equiv ne\left (\tilde{q}\right )$ are derived by simple differentiations:

$$\displaystyle{ \frac{\partial \tilde{E}} {\partial \tau } = \frac{n\left (e^{{\prime}}\right )^{2}} {\pi _{qq}} < 0,\qquad \frac{\partial \tilde{E}} {\partial n} = \frac{\left (\mu -1\right )\left (\epsilon -n\right )+\kappa } {\bar{\epsilon }-\epsilon } \tilde{e} \lesseqgtr 0\quad \Leftrightarrow \quad \left (\mu -1\right )\epsilon +\epsilon _{2} \lesseqgtr 0. }$$

(17.8)

As expected, an increase in the emission tax reduces total emission. However, this assertion is not always true in the long-run equilibrium.

The effects of entry should be intensively discussed. The term, $\left (\mu -1\right )\left (\epsilon -n\right )$, in the middle expression of the numerator of Eq. (17.8) can be called the emission divisionalization effect. Dividing up a firm causes the individual output to shrink (i.e., business-stealing) or expand (i.e., business-augmenting), given that ε < n or > n. On the other hand, the emission change can be greater or smaller than the output change depending upon μ > 1 or < 1.¹² When the emission is output-elastic (i.e., μ > 1) and the business-stealing effect is present (i.e., ε < n), the divisionalization effect is negative. Thus the entry of a firm reduces the individual output, and thus the emission will lower, to a lesser extent, the output reduction. Therefore, total emission may increase in the event of entry.

Now we establish the first proposition:

Proposition 17.1

In the short-run equilibrium in which the number of firms is exogenously given, (1) an increase in the emission tax rate always reduces total emission.

(2) If the emission is elastic with respect to output (i.e., μ > 1) and the inverse demand function is sufficiently concave (i.e., $\epsilon < n -\kappa /\left (\mu -1\right )$ ), entry of a new firm reduces total emission. Otherwise, the entry of a new firm raises total emission.

Proof

See Appendix.

2.2 Long-Run Equilibrium

In the long-run equilibrium in which all the profits are driven to zero by free entry, the number of firms is endogenously determined as a function of the tax rate, that is, $n = n\left (\tau \right )$, and thus $q = q\left (\tau \right ) \equiv \tilde{ q}(\tau,n\left (\tau \right ))$. Therefore, the effect of a change in the emission tax is found by totally differentiating the equilibrium conditions, (17.1) and (17.2). In Appendix, the long-run equilibrium comparative static results are derived as follows¹³:

$$\displaystyle\begin{array}{rcl} \frac{dq} {d\tau } & =& \frac{p^{{\prime}}qe} {Hn} \left (\epsilon -\epsilon _{1}\right ) \gtreqless 0\quad \Leftrightarrow \quad \epsilon \lesseqgtr \epsilon _{1} \equiv -n\left (\mu -1\right ),{}\end{array}$$

(17.9a)

$$\displaystyle\begin{array}{rcl} \frac{dn} {d\tau } & =& \frac{p^{{\prime}}e} {H} \left (\epsilon _{3}-\epsilon \right ) \gtreqless 0\quad \Leftrightarrow \quad \epsilon \gtreqless \epsilon _{3} \equiv \kappa +1 -\left (n - 1\right )\left (\mu -1\right ),{}\end{array}$$

(17.9b)

where H > 0 is the stability condition in the long-run equilibrium.

It should be noted that if μ = 1, then $\frac{dq} {d\tau } = \frac{p^{{\prime}}qe} {Hn} \epsilon \gtreqless 0 \Leftrightarrow p^{{\prime\prime}}\lesseqgtr 0$. In particular, when the demand is linear, there is no impact of environmental tax on the individual output. The intuition for this result is from the fact that a change in the emission tax behaves the same as in the output tax. The residual demand faced by a representative firm has a constant slope, and it is always tangent to the average overall cost curve. An increase in the tax shifts the average cost curve parallelly without changing its slope. Therefore, the tangency point moves upward, keeping the equilibrium output constant.

The long-run equilibrium results are related with the short-run counterparts in the following way:

$$\displaystyle{ \frac{dq} {d\tau } = \frac{\partial \tilde{q}} {\partial \tau } + \frac{\partial \tilde{q}} {\partial n} \frac{dn} {d\tau }. }$$

(17.10)

The first term is the direct effect of a tax hike and is negative. However, an increase in the emission tax may reduce the profitability per firms and so does the number of firms in the long run. It creates the negative business-stealing effect, and thus it expands the output per firm. This long-run or indirect effect may increase the firm’s output. However, total output declines with an increase in emission tax:

$$\displaystyle{ \frac{dQ} {d\tau } = \frac{p^{{\prime}}qe} {H} \left (\kappa +\mu \right ) < 0. }$$

(17.11)

We next check the price over-shifting in the long-run equilibrium. We calculate and evaluate the derivative at τ = 0 yields the following relationship:

$$\displaystyle{ \frac{d\left (p -\tau e/q\right )} {d\tau } = \frac{\epsilon -\epsilon _{1}} {n + n\kappa -\epsilon }\frac{e} {q} \lesseqgtr 0\quad \Leftrightarrow \quad \epsilon \lesseqgtr \epsilon _{1}. }$$

(17.12)

Since the price is equal to average overall costs $\frac{c+\tau e} {q}$ owing to free entry, the net price is the same as the average production cost $\frac{c} {q}$. Scale economies imply that the average production cost falls with output. Thus, the direction of a net price change is opposite to that of an output change.

The effect of an increase in the emission tax on the total emission, $E \equiv ne\left (q\right )$, is given by

$$\displaystyle{ \frac{dE} {d\tau } = ne^{{\prime}}\frac{dq} {d\tau } + e\frac{dn} {d\tau } = \frac{p^{{\prime}}e^{2}} {H} \left [\kappa +1 + \left (\epsilon +1\right )\left (\mu -1\right ) + n\left (\mu -1\right )^{2}\right ]. }$$

(17.13)

As in Lee (1999) and Requate (2007), suppose that μ = 1. This implies that $\frac{dE} {d\tau } = \frac{p^{{\prime}}e^{2}} {H} \left [\kappa +1\right ] < 0$, and thus an increase in the emission tax always raises the level of total pollution. To the contrary, suppose μ ≠ 1, which is the overlooked case in the previous literature. Then the following relationship is immediate:

$$\displaystyle{ \frac{dE} {d\tau } \gtreqless 0\quad \Leftrightarrow \quad \epsilon \left \{\begin{array}{c} \lesseqgtr \\ \gtreqless \end{array} \right \}\epsilon _{4} \equiv -1-n\left (\mu -1\right )-\frac{\kappa +1} {\mu -1}\text{ if }\mu \left \{\begin{array}{c} >\\ < \end{array} \right \}1. }$$

(17.14)

It can be shown that $\bar{\epsilon }-\epsilon _{4} =\mu (n - n_{0}) \lesseqgtr 0 \Leftrightarrow n \lesseqgtr n_{0} \equiv \frac{\kappa +1} {1-\mu }$. The following lemma is useful for the remaining analyses.¹⁴

Lemma 17.2

(1) If μ > 1, then $\epsilon _{4} <\epsilon _{1} <\epsilon _{2} <\epsilon _{3} <\bar{\epsilon }$ , where ε ₄ and ε ₁ are both negative. (2) If μ < 1, then (a) $0 <\epsilon _{1} <\epsilon _{2} <\epsilon _{3} <\bar{\epsilon }<\epsilon _{4}$ for n < n ₀; (b) $0 <\epsilon _{1} <\epsilon _{2} <\epsilon _{3} <\epsilon _{4} <\bar{\epsilon }$ for n > n ₀.

We are interested in identifying under what circumstances total emission increases with the emission tax. We use Lemma 17.2 to explore the sign patterns in (17.14) in Appendix. Thus, the following result is obtained:

Proposition 17.3

Consider the long-run equilibrium in a free-entry Cournot oligopoly. An increase in the emission tax rate raises total emission in the following two types of industry: (1) For an industry with the elastic emission (i.e., μ > 1 and thus ε ₄ < 0), the market demand has concavity with $\epsilon \in \left (-\infty,\epsilon _{4}\right )$ . (2) Conversely, for an industry with the inelastic emission (i.e., μ < 1 and thus ε ₄ > 0), the demand has convexity with $\epsilon \in \left (\epsilon _{4},\bar{\epsilon }\right )$ , and the equilibrium market structure is sufficiently competitive (i.e., n > n ₀).

3 Optimal Environmental Taxation

This section derives the optimal tax rate under the short-run and the long-run equilibria. Let $D\left (E\right )$ denote the environmental damage to the economy. It is assumed to satisfy D ^′ > 0 and D ^′′ ≥ 0. The social welfare is then defined as

$$\displaystyle{ W =\int _{ 0}^{nq}p\left (z\right )dz - nc\left (q\right ) - D\left (ne\left (q\right )\right ). }$$

(17.15)

The short-run welfare function, $\widetilde{W}$, is defined as W evaluated at $q =\tilde{ q}\left (n,\tau \right )$. The welfare change expression is then given by

$$\displaystyle{ dW = n\left (p - c^{{\prime}}- D^{{\prime}}e^{{\prime}}\right )dq + \left (pq - c - D^{{\prime}}e\right )dn. }$$

(17.16)

The first-best solution is obtained by setting the coefficients of both dq and dn to zero. These two equations yield p = c ^′ + D ^′e ^′ and $p = \left (c + D^{{\prime}}e\right )/q$, and thus, the first-best solution implies that $\mu = \frac{c} {D^{{\prime}}e}\left (1-\lambda \right ) + 1 > 1$.¹⁵ The first-best solution can be achieved only in the industry with output-elastic emissions.

Suppose that the regulator sets the emission tax rate so as to maximize (17.15) but that he cannot control the firms’ behavior directly. In the short-run equilibrium, n is exogenously given and thus dn = 0. Therefore, the first-order condition for short-run welfare maximization is

$$\displaystyle{ \frac{\partial \widetilde{W}} {\partial \tau } = n\left (-p^{{\prime}}\tilde{q} + \left (\tau -D^{{\prime}}\right )e^{{\prime}}\right )\frac{\partial \tilde{q}} {\partial \tau } = 0, }$$

(17.17)

where $p - c^{{\prime}} = -p^{{\prime}}\tilde{q} +\tau e^{{\prime}}$ was substituted from Eq. (17.1). Solving this for the tax rate, we get

$$\displaystyle{ \tilde{\tau }-D^{{\prime}} = \frac{p^{{\prime}}\tilde{q}} {e^{{\prime}}} < 0. }$$

(17.18)

The short-run optimal taxation falls short of the marginal environmental damage. The intuition for this result is straightforward. Oligopoly distortion induces firms to produce less, and thus the regulator has an incentive to subsidize them. Therefore, the regulator undercuts the tax rate from the traditional Pigouvian rule.

In the long-run equilibrium, n is endogenously determined and is affected by the tax rate. Therefore the first-order condition for long-run welfare maximization is

$$\displaystyle{ \frac{dW} {d\tau } = \left (\tau -D^{{\prime}}\right )\frac{dE} {d\tau } - p^{{\prime}}nq\frac{dq} {d\tau } = 0, }$$

(17.19)

where pq − c = τe and p − c ^′ = −p ^′q + τe ^′ from the equilibrium conditions, (17.1) and (17.2), were substituted. Solving the above condition gives

$$\displaystyle\begin{array}{rcl} \tau - D^{{\prime}}& =& np^{{\prime}}q\frac{dq} {d\tau } /\frac{dE} {d\tau } = \frac{p^{{\prime}}q^{2}} {e} \psi;{}\end{array}$$

(17.20a)

$$\displaystyle\begin{array}{rcl} \psi & \equiv \frac{n\left (\mu -1\right )+\epsilon } {\kappa +1+\left (\epsilon +1\right )\left (\mu -1\right )+n\left (\mu -1\right )^{2}}.&{}\end{array}$$

(17.20b)

If ψ < 0, the optimal emission tax exceeds the marginal environmental damage. First, we consider a special case of μ = 1. Then $\psi = \frac{\epsilon } {1+\kappa }$. Since κ > 0, if the demand is concave (ε < 0), the optimal emission tax exceeds the marginal environmental damage. Otherwise, the optimal emission tax falls short of the marginal environmental damage. This is a well-known result (see Lee 1999 and Requate 2007).

We extend the analyses by Lee (1999) and Requate (2007) into the more general framework where μ can be greater or smaller than unity. The condition for the optimal rate to exceed the marginal environmental damage is, therefore

$$\displaystyle{ \frac{dq} {d\tau } \cdot \frac{dE} {d\tau } = \frac{\left (p^{{\prime}}\right )^{2}qe^{3}} {H^{2}n} \left (\mu -1\right )\left (\epsilon -\epsilon _{1}\right )\left (\epsilon -\epsilon _{4}\right ) < 0. }$$

(17.21)

This condition implies that (i)ε ₄ < ε < ε ₁ for μ > 1 and, conversely, (ii)ε > ε ₄ or ε < ε ₁ for μ < 1. As for Case $\left (ii\right )$, when n < n ₀ holds, Lemma 17.2 excludes the condition of ε > ε ₄.

In summary, our first main result is as follows:

Proposition 17.4

In the long-run equilibrium in a free-entry Cournot oligopoly, the optimal emission tax rate exceeds the marginal environmental damage in the following three cases: (1) For an industry with elastic emission (i.e., μ > 1 and thus ε ₄ < ε ₁ < 0), the market demand must have concavity with $\epsilon \in \left (\epsilon _{4},\epsilon _{1}\right )$ . (2) Conversely, for an industry with inelastic emission (i.e., μ < 1 and thus ε ₄ > ε ₁ > 0), (a) the demand must have concavity or convexity with $\epsilon \in \left (-\infty,\epsilon _{1}\right )$ , and the equilibrium market structure must be sufficiently concentrated (i.e., n < n ₀); or (b) the demand must not have convexity with $\epsilon \in \left (\epsilon _{1},\epsilon _{4}\right )$ and the equilibrium market structure must be sufficiently competitive (i.e., n > n ₀).

4 Excess Entry Theorem Under the Pigouvian Tax Rule

The previous section derives the optimal pollution tax rate and shows under what conditions the optimal rate exceeds the marginal environmental damage. To find the sign of the deviation term, τ − D ^′, we need to investigate the sign of ψ, which is defined as in Eq. (17.20b). It contains the terms ε, μ, κ, and n. However, exact information on the first three terms can hardly be obtained. Such informational requirements may discourage the regulator to implement the right but complicated policy rule. Recently, Requate (2007) proposed that, in Cournot models with free entry, it is a good strategy to stick to the traditional Pigouvian tax rule and encourage more competition through tough antitrust laws. This section investigates the validity of his proposal, that is, whether the joint use of the Pigouvian rule and competition policy is subject to the informational problem.

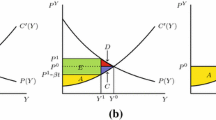
The analysis of this section relies on the seminal contributions by Mankiw and Whinston (1986) and Suzumura and Kiyono (1987). In a symmetric Cournot oligopoly, they established that the number of firms at a long-run free-entry equilibrium can be larger than the socially optimal number of firms. This is the so-called “excess entry theorem”. More specifically, reducing the number of firms from the free-entry equilibrium level leads to a welfare gain if and only if the business-stealing effect is present. In what follows, we examine the validity of the theorem under the traditional Pigouvian tax rule.

The sequence of the game is as follows. First, the antitrust authority selects the number of firms in the industry. Second, the firms make an entry decision. Third, the environmental regulator sets the emission tax equal to the marginal damage. Lastly, the firms decide output in a Cournot manner. Following Mankiw and Whinston (1986), we assume that neither regulator can control firms’ behavior directly after their entry.

In our framework, the Pigouvian tax rate is given by the marginal damage:

$$\displaystyle{ \tau = D^{{\prime}}\left (ne\left (q\right )\right ) \equiv \tau \left (n\right ). }$$

(17.22)

Under this rule, the marginal production costs become $c^{{\prime}}\left (q\right ) + D^{{\prime}}\left (ne\left (q\right )\right )e^{{\prime}}\left (q\right )$, which can be interpreted as the marginal social costs of individual production. Then the relative slope of these social marginal costs is modified into

$$\displaystyle{ \kappa _{s} \equiv 1 -\frac{c^{{\prime\prime}} + D^{{\prime}}e^{{\prime\prime}} + D^{{\prime\prime}}n\left (e^{{\prime}}\right )^{2}} {p^{{\prime}}} > 0, }$$

which constitutes one of the short-run stability conditions under the Pigouvian tax rule. The additional condition for the short-run stability is then expressed as $\epsilon < n +\kappa _{s} \equiv \bar{\epsilon }_{s}$.

We now write the short-run equilibrium condition as

$$\displaystyle{ \pi _{q}\vert _{\tau =\tau \left (n\right )} = p^{{\prime}}\left (nq\right )q + p\left (nq\right ) - c^{{\prime}}\left (q\right ) - D^{{\prime}}\left (ne\left (q\right )\right )e^{{\prime}}\left (q\right ) = 0. }$$

(17.23)

Assuming that D ^′′ = 0 is identical to the analysis in which the tax rate is exogenously given, it is, therefore, assumed that this is not the case. Totally differentiating Eq. (17.23) to obtain the comparative statics result yields

$$\displaystyle{ \frac{dq} {dn}\vert _{\tau =\tau \left (n\right )} = \frac{\epsilon -n -\delta /\mu } {\bar{\epsilon }_{s}-\epsilon } \frac{q} {n} \gtreqless 0\quad \Leftrightarrow \quad \epsilon \gtreqless n +\delta /\mu, }$$

(17.24)

where $\delta \equiv -\frac{D^{{\prime\prime}}n\left (e^{{\prime}}\right )^{2}} {p^{{\prime}}} > 0$. If the elasticity of the slope of demand, ε, lies below n + δ∕μ, then the individual output falls because of entry of a new firm, that is, the business-stealing effect prevails. Compared to the result in Eq. (17.4), we see that the cutoff value in Eq. (17.24) has the extra term, δ∕μ > 0. Therefore, we can say that for a wider range of the demand parameter ε, the Pigouvian tax rule generates the business-stealing effect. In summary, we claim the following:

Lemma 17.5

The business-stealing effect is more likely to be observed under the traditional Pigouvian tax rule than under the exogenously given tax rate.

We next evaluate the welfare effect of changing the number of firms at the free-entry, zero-profit equilibrium. From Eqs. (17.16), (17.1), and (17.2), we calculate

$$\displaystyle{ \frac{dW} {dn} = n\left (-p^{{\prime}}q + e^{{\prime}}\left (\tau -D^{{\prime}}\right )\right ) \frac{dq} {dn} + e\left (\tau -D^{{\prime}}\right ). }$$

Evaluating the above expression at the Pigouvian tax rate (17.22), we have the following relationship:

$$\displaystyle{ \frac{dW} {dn} \vert _{\tau =\tau \left (n\right )} = \left (-p^{{\prime}}nq\right ) \frac{dq} {dn}\vert _{\tau =\tau \left (n\right )}. }$$

(17.25)

Consequently, we establish our second main result:

Proposition 17.6

The excess entry theorem is more likely to hold under the traditional Pigouvian tax rule than under the exogenously given tax rate.

5 Concluding Remarks

In this paper, we identified the effects of pollution taxation and a firm’s entry in a Cournot oligopoly model. Introducing free entry and a general functional form relating output to pollution emission, we showed that the optimal emission tax rate exceeds or falls short of the marginal environmental damage to the society, depending upon the curvature of the inverse demand as well as the output elasticity of pollution emission. To implement such a complex policy rule, the regulator faces tremendous informational requirements. Therefore, as suggested by Requate (2007), it is a good strategy to stick to the traditional Pigouvian tax rule: the emission tax rate is equal to the marginal damage.

In light of informational feasibility, our policy recommendation is a joint use of the Pigouvian rule with an antitrust or competition policy that reduces the number of firms from the free-entry equilibrium level. To support this, we showed that the business-stealing effect is more likely to be observed under the Pigouvian rule than under the exogenously given tax rate. Judging whether the business-stealing effect prevails does not require much information. Hence, we established that the Pigouvian rule advocates the validity of the excess entry theorem.

Appendix

1.1 A.1 Comparative Statics

Totally differentiating the system described by Eqs. (17.1) and (17.2) yields

$$\displaystyle{ \pi _{qq}dq +\pi _{qn}dn +\pi _{q\tau }d\tau = 0,\qquad \pi _{q}dq +\pi _{n}dn +\pi _{\tau }d\tau = 0, }$$

where π _qq ≡ ∂π _q∕∂q, π _qn ≡ ∂π _q∕∂n, π _qτ ≡ ∂π _q∕∂τ, etc. and these partial derivatives are thus:

$$ \displaystyle\begin{array}{rcl} \pi _{q}& =& p^{{\prime}}nq + p - c^{{\prime}}-\tau e^{{\prime}} = p^{{\prime}}\left (n - 1\right )q,\qquad \pi _{ n} = p^{{\prime}}q^{2},\qquad \pi _{\tau } = -e, {}\\ \pi _{qq}& =& p^{{\prime\prime}}nq + \left (1 + n\right )p^{{\prime}}- c^{{\prime\prime}}-\tau e^{{\prime\prime}},\qquad \pi _{ qn} = q\left (p^{{\prime\prime}}q + p^{{\prime}}\right ),\qquad \pi _{ q\tau } = -e^{{\prime}}. {}\\ \end{array} $$

The short-run comparative static results are obtained by the first equation alone. Writing it as π _qqdq = −π _qndn −π _qτdτ yields the following results: $\frac{\partial \tilde{q}} {\partial \tau } = \frac{e^{{\prime}}} {\pi _{qq}} < 0$ and $\frac{\partial \tilde{q}} {\partial n} = -\frac{q\left (p^{{\prime\prime}}q+p^{{\prime}}\right )} {\pi _{qq}}$. From ε ≡ −Qp ^′′∕p ^′ and $\kappa \equiv 1 -\frac{c^{{\prime\prime}}+\tau e^{{\prime\prime}}} {p^{{\prime}}}$, it follows that $\pi _{qq} = \left (-p^{{\prime}}\right )\left (\epsilon -n-\kappa \right )$ and $p^{{\prime\prime}}q + p^{{\prime}} = p^{{\prime}}\left (1 -\epsilon /n\right )$, and thus upon substitution, we obtain Eq. (17.4).

The comparative statics results for the long-run equilibrium are found by writing the above system as $\left [\begin{array}{cc} \pi _{qq}&\pi _{qn}\\ \pi _{ q} & \pi _{n} \end{array} \right ]\left [\begin{array}{c} dq/d\tau \\ dn/d\tau \end{array} \right ] = \left [\begin{array}{c} -\pi _{q\tau } \\ -\pi _{\tau } \end{array} \right ]$, where $H \equiv \left \vert \begin{array}{cc} \pi _{qq}&\pi _{qn}\\ \pi _{ q} & \pi _{n} \end{array} \right \vert > 0$ is the stability condition in the long-run equilibrium. Thus, upon substitution, we have $H = p^{{\prime}}q^{2}\left (\pi _{qq} -\left (n - 1\right )\left (p^{{\prime\prime}}q + p^{{\prime}}\right )\right )$. From $\pi _{qq} = \left (-p^{{\prime}}\right )\left (\epsilon -n-\kappa \right )$ and $p^{{\prime\prime}}q + p^{{\prime}} = p^{{\prime}}\left (1 -\epsilon /n\right )$, we obtain the following relationship:

$$\displaystyle{ H = \frac{\left (p^{{\prime}}q\right )^{2}} {n} \left (n + n\kappa -\epsilon \right ) > 0\quad \Leftrightarrow \quad \epsilon < n + n\kappa. }$$

Hence, from κ > 0 and $\bar{\epsilon }\equiv n+\kappa < n + n\kappa$, it follows that the short-run stability implies the long-run stability.

We now obtain the long-run comparative static results: $\frac{dq} {d\tau } = \frac{1} {H}\left \vert \begin{array}{cc} -\pi _{q\tau }&\pi _{qn} \\ -\pi _{\tau }&\pi _{n} \end{array} \right \vert = \frac{1} {H}\left (-\pi _{q\tau }\pi _{n} +\pi _{qn}\pi _{\tau }\right ) = \frac{1} {H}q\left (qe^{{\prime}}p^{{\prime}}- e\left (p^{{\prime\prime}}q + p^{{\prime}}\right )\right )$ and $\frac{dn} {d\tau } = \frac{1} {H}\left \vert \begin{array}{cc} \pi _{qq}& -\pi _{q\tau } \\ \pi _{q} & -\pi _{\tau } \end{array} \right \vert = \frac{1} {H}\left (-\pi _{qq}\pi _{\tau } +\pi _{q\tau }\pi _{q}\right ) = \frac{1} {H}(\pi _{qq}e\ -e^{{\prime}}p^{{\prime}}\left (n - 1\right )q)$. Substituting qe ^′ = μe, $\pi _{qq} = \left (-p^{{\prime}}\right )\left (\epsilon -n-\kappa \right )$, and $p^{{\prime\prime}}q + p^{{\prime}} = p^{{\prime}}\left (1 -\epsilon /n\right )$ into these results yields the ones in Eq. (17.9).

1.2 A.2 Proof of Proposition 17.1

When μ = 1, we have $\frac{\partial \tilde{E}} {\partial n} = \frac{\kappa } {\bar{\epsilon }-\epsilon }\tilde{e} > 0$ from κ > 0 and $\bar{\epsilon }>\epsilon$. However, in the case of μ > 1, we have the sign patterns of $\frac{\partial \tilde{E}} {\partial n} \lesseqgtr 0 \Leftrightarrow \epsilon \lesseqgtr - \frac{\epsilon _{2}} {\mu -1}$. If the case of μ < 1, it follows that $\frac{\partial \tilde{E}} {\partial n} \lesseqgtr 0 \Leftrightarrow \epsilon \gtreqless - \frac{\epsilon _{2}} {\mu -1}$. Note that $\bar{\epsilon }-(- \frac{\epsilon _{2}} {\mu -1}) = \frac{\kappa \mu } {\mu -1} \gtrless 0 \Leftrightarrow \mu \gtrless 1$. If μ > 1, then $\bar{\epsilon }> - \frac{\epsilon _{2}} {\mu -1}$ is obtained. Therefore, if $\epsilon < - \frac{\epsilon _{2}} {\mu -1}$, that is, the demand is sufficiently concave, then we observe $\frac{\partial \tilde{E}} {\partial n} < 0$, that is, the entry of a firm reduces the pollution level. On the other hand, if μ < 1, then $\bar{\epsilon }< - \frac{\epsilon _{2}} {\mu -1}$ holds and thus the stability condition rules out the case of $\frac{\partial \tilde{E}} {\partial n} < 0$, that is, the entry always increases the pollution level.

1.3 A.3 Proof of Proposition 17.3

First, Suppose that μ > 1. Then we have $\bar{\epsilon }>\epsilon _{4}$. Therefore, we have the following sign pattern: $\frac{dE} {d\tau } < 0$ for $\epsilon \in \left (\epsilon _{4},\bar{\epsilon }\right )$ and $\frac{dE} {d\tau } > 0$ for $\epsilon \in \left (-\infty,\epsilon _{4}\right )$. To the contrary, suppose that μ < 1. In the case of n < n ₀, ε ₄ exceeds $\bar{\epsilon }$, and thus the stability condition implies $\frac{dE} {d\tau } < 0$. On the other hand, in the case of n > n ₀, ε ₄ falls short of $\bar{\epsilon }$. Therefore, the sign pattern is reversed from that in the case of μ > 1: $\frac{dE} {d\tau } > 0$ for $\epsilon \in \left (\epsilon _{4},\bar{\epsilon }\right )$ and $\frac{dE} {d\tau } < 0$ for $\epsilon \in \left (-\infty,\epsilon _{4}\right )$.