Elastodynamics of a Rigid-Flexible 3-RRR Mechanism with Joint Clearances

Abstract

The purpose of this paper is to analyze the elastodynamics of a rigid-flexible planar 3-RRR parallel mechanism with multiply joint clearances. In order to reduce the global system coordinates, the nature coordinate is used to model the rigid link, while the absolute nodal coordinate formulation is employed to model the flexure link. Full description of the revolute joint with clearance is given, a continuous dissipative Hertz contact model is applied to describe the contact phenomenon in the joint. Two-step Bathe integration method is utilized to solve the nonlinear system motion equations. Detailed comparisons are made among the systems under different situations. Results demonstrate that the methodology can represent the dynamic performances of the system with link flexibility and joint clearance well.

1 Introduction

Joint clearances are unavoidable due to manufacturing tolerances, assembling, wear and material deformation [1], Link flexibility also plays an important role in the dynamic performances of the mechanical system. The joint clearances and link flexibility can cause vibration and noise, decreasing the service life or even leading to failure of the mechanism [2]. Due to the increasing requirements for high precision and high speed of the mechanism, it is necessary to establish a methodology to model the multibody system with both joint clearances and link flexibility.

The subject of modeling the real joints with clearance has drawn the attentions of a large amount of researchers over the last few decades, which can be mainly divided into three categories: kinematical analysis [3, 4], dynamic analysis and experimental studies. In the area of dynamic analysis of mechanisms with joint clearances, Dubowsky and Freudenstein [5] are the pioneers. They firstly proposed a mathematical model of an elastic mechanical joint with clearance and derived the dynamical equations of motion. The most representative works in this topic is done by Ravn [6] and Flores [7–10]. They developed a continuous analysis approach for rigid multibody system with joint clearance, which is easy to integrate the contact force model into the system motion equations. This methodology allows not only to get the overall dynamic performance of the multibody system, but also to provide detailed characteristics the joint with clearance. Zhao [11] proposed a numerical approach for the modeling and prediction of wear at revolute clearance joints in flexible multibody systems by integrating the procedures of wear prediction with multibody dynamics. Realized that the revolute joint with clearance is always simplified into two parts, which cannot represent the realistic case well, Xu [12] gave a full description of the deep-groove ball bearing with clearance in a rigid planar slider-crank mechanism.

It is noticeable that, very few researchers study the mechanism with more than one degree of freedom. The 3-RRR parallel mechanism is widely used in industry applications and laboratory researches for its high moving velocity and wide range of motion [13, 14], but none of the researches has taken the joint clearances along with link flexibility into consideration in such mechanism. The main purpose of this paper is to establish a general computational methodology for analyzing the planar rigid-flexible multibody system with multiply joint clearances.

The Absolute Nodal Coordinate Formulation (ANCF) is implemented to describe the deformation of the flexible link [15]. The deformation modes of the flexure multibody system with joint clearance are associated with high frequencies, in which the explicit integration methods can be very inefficient or even fail [16]. For such a stiff system, implicit integration methods are much more efficient than explicit methods. The most popular implicit integrators are the generalized-a method, Newmark method and HHT method, but these methods may become unstable for long time simulation. To overcome this limitation, Bathe [17] proposed a two-step implicit time integration method for the large deformation system with long time durations.

This paper is organized as follows: In Sect. 2, the planar rigid and flexible beams are briefly introduced. In Sect. 3, a 3-RRR planar parallel mechanism with rigid-flexible links and multiply clearance joints is modeled. In Sect. 4, full description of the joint clearance is presented, in which the contact force model with damping is incorporated. In Sect. 5, the computational strategy for the solution of the system motion equations is described. After that, simulation results are obtained and discussed. Finally, the main conclusions are drawn.

2 Planar Rigid and Flexible Beam Element

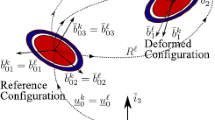
This section will present the model of rigid and flexible beams, as shown in Fig. 1.

Fig. 1

Planar beam element. a Rigid beam based on NC; b Flexible beam based on ANCF

2.1 Rigid Beam

For the rigid beam, the coordinates of the link is described using Natural Coordinates (NC) [18], see Fig. 1a. The coordinates of the link in global coordinate system are defined as

$$ \varvec{q} = \left[ {\varvec{r}_{i} ,\varvec{r}_{j} } \right]^{T} = \left[ {x_{i} ,y_{i} ,x_{j} ,y_{j} } \right]^{T} $$

(1)

There exists the following constraint equation

$$ \varPhi = \left( {x_{i} - x_{j} } \right)^{2} { + }\left( {y_{i} - y_{j} } \right)^{2} - l^{2} = 0 $$

(2)

The location of generic point along the central axis of the link is

$$ \varvec{r = }\left[ {\begin{array}{*{20}l} X \hfill \\ Y \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {x_{i} + (x_{j} - x_{i} )x/l} \hfill \\ {y_{i} + (y_{j} - y_{i} )x/l} \hfill \\ \end{array} } \right] = \varvec{S}_{r} \varvec{q} $$

(3)

where X and Y denote the position coordinates defined in the global coordinate system, x denotes the nodal coordinate along the beam central line, l denotes the element length. S _r is the shape function

$$ \varvec{S}_{r} = \left[ {\begin{array}{*{20}c} {1 - x/l} & 0 & {x/l} & 0 \\ 0 & {1 - x/l} & 0 & {x/l} \\ \end{array} } \right] $$

(4)

The mass matrix of the rigid beam can be obtained by using the principle of virtual work [18]. It is expressed as

$$ \varvec{M}_{r}^{e} { = }\rho \int\limits_{V} {\varvec{S}_{r}^{T} \varvec{S}_{r} dV} $$

(5)

in which $\rho$ is the density and V is the volume of the beam.

2.2 Flexible Beam

The planar ANCF-based deformable beam element is described by two nodes [15], as shown in Fig. 1b. The coordinates of an arbitrary point along the central axis of the beam can be defined by the third-order polynomials in the global coordinates, that is

$$ \varvec{r = }\left[ {\begin{array}{*{20}c} X \\ Y \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} } \\ {b_{0} + b_{1} x + b_{2} x^{2} + b_{3} x^{3} } \\ \end{array} } \right] = \varvec{Sq} $$

(6)

where X and Y denote the position coordinates defined in the global coordinate system, x denotes the nodal coordinate along the beam central line. S is the shape function. The absolute nodal coordinate q for node i and j can be expressed as

$$ \varvec{q = }\left[ {r_{i1} ,r_{i2} ,\frac{{\partial r_{i1} }}{\partial x},\frac{{\partial r_{i2} }}{\partial x},r_{j1} ,r_{j2} ,\frac{{\partial r_{j1} }}{\partial x},\frac{{\partial r_{j2} }}{\partial x}} \right]^{T} $$

(7)

The vector $\varvec{r}_{m} = \left[ {r_{m1} ,r_{m2} } \right]^{T}$(m = i, j) indicates the position coordinates defined in the global coordinate system, the angle $\theta_{m}$ indicates the beam cross section orientation, which can be expressed by the vector $\frac{{\partial \varvec{r}_{m} }}{\partial x} = \left[ {\frac{{\partial r_{m1} }}{\partial x},\frac{{\partial r_{m2} }}{\partial x}} \right]^{T} .$ According to the conventional finite element method, the element shape function can be obtained by

$$ \varvec{S} = \left[ {S_{1} \varvec{I}_{2} S_{2} \varvec{I}_{2} S_{3} \varvec{I}_{2} S_{4} \varvec{I}_{2} } \right] $$

(8)

where $\varvec{I}_{2}$ is the identity matrix of size two and $S_{1} = 1 - 3\xi^{2} + 2\xi^{3} ,$ $S_{2} = l\left( {\xi - 2\xi^{2} + \xi^{3} } \right),\,S_{3} = 3\xi^{2} - 2\xi^{3} ,\,S_{4} = l\left( { - \xi^{2} + \xi^{3} } \right),$ in which $\xi = x/l$.

By using the Newton-Euler formulation [15], the element equations of motion are as follows

$$ \varvec{M}^{e} {\ddot{\varvec{q}}} + \varvec{F}^{e} = \varvec{Q}^{e} $$

(9)

where $\varvec{Q}^{e}$ represents the element generalized force vector, $\varvec{M}^{e}$ denotes the element constant mass matrix

$$ \varvec{M}^{e} = \int\limits_{V} {\rho \varvec{S}^{T} \varvec{S}dV} $$

(10)

$\rho$ is density and V is the volume. F ^e denotes the element elastic force vector, which is expressed as [15]

$$ \begin{aligned} \varvec{F}^{e} & = \left( {\frac{{\partial U_{l} }}{{\partial \varvec{q}}}} \right)^{T} + \left( {\frac{{\partial U_{t} }}{{\partial \varvec{q}}}} \right)^{T} = \int\limits_{0}^{l} {EA} \varepsilon \varvec{S}_{l} \varvec{q}dx + \int\limits_{0}^{l} {EI} \varvec{S}^{{{\prime \prime }T}} \varvec{S}^{{\prime \prime }} \varvec{q}dx \\ & = \left( {\int\limits_{0}^{l} {EA} \varepsilon \varvec{S}_{l} dx} \right)\varvec{q} + \left( {\int\limits_{0}^{l} {EI} \varvec{S}^{{{\prime \prime }T}} \varvec{S}^{{\prime \prime }} dx} \right)\varvec{q} = {\mathbf{K}}_{l} \varvec{q} + {\mathbf{K}}_{t} \varvec{q} \\ \end{aligned} $$

(11)

where

$$ \begin{aligned} \varvec{K}_{l} & = \int\limits_{0}^{l} {EA\varepsilon \varvec{S}_{l} dx} = EA\int\limits_{0}^{l} {\frac{1}{2}\left( {\varvec{q}^{T} \varvec{S}_{l} \varvec{q} - 1} \right)\varvec{S}_{l} dx} \\ & = \frac{1}{2}EA\int\limits_{0}^{l} {\varvec{S}_{l} \varvec{qq}^{T} \varvec{S}_{l} dx} - \frac{1}{2}EA\int\limits_{0}^{l} {\varvec{S}_{l} dx} = \varvec{K}_{l1} + \varvec{K}_{l2} \\ \end{aligned} $$

(12)

To improve the computation efficiency, Garcia-Vallejo [19] firstly proposed an invariant matrix method to calculate the elastic force and the tangent matrix of the elastic force. Based on the following matrix transformation

$$ \left( {\varvec{S}_{l} \varvec{qq}^{T} \varvec{S}_{l} } \right)_{ij} = \varvec{q}^{T} \left( {\varvec{S}_{l} } \right)_{,i} \left( {\varvec{S}_{l} } \right)_{j,} \varvec{q} $$

(13)

The element of $\varvec{K}_{l1}$ can be expressed as

$$ \left( {\varvec{K}_{l1} } \right)_{ij} = \varvec{q}^{T} \left( {\frac{1}{2}EA\int\limits_{0}^{l} {\left( {\varvec{S}_{l} } \right)_{,i} \left( {\varvec{S}_{l} } \right)_{j,} dx} } \right)\varvec{q} = \varvec{q}^{T} \varvec{C}_{l1}^{ij} \varvec{q} $$

(14)

where $\varvec{C}_{l1}^{ij}$ is called the constant matrix of $\varvec{K}_{l1}$.

When solving the motion equations of the multibody system in an interactive way, that is, in an implicit way, the derivation of the elastic force respect to generalized coordinates will be used. It can be expressed as [19]

$$ \left( {\frac{{\partial \varvec{F}^{\varvec{e}} }}{{\partial \varvec{q}}}} \right)_{ij} = \frac{{\partial \left( {\varvec{F}^{\varvec{e}} } \right)_{i} }}{{\partial \varvec{q}_{j} }} = \left( {K_{t} + K_{l2} + K_{l1} } \right)_{ij} + \sum\limits_{k}^{8} {\sum\limits_{s}^{8} {\varvec{q}_{s} \left( {\varvec{C}_{l1}^{ik} + \left( {\varvec{C}_{l1}^{ik} } \right)^{T} } \right)_{sj} \varvec{q}_{k} } } $$

(15)

which will be the most time consuming part in simulation.

3 Modeling of the 3-RRR Mechanism

This section will describe the configuration and motion equations of a planar 3-RRR parallel mechanism. The mechanism is a symmetry structure which is composed by the fixed platform A ₁ A ₂ A ₃, the moving platform C ₁ C ₂ C ₃, three driving links A _i B _i (i = 1–3) and three passive links B _i C _i . Joints A ₁, A ₂ and A ₃ are actuators, the backlash of the motor and reducer are not considered in the analysis. Joint B ₁, B ₂, B ₃ and C ₁, C ₂, C ₃ are revolute joints with clearance, as is shown in Fig. 2.

Fig. 2

Geometry and global coordinates of the 3-RRR mechanism. a Geometry structure; b Global coordinates

The global coordinate system XOY is fixed at the center of the fixed platform. All the driving links are treated as rigid, and all the passive links are treated as flexible. Each rigid link is described by one NC beam element, while each flexible link is described by one ANCF beam element. The combination use of these two coordinates can share the same coordinates and lower the global coordinates of the system. Particularly, the moving platform is treated as rigid, and described by the reference point coordinates [x _o, y _o , θ _o ]. Thus there are totally 27 generalized coordinates in the system. 24 coordinates to describe the flexible links and 3 coordinates to describe the moving platform, as labeled in the Fig. 2b.

3.1 Without Joint Clearance

Let l ₁ and l ₂ denote the length of active link AB and passive link BC, while let l ₃ and l ₄ denote the radius of the circumscribed circle of the moving and fixed platform. The constraint equations introduced by the rigid links and revolute joints are expressed as, take the first chain A ₁ B ₁ C ₁ as an example,

$$ \varvec{\varPhi}_{{\varvec{q},1}} { = }\left[ {\begin{array}{*{20}c} {(q_{1} - x_{A1} )^{2} + (q_{2} - y_{A1} )^{2} - l_{1}^{2} } \\ {x_{o} + l_{3} \cos (\theta + 7\pi /6) - q_{5} } \\ {y_{o} + l_{3} \sin (\theta + 7\pi /6) - q_{6} } \\ \end{array} } \right] = \varvec{0} $$

(16)

In the simulation, the expected motion of the moving platform is given, the input angles can be easily obtained by the inverse kinematics of the ideal rigid mechanism. The goal is to calculate the real motions of the moving platform considering link flexibility and joint clearance. The dynamic equations of the system are needed.

Based on the ANCF, the assembly of the elements can be carried out by the conventional finite element method. The element nodal can be easily transformed into the flexible multibody system generalized coordinates. Without considering the damping of the system, the Newton-Euler equations for the rigid-flexible multibody system in Cartesian coordinates can be written as

$$ \varvec{M}{\ddot{\varvec{q}}} +\varvec{\varPhi}_{{\varvec{q}}}^{T}\varvec{\lambda}+ \varvec{F}_{e} = \varvec{F} $$

(17)

where M is the system mass matrix, λ is the Lagrange multiplier, F _e denotes the system elastic force vector, F is the external force vector.

3.2 With Joint Clearances

When considering the joint clearances, the constraints in the clearance joints are lost. Moreover, in the simulation, the inputs are given, so the position of joint B in driving link can be easily obtained, there is no need to form the constraint equations. The motion equations of the system with joint clearances are written as

$$ \varvec{M}{\ddot{\varvec{q}}} + \varvec{F}_{e} = \varvec{F}_{d} + \varvec{F}_{c} $$

(18)

where F _d is the driving force vector, F _c is the contact force vector which is introduced by the clearance joints. The key procedure is to describe the contact forces, which will be presented in the following section.

4 Modeling of the Clearance Joint

4.1 Geometry Description

In order to bring the contact forces of the clearance joints into the system motion equations, it is necessary to develop the joint clearance model. Figure 3 shows a typical revolute clearance joint.

Fig. 3

Geometry of the revolute joint with clearance

The center of bearing and journal are marked as P _i and P _j , the eccentricity vector which connects P _i and P _j is calculated by

$$ \varvec{e} = \varvec{r}_{j}^{P} - \varvec{r}_{i}^{P} $$

(19)

The unit vector of the eccentricity vector can be written as

$$ \varvec{n} = \varvec{e}/e $$

(20)

in which e is the magnitude of eccentricity vector, $e = \sqrt {\varvec{e}^{T} \varvec{e}} .$ The clearance size is

$$ \delta = e - c $$

(21)

where c is the radial clearance c = R _i − R _j . Negative of δ means that there is no contact between the journal and the bearing. Thus the detection of the instant of contact is when the sign of penetration changes between the two discrete moments in time, and such accurate moment can be found by using the Newton-Raphson method.

The contact points are denoted as Q _i and Q _j , their global coordinates and velocities are evaluated as

$$ \left\{ {\begin{array}{*{20}c} {\varvec{r}_{k}^{Q} = \varvec{r}_{k}^{P} + R_{k} \varvec{n}} \\ {\dot{\varvec{r}}_{k}^{Q} = \dot{\varvec{r}}_{k}^{P} + R_{k} \dot{\varvec{n}}} \\ \end{array} } \right. $$

(22)

where k = i, j. The relative velocity is projected onto the plane of collision and onto the normal plane of collision, obtaining a relative tangential velocity $v_{n}$ and a relative normal velocity $v_{t}$.

$$ \left\{ {\begin{array}{*{20}c} {v_{n} = (\dot{\varvec{r}}_{j}^{Q} - \dot{\varvec{r}}_{i}^{Q} )^{T} \varvec{n}} \\ {v_{t} = (\dot{\varvec{r}}_{j}^{Q} - \dot{\varvec{r}}_{i}^{Q} )^{T} \varvec{t}} \\ \end{array} } \right. $$

(23)

4.2 Contact Force Models

Knowing the penetration depth and relative velocity, the normal and tangential forces F _n and F _t are obtained. Lankarani-Nikravesh contact force model is largely used for mechanical contacts owning to its simplicity and easiness in implementation in a computational program, and also because this model accounts for the energy dissipation during the impact process [20]. The expression of the model is

$$ F_{n} = K\delta^{n} \left( {1 + \frac{{3(1 - c_{e}^{2} )}}{4}\frac{{\dot{\delta }}}{{\dot{\delta }^{( - )} }}} \right) $$

(24)

where the generalized stiffness K can be evaluated by

$$ K = \frac{4}{{3(\delta_{i} + \delta_{j} )}}\left( {\frac{{R_{i} R_{j} }}{{R_{i} - R_{j} }}} \right)^{{\frac{1}{2}}} $$

(25)

in which $\delta_{k} = \left( {1 - \nu_{k}^{2} } \right)/E_{k} \,(k = i,j)$.$\nu_{i} ,E_{i} ,R_{i}$ and $\nu_{j} ,E_{j} ,R_{j}$ are the Poisson’s ratio, the Yong’s modulus and radii of the journal and bearing respectively. $\dot{\delta }$ is the relative penetration velocity and $\dot{\delta }^{( - )}$ is the initial impact velocity. $c_{e}$ is the restitution coefficient, the exponent n is set to 1.5 for metallic surfaces.

The modified Coulomb’s friction law presented by Ambrósio [21] is used here, which is given by

$$ F_{t} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ { - c_{f} \frac{{v_{t} - v_{0} }}{{v_{1} - v_{0} }}F_{n} } \hfill \\ { - c_{f} F_{n} } \hfill \\ \end{array} \quad \begin{array}{*{20}c} {if\,v_{t} \le v_{0} } \\ {if\,v_{0} \le v_{t} \le v_{1} } \\ {if\,v_{t} \ge v_{1} } \\ \end{array} } \right. $$

(26)

where c _f is the coefficient of friction, v ₀ and v ₁ is the given tolerance for the velocity. Using the NC and ANCF method, there is no need to transform these forces into the center of the mass of each body.

5 Solving the Equations of Motion

The process of the integration of the Differential Algebraic Equations (DAEs) of motion for a flexible multibody system with joint clearance is different from that of ideal rigid body system. The high frequency responses are stimulated both by the continuous high frequency contact forces and by the finite element discretization. The Bathe integration method [17] is a composite scheme which calculates the unknown displacements, velocity and accelerations by dividing the time step h into two equal sub-steps h/2. For the first sub-step, the well-known trapezoidal rule is used, while for the second sub-step, the three-point Euler backward formula is used. The Newton interaction approach is used to solve the nonlinear equations in each sub-step. The interested readers can refer to Ref. [17] for details. The whole computational scheme can be illustrated in a flowchart shown in Fig. 4.

Fig. 4

Flowchart of the computational scheme

6 Results and Discussions

The geometric parameters of the 3-RRR mechanism are listed in Table 1, the material of all the parts are Aluminum. In the simulation, the preset trajectory of the moving platform is a circle with radius 0.1 m

Table 1 Geometry parameters of the 3-RRR mechanism

$$ \left\{ {\begin{array}{*{20}l} {q_{25} = 0.1\cos (2\pi t)\,{\text{m}}} \hfill \\ {q_{26} = 0.1\sin (2\pi t)\,{\text{m}}} \hfill \\ {q_{27} = 0\,{\text{rad}}} \hfill \\ \end{array} } \right. $$

(27)

At the start of the simulation, t = 0 s, the journal and bearing centers are defined coincident. The initial positions and velocities necessary to start the dynamic analysis are obtained from the kinematic simulation of the 3-RRR mechanism without considering link flexibility and joint clearance.

Four simulations are carried out to make comparisons, as are shown in Table 2. That is, Case 1: Rigid passive links without joint clearance; Case 2: Flexible passive links without joint clearance; Case 3: Rigid passive links with joint clearance; Case 4: Flexible passive links with joint clearance. In the simulations, the joint clearance size is taken to be 0.02 mm, which is a normal clearance size in a typical bearing with nominal dimensions. For flexible beams, the Young’s module of the passive links is set to be 7 GPa for Aluminum. Figures 5, 6, 7, 8 and 9 illustrates the simulation results of the system which are taken for two full cycles after the system steady running.

Table 2 Parameters for different cases

Fig. 5

Displacement errors of the moving platform along axis-x. a Case 2; b Case 3; c Case 4

Fig. 6

Moving accelerations of the moving platform along axis-x. a Case 2; b Case 3; c Case 4

Fig. 7

Contact forces of clearance joint B1. a Case 2; b Case 3; c Case 4

Fig. 8

Penetration depths of clearance joint B1. a Case 3; b Case 4

Fig. 9

Poincare maps for different cases. a Case 2; b Case 3; c Case 4

Figure 5 shows the displacement errors of the moving platform along axis-x direction in different cases. In Fig. 5a for Case 2, the positioning error of the platform along axis-x is around ±0.2 mm, these values are caused by the deformation of the passive link, and they are influenced by the stiffness of the flexible links. In Fig. 5b for Case 3, the errors are around ±0.2 mm, and these values will be influenced by the clearance size of the joints. In Fig. 5c for Case 4, it has the largest deviation and can be seen as the composition of Case 2 and Case 3. It indicates that both the flexure of the link and the joint clearance are the important influence factors of positioning accuracy.

In Fig. 6, the accelerations of the moving platform along axis-x for different cases are plotted, which show that these accelerations are very different with their ideal values. In Fig. 6a for Case 2, the acceleration is slightly vibrated when the link flexibility is taken into consideration. In Fig. 6b for system with joint clearances, the acceleration curve presents high frequency vibrations, which is caused by the impact of journal and bearing in clearance joints, and theses vibrations will make the system unstable and difficult to control. Moreover, the vibration amplitude get larger and the frequency get higher when both link flexibility and joint clearances are taken into consideration, which can be observed in Fig. 6c.

The same phenomena can also be observed in the curves of the contact forces represented in Fig. 7. It is certain that the high peaks of acceleration curve and the contact force curve occur at the same time. The enlarged contact forces will decrease the service life of the components, or even lead to failure of the mechanism.

The penetration depths of the clearance joint are plotted in Fig. 8. The positive value means the journal and bearing contact with each other, while the passive value means they separate with each other. It shows that for most of the time, the joint components keep contact.

The Poincare map is often used to highlight the nonlinear behavior of systems. The acceleration-x and velocity-x of moving stage are chosen to plot the Poincare map. In Fig. 9a, periodic motion is presented in flexible system. Figure 9b, c shows a non-periodic motion of the moving stage, since the curve does not repeat from cycle to cycle. It indicates that the collision between the joint components will cause chaotic motion of the multibody system.

7 Conclusions

In this paper, the dynamic analysis of a planar 3-RRR parallel mechanism is presented. Both the joint and the link flexibility are taken into consideration. The rigid driving links are molded using NC while the flexure passive links are molded using ANCF, in order to lower the global system coordinates. The continuous dissipative contact force model is employed to describe the contact phenomenon in joint clearance. Comparisons are made between the systems with and without joint clearances.

Simulation results show that the positioning accuracy of the moving platform are apparently affected by both the joint clearance and link flexibility. When the joint clearances are considered, the system performs high frequency responses, and the enlarged contact forces can decrease the service life of the mechanism. It also shows that the joint components keep contact with each other for most of the time. On the other side, the mechanism is influenced by the link flexibility in a smoother way. The 3-RRR mechanism with the flexible links is a periodical system, but it becomes non-periodical when the joint clearances are taken into consideration, as the joint clearance and link flexibility interact with each other in a nonlinear way. The future work shall focus on the control of such a complex system.