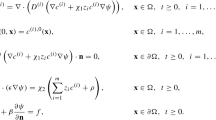Finite Element Modeling of Biomolecular Systems in Ionic Solution

Abstract

An accurate finite element method is introduced to solve the two most commonly used continuum models in computational biophysics: Poisson–Boltzmann (PB) equation and Poisson–Nernst–Planck (PNP) equations. They describe equilibrium and non-equilibrium (with diffusion existed) properties of ionic liquid, respectively. Both models involve two domains (solvent and solute) with distributed singular permanent charges inside biomolecules (solute domain) and a dielectric jump at the interface between solvent and solute. A stable regularization scheme is described to remove the singular component of the electrostatic potential induced by the permanent charges inside biomolecules, and regular, well-posed PB/PNP equations are formulated. The interface conditions for electric potential are also explicitly enforced to be satisfied. An inexact-Newton method is used to solve the nonlinear elliptic PB equation and the coupled steady-state PNP equations; while an Adams–Bashforth–Crank–Nicolson method is devised for time integration for the unsteady electrodiffusion. The numerical methods are shown to be accurate and stable by various tests of real biomolecular electrostatic and diffusion problems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

All biomolecules in cell are solvated in ionic solution which supplies an essential environment to molecular activities. These activities are generally involved in multi-scale processes. Explicit molecular dynamics (MD) or Monte Carlo (MC) simulations that includes all the solute and solvent particles are known to be limited in size and time scales of simulated systems. To overcome the shortage, implicit simulation approaches were developed to significantly reduce the degree of freedom of the system by treating the solvent as a continuum medium. The continuum models focus on the average properties of solvent through a solution of partial differential equation(s), and is therefore computationally more efficient. Furthermore, continuum model can conveniently include different types of physical interactions/processes and bridge different temporal-spatial scales, e.g. by coupling electrostatics with diffusion convection, or/and elasticity, the Navier–Stokes equations and so on. These features have made the continuum model very appealing and useful. The Poisson–Boltzmann equation (PBE) and the Poisson–Nernst–Planck equations (PNPEs) are the two most studied and established continuum models in computational molecular biology. The former is usually used for equilibrium simulation of molecular electrostatic solvation effects, and the later for non-equilibrium simulation of ionic diffusion processes interacting with biomolecular systems.

Efficiency and accuracy are two central issues in applying the PBE/PNPEs to biophysical modeling. First, a typical macromolecule may consist of a few to hundreds of thousand atoms (point charges in the PBE), which significantly challenges the current computer memory and speed. Secondly, in order to incorporate the PB electrostatics (on the fly) in a typical MD, MC, or Brownian dynamics (BD) simulation that could involve tens of millions of steps to get converged statistical results, a single solution of the PBE has to be completed within no more than a few tenths of a second on a modern workstation to meet the total wall-clock time constraint. Based on this estimation, the current solvers are still, e.g., about one to two orders of magnitude slower [56]. Thirdly, a similar demand of efficiency lies in virtual high throughput screening in drug discovery from many candidate structures and different conformations. This screening is usually based on free energy calculations (e.g., binding affinity) to an accuracy of a few kcal/mol. However, these free energies normally result from the cancellation of energies of several orders of magnitude larger terms such as electrostatic energies. This demand poses another numerical challenge for electrostatic computations with the PBE.

Finite element method (FEM) is an efficient and powerful numerical method for solution of nonlinear elliptic equation(s). Adaptive mesh refinement is a mature strategy developed in FEM to control the accuracy and efficiency of the solution. While a complicated situation in both PB and PNP models is that the solvated biomolecular systems are usually modeled by dielectrically distinct regions with singular charges distributed in the molecular region. Specific strategies are needed in FEM framework to accurately treat the singular charges and the dielectric jump at molecular boundary.

In this chapter, the two models and related methodologies will be briefly reviewed. We apply a stable regularization scheme to remove the singular component of the electrostatic potential induced by the permanent charges inside biomolecules, and formulate a regular, well-posed PB equation. The interface conditions can be explicitly enforced in the solution through using boundary conforming meshes in the FEM simulations. Then, a corresponding FEM algorithm is given. Similar regularization scheme and interface condition treatment are applied to PNP system. An inexact-Newton method is used to solve the nonlinear elliptic PBE or the coupled PNP equations for steady problems; while an Adams–Bashforth–Crank–Nicolson method is devised for time integration for the unsteady electrodiffusion. The numerical methods are shown to be accurate and stable by various test problems, and are applicable to real large-scale biophysical electrostatics and electrodiffusion problems.

A mesh is required in finite element method. Molecular mesh generation is a very technical and challenging task for practical FEM simulation of biomolecular systems. The topic is briefly discussed in Sect. 4. Interested readers are refereed to chapter “Surface Triangular Mesh and Volume Tetrahedral Mesh Generations for Biomolecular Modeling” on biomolecular meshing of this book.

The rest of the chapter is organized as follows. The PB and PNP models and their FEM treatments are introduced in Sects. 2 and 3, respectively. Each section contains a brief history of the equation(s) and related methodologies, descriptions of the regularization scheme, the numerical strategies and properties for the equation(s). Numerical examples for real biomolecular electrostatics and diffusion problems are given in Sect. 5. The chapter ends with a summary in Sect. 6.

2 PB Model

Poisson–Boltzmann (PB) theory has been a well-established model in a broad range of scientific research areas. In eletrochemistry, it is known as Gouy–Chapman (GC) theory [15, 37]; in solution chemistry, it is known as Debye–Hückel theory [24]; in colloid chemistry, it is known as the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory [25, 79]; and in biophysics, it is known as PB theory [23, 47]. The Poisson–Boltzmann equation (PBE) represents a typical implicit solvent model, and provides a simplified continuum description of the discrete particle (e.g., water, ion, and/or protein molecule) distributions in solution. In particular, the PBE describes the electrostatic interaction and ionic density distributions of a solvated system at the equilibrium state. Since the first application of the PBE in a biomolecular system [80], a large amount of literatures and many solution techniques have been produced in this area and directed to studies of diverse biological processes.

A number of review papers can be found that focus on the physical fundamentals [66, 71], brief history [30], the methodology and applications in biomolecular modeling [3, 6], the methodological developments in both PB and the related generalized Born models [51]. A more recent review [58] focused on the numerical aspects of PB methodology covering several major numerical methods. This chapter will present detailed techniques in use of finite element approach.

Solvated biomolecular systems are usually modeled by dielectrically distinct regions with singular charges distributed in the molecular region. Systems without singular charges or dielectric discontinuities are usually found in simplified models with planar or cylindrical boundary geometries in electrochemistry and biopolymer science, and can be regarded as a special case of the systems in this investigation. Figure 1 schematically illustrates a solvated biomolecular system occupying a domain Ω with a smooth boundary ∂Ω. The solute (molecule) region is represented by Ω _m and the solvent region by Ω _s . The dielectric interface Γ is defined by the molecular surface, which can be defined as the solvent-excluded surface, solvent-accessible surface, Gaussian surface [81], or some other appropriately defined solvent-molecular interface. n is the unit normal vector at Γ, pointing from Ω _m to Ω _s . The nonlinear Poisson–Boltzmann equation in Ω reads

$$ -\nabla\cdot(\varepsilon\nabla u) - \lambda\sum_{j=1}^{K} c_j q_j e^{-\beta q_j u} = \sum _{i=1}^{N} q_i \delta(x-x_i),\quad x \in\varOmega, $$

(1)

where ε is a spatial-dependent dielectric coefficient, the characteristic function λ=0 in Ω _m (impenetrable to ions) and 1 in Ω _s , c _j is the bulk density of mobile ion species j with charge q _j , β=1/kT, k is the Boltzmann constant, T is the absolute temperature, q _i is the singular charge located at x _i within solute region. For symmetric 1:1 salt (the bulk densities of cation and anion need to be equal, C ₊=C ₋=C, to satisfy the neutrality condition), to simplify the presentation we use

$$ -\nabla\cdot(\varepsilon\nabla u) + \lambda\kappa^2\sinh( u) = \rho^f,\quad x \in\varOmega, $$

(2)

and

$$ -\nabla\cdot(\varepsilon\nabla u) + \lambda\kappa^2 u = \rho^f,\quad x \in\varOmega, $$

(3)

for the linearized Poisson–Boltzmann equation in case of weak electrostatic potential, where κ ²=2βe ² C absorbing the related parameters (e is the elementary charge), and u→βeu and ρ ^f→βeρ ^f are the scaled electrostatic potential and singular charge distribution, respectively. Note that κ=0 in Ω _m because the mobile ions only present in the solvent region Ω _s . An additional region called the Stern layer might be present in some Poisson–Boltzmann models. This Stern layer is part of the solvent but is not penetrable for the mobile ions so κ=0 there. The transition from the low-dielectric solute region to the high-dielectric solvent region is usually modeled to be abrupt, which gives rise to a dielectric interface Γ. This interface is usually identified as the molecular surface. There are two conditions on Γ needed to be satisfied from the dielectric theory:

$$ u_m = u_s,\qquad \varepsilon_m \frac{\partial u_m}{\partial n} = \varepsilon_s \frac{\partial u_s}{\partial n},\quad x \in\varGamma. $$

(4)

These conditions are explicitly used in boundary integral equations based approaches, but may not be exactly satisfied in other approaches such as the traditional finite difference methods, or finite element methods without special interface treatment. An approximated Dirichlet boundary condition is normally imposed on ∂Ω. The dielectric permittivity is usually assumed to be a piecewise constant with ε=ε _m ε ₀ in Ω _m and ε=ε _s ε ₀ in Ω _s , where ε ₀ is the dielectric constant of vacuum. This is indispensable to the regularization schemes to be introduced later. The internal dielectric interface separating the molecules and solvent regions is defined to be the molecular surface, but other definitions of dielectric interface might apply also. Typical values of ε _m and ε _s are 2 and 80, respectively. The singular charge distribution within biomolecules, discontinuous dielectric constant, exponential nonlinearity at strong potential, and the highly irregular molecular surface constitute the most prominent features of the Poisson–Boltzmann equation.

Fig. 1

2-D schematic illustration of the computational domain modeling a solvated biomolecular system. The biomolecular (solute) region is Ω _m with dielectric constant ε _m and the aqueous solution (solvent) is domain Ω _s with dielectric constant ε _s . The molecular surface is $\varGamma= \bar{\varOmega}_{s} \cap\bar{\varOmega}_{m}$. The circles with plus or minus sign inside represent the diffusive charged particles which move only in Ω _s . The singular charges inside molecules are signified by plus or minus sign in Ω _m . The active reaction center Γ _a ⊂Γ is also highlighted in red where a different boundary condition may be applied in the PNP model

2.1 Regularization Schemes of the Poisson–Boltzmann Equation

The presence of the singular charge distribution in the PBE indicates that its solution is not continuous and does not belong to H ¹(Ω) [16], which directly challenges the solution theory of standard finite difference methods, finite volume methods or finite element methods for the PBE. In many finite difference or finite element solvers of the Poisson–Boltzmann equation, the singular charges are distributed onto the grid points near the singular charges by using polynomial interpolations. These approximations work well for electrostatic solvation energy ΔG _ele calculations. The solvation energy is defined as

$$ \varDelta G_{ele} = G_{sys} - G_{ref}, $$

(5)

where G _sys is the electrostatic free energy of the biomolecular system in the solvated state and the G _ref is the electrostatic free energy of the system assuming it is in space of uniform dielectric constant ε _m and without mobile ions. By using a finite difference method, finite volume method or a finite element method, the PBE is solved twice with corresponding parameters for G _sys and G _ref , respectively. Linear interpolation or higher order polynomial interpolation are usually used in these numerical methods for approximating the singular charge distribution. Although the potentials from these two calculations might suffer from large error near the singular charges, it is believed that this error would cancel in computing the ΔG _ele via Eq. (5) if the same mesh and charge interpolation are used in these two solutions of the PBE. This treatment is widely applied in computational chemistry and is somehow validated by many numerical experiments [28, 29, 35, 36, 61, 74, 86, 89]. However, the quality of the potential near the molecular surface is actually critically dependent on the specific treatment of the singular charges [32]. If the gradient of the electrostatic potential is needed, such as force calculation on atoms in the MD simulation, or electric field calculation at the boundary in the diffusion-reaction simulation by PNP equations studied in next section, more rigorous treatments of the singular charges are needed.

The regularization schemes aim at removing the singular component of the potential from the equation such that the remaining component has higher regularity and thus is solvable by using general numerical methods. The straightforward decomposition [36] considers the singular Coulomb potential u ^s of all singular charges

$$ -\varepsilon_m \varDelta u^s = \rho^f\quad\mbox{in }\varOmega $$

(6)

The corresponding regular potential component u ^r is then found by subtracting Eq. (6) from Eq. (2) to be

$$ -\nabla\cdot\bigl(\varepsilon\nabla u^r\bigr) + \lambda\kappa^2 \sinh\bigl(u^r + u^s\bigr) = 0 \quad\mbox{in } \varOmega, \\ $$

(7)

The singular component ϕ ^s should also be subtracted from the interface conditions (4), generating the following interface conditions for Eq. (8):

$$ u^r_s - u^r_m = 0,\qquad \varepsilon_s \frac{\partial u^r_s}{\partial n} - \varepsilon_m \frac {\partial u^r_m}{\partial n} = (\varepsilon_m - \varepsilon_s) \frac{\partial u^s}{\partial n},\quad x \in \varGamma. $$

(8)

This approach is applied to solve the Poisson–Boltzmann equation by Zhou et al. [89] to completely remove the self-energy so that the equation need not to be solved twice for computing the electrostatic energy. Another slightly different decomposition but leading to quite different numerical strategies using a similar equation as (6) but with varying dielectric were proposed in a hybrid finite difference/boundary element method [12] and a hybrid finite element/boundary element method [57, 87] for solving the nonlinear PBE. These two methodologies take the advantage of boundary element method to conveniently handle the singular point charges and also leads to stable and accurate numerical solution. The removal of the singular potential makes it possible for the first time to analyze the Poisson–Boltzmann equation rigorously in Sobolev spaces [16]. However, it is found that the first scheme suffers a numerical instability that will lead to a substantial error in FEM numerical solution of the full potential [45]. This is because that the total potential ϕ is relatively weak while the singular potential ϕ ^s and the regular potential are both strong. In particular, the regular potential in Ω _s is larger than the total potential ϕ by ε _s /ε _m ≈40 times. Consequently, when the numerical solution of ϕ ^h is added to the analytical solution of ϕ ^s to get the total potential, the relative numerical error will be amplified by about 40 times. For this reason we will apply a stable decomposition in this FEM study. This decomposition is first introduced by Chern et al. for solving the PBE with an interface method [19], and is implemented later in finite different method [32] and finite element method [58, 59].

We define the singular component u ^s to be the restriction on Ω _m of the solution of

$$ -\varepsilon_m \varDelta\phi^s(x) = \rho^f(x),\quad x \in\mathbb{R}^3, $$

(9)

and the harmonic component u ^h(x) to be the solution of a Laplace equation:

$$ \everymath{\displaystyle}\begin{array}{rcl} -\varDelta u^h(x) & =& 0,\quad x \in \varOmega_m, \\[4pt] u^h(x) & =& - u^s(x),\quad x \in\varGamma. \end{array} $$

(10)

It is seen that u ^s(x) can be given analytically by the sum of Coulomb potentials. This u ^s(x) is then used to compute the boundary condition for u ^h(x), the latter is to be solved numerically from Eq. (10), for which we use a finite element method in this study. Subtracting these two components from Eq. (2) we get the governing equation for the regular component u ^r(x):

$$ -\nabla\cdot \bigl( \varepsilon\nabla u^r(x) \bigr) + \lambda \kappa^2 \sinh\bigl(u^r(x)\bigr) = 0,\quad x\in\varOmega, $$

(11)

and the interface conditions

$$ u^r_s - u^r_m = 0,\qquad \varepsilon_s \frac{\partial u^r_s}{\partial n} - \varepsilon_m \frac{\partial u^r_m}{\partial n} = \varepsilon_m \frac{\partial(u^s + u^h)}{\partial n},\quad x \in\varGamma. $$

(12)

It is worth noting that there is no decomposition of the potential in the solvent region, thus ϕ(x)=ϕ ^r(x) in Ω _s . There is no decomposition in Ω _s in the second scheme, and thus the numerical solution of ϕ ^r in Ω _s does not suffer the instability [45].

2.2 Finite Element Methods

The adaptive finite element method developed by Holst et al. in [4, 16, 41, 44] tackled some of the numerical issues of the Poisson–Boltzmann equation. This method uses the piecewise-linear finite element and a well-defined error indicator for driving the local mesh refinement [16, 41]. The nonlinear Poisson–Boltzmann equation is solved using Newton-AMG iterations [42, 43, 46]. After discretization by either finite difference or finite element techniques, the inexact Newton-AMG approach results in linear memory and computational complexity solution of the nonlinear algebraic equations produced by finite difference, finite volume, or finite element discretization methods. In the case of adaptivity, non-standard variations of multigrid solvers must be used to preserve both linear memory and linear computational complexity; see [2, 45] for a detailed discussion.

Instead of using the Newton-AMG iterations for the nonlinear PBE, the finite element method of Shestakov et. al [75] uses Newton–Krylov iterations for the nonlinearity. The applications of this finite element method have not been extended from colloid systems with rather simple geometry to biomolecular systems with complicated dielectric interfaces. A mortar finite element discretization was also introduced recently by Xie et al. for numerical solutions of the PBE, which explicitly computed dielectric interface so that the interface conditions are satisfied naturally [82].

Though the new regularization scheme [19] and inclusion of molecular surface have been practically used for PB solution for real biomolecule [32, 58, 59], the analysis of a convergent adaptive finite element method was only made recently [45]. With this scheme, the accuracy of the potential near the molecular surface is substantially improved, becoming comparable to that of the interface Poisson–Boltzmann solvers [45, 86]. The finite element method advanced by Cortis et al. [21] makes use of the similar Galerkin formulation but lack a treatment of the nonlinear Poisson–Boltzmann equation. Moreover, there is no enforcement of the interface conditions on the molecular surface so the results of this method agree well with those of DelPhi. A recently proposed discontinuous Galerkin method for elliptic interface problems [38] might also be customized for solving the Poisson–Boltzmann equation provided a good description of the molecular surface.

Now we describe the FEM computational algorithm with the new regularization scheme for 3D molecular simulations. To consider the finite element solution of the PBE (11) (Eq. (10) is a simpler and special case), we define the solution space

$$ H := \bigl\{ u \in H_0^1(\varOmega) \bigr\} $$

(13)

and its finite dimensional subspace

$$ S := \bigl\{ u \in P_1(\varOmega) \bigr\}, $$

(14)

where P ₁ is the space consisting of piecewise linear tetrahedral finite elements. Functions in the space

satisfy the Dirichlet boundary condition on the exterior boundary ∂Ω. We assume that the finite elements are regular and quasi-uniform. The weak formulation of the problem now is:

Find u=∈S such that

$$ \bigl\langle F(u), v\bigr\rangle = 0 \quad \forall v \in S. $$

(15)

Here the nonlinear mapping F:H↦H ^∗ and 〈⋅,⋅〉 is the standard duality paring between the dual space H ^∗ and H. Specifically, the nonlinear weak form 〈F(u),v〉 is defined to be

$$ \bigl\langle F(u),v \bigr\rangle = ( \varepsilon\nabla u, \nabla v ) + \bigl( \lambda\kappa^2\sinh u, v\bigr) + \langle p, v\rangle_{\varGamma}, $$

(16)

where

$$p = \varepsilon_m \frac{\partial(u^s + u^h)}{\partial n} $$

is the jump in electric displacement defined in Eq. (12), 〈⋅,⋅〉 _Γ denotes the L ₂ inner product defined on the interface Γ, and the L ₂ scalar inner product over the domain Ω is denoted by (⋅,⋅). It is worth noting that the interface integral 〈⋅,⋅〉 _Γ is conveniently and directly evaluated in FEM by using a boundary conforming mesh (Γ is a collection of some faces of the tetrahedral mesh). This type of meshes, as generated by TMSmesh [17] are used in all of our FEM simulations. To solve the nonlinear problem (15) we employ the damped inexact-Newton method [41] which necessitates the Gâteaux derivative DF(u) defined by the bilinear form

(17)

With these well-defined operators the complete algorithm can be given as follows:

Algorithm 1

• Choose the initial approximation u, the nonlinear tolerance ε, the residual r in approximately solving the linear system, and the damping factor c.

• Do until |〈F(u),v〉|<ε

  • 1. Solve the correction w from 〈DF(u)w,v〉=−〈F(u),v〉+r.

  • 2. u⇐u+cw.

A constant damping parameter c=1 is chosen in this study. We note here that the step in the algorithm to solve the correction w leads to a linear system to be solved. Denoting the solution u(x) by its expansion in the test function space, i.e., u(x)=∑ _j a _j v _j (x), the weak form (16) essentially produces two matrices: a stiff matrix A associated with the product ε∇u⋅∇v and the mass matrix M associated with the product λκ ² w(coshu)v. The solution of w(x) (correction of u(x) at each Newton iteration step) from the bilinear form (17) is therefore equivalent to the solution of a linear algebraic system

$$ (A + M) \mathbf{a} = -\mathbf{f}, $$

(18)

where unknown vector a={a _j } is the expansion coefficients of w(x), and vector f is 〈F(u),v〉 for all given test functions v. The system of equations implied by Eq. (16) and the linearization Eq. (17) are then solved by a FEM software package like FETK [40] or PHG [85].

3 PNP Model

Under non-equilibrium condition(s), net ionic fluxes are produced in solution, to which case the PB model does not apply. The diffusive fluxes and the relevant electrostatic interactions in ionic solution are described as electrodiffusion. When small charged molecules are approximated as diffusive ions, the electrodiffusion framework can also be adopted to study their transportation and/or diffusion-reaction processes. Electrodiffusion is a rate-limiting step in numerous biological processes, such as ligand-enzyme binding, protein-protein diffusive encounter. An example is neurotransmission within synapses between adjacent nerve cells [9]. The kinetic properties of these processes are mostly governed by the multi-scale electrodiffusion of charged molecules in aqueous solution with various ionic concentrations, molecular charges and complicated solvent-solute interface geometries. The continuum model is more straightforward and efficient to determine the kinetics than discrete particle simulations. Furthermore, continuum electrodiffusion models can be readily modified to incorporate other types of physical interactions, such as varying molecular conformation or flow convection, by coupling with elasticity equation or the Navier–Stokes equations. These appealing features have made the continuum electrodiffusion models very useful not only for the quantitative analysis of the biological ion channels [27, 33], substrate-enzyme diffusion-reactions [54, 76, 77], and cellular electrophysiology [62, 63], but also for investigating ion-separation membranes in non-biological applications [72] and the transport of electrons and holes in semiconductors [49].

The Poisson–Nernst–Planck equations are commonly used to describe the electrodiffusion of mobile ions and charged substrates, all modeled as diffusive particles with vanishing size, in solvated biomolecular systems. Here the electrostatic potential is induced by the mobile ions, charged substrates, and the fixed charges carried by biomolecules. The system setup is similar to the PB case (see Fig. 1). The diffusive particles (ions and substrates) are distributed in Ω _s . Charged substrates might react with the biomolecules on a part of the molecular surface Γ _a , for which a suitable boundary condition for the diffusion equations of the particles is needed. On the non-reactive molecular surface Γ∖Γ _a appropriate boundary condition is needed to model the vanishing macroscopic flux. In a typical solvated biomolecular system there are multiple species of ions and substrates; each species may have its own boundary condition on molecular surface. We assume that the exterior boundary ∂Ω is connected to a particle reservoir maintained at constant concentrations, and hence a Dirichlet boundary condition for particle concentration can be applied. Compared to the pure diffusion [78], or the Nernst–Planck equation (also called Smoluchowski equation) [77] which characterizes diffusional drift by a given fixed potential, the Poisson–Nernst–Planck model is able to generate a self-consistent, full electrostatic potential and the non-equilibrium densities of ions/substrates [57, 87]. Similar to PBE, the PNP equations for describing the electrodiffusion around the biomolecules modeled at atomistic level also have the two features: presence of singular permanent charges and highly irregular surfaces not penetrable to diffusive particles.

Mathematical analysis of the Poisson–Nernst–Planck equations have been developed long after the introduction of the equation by Nernst and Planck [65, 67]. The existence and stability for the solutions of the steady PNP equations are established by Jerome [48] in studying the steady Van Roostbroeck model for electron flows in semiconductors, via a delicate construction of a Schauder fixed point mapping. Although this mapping is not shown to be contractive, an alternative pseudo-monotone mapping is constructed which guarantees the convergence of the Galerkin approximations of the equations. It noted that the permanent charges in this study are located in the same domain as that in the diffusion process, and are assumed to be in L ^∞ which ensures the H ¹∩L ^∞ regularity of the electrostatic potential and the charge densities. Existence and long time behavior of the unsteady PNP equations were studied in [10]. The analysis and computation of the PNP equations can be further simplified by reducing the 3-D system to 1-D models. Singular perturbation methods and asymptotic analysis can then be applied to study the solution properties of these simplified 1-D equations. For example, 1-D steady PNP equations for modeling physiological channels are investigated in [8, 53] in the absence of permanent charges by using various singular perturbation theories. The effects of the permanent charges are considered in [1, 26], where the permanent charge density is vanishing in the reservoirs at the two ends of the channel and is constant at the center of the channel. The piecewise constant form of the permanent charges implies that the electrostatic potential and ionic densities are still differentiable. The reduction of the dimensionality greatly simplifies the mathematical analysis of the electrodiffusion systems, and the results provide useful guide lines for the analysis of the corresponding fully 3-D systems at some limit cases. As a trade-off they are generally unable to reproduce the diffusion and reaction processes that critically depend on the geometry of the system and complicated boundary conditions.

In contrast to the limited amount of work on the mathematical analysis of the PNP equations for biophysical applications, numerical computations with the PNP and the PNP-like systems have been widely conducted by computational physicists and biophysicists. Finite difference methods are particularly popular due to the simplicity in their implementation, and have been applied to a large extent to 1-D or 3-D ion conduction characteristics of biological ion channels or other transmembrane pores [11, 14, 20, 27, 52]. The lattice nature of the finite difference method makes it difficult to model the highly irregular surface of the ion channel or the active sites of the enzymes. This difficulty can be readily overcome by using finite element methods, which have been well developed for simulating semiconductor devices [31, 50] and were recently introduced to simulate the electrodiffusion with realistic molecular structures [76, 77]. In many of the PNP solvers developed thus far such as [11, 14, 52] the electrostatic part is solved by using well-established finite difference or finite element Poisson–Boltzmann solvers [5, 13, 34]. These PB solvers use polynomial interpolations to approximate the singular charges. As described in last section, the treatments do not supply an electric field of high fidelity at molecular boundary to the Nernst–Planck equation. A similar decomposition scheme to that used in the PB equation will be adopted for the PNP equations.

The objective of this section is to present the regularized PNP equations with singular permanent charges, and to develop finite element methods for them with realistic biomolecular structures. A symmetric transformation of PNP will be mentioned. We will show that the electrostatic potential that couples the Nernst–Planck equation is indeed the regular component. Therefore the framework established in [48] for general L ₂ permanent charges could be utilized to show the well-posedness of the regularized PNP system. An inexact-Newton method will be used to solve the nonlinear differential equations. Since the Poisson–Nernst–Planck equations can be derived from the first variations of a free energy functional, the Newton-like methods can produce a convergent solution that corresponds to the minimization of the free energy.

3.1 PNP Equations

The continuum PNP equations can be derived via different routes. They can be obtained from the microscopic model of Langevin trajectories in the limit of large damping and absence of correlations of different ionic trajectories [64, 73], or from the variations of the free energy functional that includes the electrostatic free energy and the ideal component of the chemical potential [33]. The former gives the PNP model a sound theoretical basis while the latter provides a flexible framework to include more physical interactions, most prominently the correlations among particles with finite sizes, into the continuum model. In this chapter, we are concentrated in the development of numerical techniques for the standard nonlinear PNP equations, i.e., we treat all diffusive particles, including mobile ions and charged substrates, as particles with vanishing size. This is a reasonable assumption in case that solution is dilute and the characteristic dimension of space for diffusion is much larger than the particle size.

We obtain the PNP equations by coupling the Nernst–Planck equation

$$ \frac{\partial\rho_i}{\partial t} = \nabla\cdot D_i ( \nabla \rho_i + \beta q_i \rho_i \nabla\phi ),\quad x \in \varOmega_s, 1 \le i \le n, $$

(19)

and the electrostatic Poisson equation with interface $\varGamma= \bar{\varOmega}_{s} \cap\bar{\varOmega}_{m}$:

$$ -\nabla\cdot ( \varepsilon\nabla\phi ) - \lambda\sum _i q_i \rho_i = \rho^f,\quad x \in\varOmega, $$

(20)

where ρ _i (x,t) is the concentration of the i-th species particles carrying charge q _i , D _i (x) is the spatial-dependent diffusion coefficient, and ϕ is the electrostatic potential. The interface conditions for PE is similar to that for PBE. If the mobile charge density ρ _i (x) in Eq. (20) is assumed to follow the Boltzmann distribution, the equation converts to the nonlinear Poisson–Boltzmann equation. The readers are referred to [58] for discussions on the derivation and relations of these equations. The time-dependence of the electrostatic potential is seen from the appearance of time-dependent particle concentrations in Eq. (20).

Because the singular charge ρ ^f(x) poses the same numerical issue to the Poisson equation as to the PBE, a similar potential decomposition as described in the PB model (the second scheme) is adopted here to achieve a stable FEM solution for the Poisson equation. The singular and harmonic components follow the equation and boundary condition as in (9) and (10). The governing equation for the regular component ϕ ^r(x):

$$ -\nabla\cdot \bigl( \varepsilon\nabla\phi^r(x,t) \bigr) - \lambda \sum_i q_i \rho_i(x,t) = 0,\quad r\in\varOmega, $$

(21)

and the interface conditions

$$ \phi^r_s - \phi^r_m = 0,\qquad \varepsilon_s \frac{\partial\phi^r_s}{\partial n} - \varepsilon_m \frac{\partial\phi^r_m}{\partial n} = \varepsilon_m \frac{\partial(\phi^s + \phi^h)}{\partial n},\quad x \in \varGamma. $$

(22)

It is worth noting that there is no decomposition of the potential in the solvent region, thus ϕ(x)=ϕ ^r(x) in Ω _s . Hence the final regularized Poisson–Nernst–Planck equations consist of the regularized Poisson equation (21) and

$$ \frac{\partial\rho_i(x)}{\partial t} = \nabla\cdot D_i(x) \bigl( \nabla \rho_i(x) + \beta q_i \rho_i(x) \nabla \phi^r(x) \bigr),\quad x \in\varOmega_s. $$

(23)

To simplify the presentation we use ϕ to denote the electrostatic potential coupled with the Nernst–Planck equation, but keep in mind that the singular and harmonic components are to be added to get the full potential inside molecules.

The singular and harmonic components only need to be solved one time a priori the coupled solutions of the regularized PNP equations. Indeed, it is the regular potential in solvent region that couples the Nernst–Planck equation and the regular Poisson equation. The singular and harmonic components serve only for providing a fixed interface conditions for solving the regular component, which varies with the ionic concentrations.

We apply the following boundary conditions for the PNP equations. The approximate Debye law is used to compute the value of ϕ ^r=ϕ on the exterior boundary ∂Ω:

$$\phi(x) = \sum_{j} \frac{q_j e^{-|x - x_j|/\lambda_d}}{\varepsilon_s |x -x_j|}, $$

where λ _d being the Debye length computed from the bulk concentrations of all species of charged particles. For all species of particles ρ _i on ∂Ω is given by its bulk concentration. A zero macroscopic normal flux

$$D_i ( \nabla\rho_i + \beta q_i \rho_i \nabla\phi ) \cdot n = 0 $$

is prescribed on the non-reactive molecular surface Γ∖Γ _a with outer normal vector n for all species. For particles that react with the molecule on the surface Γ _a we apply the homogeneous Dirichlet boundary condition, i.e., ρ _i =0. This models the fact that the diffusion time scale is much larger than the reactive time scale, and that in the solution there is a sufficient large number of solute molecules which are able to hydrolyze all substrates that migrate to the reaction centers of solute molecules. The non-zero flux on the reactive surface makes the particle concentrations described by PNP differ fundamentally from the Boltzmann distribution, which can be reproduced if the macroscopic flux is vanishing everywhere [72].

3.2 Finite Element Algorithms

The numerical methods are focused at some major aspects of the PNP model: the nonlinearity of the system due to the drift term; the coupling between Poisson and NP equations for both steady and unsteady diffusions.

3.2.1 Steady-State Diffusion

We first consider the finite element solution of the steady state PNP equations (21), (23). To this end we define the solution space

$$ H := \bigl\{ (\phi, \rho) \in H_0^1(\varOmega) \times H_{0_1}^1(\varOmega_s) \times \cdots\times H_{0_n}^1(\varOmega_s) \bigr\} $$

(24)

and its finite dimensional subspace

$$ S := \bigl\{ (\phi, \rho) \in P_1(\varOmega) \times \bigl( P_1(\varOmega_s) \bigr)^n \bigr\}, $$

(25)

where the vector $\rho= \{ \rho_{j} \}_{j=1}^{n}$, and P ₁ is the space consisting of piecewise linear tetrahedral finite elements. Functions in the space

satisfy the Dirichlet boundary condition on the exterior boundary ∂Ω and the essential or Dirichlet boundary condition on the molecular surface Γ if there is one. We assume that the finite elements are regular and quasi-uniform. The weak formulation of the problem now is:

Find u=(ϕ,ρ)∈S such that

$$ \bigl\langle F(u), v\bigr\rangle = 0,\quad \forall v=(\psi, \eta) \in S. $$

(26)

Here the nonlinear mapping F:H↦H ^∗ and 〈⋅,⋅〉 is the standard duality paring between the dual space H ^∗ and H. Specifically, the nonlinear weak form 〈F(u),v〉 is defined to be

$$ \bigl\langle F(u),v \bigr\rangle = \left [ \matrix{ ( \varepsilon\nabla\phi, \nabla\psi) - (\lambda\sum_{i} q_i \rho_i, \psi) + \langle p, \psi\rangle_{\varGamma} \cr ( D_i \nabla\rho_i, \nabla\eta_i) + (D_i \beta q_i \rho_i \nabla \phi, \nabla\eta_i) } \right ], $$

(27)

where

$$p = \varepsilon_m \frac{\partial(\phi^s + \phi^h)}{\partial n} $$

is the jump in electric displacement defined in Eq. (22), 〈⋅,⋅〉 _Γ denotes the L ₂ inner product defined on the interface Γ, and the L ₂ scalar inner product over the domain Ω or Ω _s is denoted by (⋅,⋅). To solve the nonlinear problem (26) we employ the damped inexact-Newton method [41] which necessitates the Gâteaux derivative DF(u) defined by the bilinear form

(28)

where w=(φ,ζ). With these well-defined operators the complete algorithm can be given as follows:

Algorithm 2

• Choose the initial approximation u=(ϕ,ρ), the nonlinear tolerance ε, the residual r in approximately solving the linear system, and the damping factor c.

• Do until |〈F(u),v〉|<ε

  • 1. Solve the correction w from 〈DF(u)w,v〉=−〈F(u),v〉+r.

  • 2. u⇐u+cw.

A constant damping parameter c=1 is chosen in this study, with which the convergence is reached in less than 20 steps in all simulations.

It is noted here that the above algorithm solves the steady-state PNP equations as a whole system. A commonly used approach is also to solve the NPEs and PE separately. That means iteration is needed between NPEs and PE until the solutions are self-consistently converged. A standard Gummel iteration proceeds as following: given any initial solution function ϕ ⁰ (or ρ ⁰), solve the NP equations Eq. (23) in steady state (or the PE (21)) to get a solution ρ ⁰ (ϕ ⁰), then solve the PE (NPEs) with these ρ ⁰ (ϕ ⁰) to get an updated solution ϕ ¹ (ρ ¹), and with ϕ ¹ (ρ ¹) get an updated solution of NPEs ρ ² (ϕ ² of the PE), continue this iteration until approaching a converged solution (ρ, ϕ) of the PE and the NPEs. It is found that the standard Gummel iteration converges slowly, and may diverge in some circumstances. A γ-iteration procedure for the iteration between the NP and PE as used in our former PNP solution [55, 57] appears helpful in assisting convergence of solution for the PNP system. When obtained a solution (ρ _n , ϕ _n ) of the PNP equations at the n-th step during the iterations between solutions of the PE and NPEs, we modify them for use in next iteration step by a γ-relaxation

(29)

(30)

It is found that usually under-relaxation, i.e. γ<1 is helpful or necessary for large-sized PNP system, while over-relaxation does not help the convergence.

3.2.2 Unsteady-State Diffusion

For time-dependent problems the elliptic equation for the electrostatic potential and parabolic equations for the particle concentrations are solved sequentially. The weak form of the unsteady Nernst–Planck equation for i-th species of particle is

(31)

Various schemes can be used for the time discretization of this equation. For example, Prohl and Schmuck proposed convergent schemes based on different types of fixed-point mappings [68]. Due to the nonlinearity of the equation, the application of these and high order methods such as a third-order Runge–Kutta method or its combination with the exponential time differencing (ETD) method [22, 60] demands solving the electrostatic potential multiple times in each step of time evolution. To reduce the computational cost and maintain the stability, we adopt the Crank–Nicolson method for the time discretization. This gives rise to the following semi-discrete equation at t _n+1/2 for n>0:

(32)

for a constant time increment Δt. Here the electrostatic potential ϕ ^n+1/2 is solved from the Poisson equation (21) with particle concentrations at t _n+1/2 computed with an Adams–Bashforth scheme

$$ -\nabla\cdot \bigl( \varepsilon\nabla\phi^{n+1/2} \bigr) - \lambda\sum _i q_i \frac{3\rho_i^n - \rho_i^{n-1}}{2} = 0. $$

(33)

We then use the inexact-Newton approach presented above to solve $\rho_{i}^{n+1}$ from the equation

$$ \bigl\langle F\bigl(\rho_i^{n+1/2}\bigr),v\bigr\rangle = 0. $$

(34)

To this end we need the Gâteaux derivative $DF(\rho_{i}^{n+1})$, which is now defined by

(35)

where $w \in H^{1}_{0_{i}}$. The solutions of (34)–(35) follow Algorithm 2 with residual r=0. Since Eq. (32) is linear in $\rho_{i}^{n+1}$, only one solution of w is needed for an arbitrary initial guess of $\rho_{i}^{n+1}$ at each time step. We note that a similar Adams–Bashforth–Crank–Nicolson (ABCN) method was used for solving the Navier–Stokes equations and ensuring divergence-free velocity field [69, 84]. The extrapolation of source term at t _n , t _n−1 in Eq. (33) is similar to the construction of the pressure Poisson equation at t _n+1/2 in those studies.

3.2.3 A Symmetric Transform of the Electro-Diffusion Equations

We here introduce a commonly used transformation to the NP equations, which might be useful in future PNP-like simulations in biomolecular systems. It is known that by introducing the Slotboom variables

$$ \bar{D}_i = D_i e^{-\beta q_i \phi},\qquad \bar{\rho}_i = \rho_i e^{\beta q_i \phi}, $$

(36)

the Nernst–Planck equation can be transformed to be

$$ \frac{\partial (\bar{\rho}_i e^{-\beta q_i \phi} )}{\partial t} = \nabla\cdot ( \bar{D}\nabla \bar{\rho}). $$

(37)

These transformations, frequently used in solving the PNP equations for semiconductor device simulations [7, 49], hence give rise to a symmetric, uniformly elliptic operator in case of a fixed potential. The application of transformations (36) to the electrostatic Poisson equation (21) will lead to

$$ -\nabla\cdot(\varepsilon\nabla\phi) - \lambda\sum_{i} q_i \bar{\rho}_i e^{-\beta q_i \phi} = 0. $$

(38)

While the Eq. (38) appears identical to the nonlinear Poisson–Boltzmann equation, the actual particle concentrations, nevertheless, do not follow the Boltzmann distribution if there is a non-zero macroscopic flux inside the domain or on the boundary.

We also consider the finite element solution of transformed PNP equations (37), (38). For which the solution $u=(\phi,\bar{\rho})$ contains the transformed particle concentrations and nonlinear weak form 〈F(u),v〉 is given by

$$ \bigl\langle F(u),v \bigr\rangle = \left [ \matrix{ ( \varepsilon\nabla\phi, \nabla\psi) - (\lambda\sum_{i} q_i \bar{\rho}_i e^{-\beta q_i \phi}, \psi) + \langle p, \psi\rangle_{\varGamma} \cr\noalign{\vspace*{2pt}} ( \bar{D}_i \nabla \bar{\rho}_i, \nabla \bar{\eta}_i) } \right ], $$

(39)

where $v = (\psi, \bar{\eta})$. Accordingly, the bilinear form now is

(40)

where $w = (\varphi, {\bar{\zeta}})$. The complete algorithm for solving the transformed PNP equations is the same as Algorithm 2 but with 〈F(u),v〉 and 〈DF(u)w,v〉 defined by (39) and (40), respectively. It is worth noting that the operator DF(u)w defining the linearized equation for solving correction variable w is not symmetric regardless of the transformation due to the nonlinearity of the PNP model.

It is worth noting that the Slotboom variables are associated with the weighted inner product in many finite element approximations of semiconductor NP equations [31], for which exponential fitting techniques are usually used to obtain numerical solutions free of non-physical spurious oscillations. Although the solutions in our numerical experiments and biophysical applications presented below do not show significant non-physical oscillations, these methods can be adopted if needed. Our previous work [59] analyzed the condition number of the transformed NP equations (37) and shew that the Slotboom variables (36) can lead to quick growth of the condition number either due to large molecular permanent charge(s) or due to large difference in potential near molecular surface. However, the partial charge carried by any atom in real biomolecule is generally smaller than 2 folds of the elementary charge. Besides, solving the non-linear equation (38), instead of the linear form (21), at each step results in improved solution for the potential, especially when the density solutions of NPEs from last step deviate largely from the correct ones during the iteration. This can actually make the solution of the PNP equations converged within less iteration steps for real protein systems. The numerical properties of the Slotboom transformation or similar transform in other system [55] and its application to solution of nonlinear coupled systems need further systematic exploration. As an illustration of the usage of FEM, we shall still use the primitive formulation in this book.

3.3 PB Model as a Special Case of PNP Model

Physically, the equilibrium state is a special case of non-equilibrium state when no flux existed for any ionic species. This implies that the PB results can be obtained from the PNP system. The mathematical procedure corresponds to a relaxation of the total energy of the solvated solute-ions system.

To this end, we can numerically solve the PNPEs (either steady state or non-steady state, but non-steady state needs finally reach steady state) using the similar boundary conditions as in the usual solution of the PBE for ϕ, such as ϕ=0 or the Debye–Huckel approximation, at the outer boundary ∂Ω, and using the ionic bulk densities as boundary conditions for ρ _i . In addition, we use a reflective condition for each ion species in the molecular interface Γ (no Γ _a for PB calculation) to enforce zero-flux across the interface

$$J(r)_i = 0,\quad r \in\varGamma. $$

Then, the solution leads to the PB results. The reason is as following: We know that the steady state PNP system has only one solution [55], and we also know that the solution of zero-flux-everywhere J _i =0 (equilibrium) is a solution of the PNP system (see Eq. (19)) satisfying the interface condition, which is corresponding to the special case of the PB model. The equilibrium distribution with zero-flux condition

$$J_i=D_i(r) \bigl(\nabla\rho_i(r,t) + \beta\rho_i(r,t) q_i\nabla\phi(r) \bigr) =0 $$

can be seen equivalent to the Boltzmann distribution condition

$$\rho_i \sim e^{-\beta q_i \phi}. $$

Therefore, the PNP solution obtained from above procedure with zero-flux conditions at Γ must satisfy the zero-flux condition everywhere. This indicates that the solution of PNP is exactly the solution of the PBE. The equivalence is numerically proven true in our previous work [57], where it was shown that PBE and PNPE have essentially the same results despite a small numerical error. This fact leads to an indirect approach to solve the PB model, which sometimes shows indispensable advantage to treat certain difficult modified PB models [55].

4 Finite Element Implementation and Mesh Generation

As described above, FEM is convenient to treat the nonlinearity and complex geometries. When qualified mesh generation is available, FEMs can achieve good performance in the accuracy and memory demands.

The numerical implementation of Algorithm 1 for solving Eq. (15) for PBE, and of Algorithm 2 for solving Eq. (26), Eq. (34) and the Poisson equation (33) for the PNPEs are carried out using FETK, an expandable collection of the adaptive finite element method (AFEM) software libraries [40]. Standard linear finite element spaces and Galerkin approximation are adopted in these solutions. Recently we also improved the algorithm stability and developed a parallel solver for these equations by using the parallel AFEM software package PHG [85]. The work will be reported [83].

A volumeric mesh is prerequisite to FEM calculations. How to stably, efficiently generate a molecular mesh with correct representation of the irregular and complex molecular boundary is a challenging task in the area of mathematical continuum modeling of biomolecular systems. A mesh generation tool chain described in our former work [57] only works for not big biomolecular systems. We recently developed a new technique and software TMSmesh [17] for molecular surface meshing for general larger systems. And based on this, a tool chain can be setup for volume mesh generation. Interested readers are referred to chapter “Surface Triangular Mesh and Volume Tetrahedral Mesh Generations for Biomolecular Modeling” on molecular mesh generation of the book. It is worth noting that for PNP system, the Poisson equation and the NP equations are solved in different domains, and usually only one file of the mesh in the entire Ω and conforming to Γ is necessary for input to the code. One way to tackle this issue as in [59] is that the mesh of $\bar{\varOmega}_{s}$ is extracted by a subprogram embedded in the solver when solving the NP equations. Another way is to solve the NP equations in the entire domain Ω, but with special numerical treatments in domain Ω _m [83].

Combined with our new mesh generation tool TMSmesh [17], the FEM solver can serve as a standalone, complete computational tool for modeling protein/DNA systems in ionic solution.

5 Numerical Experiments and Biophysical Applications

Because PB results can be generated from the more general PNP model, and the main numerical properties of the PB solution are similar to that of the PNP solution due to similar FEM schemes applied to treat the singular charges and interface conditions, in this section we will mainly focus on numerical experiments and applications of the PNP model.

5.1 Steady-State Diffusion: Numerical Accuracy

Due to the intrinsic nonlinearity of the equation, the analytical solutions for the steady-state PNP equations are not available in general, even for the simplest problems such as the electrodiffusion in the spherical annulus exterior to a charged sphere. Here we choose two examples to examine the accuracy of our algorithm. The first example is to solve the Nernst–Planck system for the concentration of a single species at a given potential ϕ(r)=Q/(ε _s r) in a spherical annulus:

$$ \everymath{\displaystyle}\begin{array}{c} -\frac{1}{r^2} \frac{d}{dr} \biggl( r^2 D \biggl(\frac{d \rho}{dr} - \beta\rho q \frac{Q}{\varepsilon_s r^2} \biggr) \biggr) = 0, \quad r_1 < r < r_2 \\[10pt] \rho(r_1) = 0,\qquad \rho(r_2) = \rho_0, \end{array} $$

(41)

where ρ ₀ is the bulk concentration. Note here we are applying a reactive boundary condition on the whole sphere r=r ₁. The analytical solution for Eq. (41) is

$$ \rho(r) = \rho_0 \frac{e^{-\beta w(r)} - e^{-\beta w(r_1)}}{e^{-\beta w(r_2)} - e^{-\beta w(r_1)}}, \quad\mbox{where } w(r) = \frac{q Q}{\varepsilon_s r}. $$

(42)

The reactive rate constant k _r is then computed from the flux J(r) on the reactive surface via

$$ -k_r \equiv\frac{\int_{S_A} J(r)\, ds(r)}{\rho_0} = \frac{4 \pi r_1^2 J(r_1) }{\rho_0} = 4 \pi D w(r_1) r_1 \frac{-e^{-\beta w(r_1)}}{e^{-\beta w(r_2)} - e^{-\beta w(r_1)}} $$

(43)

where S _A is the reactive surface. In this case we choose r ₁=1, r ₂=40, ε _s =78ε ₀, ρ ₀=50 mM, $D = 78000 \mbox{ \AA /$\mu$s}$, q=−1, Q=1, and thus the exact k _r =2.5315×10¹¹ M⁻¹ min⁻¹. Table 1 lists the relative L ₂ errors of the computed particle concentration, the asymptotic order of error reduction and the reaction rate constants. These results demonstrate that our finite element method is convergent for this problem, with an asymptotic rate of convergence close to 2 as anticipated for a linear finite element method. It is also noticed that the errors in the computed reactive rate constant are large for all the mesh sizes considered. This is related to the very large gradient of concentration close the reactive surface, as seen in Fig. 2 where the exact and computed concentration profiles are plotted. Physically, this large gradient is induced by the electrostatic attraction of the negatively charged particles to the positively charged sphere. In this study we use finite element meshes refined toward the molecular surface to improve the local numerical resolution. Other higher order methods can also be introduced to this problem to resolve this large gradient and improve the numerical accuracy.

Fig. 2

The exact and computed concentration profiles for the Nernst–Planck equation in the spherical annulus 1<r<40 for a given potential. The x-axis is truncated at r=10 in the illustration. h _max =3.277

Table 1 Accuracy of the numerical solutions for Eq. (41)

The second example is to solve the full steady-state PNP equations for two species of particles, one carries charge −1 and the other has charge +1, in the same spherical annulus as in the last example. We prescribe the flux J(r)=0 for both species on the unit sphere, and the particle concentrations on the exterior boundary are set to be the respective bulk concentrations. The macroscopic flux of either species of particles is therefore zero everywhere in the domain, and thus the PNP model shall produce the nonlinear PBE and the particle concentrations shall follow the Boltzmann distribution. This criterion is used to examine the numerical solutions of the PNP equations. We would note that there is no analytical solution of the potential available for the nonlinear PBE. Rather, we will compare the computed concentration profiles of the PNP equations and those predicted by using the Boltzmann distribution and the computed electrostatic potential. In particular, let the numerical solutions of the potential and the particle concentration be ϕ and ρ, and the exact solutions of them be $\hat{\phi}$ and $\hat{\rho}$, respectively. Let the particle concentration computed from the solved potential ϕ be $\tilde{\rho}$, then the error we are measuring is $\rho- \tilde{\rho}$. It follows that for any Sobolev norm ∥⋅∥ we have

(44)

where the constant C is independent of the numerical methods. This estimate suggests that the error we are measuring has the same rate of convergence as the error of solutions of the PNP equations. Table 2 shows that the rate with respect to L ₂ norm is about 1, which is close to the one predicted for the linear elliptic interface problems in [18]. Figure 3 plots the computed particle concentration and that predicted by the Boltzmann distribution. The flattening of the profile close to r=1 indicates the vanishing concentration due to the electrostatic repulsion and the vanishing macroscopic flux as prescribed by the boundary condition.

Fig. 3

Computed concentration profiles and the Boltzmann distribution for particles with q=1. h _max =3.277

Table 2 L ₂ errors between the computed particle concentrations and those predicted by the Boltzmann distribution

5.2 Accuracy for Solving the Unsteady-State Diffusion

To examine the accuracy of the time integration method we design a problem that has the essential features of the PNP and admits an analytical solution:

(45)

(46)

This equation is solved in the spherical annulus 1≤r≤4. The analytical solutions for ϕ and ρ are prescribed to be

(47)

(48)

These two analytical solutions determine the functions f(r), g(r) and the Dirichlet boundary conditions for both equations. A very fine mesh with 40859 unknowns is used to ensure that the error due to the time discretization is dominant in the numerical approximation. The equations are integrated to t=200 with various time increments Δt and fixed parameter δ=0.01. The relative L ₂ errors are collected in Table 3, which features a convergence of approximately second-order for both variables. This agrees with the convergence of the ABCN scheme applied for solving the Navier–Stokes equations [69]. It is worth noting that here we are using large time increments in time integration; the convergence properties we observed in this study agree with the theoretical analysis [39] which proves that the ABCN for time-dependent Navier–Stokes equations is almost unconditionally stable.

Table 3 Numerical error and asymptotic order of convergence for time integration

5.3 Biophysical Applications: Diffusion-Reaction Study of AChE-ACh System

Finally we apply the regularized PNP solver to compute the reaction rate constant of neurotransmitter acetylcholine (ACh) at the reaction center of the enzyme acetylcholinesterase (AChE). The electrodiffusion reaction for the same system has been studied by using the Smoluchowski equation [77], in which the electric field is fixed and approximated by a PB solution. This approximation agrees with the underlying assumption of the well-known Debye–Hückel limiting law (DHL) describing the ionic screening effect to reaction rate constant. The DHL for AChE-ACh system is [70]:

$$k_{\mathrm{on}} = \bigl(k_{\mathrm{on}}^0 - k_{\mathrm{on}}^H \bigr)10^{-1.18|z_Ez_I|\sqrt{I}}+ k_{\mathrm{on}}^H, $$

where k _on, $k_{\mathrm{on}}^{0}$, and $k_{\mathrm {on}}^{H}$ are second-order association rate constants at the specified ionic strength I, zero ionic strength, and infinite ionic strength, respectively. z _E and z _I are the charges of the enzyme and substrate involved in the interaction. With the same assumption, Song et al.’s numerical results recover the DHL. The more complete PNP model also takes into account the charged substrate influence to the electric field around the enzyme, therefore leads to improved rate prediction. Here, we will show by using a more sophisticated PNP model the reaction rate coefficient obviously depends not only on the ionic strength, but also on the substrate concentration itself [54, 57, 87]. We treat the ACh molecules as particles with +1 charge. The computation domain is chosen to be a ball with a radius 400 Å centered at the geometric center of the AChE molecule. We consider two species of background “spectator” ions (non-reactive), one is cation with +1 charge and the other is anion with −1 charge. The boundary conditions for these two species of particles are therefore J _i (r)=0 on the whole surface of AChE. The reaction center of the AChE is signified in Fig. 4 in red where ρ _i =0 is set for ACh as the reactive boundary conditions, and on the rest surface the J _i (r)=0 is prescribed. Suppose that C ₊ and C ₋ are the bulk concentrations of cation and anion respectively, and that C _subs is the bulk concentration of substrate ACh. These bulk concentrations are used as the outer boundary conditions of the diffusion domain in solving the NP equations. Therefore, to make a closer connection with physiology, it is reasonable to consider a neutrality condition of the bulk solution in this work as C ₊+C _subs−C ₋=0. The same mesh as that in [87] is used in this study. The electrostatic potential on the surface of AChE is shown in Fig. 4 along with the surface mesh and a close view of the potential around the reaction center. The surface potential is smooth overall and the negative potential near the reaction center is well reproduced.

Fig. 4

The discretized molecular surface of AChE with the region around the reaction center colored red (left); The electrostatic potential on the surface (middle) and the surface potential around the reaction center (right). Ionic strength = 50 mM

The reaction rate coefficient is shown as a function of ionic strength (= “spectator” + bulk substrate) for different prescribed substrate concentrations in Fig. 5(a) and as a function of bulk substrate concentration for different prescribed ionic strengths in Fig. 5(b). The results show that the reaction rate coefficients strongly depend on both ionic strength and substrate concentration. At very low substrate concentration, e.g., 1 mM or less, the results show asymptotic agreement with the DHL (see red line in Fig. 5(a)). The find also agrees with the continuum model when the substrate density is not coupled into the full electric field [57, 77, 87]). However, at moderate concentrations of the substrate, the curves are shifted. A general trend is observed: the rate coefficient increases as the bulk/distant concentration of substrate increases for a fixed overall ionic strength. For instance, for a fixed ionic strength of 300 mM (C ₊+C _subs=300 mM), the rate coefficient is 1.36×10¹¹ M⁻¹ min⁻¹ for C _subs=1 mM and is increased to 3.28×10¹¹ M⁻¹ min⁻¹ for C _subs=300 mM. The physical origins of the observed behavior can be explained as follows. If substrate concentration is not considered, as in most previous work based on the DHL, the concentration of the counter ion of the enzyme, i.e., C ₊ here, is equal to the concentration of the co-ion, i.e., C ₊=C ₋. The counter ions are attracted and concentrated around the negatively charged active site, which serves to screen the Coulomb interaction between ACh molecules and AChE, hence slowing the association. When C _subs is considered in the PNP model, to maintain the same ionic strength, C ₊ needs to be reduced by C _subs compared with that in the familiar Debye–Hückel theory. This leads to a thinner counter-ion atmosphere around the active site, and it can not be compensated by the additional substrate (ACh) density that is relatively low due to reactant depletion that results from the absorbing boundary condition. In other words, in the resulting non-equilibrium state, the sum of counter-ion density and ACh density near the active site is lower than that obtained with the Boltzmann distribution for a +1e particle. The consequences are a reduced overall screening effect and thereby an enhanced reaction rate.

Fig. 5

Reaction rate coefficients for ACh-AChE reaction system. p ₀ is bulk substrate concentration (C _subs); I is total ionic strength (spectator ions plus substrate)

The ionic atmosphere always screens the electrostatic interactions, and hence reduces the rate coefficients. At very high ionic strength, due to strong ionic screening effects, the electrostatic interactions become very weak. This is close to the pure diffusion case, and all the rate constants for different substrate concentrations are close to the pure diffusion-reaction rate constant.

The phenomena observed in above rate coefficient predictions are expected to be general for attractive substrate-enzyme systems.

6 Conclusions

A finite element method is described for solving the PBE and PNP equations with permanent atomic charges within molecular region. The electrostatic PB or Poisson equation is regularized by analytically removing the singular component of the electrostatic potential from the numerical solution. A harmonic component is defined inside biomolecules to partially compensate the removed singular component such that the remaining electrostatic component is continuous on the molecular surface. This remaining regular component is governed by an elliptic interface problem, with interface conditions computed from the singular and the harmonic components. For PNP system, it is shown that the diffusion in the solvent region is completely drifted by the regular component, which gives rise to regularized Poisson–Nernst–Planck equations. An inexact-Newton method was used to solve the regular PBE and the regular steady-state PNP systems. For unsteady diffusion a second-order Adams–Bashforth–Crank–Nicolson method is proposed for time integration. Various test problems to examine the accuracy and the stability of the proposed 3D finite element methods and time integration scheme.

In the application to simulations of the electro-diffusion controlled reaction processes, we find that the DHL only applies to very dilute situations. Our numerical results show that for electrostatically steered diffusion-controlled reaction processes, the rate coefficients strongly depend on both ionic strength and substrate concentration. In particular, at the same ionic strength, the current model predicts that increasing substrate concentration results in significant increase in rate coefficients for the attractive substrate-enzyme systems in case the product concentration can be ignored (the product effects is not considered in current model).

We also show that the non-linear PB model is a special case of the PNP model, and can be implicitly achieved through the solution of the PNP model by appropriately controlling the boundary/interface conditions. By taking such an advantage, a recent work [55] shew that a more complicated, non-uniform ionic size-modified PB model can be numerically achieved through solution of a size-modified PNP model. This indicates that PNP-like model seems a powerful framework to achieve extended PB or PNP models beyond the current mean field approximation. Because all of those models, in addition to possessing all the features such as permanent charges, irregular interface and so on as aforementioned, are intrinsically strong non-linear, and may be coupled, finite element method can serve as a powerful tool for numerical simulation of these models. The other type of nonlinear models, such as a coupled elastic equation and a Poisson equation describing the elastic deformation of a protein-membrane interacting system was also effectively solved using a finite element method [88].

The accurate and stable FEM scheme can also achieve high efficiency with contemporary developments in adaptive, multi-level multi-grid, and parallelization techniques in FEM area. Some FEM soft packages, such as FETK [40] that uses AMG technique, PHG [85] that is parallelized, are also available. This makes it a promising numerical method for some future applications to such as supermolecular energy/mechanics analysis, ion-channel simulation, molecular conformation sampling, and multi-scale multi-physics modeling of other molecular/cellular activities. Finally, the current FEM PB/PNP solvers, combining with our new mesh generation tool TMSmesh [17], can be standalone and complete computational tools for modeling protein/DNA systems in ionic solution.