1 Introduction

The Poisson–Nernst–Planck (PNP) equations is a coupled continuum model widely used to describe the dynamics of ion transport in membrane channels. In this model, the ions satisfy the Nernst–Planck equation:

$$\begin{aligned} \partial _t c^{(i)} = \nabla \cdot \left\{ D^{(i)} \left( \nabla c^{(i)} + \frac{z_i e}{k_B T} c^{(i)} \nabla \psi \right) \right\} , \quad i = 1, \ldots ,m, \end{aligned}$$
(1.1)

where \(c^{(i)}=c^{(i)}(t,\mathbf{x})\) is the local concentration of the i-th ion species, \(D^{(i)}=D^{(i)}(\mathbf{x})\) is the diffusion coefficient, \(z_i\) is the valence of the ion, e is the unit charge of a proton, \(k_B\) is the Boltzmann’s constant, T is the absolute temperature, and \(\psi =\psi (t,\mathbf{x})\) is the electrostatic potential related to ion concentrations via the Poisson equation:

$$\begin{aligned} -\nabla \cdot \left( \epsilon \nabla \psi \right) = \sum _{i=1}^m z_ie \,c^{(i)}+\rho , \end{aligned}$$
(1.2)

where \(\epsilon =\epsilon (\mathbf{x})\) is the permittivity of the electrolyte and \(\rho =\rho (\mathbf{x})\) is the permanent charge density of the system. The PNP equations (1.1) and (1.2) are usually posed in a bounded domain with proper boundary and initial conditions (see Sect. 2.3 for details). Although termed by Eisenberg et al. [9, 10] in the 1990s to study the ion channels, the PNP equations have a long history in the broader context to describe charge transport, where they are often called drift-diffusion-Poisson equations, see for instance in semiconductor modeling [17]. For a review of recent development of more generalized PNP equations and related models, the readers are referred to [22].

Solutions to the PNP equations satisfy a few important physical properties: mass conservation, positivity, energy dissipation, etc. When designing numerical methods, it would be desirable to maintain the same properties at the discrete level, preferably with a mild constraint on time step \(\Delta t\) and spatial size \(\Delta x\), so that the long time simulation can be done accurately and efficiently. Our goal in this work is to construct a structure-preserving numerical method for the PNP equations.

Searching the literature, there have been numerous studies in recent years devoted to numerical simulation of the PNP equations. Many of them also aim to preserve the structure of the solutions. Without being exhaustive, we mention a few closely related works. Among the explicit methods, the finite difference scheme in [15] is able to preserve the positivity under a parabolic CFL condition (\(\Delta t=O(\Delta x^2)\)), and the energy decay can be shown for the semi-discrete scheme (time is continuous). Later a DG version is developed in [16], where the positivity and fully discrete energy decay can be achieved still under a parabolic CFL condition. Among the implicit methods, the finite difference scheme in [12] obtains second order in time using a combination of the trapezoidal rule and backward differentiation formula. The scheme is positive, however, under a parabolic CFL condition and an additional constraint on spatial size. An energy-preserving version is recently presented in [11], where the energy decay rate is shown to be consistent up to \(O(\Delta x^2+\Delta t^2)\). Finally, the finite element method in [18] employs the fully implicit backward Euler scheme to obtain the discrete energy decay. We mention that this time discretization only works for certain boundary conditions and would not work (or require extra conditions) for the general boundaries we considered in this paper (see Remark 3.3).

From the above discussions, we can see that to obtain both unconditional positivity and discrete energy decay is very difficult and it generally requires one to go from explicit to implicit schemes. Even so, a delicate treatment for the drift and diffusion terms are necessary. Our main contribution in this work is the time discretization, which is inspired by the recent work [2]. Specifically, we propose a semi-implicit finite difference scheme for the PNP equations that is first order in time and second order in space. For generality, we consider an inhomogeneous Robin type boundary condition for the Poisson equation which includes Dirichlet and Neumann boundaries as subcases. The fully discrete scheme is proved to be mass conservative, unconditionally positive and energy dissipative. As a result of fully discrete energy decay, the numerical solution would converge to the solution of the (time independent) Poisson–Boltzmann equation, i.e., the scheme is steady-state preserving. To solve the nonlinear system resulting from the semi-implicit time discretization, we propose a simple fixed point iteration. Although we are not able to prove the convergence of the iterative scheme, we demonstrate numerically its fast convergence using a series of examples. Moreover, we provide a rigorous proof of the solvability of the semi-discrete scheme (space is continuous). To the best of our knowledge, this is the first numerical method for the PNP equations that achieves simultaneously unconditional positivity and fully discrete energy decay, and works for a large class of boundary conditions.

For completeness, let us mention a few analytical work related to well-posedness and long time behavior of the PNP equations. Using a generalization of the Hopf-Cole variable transformation, existence of a global classical solution and convergence to stationary solution was proved in [14] for a simplified 1D single species PNP model. In [3], the weak solution of a multi-D single species PNP model was studied and the well-posedness locally in time was proved. This result is improved to the two species case in [5], where the global in time existence of the solution was obtained. The long time asymptotic behavior with exponential convergence to steady states was obtained in [1, 4].

The rest of this paper is organized as follows. In Sect. 2.3, we give a brief introduction of the PNP equations in a bounded domain along with the basic properties. In Sect. 3, we describe in detail the fully discrete scheme in 1D and prove its properties: mass conservation, unconditional positivity, and energy dissipation. In addition, we prove the solvability of the semi-discrete scheme and propose a simple fixed point iteration to solve the fully discrete scheme. Extension to 2D is also discussed. Numerical examples are provided in Sect. 4 to demonstrate the convergence and properties of the proposed scheme. Concluding remarks are given in Sect. 5.

2 The PNP equations: initial boundary value problem and basic properties

In this section, we describe the initial boundary value problem of the PNP equations and summarize its basic properties.

2.1 Non-dimensionalization

To begin with, we first non-dimensionalize the Eqs. (1.1) and (1.2) by introducing the following rescaled quantities:

$$\begin{aligned} {\hat{c}}^{(i)}= & {} \frac{c^{(i)}}{c_0}, \quad {\hat{\psi }} = \frac{\psi }{\psi _0}, \quad {\hat{\rho }}= \frac{\rho }{ec_0}, \quad \nonumber \\ \hat{ \mathbf{x}}= & {} \frac{\mathbf{x}}{x_0}, \quad {\hat{D}}^{(i)} = \frac{D^{(i)}}{D_0}, \quad {\hat{t}} = \frac{t }{x_0^2/D_0}, \quad {\hat{\epsilon }} = \frac{\epsilon }{\epsilon _0}, \end{aligned}$$
(2.3)

where \(c_0, \psi _0,\dots \) are the characteristic values of the corresponding quantities. Then (1.1) and (1.2) can be rewritten as

$$\begin{aligned} \frac{D_0}{x_0^2}\partial _{{\hat{t}}} {{{\hat{c}}}}^{(i)}&= \frac{D_0}{x_0^2}\nabla \cdot \left\{ {{\hat{D}}^{(i)}} \left( \nabla {{{{\hat{c}}}}^{(i)}} + \psi _0 \frac{z_i e}{k_B T} {{{{\hat{c}}}}^{(i)}} \nabla {{{\hat{\psi }}}} \right) \right\} , \end{aligned}$$
(2.4)
$$\begin{aligned} -\frac{\psi _0 \epsilon _0}{x_0^2}\nabla \cdot \left( {\hat{\epsilon }} \nabla {\hat{\psi }}\right)&= e c_0 \left( \sum _{i=1}^{m} z_i {{{\hat{c}}}}^{(i)}+ {{{\hat{\rho }}}}\right) . \end{aligned}$$
(2.5)

Define

$$\begin{aligned} \chi _1 := \frac{e\psi _0}{k_B T}, \quad \chi _2 := \frac{e c_0 x_0^2}{\psi _0 \epsilon _0}, \end{aligned}$$
(2.6)

we obtain the non-dimensionalized PNP equations as (dropping \(\hat{}\) for simplicity):

$$\begin{aligned} \partial _t c^{(i)}&= \nabla \cdot \left( D^{(i)} \left( \nabla c^{(i)} + \chi _1 z_i c^{(i)} \nabla \psi \right) \right) , \end{aligned}$$
(2.7)
$$\begin{aligned} -\nabla \cdot (\epsilon \nabla \psi )&= \chi _2 \left( \sum _{i=1}^m z_i c^{(i)}+\rho \right) . \end{aligned}$$
(2.8)

Here \(\chi _1\) is the ratio of the electric potential energy and thermal energy; \(\chi _2\) is the inverse square of the scaled Debye length. For more physical background of these dimensionless parameters, we refer the interested reader to Sect. 2.3 of [12].

2.2 Initial and boundary value problem

When the PNP equations are imposed in a connected bounded domain \(\Omega \subset {\mathbb {R}}^d\), proper initial and boundary conditions need to be supplemented.

For the Nernst–Planck equation (2.7), the initial condition is given by

$$\begin{aligned} c^{(i)}(0,\mathbf{x}) = c^{(i),0}(\mathbf{x}), \quad \mathbf{x} \in \Omega , \quad i=1,\dots ,m, \end{aligned}$$
(2.9)

and the initial value of \(\psi \) is given by solving the Poisson equation (2.8) subject to (2.9).

For the boundary, one usually assumes the no-flux boundary condition for the Nernst–Planck equation, i.e.,

$$\begin{aligned} D^{(i)} \left( \nabla c^{(i)} + \chi _1 z_i c^{(i)} \nabla \psi \right) \cdot \mathbf{n} = 0, \quad \mathbf{x} \in \partial \Omega , \ \ t\ge 0, \quad i=1,\ldots ,m,\qquad \end{aligned}$$
(2.10)

where \(\mathbf{n}\) is the unit outward normal at the boundary point \(\mathbf{x}\in \partial \Omega \). Boundary condition for the Poisson equation can be various. Here we consider a general boundary condition:

$$\begin{aligned} \alpha \psi + \beta \frac{\partial {\psi }}{\partial \mathbf{n}} = f, \quad \mathbf{x} \in \partial \Omega ,\quad t\ge 0,\qquad \end{aligned}$$
(2.11)

where \(\alpha ,\beta \) are some constants and \(f=f(\mathbf{x})\) is a given function on \(\partial \Omega \). Note that

  • when \(\alpha \ne 0, \beta \ne 0\), (2.11) is the Robin boundary condition;

  • when \(\alpha \ne 0, \beta = 0\), (2.11) reduces to the Dirichlet boundary condition;

  • when \(\alpha = 0, \beta \ne 0\), (2.11) reduces to the Neumann boundary condition. Solution to the Neumann problem can only be unique up to a constant. Also the following compatibility condition is required:

    $$\begin{aligned} \chi _2 \int _{\Omega } \left( \sum _{i=1}^m z_i c^{(i),0} +\rho \right) \, \mathrm{d} \mathbf{x} + \frac{1}{\beta } \int _{\partial \Omega } {\epsilon f} \, \mathrm{d}{} \mathbf{s} = 0. \end{aligned}$$
    (2.12)

Putting everything together, we have the following initial boundary value problem for the PNP equations:

figure a

2.3 Basic properties

Here we list a few important properties of the problem (2.13)–(2.17), which will serve as a guidance in designing numerical schemes.

  1. 1.

    Mass conservation:

    $$\begin{aligned} \int _{\Omega } c^{(i)}(t,\mathbf{x}) \,\mathrm{d}{} \mathbf{x}= \int _{\Omega } c^{(i),0}(\mathbf{x}) \,\mathrm{d}{} \mathbf{x}, \quad \forall t>0,\ i= 1, \ldots ,m. \end{aligned}$$
    (2.18)
  2. 2.

    Positivity:

    $$\begin{aligned} c^{(i),0}(\mathbf{x}) \ge 0\ \Rightarrow \ c^{(i)}(t,\mathbf{x}) \ge 0, \quad \forall t>0, \ \mathbf{x} \in \Omega ,\ i= 1, \ldots ,m. \end{aligned}$$
    (2.19)
  3. 3.

    Energy dissipation:

    $$\begin{aligned} \frac{\mathrm{d}{\tilde{E}}}{\mathrm{d}t}= & {} -\sum _{i=1}^m \int _{\Omega } D^{(i)} c^{(i)} \left| \nabla \big ( \log c^{(i)} + \chi _1 z_i \psi \big )\right| ^2 \, \mathrm{d}\mathbf{x}\nonumber \\&+\frac{\chi _1}{2\chi _2}\int _{\partial \Omega }\epsilon \left( \psi \frac{\partial \psi _t}{\partial \mathbf{n}}-\psi _t \frac{\partial \psi }{\partial \mathbf{n}}\right) \, \mathrm{d}{} \mathbf{s}, \end{aligned}$$
    (2.20)

    where the free energy \({\tilde{E}}\) is defined as

    $$\begin{aligned} {\tilde{E}} =\int _{\Omega } \sum _{i=1}^m \left( c^{(i)} \log c^{(i)}\right) \, \mathrm{d}{} \mathbf{x}+ \frac{ \chi _1 }{2} \int _{\Omega } \left( \sum _{i=1}^{m} z_i c^{(i)}+\rho \right) \psi \, \mathrm{d}{} \mathbf{x}. \end{aligned}$$
    (2.21)

    Note that using the boundary condition (2.17) and f does not depend on time, the last term on the right hand side of (2.20) can be written equivalently as

    $$\begin{aligned} \frac{\chi _1}{2\chi _2}\int _{\partial \Omega }\epsilon \left( \psi \frac{\partial \psi _t}{\partial \mathbf{n}}-\psi _t \frac{\partial \psi }{\partial \mathbf{n}}\right) \, \mathrm{d}{} \mathbf{s} = {\left\{ \begin{array}{ll} \displaystyle \frac{\chi _1}{2\chi _2 \alpha } \int _{\partial \Omega } \epsilon f \frac{\partial \psi _t}{\partial \mathbf{n}}\, \mathrm{d}{} \mathbf{s},&{} \text {if }\alpha \ne 0,\\ \displaystyle -\frac{\chi _1}{2\chi _2 \beta } \int _{\partial \Omega } \epsilon f \psi _t\, \mathrm{d}{} \mathbf{s},&{} \text {if }\beta \ne 0. \end{array}\right. }\nonumber \\ \end{aligned}$$
    (2.22)

    Therefore, to make (2.20) dissipative, one can choose

    $$\begin{aligned} E={\tilde{E}}+ {\left\{ \begin{array}{ll} \displaystyle -\frac{\chi _1}{2\chi _2 \alpha } \int _{\partial \Omega } \epsilon f \frac{\partial \psi }{\partial \mathbf{n}}\, \mathrm{d}{} \mathbf{s},&{} \text {if } \alpha \ne 0,\\ \displaystyle \frac{\chi _1}{2\chi _2 \beta } \int _{\partial \Omega } \epsilon f \psi \, \mathrm{d}{} \mathbf{s},&{} \text {if } \beta \ne 0. \end{array}\right. } \end{aligned}$$
    (2.23)

    Then one has

    $$\begin{aligned} \frac{\mathrm{d} E}{\mathrm{d}t} = -\,\sum _{i=1}^m \int _{\Omega } D^{(i)} c^{(i)} \left| \nabla \big ( \log c^{(i)} + \chi _1 z_i \psi \big )\right| ^2 \, \mathrm{d}{} \mathbf{x}\le 0. \end{aligned}$$
    (2.24)
  4. 4.

    Steady state: the energy dissipation implies that the steady state of the system is achieved when

    $$\begin{aligned} \nabla \left( \log c^{(i),\infty } + \chi _1 z_i \psi ^{\infty }\right) =0, \quad i=1,\dots ,m, \end{aligned}$$
    (2.25)

    which integrates to the equilibrium

    $$\begin{aligned} c^{(i),\infty }=\lambda _i e^{-\chi _1z_i \psi ^{\infty }}, \quad \text {with } \lambda _i= \frac{\int _\Omega c^{(i),0} \,\mathrm{d} \mathbf{x}}{\int _\Omega e^{-\chi _1 z_i\psi ^{\infty }}\, \mathrm{d} \mathbf{x}}. \end{aligned}$$
    (2.26)

    Substituting \(c^{(i),\infty }\) into the Poisson equation (2.16) leads to

    $$\begin{aligned} -\nabla \cdot (\epsilon \nabla \psi ^{\infty }) =\chi _2 \left( \sum _{i=1}^m \lambda _i z_i e^{- \chi _1 z_i\psi ^{\infty }} +\rho \right) ,\quad \mathbf{x} \in \Omega , \end{aligned}$$
    (2.27)

    which together with the boundary condition (2.17) constitute the (nonlinear) Poisson–Boltzmann equation.

3 Numerical schemes

In this section, we describe the proposed numerical scheme for the initial boundary value problem (2.13)–(2.17). For simplicity, we assume \(\chi _1 = \chi _2 = 1\) in the following.

Before going into detail, we first summarize the key ingredients in our method.

  • The first ingredient is to reformulate the Nernst–Planck equation (2.13) as

    $$\begin{aligned} \partial _t c^{(i)} = \nabla \cdot \left( D^{(i)} M^{(i)} \nabla \left( \frac{c^{(i)}}{M^{(i)}}\right) \right) , \quad \text {where } M^{(i)} = e^{-z_i\psi }. \end{aligned}$$
    (3.28)

    Accordingly, the no-flux boundary condition (2.15) becomes

    $$\begin{aligned} \nabla \left( \frac{c^{(i)}}{M^{(i)}}\right) \cdot \mathbf{n}=0. \end{aligned}$$
    (3.29)

    Note that this is the Scharfetter-Gummel transform widely used in semiconductor community [20].

  • The second ingredient is the spatial discretization. As both (3.28) and the Poisson equation (2.16) are diffusive type equations, it is simple and natural to use the central finite difference.

  • The third ingredient (which is our main contribution) is a semi-implicit time discretization

    $$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{c^{(i),n+1} - c^{(i),n}}{\Delta t} = \nabla \cdot \left( D^{(i)} M^{(i),*} \nabla \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) \right) , \\ \displaystyle -\nabla \cdot (\epsilon \nabla \psi ^{n+1} )= \sum _{i=1}^m z_i c^{(i),n+1} + \rho , \end{array}\right. } \end{aligned}$$
    (3.30)

    where \(M^{(i),*}= e^{-z_i\psi ^*}\) and the potential \(\psi ^{*}\) is chosen as

    $$\begin{aligned} \psi ^{*}=\frac{\psi ^n + \psi ^{n+1}}{2}. \end{aligned}$$
    (3.31)

3.1 Fully discrete scheme in 1D

We now describe in detail the proposed scheme in 1D. Assume the domain \(\Omega = [a,b]\), then the PNP system reads

figure b

We partition the interval [a, b] into N uniform cells with mesh size \(\Delta x=(b-a)/N\). The cell centers \(x_j = a +(j-1/2) \Delta x\), \(j=1,\ldots ,N\) are chosen as the grid points; and the cell interfaces are given by \(x_{j+1/2} = a + j\Delta x\), \(j=0,\ldots ,N\) (note that \(x_{1/2}=a, x_{N+1/2}=b\)). Let \(t_n = n \Delta t\) be the discrete time step and we denote the numerical approximation of a function u(t, x) at \((t_n,x_j)\) by \(u_j^n\).

We first discretize the Nernst–Planck equation (3.32) in space by a second-order central difference scheme:

$$\begin{aligned} \partial _t c^{(i)}_j= \frac{1}{\Delta x^2} \left( D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i)}_{j+\frac{1}{2}}{\hat{g}}_{j+\frac{1}{2}}^{(i)} - D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i)}_{j-\frac{1}{2}}{\hat{g}}_{j-\frac{1}{2}}^{(i)}\right) , \quad j=1,\cdots ,N,\nonumber \\ \end{aligned}$$
(3.38)

where \({\hat{g}}_{j+\frac{1}{2}}^{(i)}\) is defined by

$$\begin{aligned} {\hat{g}}_{j+\frac{1}{2}}^{(i)}=\left( \frac{c^{(i)}}{M^{(i)}}\right) _{j+1}-\left( \frac{c^{(i)}}{M^{(i)} }\right) _j, \quad j=1,\dots ,N-1. \end{aligned}$$
(3.39)

At the boundary (\(j=0,N\)), due to the no-flux boundary condition (3.34), we set

$$\begin{aligned} {\hat{g}}_{\frac{1}{2}}^{(i)}={\hat{g}}_{N+\frac{1}{2}}^{(i)}=0. \end{aligned}$$
(3.40)

\(D^{(i)}_{j+\frac{1}{2}}\) is the value of the diffusion coefficient \(D^{(i)}\) at \(x_{j+\frac{1}{2}}\). \({\overline{M}}^{(i)}_{j+\frac{1}{2}}\) is an approximation to \(M^{(i)}\) at \(x_{j+\frac{1}{2}}\) and we take

$$\begin{aligned} {\overline{M}}^{(i)}_{j+\frac{1}{2}}=\frac{M_{j}^{(i)}+M_{j+1}^{(i)}}{2}, \quad M^{(i)}_j=e^{-z_i\psi _j}, \quad j=1,\dots ,N-1. \end{aligned}$$
(3.41)

Remark 3.1

We remark that the choice of \({\overline{M}}^{(i)}_{j+\frac{1}{2}}\) is not unique. As long as it is a second order, positive approximation to \(M^{(i)}\) at \(x_{j+\frac{1}{2}}\), all the properties derived in Sect. 3.1.1 can be carried over.

For the Poisson equation (3.35), we also use the central difference scheme:

$$\begin{aligned} - \frac{1}{\Delta x^2} \left( \epsilon _{j+\frac{1}{2}} {\hat{\psi }}_{j+\frac{1}{2}} - \epsilon _{j-\frac{1}{2}} {\hat{\psi }}_{j-\frac{1}{2}}\right) =\sum _{i=1}^m z_i c^{(i)}_j+ \rho _j,\quad j=1,\cdots ,N, \end{aligned}$$
(3.42)

where \(\epsilon _{j+\frac{1}{2}}\) is the value of the permittivity \(\epsilon \) at \(x_{j+\frac{1}{2}}\), and \( {\hat{\psi }}_{j+\frac{1}{2}}\) is defined by

$$\begin{aligned} {\hat{\psi }}_{j+\frac{1}{2}}=\psi _{j+1}-\psi _j, \quad j=0,\dots ,N. \end{aligned}$$
(3.43)

To obtain \(\psi _0\) and \(\psi _{N+1}\), note that the boundary condition (3.36), (3.37) can be discretized as

$$\begin{aligned} \alpha \frac{\psi _{1} + \psi _{0}}{2} - \beta \frac{\psi _{1} - \psi _{0}}{\Delta x} = f_a, \quad \alpha \frac{\psi _{N+1} + \psi _{N}}{2} + \beta \frac{\psi _{N+1}- \psi _{N}}{\Delta x} = f_b, \end{aligned}$$
(3.44)

using which we can represent

$$\begin{aligned} {\hat{\psi }}_{\frac{1}{2}}&:=\psi _1-\psi _0=\frac{2\alpha \Delta x}{\alpha \Delta x+2\beta }\psi _1-\frac{2 \Delta x}{\alpha \Delta x+2\beta }f_a, \end{aligned}$$
(3.45)
$$\begin{aligned} {\hat{\psi }}_{N+\frac{1}{2}}&:=\psi _{N+1}-\psi _N=-\,\frac{2\alpha \Delta x}{\alpha \Delta x+2\beta }\psi _N+\frac{2 \Delta x}{\alpha \Delta x+2\beta }f_b. \end{aligned}$$
(3.46)

Remark 3.2

\({\hat{\psi }}_{\frac{1}{2}}\) and \({\hat{\psi }}_{N+\frac{1}{2}}\) may not be well-defined in the case of Robin boundary (when \(\alpha \ne 0\), \(\beta \ne 0\)). In this case, we assume \(\Delta x \ne -2\beta /\alpha \).

For brevity, we write the scheme (3.42) in a matrix vector multiplication form:

$$\begin{aligned} P{\varvec{\Psi }} = \mathbf{h}, \end{aligned}$$
(3.47)

where

$$\begin{aligned} P= & {} \begin{pmatrix} p_{1,1} &{} -\epsilon _{\frac{3}{2}} &{} &{} &{} \\ -\epsilon _{\frac{3}{2}} &{} (\epsilon _{\frac{3}{2}}+ \epsilon _{\frac{5}{2}}) &{} -\epsilon _{\frac{5}{2}} &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{}-\epsilon _{N-\frac{3}{2}} &{} (\epsilon _{N-\frac{3}{2}}+\epsilon _{N-\frac{1}{2}}) &{} -\epsilon _{N-\frac{1}{2}} \\ &{} &{} &{} -\epsilon _{N-\frac{1}{2}} &{} p_{N,N} \end{pmatrix},\quad {\Psi }=\begin{pmatrix} {\psi _{1}} \\ {\psi _{2}} \\ \vdots \\ {\psi _{N}} \end{pmatrix},\quad \nonumber \\ \mathbf{h}= & {} \begin{pmatrix} {h_{1}} \\ {h_{2}} \\ \vdots \\ {h_{N}} \end{pmatrix}, \end{aligned}$$
(3.48)

with

$$\begin{aligned}&{\left\{ \begin{array}{ll} \displaystyle p_{1,1} = \frac{2 \alpha \Delta x }{\alpha \Delta x + 2 \beta } \epsilon _{\frac{1}{2}}+\epsilon _{\frac{3}{2}}, \\ \displaystyle p_{N,N} = \epsilon _{N-\frac{1}{2}} + \frac{2 \alpha \Delta x }{\alpha \Delta x + 2 \beta } \epsilon _{N+\frac{1}{2}}, \end{array}\right. }\\&\quad {\left\{ \begin{array}{ll} \displaystyle h_1 =\Delta x^2\left( \sum _{i=1}^m z_i c^{(i)}_1+ \rho _1\right) + \frac{2\Delta x}{\alpha \Delta x+2\beta } \epsilon _{\frac{1}{2}}f_a,\\ \displaystyle h_j =\Delta x^2\left( \sum _{i=1}^m z_i c^{(i)}_j+ \rho _j\right) ,\quad j=2,\dots ,N-1,\\ \displaystyle h_N = \Delta x^2 \left( \sum _{i=1}^m z_i c^{(i)}_N+ \rho _N\right) + \frac{2\Delta x}{\alpha \Delta x+2\beta } \epsilon _{N+\frac{1}{2}}f_b. \end{array}\right. } \end{aligned}$$

Now let us add the time discretization as outlined in (3.30). Define

$$\begin{aligned} M_j^{(i),*} = e^{-z_i\psi _j^*}, \quad \psi _j^{*} = \frac{\psi _j^{n} + \psi _j^{n+1} }{2}, \end{aligned}$$
(3.49)

then (3.38) with time discretization reads

$$\begin{aligned}&\frac{c_j^{(i),n+1}-c_j^{(i),n}}{\Delta t} = \frac{1}{\Delta x^2} \left\{ D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _j\right] \right. \nonumber \\&\quad \left. -D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{j-1}\right] \right\} , \quad j=2,\dots ,N-1; \end{aligned}$$
(3.50)

and for \(j=1\) and N:

$$\begin{aligned}&\frac{c_1^{(i),n+1}-c_1^{(i),n}}{\Delta t} = \frac{1}{\Delta x^2} \left\{ D^{(i)}_{\frac{3}{2}} {\overline{M}}^{(i),*}_{\frac{3}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{2}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _1\right] \right\} , \end{aligned}$$
(3.51)
$$\begin{aligned}&\frac{c_N^{(i),n+1}-c_N^{(i),n}}{\Delta t} = \frac{1}{\Delta x^2} \left\{ -D^{(i)}_{N-\frac{1}{2}} {\overline{M}}^{(i),*}_{N-\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{N}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{N-1}\right] \right\} . \end{aligned}$$
(3.52)

Rearranging terms in (3.50) yields

$$\begin{aligned}&\left[ M^{(i),*}_j +\frac{\Delta t}{\Delta x^2}\left( D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}} +D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}}\right) \right] \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j \nonumber \\&\quad -\frac{\Delta t}{\Delta x^2} D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}} \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1} -\frac{\Delta t}{\Delta x^2} D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}} \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j-1}\nonumber \\&=c^{(i),n}_j, \quad j=2,\dots ,N-1. \end{aligned}$$
(3.53)

Similarly, (3.51) (3.52) become

$$\begin{aligned}&\left[ M^{(i),*}_1 +\frac{\Delta t}{\Delta x^2} D^{(i)}_{\frac{3}{2}} {\overline{M}}^{(i),*}_{\frac{3}{2}} \right] \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _1-\frac{\Delta t}{\Delta x^2} D^{(i)}_{\frac{3}{2}} {\overline{M}}^{(i),*}_{\frac{3}{2}} \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{2} =c^{(i),n}_1, \end{aligned}$$
(3.54)
$$\begin{aligned}&\left[ M^{(i),*}_N +\frac{\Delta t}{\Delta x^2} D^{(i)}_{N-\frac{1}{2}} {\overline{M}}^{(i),*}_{N-\frac{1}{2}} \right] \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _N-\frac{\Delta t}{\Delta x^2} D^{(i)}_{N-\frac{1}{2}} {\overline{M}}^{(i),*}_{N-\frac{1}{2}} \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{N-1}\nonumber \\&\quad =c^{(i),n}_N. \end{aligned}$$
(3.55)

The schemes (3.53)–(3.55) can be written in a matrix vector multiplication form:

$$\begin{aligned} A^{(i)}{} \mathbf{g}^{(i)}= \mathbf{c}^{(i),n}, \end{aligned}$$
(3.56)

if we define

$$\begin{aligned} A^{(i)} =\begin{pmatrix} a^{(i)}_{1,1} &{} a^{(i)}_{1,2} &{} &{} \\ a^{(i)}_{2,1} &{} a^{(i)}_{2,2} &{} a^{(i)}_{2,3} &{} \\ &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} a^{(i)}_{N,N-1} &{} a^{(i)}_{N,N} \end{pmatrix}, \quad \mathbf{g}^{(i)}=\begin{pmatrix} c^{(i),n+1}_1/M^{(i),*}_1 \\ c^{(i),n+1}_2/M^{(i),*}_2 \\ \vdots \\ c^{(i),n+1}_N/M^{(i),*}_N \end{pmatrix},\; \mathbf{c}^{(i),n}=\begin{pmatrix} {c_{1}^{(i),n}} \\ {c_{2}^{(i),n}} \\ \vdots \\ {c_{N}^{(i),n}} \end{pmatrix},\nonumber \\ \end{aligned}$$
(3.57)

where the entries of the matrix \(A^{(i)}\) are given by

$$\begin{aligned}&{\left\{ \begin{array}{ll} \displaystyle a^{(i)}_{1,1} = M_{1}^{(i),*}+ \frac{\Delta t}{\Delta x^2} D^{(i)}_{\frac{3}{2}} {\overline{M}}^{(i),*}_{\frac{3}{2}}, \\ \displaystyle a^{(i)}_{N,N} = M_{N}^{(i),*}+\frac{\Delta t}{\Delta x^2} D^{(i)}_{N-\frac{1}{2}} {\overline{M}}^{(i),*}_{N-\frac{1}{2}}, \end{array}\right. }\nonumber \\&\quad {\left\{ \begin{array}{ll} \displaystyle a^{(i)}_{j,j} = M_{j}^{(i),*} + \frac{\Delta t}{\Delta x^2} \left( D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}} +D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}}\right) , \quad j=2,\dots ,N-1, \\ \displaystyle a^{(i)}_{j,j-1} =-\, \frac{\Delta t}{ \Delta x^2} D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}}, \quad j=2,\dots , N, \\ \displaystyle a^{(i)}_{j,j+1} =-\, \frac{\Delta t}{\Delta x^2} D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}, \quad j=1,\dots ,N-1; \end{array}\right. } \end{aligned}$$

Therefore, together with the system (3.47), we obtain the following fully discrete scheme for the PNP system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle A^{(i)}\left( \mathbf{M}^{(i),*}\right) \mathbf{g}^{(i)}\left( \mathbf{c}^{(i),n+1},\mathbf{M}^{(i),*}\right) = \mathbf{c}^{(i),n},\\ \displaystyle P{\varvec{\Psi }}^{n+1} = \mathbf{h}\left( \mathbf{c}^{(i),n+1}\right) , \end{array}\right. } \end{aligned}$$
(3.58)

where with a little abuse of notations, the dependence of vectors is indicated.

We state the following lemma which will be useful later.

Lemma 3.1

The matrix \(A^{(i)}\left( \mathbf{M}^{(i),*}\right) \) as defined in (3.57) is symmetric positive definite and strictly diagonally dominant, provided \({\overline{M}}^{(i),*}_{j+\frac{1}{2}}\) is a second-order, positive approximation to \(M^{(i),*}\) at \(x_{j+\frac{1}{2}}\). In particular, the choice

$$\begin{aligned} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}=\frac{M_{j}^{(i),*}+M_{j+1}^{(i),*}}{2} \end{aligned}$$
(3.59)

suffices.

Proof

By definition, \(M_{j}^{(i),*}=e^{-z_i\psi _j^*}>0\), and \({\overline{M}}^{(i),*}_{j+\frac{1}{2}}\) is required to be positive, then the entries of \(A^{(i)}\) satisfy

$$\begin{aligned} a^{(i)}_{j,j}>0, \quad a^{(i)}_{j,k}\le 0, \ \ j\ne k. \end{aligned}$$
(3.60)

Furthermore,

$$\begin{aligned} |a^{(i)}_{j,j}|>\sum _{j \ne k} |a^{(i)}_{j,k}|. \end{aligned}$$
(3.61)

Hence the conclusion is immediate. \(\square \)

3.1.1 Properties of the fully discrete scheme

In this section, we prove the properties of the fully discrete scheme (3.58). These are parallel to the theoretical properties listed in Sect. 2.3.

Define the total mass of the i-th ion species at time step \(t_n\) as

$$\begin{aligned} C^{(i)}_{\Delta }(t_n) =\Delta x \sum _{j=1}^{N} c^{(i),n}_j. \end{aligned}$$
(3.62)

Then we have

Theorem 3.1

(Mass conservation) The fully discrete scheme (3.58) is always mass conservative for each ion species:

$$\begin{aligned} C^{(i)}_{\Delta }(t_n) = C^{(i)}_{\Delta }(t_{n+1}),\quad i=1,\ldots ,m. \end{aligned}$$
(3.63)

Proof

Using (3.50), (3.51) and (3.52), it is easy to see

$$\begin{aligned} C^{(i)}_{\Delta }(t_{n+1})- C^{(i)}_{\Delta }(t_n)=\Delta x\sum _{j=1}^N \left( c^{(i),n+1}_j-c^{(i),n}_j\right) =0. \end{aligned}$$
(3.64)

This proves the numerical mass conservation. \(\square \)

Theorem 3.2

(Positivity preserving) The fully discrete scheme (3.58) is unconditionally positivity-preserving, i.e., if \(c^{(i),n}_j \ge 0\) for all \(j = 1,\ldots ,N\), then

$$\begin{aligned} c^{(i),n+1}_j \ge 0, \quad j = 1,\ldots ,N, \end{aligned}$$
(3.65)

for each species \(i=1,\dots ,m\).

Proof

Lemma 3.1 implies that the matrix \(A^{(i)}\left( \mathbf{M}^{(i),*}\right) \) in the scheme (3.58) is a M-matrix, i.e., it is inverse positive (\((A^{(i)})^{-1}\) exists and each entry of \((A^{(i)})^{-1}\) is non-negative). Therefore, if \(c^{(i),n}_j\ge 0\), by solving the first linear system in (3.58), we have \(g^{(i)}_j\ge 0\). Since \(M_j^{(i),*}>0\), then \(c_j^{(i),n+1}=g^{(i)}_jM_j^{(i),*}\ge 0\). \(\square \)

Define the discrete free energy at time step \(t_n\) as

$$\begin{aligned} E_{\Delta } (t_n)= & {} \Delta x\sum _{j=1}^N \sum _{i=1}^m c^{(i),n}_j \log c^{(i),n}_j+ \frac{\Delta x}{2} \sum _{j=1}^N \left( \sum _{i=1}^m z_i c^{(i),n}_j +\rho _j\right) \psi _j^n \nonumber \\&+ \frac{ \epsilon _{\frac{1}{2}} f_a \psi _1^n + \epsilon _{N+\frac{1}{2}} f_b \psi _N^n}{\alpha \Delta x + 2 \beta }, \end{aligned}$$
(3.66)

where we assume \(\Delta x \ne -2\beta /\alpha \) when both \(\alpha \) and \(\beta \) are nonzero. Then we have

Theorem 3.3

(Energy dissipation) The fully discrete scheme (3.58) is unconditionally energy-dissipative:

$$\begin{aligned}&E_{\Delta }(t_{n+1}) -E_{\Delta } (t_n) \nonumber \\&\quad \le -\frac{\Delta t}{\Delta x} \sum _{j=1}^{N-1} \sum _{i=1}^m D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{j}\right] \nonumber \\&\qquad \times \left[ \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1} -\log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j\right] \nonumber \\&\quad \le 0. \end{aligned}$$
(3.67)

Proof

Using the definition (3.66), we have

$$\begin{aligned}&E_{\Delta }(t_{n+1})-E_{\Delta }(t_n)\nonumber \\&\quad =\Delta x \sum _{j=1}^N \sum _{i=1}^m \left( c^{(i),n+1}_j \log c^{(i),n+1}_j-c^{(i),n}_j \log c^{(i),n}_j\right) \nonumber \\&\qquad + \frac{\Delta x}{2} \sum _{j=1}^N \sum _{i=1}^m z_i \left( c^{(i),n+1}_j \psi _j^{n+1}- c^{(i),n}_j \psi _j^n\right) \nonumber \\&\qquad + \frac{\Delta x}{2}\sum _{j=1}^N \rho _j \left( \psi _j^{n+1}-\psi _j^n\right) + \frac{ \epsilon _{\frac{1}{2}} f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}} f_b (\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x + 2 \beta }\nonumber \\&\quad =\Delta x \sum _{j=1}^N\sum _{i=1}^m \left[ c^{(i),n+1}_j \log c^{(i),n+1}_j - c^{(i),n}_j \log c^{(i),n}_j + \left( c^{(i),n}_j - c^{(i),n+1}_j\right) \log c^{(i),n+1}_j\right] \nonumber \\&\qquad +\Delta x \sum _{j=1}^N \sum _{i=1}^m\left( c^{(i),n+1}_j - c^{(i),n}_j\right) \left( \log c^{(i),n+1}_j + z_i \psi _j^{*}\right) \nonumber \\&\qquad +\Delta x\sum _{j=1}^N \sum _{i=1}^m z_i \left[ \frac{1}{2} \left( c^{(i),n+1}_j \psi _j^{n+1} - c^{(i),n}_j\psi _j^n\right) + \left( c^{(i),n}_j - c^{(i),n+1}_j\right) \psi _j^{*} \right] \nonumber \\&\qquad + \frac{\Delta x}{2} \sum _{j=1}^N \rho _j (\psi _j^{n+1} - \psi _j^n) + \frac{\epsilon _{\frac{1}{2}}f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}}f_b(\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x+ 2 \beta }\nonumber \\&\quad =I + II + III, \end{aligned}$$
(3.68)

where the three parts are defined as:

$$\begin{aligned} I&:= \Delta x \sum _{j=1}^N\sum _{i=1}^m \left[ c^{(i),n+1}_j \log c^{(i),n+1}_j - c^{(i),n}_j \log c^{(i),n}_j + \left( c^{(i),n}_j - c^{(i),n+1}_j\right) \log c^{(i),n+1}_j\right] ,\nonumber \\ II&:= \Delta x \sum _{j=1}^N \sum _{i=1}^m\left( c^{(i),n+1}_j - c^{(i),n}_j\right) \left( \log c^{(i),n+1}_j + z_i \psi _j^{*}\right) , \nonumber \\ III&:= \Delta x\sum _{j=1}^N \sum _{i=1}^m z_i \left[ \frac{1}{2} \left( c^{(i),n+1}_j \psi _j^{n+1} - c^{(i),n}_j\psi _j^n\right) + \left( c^{(i),n}_j - c^{(i),n+1}_j\right) \psi _j^{*} \right] \nonumber \\&+ \frac{\Delta x}{2} \sum _{j=1}^N \rho _j (\psi _j^{n+1} - \psi _j^n) + \frac{\epsilon _{\frac{1}{2}}f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}}f_b(\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x+ 2 \beta }. \end{aligned}$$
(3.69)

For part I,

$$\begin{aligned} I=&\Delta x\sum _{j=1}^N\sum _{i=1}^m c^{(i),n}_j \left( \log c^{(i),n+1}_j - \log c^{(i),n}_j\right) = \Delta x \sum _{j=1}^N \sum _{i=1}^m c^{(i),n}_j \log \frac{c^{(i),n+1}_j}{c^{(i),n}_j}\nonumber \\ \le&\Delta x\sum _{j=1}^N \sum _{i=1}^m c^{(i),n}_j \left( \frac{c^{(i),n+1}_j}{c^{(i),n}_j} -1 \right) = 0, \end{aligned}$$
(3.70)

where \(\log x\le x-1\) (\(x>0\)) is used in the inequality and mass conservation is used in the last equality.

For part II,

$$\begin{aligned} II&= \Delta x \sum _{j=1}^N \sum _{i=1}^m \left( c^{(i),n+1}_j - c^{(i),n}_j\right) \left( \log c^{(i),n+1}_j - \log M^{(i),*}_j \right) \nonumber \\&= \Delta x \sum _{j=1}^N \sum _{i=1}^m \left( c^{(i),n+1}_j - c^{(i),n}_j\right) \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j \nonumber \\&=\frac{\Delta t}{\Delta x} \sum _{j=1}^{N-1} \sum _{i=1}^m D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _j\right] \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j \nonumber \\&\quad -\frac{\Delta t}{\Delta x} \sum _{j=2}^{N} \sum _{i=1}^m D^{(i)}_{j-\frac{1}{2}} {\overline{M}}^{(i),*}_{j-\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{j-1}\right] \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j \nonumber \\&=\frac{\Delta t}{\Delta x} \sum _{j=1}^{N-1} \sum _{i=1}^m D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _j\right] \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j \nonumber \\&\quad -\frac{\Delta t}{\Delta x} \sum _{j=1}^{N-1} \sum _{i=1}^m D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{j}\right] \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1} \nonumber \\&=-\,\frac{\Delta t}{\Delta x} \sum _{j=1}^{N-1} \sum _{i=1}^m D^{(i)}_{j+\frac{1}{2}} {\overline{M}}^{(i),*}_{j+\frac{1}{2}}\left[ \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1}-\left( \frac{c^{(i),n+1}}{M^{(i),*} }\right) _{j}\right] \nonumber \\&\quad \times \left[ \log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _{j+1} -\log \left( \frac{c^{(i),n+1}}{M^{(i),*}}\right) _j\right] \nonumber \\&\le 0, \end{aligned}$$
(3.71)

where \(M^{(i),*}=e^{-z_j\psi _j^*}\) is used in the first equality and the schemes (3.50)–(3.52) are used in the third equality. Using \(\log \) is a non-decreasing function, we obtained the last inequality.

For part III,

$$\begin{aligned} III=&\Delta x\sum _{j=1}^N \sum _{i=1}^m z_i \left[ \frac{1}{2} \left( c^{(i),n+1}_j - c^{(i),n}_j \right) \left( \psi _j^{n+1}+\psi _j^n\right) + \left( c^{(i),n}_j - c^{(i),n+1}_j\right) \psi _j^{*} \right] \nonumber \\&+ \frac{\Delta x}{2} \sum _{j=1}^N\left[ \left( \sum _{i=1}^m z_ic_j^{(i),n}+\rho _j\right) \psi _j^{n+1} - \left( \sum _{i=1}^m z_ic_j^{(i),n+1}+\rho _j\right) \psi _j^{n} \right] \nonumber \\&+ \frac{\epsilon _{\frac{1}{2}}f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}}f_b(\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x+ 2 \beta }\nonumber \\ =&\frac{\Delta x}{2} \sum _{j=1}^N\left[ \left( \sum _{i=1}^m z_ic_j^{(i),n}+\rho _j\right) \psi _j^{n+1} - \left( \sum _{i=1}^m z_ic_j^{(i),n+1}+\rho _j\right) \psi _j^{n} \right] \nonumber \\&+ \frac{\epsilon _{\frac{1}{2}}f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}}f_b(\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x+ 2 \beta }\nonumber \\ =&- \frac{1}{2\Delta x} \sum _{j=1}^N\left[ \left( \epsilon _{j+\frac{1}{2}} {\hat{\psi }}_{j+\frac{1}{2}}^n - \epsilon _{j-\frac{1}{2}} {\hat{\psi }}_{j-\frac{1}{2}}^n\right) \psi _j^{n+1} \right. \nonumber \\&\left. \quad - \left( \epsilon _{j+\frac{1}{2}} {\hat{\psi }}_{j+\frac{1}{2}}^{n+1} - \epsilon _{j-\frac{1}{2}} {\hat{\psi }}_{j-\frac{1}{2}}^{n+1}\right) \psi _j^{n} \right] \nonumber \\&+ \frac{\epsilon _{\frac{1}{2}}f_a (\psi _1^{n+1}-\psi _1^n) + \epsilon _{N+\frac{1}{2}}f_b(\psi _N^{n+1}-\psi _N^n)}{\alpha \Delta x+ 2 \beta }\nonumber \\ =\,&0, \end{aligned}$$
(3.72)

where \(\psi ^*_j=\frac{\psi ^n_j+\psi ^{n+1}_j}{2}\) is used to obtain the second equality and the scheme (3.42) is used in the third one. The last equality is obtained by using the following formula. For a sequence \(\{\phi _j\}_{j=1}^N\), one has

$$\begin{aligned}&\sum _{j=1}^N \phi _j \left( \epsilon _{j+\frac{1}{2}} {\hat{\psi }}_{j+\frac{1}{2}} - \epsilon _{j-\frac{1}{2}}{\hat{\psi }}_{j-\frac{1}{2}}\right) \nonumber \\&=\left( \phi _N \epsilon _{N+\frac{1}{2}} {\hat{\psi }}_{N+\frac{1}{2}}-\phi _1\epsilon _{\frac{1}{2}}{\hat{\psi }}_{\frac{1}{2}}\right) -\sum _{j=1}^{N-1}\epsilon _{j+\frac{1}{2}} {\hat{\psi }}_{j+\frac{1}{2}}(\phi _{j+1}-\phi _j)\nonumber \\&=-\,\frac{2\alpha \Delta x}{\alpha \Delta x+2\beta }\left( \epsilon _{\frac{1}{2}} \phi _1 \psi _1+ \epsilon _{N+\frac{1}{2}}\phi _N\psi _N\right) -\sum _{j=1}^{N-1}\epsilon _{j+\frac{1}{2}} (\psi _{j+1}-\psi _j)(\phi _{j+1}-\phi _j)\nonumber \\&\quad +\frac{2\Delta x}{\alpha \Delta x+2\beta }\left( \epsilon _{\frac{1}{2}}\phi _1f_a+\epsilon _{N+\frac{1}{2}}\phi _Nf_b\right) , \end{aligned}$$
(3.73)

where the summation by parts is used in the first equality; (3.43), (3.45) and (3.46) are used in the second equality.

Combing parts I, II, and III, the theorem is proved. \(\square \)

Remark 3.3

If one considers the fully implicit time discretization, i.e., \(\psi ^*_j=\psi ^{n+1}_j\), a similar calculation as above would also show the energy decay property, but based on the additional assumption that \(\alpha \) and \(\beta \) have the same sign. To be precise, the energy estimate of the semi-discrete scheme would read

$$\begin{aligned} E(t_{n+1}) - E(t_{n})\le & {} T_B - \Delta t \sum _{i=1}^m \int _{\Omega } c^{(i),n+1} \left| \nabla \left( \log c^{(i),n+1} + z_i \psi ^{*}\right) \right| ^2 \mathrm{d}{} \mathbf{x},\nonumber \\ \end{aligned}$$
(3.74)

where the boundary term is given as

$$\begin{aligned} \frac{\partial {\psi ^{n+1}}}{\partial \mathbf{n}} T_B = {\left\{ \begin{array}{ll} \displaystyle -\int _{\partial \Omega } \epsilon \frac{\beta }{2\alpha } \left( \frac{\partial {\psi ^{n+1}}}{\partial \mathbf{n}} -\frac{\partial {\psi ^{n}}}{\partial \mathbf{n}}\right) ^2\,\mathrm{d} \mathbf{s},&{} \text {if } \alpha \ne 0,\\ \displaystyle -\int _{\partial \Omega } \epsilon \frac{\alpha }{2\beta } \left( \psi ^{n+1} -\psi ^{n}\right) ^2\,\mathrm{d} \mathbf{s},&{} \text {if } \beta \ne 0. \end{array}\right. } \end{aligned}$$
(3.75)

This is exactly what proposed in [18]. We point out that \(\alpha \) and \(\beta \) come from the physical boundary condition and their signs are not definite. Therefore, our semi-implicit time discretization is more general and works for a larger class of boundary conditions.

As a consequence of the fully discrete energy decay, we have the following

Theorem 3.4

(Steady-state preserving) Assume the discrete energy \(E_{\Delta } (t_n)\) is bounded from below, the fully discrete scheme (3.58) is steady-state preserving, i.e., for fixed \(\Delta x\), when time step \(n\rightarrow \infty \), the numerical solutions \(c_j^{(i),\infty }\) and \(\psi _j^\infty \) become the (second order) numerical solutions to the limiting Poisson–Boltzmann equation

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle - (\epsilon \psi ^{\infty }_x)_x =\sum _{i=1}^m z_i c^{(i),\infty } +\rho , \quad \quad x\in [a,b],\\ &{}\displaystyle \alpha \psi ^\infty (a) - \beta \psi ^{\infty }_x(a) = f_a, \quad \alpha \psi ^\infty (b) + \beta \psi ^{\infty }_x(b) = f_b, \end{array}\right. } \end{aligned}$$
(3.76)

where

$$\begin{aligned} c^{(i),\infty }=\lambda _ie^{- z_i\psi ^{\infty }}, \quad \lambda _i= \frac{\int _a^b c^{(i),0} \,\mathrm{d} {x}}{\int _a^b e^{-z_i\psi ^{\infty }}\,\mathrm{d} {x}}. \end{aligned}$$
(3.77)

Proof

Since the discrete energy sequence \(\{E_{\Delta } (t_n)\}\) is monotonically decreasing and bounded from below, the limit \(\lim _{n\rightarrow \infty }E_{\Delta } (t_n)=E_{\Delta }(t_{\infty })\) exists. Taking \(n\rightarrow \infty \) in (3.67), we have

$$\begin{aligned} c_j^{(i),\infty }=\lambda _iM_j^{(i),\infty }=\lambda _ie^{-z_i\psi _j^{\infty }}, \quad \text {for all } i=1,\dots ,m, \ j=1,\dots ,N, \end{aligned}$$
(3.78)

where \(\lambda _i\) is some constant depending only on i and can be obtained by

$$\begin{aligned} \lambda _i=\frac{\sum _{j=1}^Nc_j^{(i),\infty }}{\sum _{j=1}^N e^{-z_i\psi _j^{\infty }}}=\frac{\sum _{j=1}^Nc_j^{(i),0}}{\sum _{j=1}^N e^{-z_i\psi _j^{\infty }}}, \end{aligned}$$
(3.79)

where we used the mass conservation. Finally substituting \(c_j^{(i),\infty }\) into the system (3.47), we have

$$\begin{aligned} P{\varvec{\Psi }}^{\infty } = \mathbf{h}\left( \mathbf{c}^{(i),\infty }\right) , \end{aligned}$$
(3.80)

which is a second order finite difference discretization to the limiting Poisson–Boltzmann equation (3.76). \(\square \)

Remark 3.4

We mention that there is a different line of research to develop schemes that preserve the steady state directly. The so-called Chang-Cooper scheme for the linear Fokker–Planck equation is the one of the pioneer work [8]. See also [7, 19] for recent development on nonlinear Fokker–Planck equations.

3.1.2 Fixed point iteration to solve the fully discrete scheme

The system (3.58) is implicit and fully coupled. To solve it, we propose a simple fixed point iteration. The following algorithm describes how the iterations are performed at time step \(t_n\) to compute the solutions \(c_j^{(i),n+1}\) and \(\psi ^{n+1}_j\) (\(i=1,\dots ,m\); \(j=1,\dots ,N\)) at time step \(t_{n+1}\).

Note that in each iteration, we need to solve two linear systems (3.82) and (3.84). Both of them can be solved efficiently using sparse linear solvers. Furthermore, the matrix \(A^{(i)}\left( \mathbf{M}^{(i),(l)}\right) \) is a M-matrix (by Lemma 3.1), hence the solution \(c^{i,(l)}\) obtained in internal steps is guaranteed to be positive. For the Poisson equation, special care is needed for the Neumann boundary condition since the solution is unique up to a constant. Here we choose one solution by setting \(\psi _1 = 0\).

The above fixed point iteration is just one strategy to solve the nonlinear system and our numerical experiments show that it generally converges in several steps (less than 10). One could also use Newton’s method to achieve potentially faster convergence. We leave the convergence studies of different iterative methods to future work (see [6] for a related study). Nonetheless, to better understand the proposed time discretization, we do provide in this work a proof of the solvability of the semi-discrete scheme (3.30).

figure c

3.1.3 Solvability of the semi-discrete scheme

To prove the solvability of the semi-discrete scheme (3.30), we consider \(D^{(i)}=\epsilon =1\) for simplicity and rewrite it as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{c^{(i),n+1} -c^{(i),n}}{\Delta t}= \Delta c^{(i),n+1} + \frac{1}{2}\nabla \cdot \left( z_i c^{(i),n+1} \nabla \left( \psi ^n+ \psi ^{n+1}\right) \right) , \\ \displaystyle -\Delta \psi ^{n+1} =\sum _{i=1}^m z_i c^{(i),n+1} + \rho . \end{array}\right. } \end{aligned}$$
(3.85)

The boundary condition is given as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \left( \nabla c^{(i),n+1} + \frac{1}{2}z_i c^{(i),n+1} \nabla \left( \psi ^n+ \psi ^{n+1}\right) \right) \cdot \mathbf{n}=0, \\ \displaystyle \nabla {\psi }^{n+1}\cdot \mathbf{n}= 0. \end{array}\right. } \end{aligned}$$
(3.86)

Note that the homogeneous Neumann boundary condition is assumed for the Poisson equation in our analysis, which is a bit less general than what we considered for the rest of the paper.

Definition 3.1

Given \(\left( \{c^{(i),n}\}_{i=1}^m,\psi ^{n} \right) \in H^1(\Omega )\), we say that \(\left( \{c^{(i),n+1}\}_{i=1}^m,\psi ^{n+1} \right) \in H^1(\Omega )\) is a weak solution of (3.85), (3.86), if it satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t} \int _{\Omega } \left( c^{(i),n+1} -c^{(i),n}\right) \phi \ \mathrm{d}{} \mathbf{x}+ \int _{\Omega } \nabla c^{(i),n+1}\cdot \nabla \phi \ \mathrm{d}{} \mathbf{x}\\ \quad = - \frac{1}{2} \int _{\Omega } z_i c^{(i),n+1} \nabla \left( \psi ^n+ \psi ^{n+1}\right) \cdot \nabla \phi \ \mathrm{d}{} \mathbf{x}, \\ \displaystyle \int _{\Omega } \nabla \psi ^{n+1}\cdot \nabla \phi \ \mathrm{d}\mathbf{x} =\int _{\Omega } \left( \sum _{i=1}^m z_i c^{(i),n+1} + \rho \right) \phi \ \mathrm{d}{} \mathbf{x}, \end{array}\right. } \end{aligned}$$
(3.87)

for all test function \(\phi \in H^1(\Omega )\).

We now state the solvability theorem for problem (3.85), (3.86).

Theorem 3.5

Let \(\Omega \) be a bounded, open subset of \({\mathbb {R}}^d\)\((d\le 3)\), and \(\partial \Omega \) is \(C^1\), then the semi-discrete scheme (3.85), (3.86) has a weak solution \(\left( \{c^{(i),n+1}\}_{i=1}^m,\psi ^{n+1} \right) \) when \(\Delta t\) is sufficiently small.

The proof of this theorem is provided in the Appendix, which follows a similar line of the well-posedness theory for the PNP equations [3, 5, 21].

3.2 Fully discrete scheme in 2D

The extension of the 1D scheme to multi-D in the rectangular domain is straightforward. Here for completeness, we briefly present the scheme in 2D.

Consider the domain \(\Omega =[a,b] \times [c,d]\), then the 2D PNP system reads

figure d

We partition \(\Omega \) into \(N_x\) and \(N_y\) uniform cells in each dimension with mesh size \(\Delta x = (b-a)/N_x, \Delta y=(d-c)/N_y\), respectively. The interior grid points are chosen as \((a +(j-1/2) \Delta x,c +(k-1/2)\Delta y)\), \(j=1,\ldots ,N_x, \ k=1,\ldots ,N_y\), and the numerical approximation of a function u(t, x, y) at this point and time step \(t_n\) is denoted by \(u_{j,k}^n\). Cell interface values are defined similarly as in 1D.

The fully discrete scheme for the Nernst–Planck equation (3.88) is given as follows:

$$\begin{aligned} \frac{c^{(i),n+1}_{j,k} -c^{(i),n}_{j,k}}{\Delta t} =&\frac{1}{\Delta x^2} \left[ D_{j+\frac{1}{2},k}^{(i)} {\overline{M}}_{j+\frac{1}{2},k}^{(i),*} {\hat{g}}^{(i),n+1}_{j+\frac{1}{2},k} - D_{j-\frac{1}{2},k}^{(i)} {\overline{M}}_{j-\frac{1}{2},k}^{(i),*} {\hat{g}}^{(i),n+1}_{j-\frac{1}{2},k}\right] \nonumber \\&+ \frac{1}{\Delta y^2} \left[ D_{j,k+\frac{1}{2}}^{(i)} {\overline{M}}_{j,k+\frac{1}{2}}^{(i),*} {\hat{g}}^{(i),n+1}_{j,k+\frac{1}{2}} - D_{j,k-\frac{1}{2}}^{(i)} {\overline{M}}_{j,k-\frac{1}{2}}^{(i),*} {\hat{g}}^{(i),n+1}_{j,k-\frac{1}{2}}\right] ,\nonumber \\ \end{aligned}$$
(3.95)

where

$$\begin{aligned}&{\hat{g}}^{(i),n+1}_{j+\frac{1}{2},k} = \frac{c^{(i),n+1}_{j+1,k}}{M_{j+1,k}^{(i),*}} - \frac{c^{(i),n+1}_{j,k}}{M_{j,k}^{(i),*}},\quad {\hat{g}}^{(i),n+1}_{j,k+\frac{1}{2}} =\frac{c^{(i),n+1}_{j,k+1}}{M_{j,k+1}^{(i),*}} - \frac{c^{(i),n+1}_{j,k}}{M_{j,k}^{(i),*}}, \end{aligned}$$
(3.96)
$$\begin{aligned}&{\overline{M}}_{j+\frac{1}{2},k}^{(i),*} = \frac{1}{2} \left( {M}_{j,k}^{(i),*} + {M}_{j+1,k}^{(i),*}\right) , \quad {\overline{M}}_{j,k+\frac{1}{2}}^{(i),*} = \frac{1}{2} \left( {M}_{j,k}^{(i),*} + {M}_{j,k+1}^{(i),*}\right) ,\qquad \end{aligned}$$
(3.97)

and

$$\begin{aligned} M_{j,k}^{(i),*} = e^{- z_i \psi _{j,k}^{*}},\quad \psi _{j,k}^{*} = \frac{1}{2}\left( \psi _{j,k}^{n} + \psi _{j,k}^{n+1}\right) . \end{aligned}$$
(3.98)

At the boundary

$$\begin{aligned} {\hat{g}}^{(i),n+1}_{\frac{1}{2},k} = {\hat{g}}^{(i),n+1}_{N_x+\frac{1}{2},k}=0,\quad {\hat{g}}^{(i),n+1}_{j,\frac{1}{2}} = {\hat{g}}^{(i),n+1}_{j,N_y+\frac{1}{2}}=0. \end{aligned}$$
(3.99)

For the Poisson equation (3.92), the scheme is given as

$$\begin{aligned}&\sum _{i=1}^m z_i c_{j,k}^{(i),n+1} + \rho _{j,k} \nonumber \\&\quad = -\frac{1}{\Delta x^2} \left[ \epsilon _{j-\frac{1}{2},k} \psi _{j-1,k}^{n+1} - (\epsilon _{j-\frac{1}{2},k} + \epsilon _{j+\frac{1}{2},k})\psi _{j,k}^{n+1} + \epsilon _{j+\frac{1}{2},k}\psi _{j+1,k}^{n+1} \right] \nonumber \\&\qquad - \frac{1}{\Delta y^2} \left[ \epsilon _{j,k-\frac{1}{2}} \psi _{j,k-1}^{n+1} - (\epsilon _{j,k-\frac{1}{2}} + \epsilon _{j,k+\frac{1}{2}})\psi _{j,k}^{n+1} + \epsilon _{j,k+\frac{1}{2}}\psi _{j,k+1}^{n+1} \right] , \end{aligned}$$
(3.100)

where the boundary terms are defined through

$$\begin{aligned}&\alpha \frac{\psi ^{n+1}_{1,k}+\psi ^{n+1}_{0,k}}{2}- \beta \frac{\psi ^{n+1}_{1,k}-\psi ^{n+1}_{0,k}}{\Delta x}= f_a,\nonumber \\&\alpha \frac{\psi ^{n+1}_{N_x+1,k}+\psi ^{n+1}_{N_x,k}}{2} + \beta \frac{\psi ^{n+1}_{N_x+1,k}-\psi ^{n+1}_{N_x,k}}{\Delta x} = f_b, \end{aligned}$$
(3.101)
$$\begin{aligned}&\alpha \frac{\psi ^{n+1}_{j,1}+\psi ^{n+1}_{j,0}}{2} -\beta \frac{\psi ^{n+1}_{j,1}-\psi ^{n+1}_{j,0}}{\Delta y} = f_{c},\nonumber \\&\alpha \frac{\psi ^{n+1}_{j,N_y+1}+\psi ^{n+1}_{j,N_y}}{2} + \beta \frac{\psi ^{n+1}_{j,N_y+1}-\psi ^{n+1}_{j,N_y}}{\Delta y} = f_d. \end{aligned}$$
(3.102)

For the 2D scheme, we can also show the following properties: mass conservation, positivity preserving, and energy dissipation, which we give without proof.

Theorem 3.6

(Mass conservation) The fully discrete scheme (3.95), (3.100) is always mass conservative:

$$\begin{aligned} C^{(i)}_{\Delta }(t_n) = C^{(i)}_{\Delta }(t_{n+1}),\quad i=1,\ldots ,m. \end{aligned}$$
(3.103)

where

$$\begin{aligned} C_{\Delta }^{(i)}(t_n) = \Delta x \Delta y\sum _{j=1}^{N_x} \sum _{k=1}^{N_y} c_{j,k}^{(i),n} \end{aligned}$$
(3.104)

is the total mass of the ith ion species at \(t_n\).

Theorem 3.7

(Positivity preserving) The fully discrete scheme (3.95), (3.100) is unconditionally positivity-preserving, i.e., if \(c^{(i),n}_{j,k} \ge 0\) for all \(j= 1,\ldots ,N_x, \ k=1,\ldots ,N_y\), then

$$\begin{aligned} c^{(i),n+1}_{j,k} \ge 0, \quad j= 1,\ldots ,N_x, \ k=1,\ldots ,N_y, \end{aligned}$$
(3.105)

for each \(i=1,\dots ,m\).

Theorem 3.8

(Energy dissipation) The fully discrete scheme (3.95), (3.100) is unconditionally energy-dissipative:

$$\begin{aligned} E_{\Delta }(t_{n+1}) \le E_{\Delta } (t_n), \end{aligned}$$
(3.106)

where the discrete free energy at \(t_n\) is defined as

$$\begin{aligned} E_{\Delta }(t_n)=&\Delta x \Delta y \sum _{i=1}^m \sum _{j=1}^{N_x} \sum _{k=1}^{N_y} c_{j,k}^{(i),n} \log c_{j,k}^{(i),n} \nonumber \\&+ \frac{\Delta x \Delta y}{2} \sum _{j=1}^{N_x} \sum _{k=1}^{N_y} \psi _{j,k}^n \left( \sum _{i=1}^mz_i c_{j,k}^{(i),n} + \rho _{j,k} \right) \nonumber \\&+ \sum _{k=1}^{N_y} \frac{\epsilon _{\frac{1}{2},k}f_a\psi _{1,k}^n + \epsilon _{N_x+\frac{1}{2},k}f_b\psi _{N_x,k}^n}{\alpha \Delta x + 2\beta }\nonumber \\&+\sum _{j=1}^{N_x} \frac{\epsilon _{j,\frac{1}{2}}f_{c}\psi _{j,1}^n + \epsilon _{j,N_y+\frac{1}{2}}f_{d}\psi _{j,N_y}^n}{\alpha \Delta y + 2\beta }. \end{aligned}$$
(3.107)

4 Numerical examples

In this section, we perform several numerical tests to demonstrate the convergence and properties of the proposed scheme. We will consider both 1D and 2D examples, and in particular, a practical example with physical parameters specifically suited toward the modeling of ion channels. The tolerance for fixed point iteration is set as \(\text {tol} = 10^{-8}\) for all the tests except the tolerance test in Sect. 4.2.

4.1 Accuracy test: manufactured solution

We first examine the accuracy of our scheme using a manufactured solution. Consider the following 1D single-species PNP system with a source term

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t c = \partial _x\left( \partial _x c + c \partial _x \psi \right) + h ,&{} x\in [0,1], \ \ t\ge 0, \\ c(0,x)= x^2(1-x)^2, &{} x\in [0,1],\\ -\partial _{xx}\psi = c,&{} x\in [0,1], \ \ t\ge 0, \\ \psi (t,0)= 0,\quad \psi (t,1) =-\,\frac{1}{60}e^{-t},&{} t \ge 0, \\ \partial _x c + c \partial _x \psi = 0,&{} x=0,1, \ \ t \ge 0, \end{array}\right. } \end{aligned}$$
(4.108)

where h is given by

$$\begin{aligned}&h(t,x) = \left( \frac{9}{5}x^8 - \frac{36}{5} x^7 + \frac{161}{15}x^6 - 7x^5 +\frac{5}{3} x^4\right) e^{-2t}\nonumber \\&\quad -\left( x^4 -2x^3 +13x^2 -12x +2\right) e^{-t}. \end{aligned}$$

For this system, one can construct the exact solution as

$$\begin{aligned} c(t,x) = x^2(1-x)^2 e^{-t}, \quad \psi (t,x) = -\,\left( \frac{1}{30}x^6 -\frac{1}{10}x^5 + \frac{1}{12}x^4\right) e^{-t}.\qquad \quad \end{aligned}$$
(4.109)

We verify the order of the proposed scheme in both space and time. The results are shown in Tables 1 and 2, where the error of a numerical solution \(u_j^n\) is computed as

$$\begin{aligned} \Vert u^{\text {num}}-u^{\text {ext}}\Vert _{l^2}:= \left( \Delta x \sum _j |u_{j} ^n - u^{\text {ext}}(t_n,x_j)|^2\right) ^{1/2} \end{aligned}$$
(4.110)

at time \(t_n=0.5\). These results imply that our scheme is indeed first order accurate in time and second order accurate in space.

Table 1 Table of errors with different time step sizes \(\Delta t\)
Full size table
Table 2 Table of errors with different spatial mesh sizes \(\Delta x\)
Full size table

4.2 1D multiple species

Next we apply our scheme to solve the 1D two-species PNP system (3.32)–(3.37) and verify its properties. Two different tests are performed:

  1. Case 1

    The Dirichlet boundary value problem in domain \([-1,1]\) with \(D^{(1)}=D^{(2)}=\epsilon =1\), \(z_1 =1, z_2 =-\,1,\rho =0\), the initial and boundary conditions are chosen as

    $$\begin{aligned} {\left\{ \begin{array}{ll} c^{(1)}(0,x) = 2-x^2, \quad c^{(2)}(0,x)=x^2, \\ \psi (t,-1)= -\,1, \quad \psi (t,1)= 1. \end{array}\right. } \end{aligned}$$
    (4.111)
  2. Case 2

    The Neumann boundary value problem in domain [0, 1] with \(D^{(1)}=D^{(2)}=\epsilon =1\), \(z_1 =1, z_2 =-\,2,\rho =x\), the initial and boundary conditions are chosen as

    $$\begin{aligned} {\left\{ \begin{array}{ll} c^{(1)}(0,x) = 2+x+\sin (2\pi x), \quad c^{(2)}(0,x)=1+x,\\ \partial _x \psi (t,0) =\partial _x \psi (t,1) = 0. \end{array}\right. } \end{aligned}$$
    (4.112)

Figure 1 shows the time evolution of the ion concentrations \(c^{(1)}\), \(c^{(2)}\) and the electrostatic potential \(\psi \). One can see that the proposed scheme works well with a large time step and spatial mesh size in both cases.

To verify the energy dissipation and mass conservation, we plot in Fig. 2 the time evolution of the discrete free energy \(E_{\Delta }(t_n)\) and the total mass \(C^{(1)}_{\Delta }(t_n)\), \(C^{(2)}_{\Delta }(t_n)\). Although not shown here, the positivity of the ion concentrations is also checked and no negative values are detected.

Fig. 1
figure 1

Time evolution of the ion concentrations \(c^{(1)}\), \(c^{(2)}\) and the potential \(\psi \). Top row: Case 1 \(\Delta t=0.05\), \(\Delta x=0.05\). Bottom row: Case 2 \(\Delta t=0.01\), \(\Delta x=0.05\)

Full size image
Fig. 2
figure 2

Time evolution of the discrete energy \(E_{\Delta }(t_n)\) and the total mass \(C_{\Delta }^{(1)}(t_n)\), \(C_{\Delta }^{(2)}(t_n)\). Top row: Case 1. Bottom row: Case 2. Spatial mesh size is fixed at \(\Delta x = 0.001\). Different time steps are chosen as indicated in the figures

Full size image

Next, we check how the tolerance threshold in the fixed point iteration will affect the accuracy. The numerical solution with tolerance \(\text {tol} = 10^{-10}\) is chosen as a reference solution. For Case 1, we check the maximum error for the ion concentrations and electrostatic potential at time \(t = 0.2\). For Case 2, the maximum error is inspected at time \(t = 0.1\). The results in Tables 3 and 4 indicate that our scheme will achieve better accuracy with lower tolerance.

In [4], the exponential convergence towards the steady states was proved for the PNP system

$$\begin{aligned} W(t) \le W(0) e^{-\lambda t}, \quad \text { for } \lambda = \lambda (\Omega ), \end{aligned}$$
(4.113)

where W(t) is the entropy functional defined as \(W(t) = {\tilde{E}}(t) - {\tilde{E}}(t_\infty )\). Here we try to verify such a property for our numerical solution. In Fig. 3, the discrete entropy functional \(W_{\Delta }(t_n) = E_{\Delta }(t_n) - E_{\Delta }(t_{\infty })\) is plotted for both cases, where the exponential convergence is evident.

Table 3 Table of errors for Case 1 at time \(t = 0.2\) with different tolerance \(\text {tol} = 10^{-2},10^{-3},10^{-4},10^{-5}\)
Full size table
Table 4 Table of errors for Case 2 at time \(t = 0.1\) with different tolerance \(\text {tol} = 10^{-2},10^{-3},10^{-4},10^{-5}\)
Full size table
Fig. 3
figure 3

Time evolution of the discrete entropy functional \(W_{\Delta }(t)\) in semi-log plot. Left: Case 1. Right: Case 2. Spatial mesh size is fixed at \(\Delta x = 0.001\). Different time steps are chosen as indicated in the figures. For both cases, we consider the numerical solution at \(t=5\) as the steady state

Full size image

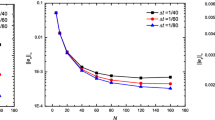
Finally, to demonstrate the convergence of the fixed point iteration, we record the number of iterations at each time step in Fig. 4. We can see that the method converges in less than 10 iterations, and this number decreases as the solution approaches the steady state.

Fig. 4
figure 4

Number of fixed point iterations needed at each time step (the convergence tolerance is set as \(\max _j |c_j^{(i),(l+1)}-c_j^{(i),(l)}|\le 10^{-8}\)). Left: Case 1. Right: Case 2. Spatial mesh size is fixed at \(\Delta x = 0.001\). Different time steps are chosen as indicated in the figures

Full size image

4.3 2D single species

We now apply our scheme to solve the 2D single-species PNP system (3.88)–(3.94). Let \(\Omega = [0,1]\times [0,1]\) be the computational domain and \(D^{(1)}=\epsilon =z_1=1\), \(\rho =0\). Two different boundary and initial conditions are considered:

  1. Case 1

    \(c(0,x,y) = 4, \ \alpha =0,\ \beta =1,\ f_a=f_b=f_c=f_d=-\,1\);

  2. Case 2

    \(c(0,x,y) = 2, \ \alpha =0,\ \beta =1,\ f_a=f_b=-\,1,\ f_c=f_d=0\).

The time evolution of the ion concentration in both cases are shown Figs. 5 and 6, respectively. The energy dissipation is demonstrated in Fig. 7. Finally, the positivity of the ion concentration is also checked and no negative values are detected.

Fig. 5
figure 5

Case 1: time evolution (contour plot) of the ion concentration c. Time step and spatial mesh size are chosen as \(\Delta x = 0.01\) and \(\Delta t = 0.01\)

Full size image
Fig. 6
figure 6

Case 2: time evolution (contour plot) of the ion concentration c. Time step and spatial mesh size are chosen as \(\Delta x = 0.01\) and \(\Delta t = 0.01\)

Full size image
Fig. 7
figure 7

Time evolution of the discrete free energy \(E_{\Delta }(t_n)\). Left: Case 1. Right: Case 2. Spatial mesh size is fixed at \(\Delta x = 0.01\). Different time steps are chosen as indicated in the figures

Full size image

4.4 KcsA model with spatially dependent diffusion coefficients

In the ion channels, values of the diffusion coefficients depend on ion species and channels. They affect only the convergence rate of the system to the steady state. In this test, we apply our scheme to a simplified KcsA model with spatially dependent diffusion coefficients [13] to verify the impact of diffusion coefficients.

We consider the KcsA model in domain \([-1,1]\) with \(\epsilon =1\), \(z_1 =1, z_2 =-\,1,\rho =0\), the initial and boundary conditions are chosen as

$$\begin{aligned} {\left\{ \begin{array}{ll} c^{(1)}(0,x) = 2-x^2, \quad c^{(2)}(0,x)=x^2, \\ \psi (t,-1)= -\,1, \quad \psi (t,1)= 1. \end{array}\right. } \end{aligned}$$
(4.114)

Then we separate the domain into three regions:

  1. (a)

    channel outside (CO): \(0.7 \le |x|\le 1\);

  2. (b)

    selectivity filter (SF): \(-0.1<x<0.7\);

  3. (c)

    intracellular (IC): \(-0.7< x < -0.1\).

Outside the channel the diffusion coefficients are set as \(D^{(1)} = D^{(2)} = 1\). We test three diffusion coefficient profiles:

  1. (i)

    \(D^{(i)}\) is reduced to 0.4 in SF;

  2. (ii)

    \(D^{(i)}\) is reduced to 0.4 in SF and 0.8 in IC;

  3. (iii)

    \(D^{(i)}\) is reduced to 0.4 in both SF and IC.

The time evolution of the ion concentrations and energy are presented in Figs. 8 and 9. These three systems do converge to the same steady state with different rates.

Fig. 8
figure 8

Time evolution of the ion concentrations in KcsA model. First column: case i. Second column: case ii. Third column: case iii. Time step and spatial mesh size are chosen as \(\Delta t =0.05 \) and \(\Delta x = 0.05\)

Full size image
Fig. 9
figure 9

Time evolution of the energy in KcsA model. Time step and spatial mesh size are chosen as \(\Delta t =0.05 \) and \(\Delta x = 0.05\)

Full size image

4.5 Gouy–Chapman model

In this final test, we simulate the so-called Gouy-Chapman model widely used to describe the double layer structure in ion channels.

We consider the 1D two-species PNP system (3.32)–(3.37) in domain \([-1,1]\) with \(D^{(1)} = D^{(2)} =\epsilon = 1\), \(z_1 = 1\), \(z_2 = -\,1\), and \(\rho =0\). The dimensionless parameters \(\chi _1\) and \(\chi _2\) are chosen as \(\chi _1 = 3.1, \chi _2 = 125.4\), which are taken from the work [12]. A uniform initial condition is assumed \(c^{(i)}(x,0) =1, i= 1,2\) for all \(-1\le x \le 1\) and the boundary condition for the Poisson equation is given by \(\alpha =1, \beta = 4.63 \times 10^{-5},f_a = 1, f_b = -\,1\).

Figure 10 shows the time evolution of the ion concentrations and the electrostatic potential. Beginning with the linear profile, the electrostatic potential becomes zero in the bulk region (away from the boundary) and increases drastically in the diffuse layers (close to the boundary) at the steady state. Notice that the presence of diffuse layers requires a small spatial mesh size in numerical simulations. The solution will be far away from the thin layer solution if the mesh size is large, for example, \(\Delta x > 0.05\).

Fig. 10
figure 10

Time evolution of the ion concentrations and the electrostatic potential in Gouy-Chapman model. Time step and spatial mesh size are chosen as \(\Delta t =0.00125\) and \(\Delta x = 0.02\)

Full size image

5 Conclusion

We have introduced a semi-implicit finite difference scheme for the PNP equations in a bounded domain. A general boundary condition for the Poisson equation which includes (nonhomogeneous) Dirichlet, Neumann, and Robin boundaries as subcases were considered. The proposed scheme is first order in time and second order in space. The fully discrete scheme was proved to be mass conservative, unconditionally positive and energy dissipative (hence preserving the steady state). The solvability of the semi-discrete scheme was investigated and a fixed point iteration was proposed to solve the fully discrete scheme. Numerical examples were presented to demonstrate the accuracy and efficiency of the proposed scheme. Note that the fixed point iteration employed in this work is not necessarily the best method to solve the implicit scheme. We will investigate different iterative methods such as Newton’s method in future work. Also, it would be interesting and challenging to develop a high order in time scheme which preserves the same properties as the first order one.