Atomic Force Microscopy: Imaging and Rheology of Living Cells

Abstract

Atomic force microscopy (AFM) has been widely used for characterizing physical properties of adherent living cells because it provides high-resolution images and accurate measurements of mechanical properties without modifications to the cells. In this chapter, we review recent advances in AFM single-cell imaging and rheology. Techniques for AFM imaging and mechanical measurements of living cells are first reviewed. We then discuss how rheological properties of cells, which are described as power-law rheology model, are quantified for single-cell diagnostics. In addition to micro- and nano-measurements of cell moduli, we introduce an AFM method combined with a micro-fabricated substrate as a force sensor for investigating how forces propagate inside cells through the cytoskeleton, which is deeply associated with various cell functions. Finally, we reviewed scanning ion conductance microscopy, which allows us to obtain noncontact image of cell membrane topography and to quantify cell membrane fluctuations that are inaccessible to AFM.

15.1 Principles of AFM

15.1.1 Imaging

Atomic force microscopy (AFM) [1] is a scanning probe technique that has been adapted for high-resolution imaging, characterization of mechanical properties, and manipulation of living cells. AFM uses a cantilever as a sensor (Fig. 15.1) of forces between a sample surface and a probe tip attached at the end of the cantilever. The forces are detected by either cantilever deflection, damped vibration amplitude, or frequency and/or phase shifts [2, 3]. During image acquisition, the cantilever is raster scanned laterally (x–y axes) over the sample surface, while its vertical position (z-axis) is regulated with a feedback circuit that maintains a constant force between the probe and sample. For high-resolution imaging, a sharp probe tip (<20 nm radius) is required.

Fig. 15.1

Principles of AFM. The force between the cantilever tip and the sample is detected by deflection of the cantilever and an optical lever coupled with a position-sensitive photodetector (PSD). The PSD signal is used to regulate the force

In contact mode AFM operation, the force between the tip and the surface is kept constant by maintaining a static deflection of the cantilever (Fig. 15.2a). Thus, the z-position corresponds to the topography of the cell sample. In the case of soft samples such as cells, the contact force may cause local deformation (Figs. 15.2c and 15.3a). To minimize deformation, the contact force should be <1 nN [4], and a low-stiffness (∼0.1 N/m) cantilever should be used.

Fig. 15.2

Imaging modes of AFM: (a) contact mode and (b) AM mode. The sample is a hard elastic material with a soft viscoelastic region. (c) Topography and (d) deflection images in contact mode. (e) Topography and (f) phase-shift images in AM mode

Fig. 15.3

Contact mode height (a) and deflection (b) images of a living cell showing cytoskeletal structures (Reprinted with permission from [5])

The deflection of the cantilever would be unchanged if the feedback was perfectly regulated. During imaging, however, the deflection signal changes slightly with abrupt changes in the cell surface morphology. The corresponding error signal can be used to construct images in which changes in topography are sharply identified (Fig. 15.2d). In Fig. 15.3, a deflection error image reveals underlying cytoskeletal structures more clearly than the corresponding topography (z-piezo) image [5].

In contact mode, the scanning tip may generate lateral forces that could drag the cell surface. To reduce lateral forces, amplitude modulation (AM) mode or “tapping” mode AFM was developed. For intermittent contact, the cantilever is continuously oscillated in the z-direction (Fig. 15.2d). The small amplitude of the oscillation near the cantilever’s fundamental resonance frequency f ₀ is used as the feedback signal for maintaining intermittent contact during topographic image acquisition. As in contact mode, the intermittent contact force and lateral forces could also deform a soft sample surface (Fig. 15.2e). The phase difference between the oscillation drive signal and the oscillating cantilever is sensitive to the change in the topography and reflects energy dissipation in the sample (Fig. 15.2f).

AM mode is used for high-speed AFM (HS-AFM) [6, 7], at video rates for high-resolution observation of dynamic processes. Recently, HS-AFM combined with a wide-area scanner was used to acquire video images of endocytosis on a living cell surface (Fig. 15.4) [8].

Fig. 15.4

HS-AFM images showing the dynamics of endocytosis (dotted circles) in HeLa cells. Scan range and imaging rate are 5 × 5 μm and 5 s/frame over 200 × 200 pixels (Reprinted with permission from [8])

When the cantilever is oscillated at frequency f ₀, the motion of the cantilever also includes higher harmonic modes (2f ₀, 3f ₀, etc.) because of nonlinear interactions between the AFM tip and the sample [9]. The interaction of the harmonic components with the cell surface can be employed to characterize local stiffness, stiffness gradients, and viscoelastic dissipation at high resolution [10].

In a technique called scanning near-field ultrasonic holography (SNFUH), the sample and the cantilever are simultaneously excited at different ultrasonic frequencies (MHz) f _S and f _C, respectively (Fig. 15.5). The ultrasonic vibration of the cantilever allows us to generate images of subsurface structures in cells because the mechanical waves propagate through the cell and are perturbed by internal structures [11, 12]. The amplitude and the phase shift reflect the local mechanical properties of the subsurface structures. In Fig. 15.5, SNFUH images of nanoparticles embedded in red blood cells are clearly shown [11, 12]. The imaging depth strongly depends on the material properties of the sample [13], but the mechanism of SNFUH imaging is not fully understood.

Fig. 15.5

(Left) Schematic of scanning near-field ultrasonic holography (SNFUH). The cantilever and the sample are vibrated at fc and fs ultrasonic frequencies, respectively. The AFM cantilever is locked in at the frequency difference |fc-fs|, providing information about local intracellular nano-mechanical structures. (Right) Images of nanoparticles in red blood cells (Reprinted with permission from [11])

15.1.2 AFM Probe

The shape of the AFM probe in the region that interacts directly with the sample surface affects imaging resolution as well as mechanical properties. Sharp tips required for a high-resolution imaging are more likely to damage soft cells with fragile structures. Moreover, the exact profile of a sharp tip is hard to determine precisely, precluding quantitative mechanical measurements. For those reasons, a silica or polystyrene colloidal bead [14] with a well-defined spherical shape is widely used for force measurements on cells. It can be attached to a cantilever in various ways (Fig. 15.6). When the bead of the colloidal probe cantilever contacts the cell surface in a liquid environment, the liquid between the cantilever and the cell surface is highly confined and squeezed. This enhances viscous damping of the cantilever and affects the rheological observations. Because the squeezing effect can be reduced by increasing the distance between the cantilever and the surface [17], attaching the bead to the apex of the probe (Fig. 15.6c, d) is suitable for single-cell rheology.

Fig. 15.6

Different mounting geometries for a colloidal bead probe on a cantilever. (a) Attached to a tip-less cantilever. (b) Attached beside a sharp tip. (c) Attached at the apex of a sharp tip. Reprinted with permission from [15]. (d) Electron microscope image of a probe attached as in (c) (Reprinted with permission from [16])

Adhesion between the colloidal bead and the cell surface should be minimized for single-cell rheology because the Hertz model [2, 3, 18, 19], which is the standard model for estimating contact mechanics, assumes that there is no adhesion between contacting materials. Hydrophobic perfluorodecyltrichlorosilane-coated colloidal beads [20] work well to prevent adhesion to the cell surface during force measurements.

15.1.3 Force Measurements

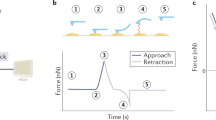
Elastic properties, i.e., reversible deformation of cells, are estimated from the relationship between the loading force F and the normal displacement Z of the AFM probe as it deforms the cell surface (Fig. 15.7a). The indentation δ in the cell surface is determined by subtracting the cantilever deflection d from the displacement Z. The loading force is estimated from Hook’s law (F = kd), where the spring constant k of the cantilever can be determined by thermal fluctuations [21].

Fig. 15.7

(a) Force curve measurements. (i) The cantilever is separated from the sample surface and no deflection occurs. (ii) The AFM cantilever probe contacts the cell surface at the position Z = 0. (iii) The AFM probe indents the cell sample a Z from the position in (ii). The deflection of the cantilever is d, while the indentation is δ, where δ = Z – d (Reprinted with permission from [15]). (b) Characteristic features of force–distance curves measured in viscoelastic materials

F(δ) depends on the shape of the AFM probe. According to the Hertz model for a spherical probe with radius R [2, 3, 18, 19], F is given by

$$ F=\frac{4}{3}\frac{E{R}^{1/2}}{1-{\nu}^2}{\delta}^{3/2}, $$

(15.1)

where ν is Poisson’s ratio, which is assumed to be 0.3–0.5 for cells [2, 3], and E is Young’s modulus. E has been measured in various animal cells [2, 3], and its spatial heterogeneity has been resolved [5, 22, 23]. In one case, local values of E were attributed to actin filaments rather than microtubules and intermediate filaments [5].

Cells are not completely elastic, but behave more like a compliant viscoelastic material. Therefore, because of energy dissipation in the cells, force–distance curves tend to exhibit hysteresis between approach and retraction (Fig. 15.7b) [24]. Thus, E estimated by force–distance curve measurements may depend on the speed of approach or retraction. Because it increases with increasing speed (Fig. 15.7b), E from force curve measurements is an “apparent” Young’s modulus. Thus, frequency and/or time domain AFM measurements are indispensable for quantifying intrinsic mechanical properties of cells.

15.1.4 Frequency Domain AFM

In the force modulation mode [25–27], the dynamic response due to an external periodic strain is measured (Fig. 15.8a). The strain is due to a cantilever that is sinusoidally oscillated with fixed amplitude (usually 10–50 nm) at several frequencies during indentation. The amplitude and phase shift of the cantilever displacement are measured with a lock-in amplifier.

Fig. 15.8

Schematics of AFM rheology measurements: (a) force modulation mode, (b) stress relaxation, and (c) creep relaxation (Reprinted with permission from [15])

Using the Hertz model from Eq. 15.1, the complex loading force F* with a small complex amplitude indentation oscillation ${\delta}_1^{\ast }$ around an operating indentation δ ₀ is approximately expressed [25–30] by a first-order Taylor expansion:

$$ {F}^{\ast }=\frac{4{R}^{1/2}}{3\left(1-{\nu}^2\right)}\left({E}_0{\delta}_0^{3/2}+\frac{3}{2}{E}_1^{\ast }{\delta}_0^{1/2}{\delta}_1^{\ast}\right), $$

(15.2)

where E ₀ is Young’s modulus at zero frequency and ${E}_1^{\ast }$ is the frequency-dependent Young’s modulus, given by $2\left(1+\nu \right){G}^{*}$ [19]. Since the oscillating probe experiences hydrodynamic drag forces ${F}_{\mathrm{d}}^{\ast }$ [17], G ^* is given by

$$ {G}^{\ast }=G^{\prime }+iG^{{\prime\prime} }=\frac{1-\nu }{4{\left(R{\delta}_0\right)}^{1/2}}\left[\frac{F_1^{\ast }}{\delta_1^{\ast }}-ib(0)f\right], $$

(15.3)

where ${F}_1^{\ast }=2{\left(R{\delta}_0\right)}^{1/2}{E}_1^{\ast }{\delta}_1^{\ast }/\left(1-{\nu}^2\right)$ and b is the drag factor [17]. F ^*_d at a separation distance h between the sample surface and the probe with ${\delta}_1^{\ast }$ is defined as F ^*_d /δ ^*₁ = ib(h)f. The value b(0) can be determined by the extrapolation of b(h) measured at an oscillating frequency [17]. The phase shift and amplitude of the AFM instrument at different frequencies can be calibrated with a stiff cantilever in contact with a clean glass substrate in air [17, 28]. By using this method, G ^* for several cell types has been measured in detail.

15.1.5 Time Domain AFM

In AFM stress relaxation [16, 20, 24, 31–33], Z is kept constant at the position where the initial force is applied, and F is measured as a function of time t (Fig. 15.8b). The cantilever defection d and the corresponding indentation δ both change during stress relaxation. This situation is not like conventional stress relaxation measurements where the strain is kept a constant value and the stress is measured as a function of t. In cell experiments, the change in d is typically about 1 % (10 nm) of that for δ (1 μm). Therefore, it is assumed that d is approximately constant relative to δ. According to the Hertz model, in which the contact radius a is dependent only on δ with a fixed probe radius R, the average stress is F/(πa ²).

Since F, δ, and E are time dependent, and based on the Hertz model of Eq. 15.1, F is given by

$$ F(t)=\frac{4{R}^{1/2}E(t)}{3\left(1-{\nu}^2\right)}{\delta}^{3/2}(t), $$

(15.4)

where E(t) is the relaxation modulus at t.

In the case of stress relaxation with a constant indentation δ ₀, F(t) is proportional to E(t)H(t) by Eq. 15.4, using the Heaviside step function H(t) [32, 34]. As shown below, G(f) for cells follows a single power law of frequency f ^α at low frequencies. Since the relaxation modulus in the Laplace domain E(f) is proportional to f ^α from the relation $E(f)=2\left(1+\nu \right)G(f)$ (in the case where ν is independent of t) [19], F(f) is proportional to ${f}^{\alpha -1}$. Therefore, the inverse Laplace transform of F(f) yields the functional form of the loading force for stress relaxation: $F(t)\propto {t}^{-\alpha }$. Since cells are generally soft, F decreases significantly over long time periods and may approach zero. Therefore, stress relaxation, when compared to creep relaxation, is insensitive for long-term measurements of cell rheology. Furthermore, large initial loading forces required to enhance the signal-to-noise ratio for stress relaxation curves over long times cause large deformations in cells. This may also induce the cells to actively escape from the stress.

Creep relaxation of single cells can also be performed by AFM [20, 35]. In this case, the probe contacts the cell surface at a constant F under feedback, and Z is monitored as a function of t (Fig. 15.8c). Because the contact radius a changes during creep relaxation, the stress applied to the cell is not constant and decreases with t. The relationship between a(t) and the creep compliance J(t) becomes ${a}^3(t)\propto J(t)$ [18]. If G(f) follows a single power law of the form f ^α, J(t) is proportional to t ^α. Moreover, by using ${a}^2(t)=R\delta$ [18, 19], the indentation for creep relaxation is given by $\delta (t)\propto {t}^{2\alpha /3}$. For soft cells during creep measurements, δ significantly increases over long time periods, allowing us to easily monitor the relaxation. Conversely, the observed relaxation curve may reflect the highly heterogeneous cell structure with depth. Fluctuation and active movement of the cell also occur because of large δ.

15.2 Single-Cell Rheology

15.2.1 High-Throughput Measurements

Among single cells of the same source and type, rheological properties exhibit spatial, temporal, and intrinsic variations. High-throughput techniques, based on magnetic or optical trapping with micron-sized beads [36–42], micro-fluidic systems [43, 44], and AFM with micro-fabricated substrates [45–48], have been developed to characterize large numbers of cells.

Magnetic twisting cytometry (MTC) is one of the most common methods for investigating rheology statistics of adherent cells. A micron-sized magnetic bead is attached to a cell surface via binding proteins, and the cell modulus is estimated from the displacement of the beads under a periodic, external magnetic force (Fig. 15.9a). Lateral [36–42] or vertical [49] displacement of a large number of microbeads can be simultaneously monitored with optical microscopy. The disadvantages of MTC are that the contact geometry and the degree of binding between the microbeads and the cell surface are not well known, and the positions on the cell surfaces are not precisely controlled. Thus, it is difficult to assess cell-to-cell variations from the experimental data. Furthermore, focal adhesion complexes form at the microbead binding sites; thus, local reorganization of the cytoskeleton may alter the rheology [28].

Fig. 15.9

Depiction of single-cell rheology for a large number of cells: magnetic twisting cytometry (MTC), micro-fluidic optical stretcher, and AFM on a micro-fabricated substrate

Micro-fluidic techniques can provide very high-throughput measurements of single-cell rheology. Suspended cells flowing in micro-channels can be deformed by optical pressure (Fig. 15.9b) [43] or hydrodynamic forces [44], and the deformability of whole cells floating in a micro-fluidic chamber is estimated. One disadvantage is that adherent cells have to be detached from their substrate, which may perturb intracellular structures that, in turn, affect cell mechanics.

With micro-fabricated substrates, one can use AFM to characterize the rheology of a large number of single cells rapidly (Fig. 15.9c). It has the advantage of measuring mechanical properties of single adherent cells at any region on the surface without cell surface modification [2, 3]. Thus, AFM is a less-invasive technique for measuring intrinsic mechanical features of single cells.

15.2.2 Power-Law Rheology Model

Because cells have internal organelles, their spatial–temporal rheological properties will vary from cell to cell. In spite of the structural complexities, the rheology of cells has been widely explained in terms of linear viscoelastic [34] or structural dampening models [36, 37, 50, 51].

In linear viscoelastic models, the cell is simulated with linear springs and linear viscous dashpots, and inertia effects are neglected. Therefore, creep and stress relaxations are sums of single-exponential functions in the time domain [34].

Power-law behaviors as a function of f have been observed for cell rheology with MTC and AFM. G′ exhibits one single-power-law behavior in the range of 10⁰–10² Hz, whereas, for other frequency ranges, other power-law models have been proposed: single (Fig. 15.10a) [36, 37] and multiple (Fig. 15.10b) [38, 52].

Fig. 15.10

Power-law models of G′ as a function of f. (a) Single-power-law model for single cells under different conditions and (b) multiple-power-law model

Fabry et al. reported that G′ followed a single-power-law function over 10⁻²–10³ Hz, where the exponent α depended on the cytoskeletal architecture, regardless of modifications by chemical drugs, and appeared to cross at G′ = g ₀ at a high frequency f = Φ₀ [36, 37] (Fig. 15.10a). In this model, the complex shear modulus G ^* is given by the structural damping model [36, 37, 50, 51]:

$$ {G}^{\ast }={G}_0\left(1+i\eta \right)\;{\left(\frac{f}{f_0}\right)}^{\alpha}\Gamma \left(1-\alpha \right) \cos \left(\pi \alpha /2\right)+i\mu f, $$

(15.5)

where η is the hysteresivity, which is expressed by tan(πα/2), G ₀ is a modulus scale factor at a frequency scale factor of f ₀, and Γ denotes the gamma function. The α-value was 0.1–0.4 depending on cell type, where α = 0 is solid-like and α = 1 is fluidlike. The Newtonian viscous term μf is small, except at high frequencies. Single power laws have been discussed in detail in terms of soft glassy rheology (SGR) [50, 53, 54].

In contrast, two power-law exponents in the frequency domain have been observed; they cross over at around 10⁰ Hz or 10² Hz (Fig. 15.10b). The exponent for the lower frequencies was 0.5, because of noncovalent protein–protein bond rupture during near-equilibrium loading [52]. Meanwhile, the exponent for the higher frequencies was about 0.75, because of entropic fluctuations of semi-flexible filaments and soft-glass-like dynamics [38].

Multiple-power-law cell rheology has also been observed in time domain experiments. Overby et al. reported that α = 0.18 for pulling a single cell in a creep experiment over several seconds and α = 0.5 for longer time scales [55]. Using magnetic microbeads, Stamenovic et al. reported that in creep experiments of single cells over a wide range of time scales, there were two power-law regimes with an intervening plateau over 10 s [56]. Desprat et al. employed a uniaxial stretching rheometer to observe that the creep function of pulling a whole cell follows a power-law exponent of 0.24 for periods <200 s, while for periods >200 s, the exponent increased to ≈ 0.5 [57]. These studies commonly showed that in the intermediate frequency range of 10⁰–10² Hz, the single power law is an intrinsic feature of cell mechanics and is valid at size scales from a few tens of nanometers to the entire cell. However, it is not elucidated whether passive and active cell behaviors are involved in the mechanics over longer time scales.

15.2.3 Ensemble Averaged Single-Cell Rheology

15.2.3.1 Frequency Domain AFM

Mahaffy et al. used force modulation mode with a colloidal probe on an AFM cantilever to measure the mechanical properties of cells as a function of indentation depth δ and estimated the viscoelastic parameters and Poisson’s ratio quantitatively [29, 30]. Using the AFM model in Eq. 15.3, Alcaraz et al. revealed a characteristic feature of averaged G′ and G″ for single cells as a function of f [28]. The typical behavior of G* is shown in Fig. 15.11. G′ increased linearly in a log–log scale, exhibiting a weak power-law dependence on oscillation frequency. Conversely, G″ displayed a similar frequency dependence at values <10 Hz, and the frequency dependence was more pronounced at higher frequencies. The results fit the structural damping model shown in Eq. 15.5. This power-law frequency dependence has been observed with AFM in different cell types [45, 58, 59]. However, the absolute values of G′ and G″ were different between cell types.

Fig. 15.11

Storage modulus G′ (left) and loss modulus G″ (right) of adherent mouse fibroblast cells

15.2.3.2 Time Domain AFM

Darling et al. measured the stress relaxation of single cells for ≈ 60 s with a colloidal probe cantilever [32, 33]. They observed that the stress relaxation was a single-exponential function, obeying a linear viscoelastic model. Moreno-Flores et al. reported that heterogeneities in single-cell rheology could be imaged with stress relaxation AFM [60].

Wu et al. investigated the relationship between viscoelastic properties and the cytoskeletal architecture of cells by using creep relaxation AFM. They demonstrated that creep relaxation for 60 s could be fit with a standard linear solid model consisting of two springs and one dashpot [35]. The creep relaxation of cells treated with various chemical drugs affecting the cytoskeleton was examined. Cytochalasin D (cytoD), which depolymerizes actin filaments, reduced both elasticity and viscosity, whereas nocodazole or colcemid, which depolymerizes microtubules, exhibited a marked increase in elasticity and a slight increase in viscosity. Thus, changes in cytoskeletal structure can be detected by using AFM in the time domain.

The results from stress and creep relaxation experiments are inconsistent with those obtained with force modulation mode, where power-law behavior in the frequency domain has been widely observed. In this context, the relaxation behavior of individual cells placed and cultured in microarray wells was characterized with AFM by averaging several relaxation curves (Fig. 15.12) [20]. Tails in both stress and creep relaxation curves at long times follow single power laws over 60 s. Also, α = 0.1–0.4, which varies between cells and has an average value in good agreement with that estimated from the force modulation mode [45].

Fig. 15.12

Linear plots of the averaged AFM stress (a) and creep (b) relaxation curves for NIH3T3 cells on a microarray. The insets show the corresponding relaxations on logarithmic axes. Solid lines represent the fit of the power-law functions described in the main text (Reprinted with permission from [20])

15.2.4 Cell-to-Cell Variability

15.2.4.1 Statistics of Single-Cell Rheology

The statistics of single-cell rheology is crucial to reveal a universal behavior of single cells and to conduct single-cell diagnostics automatically. Hoffman et al. found that the distribution of G ^* measured by MTC followed a lognormal and that the amplitude of the rocking motion or mean-square displacement of beads in cells varied dramatically for different methods [40]. Moreover, Massiera et al. showed that by using MTC and laser tracking micro-rheology, the magnitude of G ^* at a low frequency exhibited a lognormal distribution, whereas the single-power-law exponent was a normal Gaussian [41]. Using optical trapping and uniaxial stretching of single cells, Balland et al. also showed that α is distributed normally over a cell population and that the prefactors of G* and J follow a lognormal distribution [42].

The statistical properties of single-cell rheology were investigated with AFM on a microarray of wells [45] (Fig. 15.13). Experimental variation is minimized because the cell shape is highly controlled in each well and the measurement position of cell is well defined. Force measurements are automatically performed at the centers of each well without confirming the cell positions. Figure 15.14 shows the distributions of single cells cultured in the wells [45]. We observed four characteristic features from the number distributions of mouse fibroblast cells [47]. First, ${G}^{\ast }$ consistently exhibited a lognormal distribution. Second, the geometric mean of ${G}^{\ast }$ ($\overline{G}^{\prime }$ and $\overline{G}^{{\prime\prime} }$) shifted to higher values with increasing f. Third, the distribution of G′ became narrower with f, and the distributions of G″ were narrower than those of G′. Fourth, the distribution of ${G}^{\ast }$ for the cytoD-treated cells was narrower than that of the untreated cells.

Fig. 15.13

Schematic of AFM for microarrays of cells. Force modulation mode measurements are automatically examined at the centers of the wells after a specific cell is chosen with optical microscopy (Reprinted with permission from [47])

Fig. 15.14

Distributions of the storage G′ (left) and loss G″ (right) moduli of untreated fibroblast cells in microarray wells at different frequencies: (a) 5, (b) 100, and (c) 200 Hz. The solid line represents the fitted result using a lognormal distribution function

${\overline{G}}^{\prime }$ and ${\overline{G}}^{{\prime\prime} }$ increased with f and closely followed the structural damping in Eq. 15.5 (Fig. 15.15a, b). The depolymerization of actin filaments resulted in a decrease in ${\overline{G}}_0$ and an increase in the arithmetic mean of α, 〈α〉, which were similar to those characteristics measured with MTC [36, 37, 61, 62]. The standard deviation of the complex modulus ${\sigma}_{\ln {G}^{\ast }}$ was reduced in the treated cells (Fig. 15.15c, d), indicating a strong coupling between cell-to-cell variation and the cytoskeleton, where σ _X represents the standard deviation of X. The ${\sigma}_{\ln {G}^{\ast }}$ in the untreated and treated cells crossed at the point where the extrapolated lines of ${\overline{G}}^{\prime }$ for the treated and untreated cells intersect; this was defined as ${\overline{G}}^{\prime }={\overline{g}}_0$ at $f={\overline{\varPhi}}_0$ (Fig. 15.15) [36, 37].

Fig. 15.15

Frequency dependences of ${\overline{G}}^{*}$ (${\overline{G}}^{\prime }$ (a) and ${\overline{G}}^{{\prime\prime} }$ (b)) of untreated (circle) and treated (square) cells. Solid lines in (a) and (b) are fits to Eq. 15.3. The point where the curves of ${\overline{G}}^{\prime }$ intersect is defined as ${\overline{G}}^{\prime }={\overline{g}}_0$ at $f={\overline{\varPhi}}_0$. Frequency dependence of ${\sigma}_{\ln {G}^{\prime }}$ (c) and ${\sigma}_{\ln {G}^{\prime }}$ (d) of untreated (circle) and treated (square) cells. Solid lines in (c) are fits to Eq. 15.8 (Reprinted with permission from [47])

Regarding the parameters of the single-power-law rheology in Eq. 15.5, G ₀ was lognormal with a narrower distribution after cytoD treatment. The power-law exponent α exhibited a Gaussian distribution that also became narrower after cytoD treatment, whereas μ had a lognormal distribution, and its mean value did not change significantly after treatment (Fig. 15.16).

Fig. 15.16

Distributions of (a) G ₀ on a logarithmic scale, (b) α on a linear scale, and (c) μ on a logarithmic scale of untreated (white) and treated (gray) cells. Inset in (c) shows the distribution of μ on a linear scale. Solid and dashed lines represent the fitted results of untreated and treated cells, respectively, using a lognormal distribution function (a and c) and to a normal distribution function (b and inset in c) (Reprinted with permission from [47])

15.2.4.2 Standard Deviation of Cell Storage Modulus

In the single-power-law rheology model, G′ for each cell is expressed as

$$ {G}^{\prime }={g}_0{\left(\frac{f}{\varPhi_0}\right)}^{\alpha }, $$

(15.6)

where Φ ₀ can be estimated by extrapolating G′ vs. f curves acquired under various conditions. Data for single cells specified by (g ₀, Φ ₀) varies considerably [47], indicating that cells exhibit mechanical variability that corresponds to the variation in potential energy that a cytoskeletal element must overcome to escape the glass transition, according to the SGR model [50, 53, 54].

Since lng(α) is approximately linear with respect to α [47, 63], the linear relation between lnG ₀ and α for each cell in Eq. 15.6 is given by

$$ \ln {G}_0= \ln {\overline{g}}_0-\left[ \ln \left(\frac{{\overline{\varPhi}}_0}{f_0}\right)+\frac{d \ln g\left(\alpha \right)}{d\alpha}\right]\alpha, $$

(15.7)

where ${\overline{g}}_0$ and ${\overline{\varPhi}}_0$ are the geometric mean of g ₀ and Φ ₀, respectively.

From Eq. 15.7, we obtain

$$ {\sigma}_{\ln {G}^{\prime }}={\sigma}_{\ln {g}_0}+\left( \ln {\overline{\varPhi}}_0- \ln f\right){\sigma}_{\alpha }, $$

(15.8)

which shows that ${\sigma}_{\ln {G}^{\prime }}$ is proportional to ln f with a slope of $-{\sigma}_{\alpha }$ at $f<{\overline{\varPhi}}_0$, which is the frequency-dependent component in terms of the SGR model. The variation, from all sources, in the mechanical responses is characterized by ${\sigma}_{\ln {g}_0}$ at $f={\overline{\varPhi}}_0$, which is the purely elastic component in the SGR model. It was found experimentally that ${\tilde{\sigma}}_{\ln {G}^{\prime }}$, which is defined as ${\sigma}_{\ln {G}^{\prime }}-{\sigma}_{\ln {g}_0}$ and is a function of f, was highly invariant for different cell samples cultured in different dishes (Figs. 15.17 and 15.18).

Fig. 15.17

${\sigma}_{\ln {G}^{\prime }}$ as a function of f as shown in Eq. 15.8. ${\tilde{\sigma}}_{\ln {G}^{\prime }}$, which is defined as ${\sigma}_{\ln {G}^{\prime }}-{\sigma}_{\ln {g}_0}$, is the frequency-dependent component that is experimentally invariant among different cell samples of the same cell type

Fig. 15.18

${\tilde{\sigma}}_{\ln {G}^{\prime }}$, which represents ${\sigma}_{\ln {G}^{\prime }}-{\sigma}_{\ln {g}_0}$ as a function of ln f. One array has untreated (closed rectangle) and treated (open rectangle) cells measured at the center of wells, whereas the other has untreated cells measured at the centers of microarray wells having 20 μm (closed triangle) or 4.5 μm spacing from the centers (open triangle). Solid lines are fits to Eq. 15.8 (Reprinted with permission from [47])

In Fig. 15.18, ${\tilde{\sigma}}_{\ln {G}^{\prime }}\;vs.\;f$ shows that (1) ${\tilde{\sigma}}_{\ln {G}^{\prime }}$ for cells treated with cytoD was largely reduced relative to that for control cells, and (2) ${\tilde{\sigma}}_{\ln {G}^{\prime }}$ away from the center of the wells, but still within the nuclear boundary, was smaller than the corresponding value at the center. The results reveal that the frequency dependence of ${\tilde{\sigma}}_{\ln {G}^{\prime }}$ varies with the integrity of the actin network and that the cell-to-cell mechanical variation exhibits a spatial dependence. The cell-to-cell variation of G′ in the frequency domain is depicted schematically in Fig. 15.19.

Fig. 15.19

Schematic of G′ of untreated cells (a) and cytoD-treated cells (b) at different frequencies. The cell-to-cell variation of G′ depends on intracellular locations: the distribution narrows when changing from cell center to cell nucleus boundaries. The spatial component of the cell-to-cell variation of G′ between untreated and treated cells decreases with increasing f, and consequently both cells become spatially homogeneous at $f={\overline{\varPhi}}_0$ beyond the SGR region (see Eq. 15.8), but the cell-to-cell variation still exists at $f={\overline{\varPhi}}_0$. The spatial variation of G′ for the untreated cells in the SGR region is larger than that for treated cells. One experimental condition is that G ^′_a (σ_II) and G ^′_b (σ_I) represent values measured at off-center and center locations, respectively, while the other G ^′_a (σ_I) and G ^′_b (σ_II) are those of the untreated and treated cells, respectively (c) (Reprinter with permission from [47])

In SGR, the power-law exponent of G′ is related to the probability of transitions between the potential wells, where the transition rate decreases with a decreasing value of the exponent [50, 53, 54]. SGR elements and energy wells can be identified with myosin motors and the binding energies between myosin and actin, respectively [50], suggesting that the depolymerization of actin filaments by cytoD reduces actin–myosin interactions and enhances the spatial homogeneity of the interactions.

Cells interact mechanically with neighboring cells. The microarray wells were not completely separated, so that neighboring cells were in partial contact. There have been no reported data regarding the influence of cell-to-cell contact on mechanical measurements [52]. Recently, an AFM study in which NIH3T3 cell migration was highly inhibited on micro-patterned substrates revealed that the power law of G* is not significantly influenced by cell-to-cell contact [64]. Micro-patterned substrates have been widely used for investigating the relationship between cell mechanics and intracellular cytoskeletal structures. Thus, AFM of cells on micro-patterned substrates should be a good way to characterize single-cell mechanical variations.

15.2.4.3 Cancer Cell Detections

The mechanics of living cells are extremely important for understanding motility, division, and adhesion [1–4]. Furthermore, mechanical properties may also be used to distinguish between normal and abnormal cells. Deformability is widely used to identify cancer cells [43, 44]. Optical stretchers [43] and deformability cytometry [44] both employ micro-fluidic chambers, in which suspended cells are deformed by either optical pressure (optical stretching) or hydrodynamic forces (deformability cytometer), and the deformations are monitored with a high-speed camera system [43, 44].

To diagnose unmodified single cells attached on substrate, Lekka et al. [65] used AFM to show that Young’s modulus E of normal human epithelial cells was one order of magnitude higher than cancer cells. Cross et al. [66] also reported that an ex vivo AFM mechanical analyses of patient cancer cells correlated well with conventional immune-histochemical testing. As mentioned before, the G ₀ value, which is related to E, is dependent on the measurement position. Therefore, AFM cancer cell detection is expected to be more precise on micro-fabricated substrates.

AFM has been used to characterize normal and cancerous tissues to understand how the transformation from health to malignancy alters the mechanical properties within the tumor microenvironment [67]. The spatial distributions of E on normal and benign tissues had a single distinct peak, indicating uniform stiffness. In contrast, malignant breast tissues had a broad distribution because of tissue heterogeneity, with a prominent low-stiffness peak representative of cancer cells. The results suggest that AFM provides quantitative indicators at the tissue level for clinical diagnostics of breast cancer with translational significance.

15.3 Single-Cell Dynamics

15.3.1 Force Propagation in Cells

When adherent cells contact a substrate, they form focal contacts that are adhesion sites at the cell–substrate interface formed by integrin receptors. The cells then form stress fibers that are coalesced actin filaments to anchor at the focal contacts and increase stiffness in response to stress applied to the integrins. CSK filaments and nuclear scaffolds are discretely connected to each other in response to external static forces [68, 69]. Force measurements using both magnetic microbeads [70–73] and an elastic micro-pillar [74] revealed that static forces propagate across discrete CSK elements over long distance through the cytoplasm in adherent cells, indicating that pre-stress in the actin bundles is the key determinant of how far a force can propagate. This is known as “action at a distance” behavior [70–73].

AFM has been used to investigate how mechanical perturbations propagate in cells. For example, Rosenbluth and Crow et al. measured the magnitude and timing of intracellular stress propagation, using AFM and fluorescent particle tracking, and showed that AFM deformation of the cell surface exhibited distance dependence that could be eliminated by disruption of the actin cytoskeleton [75]. Silberberg et al. reported that mitochondria displacements, which are markers of microtubule displacements and deformation, were much less sensitive to AFM loading forces at apical surfaces, suggesting that filamentous structures other than actin filaments propagated less mechanical force from apical to basal cell surfaces [76].

A new AFM technique combined with a micro-post substrate [77] was used to characterize the mechanical response of CSK filaments at focal adhesions. Apical and basal cell surfaces were pre-coated with an adhesive protein (fibronectin) and then bound to both a colloidal bead on an AFM cantilever and to polydimethylsiloxane (PDMS) micro-posts [77, 78] (Fig. 15.20). The cantilever was oscillated normal to the substrate surface with amplitude for a period T at frequency f, while a time series of images of cells on the micro-posts were acquired.

Fig. 15.20

Schematic of AFM of cells atop a micro-post substrate, for measuring force propagation from apical to basal surfaces through the cytoskeleton

Cells exhibited a power-law rheology with α ~ 0.2 at the apical surface, but had no apparent out-of-phase response at the basal surface, thus indicating that the cytoskeletal filaments behave in an elastic manner. As shown in Fig. 15.21, a periodic change in force was observed at these frequencies, but no apparent phase shift in the force magnitude was observed at these frequencies (Fig. 15.21a). The response to the force at the basal cell surface appeared in phase, even at the higher frequency (0.5 Hz) at which the rheological properties of cells were clear for apical surfaces (Fig. 15.21b). At the lower frequency, the response to the force was no longer periodic but more complex. Moreover, force profiles that exhibited periodic responses (Fig. 15.21) were asymmetric, and some (depicted by arrows in Fig. 15.21) showed plateau responses to low forces. These results indicate that the lateral force at the basal cell surface readily propagated when a strong force was applied normal to the apical surface.

Fig. 15.21

(a) AFM data from cells cultured on PDMS micro-posts that were pre-coated with fibronectin. A fibronectin-coated colloidal bead attached at the apex of an AFM tip was bound to the apical cell surface with an initial loading force less than 500 pN for 30 min. An oscillatory pulling force was applied in the frequency range of 0.01–0.5 Hz for three periods (0 < t < 3 T), while the deflection of the micro-post was measured by phase-contrast or bright-field microscopy. (b) Optical microscopic image of micro-posts. An objective lens with a long working distance was focused on the tops of the micro-posts. (c) Red arrows indicate cell pre-stress, estimated from the deflection of the micro-posts (letters A–D). Time series of lateral force magnitude applied to micro-posts during external modulation at different frequencies by AFM. Letters correspond to those in (b). Reprinted with permission from [79]

The direction of the propagated force was correlated with pre-stress, indicating that the lateral force applied to the micro-posts at the basal surface is directly associated with forces propagated through CSK [79]. The heterogeneities of long-distance force propagation are most likely associated with the deformation of the nucleus [68, 69], remodeling of actin filaments in local regions [80], and entanglement of CSK filaments [81].

15.3.2 Cell Membrane Fluctuations

Scanning ion conductance microscopy (SICM) [82] is used to detect a cell surface at a local position in the noncontact region through an ion current I that flows through the small bore of a pipette (typically 100 nm in diameter) [83–86] (Fig. 15.22a, b). The basic principle of SICM is that I monotonically decreases as the tip approaches the sample surface (Fig. 15.22c); thus, I is used to regulate the tip–surface distance D without tip–surface contact. High-resolution images of microvilli formation and assembly [84] on apical epithelial cell surfaces and fragile neuron cells [85] have been acquired without substantial cell deformation. As described below, the I–D curve provides information about the dynamics of cell surfaces such as membrane fluctuations.

Fig. 15.22

(a) Schematic of SICM instrument. (b) Scanning electron micrograph of a nano-pipette tip used in this study. The inner and outer diameters were ≈ 100 nm and ≈ 200 nm, respectively. (c) I–D curves measured on a silicon substrate (filled circle) and a flat PDMS substrate (open circle). The solid lines represent fits to Eq. 15.9 (Reprinted with permission from [92])

Because cell membranes are flexible and undergo morphological changes with different biological functions, the characterization of cell surface fluctuations is crucial for a better understanding of cell function and dynamics. The thicknesses of adherent mammalian cells have been determined by optical techniques [87–89]. However, the refractive index of a cell may fluctuate because of modulations in the intracellular cytoskeletal network and/or the displacement of subcellular organelles. Pelling et al. demonstrated that AFM can measure local temperature-dependent nano-mechanical motion in yeast cell walls [90]. However, an AFM tip may perturb mammalian cell surfaces because they are much softer than yeast cells [91]. Being a noncontact probe, SICM allows us to safely measure flexible cell surface positions and to quantify nanoscale fluctuations on adherent cell membranes [92].

Figure 15.23 illustrates the method for estimating cell surface fluctuations from I–D curves. The cell surface position z _s(x, t) at time t at a normalized lateral position x is z _s(x, t) = z ₀(x) + δz _s(x, t), where z ₀(x) is the average z-position of the apical cell surface and δz _s(x, t) is the fluctuation around z ₀(x), i.e., $\left\langle \delta {z}_{\mathrm{s}}(x)\right\rangle =0$, where < X > is the X ensemble or time average. It is assumed that the cell surfaces fluctuate with a Gaussian stochastic distribution P about the root-mean-square (RMS) displacement of surface fluctuations 〈δz ²_s 〉^1/2, as given by

Fig. 15.23

Schematic of apical cell surface fluctuation measurements with SICM. The apical cell surfaces fluctuate with δz _s (x, t) around z = z ₀(x) at a normalized lateral position x (0 and 1 at the cell edge and 1/2 at the cell center) at time t. The apical cell surface position is statistically expressed as a Gaussian stochastic distribution P of the RMS displacement of surface fluctuations, which is the apparent amplitude of the cell surface fluctuation. In this case, <I > follows Eq. 15.11 (Reprinted with permission from [92])

$$ P\left({z}_{\mathrm{s}}-{z}_0,\left\langle \delta {z}_{\mathrm{s}}^2\right\rangle \right)=\frac{1}{\sqrt{2\pi \left\langle \delta {z}_{\mathrm{s}}^2\right\rangle }}\kern0.3em \exp \left\{-{\left({z}_{\mathrm{s}}-{z}_0\right)}^2/\left(2\left\langle \delta {z}_{\mathrm{s}}^2\right\rangle \right)\right\}. $$

(15.9)

The I–D curve for a solid substrate is modeled as [93]

$$ {I}_0\left(z-{z}_0\right)={I}_{\mathrm{sat}}{\left[1+\frac{\zeta }{z-{z}_0}\right]}^{-1}, $$

(15.10)

where z is the tip position, z ₀ is sample surface position with no fluctuations, I _sat is the ion current when the pipette is far from the surface, and ζ is a function of the inner radius of the tip opening, the inner radius of the tip base, the tip length, and the conductivity of the electrolyte in solution in the pipette [93]. ζ is experimentally determined for I _sat. Thus, when cell fluctuations obey Eq. 15.9, the average 〈I〉, measured at z on cells at z ₀ with 〈δz ²_s 〉^1/2, is given by

$$ \left\langle I\left(z-{z}_0\left\langle \delta {z}_{\mathrm{s}}^2\right\rangle \right)\right\rangle ={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{I}_0\left(z-{z}_{\mathrm{s}}\right)P\left({z}_{\mathrm{s}}-{z}_0,\left\langle \delta {z}_{\mathrm{s}}^2\right\rangle \right)d{z}_s}, $$

(15.11)

where z ₀ and 〈δz ² _s 〉 are fitting parameters. The measured dynamic range of the cell surface fluctuations is limited by the bandwidth of the SICM preamplifier.

Figure 15.24a shows I–D curves for epithelial Madin–Darby canine kidney (MDCK) cell sheets that were almost fully confluent where translational cell migration were highly restricted. For the fixed cells, the RMS displacement of surface fluctuations was 6.5 nm, which is consistent with that determined by optical techniques for fixed red blood cells [94]. The displacements significantly increased to 60 nm in untreated and microtubule-depolymerized, colchicine (col)-treated cells and to 105 nm in actin-depolymerized, latrunculinA (latA)-treated cells.

Fig. 15.24

(a) I–D curves of fixed (purple), untreated cells (blue), latA-treated cells (red), and col-treated cells (green). The solid lines are fits to Eq. 15.11. (b) RMS displacements of surface fluctuations (defined in Eq. 15.9) of fixed cells (purple line), untreated cells (blue line), col-treated cells (green line), and latA-treated cells (red line) measured in lines crossing over the center of the cells (the data were fitted as parabolas) (Reprinted with permission from [92])

Figure 15.24b plots the RMS displacement of surface fluctuations estimated at different positions on the cell surface. In the untreated cells, the fluctuations exhibited a clear spatial dependence that increased toward the cell center. Specifically, the RMS displacement was 46 nm at the cell edge and 71 nm at the cell center. In contrast, no spatial dependence was observed in the fixed cells. Moreover, in the latA-treated cells, the spatial dependence was significantly reduced. The investigation demonstrated that SICM is the powerful technique for exploring spatial heterogeneities in epithelial cell surface fluctuations, which are strongly associated with the underlying cytoskeleton.

15.4 Summary

In this chapter, we described AFM techniques for imaging live cells and for measuring single-cell rheology parameters. While AFM imaging of surface topography is well established, imaging of inner structures of cells has great potential. Regarding single-cell rheology, AFM of cells attached to micro-fabricated substrates allows us to characterize frequency- and time-dependent mechanical properties and to quantify cell-to-cell variability, i.e., single-cell diagnostics. We emphasize that AFM biological techniques are still rapidly developing and will be applied more broadly to explore rheological properties of cells, to characterize tissues and organs for bioengineering and for medical applications.