Vibration Control and Structural Damping of a Rotating Beam by Using Piezoelectric Actuators

Abstract

In this paper, the application of piezoelectric vibration control in flexible multibody systems is studied and verified. Exemplarily, beam-type structures are considered that are subject to inertial and external forces. The equations of motion for three-dimensional flexible and torsional vibrations are presented considering the influence of piezoelectric actuation strains. In the framework of Bernoulli-Euler beam theory the shape control solution is derived, i.e. the distribution of actuation strains such that the flexible displacements are completely compensated. For the experimental verification, a laboratory model has been developed, in which the theoretical distribution of actuation strains is discretized by piezoelectric patches. A suitable control algorithm is implemented within a dSpace environment. Finally, the results are validated by numerical computations utilizing ABAQUS and HOTINT, and verified by experimental evaluation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

15.1 Introduction

Recently, the interest in vibration compensation by means of distributed actuation has increased rapidly. On the one hand, structures become more and more light-weighted, on the other hand there are considerable advances in the development of materials suitable for such kinds of actuators and sensors. This paper concentrates on the application of piezoelectric transducers in order to control flexible vibrations in beams, which are important components of many multibody systems.

Piezoelectric transducers can be used for sensing and actuation, utilizing either the direct or the converse piezoelectric effect, respectively [1]. An efficient possibility for realisation is to apply piezoelectric patches on the surfaces of beams. Depending on the type of the piezoelectric material, and on the position of the patch on the beam, such transducers can be used for sensing and actuation of bending and torsional modes. Vibration compensation by piezoelectric materials has been extensively treated in the literature. The exact compensation of flexible displacements by distributed actuation has been denoted as shape control, for a review see Irschik [2].

An exact solution in the framework of Bernoulli-Euler beam theory for the complete compensation of plane bending vibrations under influence of rigidbody motions has been presented by Zehetner and Irschik [3]. Torsional vibration control has been investigated by Zehetner and Krommer [4], where it has been shown how piezoelectric transducers can be used for torsional sensing and actuation. A comparison of some specific piezoelectric materials for the application of torsional actuation and sensing has been shown in [5].

There are several possibilities for the practical realisation of the spatial distribution, i.e. the shape of the actuators and sensors. For instance, shaped piezoelectric layers can be applied on the beam. Other possibilities would be shaped electrodes or functionally graded material properties. These strategies enable the exact distribution of the necessary actuation strains, but are very extensive. Thus, patch approximations are more suitable for practical applications. A patch approximation for the control of vibrations of a rotating beam has been investigated numerically by Zehetner and Gerstmayr [6], and first experimental results have been presented in [7] and [8].

Goal of this work is the derivation and verification of a mechanical model for the control of three-dimensional flexural and torsional beam vibrations caused by external forces and inertial forces due to rigidbody motions. The theoretical results are validated by numerical computations using the finite element software ABAQUS and the multibody dynamics simulation code HOTINT, mainly developed by Gerstmayr [9].

Finally, the theoretical results are verified by experimental investigations. For this sake, a laboratory model has been set up, in which 48 piezoelectric patches are applied on a rectangular hollow beam. The beam is fixed on a motor, such that it performs a rotational rigid body motion. Within a dSpace environment control algorithms are implemented and tested. It turns out that the flexible vibrations can be reduced significantly, and that theoretical, numerical and experimental results show a very good coincidence.

15.2 Piezoelectric Actuators and Sensors

Piezoelectric layers can be used as actuators and sensors in various ways. Here, we consider piezoelectric patches that are attached on the surfaces of a beam. We distinguish between two operational modes:

• Extension mode. The electric field component in thickness direction corresponds to extension strains as shown in Fig. 15.1. Bending actuators and sensors are realized by placing such devices symmetrically on the upper and lower surface of the beam and applying an electric field in opposite direction (extension and contraction). Such a behaviour is provided e.g. by the piezoelectric ceramic PZT (lead zirconate titanate). Extension with a predominating axis can be realized by makro-fiber composites (MFC) consisting of PZT stripes embedded in epoxy-substrate. Torsional actuation and sensing can be realized by placing such layers at an angle of 45° with respect to the rod axis as shown in Fig. 15.1.

  Fig. 15.1

  

  Piezoelectric extension mode

• Shear mode. The electric field in thickness direction corresponds to shear strains as shown in Fig. 15.2. Such a behaviour is shown e.g. by the piezoelectric material ADP (ammonium dihydrogen phosphate). The shear mode can be utilized for torsional sensing and actuation as shown in Fig. 15.2.

  Fig. 15.2

  

  Piezoelectric shear mode

15.3 Constitutive Equations

The constitutive equations for piezoelectric materials relate the mechanical strain $\varepsilon = {{[{{\varepsilon }_{{xx}}}\:{{\varepsilon }_{{yy}}}\:{{\varepsilon }_{{zz}}}\:{{\gamma }_{{yz}}}\:{{\gamma }_{{xz}}}\:{{\gamma }_{{xy}}}]}^T}$, stress $\sigma = {{[{{\sigma }_{{xx}}}\:{{\sigma }_{{yy}}}\:{{\sigma }_{{zz}}}\:{{\tau }_{{yz}}}\:{{\tau }_{{xz}}}\:{{\tau }_{{xy}}}]}^T}$, electrical field $\mathbf{ E} = {{[{{E}_x}\;\:{{E}_y}\;\:{{E}_z}]}^T}$ and dielectric displacement $\mathbf{ D} = {{[{{D}_x}\;\:{{D}_y}\;\:{{D}_z}]}^T}$, cf. Tauchert [10], in the form

$$ \sigma = {\ Q} \cdot \left( {\varepsilon - \ dE} \right), $$

(15.1)

$$ D = \ \eta \cdot E + d\sigma, $$

(15.2)

where Q is the 6 × 6 matrix of elasticity coefficients, d the 6 × 3 matrix of piezoelectric coefficients and $\eta$ the 3 × 3 matrix of dielectric coefficients. The coefficients of the matrices depend on the specific type of piezoelectric material. Examples for PZT, ADP and MFC are summarized in the Appendix.

In beam-type structures it is assumed that the stress components ${{\sigma }_{{yy}}}$, ${{\sigma }_{{zz}}}$ and ${{\tau }_{{yz}}}$ can be neglected, such that (15.1) and (15.2) reduce to

$$ \begin{array}{llllll} {{\sigma }_{{xx}}} & = \mathop{{\overline Q }}\nolimits_{{11}} ({{\varepsilon }_{{xx}}} - \varepsilon_{{xx}}^0), \\{{\tau }_{{xz}}} & = {{Q}_{{55}}}({{\gamma }_{{xz}}} - \gamma_{{xz}}^0), \\{{\tau }_{{xy}}} & = {{Q}_{{66}}}({{\gamma }_{{xy}}} - \gamma_{{xy}}^0),\end{array} $$

(15.3)

and

$$ {{D}_z} = {{\eta }_{{33}}}({{E}_z} - E_z^0), $$

(15.4)

where $\mathop{{\overline Q }}\nolimits_{{11}} = S_{{11}}^{{ - 1}}$ is the effective Young modulus, ${{S}_{{11}}}$ is the first component of the compliance matrix $\mathbf{ S} = {\mathbf{ Q}^{{ - 1}}}$. In (15.3), $\varepsilon_{{xx}}^0$, $\gamma_{{xz}}^0$ and $\gamma_{{xy}}^0$ are piezoelectric eigenstrains representing the converse piezoelectric effect, cf. Mura [11] for the definition of eigenstrains. Accordingly, $E_z^0$ is the electric eigenfield, a generalized formulation for the direct piezoelectric effect which has been introduced by Irschik et al. [12]. Eigenstrains and the eigenfield depend on the material properties, e.g. for PZT there is

$$ \varepsilon_{{xx}}^0 = {{d}_{{31}}}{{E}_z},\ \gamma_{{xy}}^0 = \gamma_{{xz}}^0 = 0,\quad E_z^0 = \frac{{{{d}_{{31}}}}}{{{{\eta }_{{33}}}}}{{\sigma }_{{xx}}}, $$

(15.5)

and for ADP

$$ \varepsilon_{{xx}}^0 = 0,\ \gamma_{{xy}}^0 = {{d}_{{36}}}{{E}_z},\ \gamma_{{xz}}^0 = 0,\quad E_z^0 = \frac{{{{d}_{{36}}}}}{{{{\eta }_{{33}}}}}{{\tau }_{{xy}}}. $$

(15.6)

Assuming that the piezoelectric transducers are relatively thin, the electric field components in the plane of the layers are neglected ${{E}_x} = {{E}_y} = 0$, and the electric field is constant in thickness direction and proportional to the applied voltage ${{U}_{{el}}}$,

$$ {{E}_z} = \frac{{{{U}_{{el}}}}}{{{{h}_L}}}, $$

(15.7)

${{h}_L}$ is the thickness of the piezoelectric layer.

15.4 Kinematics

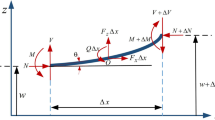
Figure 15.3 shows a flexible beam fixed to a rigid base in point B. A floating reference frame is introduced with origin in point B. In the undeformed configuration, $x$ coincides with the beam axis, and $(y,z)$ is the cross-sectional plane. The position of B with respect to an inertial frame is described by the position vector ${{{\mathbf{x}}}_B}(t)$, and the orientation of the floating frame by the rotation matrix ${{{\mathbf{A}}}_B}(t)$. Hence, ${{{{x}}}_B}$ and ${{{\mathbf{ A}}}_B}$ represent the rigidbody motion of the beam.

Fig. 15.3

Moving cantilever beam, ideally fixed on a rigid base

The deformed beam axis is given by the flexible displacements $u(x,t)$, $\vee(x,t)$, $w(x,t)$ as shown in Fig. 15.3. According to Bernoulli-Euler beam theory the cross-sections remain undeformed and perpendicular to the beam axis. According to Saint Venant’s theory of torsion, the cross-section performs a rigidbody rotation around the beam axis with the torsional angle $\chi (x,t)$, and an axial displacement (cross-sectional warping) expressed by Saint Venant’s warping function $\varphi (y,z)$. It has been shown by Zehetner [13] that eigenstrains cause an additional cross-sectional warping which can be formulated by the warping function ${{\phi }^0}(y,z,{{\varepsilon }^0}(t))$. Thus, the displacement field of the beam is expressed by

$$ \mathbf{ u} = \left[ {\begin{array}{llllll} {u - y\vee \ ^\prime - zw \ ^\prime + \chi \ ^\prime \varphi } \\{\vee - z\chi } \\{w + y\chi } \\\end{array} } \right] + \left[ {\begin{array}{llllll} {{{\phi }^0}} \\0 \\0 \\\end{array} } \right] - \frac{1}{2}\left[ {\begin{array}{llllll} {2\chi (yw \ ^\prime - z\vee \ ^\prime )} \\{z\vee \ ^\prime w \ ^\prime + y(\mathop{{\vee \ ^\prime }}\nolimits^2 + {{\chi }^2})} \\{y\vee \ ^\prime w \ ^\prime + z(\mathop{{w \ ^\prime }}\nolimits^2 + {{\chi }^2})} \\\end{array} } \right]. $$

(15.8)

The first term represents the displacements according to linear Bernoulli-Euler beam theory and Saint Venant’s theory of torsion. The second term stands for the additional cross-sectional warping due to eigenstrains, and the third term contains second order terms which enable the consideration of dynamic stiffening effects and stability investigations.

For laminated cross-sections as shown in Figs. 15.1 and 15.2, the Saint Venant warping function $\varphi (y,z)$ is given by the boundary value problem

$$ \begin{array}{llllll} {{Q}_{{66}}}\frac{{{{\partial }^2}\varphi }}{{\partial {{y}^2}}} + {{Q}_{{55}}}\frac{{{{\partial }^2}\varphi }}{{\partial {{z}^2}}} & = 0, \\\partial A:\quad {{Q}_{{66}}}\left( {\frac{{\partial \varphi }}{{\partial y}} - z} \right){{n}_y} + {{Q}_{{55}}}\left( {\frac{{\partial \varphi }}{{\partial z}} + y} \right){{n}_z} & = 0, \\\partial I:\quad \left[\kern-0.15em\left[ {{{Q}_{{66}}}\left( {\frac{{\partial \varphi }}{{\partial y}} - z} \right){{n}_y} + {{Q}_{{55}}}\left( {\frac{{\partial \varphi }}{{\partial z}} + y} \right){{n}_z}} \right]\kern-0.15em\right] & = 0, \\\left[\kern-0.15em\left[ \varphi \right]\kern-0.15em\right] & = 0,\end{array} $$

(15.9)

ny and nz are the components of the outer normal vector. A derivation can be found e.g. in Rand and Rovenski [14]. Besides the boundary conditions at the boundary $\partial A$ of the cross-section, interface conditions have to be satisfied at the interface $\partial I$ between two layers in order to obtain continuous displacement and stress distributions. In this context, the notation $\left[\kern-0.15em\left[ \cdot \right]\kern-0.15em\right]$ stands for the difference of a quantity at the interface.

The additional warping function ${{\phi }^0}(y,z,{{\varepsilon }^0}(t)$ is expressed by a similar boundary problem

$$ \begin{array}{llllll} {{Q}_{{66}}}\frac{{{{\partial }^2}{{\phi }^0}}}{{\partial {{y}^2}}} + {{Q}_{{55}}}\frac{{{{\partial }^2}{{\phi }^0}}}{{\partial {{z}^2}}} & = 0, \\\partial A:\quad {{Q}_{{66}}}\left( {\frac{{\partial {{\phi }^0}}}{{\partial y}} - \gamma_{{xy}}^0} \right){{n}_y} + {{Q}_{{55}}}\left( {\frac{{\partial {{\phi }^0}}}{{\partial z}} - \gamma_{{xz}}^0} \right){{n}_z} & = 0, \\\partial I:\quad \left[\kern-0.15em\left[ {{{Q}_{{66}}}\left( {\frac{{\partial {{\phi }^0}}}{{\partial y}} - \gamma_{{xy}}^0} \right){{n}_y} + {{Q}_{{55}}}\left( {\frac{{\partial {{\phi }^0}}}{{\partial z}} - \gamma_{{xz}}^0} \right){{n}_z}} \right]\kern-0.15em\right] & = 0, \\\left[\kern-0.15em\left[ {{{\phi }^0}} \right]\kern-0.15em\right] & = 0,\end{array} $$

(15.10)

the derivation as well as an analytical solution for rectangular laminated cross-sections can be found in Zehetner [13]. Note that (15.9) and (15.10) hold for any kind of laminated cross-sections and material behaviour according to Sect. 15.3.

15.5 Equations of Motion

The equations of motion for the beam in Fig. 15.3 can be derived e.g. by applying D’Alembert’s principle. A detailed derivation can be found in Zehetner [15]. As excitations we consider inertial forces due to rigidbody motions as well as distributed and concentrated external forces. With the kinematical assumptions in (15.8) and the constitutive equations in (15.3) we obtain the equations of motion for longitudinal, transversal and torsional beam vibrations

$$ \begin{array}{llllll} f_x^e - {{N}^a} \ ^\prime & = \mu (\ddot{u} + {{a}_1}) - ({{A}_{{11}}}u \ ^\prime ) \ ^\prime , \\f_y^e + M_z^a{ \ ^\prime \ ^\prime } & = \mu (\ddot{\vee} + {{a}_2}) + ({{D}_{{22}}}\vee \ ^\prime \ ^\prime ) \ ^\prime \ ^\prime - (N\vee \ ^\prime - \tfrac{1}{2}\;{{M}_x}w \ ^\prime \ ^\prime ) \ ^\prime + ({{M}_y}\chi + \tfrac{1}{2}\;{{M}_x}w \ ^\prime ) \ ^\prime \ ^\prime , \\f_z^e - M_y^a{ \ ^\prime \ ^\prime }{ } & = \mu (\ddot{w} + {{a}_3}) + ({{D}_{{11}}}w \ ^\prime \ ^\prime ) \ ^\prime \ ^\prime - (Nw \ ^\prime + \tfrac{1}{2}\;{{M}_x}\vee \ ^\prime \ ^\prime ) \ ^\prime + ({{M}_z}\chi - \tfrac{1}{2}\;{{M}_x}\vee \ ^\prime ) \ ^\prime \ ^\prime , \\m_x^e - M_x^a{ \ ^\prime }{ } & = {{I}_x}(\ddot{\chi } + {{\alpha }_1}) - ({{C}_{{11}}}\chi \ ^\prime ) \ ^\prime + {{M}_z}w \ ^\prime \ ^\prime + {{M}_y}\vee \ ^\prime \ ^\prime ,\end{array} $$

(15.11)

with kinematic boundary conditions for the clamped end,

$$ x = 0:\quad u = \vee = \vee \ ^\prime = w = w \ ^\prime = \chi = \chi \ ^\prime = 0, $$

(15.12)

and dynamic boundary conditions at the free end,

$$ \begin{array}{llllll} x = L:\quad F_x^e + {{N}^a} & = {{A}_{{11}}}u \ ^\prime , \\F_y^e - M_z^a{ \ ^\prime } & = - ({{D}_{{22}}}\vee \ ^\prime \ ^\prime ) \ ^\prime + N\vee \ ^\prime - \tfrac{1}{2}\;M_x^ew \ ^\prime \ ^\prime - ({{M}_y}\chi + \tfrac{1}{2}\;{{M}_x}w \ ^\prime ) \ ^\prime , \\M_z^e + M_z^a & = {{D}_{{22}}}\vee \ ^\prime \ ^\prime + {{M}_y}\chi + \tfrac{1}{2}\;{{M}_x}w \ ^\prime , \\F_z^e + M_y^a{ \ ^\prime } & = - ({{D}_{{11}}}w \ ^\prime \ ^\prime ) \ ^\prime + Nw \ ^\prime + \tfrac{1}{2}\;{{M}_x}\vee \ ^\prime \ ^\prime - ({{M}_z}\chi - \tfrac{1}{2}\;{{M}_x}\vee \ ^\prime ) \ ^\prime , \\M_y^e + M_y^a & = - {{D}_{{11}}}w \ ^\prime \ ^\prime - {{M}_z}\chi + \tfrac{1}{2}\;{{M}_x}\vee \ ^\prime , \\M_x^e + M_x^a & = {{C}_{{11}}}\chi \ ^\prime .\end{array} $$

(15.13)

In (15.11)–(15.13), $f_x^e$, $f_y^e$, $f_z^e$ and $m_x^e$ are effective distributed external forces and torque per unit length, respectively. These effective quantities consider external forces and inertial forces due to the rigidbody motion. $F_x^e$, $F_y^e$, $F_z^e$, $M_x^e$, $M_y^e$ and $M_z^e$ are external concentrated forces acting at the free beam end, e.g. joint forces or manipulator forces. $\mu$ is the mass per unit length, ${{A}_{{11}}}$ the longitudinal stiffness, ${{D}_{{11}}}$ and ${{D}_{{22}}}$ are the bending stiffnesses, and ${{C}_{{11}}}$ is the torsional stiffness. ${{a}_1}$, ${{a}_2}$, ${{a}_3}$ and ${{\alpha }_1}$ are accelerations corresponding to the flexible displacements $u$, $\vee$, $w$ and $\chi$, for details see Ref. [15].

The influence of the piezoelectric effect is represented by the actuating force and moments ${{N}^a}$, $M_z^a$, $M_y^a$ and $M_x^a$. Using the piezoelectric material PZT we obtain

$$ \begin{array}{llllll} {{N}^a} & = \frac{{{{U}_{{el}}}}}{{{{h}_L}}}\int_A \mathop{{\overline Q }}\nolimits_{{11}} {{d}_{{31}}}\;\:dA, \\M_z^a & = \frac{{{{U}_{{el}}}}}{{{{h}_L}}}\int_A \mathop{{\overline Q }}\nolimits_{{11}} {{d}_{{31}}}y\;\:dA, \\M_y^a & = \frac{{{{U}_{{el}}}}}{{{{h}_L}}}\int_A \mathop{{\overline Q }}\nolimits_{{11}} {{d}_{{31}}}z\;\:dA.\end{array} $$

(15.14)

On the other hand, using patches made of the material ADP, and using the substitution ${{\phi }^0} = \mathop{{\overline \phi }}\nolimits^0 {{U}_{{el}}}$, we obtain the actuating torque

$$ M_x^a = - \frac{{{{U}_{{el}}}}}{{{{h}_L}}}\left( {\int_{{{{A}_p}}} {{Q}_{{66}}}{{d}_{{36}}}z\;\:dA - \int_A \left( {{{Q}_{{55}}}\frac{{\partial \mathop{{\overline \phi }}\nolimits^0 }}{{\partial z}}y - {{Q}_{{66}}}\frac{{\partial \mathop{{\overline \phi }}\nolimits^0 }}{{\partial y}}z} \right)\:dA} \right). $$

(15.15)

15.6 Shape Control

From (15.11)–(15.13) we can immediately derive relations for the actuating forces and moments in order to compensate the external excitations (shape control), i.e. homogenous equations of motion are obtained if the left hand sides of (15.11)–(15.13) vanish, hence

$$ \begin{array}{llllll} {{N}^a}{ \ ^\prime } = f_x^e,\ M_z^a{ \ ^\prime \ ^\prime } = - f_y^e,\ M_y^a{ \ ^\prime \ ^\prime } = f_z^e,\ M_x^a{ \ ^\prime } = m_x^e \\x = L:\ \quad{{N}^a} = - F_x^e,\ M_z^a{ \ ^\prime } = F_y^e,\ M_z^a = - M_z^e, \\M_y^a{ \ ^\prime } = - F_z^e,\ M_y^a = - M_y^e,\ M_x^a = - M_x^a.\end{array} $$

(15.16)

Integrating (15.16) yields the spatial distribution of actuating forces and moments in order to compensate external excitations and the influence of the rigidbody accelerations. If the motion starts from rest (homogenous initial conditions), and if no buckling effects occur, then the elastic displacements are compensated exactly. Note that buckling phenomena can also be investigated since second order terms are considered in the equations of motion.

A common strategy for the practical realisation of distributed actuation is an approximation by a patch discretisation [16]. The latter will be discussed in more detail by means of the examples in the subsequent section.

15.7 Examples

In order to verify the theoretical results of the above sections, two examples are considered. First, a flexible manipulator is studied numerically, and secondly, numerical and experimental results concerning a rotating beam are presented.

15.7.1 Flexible Manipulator—Numerical Simulations

Figure 15.4 shows a flexible manipulator: A flexible beam is fixed on a rigid base moving in $\boldsymbol z$-direction with the acceleration ${{a}_3}$. At the free beam end, the mass $M$ is fixed with its center of gravity located at a distance of $r$ with respect to the beam axis. The effective excitations due to the acceleration ${{a}_3}$ are represented by

Fig. 15.4

Flexible manipulator

$$ f_z^e = - \mu {{a}_3}(t),\quad \quad F_z^e = - M{{a}_3}(t). $$

(15.17)

In the following, it is assumed that the influence of the tip mass $M$ dominates, such that the distributed force $f_z^e$ is neglected. Moreover, longitudinal and transversal vibrations in $y$-direction are neglected. Due to the force $F_z^e$, transversal vibrations in $z$-direction and torsional vibrations are excited. Inserting (15.17) into (15.16) and integrating yields the actuating bending moment $M_y^a$ and the actuating torque $M_x^a$ as

$$ M_y^a(x,t) = - LM{{a}_3}(t)\left( {1 - \frac{x}{L}} \right),\quad M_x^a(x,t) = - Mr{{a}_3}(t). $$

(15.18)

The spatial distribution of $M_y^a$ is linear with respect to the longitudinal coordinate $x$, and $M_x^a$ is constant. The realisation of actuation is shown in Fig. 15.4. Two piezoelectric layers are bonded ideally on the surfaces of the beam: One layer made of ADP is placed on the back side of the beam, using an electrode with constant width. On the second side, a PZT layer is attached. The width of the electrode corresponds to the linear spatial distribution of the actuating moment $M_y^a$ in (15.18). The voltage of the actuators is obtained from (15.14) and (15.15).

In order to verify (15.18), a Finite Element model has been implemented using ABAQUS. The beam and the piezoelectric layers have been discretized by 3D-continuum elements of type C3D8R (reduced integration) and C3D8E (piezoelectric elements). As actuator voltage, the results of beam theory are applied. Note that this simulation model considers several electro-mechanical coupling effects and refinements in contrast to beam theory. Thus, this model is supposed to be suitable for a validation of the theoretical results.

The numerical results for the tip deflection $w(x = L)$ and the torsional angle $\chi (x = L)$ are shown in Fig. 15.5, for the case with and without actuation. The results show a significant reduction of the amplitude due to the actuation. The remaining vibrations are caused by the mass of the beam which has been neglected. All in all the results show a good coincidence between theoretical and Finite Element solution.

Fig. 15.5

Numerical simulation results for the beam end $x = L$

15.7.2 Rotating Beam—Experimental Verification

As a second example, a rotating beam with rectangular hollow cross-section is considered as schematically shown in Fig. 15.6. The according laboratory setup is shown in Fig. 15.7. On the beam, i.e. inside and outside of the hollow cross-section, a number of 48 piezoelectric patches has been applied. In order to reduce the number of circuits for the electrical power supply, groups of three patches have been connected. Between these groups strain gauges have been applied for sensing. For monitoring, an acceleration sensor has been placed at the free beam end.

Fig. 15.6

Rotating beam with piezoelectric patches

Fig. 15.7

Experimental setup

The effective excitation of the beam is the transversal distributed inertial force per unit length

$$ f_z^e = - \rho A{{x}^2}\ddot{\varphi }, $$

(15.19)

caused by the rigidbody rotation angle $\varphi (t)$. Inserting into (15.16) and integrating with respect to the axial coordinate $x$ yields the actuating moment

$$ M_y^a = \tfrac{1}{3}\;\rho A{{L}^3}\ddot{\varphi }{{\left( {1 - \xi } \right)}^2}\left( {1 + \tfrac{1}{2}\;\xi } \right). $$

(15.20)

This cubic spatial distribution is discretized by means of four groups of three patches as shown in Fig. 15.8. The actuating moment of a piezoelectric patch is obtained from (15.14). With the Young modulus of the patch ${{E}_p}$, the width $b$ and the height $h$ of the beam, we obtain the actuating bending moment of the $i$-th patch

$$ M_y^{{a,i}} = \tfrac{1}{2}\;{{E}_p}{{d}_{{31}}}b(h + {{h}_L}){{k}_i}{{U}_e}l(t), $$

(15.21)

where the gains ${{k}_i}$ are weighting factors in order to realize the cubic distribution of the actuating moment as given in (15.20). Following the strategy presented in Ref. [16], the coefficients are found to be ${{k}_1} = 1$, ${{k}_2} = \tfrac{1}{2}$, ${{k}_3} = \tfrac{1}{5}$ and ${{k}_4} = \tfrac{1}{{28,5}}$.

Fig. 15.8

Patch discretisation

Figure 15.9 shows the control strategy consisting of two parts: First, the feed forward shape control $M_a^{{f\;f}}$ is implemented with an estimation of the rigidbody acceleration $\ddot{\varphi }$.

Fig. 15.9

Control strategy

Due to several uncertainties of the system it is not possible to completely compensate the vibrations by feed forward control only. Thus, strain gauges between the patches are used as sensors to measure the average curvature $\bar{\kappa }$. The error of the curvature ${{e}_k}$, i.e. the difference of prescribed and measured curvature, is the input of the feedback controller. As a first account, a P-control law has been implemented. For monitoring, the acceleration ${{a}_L} = a(x = L)$ of the free beam end is measured.

In order to optimize the control parameters, a simulation model has been implemented using the multibody dynamics simulation code HOTINT. The model is based on a Finite Element Formulation using Bernoulli-Euler beam elements which considers large deformation strains as well as the varying stiffness due to the piezoelectric patches. A motor model is implemented considering stiffness, damping and friction. The parameters of the simulation model have been calibrated to the experiment using appropriate identification strategies.

As a first investigation, the motor angle has been prescribed in sinusoidal form, the frequency coinciding with the first eigenfrequency of the beam, ${{f}_1} = 20\:{\text{Hz}}$. Figure 15.10 shows a comparison of simulation (left picture) and experiment (right picture) for the tip acceleration of the beam. In both cases, the amplitude of the vibration is reduced significantly. The results show a very good coincidence even in the considered resonant case.

Fig. 15.10

Time response for harmonic excitation of the first eigenfrequency

As a second example, a triangular velocity profile has been prescribed as rigidbody motion. Figure 15.11 shows the measured time response and the frequency response of the tip acceleration, i.e. at the free beam end. The result shows that the amplitude of the vibration is reduced significantly with the implemented control strategy.

Fig. 15.11

Time response of a triangular velocity profile

15.8 Conclusions

In this paper, piezoelectric vibration control of three-dimensional flexural and torsional beam vibrations has been treated. External and inertial forces due to rigidbody motions are considered as excitations. The equations of motion have been derived in the framework of Bernoulli-Euler beam theory, and an extension of Saint Venant’s theory of torsion. Laminated cross-sections and the influence of piezoelectric strains are considered. In the framework of beam theory, an exact shape control solution has been presented, i.e. the distribution of piezoelectric actuation strains in order to completely compensate the elastic beam vibrations. For the practical realisation, a patch approximation has been introduced. The theoretical results have been verified by means of numerical and experimental investigations, showing a very good coincidence. The results also show that a significant reduction of the flexible vibrations is possible with the presented strategy.

Appendix

Lead zirconate titanate (PZT)

$$ \mathbf{ Q} = \left[ {\begin{array}{llllll} {{{Q}_{{11}}}} & {{{Q}_{{12}}}} & {{{Q}_{{13}}}} & 0 & 0 & 0 \\{{{Q}_{{12}}}} & {{{Q}_{{11}}}} & {{{Q}_{{13}}}} & 0 & 0 & 0 \\{{{Q}_{{13}}}} & {{{Q}_{{13}}}} & {{{Q}_{{33}}}} & 0 & 0 & 0 \\0 & 0 & 0 & {{{Q}_{{55}}}} & 0 & 0 \\0 & 0 & 0 & 0 & {{{Q}_{{55}}}} & 0 \\0 & 0 & 0 & 0 & 0 & {{{Q}_{{66}}}} \\\end{array} } \right],\quad \mathbf{ d} = \left[ {\begin{array}{llllll} 0 & 0 & {{{d}_{{31}}}} \\0 & 0 & {{{d}_{{32}}}} \\0 & 0 & {{{d}_{{33}}}} \\0 & {{{d}_{{24}}}} & 0 \\0 & 0 & {{{d}_{{15}}}} \\0 & 0 & 0 \\\end{array} } \right]. $$

(15.22)

Ammonium dihydrogen phosphate (ADP)

$$ \mathbf{ Q} = \left[ {\begin{array}{llllll} {{{Q}_{{11}}}} & {{{Q}_{{12}}}} & {{{Q}_{{13}}}} & 0 & 0 & 0 \\{{{Q}_{{12}}}} & {{{Q}_{{11}}}} & {{{Q}_{{13}}}} & 0 & 0 & 0 \\{{{Q}_{{13}}}} & {{{Q}_{{13}}}} & {{{Q}_{{33}}}} & 0 & 0 & 0 \\0 & 0 & 0 & {{{Q}_{{55}}}} & 0 & 0 \\0 & 0 & 0 & 0 & {{{Q}_{{55}}}} & 0 \\0 & 0 & 0 & 0 & 0 & {{{Q}_{{66}}}} \\\end{array} } \right],\quad \mathbf{ d} = \left[ {\begin{array}{llllll} 0 & 0 & 0 \\0 & 0 & 0 \\0 & 0 & 0 \\{{{d}_{{25}}}} & 0 & 0 \\0 & {{{d}_{{25}}}} & 0 \\0 & 0 & {{{d}_{{36}}}} \\\end{array} } \right]. $$

(15.23)

Macro fiber composite (MFC)

$$ \mathbf{ Q} = \left[ {\begin{array}{llllll} {{{Q}_{{11}}}} & {{{Q}_{{12}}}} & {{{Q}_{{13}}}} & 0 & 0 & {{{Q}_{{16}}}} \\{{{Q}_{{12}}}} & {{{Q}_{{11}}}} & {{{Q}_{{13}}}} & 0 & 0 & {{{Q}_{{16}}}} \\{{{Q}_{{13}}}} & {{{Q}_{{13}}}} & {{{Q}_{{33}}}} & 0 & 0 & {{{Q}_{{36}}}} \\0 & 0 & 0 & {{{Q}_{{55}}}} & {{{Q}_{{45}}}} & 0 \\0 & 0 & 0 & {{{Q}_{{45}}}} & {{{Q}_{{55}}}} & 0 \\{{{Q}_{{16}}}} & {{{Q}_{{16}}}} & {{{Q}_{{36}}}} & 0 & 0 & {{{Q}_{{66}}}} \\\end{array} } \right],\quad \mathbf{ d} = \left[ {\begin{array}{llllll} {{{d}_{{11}}}} & {{{d}_{{12}}}} & 0 \\{{{d}_{{12}}}} & {{{d}_{{11}}}} & 0 \\{{{d}_{{13}}}} & {{{d}_{{13}}}} & 0 \\0 & 0 & {{{d}_{{35}}}} \\0 & 0 & {{{d}_{{35}}}} \\{{{d}_{{16}}}} & {{{d}_{{16}}}} & 0 \\\end{array} } \right]. $$

(15.24)