Abstract
Weakly Aggregative Modal Logic (\(\textsf {WAML}\)) is a collection of disguised polyadic modal logics with n-ary modalities whose arguments are all the same. \(\textsf {WAML}\) has some interesting applications on epistemic logic and logic of games, so we study some basic model theoretical aspects of \(\textsf {WAML}\) in this paper. Specifically, we give a van Benthem-Rosen characterization theorem of \(\textsf {WAML}\) based on an intuitive notion of bisimulation and show that each basic \(\textsf {WAML}\) system \(\mathbb {K}_n\) lacks Craig Interpolation.
The main work of the first author was completed during his Ph.D. at Peking University.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
You are invited to a dinner party for married couples after a logic conference in China. The host tells you the following facts:
-
at least one person of each couple is a logician and
-
at least one person of each couple is Chinese.
Given these two facts, can you infer that at least one person of each couple is a Chinese logician? The answer is clearly negative, since there might be a couple consisting of a foreign logician and a Chinese spouse who is not a logician.
Now, suppose that the host adds another fact:
-
at least one person of each couple likes spicy food.
What do you know now? Actually, you can infer that for each couple, one of the two people must be either:
-
a Chinese logician, or
-
a logician who likes spicy food, or
-
a Chinese who likes spicy food.
This can be verified by the Pigeonhole Principle: for each couple, there is a logician, a Chinese, and a fan for spicy food, thus there must be at least one person of the couple who has two of those three properties. This can clearly be generalized to n-tuples of things w.r.t. \(n+1\) properties.
Now, going back to logic, if we express “at least one person of each couple has property \(\varphi \)” by \(\Box \varphi \) then the above reasoning shows that the following is not valid:
On the other hand, the following should be valid:
In general, if \(\Box \varphi \) expresses “at least one thing of each (relevant) n-tuple of things has property \(\varphi \)” then the following is intuitively valid:
Note that \(\mathtt {K}_1\) is just \(\mathtt {C}\), which is a theorem in the weakest normal modal logic \(\mathbb {K}\). \(\mathtt {C}\) is sometimes called the Closure of Conjunction [11], or Aggregative Axiom [20], or Adjunctive Axiom [6]. Clearly, when \(n\ge 2\), \(\mathtt {K}_n\) are weaker versions of \(\mathtt {C}\). The resulting logics departing from the basic normal modal logics by using weaker aggregative axioms \(\mathtt {K}_n\) instead of \(\mathtt {C}\) are called Weakly Aggregative Modal Logics (WAML) [32]. There are various readings of \(\Box p\) under which it is intuitive to reject \(\mathtt {C}\) besides the one we mentioned in our motivating party story. For example, if we read \(\Box p\) as “p is obligatory” as in deontic logic, then \(\mathtt {C}\) is not that reasonable since one may easily face two conflicting obligations without having any single contradictory obligation [32]. As another example, in epistemic logic of knowing how [16, 35], if \(\Box p\) expresses “knowing how to achieve p”, then it is reasonable to make \(\mathtt {C}\) invalid: you may know how to open a door and know how to close the door, but you can never know how to make the door both open and closed.
Coming back to our setting where \(\mathtt {K}_n\) are valid, the readings of \(\Box \varphi \) in those axioms may sound complicated, but they are actually grounded in a more general picture of Polyadic Modal Logics (\({{\textsf {\textit{PML}}}}\)) which studies the logics with n-ary modalities. Polyadic modalities arose naturally in the literature of philosophical logic, particularly for the binary ones, such as the until modality in temporal logic [21], instantial operators in games-related neighborhood modal logics [34], relativized knowledge operators in epistemic logic [9, 36], Routley and Meyer’s ternary accessibility relation semantics in relevance logics [29, 30], and the conditional operators in the logics of conditionals [8]. Following the notation in [10], we use \(\nabla \) for the n-ary generalization of the \(\Box \) modality when \(n>1\).Footnote 1 The semantics of \(\nabla (\varphi _1, \dots , \varphi _n)\) is based on Kripke models with \(n+1\)-ary relations R [10, 20]:
\(\nabla (\varphi _1, \dots , \varphi _n)\) holds at s iff for all \(s_1, ..., s_n\) such that \(Rss_1\dots s_n\) there exists some \(i\in [1,n]\) such that \(\varphi _i\) holds at \(s_i\).
We will call \(\nabla \) the normal polyadic modal operator and one should also notice that, by contrast, in those examples with unary operators we just mentioned above, the unary operators are not normal.Footnote 2 However, the reading we mentioned for \(\Box \varphi \) in our motivating story is simply the semantics for \(\nabla (\varphi _1, \dots , \varphi _n)\) where \(\varphi _1=\dots =\varphi _n\): notice how they share the same \(\forall \exists \) quantifier alternation pattern. Thus, the formulas \(\Box \varphi \) under the new reading can be viewed as special cases of the modal formulas in polyadic modal languages. Due to the fact that the arguments are the same in \(\nabla (\varphi , \dots , \varphi )\), we can also call the \(\Box \) the diagonal n-modalities.Footnote 3 In this light, we may call the new semantics for \(\Box \varphi \) the diagonal n-semantics (given frames with \(n+1\)-ary relations).
Diagonal modalities also arise in other settings in disguise. For example, in epistemic logic of knowing value [18], the formula \(\mathsf {Kv}(\varphi , c)\) says that the agent knows the value of c given \(\varphi \), which semantically amounts to that for all the pairs of \(\varphi \) worlds that the agent cannot distinguish from the actual worlds, c has the same value. In other words, in every pair of the indistinguishable worlds where c has different values, there is a \(\lnot \varphi \) world, which can be expressed by \(\Box ^c \lnot \varphi \) with the diagonal 2-modality (\(\Box ^c\)) based on intuitive ternary relations (see details in [18]). As another example in epistemic logic, [13] proposed a local reasoning operator based on models where each agent on each world may have different frames of mind (sets of indistinguishable worlds). That one agent believes \(\varphi \) then means that in one of his current frame of mind, \(\varphi \) is true everywhere. This belief modality can also be viewed as the dual of a diagonal 2-modality (noticing the quantifier alternation \(\exists \forall \) in the informal semantics).
Yet another important reason to study diagonal modalities comes from the connection with paraconsistent reasoning established by Schotch and Jennings [32]. In a nutshell, [32] introduces a notion of n-forcing where a set of formulas \(\varGamma \) n-forces \(\varphi \) (\(\varGamma \vdash _n\varphi \)) if for each n-partition of \(\varGamma \) there is a cell \(\varDelta \) such that \(\varphi \) follows from \(\varDelta \) classically w.r.t. some given logic (\(\varGamma \vdash \varphi \)). This leads to a notion of n-coherence relaxing the notion of consistency: \(\varGamma \nvdash _n \bot \) (\(\varGamma \) is n-coherent) iff there exists an n-partition of \(\varGamma \) such that all the cells are classically consistent. These notions led the authors of [32] to the discovery of the diagonal semantics for \(\Box \) based on frames with \(n+1\)-ary relations, by requiring \(\Box (u)=\{\varphi \mid u\vDash \Box \varphi \}\) to be an n-theory based on the closure over n-forcing, under some other minor conditions. Since the derivation relation of basic normal modal logic \(\mathbb {K}\) can be characterized by a proof system extending the propositional one with the rule \(\varGamma \vdash \varphi /\Box (\varGamma )\vdash \Box \varphi \) where \(\Box (\varGamma )=\{\Box \varphi \mid \varphi \in \varGamma \}\), it is interesting to ask whether adding \(\varGamma \vdash _{n} \varphi /\Box (\varGamma )\vdash _n \Box \varphi \) characterizes exactly the valid consequences for modal logic under the diagonal semantics based on frames with n-ary relations. Apostoli and Brown answered this question positively in [5] 15 years later, and they characterize \(\vdash _n\) by a Gentzen-style sequent calculus based on the compactness of \(\vdash _n\) proved by using a compact result for coloring hypergraphs.Footnote 4 Moreover, they show that the WAML proof systems with \(\mathtt {K}_n\) are also complete w.r.t. the class of all frames with \(n+1\)-ary relations respectively. The latter proof is then simplified in [26] without using the graph theoretical compactness result. This completeness result is further generalized to the extensions of WAML with extra one-degree axioms in [4]. The computational complexity issues of such logics are discussed in [1], and this concludes our relatively long introduction to WAML, which might not be that well-known to many modal logicians.
In this paper, we continue the line of work on WAML by looking at the model theoretical aspects. In particular, we mainly focus on the following two questions:
-
How to characterize the expressive power of WAML structurally within first-order logic over (finite) pointed models?
-
Whether WAML has Craig Interpolation?
For the first question, we propose a notion of bisimulation to characterize WAML within the corresponding first-order logic. The answer for the second question is negative, and we will provide counterexamples in this paper to show WAML (in particular, each \(\mathbb {K}_n\) for \(n \ge 2\)) does not have Craig Interpolation.
In the rest of the paper, we lay out the basics of WAML in Sect. 2, prove the characterization theorem based on a bisimulation notion in Sect. 3, and give counterexamples for the interpolation theorem in Sect. 4 before concluding with future work in Sect. 5.
2 Preliminaries
In this section we review some basic definitions and results in the literature.
2.1 Weakly Aggregative Modal Logic
The language for \(\textsf {WAML}\) is the same as the language for basic (monadic) modal logic.
Definition 1
Given a set of propositional letters \(\varPhi \) and a single unary modality \(\Box \), the language of \(\textsf {WAML}\) is defined by:
where \(p\in \varPhi \). We define \(\top \), \(\varphi \vee \psi \), \(\varphi \rightarrow \psi \), and \(\Diamond \varphi \) as usual.
However, given n, \(\textsf {WAML}\) can be viewed as a fragment of polyadic modal logic with a n-ary modality, since \(\Box \varphi \) is essentially \(\nabla (\varphi , \ldots , \varphi )\). Notation: in the sequel, we use \(\textsf {WAML}^n\), where \(n>1\), to denote the logical framework with the semantics based on n-models defined below:
Definition 2
(n-Semantics). An n-frame is a pair \(\langle W, R \rangle \) where W is an nonempty set and R is an \(n+1\)-ary relation over W. An n-model \(\mathcal {M}\) is a pair \(\langle \mathcal {F}, V \rangle \) where the valuation function V assigns each \(w\in W\) a subset of \(\varPhi \). We say \(\mathcal {M}\) is an image-finite model if there are only finitely many n-ary successors of each point. The semantics for \(\Box \varphi \) (and \(\Diamond \varphi \)) is defined by:
According to the above semantics, it is not hard to see that the aggregation axiom \(\Box \varphi \wedge \Box \psi \rightarrow \Box (\varphi \wedge \psi )\) in basic normal modal logic is not valid on n-frames for any \(n > 1\).
[32] proposed the following proof systems \(\mathbb {K}_n\) for each n.
Definition 3
(Weakly aggregative modal logic). The logic \(\mathbb {K}_n\) is a modal logic including propositional tautologies, the axiom \(\mathtt {K}_n\) and closed under the rulesFootnote 5 \(\mathtt {N}\) and \(\mathtt {RM}\):

It is clear that \(\mathtt {K}_1\) is just the aggregation axiom \(\mathtt {C}\) and thus \(\mathbb {K}_1\) is just the normal monadic modal logic \(\mathbb {K}\). It can also be shown easily that for each \(n > m\), \(\mathbb {K}_n\) is strictly weaker than \(\mathbb {K}_m\). In fact, many familiar equivalences in normal modal logics, like the equivalence between \(\Diamond \top \) and \( \Box p \rightarrow \Diamond p\), no longer hold in \(\mathbb {K}_n\) for \(n > 1\). Semantically speaking, while \(\Box p \rightarrow \Diamond p\)’s validity corresponds to seriality on 1-frames (usual Kripke frames), its correspondence on 2-frames is not even elementary (\(\Diamond \top \) still corresponds to each point having at least a successor tuple).
After being open for more than a decade, the completeness for \(\mathbb {K}_{n}\) over n-models was finally proved in [5] and [4], by reducing to the n-forcing relation proposed in [32]. In [26], a more direct completeness proof is given using some non-trivial combinatorial analysis to derive a crucial theorem of \(\mathbb {K}_n\).
3 Characterization via Bisimulation
In this section, we introduce a notion of bisimulation for \(\textsf {WAML}\) and prove the van Benthem-Rosen Characteristic Theorem for WAML.Footnote 6
Definition 4
(\(wa^n\)-bisimulation). Let \(\mathcal {M}=(W,R,V)\) and \(\mathcal {M}'=(W',R',V')\) be two n-models. A non-empty binary relation \(Z\subseteq W\times W'\) is called a \(wa^n\)-bisimulation between \(\mathcal {M}\) and \(\mathcal {M}'\) if the following conditions are satisfied:
-
inv
If \(wZw'\), then w and \(w'\) satisfy the same propositional letters (in \(\varPhi \)).
-
forth
If \(wZw'\) and \(Rwv_{1},\ldots ,v_{n}\) then there are \(v_{1}',\ldots ,v_{n}'\) in \(W'\) s.t. \(R'w'v_{1}',\ldots ,v_{n}'\) and for each \(v'_j\) there is a \(v_i\) such that \(v_i Z v'_j\) where \(1\le i,j\le n\).
-
back
If \(wZw'\) and \(R'w'v_{1}',\ldots ,v_{n}'\) then there are \(v_{1},\ldots ,v_{n}\) in W s.t. \(Rwv_{1},\ldots ,v_{n}\) and for each \(v_i\) there is a \(v'_j\) such that \(v_i Z v'_j\) where \(1\le i,j\le n\).
When Z is a bisimulation linking two states w in \(\mathcal {M}\) and \(w'\) in \(\mathcal {M}'\) we say that w and \(w'\) are \(\varPhi \)-\(wa^n\)-bisimilar  .
.
Remark 1
Observe the two subtleties in the above definition: i, j in the forth and back conditions are not necessarily the same, thus we may not have an aligned correspondence of each \(v_i\) and \(v_i'\); in the second part of the forth condition, we require each \(v_j'\) to have a corresponding \(v_i\), not the other way around. Similar in the back condition. This reflects the quantifier alternation in the semantics of \(\Box \) in \(\textsf {WAML}^n\).
Example 1
Consider the following two 2-models where \(\{\langle w,w_1,w_2 \rangle ,\) \(\langle w,w_2,w_3 \rangle \}\) is the ternary relation in the left model, and \(\{\langle v,v_1,v_2 \rangle \}\) is the ternary relation in the right model.

\(Z=\{\langle w,v \rangle , \langle w_1, v_1 \rangle , \langle w_2, v_2 \rangle , \langle w_2, v_1 \rangle \}\) is a \(wa^2\)-bisimulation. A polyadic modal formula \(\lnot \nabla \lnot (p, \lnot p)\), not expressible in \(\textsf {WAML}^2\), can distinguish w and v.
It is easy to verify that  is indeed an equivalence relation and we show \(\textsf {WAML}^n\) is invariant under it.
is indeed an equivalence relation and we show \(\textsf {WAML}^n\) is invariant under it.
Proposition 1
Let \(\mathcal {M}=(W,R,V)\) and \(\mathcal {M}'=(W',R',V')\) be two n-models. Then for every \(w\in W\) and \(w'\in W'\),  implies \(w\equiv _{\textsf {WAML}^n} w'\). In words, \(\textsf {WAML}^n\) formulas are invariant under \(wa^n\)-bisimulation.
implies \(w\equiv _{\textsf {WAML}^n} w'\). In words, \(\textsf {WAML}^n\) formulas are invariant under \(wa^n\)-bisimulation.
Proof
We consider only the modality case. Suppose that  and \(w\,\models \,\Diamond \varphi \). Then there are \(v_{1},\ldots ,v_{n}\) s.t. \(Rwv_{1},\ldots ,v_{n}\), and each \(v_{i}\,\models \,\varphi \). By the forth condition, there are \(v_{1}',\ldots ,v_{n}'\) in \(W'\) s.t. \(Rw'v_{1}',\ldots ,v_{n}'\) and for each \(v'_j\) there is a \(v_i\) such that \(v_i Z v'_j\). From the I.H. we have each \(v_{i}'\,\models \,\varphi \). As a result, \(w'\,\models \,\Diamond \varphi \). For the converse direction just use the back condition.
and \(w\,\models \,\Diamond \varphi \). Then there are \(v_{1},\ldots ,v_{n}\) s.t. \(Rwv_{1},\ldots ,v_{n}\), and each \(v_{i}\,\models \,\varphi \). By the forth condition, there are \(v_{1}',\ldots ,v_{n}'\) in \(W'\) s.t. \(Rw'v_{1}',\ldots ,v_{n}'\) and for each \(v'_j\) there is a \(v_i\) such that \(v_i Z v'_j\). From the I.H. we have each \(v_{i}'\,\models \,\varphi \). As a result, \(w'\,\models \,\Diamond \varphi \). For the converse direction just use the back condition.
Theorem 1
(Hennessy-Milner Theorem for \({\mathbf {\mathsf{{WAML}}}}^n\)). Let \(\mathcal {M}=(W,R,V)\) and \(\mathcal {M}'=(W',R',V')\) be two image-finite n-models. Then for every \(w\in W\) and \(w'\in W'\),  iff \(w\equiv _{\textsf {WAML}^n} w'\).
iff \(w\equiv _{\textsf {WAML}^n} w'\).
Proof
As in basic modal logic, the crucial part is to show \(\equiv _{\textsf {WAML}^n}\) is indeed a \(wa^n\)-bisimulation and we only verify the forth condition. Suppose towards contradiction that \(Rwv_1\dots v_n\) but for each \(v_1'\dots v'_n\) such that \(R'w'v_1'\dots v'_n\) there is a \(v'_j\) such that it is not \(\textsf {WAML}^n\)-equivalent to any of \(v_i\). In image-finite models we can list such \(v'_j\) as \(u_1\dots u_m\). Now for each \(u_k\) and \(v_i\) we have \(\varphi _k^i\) which holds on \(v_i\) but not on \(u_k\). Now we consider the formula \(\psi =\Diamond (\bigvee _{1\le i\le n}\bigwedge _{1\le k\le m} \varphi _k^i)\). It is not hard to see that \(\psi \) holds on w but not \(w'\), hence contradiction.
Like in normal modal logic, we can also define a notion of k-bisimulation of \(\textsf {WAML}^n\), by restricting the maximal depth we may go to.
Definition 5
(k-\(wa^n\)-bisimulation). Let \(\mathcal {M}=(W,R,V)\) and \(\mathcal {M}'=(W',R',\) \(V')\) be two n-models. w and \(w'\) are 0-\(wa^n\)-bisimilar ( ) iff \(V(v)=V'(v')\).
) iff \(V(v)=V'(v')\).  iff
iff  and the follow two conditions are satisfied:
and the follow two conditions are satisfied:
-
forth
If
 and \(Rvv_{1},\ldots ,v_{n}\) then there are \(v_{1}',\ldots ,v_{n}'\) in \(W'\) s.t. \(R'v'v_{1}',\ldots ,v_{n}'\) and for each \(v'_j\) there is a \(v_i\) such that
and \(Rvv_{1},\ldots ,v_{n}\) then there are \(v_{1}',\ldots ,v_{n}'\) in \(W'\) s.t. \(R'v'v_{1}',\ldots ,v_{n}'\) and for each \(v'_j\) there is a \(v_i\) such that  where \(1\le i,j\le n\).
where \(1\le i,j\le n\). -
back
If
 and \(R'v'v_{1}',\ldots ,v_{n}'\) then there are \(v_{1},\ldots ,v_{n}\) in W s.t. \(Rvv_{1},\ldots ,v_{n}\) and for each \(v_i\) there is a \(v'_j\) such that
and \(R'v'v_{1}',\ldots ,v_{n}'\) then there are \(v_{1},\ldots ,v_{n}\) in W s.t. \(Rvv_{1},\ldots ,v_{n}\) and for each \(v_i\) there is a \(v'_j\) such that 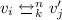 where \(1\le i,j\le n\).
where \(1\le i,j\le n\).
We can translate each \(\textsf {WAML}^n\) formula to an equivalent \(\textsf {FOL}\) formula with one free variable and one \(n+1\)-ary relation symbol, thus \(\textsf {WAML}^n\) is also compact.
Definition 6
(Standard translation). \(ST:\textsf {WAML}^{n}\rightarrow \textsf {FOL}\):
By following a similar strategy as in [27], we will show a van Benthem-Rosen characterization theorem for \(\textsf {WAML}^n\): a \(\textsf {FOL}\) formula is equivalent to the translation of a \(\textsf {WAML}^n\) formula (over finite n-models) if and only if it is invariant under \(wa^n\)-bisimulations (over finite n-models).
First we need to define a notion of unraveling w.r.t. n-ary models similarly to models with binary relations. We use an example of a graph with ternary relations to illustrate the intuitive idea behind the general n-ary unraveling, which is first introduced in [28].
Example 2
Given the 2-model with ternary relations \(\langle \{w,v,u,t\},\) \(\{\langle w, u,t \rangle ,\) \(\langle u,t,u \rangle ,\) \(\langle t,w,v \rangle \}, V \rangle \). It is quite intuitive to first unravel it into a tree with pairs of states as nodes, illustrated below:

To turn it into a 2-model, we need to define the new ternary relations. For each triple \(\langle s_0,s_1,s_2 \rangle \) of pairs, \(\langle s_0, s_1, s_2 \rangle \) is in the new ternary relation iff \(s_1\) and \(s_2\) are successors of \(s_0\) in the above graph and the triple of underlined worlds in \(s_0, s_1, s_2\) respectively is in the original ternary relation, e.g., \(\langle u,\underline{t} \rangle ,\langle \underline{w},v \rangle ,\langle w,\underline{v} \rangle \) is in the new ternary relation since \(\langle t,w,v \rangle \) is in the original ternary relation.
In general, we can use the n-tuples of the states in the original model together with a natural number \(k\in [1,n]\) as the basic building blocks for the unraveling of an n-model, e.g., \(\langle w, v, u, 2 \rangle \) means the second the state is the underlined one. To make the definition uniform, we define the root as the sequence \(\langle w,\dots ,w,1 \rangle .\) Like the unraveling for a binary graph, formally we will use sequences of such building blocks as the nodes in the unraveling of a n-model, e.g., the left-most node \(\langle \underline{t},u \rangle \) in the above example will become \(\langle \langle w,w,1 \rangle ,\langle u,t,1 \rangle ,\langle t, u ,1 \rangle \rangle \). This leads to the following definition.
Definition 7
Given an n-model \(\mathcal {M}=\langle W,R,V\rangle \) and \(w\in W\), we first define the binary unraveling \(\mathcal {M}^b_{w}\) of \(\mathcal {M}\) around w as \(\langle W_w, R^b, V' \rangle \) where:
-
\(W_w\) is the set of sequences \(\langle \langle \mathbf {v}_0,i_0\rangle ,\langle \mathbf {v}_{1},i_{1}\rangle ,\ldots ,\langle \mathbf {v}_{m},i_{m}\rangle \rangle \) where:
-
\(m\in \mathbb {N}\);
-
for each \(j\in [0,m]\), \(\mathbf {v}_{j}\in W^n\) and \(i_{j}\in [1, n]\) such that \(R(\mathbf {v}_{j}[i_{j}])\mathbf {v}_{j+1}\);
-
\(\mathbf {v}_0\) is the constant n-sequence \(\langle w,\dots ,w\rangle \) and \(i_0=1\);
-
-
\(R^bss'\) iff \(s'\) extends s with some \(\langle \mathbf {v}, i \rangle \)
-
\(V'(s)=V(r(s))\), where \(r(s)= \mathbf {v}_m[i_m]\) if \(s=\langle \dots , \langle \mathbf {v}_m,i_m \rangle \rangle \).
The unraveling \(\mathcal {M}_w=\langle W_w, R', V' \rangle \) is based on \( \mathcal {M}^b_w\) by defining \(R's_0 s_1\dots s_n \) iff \(Rr(s_0)r(s_1)\dots r(s_n)\) and \(R^bs_0s_i\) for all \(i\in [1,n]\). Let the bounded unraveling \(\mathcal {M}_w|_l\) be the submodel of \(\mathcal {M}_w\) up to level l.
Remark 2
The unravelling \(\mathcal {M}_w\) itself is not totally “tree-like”, since there may be some node w occurs in both an n-tuple successor of x and an n-tuple successor of y for \(x \ne y\). But clearly \(\mathcal {M}^b_w\) is a tree, and in \(\mathcal {M}_w\), if \(Rs_0\dots s_n\) then \(s_1\dots s_n\) are at the next “level” of \(s_0\). The latter property is crucial in the later proofs, but due to space issues, we have to omit the details here.
r defined above reveals the corresponding state of s in the original model \(\mathcal {M}\). It is not hard to show the following.
Proposition 2
The above r (viewed as a relation) is a \(wa^n\)-bisimulation between \(\mathcal {M}_{w}\) and \(\mathcal {M}\). Actually r is a p-morphism (over n-models) from \(\mathcal {M}_w\) to \(\mathcal {M}\).
Now we have all the ingredients to prove the following characterization theorem. Note that the characterization works with or without the finite model constraints.
Theorem 2
A first-order formula \(\alpha (x)\) is invariant under  (over finite models) iff \(\alpha (x)\) is equivalent to a \(\textsf {WAML}^n\) formula (over finite models).
(over finite models) iff \(\alpha (x)\) is equivalent to a \(\textsf {WAML}^n\) formula (over finite models).
Following the general strategy in [27], the only non-trivial part is to show that the FOL formula \(\alpha (x)\) that is invariant under \(wa^n\)-bisimulation has some locality property w.r.t. its bounded unraveling \(\mathcal {M}_w|_l\) for some l. Due to lack of space, we only show the following lemma and give a proof sketch here. For other relatively routine parts of the proof, see [27].
Lemma 1
(locality). An FOL formula \(\alpha (x)\) is invariant under  (over finite models) implies that for some \(l \in \mathbb {N} \), for any n-model \(\mathcal {M},w\): \(\mathcal {M},w\Vdash \alpha (x)[w]\) iff \(\mathcal {M}_w|_{l}\Vdash \alpha (x)[(\langle \mathbf {w},1) \rangle ]\).
(over finite models) implies that for some \(l \in \mathbb {N} \), for any n-model \(\mathcal {M},w\): \(\mathcal {M},w\Vdash \alpha (x)[w]\) iff \(\mathcal {M}_w|_{l}\Vdash \alpha (x)[(\langle \mathbf {w},1) \rangle ]\).
Here we explain the most important ideas behind the proof. First of all, like in [27], we take \(l=2^q-1\) where q is the quantifier rank of \(\alpha (x)\), and build two bigger models \(\mathcal {M}^*, w^*\) and \(\mathcal {N}^*, v^*\) which are \(wa^n\)-bisimilar to \(\mathcal {M},w\) and \(\mathcal {M}_w|_{l}, w\) respectively using our new unraveling notion. Then we show that in the q-round EF game between the bigger n-models Duplicator has a winning strategy. To specify the strategy, which is essentially letting the duplicator to keep some “safe zones” for extensions of partial isomorphisms, we need to define the distance of points in n-models. Let the distance between s and \(s'\) (notation \(d(s,s')\)) be the length of the shortest (undirected) path between s and \(s'\) via a new relation binary \(R^{c}\) where \(R^{c}xy\) iff \(Rxy_{1}\ldots y_{n}\) and \(y=y_{i}\) for some \(i\in [1, n]\). We set \(d(s, s')=\omega \) if s and \(s'\) are not connected by any such path. It is easy to see that in the unraveling \(\mathcal {M}_w\), \(d(s, s')\) is exactly the distance in the usual sense between \(s, s'\) in the tree \(\mathcal {M}_w^b\). Then, the winning strategy looks exactly like the one in [27] for binary models. The key point to show that the same strategy is a winning strategy in the new setting is that when building the correct induction hypothesis, we need to define two “neighborhoods” of a node–a big one and a small one. In particular, first let \((a_{i},b_{i})\) be the pair selected at i round where each \(a_{i}\in \mathcal {M}^{*}\) and \(b_{i}\in \mathcal {N}^{*}\), where by the rule of the game, \(a_{0}=w^{*}\) and \(b_{0}=v^{*}\). Then define \(S(m)=\{a_{i}\mid i\le m\}\), \(N_{i}(m)\) to be the neighborhood of \(a_{i}\) within distance of \(2^{q-m}-1\), and \(N_{i}^{^{\prime }}(m)\) to be the neighborhood of \(a_{i}\) within distance of \(2^{q-(m+1)}\). Here the N and \(N^{^{\prime }}\) are the two “neighborhoods”. Then finally the induction hypothesis can be correctly formulated as the following.
After m rounds (\(0\le m\le q\)), the following two hold.
- 1.
The selected points form a partial isomorphism I: \(\mathcal {M}^{*}\rightarrow \mathcal {N}^{*}\).
- 2.
If \(m<q\) then there is a sequence \((I_{0},\ldots ,I_{m})\) s.t. for each \(i\le m\),
- (a)
\(I_{i}\supseteq I\) is a partial isomorphism with \(Dom(I_{i})=N_{i}(m)\cup S(m)\);
- (b)
\(\forall h,j\le m\forall x\in N_{h}^{^{\prime }}(m)\cap N_{j}^{^{\prime }}(m)(I_{h}(x)=I_{j}(x))\).
In Otto’s original proof in [27], the induction hypothesis is not very clear, and we think it is necessary to give such an explicit formulation here.
Remark 3
It is not hard to show that under our distance notion, for each x, y, z in the model, \(d(x,z) \ge d(x,y)-d(y,z)\), i.e., \(d(x,z)+d(z,y) \ge d(x,y)\) which is a more usual form of the triangle inequality. This justifies the new distance notion. To see why a similar strategy like the one in [27] for binary models works, note that our unraveling \(\mathcal {M}_w\) is essentially based on a tree \(\mathcal {M}_w^b\) by definition, and the n-ary relation over such a tree structure has a very special property: if \(Rs_0\dots s_n\) then \(s_1\dots s_n\) are immediate successors of \(s_0\) in the binary unraveling as mentioned in Remark 2. This leads to the following crucial property we will use repeatedly: if we already established a partial isomorphism I between S and N (w.r.t. also n-ary relations), and \(x\not \in S\) is not directly connected to anything in S, and \(y\not \in N\) is also not directly connected to anything in N then \(I\cup \{(x,y)\}\) extending I is again a partial isomorphism.
Finally, the bound \(l=2^{q}-1\) in the above proof, which we choose uniformly for every n, is actually not “optimal”, since for a larger n, we can have a lower bound. Especially, when \(n > q\), even \(l=1\), the Duplicator could have a winning strategy, since any bijection will be a partial isomorphism. So the distance we define here is not a appropriate one for us to find the minimal bound l. Here we conjecture that the bound should be the least integer l s.t. \(l \ge (2^{q}-1)/n\).
4 Interpolation
By a standard strategy in [19], we know that the basic polyadic modal logics (\(\textsf {PML}\)) have the Craig Interpolation theorem. What’s more, in [31], the authors proved that the minimal monotonic modal logic M has Uniform Interpolation. Furthermore, we know that the basic modal logic \(\mathbb {K}\) also has Uniform Interpolation from [3] and [2]. From the following three aspects we may conjecture that the basic \(\textsf {WAML}\) systems \(\mathbb {K}_{n}\) should have interpolation too:
-
1
\(\textsf {WAML}\) can be treated as a fragment of \(\textsf {PML}\).
-
2
\(\mathbb {K}_{n}\) is regarded as a general version of \(\mathbb {K}\), since \(\mathbb {K}\) is just \(\mathbb {K}_{1}\).
-
3
\(\mathbb {K}_{n}\) can be viewed as a special kind of monotonic modal logics.
But in fact no \(\mathbb {K}_{n}\) has the Craig Interpolation Property for \(n \ge 2\). The first counterexample for interpolation we found is for \(\mathbb {K}_{3}\), which is relatively easy to understand and can be readily generalized to all \(\mathbb {K}_{n}\) for \(n \ge 3\). Later we found a counterexample for \(\mathbb {K}_{2}\), which is slightly more complicated. Here we first give the two counterexamples for \(\mathbb {K}_2\) and \(\mathbb {K}_3\) and then provide the general construction for \(\mathbb {K}_n\) (\(n \ge 3\)). But before we state the counterexamples, let us first clarify what do we mean by “a counterexample” of the Craig Interpolation Property for \(\mathbb {K}_n\).
Lemma 2
Let n be a non-zero natural number. If there are two pointed n-models \(\mathcal {M}, w\) and \(\mathcal {N}, v\) and two formulas \(\varphi \) and \(\psi \) such that
-
1.
\(\mathcal {M}, w\,\models \,\varphi \) and \(\mathcal {N}, v\,\models \,\psi \);
-
2.
\(\mathbb {K}_n \vdash \varphi \rightarrow \lnot \psi \);
-
3.
letting \(\varPhi '\) be the set of all the propositional letters that appear both in \(\varphi \) and \(\psi \), for any formula \(\gamma \) in \(\textsf {WAML}\) such that only letters in \(\varPhi '\) appear, \(\mathcal {M}, w\,\models \,\gamma \) iff \(\mathcal {N}, v\,\models \,\gamma \);
then \(\mathbb {K}_n\) lack the Craig Interpolation Property.
Proof
Assume for contradiction that \(\mathbb {K}_n\) has the Craig Interpolation Property. Then since \(\mathbb {K}_n \vdash \varphi \rightarrow \lnot \psi \), there is a interpolant \(\gamma \) such that
-
\(\mathbb {K}_n \vdash \varphi \rightarrow \gamma \) and \(\mathbb {K}_n \vdash \gamma \rightarrow \lnot \psi \);
-
only letters in \(\varPhi '\) appear in \(\gamma \).
Now since \(\mathcal {M}, w\,\models \,\varphi \) with \(\mathcal {M}\) being an n-model and \(\mathbb {K}_n \vdash \varphi \rightarrow \gamma \), by soundness, \(\mathcal {M}, w\,\models \,\gamma \). Then \(\mathcal {N}, v\,\models \,\gamma \) by 3. Then using \(\mathbb {K}_n \vdash \gamma \rightarrow \lnot \psi \) and soundness again, \(\mathcal {N}, v\,\models \,\lnot \psi \), contradicting \(\mathcal {N}, v\,\models \,\psi \).
Given this proposition, a pair of pointed n-models and a pair of formulas satisfying the antecedent constitute a counterexample of the Craig Interpolation property. Now we proceed to provide them for each \(\mathbb {K}_n\) with \(n \ge 2\).
Example 3
Consider the following two 2-models where \(\{\langle w,w_1,w_1 \rangle ,\) \(\langle w,w_2,w_3 \rangle \}\) is the ternary relation in the left model \(\mathcal {M}_2\), and \(\{\langle v,v_1,v_2 \rangle \}\) is the ternary relation in the right model \(\mathcal {N}_2\), where the valuations are as in the diagram.

Then set \(\varphi _2 = \Box (\lnot p \vee \lnot q) \wedge \Diamond q\) and \(\psi _2 = \Box (p \wedge r) \wedge \Box (p \wedge \lnot r)\). It is easy to see that \(\mathcal {M}_2, w\,\models \,\varphi _2\) and \(\mathcal {N}_2, v\,\models \,\psi _2\). To see that \(\mathbb {K}_2\vdash \varphi _2 \rightarrow \lnot \psi _2\), consider the following derivation, where to make long Boolean combinations readable, we write negation of propositional letters as overline, omit \(\wedge \) between purely Boolean formulas and replace \(\vee \) with |.

Here PL means propositional reasoning. Hence we are done with the first two points for this pair of models and formulas to be a counterexamples. For the last point, note that \(Z=\{\langle w,v \rangle , \langle w_1, v_1 \rangle , \langle w_1, v_2 \rangle , \langle w_2, v_1 \rangle ,\langle w_2, v_2 \rangle \}\) is a \(wa^2\)-bisimulation when \(\varPhi = \{p\}\). Hence by Proposition 1, for any formula \(\gamma \) with p the only propositional letter, \(\mathcal {M}_2, w\,\models \,\gamma \) iff \(\mathcal {N}_2, v\,\models \,\gamma \). But p is the only common propositional letters in \(\varphi _2\) and \(\psi _2\). Clearly, now \(\mathcal {M}, w\), \(\mathcal {N}, v\), \(\varphi _2\), and \(\psi _2\) form a counterexample to the Craig Interpolation Property for \(\mathbb {K}_2\).
Example 4
Consider the following two 3-models where \(\{\langle w,w_1,w_2,w_3 \rangle \}\) is the relation in \(\mathcal {M}_3\) and \(\{\langle v,v_1,v_2,v_3 \rangle \}\) is the relation in \(\mathcal {N}_3\).

Then set \(\varphi _3= \Box p\bar{q} \wedge \Box pq \wedge \Diamond (p|\bar{p})\), \(\psi _3= \Box \bar{p}r \wedge \Box \bar{p}\bar{r} \wedge \Diamond (p|\bar{p})\). Clearly \(\mathcal {M}_3, w\,\models \,\varphi _3\) and \(\mathcal {N}_3, v\,\models \,\psi _3\). Further, \(\mathbb {K}_2 \vdash \varphi _3 \rightarrow \lnot \psi _3\) since we have the following derivation.

Finally, note that \(Z=\{\langle w,v \rangle , \langle w_1, v_3 \rangle , \langle w_2, v_3 \rangle , \langle w_3, v_1 \rangle ,\langle w_3, v_2 \rangle \}\) is a \(wa^3\)-bisimulation if \(\varPhi = \{p\}\).
The above example can be naturally generalized for each \(\mathbb {K}_n\) with \(n > 3\). Let m be the least natural number s.t. \(2^{m} \ge n-1\) and pick m many distinct propositional letters \(r_1, \ldots , r_m\) from \(\varPhi \). Then for each i from 1 to \(n-1\), we can associate a distinct conjunction of literals \(\rho _i\) using \(r_j\)’s so that \(\rho _i \wedge \rho _{i'}\) are incompatible for each \(i \not = i'\). Then we can state the general counterexample.
Example 5
Consider the following two n-models where \(\{\langle w,w_1,...,w_n \rangle \}\) is the relation in \(\mathcal {M}_n\), and \(\{\langle v,v_1,...,v_n \rangle \}\) is the relation in \(\mathcal {N}_n\).

Set \(\varphi _n = \Box (p \wedge \lnot q) \wedge \Box (p \wedge q) \wedge \Diamond \top \) and \(\psi _n = \bigwedge _{i = 1}^{n-1}\Box (\lnot p \wedge \rho _{i}) \wedge \Diamond \top \). Clearly \(\mathcal {M}_n, w\,\models \,\varphi _n\) and \(\mathcal {N}_n, v\,\models \,\psi _n\). It is also easy to see that by \(\mathtt {K}_n\), we can derive \((\Box (p \wedge \lnot q) \wedge \Box (p \wedge q) \wedge \bigwedge _{i = 1}^{n-1}\Box (\lnot p \wedge \rho _i)) \rightarrow \Box \bot \). With this we can then easily derive \(\varphi _n \rightarrow \lnot \psi _n\) in \(\mathbb {K}_n\). Finally, note that p is the only common propositional letter in \(\varphi _n\) and \(\psi _n\) and that \(Z=\{\langle w,v \rangle , \langle w_1, v_1 \rangle , \langle w_2, v_1 \rangle \} \cup \{w_3,...,w_n\} \times \{v_2,...,v_n\} \) is a \(wa^n\)-bisimulation when \(\varPhi = \{p\}\).
With the examples and Lemma 2, the main theorem of this section follows.
Theorem 3
For any \(n \ge 2\), \(\mathbb {K}_n\) does not have the Craig Interpolation Property.
Remark 4
Note that the Lemma 2 uses only the soundness of the logics. Hence for any extension of \(\mathbb {K}_n\) that is sound on \(\mathcal {M}_n\) and \(\mathcal {N}_n\), it still lacks the Craig Interpolation Property. For example, we may extend \(\mathbb {K}_n\) with \(\mathtt {4}\) and our examples still work since \(\mathtt {4}\) is valid on the underlying frames.
5 Conclusion
In this paper, we proved two results about \(\textsf {WAML}\): first, \(\textsf {WAML}\) have a van Benthem-Rosen characterization, and second, \(\textsf {WAML}\) do not have Craig Interpolation Property (CIP). We conclude with two potentially promising lines of further investigation.
First, the main part of the completeness proof of \(\mathbb {K}_n\) over n-models is to solve some combinatorial puzzle [26]. Due to the semantics of \(\textsf {WAML}\) there is a natural link between combinatorics and \(\textsf {WAML}\) as also shown in the use of graph coloring problem in [5]. As future work, we would like to explore the possibility of using \(\textsf {WAML}\) to express interesting combinatorial properties in graph theory, like the one in [25].
Second, even though we proved that \(\textsf {WAML}\) do not have Craig Interpolation Property, it doesn’t mean that the same must be the case under further constraints (stronger logics). For instance, the counterexample in our paper cannot show that \(\mathbb {K}_n \oplus \mathtt {T}\) lacks CIP since the logic is not sound on the frames of the models we provided. What remains to be done then is to chart the map of CIP among the logics extending \(\mathbb {K}_n\)’s and look for more general methods.
Lastly, if we change all the \(\Box \) in \(\mathbb {K}_n\) into \(\Diamond \), we get the following formula:
In basic normal modal logics, this formula characterizes frames where each world has at most n accessible worlds and is equivalent (assuming the normality of \(\Box \)) to what is commonly called the \(\mathtt {Alt}_n\) in the literature [33]. It is not too hard to observe that the strategy we gave in Sect. 4 can be used to show that for each \(n \ge 3\), normal modal logic \(\mathtt {K}\oplus \mathtt {K}_{n}^{*}\) lacks CIP. It seems that, more abstractly speaking, the counterexamples exist because the logic can reason about with the help of extra propositional letters, but cannot express directly, whether there are many accessible worlds satisfying a property. Note that counting the number of accessible worlds satisfying a property is intuitively important and has been studied in Description Logics (DL) [7] and Graded Modal Logics (GML) [12, 15, 17]. There are already some CIP work in those logics, like [23], and we conjecture that CIP may return when we add modalities that talk directly about numbers.
Notes
- 1.
This is not to be confused with the non-contingency operator, which is also denoted as \(\nabla \) in non-contingency or knowing whether logics [14].
- 2.
One can find a model theoretical survey on \(\textsf {PML}\) in [22].
- 3.
Name mentioned by Yde Venema via personal communications.
- 4.
Other connections between WAML and graph coloring problems can be found in [24] where the four-color problem is coded by the validity of some formulas in the WAML language.
- 5.
This rule can be simplified by the axiom \(\Box \top \) since we have \(\mathtt {RM}\) here.
- 6.
We have another proof for the Characterization theorem over arbitrary n-models, using tailored notions of saturation and ultrafilter extension for \(\textsf {WAML}^n\), due to the space limit we only present the proof which also works for finite models.
References
Allen, M.: Complexity results for logics of local reasoning and inconsistent belief. In: Proceedings of the 10th Conference on Theoretical Aspects of Rationality and Knowledge, pp. 92–108. National University of Singapore (2005)
Andréka, H., Németi, I., van Benthem, J.: Modal languages and bounded fragments of predicate logic. J. Philos. Logic 27(3), 217–274 (1998)
Andréka, H., Van Benthem, J., Németi, I.: Back and forth between modal logic and classical logic. Logic J. IGPL 3(5), 685–720 (1995)
Apostoli, P.: On the completeness of first degree weakly aggregative modal logics. J. Philos. Logic 26(2), 169–180 (1997)
Apostoli, P., Brown, B.: A solution to the completeness problem for weakly aggregative modal logic. J. Symbolic Logic 60(3), 832–842 (1995)
Arló Costa, H.: Non-adjunctive inference and classical modalities. J. Philos. Logic 34(5), 581–605 (2005)
Baader, F., Horrocks, I., Sattler, U.: Description logics. Found. Artif. Intell. 3, 135–179 (2008)
Beall, J., et al.: On the ternary relation and conditionality. J. Philos. Logic 41(3), 595–612 (2012)
van Benthem, J., van Eijck, J., Kooi, B.: Logics of communication and change. Inf. Comput. 204(11), 1620–1662 (2006)
Blackburn, P., De Rijke, M., Venema, Y.: Modal Logic, vol. 53. Cambridge University Press, Cambridge (2002)
Chellas, B.F.: Modal Logic: An Introduction. Cambridge University Press, Cambridge (1980)
De Caro, F.: Graded modalities, ii (canonical models). Studia Logica 47(1), 1–10 (1988). https://doi.org/10.1007/BF00374047
Fagin, R., Halpern, J., Moses, Y., Vardi, M.: Reasoning About Knowledge. MIT Press, Cambridge (1995)
Fan, J., Wang, Y., van Ditmarsch, H.: Contingency and knowing whether. Rev. Symbol. Logic 8, 75–107 (2015)
Fattorosi-Barnaba, M., De Caro, F.: Graded modalities. I. Studia Logica 44(2), 197–221 (1985). https://doi.org/10.1007/BF00379767
Fervari, R., Herzig, A., Li, Y., Wang, Y.: Strategically knowing how. In: Proceedings of IJCAI 2017, pp. 1031–1038 (2017)
Fine, K., et al.: In so many possible worlds. Notre Dame J. Formal Logic 13(4), 516–520 (1972)
Gu, T., Wang, Y.: “Knowing value” logic as a normal modal logic. In: Proceedings of AiML, vol. 11, pp. 362–381 (2016)
Hansen, H., Kupke, C., Pacuit, E.: Neighbourhood structures: bisimilarity and basic model theory. Logical Meth. Comput. Sci. 5(2) (2009). https://doi.org/10.2168/LMCS-5(2:2)2009
Jennings, R.E., Schotch, P.K.: Some remarks on (weakly) weak modal logics. Notre Dame J. Formal Logic 22(4), 309–314 (1981)
Kamp, H.: Tense logic and the theory of linear order. Ph.D. thesis, UCLA (1968)
Liu, J.: Model theoretical aspects of polyadic modal logic: an exposition. Stud. Logic 12(3), 79–101 (2019)
Lutz, C., Wolter, F.: Foundations for uniform interpolation and forgetting in expressive description logics. In: Twenty-Second International Joint Conference on Artificial Intelligence (2011)
Nicholson, T., Allen, M.: Aggregative combinatorics: an introduction. In: Student Session of 2nd North American Summer School in Language, Logic, and Information, pp. 15–25 (2003)
Nicholson, T., Allen, M.: Aggregative combinatorics: an introduction. In: Proceedings of the Student Session, 2nd North American Summer School in Logic, Language, and Information (NASSLLI-03), pp. 15–25 (2003)
Nicholson, T., Jennings, R.E., Sarenac, D.: Revisiting completeness for the \({K}_{n}\) modal logics: a new proof. Logic J. IGPL 8(1), 101–105 (2000)
Otto, M.: Elementary proof of the van Benthem-Rosen characterisation theorem. Technical report 2342 (2004)
de Rijke, M.: Extending modal logic. Ph.D. thesis, ILLC, University of Amsterdam (1993)
Routley, R., Meyer, R.K.: The semantics of entailment – II. J. Philos. Logic 1(1), 53–73 (1972)
Routley, R., Meyer, R.K.: The semantics of entailment – III. J. Philos. Logic 1(2), 192–208 (1972)
Santocanale, L., Venema, Y., et al.: Uniform interpolation for monotone modal logic. Adv. Modal Logic 8, 350–370 (2010)
Schotch, P., Jennings, R.: Modal logic and the theory of modal aggregation. Philosophia 9(2), 265–278 (1980)
Segerberg, K.: An Essay in Classical Modal Logic. Filosofiska Föreningen Och Filosofiska Institutionen Vid Uppsala Universitet, Uppsala (1971)
Van Benthem, J., Bezhanishvili, N., Enqvist, S., Yu, J.: Instantial neighbourhood logic. Rev. Symbolic Logic 10(1), 116–144 (2017)
Wang, Y.: A logic of goal-directed knowing how. Synthese 195(10), 4419–4439 (2018)
Wang, Y., Fan, J.: Conditionally knowing what. In: Proceedings of AiML, vol. 10, pp. 569–587 (2014). www.aiml.net/volumes/volume10/Wang-Fan.pdf
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Liu, J., Wang, Y., Ding, Y. (2019). Weakly Aggregative Modal Logic: Characterization and Interpolation. In: Blackburn, P., Lorini, E., Guo, M. (eds) Logic, Rationality, and Interaction. LORI 2019. Lecture Notes in Computer Science(), vol 11813. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-60292-8_12
Download citation
DOI: https://doi.org/10.1007/978-3-662-60292-8_12
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-60291-1
Online ISBN: 978-3-662-60292-8
eBook Packages: Computer ScienceComputer Science (R0)




 and
and  where
where  and
and 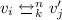 where
where