Keywords

1 Introduction

As a commonly used high-precision positioning technology, the real-time kinematic (RTK) has proven its efficient and reliable performance during the past a few years. However, both its availability and reliability deteriorate dramatically under some challenging conditions, for instance, the longer baselines than 15 km, deep open pit mines and urban canyon [1]. Especially for the single-system situation, in challenging observation conditions, not all available satellites are visible. In addition, affected by observation noises and atmospheric errors, the initialization often takes tens of seconds or even more depending on the number of tracked satellites, the baseline length and the observation environment [2, 3]. The fundamental reason is that the integer ambiguity cannot be resolved reliably. Integer ambiguity resolution (AR) is a prerequisite for precise RTK positioning [4–6]. The positioning accuracy can reach centimetre level if the ambiguities are correctly resolved. Otherwise the decimetre level even larger positioning bias will be introduced duo to the wrong ambiguities.

As the China’s Navigation Satellite System (BDS) had provided regional service by the end of 2012, it has been one of the four global navigation satellite systems, together with the US system GPS, the Russian system GLONASS and the European system Galileo. Multi-constellation combination brings multiple satellites compared with single system, thus provides more redundant observation information. This contributes to the improvement of positioning stability [1, 7, 8]. Besides, multi-constellation combination will also contribute to AR, especially the geometry-based model, mainly for it can improve the ambiguity precision and thus improve the AR success rate [9, 10]. However for the systematic bias, for instance caused by atmospheric errors typically, the multi-constellation combination helps little. The existing commonly used RTK technology usually resolves the basic ambiguities, i.e. L1 (B1) or L2 (B2) ambiguities. The wavelengths of these basic carrier measurements are about from 18 to 25 cm. That is say, if the systematic bias reaches near half of the wavelength, the ambiguity can hardly be resolved correctly. Even if the ambiguity can be resolved correctly, it will take long time. That is the primary reason that the current RTK can just reach no more than 15 km. For the longer baseline, especially for the low-elevation satellites, atmospheric errors cannot be neglected, relatively to the wavelengths of basic carrier measurements.

In this contribution, in order to weaken the influence of atmospheric errors on AR, we proposed a reliable RTK positioning method. It takes advantage that wide-lane combination has much more longer wavelength, and the multi-constellation combined wide-lane ambiguity-fixed observations are directly used to positioning calculation. In the paper, firstly, the GPS/GLONASS/BDS combined geometry-based wide-lane AR model is introduced in Sect. 38.2. Then in Sect. 38.3, we introduce a partial ambiguity resolution (PAR) method to avoid the influence of extreme errors from low-elevation satellites. Lastly in Sect. 38.4, a typical example with real-data is given to reflect the benefits of the proposed method.

2 WL Ambiguity Resolution Model

2.1 Observation Model

Without loss of simplicity, the basic DD pseudorange and carrier observation equations can be expressed as below:

$$ \Delta \nabla P_{i} = \Delta \nabla \rho + \Delta \nabla T + \Delta \nabla I_{i} + \Delta \nabla \varepsilon_{{P_{i} }} $$
(38.1)
$$ \lambda_{i} \cdot \Delta \nabla \varphi_{i} = \Delta \nabla \rho + \Delta \nabla T - \Delta \nabla I_{i} + \lambda_{i} \cdot \Delta \nabla N_{i} + \Delta \nabla \varepsilon_{{\phi_{i} }} $$
(38.2)

where \( \Delta \nabla ( \cdot ) \) is the double-difference operator; P and φ are pseudorange and carrier measurements respectively; λ is the wavelength; all the items with the subscript i represent the corresponding items in the \( i{\text{th}} \) frequency; ρ is the satellite-station distance; T is tropospheric delay; I is ionospheric delay; N is integer ambiguity; ϕ is the carrier observation by distance; \( \varepsilon_{{P_{i} }} \) and \( \varepsilon_{{\phi_{i} }} \) are measurement noises of pseudorange and carrier respectively. Specifically for GLONASS, which adopt the Frequency Division Multiple Access (FDMA) model, \( \lambda_{i} \cdot \Delta \nabla \varphi_{i} \) and \( \lambda_{i} \cdot \Delta \nabla N_{i} \) can be further described as Eq. (38.3a, 38.3b):

$$ \lambda_{i} \cdot \Delta \nabla \varphi_{i} = \lambda_{i,k} \nabla \varphi_{i,k} - \lambda_{i,r} \nabla \varphi_{i,r} $$
(38.3a)
$$ \lambda_{i} \cdot \Delta \nabla N_{i} = \lambda_{i,k} \nabla N_{i,k} - \lambda_{i,r} \nabla N_{i,r} $$
(38.3b)

Based on the basic observation equations, the DD wide-lane measurement and corresponding observation equation can be expressed as Eqs. (38.4) and (38.5):

$$ \Delta \nabla \phi_{wl} = \lambda_{wl} \cdot (\Delta \nabla \varphi_{1} - \Delta \nabla \varphi_{2} ) $$
(38.4)
$$ \Delta \nabla \phi_{wl} = \Delta \nabla \rho + \Delta \nabla T - \Delta \nabla I_{wl} + \lambda_{wl} \cdot \Delta \nabla N_{wl} + \Delta \nabla \varepsilon_{{\phi_{wl} }} $$
(38.5)

Similarly to Eq. (38.3a, 38.3b), \( \Delta \nabla \phi_{wl} \) and \( \lambda_{wl} \cdot \Delta \nabla N_{wl} \) can also be further described as Eqs. (38.6) and (38.7):

$$ \Delta \nabla \phi_{wl} = \lambda_{wl,k} \cdot \nabla \varphi_{wl,k} - \lambda_{wl,r} \cdot \nabla \varphi_{wl,r} $$
(38.6)
$$ \lambda_{wl} \cdot \Delta \nabla N_{wl} = \lambda_{wl,k} \cdot \nabla N_{wl,k} - \lambda_{wl,r} \cdot \nabla N_{wl,r} $$
(38.7)

2.2 Wide-Lane Ambiguity Resolution with Geometry-Based Model

In geometry-based model, the unknown baseline vector parameters and wide-lane ambiguities are estimated together. The two pseudorange equations on \( f_{1} \) and \( f_{2} \), and the wide-lane carrier equations are all used. The matrix form of calculating equation is as Eq. (38.8):

$$ \left[ {\begin{array}{*{20}c} {A^{G} } & {B^{G} } & {} & {} \\ {A^{R} } & {} & {B^{R} } & {} \\ {A^{C} } & {} & {} & {B^{C} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\text{d} X} \\ {\Delta \nabla N_{wl}^{G} } \\ {\Delta \nabla N_{wl}^{R} } \\ {\Delta \nabla N_{wl}^{C} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Delta \nabla L^{G} } \\ {\Delta \nabla L^{R} } \\ {\Delta \nabla L^{C} } \\ \end{array} } \right] $$
(38.8)

where the superscript ‘G’, ‘R’, ‘C’ represent GPS, GLONASS, and BDS respectively; A is coefficient matrix of baseline vector parameters; B is coefficient matrix of DD ambiguities; dX represents the baseline vector parameters; \( \Delta \nabla L \) is DD constant term matrix after linearization. From Eq. (38.8) we can calculate and get the float wide-lane ambiguity \( \Delta \nabla \hat{N}_{wl} \) and its variance-covariance matrix (vc-matrix) \( Q_{{\hat{N}_{wl} }} \). In order to make the DD ambiguity of GLONASS able to be calculated, we separate the DD ambiguity from Eq. (38.7) and rewrite it as (38.9) :

$$ \lambda_{wl} \cdot \Delta \nabla N_{wl} = \lambda_{wl,k} \cdot [(\nabla N_{wl,k} - \nabla N_{wl,r} ) + (1 - \frac{{\lambda_{wl,r} }}{{\lambda_{wl,k} }}) \cdot \nabla N_{wl,r} ] $$
(38.9)

where \( \nabla N_{wl,k} - \nabla N_{wl,r} \) is the DD wide-lane ambiguity which will be searched and fixed. From Eq. (38.9) we know, in order to separate DD wide-lane ambiguity of GLONASS, we need at first to know the station-single-difference wide-lane ambiguity of the reference satellite. It can be calculated using the Melbourne-Wübbena combination [11, 12], as Eq. (38.10).

$$ \nabla N_{wl,r} = \nabla \varphi_{wl,r} - \frac{1}{{\lambda_{wl,r} }} \cdot \frac{{f_{1,r} \cdot \nabla P_{1,r} + f_{2,r} \cdot \nabla P_{2,r} }}{{f_{1,r} + f_{2,r} }} $$
(38.10)

The calculation of \( \nabla N_{wl,r} \) is mainly affected by the measurement noises, especially the pseudorange noise. This problem can be solved through averaging method. In fact, the influence coefficient of the \( \nabla N_{wl,r} \) on \( \nabla N_{wl,k} - \nabla N_{wl,r} \) is \( (1 - \lambda_{wl,r} /\lambda_{wl,k} ) \). And \( \lambda_{wl,r} /\lambda_{wl,k} \) is a value near to one, so the bias of \( \nabla N_{wl,r} \) will just has very small effect on \( \nabla N_{wl,k} - \nabla N_{wl,r} \). It can be calculated that even if \( \nabla N_{wl,r} \) has a ten-cycle bias, the influence on \( \nabla N_{wl,k} - \nabla N_{wl,r} \) will be smaller than 0.05 cycle. After being processed by Eqs. (38.9) and (38.10), the DD wide-lane ambiguities of GLONASS can be search to integers like GPS or BDS.

3 Partial Ambiguity Resolution Method

From the method described in Sect. 38.2, we can get the float wide-lane DD ambiguities of all the three systems and the corresponding vc-matrix. We know that affected by atmospheric delays, measurement noises and multipath effects, the measurements of low-elevation satellites generally have the much lower accuracy. If we fix all the ambiguities simultaneously, the low-elevation ones may influence the search system and make the search result unable to pass the acceptance test. So we can divide the ambiguities into two parts, of which the one is easy to be fixed, and of course the other one is not or maybe not to be fixed. As shown in Eq. (38.11), we suppose that \( \hat{N}_{a} ,\;Q_{{\hat{N}_{a} }} \) and \( \hat{N}_{b} ,\;Q_{{\hat{N}_{b} }} \) are the ambiguities and vc-matrix of the two parts respectively, as in Eq. (38.11).

$$ \left[ {\begin{array}{*{20}c} {\hat{N}_{a} } \\ {\hat{N}_{b} } \\ \end{array} } \right]\quad \left[ {\begin{array}{*{20}c} {Q_{{\hat{N}_{a} }} } & {Q_{{\hat{N}_{a} \hat{N}_{b} }} } \\ {Q_{{\hat{N}_{b} \hat{N}_{a} }} } & {Q_{{\hat{N}_{b} }} } \\ \end{array} } \right] $$
(38.11)

If we can fix \( \hat{N}_{a} \) reliably and the number of ambiguities in \( \hat{N}_{a} \) is enough, we can directly use the fixed ambiguities to positioning calculation. Of course we can also use the fixed ambiguities to improve the accuracies of the remaining ambiguities and their vc-matrix, which can be referred from [13, 14]. In this paper we mainly consider the former, that is to say we directly use the selected fixed ambiguities to positioning calculation. However, the important thing is how to determine the subset. In this paper we get the subset by the following steps:

  1. (1)

    Sort the elevations of all satellites as an ascend order, and we can get the new elevation set like Eq. (38.12)

    $$ E = \left\{ {e_{1} ,\,e_{2} , \ldots ,e_{n} {\kern 1pt} {\kern 1pt} |{\kern 1pt} {\kern 1pt} {\kern 1pt} e_{1} \, < \,e_{2} \, < \, \cdots \, < \,e_{n} {\kern 1pt} } \right\} $$
    (38.12)

    where \( e_{i} \) represent the elevation in \( i{\text{th}} \) order.

  2. (2)

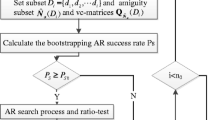
    Set the cut-off elevation \( e_{c} \) at \( e_{1} \), and we can get the subset \( \hat{N}_{a} (e_{1} ) \) and \( Q_{{\hat{N}_{a} }} (e_{1} ) \).Then the LAMBDA method [15] is applied into the ambiguity search process. If the search results meet the following three conditions, the fixed ambiguities can be considered to pass the acceptance test and be used into the flowing positioning calculation.

    1. (a)

      The bootstrapping AR success rate \( P_{s} \), calculated according to Eq. (38.13) from the decorrelated vc-matrix [16] is larger than the set threshold, \( P_{0} \);

      $$ P_{s} = \prod\limits_{j = i}^{n} {\left( {2\Phi (\frac{1}{{2\sigma_{{\hat{z}_{j|J} }} }}) - 1} \right)} $$
      (38.13)

      where \( \Phi (x) = \int_{ - \infty }^{x} {\frac{1}{{\sqrt {2\pi } }}\exp \{ - \frac{1}{2}\nu^{2} \} d\nu } \) and \( \sigma_{{\hat{z}_{j|J} }} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\kern 1pt} {\kern 1pt} j = i, \ldots ,n,{\kern 1pt} {\kern 1pt} {\kern 1pt} J = \{ j + 1, \ldots ,n\} {\kern 1pt} {\kern 1pt} ) \) denote the conditional standard deviations of the decorrelated ambiguities.

    2. (b)

      The ratio of the second minimum quadratic form of integer ambiguities residuals and the minimum one [17], which is shown in Eq. (38.14), is larger than the set threshold, \( t_{0} \);

      $$ ratio = \frac{{\parallel \hat{N}_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N}_{a2} \parallel_{{{\kern 1pt} {\kern 1pt} Q_{{\hat{N}_{a} }} }} }}{{\parallel \hat{N}_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N}_{a1} \parallel_{{{\kern 1pt} {\kern 1pt} Q_{{\hat{N}_{a} }} }} }} $$
      (38.14)

      where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N}_{a1} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N}_{a2} \) are the ambiguity candidates with the minimum and second minimum quadratic form respectively; \( \parallel \cdot \parallel_{{{\kern 1pt} {\kern 1pt} Q_{{\hat{N}_{a} }} }} = ( \cdot )^{\text{T} } Q_{{\hat{N}_{a} }}^{ - 1} ( \cdot ) \).

    3. (c)

      The number of ambiguities in the subset is larger than the set minimum threshold \( n_{0} \) and the cut-off elevation is smaller than the set maximum threshold \( e_{c0} \). The two conditions are set to ensure the selected satellites are still enough to get reliable positioning results, since too few or too high cut-off-elevation satellites are not adverse to the positioning stability, especially for the vertical direction.

  3. (3)

    If the conditions in Step (2) cannot be met, the cut-off elevation will be set at \( e_{2} \). Then the Step (2) will be repeated. Of course if cut-off elevation at \( e_{2} \) is still unable to pass the acceptance test, the procedure will be continued with larger cut-off elevation. But if it runs into and meets the condition (c), the circulation will be stopped and the current epoch keeps the ambiguities float.

    The procedure of the ambiguity subset selection method in PAR can also be expressed in Fig. 38.1. In the experiments of Sect. (38.4), \( P_{0} \) is set at 0.999; t at 3.0; \( n_{0} \) at 10 and \( e_{c0} \) at 35°.

    Fig. 38.1
    figure 1

    The flowchart of ambiguity subset selection method in PAR model

    Full size image

4 Experiments

A 19.7-km baseline GNSS data is used to test the effects of the proposed RTK positioning method. The data contains observations from GPS, GLONASS and BDS systems. For lack of space, we just list and analyze the results from a selected typical period in detail. However, the method should be suitable for any other periods.

Figure 38.2 shows the residuals of DD wide-lane ambiguity-fixed carrier observations from three low-elevation satellites. The residuals mainly compose by two parts: ones are random items caused by the noises of carrier measurements, and the other ones are systematic items caused by atmospheric errors, i.e. tropospheric and ionospheric errors. We can see the residuals reach a considerable magnitude even larger than ten centimeters. Although the ionospheric errors in wide-lane observations are not equivalent to those in L1 or L2 observations, the absolute magnitude not differ significantly. For instance in GPS, the ionospheric error in the wide-lane observation is −1.283 times and −0.779 times from that in L1 or L2 observation. The similar results can also be obtained in GLONASS and BDS. So it can be seen the atmospheric errors will affect a lot to the L1 or L2 ambiguity resolution, where the corresponding wavelengths just range about from 19 to 25 cm.

Fig. 38.2
figure 2

Residuals of DD wide-lane ambiguity-fixed carrier observations from three low-elevation satellites. a G29. b R02. c C14

Full size image

Figure 38.3 shows the number of DD ambiguities to be fixed in several situations, including the three single-system situations of GPS, GLONASS and BDS, full ambiguity resolution (FAR) and PAR situations of G/R/C combination. We can see the G/R/C combined model almost triple the ambiguities in the single-system. And except the epochs where new satellite around, the number ambiguities in PAR model is almost the same with that in FAR model. This implies that the PAR model uses almost the same observation information with FAR. Figure 38.4 shows the success rates at the initial twenty epochs of AR in the five situations. As we can see, the G/R/C combined AR model dramatically improves the success rate, since the multi-constellation combination provides more redundant observation information. And this is the main contribution what multi-constellation combination takes to AR.

Fig. 38.3
figure 3

Number of ambiguities to be fixed in the five situations

Full size image
Fig. 38.4
figure 4

Success rate of AR in the five situations

Full size image

Figures 38.5 and 38.6 show the AR ratio values of G/R/C combined model and single-system model respectively. From Fig. 38.5 we can see, although in most time the single-system can get good ratio values larger than three, there are still some time where the ratio values are smaller than the threshold, for instance in the initial seventy epochs of GPS and the epochs around the time when the new satellite arises. Figure 38.6 show the FAR and PAR results both with G/R/C combined model, in which we can see at the initial phase, the ratio values are much larger than that of any single-system. When there has the new rising satellite, the FAR model suffers from the poor ambiguity precision and large ambiguity bias of low-elevation satellite, so the ratio drops suddenly. Nevertheless, the PAR model can avoid this problem. The reason is that the new rising satellite is removed adaptively according to the PAR criterions, and thus not involved in the ambiguity search and fixing. In the later epochs, as the elevation increases and the ambiguity precision improve, the ‘new rising’ ambiguity will be adopted in the ambiguity fixing. Although the ratio also drops a lot, it still meets the criterions, thus still ensure the AR reliability.

Fig. 38.5
figure 5

Ratio in single-system AR

Full size image
Fig. 38.6
figure 6

Ratio in FAR and PAR model with G/R/C combination

Full size image

After fixing the wide-lane ambiguities by the PAR method, the fixed integer wide-lane ambiguities can be backtracked into the model like Eq. (38.8), and the positioning results can be calculated. The positioning biases of north, east and up (N/E/U in Fig. 38.7) directions are shown in Fig. 38.7. We can see the positioning biases of three directions are all within ±10 cm, especially the north and east, almost within ±5 cm. Affected by the residual atmospheric errors, the positioning results reflect some systematic biases especially in the up direction. However this may be already enough for many practical positioning applications.

Fig. 38.7
figure 7

Positioning bias of the G/R/C combined PAR model

Full size image

5 Conclusion

The paper proposes a reliable RTK positioning method based on partial wide-lane ambiguity resolution from GPS/GLONASS/BDS Combination. The unified G/R/C geometry-based wide-lane AR model and the PAR method are introduced in detail. Real G/R/C baseline data is also calculated as typical example to reflect the benefits of the proposed method. Main conclusions are as follows:

  1. (1)

    The method takes advantage that wide-lane observation has much longer wavelength and ambiguity easy to be fixed. So the wide-lane AR suffers much less from the atmospheric errors compared with the AR of basic observation, i.e. L1(B1) or L2(B2).

  2. (2)

    Combined with the single-system based AR model, multi-constellation combination can significantly improve the wide-lane AR effects, including the AR success rate, ratio and initialization speed, as multi-constellation combination provides more redundant observation information.

  3. (3)

    The proposed PAR method can effectively avoid the negative influence of new rising satellites, as it removes the new rising satellite(s) adaptively according to the PAR criterions thus ensure the AR stability. At the same time the PAR model uses almost the same satellites except removed new rising satellite(s). So the fixed ambiguities are enough to directly used in positioning calculation.

  4. (4)

    The positioning accuracy with G/R/C combined ambiguity-fixed wide-lane observations can still reach centimetre level.