Keywords

1 Introduction

Today, the Global Navigation Satellite System (GNSS) has been widely used for a multitude of applications around the world. Multi-GNSS differential positioning requires different reference satellite for each system, which is referred to as loose combining (LC) [1], and the performance of BDS/GPS dual/triple frequency was investigated by Gao et al. [2, 3]. On the other hand, combining observations on same frequencies from multi-GNSS in one positioning model with a common pivot satellite, which is the so-called tight combining (TC) [4], can introduce at least one more redundancy and will be beneficial to ambiguity resolution (AR) performance which is essential to high-precision mixed-constellation RTK positioning. The performance in terms of accuracy, availability and reliability of GPS only is largely a function of the number of satellite being tracked. Thus, the GPS real-time kinematic (RTK) positioning solution is degraded in urban canyon environment or in deep open cut mines where the number of visible satellite is limited [5]. The Galileo in EU is a one of the aiding solutions to add more functioning satellites which shares two overlapping frequencies (e.g. L1/E1 and L5/E5a) with GPS [6]. However, proper handling of the GNSS hardware biases known as differential inter-system bias (DISB) [7] is the prerequisite for integrating GPS and Galileo in one rigorous model. Studies on DISB have become the focus in the GNSS community. The GPS-Galileo ISB was first carried out by Montenbruck in CONGO network experiment [8]. Odijk and Teunissen pointed out that the range ISB can be estimated along with the coordinate parameters, while the phase ISB can be lump together with ambiguity parameters [9], however, this will not do any impact on the positioning results. A particle filter-based method for estimation of ISB was proposed by Tian et al. [10]. In addition to identical frequencies, DISB model between GPS and BDS on different frequencies was also studied and verified by Gao et al. [11].

Correct estimates of the carrier phase integer ambiguities are the prerequisite for high-precision positioning, since incorrect ambiguity fixing can lead to largely biased positioning solutions. However, it is not easy to fix all ambiguities simultaneously. In such cases, it may be beneficial to consider partial ambiguity resolution (PAR) techniques, which resolve only a subset of ambiguities. The important thing is how to determine the subset. Choice of an ambiguity subset could be based on ambiguity variance, pre-defined subset sizes, elevation ordering and linear combinations [12]. Parkins proposed a PAR method to deal with the presence of biased observations [13], but it is very time-consuming. An elevation-based technique was applied to the GPS/BDS/GLONASS RTK positioning by Gao et al. [14]. Unlike the usual method, a modified partial ambiguity resolution procedure is proposed by Wang and Feng [15], where the indices of both the success rate and the ratio test are combined to find an optimal ambiguity subset to be fixed. It was widely demonstrated that the PAR strategy could obviously shorten the time to reach centimeter level accuracy for long baselines, and considerably extend the range for instantaneous RTK positioning [16].

Although many studies have been focused on the DISB with zero/ultra-short or medium-baseline experiments, the effect of application under long baseline conditions remains to be further studied. Therefore, this paper aims to make a preliminary assessment of the DISB application in the case of long baseline. In the following, Sect. 2 details the mathematical derivations of TC observation model, DISB estimation model and PAR procedure; Sect. 3 presents the data and models used in the experiments; Sect. 4 analysis the results of estimated DISB, performance of AR and positioning accuracy; finally, Sect. 5 summarizes the main point of this paper.

2 Methods

2.1 Intra-system and Inter-system Observation Model

For GPS and Galileo, the discrepancy in coordinate and time systems may be negligible in most applications. They transmitted signals on identical frequencies of L1/E1 and L5/E5a, which enables only one common pivot satellite once the DISB is calibrated. For long baselines, the differential atmospheric delays between receivers need to be considered. The between-receiver SD observation equations for GPS or Galileo can be expressed as

$$ \begin{aligned} \Delta L_{{r_{1} r_{2} }}^{S} & = \Delta \rho_{{r_{1} r_{2} }}^{S} + \Delta dt_{{r_{1} r_{2} }} + \Delta T_{{r_{1} r_{2} }}^{S} - \mu \cdot \Delta I_{{r_{1} r_{2} }}^{S} + \lambda \cdot \Delta N_{{r_{1} r_{2} }}^{S} + b_{{r_{1} r_{2} }}^{S} \\ \Delta P_{{r_{1} r_{2} }}^{S} & = \Delta \rho_{{r_{1} r_{2} }}^{S} + \Delta dt_{{r_{1} r_{2} }} + \Delta T_{{r_{1} r_{2} }}^{S} + \mu \cdot \Delta I_{{r_{1} r_{2} }}^{S} + B_{{r_{1} r_{2} }}^{S} \\ \end{aligned} $$
(1)

where, \( \Delta \) is the between-receiver SD operator; \( L \) is the carrier observation and \( P \) is pseudorange observation; The superscript \( S \) represents the satellite of GPS or Galileo and the subscript \( r \) represents different receivers; \( \rho \) is the distance between satellite and receiver; \( dt \) denotes the receiver clock error; \( \lambda \) denotes the wavelength; \( b \) denotes the hardware phase delay, which also contains the initial phase in the receiver; \( N \) denotes the integer phase ambiguity; \( T \) denotes the tropospheric delay, and \( I \) denotes the ionospheric delay; \( \mu \) is the ionospheric scale factor; \( B \) denotes the hardware code delay in the receiver for GPS or Galileo.

Based on SD observation equations, the classical intra-system DD observation can be formed, where the receiver-dependent bias can be eliminated. Here, we choose \( G_{1} \) as the reference satellite for GPS and \( E_{1} \) for Galileo, we can obtain

$$ \begin{aligned} \nabla \Delta L_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} - \mu \cdot \nabla \Delta I_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} + \lambda \cdot \nabla \Delta N_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} \\ \nabla \Delta P_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} + \mu \cdot \nabla \Delta I_{{r_{1} r_{2} }}^{{G_{1} G_{s} }} \\ \nabla \Delta L_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} - \mu \cdot \nabla \Delta I_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} + \lambda \cdot \nabla \Delta N_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} \\ \nabla \Delta P_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} + \mu \cdot \nabla \Delta I_{{r_{1} r_{2} }}^{{E_{1} E_{s} }} \\ \end{aligned} $$
(2)

where, \( \nabla \Delta \) is the double-differential operator; \( G \) and \( E \) represents satellites of GPS and Galileo respectively. The meaning of other characters is as described above.

The inter-system DD observation equations between GPS and Galileo on same frequencies can also be built in a similar way, but the hardware delays cannot be eliminated. The corresponding models can be expressed as

$$ \begin{aligned} \nabla \Delta L_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta I_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \lambda \cdot \nabla \Delta N_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \nabla \Delta b_{{r_{1} r_{2} }}^{GE} \\ \nabla \Delta P_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} & = \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \nabla \Delta T_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \nabla \Delta I_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \nabla \Delta B_{{r_{1} r_{2} }}^{GE} \\ \end{aligned} $$
(3)

where, \( \nabla \Delta b_{{r_{1} r_{2} }}^{GE} \) and \( \nabla \Delta B_{{r_{1} r_{2} }}^{GE} \) represent the phase and code DISB between GPS and Galileo on overlapping frequencies. Odijk and Teunissen [7] and Paziewski et al. [6] have studied the DISB on same frequencies and demonstrated that the DISB is rather stable in time and related to the receiver type and signal frequency. Therefore carrier phase and code ISBs for a particular receiver pair can be estimated once and introduced as a known correction in GPS/Galileo tightly combined processing.

In order to avoid the hand-over problem of reference satellites in traditional DD model, we made some adjustments where the estimated DD tropospheric delay is expressed in the form of zero-differenced and the estimated DD ionospheric delay, DD ambiguities are all maintain the form of between-receiver single difference.

$$ \begin{aligned} \nabla \Delta L_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta b_{{r_{1} r_{2} }}^{{GE}} & = \nabla \Delta \rho _{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \left( {M_{{r_{2} }}^{{E_{s} }} - M_{{r_{2} }}^{{G_{1} }} } \right)T_{{r_{2} }} - \left( {M_{{r_{1} }}^{{E_{s} }} - M_{{r_{1} }}^{{G_{1} }} } \right)T_{{r_{1} }} - \mu \cdot \left( {\Delta I_{{r_{1} r_{2} }}^{{E_{s} }} - \Delta I_{{r_{1} r_{2} }}^{{G_{1} }} } \right) \\ & \quad + \lambda \cdot \left( {\Delta N_{{r_{1} r_{2} }}^{{E_{s} }} - \Delta N_{{r_{1} r_{2} }}^{{G_{1} }} } \right) \\ \nabla \Delta P_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta B_{{r_{1} r_{2} }}^{{GE}} & = \nabla \Delta \rho _{{r_{1} r_{2} }}^{{G_{1} E_{s} }} + \left( {M_{{r_{2} }}^{{E_{s} }} - M_{{r_{2} }}^{{G_{1} }} } \right)T_{{r_{2} }} - \left( {M_{{r_{1} }}^{{E_{s} }} - M_{{r_{1} }}^{{G_{1} }} } \right)T_{{r_{1} }} + \mu \cdot \left( {\Delta I_{{r_{1} r_{2} }}^{{E_{s} }} - \Delta I_{{r_{1} r_{2} }}^{{G_{1} }} } \right) \\ \end{aligned} $$
(4)

where \( M \) is the mapping function of tropospheric delay, here the niell mapping function is used.

After making the above adjustments to the model, the unknown state \( x \) vector is defined as:

$$ x = \left( {X,Y,Z,T_{{r_{2} }} ,T_{{r_{1} }} ,I_{1} ,I_{2} , \ldots ,I_{Maxsat} ,N_{1} ,N_{2} , \ldots ,N_{Maxsat \cdot numfreq} } \right) $$
(5)

where, \( Maxsat \) and \( numfreq \) represents the number of satellites and frequencies respectively.

2.2 Estimation of DISB

The phase and code ISBs can be estimated precisely on zero or ultra-short baselines based on Eq. (3) where differential atmosphere errors could be ignored. Due to the integer part of DISB is linearly dependent with ambiguity so they can be lumped together, so we could only get the fractional part of the phase DISB. Of course, this rank deficiency problem do not exist in the estimation of code DISB. The code and fractional part of phase DISB can be calculated through the following equation,

$$ \begin{aligned} \nabla \Delta b_{{r_{1} r_{2} ,fractional}}^{GE} & = \left( {\nabla \Delta L_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} } \right)/\lambda - \left[ {\left( {\nabla \Delta L_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} } \right)/\lambda } \right] \\ \nabla \Delta B_{{r_{1} r_{2} }}^{GE} & = \nabla \Delta P_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} - \nabla \Delta \rho_{{r_{1} r_{2} }}^{{G_{1} E_{s} }} \\ \end{aligned} $$
(6)

where, the \( \left[ \cdot \right] \) denotes rounding function.

2.3 Strategy of Partial Ambiguity Resolution

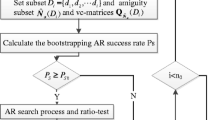
In the multi-constellation RTK processing, it is not easy to fix all ambiguities reliably, however, one could have sufficient confidence to fix a subset of the ambiguities, which is referred to as partial ambiguity resolution (PAR) [17]. As we all know, the low-elevation ambiguities suffer much more from observation noise, multipath effects and the residual atmospheric delays, and thus have lower accuracies and also take longer to converge to a certain degree of precision. Therefore it is generally hard to fix these ambiguities correctly due to its poor accuracy and high correlation with others. In the other hand, if we fix all the ambiguities simultaneously, the low-elevation ones may influence the search system and make the search result unable to pass the acceptance test [14]. Fortunately, the number of visible satellites greatly increases when both GPS and Galileo are used, which means a higher cut-off angle could be used. In this Section, a simple but robust PAR strategy with ambiguity subset selected based on the elevations and the number of consecutive tracking will be introduced. Figure 1 presents the flowchart of this procedure.

Fig. 1
figure 1

The flowchart of PAR procedure

Full size image

First, the procedure starts with SD float ambiguity and an initial elevation mask of 10 degrees, and the threshold number of consecutive locked is set to 10, then we could get the DD float solution and the corresponding variance. If the number of DD float ambiguity is greater than 6, the LAMBDA method is applied to get the optimal candidate. If the bootstrapping success rate and value of ratio is higher than the threshold (e.g., 0.99 and 3.0), tight constraints is applied on ambiguities which is the so-called “Fix and Hold”, and the ambiguity-fixed solution is achieved. Otherwise, the elevation mask of AR will increase by 5°, and repeat the LAMBDA search and AR test. Until the number of DD ambiguities is less than 6, the iteration will be terminated and only a float solution is achieved at this epoch.

3 Data Processing

Similar to earlier DISB studies, the estimation of code and phase DISBs on overlapping frequencies L1/E1 and L5/E5a is achieved through zero and ultra-short baselines, since the atmospheric effects can be ignored. Here, three MGEX stations (CUT0, CUT2, CUTC) in campus of Curtin University, Australia is selected. As mentioned earlier, the purpose of DISB calibration is to improve the performance of ambiguity resolution which is essential to high-precision mixed-constellation RTK positioning. The calibration of DISB is verified with 3 long baselines range from 570 to 1200 km which is formed by PERT, MRO1 and KARR in Australia. It is worth mentioning that the coordinates of the MGEX stations are known and have an accuracy of a few millimeters. Detailed information for each baseline is shown in Table 1. All stations are equipped with Trimble NETR9 receiver but different firmware version. The data were collected on DOY 300, 2017 with the sampling interval of 30 s.

Table 1 Baselines used in the experiment of estimation and calibration of DISB
Full size table

Table 2 summarizes the detailed processing strategy for long baseline RTK positioning. Precise orbit at intervals 5 min provided by MGEX (e.g., GFZ) were used since the accuracy of broadcast ephemeris is limited. For data modeling, we applied the absolute phase centers [18], the phase-wind up effects [19] and the station displacement models proposed by IERS Convensions 2010 [20]. A cut-off angel of 10° was set for usable measurement and an elevation-dependent weighting strategy was applied to measurements where a priori precision of 3 mm and 3 m for raw phase and code, respectively. In addition, the station coordinate was estimated as white noise process with variance of 302 m2. The bootstrapping success rate and ratio-test threshold were 0.99 and 3.0 respectively.

Table 2 Tightly combined processing strategy for long baseline
Full size table

4 Results and Discussion

In this section, we first discuss the characteristics of the code/phase DISB estimated from zero or ultra-short baseline, then analysis the ambiguity performance of long baseline RTK positioning with DISB calibration, and finally address the statistical results of positioning accuracy under LC and TC strategy.

4.1 Results of Code/Phase DISB

The estimated code and phase DISB on frequencies L1/E1 and L5/E5a calculated from Eq. (6) are shown in Figs. 2 and 3 respectively. It is obviously that the DISB is rather stable over the whole observation period regardless of the random terms caused by observation noises. The mean of phase DISB over the day is close to zero indeed and the standard deviations for both L1/E1 and L5/E5a are all within 0.02 cycles. Compared with phase DISB, the code DISB show greater noise due to the pseudorange noise and the standard deviations are all within 0.6 m. Despite the larger noise in code DISB, the amplitude is still relatively stable. The detailed statistical results is summarized in Table 3.

Fig. 2
figure 2

Estimated fractional phase (left) and code (right) DISB on L1/E1 corresponding to CUT2-CUT0 (top) and CUTC-CUT0 (bottom)

Full size image
Fig. 3
figure 3

Estimated fractional phase (left) and code (right) DISB on L5/E5a corresponding to CUT2-CUT0 (top) and CUTC-CUT0 (bottom)

Full size image
Table 3 Statistical results of fractional phase and code DISB
Full size table

It can be seen that the code and phase DISB on both frequencies estimated from CUTC-CUT0 show larger noise than that from CUT2-CUT0. This may be caused by the following two reasons: The first one is that the different firmware version over the both sides of the baseline CUTC-CUT0; The second is that the baseline CUT2-CUT0 is a zero baseline for which differential atmospheric errors are completely absent and multi-path errors are very minor while the baseline CUTC-CUT0 is a nonzero-baseline. We adopted the DISB calibration in the long baseline experiments corresponding to the receiver firmware version.

4.2 Results of AR Performance

The AR results of LC and TC for three different long baselines are shown in this section. Figure 4 shows the value of ratio (left) over the day and success rate (right) for the first 6 h. From Fig. 4, we can find that TC strategy do not significantly improve the value of ratio, but shorten the convergence time to reach the 100% success rate. This is because that during the initial period, TC strategy could provide more observations, so additional redundancies are introduced which is beneficial to the ambiguity resolution.

Fig. 4
figure 4

Ratio value (left) and bootstrapping success rate (right) corresponding to MRO1-KARR (top), PERT-MRO1 (medium), PERT-KARR (bottom) under LC and TC strategy respectively

Full size image

Figure 5 shows the AR performance in terms of TTFF (left) and the fixing rate (right) of three different long baselines under LC and TC strategy. In this paper, the TTFF was defined as the time taken for the ambiguity-fixed solution to be successfully achieved and the following 10 epochs also keep fixed. The fixing rate was defined as the ratio of the number of fixed epochs to the number of total epochs during this period. Since we apply the DISB calibration advance in TC strategy, there is more redundancies compared with LC strategy, which result in shorter convergence time to first fix, as shown in Fig. 5. The time to first fix is 70, 122, 129 min under LC strategy, while only 32, 33, 40 min under TC strategy corresponding to MRO1-KARR, PERT-MRO1, PERT-KARR baseline. Compared with results of LC strategy, TTFF is further reduced by 54.3, 72.9, 69.0% respectively. Figure 5 (right) also shows that TC strategy could slightly improve the fixing rate of epochs.

Fig. 5
figure 5

TTFF (left) and fix rate (right) of epochs correspond to different baselines

Full size image
Fig. 6
figure 6

Common view satellite number (top) and fixed period (bottom) of Galileo system corresponding to MRO1-KARR

Full size image

Figure 6 shows the common view satellite number of Galileo (top) and ambiguity fix period of Galileo (bottom) corresponding to MRO1-KARR baseline. It is easy to find that TC could achieve longer fixing period. During some period as checked in red rectangle in Fig. 6, there is only one common view Galileo satellite where double-difference ambiguity could not be formed within Galileo system and the number of satellites is dramatically changing which lead to frequent reinitialization of new rise satellites, LC could only keep float solutions, while TC could still get the fixed solutions. It come to the following conclusion that compared with LC strategy, TC strategy has a better performance in AR.

4.3 Results of Positioning

As mentioned earlier, the coordinates of three stations are precisely known from the IGS weekly solution. Baseline errors are the difference between the estimated baseline length and precise reference baseline length. Baseline errors of different combination strategy are shown in Fig. 7. The light green dotted line in the figure marked the TTFF. It is easy to find that fluctuation in the up direction is larger than that in north and east direction. Detailed precision statistics are summarized in Table 4. It must be noted that only the ambiguity-fixed solution is contained in the statistics. The 3D positioning errors is 3.4, 3.3, 4.8 cm under LC strategy, while 3.3, 3.4, 5.0 cm under TC strategy corresponding to MRO1-KARR, PERT-MRO1, PERT-KARR baseline. LC and TC strategy could both achieve centimeter-level positioning accuracy in the case of ambiguity fixed correctly. The length of PERT-KARR is almost twice of that of other two baselines and the accuracy of PERT-KARR baseline is also worse than that of other two baselines due to residual atmospheric errors, such as residual tropospheric delay and ionospheric delay.

Fig. 7
figure 7

Baseline errors for LC (left) and TC (right) strategy corresponding to MRO1-KARR (top), PERT-MRO1 (medium), PERT-KARR (bottom)

Full size image
Table 4 RMS statistics of baseline error
Full size table

5 Conclusions

We first propose a GPS/Galileo tightly combined RTK positioning model with raw carrier phase and code observations for long baselines which avoid the hand-over problem of reference satellites in traditional DD model, then the estimation of DISB model based on zero or ultra-short baseline is developed. In order to get better AR performance, a simple but robust strategy of partial ambiguity resolution is suggested, where the satellite elevation, number of consecutive tracking, success rate and ratio test are all combined to determine the subset of ambiguity. The DISB results based on zero/ultra-short baseline with different receiver firmware version shows that the code and phase DISB is rather stable over time which means that it could be corrected in advance. Three long baselines range from 570 to 1200 km were tested with DISB calibration in advance to verify the proposed model. The results shows that TC strategy do not improve the value of ratio but shorten the time to reach 100% success rate, compared with the LC strategy. At the same time, TC strategy could significantly shorten the time to first fix and improve the fixing rate of epochs slightly, which means that under some circumstances, LC strategy could only keep float solutions while the TC strategy could still get ambiguity-fixed solutions. In term of positioning accuracy, the precision in up direction is worse than that in north and east direction. Once the ambiguity is fixed correctly, both LC and TC strategy can achieve centimeter-level positioning accuracy. This paper just gives the preliminary research results about the DISB application under long baseline circumstances. Using more data for experimental verification and investigating of what performance the real-time precise products could archive are the points that we will focus on and continue to research.