1 Introduction

The interior permanent magnet synchronous motors (IPMSMs) are widely employed for the electric vehicle traction due to the high torque density and high efficiency [1,2,3]. The rotor position information is essential for the field-oriented control (FOC), but the encoder or the rotary transformer are unreliable, and increase the size and cost [4, 5]. In order to overcome these challenges, much attention and effort are focused on the sensorless rotor position estimation methods.

The sensorless control methods for IPMSM can be generally classified into two classes [6]. The first class is the high frequency injection-based method for the position estimation in the standstill and low-speed condition [7, 8]. The second class is the back electromotive force(EMF)-based method for high-speed position detection, which mainly includes the state observer, the sliding mode observer (SMO) method [9, 10], the model reference adaptive system observer (MRAS) [11] and Extended Kalman Filter(EKF) algorithm [12].

However, some above-mentioned methods have some shortcomings, such the chattering problem, the complex control parameter choice, and large amounts of computing. Therefore, the Luenberger state observer attracted a lot of attention because of the advantages of the good stability, the easy digital implementation and the low computational demand [13, 14]. However, the position estimation performance is affected by the load change [15,16,17]. In order to solve this problem, several methods have been proposed to compensate the position estimation error. Lascu has proposed a new fifth-order PLL position and speed observer and established the relationship between the current errors and the position and speed errors [18]. Zhang et al. has proposed a global time-delay compensation method based on q-axis current error, and the lag angle can be eliminated by means of the adjustment of the current error [19]. To solve the problem of calculation delay resulted from the digital computation, a current precompensation method based on dual-sampling scheme in one switching period is proposed [20].

From aforementioned analysis, the existing position error compensation strategies are mainly based on modified current errors and good error compensation performance is obtained. In sensorless control system, currents can be divided as: the command current, the feedback current from IPMSMs, and the current estimated from position observers. The feedback currents will be adjusted to follow the command currents to realize the closed-loop FOC control by the current-loop PI controllers, and the current estimated from position observers will be modulated to trace the command current or feedback current through the PI controllers when the observer comes to the equilibrium state [21]. Thus, it is difficult to find out the relationship between the errors of above three currents and rotor position errors.

In addition, the position error is proportional to the q-axis inductance error when the stator resistance error is small [22]. Since the true value of q-axis inductance is hardly to get since it changes with the q-axis current, this method is not adopted to extract the position error.

Very little literature has focused on the relationship between voltage errors and rotor position errors, since the voltage is not easy to be measured or obtained.

Furthermore, the position error cannot be fully compensated when the errors are directly added to the estimated position.

Based on the above difficulties, a position error compensation method based on the voltage output of PI controllers in the current loop is proposed in this paper for IPMSM sensorless drives, and it consists of two parts: the position error extraction model, and the position error compensation model. The original contributions of this paper lie in:

  1. 1.

    The relationship between the voltage output from PI controllers in the current loop and the position error has been found out and the position error extraction model is proposed. The voltage output of the current-loop PI-regulator is proposed to estimate the position error for the first time.

  2. 2.

    A novel position error compensation model of the rotor reference frame is proposed based on the voltage and current inputs in the two-phase stationary reference frame, not in the rotor reference frame. The core ideal of the proposed error compensation model is the rotation of the coordinate system based on the two-phase stationary reference frame. The proposed error compensation model can fully compensate the error when the error extraction is correct.

This paper is organized as follows: Section II describes the traditional rotor position observer based on the rotor rotation frame. A position error compensation method based on the voltage output of the PI controllers in the current loop is proposed for IPMSM sensorless drives in Section III. Section IV gives the experimental results of the proposed method. Section V summarizes this paper.

2 Traditional Rotor Position Observers

2.1 IPMSM Model Based on the Estimated Rotor Reference Frame

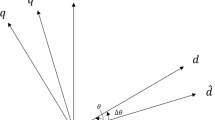
In order to design a rotor position observer for IPMSMs, two reference frames are adopted, as shown in Fig. 1) the actual rotor reference frame based on the actual rotor position and the actual rotor speed, and 2) an estimated rotor reference frame based on the estimated rotor position and the estimated rotor speed. The rotor position and speed errors are defined as \(\Delta \theta = \theta_{e} - \hat{\theta }_{e} ,\Delta \omega = \omega_{e} - \hat{\omega }_{e}\), respectively.

Fig. 1
figure 1

Actual and estimated reference frames for IPMSMs

Full size image

The IPMSM model based on the actual rotor reference frame can be expressed as:

$$u_{s}^{dq} = R_{s} i_{s}^{dq} + L_{d} \frac{{di_{s}^{dq} }}{dt} + j\omega_{e} L_{q} i_{s}^{dq} + jE_{ex}^{dq}$$
(1)

where \(u_{s}^{dq} = u_{s}^{d} + ju_{s}^{q} ,i_{s}^{dq} = i_{s}^{d} + ji_{s}^{q}\), are the voltage and current vectors, respectively. Ld and Lq are the d- and q-axis inductances, respectively, and Rs is the stator resistance. \(E_{ex}^{dq} = \omega_{e} \psi_{f} - \left( {L_{d} - L_{q} } \right)\left( {{{di_{s}^{q} } \mathord{\left/ {\vphantom {{di_{s}^{q} } {dt}}} \right. \kern-\nulldelimiterspace} {dt}} + \omega_{e} i_{s}^{d} } \right)\) is the extended electromotive force(EEMF), and ψf is rotor PM flux.

Considering the rotor position error, the voltage and current vectors based on the estimated rotor reference frame are obtained as:

$$\begin{aligned} u_{s}^{dq} & = u_{s}^{{\hat{d}\hat{q}}} e^{ - j\Delta \theta } \\ i_{s}^{dq} & = i_{s}^{{\hat{d}\hat{q}}} e^{ - j\Delta \theta } \\ \end{aligned}$$
(2)

From Eqs. (1) and (2), the IPMSM model based on the estimated rotor reference frame can be deduced as:

$$u_{s}^{{\hat{d}\hat{q}}} = R_{s} i_{s}^{{\hat{d}\hat{q}}} + \hat{L}_{d} \frac{{d\hat{i}_{s}^{dq} }}{dt} - j\hat{L}_{d} \frac{d\Delta \theta }{{dt}}i_{s}^{{\hat{d}\hat{q}}} + j\hat{\omega }_{e} \hat{L}_{q} i_{s}^{{\hat{d}\hat{q}}} + jE_{ex} e^{j\Delta \theta }$$
(3)

where \(u_{s}^{{\hat{d}\hat{q}}} = u_{s}^{{\hat{d}}} + ju_{s}^{{\hat{q}}} ,i_{s}^{{\hat{d}\hat{q}}} = i_{s}^{{\hat{d}}} + ji_{s}^{{\hat{q}}} ,\hat{L}_{d} ,\hat{L}_{q}\), are the voltage and current vectors, the d- and q-axis inductances based on the estimated rotor reference frame, respectively.

Considering the rotor position error is constant under the steady-state operation and the inductance difference is small for those two rotor reference frames, the following equations can be obtained:

$$\hat{L}_{d} \frac{d\Delta \theta }{{dt}}i_{s}^{{\hat{d}\hat{q}}} = 0$$
(4)
$$\begin{gathered} \hat{L}_{d} \left( {\Delta \theta } \right) = L_{d} \hfill \\ \hat{L}_{q} \left( {\Delta \theta } \right) = L_{q} \hfill \\ \end{gathered}$$
(5)

Then, the IPMSM model based on the estimated rotor reference frame can be simplified as:

$$u_{s}^{{\hat{d}\hat{q}}} = R_{s} i_{s}^{{\hat{d}\hat{q}}} + L_{d} \frac{{di_{s}^{{\hat{d}\hat{q}}} }}{dt} + j\hat{\omega }_{e} L_{q} i_{s}^{{\hat{d}\hat{q}}} + jE_{ex}^{{\hat{d}\hat{q}}}$$
(6)

where \(E_{ex}^{{\hat{d}\hat{q}}} = E_{ex} e^{j\Delta \theta } = E_{ex} \left[ {\begin{array}{*{20}c} { - \sin \left( {\Delta \theta } \right)} \\ {\cos \left( {\Delta \theta } \right)} \\ \end{array} } \right]\).

2.2 Establishment of the Rotor Position Observer

The rotor position observer consists of the current observer and the phase-locked loop (PLL).

A simplified IPMSM model based on Eq. (6) is adopted to design a rotor position observer in the estimated rotor reference frame. The current observer as shown in Fig. 2 can be described by:

$$u_{s}^{{\hat{d}\hat{q}}} = R_{s} \hat{i}_{s}^{{\hat{d}\hat{q}}} + L_{d} \frac{{d\hat{i}_{s}^{{\hat{d}\hat{q}}} }}{dt} + j\hat{\omega }_{e} L_{q} \hat{i}_{s}^{{\hat{d}\hat{q}}} + j\hat{E}_{ex}^{{\hat{d}\hat{q}}}$$
(7)

where \(\hat{i}_{s}^{{\hat{d}\hat{q}}} = \hat{i}_{s}^{{\hat{d}}} + j\hat{i}_{s}^{{\hat{q}}}\) are the current vector of the current observer model, and \(\hat{E}_{ex}^{{\hat{d}\hat{q}}}\) represents the EEMF in the current observer.

Fig. 2
figure 2

The diagram of the current observer

Full size image

Since the EEMF cannot be obtained or measured, the current errors are used to estimate the EEMF. Equation (7) can be rewritten as:

$$L_{d} \frac{{d\hat{i}_{s}^{{\hat{d}\hat{q}}} }}{dt} = u_{s}^{{\hat{d}\hat{q}}} - R_{s} \hat{i}_{s}^{{\hat{d}\hat{q}}} - j\hat{\omega }_{e} L_{q} \hat{i}_{s}^{{\hat{d}\hat{q}}} - \left( {K_{p} + {{K_{i} } \mathord{\left/ {\vphantom {{K_{i} } s}} \right. \kern-\nulldelimiterspace} s}} \right)\left( {\hat{i}_{s}^{{\hat{d}\hat{q}}} - i_{s}^{{\hat{d}\hat{q}}} } \right)$$
(8)

where Kp and Ki are the gain coefficients, and 1/s is the integral operator.

From Eqs. (7) and (8), the relationship between EEMF and the current errors can be expressed as

$$\hat{E}_{ex}^{{\hat{d}\hat{q}}} = E_{ex}^{{\hat{d}\hat{q}}} e^{{j\Delta \hat{\theta }}} = E_{ex}^{{\hat{d}\hat{q}}} \left[ {\begin{array}{*{20}c} { - \sin \left( {\Delta \hat{\theta }} \right)} \\ {\cos \left( {\Delta \hat{\theta }} \right)} \\ \end{array} } \right] = \left( {K_{p} + {{K_{i} } \mathord{\left/ {\vphantom {{K_{i} } s}} \right. \kern-\nulldelimiterspace} s}} \right)\left[ {\begin{array}{*{20}c} {\hat{i}_{s}^{{\hat{d}}} - i_{s}^{{\hat{d}}} } \\ {\hat{i}_{s}^{{\hat{q}}} - i_{s}^{{\hat{q}}} } \\ \end{array} } \right]$$
(9)

From Eq. (9), the \(\hat{d}\)-axis EEMF can be taken an input of PLL, since \(\sin \left( {\Delta \hat{\theta }} \right) = \Delta \hat{\theta }\) is satisfied under the small rotor position error.

The rotor position observer consists of the current observer and the phase-locked loop (PLL), as shown in Fig. 3. When the system reaches the equilibrium state under the action of PI controllers, the current error is close to zero and the estimated rotor error position fluctuates around zero.

Fig. 3
figure 3

Rotor position observer based on the rotor reference frame

Full size image

It should be noted that the estimated rotor position error is the position difference between the reference model and the observer model, and these two models are based on the estimated rotor position frame. The estimated rotor position error cannot reflect the actual rotor position error between the actual rotor frame and the estimated rotor frame. Therefore, how to obtain the actual rotor position error remains a problem.

3 Proposed Rotor Position Error Compensation Method

The proposed rotor position error compensation method contains two main parts: (1) the rotor position error extraction model, which can obtain the rotor position differences between the actual and estimated rotor frame, and (2) a rotor position error compensation model, which can correct the position output from the observer.

3.1 Rotor Position Error Extraction Under the Condition of Load Change

When IPMSM reaches the steady state in the actual rotor reference frame, Eq. (1) can be rewritten as:

$$\begin{aligned} u_{s}^{d} & = R_{s} i_{s}^{d} - \omega_{e} L_{q} i_{s}^{q} \\ u_{s}^{q} & = R_{s} i_{s}^{q} + \omega_{e} L_{d} i_{s}^{d} + \omega_{e} \psi_{f} \\ \end{aligned}$$
(10)

When the load changes, some factors will result in the advance or lag of the FOC operation, such as the algorithm excitation time, the inverter nonlinearity and the sample delay. Thus, PI controllers of the d- and q-axis current loops serve as the voltage loss compensator when the feedforward compensation is adopted shown in Fig. 4. Equation (10) can be transformed as:

$$\begin{aligned} u_{s}^{{d^{\prime}}} & = R_{s} i_{s}^{d * } - \omega_{e} L_{q} i_{s}^{q * } + u_{error}^{d} \\ u_{s}^{{q^{\prime}}} & = R_{s} i_{s}^{q * } + \omega_{e} L_{d} i_{s}^{d * } + \omega_{e} \psi_{f} + u_{error}^{q} \\ \end{aligned}$$
(11)

where \(u_{error}^{d} ,u_{error}^{q}\) are the d- and q-axis voltage error as shown in Fig. 5.

Fig. 4
figure 4

The current loop of d-axis under the actual rotor frame

Full size image
Fig. 5
figure 5

Voltage error resulting from a the lag of FOC operation b the advance of FOC operation

Full size image

Based on the \(d^{\prime} - q^{\prime}\) reference frame, the stator voltage can be expressed as:

$$\begin{aligned} u_{s}^{{d^{\prime}}} & = u_{s}^{d} \cos \left( {\Delta \theta^{{\prime }} } \right) - u_{s}^{q} \sin \left( {\Delta \theta^{{\prime }} } \right) \\ u_{s}^{{q^{\prime}}} & = u_{s}^{d} \sin \left( {\Delta \theta^{{\prime }} } \right) + u_{s}^{q} \cos \left( {\Delta \theta^{{\prime }} } \right) \\ \end{aligned}$$
(12)

Considering the position error is small, d′-axis voltage can be given as:

$$u_{s}^{{d^{\prime}}} = u_{s}^{d} - u_{s}^{q} \Delta \theta^{\prime}$$
(13)

Combining Eqs. (11) and (13), d- axis voltage error can be obtained as:

$$u_{error}^{d} = - u_{s}^{q} \Delta \theta^{{\prime }}$$
(14)

In Eq. (14), Δθ′ is a fixed parameter and can be measured by the simple calibration. The d-axis voltage error is proportional to q-axis voltage.

In the estimated rotor reference frame, considering the position error Δθ between the actual rotor frame and the estimated frame, in the estimated frame, the voltage and the current vector can be expressed as:

$$\begin{gathered} u_{s}^{{\hat{d}\hat{q}}} = u_{s}^{dq} e^{{j\left( {\Delta \theta } \right)}} \hfill \\ i_{s}^{{\hat{d}\hat{q}}} = i_{s}^{dq} e^{{j\left( {\Delta \theta } \right)}} \hfill \\ \end{gathered}$$
(15)

Substituting Eq. (15) into Eq. (1), the voltage model in the \(\hat{d}\hat{q}\)-axis can be deduced as:

$$u_{s}^{{\hat{d}\hat{q}}} = R_{s} i_{s}^{{\hat{d}\hat{q}}} + j\omega_{e} L_{q} i_{s}^{{\hat{d}\hat{q}}} + jE_{ex}^{dq} e^{{j\left( {\Delta \theta } \right)}}$$
(16)

When id = 0 control strategy is adopted, Eq. (10) can be expressed as:

$$\begin{array}{*{20}c} {u_{s}^{{\hat{d}}} = R_{s} i_{s}^{{\hat{d}}} - \hat{\omega }_{e} L_{q} i_{s}^{{\hat{q}}} - \hat{\omega }_{e} \psi_{f} \sin \left( {\Delta \theta } \right)} \\ {u_{s}^{{\hat{q}}} = R_{s} i_{s}^{{\hat{q}}} + \hat{\omega }_{e} L_{d} i_{s}^{{\hat{d}}} + \hat{\omega }_{e} \psi_{f} \cos \left( {\Delta \theta } \right)} \\ \end{array}$$
(17)

It can be seen from Eq. (17) that the position error is related to the back electromotive force constant term. Thus, the back electromotive force constant term \(\hat{\omega }_{e} \psi_{f}\) is adopted in the extraction of the rotor position error in this paper.

Considering the voltage error, Eq. (17) can be rewritten as:

$$\begin{aligned} u_{s}^{{\hat{d}}} & = R_{s} i_{s}^{{\hat{d}}} - \hat{\omega }_{e} L_{q} i_{s}^{{\hat{q}}} - \hat{\omega }_{e} \psi_{f} \sin \left( {\Delta \theta } \right) + u_{error}^{d} \\ u_{s}^{{\hat{q}}} & = R_{s} i_{s}^{{\hat{q}}} + \hat{\omega }_{e} L_{d} i_{s}^{{\hat{d}}} + \hat{\omega }_{e} \psi_{f} \cos \left( {\Delta \theta } \right) + u_{error}^{q} \\ \end{aligned}$$
(18)

The current loop of the estimated rotor frame can be designed as:

$$\begin{aligned} u_{s}^{{\hat{d}}} & = u_{s\_feed}^{{\hat{d}}} + PI\left( {\hat{d}} \right) \\ u_{s}^{{\hat{q}}} & = u_{s\_feed}^{{\hat{q}}} + PI\left( {\hat{q}} \right) \\ \end{aligned}$$
(19)

where \(PI\left( {\hat{d}} \right),PI\left( {\hat{q}} \right)\), are the voltage error estimated by PI controllers, and \(u_{s\_feed}^{{\hat{d}}} ,u_{s\_feed}^{{\hat{q}}}\) are the voltage feedforward decoupling, which can be described by:

$$\begin{array}{*{20}c} {u_{s\_feed}^{{\hat{d}}} = R_{s} i_{s}^{d*} - \hat{\omega }_{e} L_{q} i_{s}^{q*} } \\ {u_{s\_feed}^{{\hat{q}}} = R_{s} i_{s}^{q*} + \hat{\omega }_{e} L_{d} i_{s}^{d*} } \\ \end{array}$$
(20)

where \(i_{s}^{d*} ,i_{s}^{q*}\), are the d- and q-axis command currents.

From Eqs. (19) and (20), it can be obtained as:

$$\begin{aligned} 0 & = R_{s} \left( {i_{s}^{{\hat{d}}} - i_{s}^{d*} } \right) - \omega_{e} L_{q} \left( {i_{s}^{{\hat{q}}} - i_{s}^{q*} } \right) + u_{error}^{d} \\ & \quad + \hat{\omega }_{e} \psi_{f} \sin \left( {\Delta \theta } \right) + PI\left( {\hat{d}} \right) \\ \end{aligned}$$
(21)

Under the action of PI controllers in the current loop, the feedback currents are regulated around the command current values: \(i_{s}^{d*} = i_{s}^{{\hat{d}}} ,i_{s}^{q*} = i_{s}^{{\hat{q}}}\). Equation (21) can be rewritten as:

$$u_{error}^{d} + \hat{\omega }_{e} \psi_{f} \sin \left( {\Delta \theta } \right) + PI\left( {\hat{d}} \right) = 0$$
(22)

Considering the rotor position error is small, the following equation can be obtained:

$$\sin \left( {\Delta \theta } \right) = \Delta \theta$$
(23)

When id = 0 control strategy is adopted and the load changes (q-axis current changes), the rotor position error extraction model can be expressed as:

$$\frac{{\Delta u_{error}^{d} }}{{\Delta i_{s}^{{\hat{q}}} }} + \frac{{\Delta \left( {\hat{\omega }_{e} \psi_{f} \Delta \theta } \right)}}{{\Delta i_{s}^{{\hat{q}}} }} + \frac{{\Delta PI\left( {\hat{d}} \right)}}{{\Delta i_{s}^{{\hat{q}}} }} = 0$$
(24)

where \(\Delta i_{s}^{{\hat{q}}}\) is the change of q-axis current and it can be expressed as:

$$\Delta i_{s}^{{\hat{q}}} = i_{s}^{{\hat{q}}} \left( k \right) - i_{s}^{{\hat{q}}} \left( {k - 1} \right)$$
(25)

Since the FOC control adopts the estimated rotor position, \(PI\left( {\hat{d}} \right),PI\left( {\hat{q}} \right)\) keep constant. Equation (24) can be simplified as:

$$\frac{{\Delta \left( {\Delta \theta } \right)}}{{\Delta i_{s}^{{\hat{q}}} }} = - \frac{{\Delta u_{error}^{d} }}{{\Delta i_{s}^{{\hat{q}}} \hat{\omega }_{e} \psi_{f} }}$$
(26)

From Eq. (26), it can be seen that there is a good linear relationship between the variation of position error and the variation of q-axis current assuming that the flux and speed remain constant.

3.2 Rotor Position Error Compensation

When the rotor position error exits, the observer model can be expressed as:

$$u_{s}^{{\hat{d}\hat{q}}} = R_{s} \hat{i}_{s}^{{\hat{d}\hat{q}}} + j\hat{\omega }_{e} L_{q} \hat{i}_{s}^{{\hat{d}\hat{q}}} + jE_{ex} e^{{j\left( {\Delta \theta } \right)}}$$
(27)

In order to keep the rotor position error be zero, rotations are made for the voltage and current vectors in the estimated rotor position frame in the same time:

$$\begin{aligned} u_{s\_com}^{{\hat{d}\hat{q}}} & = u_{s}^{{\hat{d}\hat{q}}} e^{{j\left( { - \Delta \theta } \right)}} \\ \hat{i}_{s\_com}^{{\hat{d}\hat{q}}} & = \hat{i}_{s}^{{\hat{d}\hat{q}}} e^{{j\left( { - \Delta \theta } \right)}} \\ \end{aligned}$$
(28)

Substituting Eq. (28) into Eq. (27),

$$u_{s\_com}^{{\hat{d}\hat{q}}} = R_{s} \hat{i}_{s\_com}^{{\hat{d}\hat{q}}} + j\hat{\omega }_{e} L_{q} \hat{i}_{s\_com}^{{\hat{d}\hat{q}}} + jE_{ex}$$
(29)

It can be seen from Eq. (29) that the compensation for the voltage and current vectors can eliminate the rotor position error, since the EEMF vector is in the \(\hat{q}\)-axis direction.

Based on Eq. (28), in order to compensate the position error, a position error compensation model is proposed and it consists of two coordinate transform modules and an angel rotation module. The angle rotation module is adopted to predict the next moment angle based on the current estimated angle and the extracted error shown in Fig. 6, and its mathematical expression can be given as:

$$\theta_{e} \left( k \right) = \hat{\theta }_{e} \left( {k - 1} \right) + \hat{\omega }_{e} \left( {k - 1} \right)T + \Delta \theta$$
(30)
Fig. 6
figure 6

The principle diagram of angle rotation module

Full size image

The proposed rotor position error compensation model is proposed as shown in Fig. 7. The proposed model is based on the voltage and current inputs in the two-phase stationary reference frame, not in the rotor reference frame. The proposed model is the improvement of the traditional observer model shown in Fig. 3. The key contribution lies in applying the rotation of coordinate system to realize the error compensation.

Fig. 7
figure 7

Proposed rotor position error compensation model

Full size image

4 Experimental Verification

The proposed sensorless strategy has been verified at a IPMSM platform, as shown in Fig. 8. The major parameters of the tested motor are listed in Table 1. The tested motor is not operated under the weak magnet situation, since the study focus of this paper is the position error caused by the q-axis current changes. Thus, id = 0 control strategy is chosen in this paper.

Fig. 8
figure 8

IPMSM testing platform

Full size image
Table 1 IPMSM parameters
Full size table

Figure 9 compares the voltage error from the PI controller of the current loop based on the actual rotor reference frame and the estimated rotor reference frame when the load changes. The voltage error under the actual rotor frame varies with the q-axis current, whereas it remains constant under the estimated rotor frame. It can be seen from Fig. 9a that the voltage increases by 1 V for every 10 A increase of the q-axis current.

Fig. 9
figure 9

Voltage errors estimated by PI controllers with the q-axis currents change based on a the actual rotor reference frame b the estimated rotor reference frame

Full size image

When the q-axis current changes, the rotor position error will change accordingly, as shown in Fig. 10. For every 10 A increase of the q-axis current, the lag angle is nearly 1°. Combining that relationship shown in Fig. 9a, it can be concluded that 1 V voltage compensation corresponds to 0.93°rotor position delay when the q-axis current changes by 10 A, which satisfied the relationship obtained from Eq. (24).

Fig. 10
figure 10

Rotor position error with the q-axis currents change at 2000 rpm

Full size image

Figure 11 shows the compensation results of the rotor position error at 2000 rpm when the load changes. According to Eq. (24), the calculated rotor position error should be 1.87° (q-axis current from 20 to 40 A) and 3.98° (q-axis current from 40 to 60 A). After rotor position error compensation, the error can be compensated based on the proposed compensation model. The errors fluctuate around 0, which validates the effectiveness of the proposed rotor position error compensation strategy.

Fig. 11
figure 11

Rotor position error compensation at 2000 rpm under the condition of q-axis current a from 20 to 40 A b from 40 to 60 A

Full size image

Figure 12 shows the compensation results of the rotor position error at 3000 rpm when the load changes. According to Eq. (24), the calculated rotor position error should be 1.87° (q-axis current from 20 to 40 A) and 4.06° (q-axis current from 40 to 60 A). The rotor position error can be also compensated and finally the errors are close to 0.

Fig. 12
figure 12

Rotor position error compensation at 3000 rpm under the condition of q-axis current a from 20 to 40 A b from 40 to 60 A

Full size image

Figure 13 illustrates the transient position error at 2000 rpm. It can be seen that as the q-axis current increases and decreases, the error basically remains unchanged. The conclusions also apply to the situation at 3000 rpm shown in Fig. 14. In conclusion, the proposed rotor position compensation method can also perform well in the transient state.

Fig. 13
figure 13

Transient rotor position error with the q-axis currents change at 2000 rpm

Full size image
Fig. 14
figure 14

Transient rotor position error with the q-axis currents change at 3000 rpm

Full size image

5 Conclusion

In this paper, a position error compensation method based on the voltage output of PI controllers in the current loop is proposed for IPMSM sensorless drives. The relationship between the PI voltage output of the current loop and the position error has been found out and the position error extraction model is proposed under the condition of load change. Furthermore, a novel position error compensation model in the rotor reference frame is proposed based on the voltage and current inputs in the two-phase stationary reference frame, not in the rotor reference frame. The position error can be compensated by means of the rotation of the coordinate system. Finally, the effectiveness of the proposed method is verified experimentally. The results show that the position error fluctuates around zero after the compensation and the fluctuation amplitude is 1°.