Modeling and Simulation

Abstract

This chapter will describe the fundamental aspects and methods for the modeling and simulation of textile reinforcement structures and fiber-reinforced plastic composites (FRPCs). Due to the anisotropic material properties, the simulation of the deformation behavior of textile reinforcement structures is a complex matter. Various approaches will be introduced and simulation solutions based on kinematic models will be discussed in detail. The focus of this chapter is to assist designers and engineers in the design of preforms for complex FRPC components. To correctly configure the composite material according to the expected strains by means of Finite Element Models (FEM), extensive experimental tests for the quantification of composite characteristics are necessary. This contribution will therefore also address modeling and simulation methods based on multi-scale approaches to the determination of special mechanical values of materials.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

This chapter will describe the fundamental aspects and methods for the modeling and simulation of textile reinforcement structures and fiber-reinforced plastic composites (FRPCs). Due to the anisotropic material properties, the simulation of the deformation behavior of textile reinforcement structures is a complex matter. Various approaches will be introduced and simulation solutions based on kinematic models will be discussed in detail. The focus of this chapter is to assist designers and engineers in the design of preforms for complex FRPC components. To correctly configure the composite material according to the expected strains by means of Finite Element Models (FEM), extensive experimental tests for the quantification of composite characteristics are necessary. This contribution will therefore also address modeling and simulation methods based on multi-scale approaches to the determination of special mechanical values of materials.

15.1 Introduction

The use of computer-assisted methods for the assessment of a component design and its constructive realization has become crucial to achieve ever shorter product development cycles. Apart from that, generating geometry models to describe the product dimensions requires the characterization of material behavior of the textile composite reinforcements for purposes of modeling. Ensuring a wrinkle-free shaping of textile reinforcement structures into strongly curved shapes, sometimes even double-curved spatial contours, and realizing a load-adapted orientation of the reinforcement yarns are essential criteria in the designing of FRPC components.

The mechanical behavior of textile reinforcement structures differs considerably from that of monolithic materials. Due to the inhomogeneous structure made from fibers and yarns, locally varying material properties are common. Globally varying material properties arise from the production of textile reinforcements made from approximately similar fibers and yarns but manufactured by means of different fabric formation technologies. Due to the orientation of the reinforcement yarns, the properties of the reinforcement structures are anisotropic.

The flexible, anisotropic behavior of textile reinforcements makes the modeling of such structures for simulation processes for the purpose of specific designing and construction quite complex. Established methods can be classified according to the depth of analysis into the micro (fiber) level, the meso (yarn) level, and the macro (fabric) level. While the structure in the micro and meso scales is inhomogeneous, the macro scale allows a homogeneous approach.

The load-adapted orientation of the textile reinforcement structures of complex-shape components imposes high engineering requirements not only on the computation and simulation software to be used but also on the machines and methods suitable for production. If reinforcement structures are selected specifically and provided efficient manufacture, fiber-reinforced plastic composites allow a more cost-efficient component production in comparison to the metal materials. This requires an adaption of the geometry and designing/constructive aspects to the processed material. If this is taken into account, composite materials can be used to realize complex component geometries which could (easily) be produced with metal materials [1–6].

The current technologies used to manufacture textile preforms and precisely position them in the mold for shaping/consolidation are not sufficiently economical outside of aeronautics applications, regardless of component manufacturing method and used matrix material [7–9]. Preform production costs constitute a significant part of the total production costs.

Currently, the desired reproducibility of the preform quality and the resulting structure-mechanical component properties are not achieved due to the significant geometry alterations during the handling of textiles required in building the stack of layers and in shaping and positioning in the consolidation mold. During shaping into complex components, the load-adapted yarn orientation is partially lost, making an increased use of material necessary to ensure the safety required by the design. This is done at the expense of the lightweight construction effect and increases costs due to over-dimensioning. Improving simulation tools for the characterization of the deformation behavior of dry textile structures and fiber-reinforced plastic composites is therefore a priority. For this, the material parameters needed for the simulation have to be determined.

15.2 Deformation Behavior of Textile Semi-finished Products

15.2.1 General Discussion

For the application of textile semi-finished products made from high-performance fibers in FRPCs, it is crucial to realize the reinforcement of complex, sometimes strongly curved geometries without the formation of wrinkles. To perform this task without an excessive number of iterations in the future, a simulation of the deformation is currently a priority goal. For this, parameters characterizing the deformation behavior are required.

Tensile, flexural, and shear parameters as well as torsion rigidities [10–12] have to be taken into account in the mechanical assessment of the deformation of textile fabrics. A measuring method for the determination of torsion rigidities in textile fabrics has been developed and tested for classical textile structures, and it is also suitable for textiles made from high performance fibers. The currently available experimental examinations will have to be extended in the future to specify exact test conditions [13].

15.2.2 Tensile Values

The deformation behavior of textile fabrics under tensile loads results from the mechanical properties of the processed fibers, yarns, and the construction design [12]. Changes in length, related to the initial length of the sample, are referred to as elongations [14].

Determining the tensile values by means of tensile tests on strips according to DIN EN ISO 13934 T1 is explained in detail in Sect. 14.5.3.

Stress-strain behavior is tested using tensile tests on strips, preferably in two directions usually corresponding with the direction of the reinforcement yarns. To minimize the effects of transverse deformation the test can also be performed on biaxial tensile testers (manufacturers include Zwick GmbH & Co. KG [15], Kato Iron Works Co. Ltd [16]). The measuring sample is held in place by several clamps located on all four sides. The clamps are arranged perpendicular to the load direction or move proportional to the current change in length, controlled by computers. Tensile force is measured in both directions. The biaxial tensile test offers the possibility to test in an approximately load-adapted manner [17]. For the deformation simulation, transverse normal stiffnesses can be measured in addition to longitudinal normal stiffnesses. To gather test results with minimal spread, the clamping variations and sample shape have to be defined precisely and observed accurately. At the time of writing, no standards, but numerous recommendations on biaxial tensile tests exist. To avoid transverse deformation and the influence of the material clamping, the literature mainly discusses application-related test forms and force introductions [18–21].

15.2.3 Flexural Values

The flexural rigidity B is a measure of the resistance with which a textile fabric counters the bending moment of a defined bending change [10]. Flexural rigidity in textile fabrics depends on the fiber material used and the yarn construction. Both the rigidity of the fibers in the yarn and the construction design of the fabric significantly influence this specific value. The flexural rigidity of a fabric is commonly measured using a cantilever process, which is detailed in Sect. 14.5.4.

Extensive research at the Institute of Textile Machinery and High Performance Material Technology (ITM) at TU Dresden have shown that the currently used devices for flexural testing with cantilever methods do not offer reproducible results due to manual operation and the corresponding subjective influences. The visually determined overhanging length is included in the calculation of flexural rigidity in cubic power. Thus, even slight inaccuracies in reading the results and the insufficiently accurate scale marking can cause calculation errors of the flexural rigidity. Therefore, a new flexural rigidity measuring system (ACPM 200) was developed at the ITM [22]. The high degree of test process automation and analysis compensates the mentioned disadvantages of previous devices. Furthermore, the influence of local differences in rigidity across the sample width can be quantified. The developed device can be used for flexural rigidity tests of fabrics made from high-performance fibers.

A provision of the measured values in the form of a moment-curvature curve is required for the simulation of flexural behavior. This curve is not recorded in flexural tests on the ACMP 200. EISCHEN et al. [23] gives an indirect method to determine the moment-curvature curve, based on the cantilever method. In the first step, the X-Y coordinates along the bending curve are recorded from a side view, using a digital camera (Fig. 15.1).

Fig. 15.1

Experimentally determined bending curve

The data is computer-processed to determine the value pairs of the moments and curvatures along the overhang from the free endpoint to a locally defined endpoint. The zero point of the coordinate system is located at the free end of the sample. Programming the algorithm for the ascertainment of the bending moment—curvature curve (Fig. 15.2) can be performed with MATLAB.

Fig. 15.2

Bending curve calculated with ACPM 200 data

15.2.4 Shear Values

Shearing is the change of the angle of the crossing yarn systems caused by shear loads. The yarn intersection points form a center of rotation in which the distance of the points remains constant. Four intersection points are considered in Fig. 15.3. The originally rectangular arrangement of the points is distorted into a rhombus under shear strain. The resulting angle φ is referred to as the shear angle. When the deformation results in a maximum yarn compression, the shear angle reaches the critical value φ _kr . Further yarn compressions cannot take place in the plane. This necessarily results in the creation of wrinkles in the fabrics.

Fig. 15.3

Shear angles according to [12, 24, 25]

The shear of textile fabrics can be distinguished into two essential types of shear: simple and pure shear [26]. Figure 15.4 represents the different shear principles.

Fig. 15.4

Schematic representation of shear principles [26]: (a) simple shear, (b) pure shear

Numerous methods for the characterization of the shear behavior of fabrics have been tested. However, not all of them are suitable for tests on reinforcement textiles made from high-performance fibers.

In simple shear (Fig. 15.4a), shear loads cause not only angular changes between the yarns, but also tensile strain caused by yarn torsion at the crossing points. The distance between the two clamping lines remains constant during the entire shear process, causing a change of the length of the unclamped sample edge. If a tensile force is overlaid on shear deformation across the entire load cycle, a premature buckling of the fabric can be prevented in classical textiles. Usually, classical textiles tend to form wrinkles at low shear angles. As a shear angle of up to 8° is not sufficient for tests on textile composite reinforcements, this test method is not recommended. At greater angles, simple shear testing results in tensile deformations, which can only be realized by very high forces in textile composite reinforcements and are therefore irrelevant for the application of preforming.

Therefore, pure shear testing is recommended for tests on textile reinforcements (Fig. 15.4b). In pure shear, only the angle between the yarns is changed without yarn elongation. The distance between the clamping lines remains constant, and the sample edges do not change. This test principle is realized in bias extension tests and shear frame tests. The realization of shear in bias-extension tests can be performed on monaxial as well as biaxial tensile testers. They are tensile tests using a sample cut at a 45° angle to the yarn directions [27, 28]. In section A (Fig. 15.5), pure shear is measured. In section B, half the value of the shear measured in section A is registered. Section C does not contribute to shear force. During testing, the shear force—shear displacement diagram is recorded.

Fig. 15.5

Schematic of the bias-extension test [27]

The NAISS Company developed the TEXPROOF textile testing machine, which includes a shear test module (Fig. 15.6) [29]. The sample is affixed between two clamps, one of which is fixed, while the other can travel on a curved course. This course realizes the “Trellis” effect. The effect is triggered when the directions of introduced tensile forces do not correspond to the main directions of the reinforcement yarns. Shear with a change of the angle occurs until the reinforcement yarns are oriented in force-direction or until a maximum angle is achieved, which depends of the reinforcement geometry [29]. Independent of the sample thickness, light barriers register the shear angle at a crease height of 3 mm perpendicular to the plane.

Fig. 15.6

Shear test module TEXPROOF [29]

In the shear frame test [26–28, 30–37], pure shear is realized by fixing a square sample in a shear frame, clamped in a monaxial tensile tester at opposing corners, and deformed into a rhombus to a preset deformation distance (Fig. 15.7). Meanwhile, the force plot is recorded along the entire deformation distance. The shear angle can be calculated from the change in length of the rhombus diagonal. Clamping influences on the shear result are minimized by fixing the sample on needle bars [26]. For this test, the samples (300 mm × 300 mm) are needled onto the shear frame without tension, and secured.

Fig. 15.7

Test set-up and sample deformation principle

The deformation distance of the shear frame in these tests ranges from 60 mm (for multiaxial non-crimp fabrics) to a maximum of 100 mm (for woven fabrics). This is equivalent to shear angles of φ = 0° to φ = 28°, or φ = 0° to φ = 56.3° respectively. At the ITM, test speed is set at v _test  = 200 mm/min. During the shear test, the shear force is recorded along the traveling distance and then depicted graphically.

The shear angle can be calculated according to Eq. 15.1

$$ \varphi =90-2 \arccos \left(\frac{1}{\sqrt{2}}+\frac{h}{2a}\right) $$

(15.1)

Here, φ is the shear angle in °, h is the deformation distance of the shear frame in mm, and a is the side length of the shear frame in mm (200 mm in the test case).

At the beginning of the measurement series, reference measurements are taken with the frame without inserted sample, determining the friction forces of the shear frame during the test. The friction force is subtracted from all measurement curves as a reference curve. The deformation of the samples is also recorded with a camera during testing, and the wrinkling in Z direction is optically captured by means of the shade. The camera is positioned facing the surface normal in the center of the sample. At least three photographs per second are recommended to photographically record the sample over the entire test duration.

From the calculated shear force—shear angle diagrams, statements regarding the expectable deformability can be derived. To analyze the shear behavior, critical shear angles and the limiting angle are used, as they can be stored in the simulation tools.

To determine the limiting angle, the shear force—shear angle plot is separated into a linear and a non-linear zone as suggested by [38] (Fig. 15.8). The warning angle φ _lim is defined at the transition from linear to non-linear zone.

Fig. 15.8

Shear force—shear angle diagram with φ _lim for a woven fabric

Due to the force increase at the beginning of the shear test, the measured values at the beginning of the curve are not considered. After this increase of force, the curve transitions into a nearly linear section. This is chosen as the initial value of the regression analysis. Usually, these are measured values in a range from 5° and 10°. In the test example, the results from the difference between the measured curve and the line are characterized by fluctuations under 3 %. In the transition from the linear to the non-linear section, the deviation is significantly higher. The end of the linear section is defined at a deviation of 5 % [26].

The critical shear angle of a fabric can be determined optically, as described above. The first bulking of the sample is often subjectively detected visually from the recorded images. It is however recommended to recognize wrinkles instrumentally. Grey value image analysis or optical 3D deformation measurement systems are suitable options to detect the formation of wrinkles [26, 31].

Currently, preforms for complex FRPC components are largely manufactured manually. The textile composite reinforcements are shaped from the plane into the desired component geometry without tension. Recent developments are concerned with the automation of preform structuring. So-called “guidance systems” enable an automated laying of the reinforcement structures. These create a primary tension in the textile, which can influence wrinkling during deformation. To analyze this influence, the test device described in the following section was developed [28].

The shear measuring device built in [28] consists of a shear frame equipped with force sensors to determine primary tension and tensile force in warp and weft direction (Fig. 15.9). This allows a measuring of the tensile forces occurring in warp and weft direction during the test, and an allocation of the primary tensions to the shear deformation.

Fig. 15.9

Shear frame with force sensors [28]

To date, a variety of research efforts to determine suitable shear test methods and to apply experimental results in modeling approaches related to the deformation behavior have been conducted in parallel, but without co-ordination between individual research groups. Therefore, academic and industrial researchers founded an international group for developing and implementing a benchmarking in 2003 [31]. Shear frame and bias-extension tests for textile composite reinforcements with symmetrical or asymmetrical reinforcement yarn arrangements were performed and compared. The tests were realized on three identical woven fabrics by seven international research institutions: (NU) Northwestern University, USA; (UT) University of Twente, Netherlands; (LMSP) Laboratoire de Mécanique des Systèmes et des Procédés, France; INSA-Lyon, France; (UML) University of Massachusetts Lowell, USA; (UN) University of Nottingham, United Kingdom; (KUL) Katholieke Universiteit Leuven, Belgium; and (HKUST) Hong Kong University of Science and Technology, China. Six of the research groups delivered results based on the use of a shear frame, and four of the groups submitted findings based on bias-extension tests.

The efforts of the abovementioned [31] and other research works aim to provide recommendation of suitable testing technology and a standardized test method. In [31] no significant limitations were given regarding the conduct of the test.

The samples are square and adapted to the respective frame dimensions (145–250 mm). More details regarding sample preparation are given below. Woven fabrics are selected as test material, meaning that the reinforcement yarns are oriented in 0°/90° direction to one another. The tests are performed at different velocities ranging from 10 to 1,000 mm/min. The shear frame constructions are not identical (Fig. 15.10), but all the frames share certain characteristics. The textile reinforcements are held by the shear frame clamping mechanisms in a fashion that prevents slipping during the test. The friction between reinforcement structure and clamping is not considered. To eliminate the share of the force resulting from the shear of the selvedge reinforcement yarns, HKUST removed all clamped selvedge yarns running parallel to the clamping direction. Likewise, UT eliminated all reinforcement yarns arranged at a defined distance parallel to clamping direction, in order to prevent premature crease formation.

Fig. 15.10

Shear frames used [31]: (a) HKUST, (b) KUL, (c) UML, (d) UT, (e) LMSP, (f) UN

For bias-extension tests, samples of different sizes are used as well, and tested at different machine speeds.

The results of the study have shown that it is possible to use shear frames to obtain valuable experimental data for the characterization of the shear behavior of reinforcement structures, despite different test engineering preconditions. The mechanical conditioning of the sample can improve repeatability, as shown by the results of UML and KUL. All samples tested by UML were mechanically conditioned and gave results showing lower fluctuations. Using mechanical conditioning, the tensions remaining in the reinforcement structure from weaving are compensated (Fig. 15.11).

Fig. 15.11

Shear force—shear angle curves [31]

In order to compare different shear frame constructions, shear frame and/or sample sizes, and designs, normalization methods [27, 31, 39] were developed and presented (Fig. 15.12). After applying the normalization methods described in the study, test results are similar in the range up to 35°, which is relevant for the deformation of textile reinforcements (Fig. 15.12).

Fig. 15.12

Shear force—shear angle curves after normalization based on frame length [31]

Parallel to calculating the shear angle, optical methods are used to record wrinkle formation. As a result, it can be stated that—up to a shear angle of 35° in shear frame tests, and up to 30° in bias-extension tests—plain-woven fabrics display consistent matches with the shear angle determination based on the traversal path. At greater angles, optical wrinkling detection is recommended.

So far, this chapter has established the lack of a suitable testing standard. Currently, global research is being conducted to understand the effects of primary tension [28, 31].

As shown above, a textile-physical characterization of textile reinforcements made from high-performance fibers requires adjustments of the textile testing technology, as these textile reinforcements differ considerably from classic fabrics with regard to geometrical and structural construction.

In summary, it can be said that the deformation behavior of fabrics made from yarns produced from continuous high-performance fibers consist in shares of yarn elongation, yarn extension, yarn displacement (Fig. 15.13), and surface shearing [12, 24, 25, 38, 40]. Shear, which is the single most important specific value for the description of the deformation behavior of textile reinforcements, has been characterized in details. The other deformation mechanisms are described in the following sections.

Fig. 15.13

Basic deforming mechanisms of textile reinforcement structures [24, 25]

15.2.4.1 Yarn Elongation

Woven fabrics, knitted fabrics with biaxial or multiaxial reinforcement yarns, or non-crimp fabrics made from high-performance yarns are characterized by a minimal elongation at tensions below 100 N (which is the value required for draping). Therefore, elongation has only a miniscule share in the deformation of the textile fabric [12, 25, 28].

15.2.4.2 Yarn Extension

In fabrics produced by the interlacing (e.g. woven fabrics, braided fabrics) or inter-looping (knitted fabrics), the yarns are not oriented straight and stretched, but in waves, sinuses, or loops. Due to the change of curvature radii under loads, the yarns of the semi-finished product are stretched [25, 26]. Figure 15.13 shows the yarn stretching of a woven fabric.

15.2.4.3 Yarn Displacement

Yarn displacement often occurs in fabrics made from high-performance fiber materials at low yarn-yarn friction. Such fabrics include multiaxial non-crimp fabrics and fabrics with long floating loops (twill and atlas-woven fabrics).

The shear behavior is therefore the most important specific deformation value for modeling and simulating the shaping process of textile reinforcement structures made from high-performance fibers. The aim is to support the constructive component design in high-performance fiber composite application with an informed selection of reinforcement structures. Here, precise previous knowledge of the degree of crease-free shaping of dry reinforcement structures is crucial.

Model examination for a comparison of the deformation behavior of dry reinforcement structures can be performed by means of push-out tests.

A test setup constructed especially for the push-out test is integrated into a tensile tester (Fig. 15.14). In this setup, a cylindrically tapered hemisphere (diameter: 100 mm) pushes the textile to be tested through a ring. This ring is exchangeable, but has an internal diameter of 120 mm, and an edge radius of 2 mm in the case of the performed tests [8]. The squarely cut textile to be tested is fixed by spring-attached clamps at four points and repositioned by them in a defined manner during the test. This clamping mechanism only slightly impedes the deformation of the textile semi-finished product and does not significantly influence the course of the measurement curve. The push-out punch and ring with its bracket are clamped respectively in the bottom and top clamping device of a tensile tester (e.g. the Zwick GmbH Z100). The test records and analyses the push-out force in relation to the traverse path.

Fig. 15.14

(a) 3D model of the push-out test setup, (b) push-out test performed on a multilayered knitted fabric [8]

15.3 Computer-Assisted Simulation of the Deformation Behavior of Textile Composite Reinforcements

15.3.1 Models for Simulating the Deformation Behavior Simulation

The achievable draping behavior for a wrinkle-free shaping in complex components is of equal importance as the load-adapted reinforcement by means of single- or multilayer structures. Here, the reinforcement-adjusted yarn orientation is to be retained after shaping into the desired component contour in order to avoid a deterioration of the mechanical properties of the component by an undefined placement of the reinforcement textile.

In general, two variations of shaping are distinguished. In the first case, a rectangular cutting of the textile reinforcement is draped into a mold that matches the desired component geometry. In combination with yarn extension, and depending on the curvature, this can cause sometimes considerable yarn displacement and surface shearing, affecting the desired yarn orientation. In areas where wrinkles occur, the reinforcement structure is incised and extensively overlapped without a joining process, resulting in according with thickenings and higher component masses.

In the second case, ready-made technology is used to project the complex geometry in the plane as undistorted as possible by means of a partition into several smaller cuts. To produce a preform largely matching the component contour, the aim is to approximately project the component geometry by as few partial cuts as possible. However, further draping is required for the shaping. Angle and distance alterations of the yarns are inevitable in the process. To achieve the desired 3D component shape in a load-adapted design without later additional process steps, the smaller cuts are designed directly on the virtual geometry model [12].

The individual smaller cuts are placed in the mold either manually or by robots, or are joined into near-net shape preforms. Usually, the joining sections change the wall thickness in the joint zone.

According to [38, 41, 42] the following approximate classification can be derived for the modeling of the draping behavior of bidirectional textiles:

• the kinematic model,

• the elasticity model, and

• the particle model

The kinematic model depicts the meso structure (yarn level) of the textile by a geometric pattern with regard to the geometric boundary conditions on a surface.

In the elasticity model the textile semi-finished products, which are largely represented anisotropically and partly orthotropically, are discretized in order to determine the deformation and the yarn orientation by means of the Finite Element Method.

The particle model represents microscopic interactions describing the properties of the macroscopic system. Each yarn intersection point is represented by a particle possessing the physical characteristics of the reinforcement structure. The most probable arrangement of the intersection points is determined by establishing the minimum particle energy. This approach does not require a flat placement of the textile, allowing a simulation of the free deformation of textiles under the influence of gravity. The fiber bending is factored in.

CHERIF [38] develops a significant contribution to the drape-ability simulation of woven fabrics and multiaxial non-crimp fabrics on the basis of the Finite Element Method. Apart from the anisotropic material behavior, production-technological constrains are considered as well. To describe the mechanical material behavior, a four-noded shell element is used. The macromechanical model allows the consideration of high and non-linear shear deformation degrees at negligible elongations. Extensive experiments serve to determine the required specific values. Furthermore, geometrical non-linearities caused by the contact of reinforcement structure and shaping mold, as well as boundary conditions varying with the proceeding draping process can be simulated. To omit a repetition of any detailed deliberations on the subject, the respective literature is recommended for in-depth information.

Beyond this, the textile structure can be depicted as precisely as possible by means of a unit cell (RVE—Representative Volume Element) [43–48]. Determining the modeling parameters can be an elaborate process, but given sufficient parametrization, can be used to represent a variety of structures of the same fabric formation process. The modeling of the entire structure to simulate draping behavior on different component geometries still requires enormous computing power.

Kinematic models for the simulation of the deformation behavior of reinforcement structures have disadvantages. Even so, short computing times and the precision of calculation results make them increasingly relevant for practical applications due. Both factors may vary depending on component complexity. The disadvantages include [38]:

• Only single-layer structures are simulated. Frictions between the layers during simultaneous draping of several layers are not considered.

• The effect of any drape effectors or other shaping molds on the draping result cannot be simulated.

• The influence of a guidance system for a reproducible, preferably wrinkle-free shaping is disregarded.

Despite worldwide research efforts for the description of draping processes by means of FEM, the currently commercially available simulation tools require extensive computing times and considerable experimental effort for the determination of the required specific values.

15.3.2 Kinematic Modeling of the Deformation Behavior

As established above, shearing behavior is the most important specific value to be considered in the simulation of the deformation behavior of dry reinforcement structures. When describing the deformation, the effects of yarn elongation and yarn extension are usually omitted. In the kinematic model, only deformations based on shear are considered. The placement of the bidirectional reinforcement structure on the surface of the form is simulated. The model delivers geometrical information on the shear angles required for the deformation. The mechanical properties of the reinforcement structure are not entered in the modeling [42, 49, 50].

The crossing points of the yarn axes between the yarns are modeled as joints. Between these intersection points, the yarns behave as beams with constant length. A geometric algorithm allows the determination of the crossing points of the reinforcement structure, if the location of the point on the shape geometry and the fiber orientation direction in the point are known. The yarns between the joins are geodesically placed on the geometry. The resulting angles in the joints match the shear angles of the reinforcement structure. Shear limitations for the realization of a wrinkle-free draping may prevent the placement of the intersection points. This is always the case if the critical shear angle stored in the simulation tool is exceeded [42, 49].

Using a comparison of the calculated local shear angles to the critical shear angles of the textile semi-finished products to be used (which can differ greatly between multilayered knitted fabrics, woven fabrics, and multiaxial non-crimp fabrics), a sensible default is set for the cut parts. Usually, these algorithms do not consider loads or friction effects.

FiberSIM ^® [51], DesignConcept 3D (DC3D) [52], PAM Quickform [53], Composite Part Design (CPD) [54] are examples of commercial software packages on a geometrical basis, and contain interfaces with FE-calculation programs such as ANSYS [55] or MSC-Patran and MSC-Nastran ^® [56]. With these, the yarn orientation can be simulated and represented on the basis of a geometrically sufficiently defined reinforcement structure. The result can be transferred into FE-calculation programs and is used to recalculate load cases.

The FiberSIM ^® and DC3D software solutions are examined with regard to deformation simulation and cut generation in [57]. The simulations are based on the kinematic model.

The textile preform has to match the desired component geometry as precisely as possible. The desired component thickness is an exception, as it is only achieved after the consolidation process. The aim is to design the cutting of the reinforcement textile in a manner that creates minimum material compressions or extensions, adheres to the set reinforcement direction, and ensures a wrinkle-free deformation. The 3D data required for cut generation of the projected components can be created with commercially available 3D-CAD software solutions (such as CATIA [53], SolidWorks [58]) or implemented into the simulation software via neutral interface formats (e.g. IGES and STEP).

Using the DC3D software solution [52], the user can create virtual 3D geometry models and conduct feasibility analyses based on an automated cutting generation. The cutting contours for the realization of the desired component shape are based on the 3D geometry. To this end, cutting boundaries are set on the surface. In order to be able to represent the cutting designed in 3D in the plane, the surfaces are triangulated. Triangulation refers to the partition of an area into triangles. Triangulation can be performed curvature-dependently or uniformly.

The simulation criterion consists of minimizing changes to the edge length of the triangles, the angles in the triangle, and the areas of the triangles [12, 57]. The flattening result is influenced significantly by two boundary conditions: the starting point and the fiber orientation direction [40]. In assembling, the term flattening is used for the representation of the 3D-developed cut parts in the plane.

As reinforcement textiles can have an anisotropic stress-strain behavior, fiber orientations play a crucial part. Textile-reinforced plastic components are differently loaded in practice, and therefore the reinforcement yarns have to be oriented according to the structure-mechanical design.

Fiber orientation directions and starting point of the simulation are varied for a reference geometry (hemisphere with flat contact surface) (Fig. 15.15).

Fig. 15.15

Cuttings under variation of fiber orientation and simulations starting point [57]

The flattening analysis shows which shear angles are necessary to drape the cutting onto the shaping mold. By comparing the experimentally established critical shear angles of the textile reinforcements, the designer can judge whether the selected cutting determination is suitable for the component geometry to be realized. The designer has to decide whether the shear-induced local displacements of the reinforcement yarns are permissible for the load-adapted component design.

To achieve the desired wall thickness of the component, several layers of reinforcement structure are often required. The component geometry therefore has to be adjusted according to layer thickness in the compacted state, in order to ensure accurate cutting generation.

The FiberSIM ^® software is currently in use by leading manufacturers in aeronautics to develop fiber-reinforced plastic composite constructions.

The cutting contours are derived from the 3D geometry. As mentioned above, the cut boundaries are defined on the surface for this purpose. FiberSIM ^® works directly on the CAD representation of the component, evaluating the native geometry without transformation and approximation [51]. After the simulation of the reinforcement structure placement on the respective geometry, information concerning the necessary shear angles becomes available [42, 49]. The simulation results are represented on the surface of the geometry by means of a set of curves known as “fiber trajectories”, which reflect the final state of the semi-finished product after draping. For biaxially reinforced structures, the result is a grid on the model surface.

FiberSIM ^® contains a material database in which the basic specific values and characteristic values for a description of the shear behavior of reinforcement textiles can be stored. The calculation results are compared to the limiting angle and critical angle values under shear loads, stored in the database. The “fiber trajectories” are shown color-scaled. Areas visualized in blue display low strain, a yellow color signalizes that the limiting shear angle has already been reached, while a red color indicates that no wrinkle-free draping is possible. Figure 15.16a gives an example of this.

Fig. 15.16

(a) Shear deformation on the cutting, (b) Deviation from the defined orientation of the reinforcement yarns [57]

By means of the analysis of deviations from the selected fiber orientation direction, FiberSIM ^® offers additional control to avoid multiple iterations during preform development. One example is given in Fig. 15.16b.

As the surface area of the planar cutting deviates greatly from the surface area of the counterpart in 3D, problems during draping can be identified early on (Fig. 15.17). This proves that variations of the starting point can contribute to an optimization of the flattening result.

Fig. 15.17

Cuttings under variation of the fiber orientation and the simulation starting point [57]

The deformation analysis results of both software solutions are similar (Fig. 15.18). As can be seen from Fig. 15.19 and Table 15.1, the calculated cuttings of both software solutions can differ significantly.

Fig. 15.18

Deformation analysis [57]: (a) DC3D, (b) FiberSIM ^®

Fig. 15.19

Comparison of cuttings developed with FiberSIM ^® (dotted line) and DC3D (continuous line) [57]: (a) starting point at the cut tip (apex), fiber orientation 0° to warp direction, (b) starting point at the cut tip (apex), fiber orientation 45° to warp direction, (c) starting point at the center of the area of the cut, fiber orientation 0° to warp direction, (d) starting point at the center of the area, fiber orientation 45° to warp direction

Table 15.1 Surface area of the cuts shown in Fig. 15.19

The examined software solutions are based on different algorithms (Fishnet—FiberSIM ^® , Mosaic—DC3D), which are explained and discussed below [42, 49, 59–62].

Both algorithms use the basis algorithm of the kinematic model. All points $\overrightarrow{x}$ on a double-curved geometry surface can be represented parametrically with surface coordinates u _i [42]

$$ \overrightarrow{x}=\overrightarrow{x}\left({u}_1,{u}_2\right). $$

(15.2)

The elementary length dS of a surface segment between two closely located points is given by the first surface fundamental form

$$ d{S}^2={G}_{ij}d{u}_id{u}_j $$

(15.3)

with the coefficients

$$ {G}_{ij}=\frac{\partial \overrightarrow{x}}{\partial {u}_i}\cdotp \frac{\partial \overrightarrow{x}}{\partial {u}_j}. $$

(15.4)

In Eq. 15.3, the Einstein notation is used, which states that all indices occurring twice in a term are automatically summed up.

The biaxially reinforced textile structure is described by coordinates v _i along the directions of the reinforcement yarns. The elementary length ds of a section of the deformed textile is given by

$$ d{s}^2=\left({\delta}_{ij}+2{E}_{ij}\right)d{v}_id{v}_j. $$

(15.5)

E _ij describes the coordinates of the Green-Lagrange tensor with

$$ {E}_{11}=0,{E}_{22}=0\ \left(\mathrm{no}\ \mathrm{fiber}\ \mathrm{elongation}\right)\ \mathrm{and}\ 2{E}_{12}= \cos \alpha, $$

(15.6)

i.e. it is assumed that the deformation of the biaxially reinforced textile structure under shear is caused by pure shear at a fiber angle α. When placing the textile on the surface, the length of one surface segment is equal to that of the corresponding textile section, therefore

$$ dS=ds $$

(15.7)

applies, from which follows

$$ {G}_{ij}d{u}_id{u}_j=\left({\delta}_{ij}+2{E}_{ij}\right)\;d{v}_id{v}_j. $$

(15.8)

Using the Einstein notation, and insertion into Eq. (15.8) result in

$$ {G}_{11}d{u}_1^2+2{G}_{12}d{u}_1d{u}_2+{G}_{22}d{u}_2^2=d{v}_1^2+2 \cos \alpha d{v}_1d{v}_2+d{v}_2^2. $$

(15.9)

The draping of a biaxially reinforced textile structure onto the surface is described by the equation

$$ {u}_i={u}_i\left({v}_1,{v}_2\right). $$

(15.10)

Inserting

$$ \begin{array}{l}d{u}_1-\frac{\partial {u}_1}{\partial {v}_1}d{v}_1+\frac{\partial {u}_1}{\partial {v}_2}d{v}_2\kern1em \mathrm{and}\\ {}d{u}_2-\frac{\partial {u}_2}{\partial {v}_1}d{v}_1+\frac{\partial {u}_2}{\partial {v}_2}d{v}_2\end{array} $$

(15.11)

into Eq. (15.9) results in

$$ \begin{array}{c}\hfill d{s}^2=\left[{G}_{11}{\left(\frac{\partial {u}_1}{\partial {v}_1}\right)}^2+2{G}_{12}\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_1}+{G}_{22}{\left(\frac{\partial {u}_2}{\partial {v}_1}\right)}^2\right]d{v}_1^2+\cdots \hfill \\ {}\hfill \cdots +\left[{G}_{11}{\left(\frac{\partial {u}_1}{\partial {v}_2}\right)}^2+2{G}_{12}\frac{\partial {u}_1}{\partial {v}_2}\;\frac{\partial {u}_2}{\partial {v}_2}+{G}_{22}{\left(\frac{\partial {u}_2}{\partial {v}_2}\right)}^2\right]d{v}_2^2+\cdots \hfill \\ {}\hfill \cdots +2\left[{G}_{11}\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_1}{\partial {v}_2}+{G}_{12}\left(\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_2}+\frac{\partial {u}_1}{\partial {v}_2}\;\frac{\partial {u}_2}{\partial {v}_1}\right)+{G}_{22}\frac{\partial {u}_2}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_2}\right]d{v}_1d{v}_2=\cdots \hfill \\ {}\hfill \dots =d{v}_1^2+2 \cos \alpha d{v}_1d{v}_2+d{v}_2^2.\hfill \end{array} $$

(15.12)

A comparison of the coefficients gives

$$ \begin{array}{c}\hfill {G}_{11}{\left(\frac{\partial {u}_1}{\partial {v}_1}\right)}^2+2{G}_{12}\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_1}+{G}_{22}{\left(\frac{\partial {u}_2}{\partial {v}_1}\right)}^2=1\hfill \\ {}\hfill {G}_{11}{\left(\frac{\partial {u}_1}{\partial {v}_2}\right)}^2+2{G}_{12}\frac{\partial {u}_1}{\partial {v}_2}\;\frac{\partial {u}_2}{\partial {v}_2}+{G}_{22}{\left(\frac{\partial {u}_2}{\partial {v}_2}\right)}^2=1\hfill \\ {}\hfill {G}_{11}\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_1}{\partial {v}_2}+{G}_{12}\left(\frac{\partial {u}_1}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_2}+\frac{\partial {u}_1}{\partial {v}_2}\;\frac{\partial {u}_2}{\partial {v}_1}\right)+{G}_{22}\frac{\partial {u}_2}{\partial {v}_1}\;\frac{\partial {u}_2}{\partial {v}_2}= \cos \alpha .\hfill \end{array} $$

(15.13)

The initial and boundary conditions are necessary to solve the equations of the kinematic model numerically. As boundary conditions for

$$ \begin{array}{ccc}\hfill {v}_1=0\hfill & \hfill \mathrm{and}\hfill & \hfill {v}_2=0\hfill \end{array} $$

(15.14)

the yarns are to be placed geodesically. To numerically solve the set of non-linear equations (15.13), the biaxially reinforced textile structure is discretized in a mesh of edge length d, so that the node (i, j ) has the coordinates

$$ \begin{array}{l}{v}_1= id\kern0.5em \mathrm{and}\\ {}{v}_2=jd.\end{array} $$

(15.15)

The surface coordinates or the spatial coordinates can then be calculated for each node, from which the angle α can be determined [42, 49].

The draping is simulated in five steps:

• 1. The starting point for the placement of the reinforcement structure on the surface of the geometry is selected

• 2. The draping direction for the yarns is determined as v ₂ = 0,

• 3. The yarns with v ₂ = 0 are placed on the surface geometry along a geodesic curve,

• 4. Steps 2 and 3 are repeated for the yarns with v ₁ = 0,

• 5. All nodes (i, j ) are traversed, and the conditions set by Eq. (15.13) will be complied for each cell with nodes (i, j ) and (i − 1, j − 1)

Figure 15.20 illustrates the kinematic model for reinforcement yarns during the draping of a bidirectional reinforcement structure. For the illustration of u ₁ (v ₁, v ₂), different approaches can be used [40, 49], which are described below.

Fig. 15.20

Kinematic simulation of draping on a spherical surface, discretization of the bidirectional textile [42, 49, 57]

In the fishnet algorithm, the bidirectionally reinforced textile structure is represented by a web of intersecting yarns arranged on the surface along geodesic curves. For this, a freely selected cell will be considered below (Fig. 15.20). Initially it is assumed that the length of the edges originating in the left intersection point is known. The initial direction of the geodesic edges beginning in the upper and lower intersection point are determined, whose terminal points have to meet. The calculation rule is framed as an optimization problem of the distance between two terminal points.

As the analysis of the objective function includes the integration of a differential for geodesic curves of given length d, the problem is not solvable analytically. Therefore, Gradient and Hessian matrix are calculated numerically by the finite difference method [49]. A geodesic edge is determined by parametrically defining the reinforcement yarn on the surface by Eq. (15.2), using

$$ \begin{array}{l}{u}_1={u}_1(v)\\ {}{u}_2={u}_2(v)\end{array} $$

(15.16)

This designates the arc length v. If

$$ \frac{d\;\overrightarrow{x}}{dv}\cdotp \frac{d\;\overrightarrow{x}}{dv}=1 $$

(15.17)

and

$$ \frac{d\;\overrightarrow{x}}{dv}=\frac{\partial \overrightarrow{x}}{\partial {u}_1}{u}_1^{\prime }+\frac{\partial \overrightarrow{x}}{\partial {u}_2}{u}_2^{\prime }, $$

(15.18)

the reinforcement yarn is inextensible.

The yarn is referred to as geodesic if the position-dependent normal to the curve and the normal to the surface coincide [49]. This can be phrased as follows:

$$ \frac{d^2\overrightarrow{x}}{d{v}^2}=\frac{1}{\rho}\overline{n}. $$

(15.19)

This describes the curvature 1/ρ. With the equation

$$ \overline{n}=\frac{\overline{J}}{\left|\overline{J}\right|} $$

(15.20)

the normal to the surface is calculated, where

$$ \overline{J}=\frac{\partial \overrightarrow{x}}{\partial {u}_1}\cdotp \frac{\partial \overrightarrow{x}}{\partial {u}_2}. $$

(15.21)

The differentiation of the condition (15.17) results in

$$ \left(\frac{\partial \overrightarrow{x}}{\partial {u}_k}{u}_k^{\prime}\right)\kern0.5em \left(\frac{\partial^2\overrightarrow{x}}{\partial {u}_i\partial {u}_j}{u}_i^{\prime }{u}_j^{\prime }+\frac{\partial \overrightarrow{x}}{\partial {u}_i}{u}_i^{{\prime\prime}}\right)=0. $$

(15.22)

Considering Eq. (15.19),

$$ \left\{\begin{array}{l}{u}_1^{{\prime\prime}}\hfill \\ {}{u}_2^{{\prime\prime}}\hfill \\ {}1/\rho \hfill \end{array}\right\}=-{\left[\frac{\partial \overrightarrow{x}}{\partial {u}_1}\frac{\partial \overrightarrow{x}}{\partial {u}_2}-\overline{n}\right]}^{-1}\left\{\frac{\partial^2\overrightarrow{x}}{\partial {u}_i\partial {u}_j}{u}_i^{\prime }{u}_j^{\prime}\right\} $$

(15.23)

follows.

The first two rows are differentials of the second order for curvilineal coordinates u _k′ , while the third row gives the curvature. The initial conditions for Eq. (15.23) in the starting point are u ₁ (0) and u ₂ (0), where du ₂/du ₁ are the adequate values for the initial orientation direction. The values u′₁ (0) and u′₂ (0) include the normalization conditions (15.17) [49].

If the surface of a model geometry is described with planar triangles, the mosaic algorithm [49, 62] is used. For complex surfaces, a multitude of elements are required for a precise approximation of a curvature. A geodesic curve is reduced to a zigzag line by means of such mosaic surfaces (Fig. 15.21).

Fig. 15.21

Changes of fiber orientation in kink points [49, 57]

If the starting point and fiber orientation are given, consecutive node points on the edges of the mosaic can be defined. The fiber direction at the beginning of the consequent triangle results from the observation that the angle between the yarn and the edge does not change between triangles (α = β in Fig. 15.21). If the trajectories AB and AC in any given cell ABCD are known, the initial directions of the trajectories BD and CD have to be defined in a way that ensures that the end points coincide at D. In turn, this is equivalent to an optimization problem, which has previously been explained for the fishnet algorithm [49]. The quality of the mosaic algorithm is impaired by a constant error caused by the discretization of the surface.

In summary it can be stated that the determination of the optimum between structure-mechanical requirements and shaping possibilities (separation into individual cuttings) has to be made accurately for each individual case. For this purpose, the abovementioned and tested simulation tools can be very helpful and reduce required development times.

15.3.3 Local Structural Fixations for the Defined Draping of Textile Structures on Strongly Curved Surfaces

During the shaping and placing of textile reinforcements for the construction of a preform, deformability plays a crucial role. As the flexible textile fabrics are very sensitive, the reinforcement yarns are at risk of being displaced in an undefined manner during handling. In addition, selvedge yarns (especially in acute-angled outlines) can become disengaged or displaced. To counter these effects, fixation agents in the form of binders can be applied to the textile reinforcements. If the binder is applied to the entire surface, the form stability of the textile is increased significantly, which usually limits the wrinkle-free deformation capacity. For this reason, only sections of the pre-assembled textile structures are fixated [63–65].

For this purpose, a method that can contribute greatly to an improvement of the preforming process will be portrayed. The developed and patented method for the structure fixation [66] realizes tailor-made local fixations with due regard to the 3D component geometry. Thus, it can solve current, sometimes substantial problems of cutting, handling, and shaping along the preform production chain. The following features characterize this software-based method, according to [66]:

• adjustment of the structural fixation according to the calculated cutting geometries,

• identification of shear deformation during spatial arrangement of the cutting into the preform geometry,

• fixation of the sections exposed to small strains/displacement by deformation,

• application of the fixation agents in a grid-like pattern or intermittently (the manner of fixation depends of the respective fabric structures and the fiber materials to be processed),

• minimization of the amount of the fixation agent with regard to the usually porous structure of the textile structure, continuous or discontinuous performance of the structural fixation in the preform production chain,

• contour-adapted stacking of fixated cuttings with due regard to the sectional drawing, and

• observance of the matrix compatibility of the fixation agent.

Sections exposed only to small displacements by the deformation are suitable as local fixation areas. These sections can be identified by calculation and flattening analyses (see Sect. 15.3.2).

The fixated areas can be arranged over lines or over areas. For the hemispherical reference geometry, the structural fixation is adjusted over lines, as shown in Fig. 15.22. The fixation lines run over the cutting in crossed and longitudinal lines, fixating all yarns running transversely and lengthwise respectively. This prevents the yarns from falling apart without fixation the edges of the cutting [64]. The amount of fixation agent is minimized in this method to achieve good deformability of the reinforcement structures into the preform and avoid negative influences on the specific mechanical values of the composite.

Fig. 15.22

Determination of the fixation lines of different cuttings [57]

Due to the significantly different fabric structures, any measures of structural fixation have to be adjusted to the textiles in question. For this purpose, they are modeled with sufficient accuracy (Fig. 15.23a), based on microscopic experiments. The illustration uses a woven reinforcement fabric as an example.

Fig. 15.23

(a) Distances between yarn centers: (top) normal distance to woven fabric plane, (bottom) in the woven fabric plane, (b) 3D woven fabric models (top view)

The following parameters are commonly required for a 3D fabric modeling:

• width of the warp and weft yarns,

• fabrics thickness,

• distance between yarn centers normal to the woven fabric plane, and

• distance between yarn centers in the woven fabric plane

The modeled woven reinforcement textiles are shown in Fig. 15.23b.

By modeling the woven fabrics, the cutting contours and structures of the textiles can be “coupled” with each other, in order to adjust the zones of local fixation to the structure (Fig. 15.24). The applied method of structural modeling is expensive and therefore rarely realizable for the multitude of used reinforcement structures in practice. Therefore, another method allowing the virtual control of the reinforcement yarn position is being developed. A grid representing the yarn course of the reinforcement structure is drawn on the 2D cutting calculated in DC3D. Adjusted for strain, this is then projected onto the virtual shaping tool (Fig. 15.24b).

Fig. 15.24

(a) Matching the woven fabric to the reference geometry, binder application, (b) virtual control of the reinforcement yarns, binder application

The structural modeling indicates the positions of reinforcement structure where binder has to be applied in order to realize the determined fixation patterns and fixate all yarns of the cutting.

15.4 Composite Material Modeling

The mechanical behavior of fiber-reinforced composite materials differs fundamentally from that of classical, monolithic materials. The significant distinguishing features are:

• locally varying material properties due to inhomogeneous composite structure,

• globally varying material properties due to changing composite configuration, and

• anisotropic material properties caused by the orientation of the reinforcement fibers

The major challenge for the designer is to find the optimum configuration of the composite material with regard to the expected load on a component. To analyze the selected component design concerning criteria such as maximum deformation or strain, FE calculation are used. For the FE models, the geometry and the constitutive laws have to be given, according to the respective material. The adaptivity and resulting multitude of possible configurations of textile composite materials and the complex material behavior require extensive experimental efforts to quantify composite properties, especially when considering the physically nonlinear behavior. Alternatively, both mechanical and other specific material values can be determined much more efficiently with modeling and simulation methods based on a multi-scale approach.

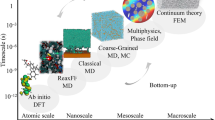
The hierarchical structure of composite materials, as shown in Fig. 15.25, allows a clear distinction between different scales, which are defined by characteristic dimensions.

Fig. 15.25

Definition of micro, meso, and macro scale, based on the hierarchical structure of composite materials

Accordingly, a distinction will be drawn here between:

• Micromechanics (<0.1 mm), which describes e.g. the influence of interfaces, or the interaction of fiber filaments and matrix,

• Mesomechanics (0.1 mm–1.0 cm), which captures the properties of the yarn/matrix bundles, their interactions, and matrix cracks, and

• Macromechanics (>1 cm) for the determination of component behavior under defined external loads

The bracketed dimensions match characteristic dimensions for the respective level of observation.

On the one hand, a multi-scale simulation is based on the constitutive relations of composite constituents, which are often characterized by a simple formulation and well-known quantification. On the other hand, the modeling, e.g. based on the FEM, represents the composite architecture. Homogenization then refers to the transition from one scale to the next coarser scale, i.e. from micro to meso, or from meso to macro. The reversal, which is the transition from one scale into the next finer scale is equivalent to a localization. With this approach and the corresponding methods, variations of the specific geometrical or material values in the micro and meso scales allow a targeted adjustment of the macroscopic properties of the composite without experiments.

In the following, the modeling of textile-reinforced composite materials on the micro and meso level will be described in greater detail. This includes the geometrical analysis of the composite on the respective observation level as well as the application of special modeling methods to efficiently generate FE models for the representation of complex reinforcement architectures.

15.4.1 Modeling the Fiber/Matrix Composite (Micro-level)

To simulate the material behavior on the micro-level and calculate the effective properties of the meso-level by means of FE-based homogenization methods, the composite (which consist of high-performance filaments and surrounding plastics) has to be modeled. The assumptions and prerequisites made for that purpose are described below.

The impregnation of the meshed non-crimp fabric structure with matrix material depends on the technological parameters of the production method. Here, it is assumed that the space between filaments is completely filled with matrix material.

As shown by the CT scan in Fig. 15.26, the filaments are arranged parallel in a roving, without local irregularities.

Fig. 15.26

CT scan of the composite

Fig. 15.27

Volume model of a multilayer non-crimp fabric

Thus, for the microscopic modeling of the representative volume element (RVE), the fiber/matrix area is considered as a UD composite.

The irregular arrangement of the filaments in the cross-section of the roving can be seen in Fig. 15.28, showing a polished composite section. Due to the high number of filaments and their statistical distribution the effective mechanical properties perpendicular to the roving alignment are independent of the orientation. Therefore, a transversely isotropic material law can be used to describe the mechanical behavior. To avoid an elaborate modeling of the statistical distribution, an equivalent, idealized UD composite with regularly arranged filaments, for which a unit cell can be defined as RVE, is considered. One prerequisite for the transversely isotropic material is an equally spaced positioning of neighboring filaments. Several possibilities are available to determine the unit cell area, where the case of an oblique parallelepiped is shown in Fig. 15.29.

Fig. 15.28

Polished section of the warp yarn area with irregular filament arrangement

Fig. 15.29

Model of a unit cell in a UD composite

Due to the periodic structure, the exterior dimensions of the model in filament direction have no influence on the effective properties and can therefore be selected freely. The acute angle enclosed by the sidelines of the cross-section is 60°. The length a of these lines can be calculated by

$$ a=\sqrt{\frac{\pi }{2\sqrt{3}\;\varphi }}\;{d}_f $$

(15.24)

if the filament diameter d _f and the fiber volume content φ are known.

15.4.2 Modeling of the Textile in the Composite (Meso-level)

15.4.2.1 Geometrical Description of the Multilayer Knitted Fabric Reinforcement (MLG Reinforcement)

Textile-technical and manufacturing engineering parameters are the basis for a description of the geometry and of the determination of independent geometry values. Furthermore, as shown in Fig. 15.30, digital shots of the textile and composite can be made with scanners or transmitted-light microscopes, and analyzed regarding their planar dimensions. The geometry values in thickness direction can be determined using CT scans, as shown in Fig. 15.26. As CT scans are expensive, the equations for the determination of spatial reinforcement geometries derived in the following section will rely solely on specific textile-technical values, and dimensions which can be established from optical images in the textile plane.

Fig. 15.30

Optical images of the MLG and the composite. (a) Scan of the MLG 3a. (b) Microscopic view of the composite

For the modeling based on the FEM for the experiments of composite behavior on the meso-level, the orientation and course of the reinforcement yarns has to be known. In order to simplify the geometrical description and thus the modeling, only the basic geometrical shapes are used, such as lines and circle segments. By using basic geometrical shapes for the yarn cross-sections, the positions of the center of gravity can be determined. The path of this center of gravity along the respective reinforcement yarn has to be known for the Binary Model, described in Sect. 15.4.2.2.

The CT scans show that an ellipse can be assumed as an approximate cross-section for the weft yarn, while a circular segment is a suitable cross-section approximation for the warp yarn. In comparison to warp and weft yarns, the loop yarn has a smaller cross-section. For simplicity, it is therefore regarded as circular.

By means of these geometrical abstractions, the reinforcement architecture of a composite with a textile reinforcement consisting of two conversely placed MLGs can be represented as shown in Fig. 15.27. For the quantitative description of the orientation, a coordinate system matching the three views in Fig. 15.31 is defined.

Fig. 15.31

Graphic definition of the MLG geometry parameters

In the definition of geometry parameters, it is assumed that variables with subscript We, Wa, and L refer to values in relation to weft, warp, or loop yarns.

15.4.2.1.1 Geometry of the Biaxial Reinforcement

The distance between the neighboring warp and weft yarns can be determined from the warp and weft yarn densities η_Wa and η_We where ${l}_{Wa}=\frac{1}{\eta We}$ and ${l}_{We}=\frac{1}{\eta Wa}$, respectively. The area of the cross-sections A _Wa and A _We can be computed based on the assumptions regarding the geometrical shape, and the dimensions D _Wa , d _Wa , D _We , and d _we , which are defined in Fig. 15.31 by

$$ \begin{array}{lll}{A}_K=\frac{2}{3}{D}_K{d}_K+\frac{d_K^3}{2{D}_K}\hfill & \mathrm{and}\hfill & {A}_S=\frac{\pi }{4}{D}_S{d}_S\hfill \end{array} $$

(15.25)

Here, the equation for A _Wa conforms to an approximation of the area of a circular section. The independent values D _Wa and D _We are easily determined from the scans and microscopic images, since they are dimensions in the composite plane. In contrast to that, d _Wa and d _We as dimensions in Z direction can only be determined by means of expansive polished sections or CT scans. Alternatively, these values can be estimated from the relations of the mass content ratio ${\overline{m}}_{Wa}$ and ${\overline{m}}_{We}$ of warp and weft yarns, which are known as textile-technical parameters. Based on the assumption that the mass densities of the rovings are approximately identical, the resulting relation is

$$ \frac{{\overline{m}}_S}{{\overline{m}}_K}=\frac{A_S{l}_S{n}_S}{A_K{l}_K{n}_K}, $$

(15.26)

where n _Wa and n _ew are the respective number of warp and weft yarn systems in the MLG. Substituting the areas A _Wa and A _We with the Eq. (15.25), neglecting the cubic part of d _K and with the definition of the ratio

$$ rd:=\frac{d_S}{d_K}=\frac{8{\overline{m}}_S{D}_K{n}_K{\eta}_K}{3\pi {\overline{m}}_K{D}_S{n}_S{\eta}_S} $$

the following equations can be derived for the computation of the warp and weft yarn thicknesses, respectively.

$$ \begin{array}{llll}{d}_K=\frac{d_{MLG}}{\left({n}_S rd+{n}_K\right){\xi}_K}\hfill & \mathrm{with}\hfill & {d}_{MLG}:=d/{n}_{MLG}\hfill & \mathrm{and}\hfill \\ {}{d}_S=\frac{\xi_K}{\xi_S} rd\kern0.5em {d}_K\hfill & \mathrm{with}\hfill & \frac{1}{2}\le {\xi}_{K/S}\le 1\hfill & \hfill \end{array} $$

(15.27)

Here, d _MLG is the thickness of an MLG in the composite. Furthermore, it is assumed that the contribution of the loop yarn to the composite thickness is negligible. The factors ξ _We and ξ _Wa describe the superposition of yarn layers by interloping. This occurs, for instance, in alternately laid biaxial knitted fabrics and can clearly be seen in the top of Fig. 15.26 for the warp yarn layer. For knitted fabrics with a double loop yarn system, the structure of the textile prevents superposition, from which follows that ξ _We  = ξ _Wa  = 1. The factors ξ _We and ξ _Wa depend extensively on the compression of the knitted fabric layers in thickness direction. For this reason, analytical solutions on a purely geometrical basis do not give satisfying results.

For an analytical approximation of the effective mechanical properties of the fiber/matrix areas in the composite, the respective fiber volume fraction has to be known. It can be determined by φ :=A ^f /A, if this domain is considered as a UD composite. The total cross-section area A can be determined from the Eq. (15.25) for the warp and weft yarns. The fiber cross-section area A ^f is calculated from the yarn fineness T _t and the thickness of the textile material ρ, as A ^f = T _t /ρ.

The coordinate Ζ _K of the warp yarn axis results from the equation

$$ {z}_K=\frac{{\left(\frac{D_K}{2}\right)}^2+{d}_K^2}{2{d}_K}-\frac{D_K^3}{12{A}_K}, $$

derived from the circle radius und the distance of the centroid to the center of the circle. With the thicknesses d _Wa and d _We , all other Ζ coordinates of the reinforcement layers can be determined. For this example considered here it follow,

$$ {z}_S={d}_K+\frac{1}{2}{d}_S. $$

15.4.2.1.2 Loop Yarn System Geometry

The loop yarn is represented strongly abstracted, with due regard to the geometrical resolution on the meso-level, and as shown in Fig. 15.31. The actual geometry of the cross-section area of the loop yarns is very variable locally. Due to the relatively small diameter, the cross-section can be simplified into a circle. To calculate the area A _L , it is also assumed that the fiber volume fraction of the loop yarn ${\varphi}_L={A}_L^f/{A}_{\mathrm{L}}$ matches the averaged value of warp and weft yarns. Therefore, the diameter can be determined by ${d}_L=2\sqrt{\frac{AL}{\uppi}}$. With the yarn diameter, the y and z coordinates of the loop yarn in the area of the warp yarn enclosure are known.

The geometry of the top area is largely determined by the radius R _L of the stitch loop. This radius can be measured in its projection onto the x-y plane as R _L in the microscopic and scan views. Since the stitch, as visible in the CT scans, is inclined downwards, it is assumed that the center is placed at height of the weft yarn axis z _We . The coordinate of the loop section in thickness direction (which is regarded as plane) can be determined with ${z}_L={z}_{We}+\frac{1}{2}{d}_{We}$. Thus, the stitch radius can be calculated from the projection radius and the z coordinates by means of

$$ {R}_M=\sqrt{{\tilde{R}}_M^2+{\left({z}_M-{z}_S\right)}^2} $$

As the center of the stitch loops (as in Fig. 15.26) is touching the weft yarn,

$$ {x}_R={l}_K-\frac{1}{2}\left({D}_S+{d}_M+2{\tilde{R}}_M\right). $$

applies to the x coordinate of the center of the circular arc. Value a ₁ describes the y distance of the contact point between the downward running loop yarns and the stitch loop (Fig. 15.31). With due regard to the yarn layer orientation, this distance can be estimated with a ₁ = l _We  − D _Wa  − 2d _L . From the intersection point of the stitch loop arc with the coordinate y = a ₁ /2 follows the equation

$$ {x}_M={x}_R+\sqrt{{\tilde{R}}^2-{\left(\frac{a_1}{2}\right)}^2} $$

With the help of the theorem of intersecting lines, the equation for the calculation of the distance a ₂ can be derived:

$$ {a}_2=\frac{l_K-{x}_M}{l_K-{x}_M+{x}_R}\left(2\tilde{R}-{a}_1\right)+{a}_1. $$

With these previously mentioned equations, the spatial geometry of the loop yarn can be described entirely.

The mentioned analyses for the determination of specific geometrical values of the MLG can be transferred analogically to other MLGs, if attention is paid to possibly varying number of warp and weft yarn systems, for instance. Furthermore, the equations can be adjusted to determine the geometry of similar textiles such as woven multiaxial non-crimp or knitted fabrics.

15.4.2.2 Finite Element Modeling with the Binary Model

15.4.2.2.1 Concept and Numerical Implementation of the Binary Model

The Binary Model was developed for the efficient modeling of textile-reinforced composites [67–69], and is used in a multitude of simulations for static, thermal, and dynamic problems [70, 71].

The central characteristic of the binary model is the separation of the mechanical composite properties. This principle is based on great differences in stiffness between the reinforcement fibers and the matrix material. In the case of the composite examined here, the Young’s modulus of the glass fibers is 25 times higher than that of the resin.

Figure 15.32 gives a schematic representation of the Binary Model for a biaxial fiber composite regarding the meso-level.

Fig. 15.32

Binary model of a biaxial fiber composite

Here, the axial stiffnesses of the fiber/matrix bundles are replaced with tows. The so-called effective medium represents all remaining properties of matrix and yarn material. In the case of a purely mechanical model, these include the Poisson’s effect as well as shear and normal stiffness of the matrix material.

With the transfer of this observation to the FE modeling, the axial stiffnesses are replaced with two-noded line elements, and the effective medium with eight-noded volume elements. The latter take up the entire space of the considered component domain. The element geometry does not have to be adjusted to the interface between matrix and yarn, as is required for a conventional FE-mesh. Therefore the shape of the elements can always match that of a cuboid, which benefits convergence and precision of the solutions.

The locations of the line elements therefore represent the center of gravity line of the respective yarn cross-section. Suitable constraints are to be used to ensure continuity of the displacement field of the superimposed volume and line elements. For this, the two following possibilities have to be distinguished.

If a node of the line elements occupies the same place as a node of the volume element, both can be replaced by a shared node.

If, as in Fig. 15.32, the direction and location of the line elements are identical to the edges of the volume elements, the node positions of line and volume elements can always be correlated.

For irregular geometries as those of the loop yarn, extensive efforts would be required to match the positions of the respective volume element with those of line elements. Therefore, a second case will be taken into account, in which the line element nodes, as shown in Fig. 15.33, can be placed in any desired location within the volume elements. For this, the continuity of the displacement field is ensured by eliminating the degrees of freedom of the node of the beam element i, here designated generally as {û}^(T). The displacement constraints between {û}^(T) and the degrees of freedom of the volume elements {û}^(EM) can be described in the equations

Fig. 15.33

Local volume element coordinates of a line element node

$$ {\left\{{\widehat{\mathbf{u}}}^i\right\}}^{(T)}=\sum_{I=1}^8\left[\begin{array}{lll}{N}_I\left({\upxi}^t\right)\hfill & 0\hfill & 0\hfill \\ {}0\hfill & {N}_I\left({\upxi}^t\right)\hfill & 0\hfill \\ {}0\hfill & 0\hfill & {N}_I\left({\upxi}^t\right)\hfill \end{array}\right]\kern0.5em {\left\{{\widehat{\mathbf{u}}}^I\right\}}^{(EM)}=:\left[{\mathbf{T}}^i\right]\;{\left\{\widehat{\mathbf{u}}\right\}}^{(EM)} $$

(15.28)

where N _I are the eight shape functions of the volume element, and ξ ^t are the local coordinates of the volume element of the line node (Fig. 15.33).

With the matrix [T ⁱ] thus determined, the constraints can be implemented as described in [72]. The number of degrees of freedom of the FE Binary Model is therefore exclusively determined by the number of volume element nodes. The FE mesh of the volume elements and the structure of the line elements of the RVE with two alternatively placed biaxial weft-knitted fabrics are given as an example of the Binary Model in Fig. 15.34.

Fig. 15.34

Binary model of the RVE with MLG reinforcement, (a) FE mesh of the volume elements, (b) Structure of the line elements

The evaluated biaxial weft-knitted fabric and the employed geometry match the example analyzed in Sect. 15.4. This FE model requires 3,927 degrees of freedom. A similar conventional FE model describing just the structure of the warp and weft yarns with volume elements only needs circa 18,200 degrees of freedom. This comparison clarifies the efficiency of the Binary Model concerning the numerical efforts. The meshing of the loop structure based on volume elements also entails considerable modeling efforts. For this reason, the mesh has to be refined significantly, which in turn further increases the number of degrees of freedom of the equation system.

The geometrical abstraction of the binary model requires a derivation of the constitutive equations which are then assigned to the line and volume elements. According to the statements of XU et al. [68], an elastic material behavior is detailed below.

15.4.2.2.2 Constitutive Equations of the Effective Medium

The mechanical properties of the effective medium for a biaxial reinforcement can be derived from the effective properties of the UD composite. These can be calculated by means of homogenizing a UD model according to Sect. 15.4.1 or by analytical approximation (see [73]). For reasons of differentiation, all values of the UD composite or of the effective medium will be designated by a superscript (UD) or (EM) respectively. Beyond that, the fiber volume fraction φ^(EM) is defined as the relation of the volumes of fiber reinforcement and RVE. The fiber orientation in the UD composite matches the x ₁ direction. The following indices of the values of the effective medium are based on the coordinate system given in Fig. 15.32.

When applying specific UD values to the characteristics of the effective medium, it is assumed that the transverse stiffness of the fiber matrix bundle significantly influences the Young’s modulus E ^(EM)₃ in thickness direction. For lateral contractions and shear moduli of the effective medium, an estimation with v ^(UD)₁₂ or G ^(UD)₁₂ respectively, is the obvious choice [68]. The remaining Young’s moduli regarding the composite planes E ^(EM)₁ and E ^(EM)₂ can be calculated from shear modulus and lateral contraction, based on a transversal isotropy where fibers are aligned with the x ₃ axis. The material properties of the linear-elastic effective medium can be summarized as:

$$ \begin{array}{l}{G}_{23}^{(EM)}={G}_{13}^{(EM)}={G}_{12}^{(EM)}={G}_{12}^{(UD)},\\ {}{v}_{23}^{(EM)}\kern1em ={v}_{13}^{(EM)}\kern1em ={v}_{12}^{(EM)}={v}_{12}^{(UD)},\\ {}\kern6em {E}_3^{(EM)}\kern1em ={E}_2^{(UD)}\kern1em \mathrm{and}\\ {}\kern3em {E}_1^{(EM)}={E}_2^{(EM)}=2\left(1+{v}_{12}^{(EM)}\right){G}_{12}^{(EM)}.\end{array} $$

(15.29)

This elastic behavior only deviates from an isotropic material because of the different Young’s moduli. As stiffnesses in textile composite are primarily determined by the reinforcement yarns, the identities of ${E}_1^{(EM)}={E}_2^{(EM)}={E}_2^{(UD)}$ can be simplifyingly assumed, as in [68]. From this follows an isotropic behavior of the effective medium.

The reinforcement architecture of MLG composites differs from that of the previously considered biaxial composite in terms of the loop structure. As the loop structure only makes up 4–14 % of the total textile mass, the structural influence on the properties of the effective medium can be neglected. The volume of the loop yarn is only taken into account for the calculation of φ^(EM).

15.4.2.2.3 Constitutive Equations of the Lines

As described in this section, the line elements in the Binary Model represent the axial stiffnesses of the filaments consolidated with matrix material in the composite material. The rovings used for warp and weft yarns do not contain twisted filament fibers. As visible from Fig. 15.26, the respective orientations of the filaments and the rovings match well, which allows the treatment of these fiber/matrix areas as a UD composite.

If the loop yarn consists of a twisted glass yarn, there are limitations to treating it as UD. But as the fiber volume content ratio of the loop yarn is relatively low in the composite, the mechanical influence of the twisted filament arrangement can be neglected. Therefore, the area of the loop yarn in the consolidated MLG can be simplistically modeled as a UD composite.

For the following derivations for a description of effective properties of the line elements, the components of the UD composites (in this case glass and epoxy resin) are treated as continua.

The elastic stiffness of the line elements can be determined analogously to the effective medium, using an analytical UD model. In consequence, the resulting Young’s modulus in orientation of the line element matches the value E ^(UD)₁ (φ) calculated from the fiber volume content ratio φ of the fiber-matrix area and the material properties of fiber and matrix.

In the FE model, line and volume elements are superimposed. This corresponds to a parallel arrangement of the axial stiffnesses of both elements. To prevent a multiple consideration of the contribution of the elastic stiffness of the matrix material, the Young’s modulus of the line element E ^{(T )} is set according to the equation

$$ \begin{array}{lll}{E}_{\beta}^{(T)}={E}_1^{(UD)}\left({\varphi}_{\beta}\right)={E}_{axial}^{(EM)}\hfill & \mathrm{with}\hfill & \beta \in \left\{\mathrm{K},\mathrm{S},\mathrm{M}\right\}\hfill \end{array} $$

(15.30)

The index β describes the relation to the respective warp, weft, and loop yarn, while E ^(EM) _axial matches the stiffness of the effective medium in the orientation of the line element.

To calculate E ^(EM) _axial , the strain state of the line element is transferred on the allocated volume element. With this, the desired value can be numerically calculated using

$$ {E}_{axial}^{(EM)}={\left\{{\varepsilon}^{-t}\right\}}^T\left[{\mathbf{C}}^{(EM)}\right]\kern0.5em \left\{{\varepsilon}^{-t}\right\} $$

(15.31)

where the vector $\left\{{\varepsilon}^{-\mathrm{t}}\right\}$ corresponds to a unit strain in orientation with the line, and the matrix [C ^(EM)] matches the material stiffness of the effective medium. In the case of an FE simulation with an elastic-plastic material law for the effective medium, the matrix in Eq. (15.31) is to be replaced with the respective consistent tangent stiffness.

15.5 Material Properties of Composite Materials, Exemplified by Multi-layered Weft-Knitted Fabrics

15.5.1 Experimental Examinations

The aim of experimental examinations of composite materials with textile reinforcement usually consists of the general study of material behavior with due regard to various material behaviors at different length scales and the quantification of effective in-plane material properties. These can be used directly, or in the calculation of structural models from the corresponding composite material, or as the basis for validation of simulation and modeling methods. Furthermore, the evaluation of tests performed on pure-resin test specimens can provide the material properties for the micro and meso models of Sect. 15.4.2.

In contrast to many monolithic materials, the properties of continuous-fiber-reinforced composites are strongly anisotropic and dependent on the type of load. In comparison to the first mentioned group of materials, this requires a significantly larger test effort for a thorough and complete experimental analysis. In general, the anisotropic properties can be examined in tensile, compression, flexural, and shear tests. In the following, these tests and the related evaluations will be considered in greater detail.

15.5.1.1 Tensile and Compression Tests

As described in Sect. 14.6.2.1, tensile and compression tests are used to examine the behavior of a material under monaxial tensile and compressive loads. The anisotropic material behavior requires an evaluation of data sets of specimens with different textile orientations. For an orthotropic behavior, tests with three different directions, e.g. 0°, 45°, and 90°, are required to determine the specific elastic in-plane values. Examinations of specimens with additional textile orientations allow a validation of the assumption of orthotropic behavior.

The experimental test method for the compression behavior is to be selected under consideration of the composite thickness d and of the regarded load spectrum. In case of risk of buckling on the specimen, a buckle support (as shown in Fig. 15.35a) needs to be used.

Fig. 15.35

Experimental devices for compression testing, (a) buckle support for thin specimens, (b) compression die for thick specimens

As discussed in Sect. 14.6.2.2, sufficiently thick composite materials can be clamped directly into the clamping jaws of the testing machine, or fixated between two compression dies, as shown in Fig. 15.35.

Measured data are generally recorded by the control computer of the testing machine. The force and traverse path can be measured by dedicated devices integrated in the tester. Strains on the specimen surface can be measured by means of strain gages. In comparison to monolithic material, strain gages have to be much longer for measurements on composite materials [74]. Unfortunately, the use of these longer strain gages is much more costly. Laser extensometers are an alternative for the determination of transverse strain. For this, two measuring markers are affixed to the specimen, and their distance is registered by a laser beam during the entire test. The control program uses these measurements to calculate the nominal strain, which is to be interpreted as an integral quantity over the area between the measuring markers. Another measurement possibility is simultaneously determining the deformation field of the opposite specimen surface with ARAMIS (by GOM GmbH, Braunschweig, Germany). This allows a simultaneous measurement of longitudinal and transverse strains, and the examination of bending deformations. A corresponding test setup is shown in Fig. 15.36.

Fig. 15.36

Tensile test with parallel measuring by ARAMIS and laser extensometer

For exemplary purposes, Fig. 15.37 compares three typical stress-strain plots from tensile test in 0°, 45°, and 90° direction with specimens made from a biaxial MLG composite material.

Fig. 15.37

Stress-strain diagram of tensile tests in 0°, 45°, and 90° directions on an MLG composite material

It is to be expected from the reinforcement architecture that the composite displays a substantially higher stiffness in the direction of the reinforcement fibers as compared to the 45° direction. The tests also prove the curve section, which can be correlated with the linear-elastic area, to be greater in the principal material axis. Furthermore, the curve section delineates itself from the subsequent inelastic behavior by the dropping of the plot. From the initially linear slope of the stress-strain curves, the Young’s modulus E ^(α) is to be determined for each test with textile orientation α. The Poisson’s ratio v ^(α) is determined from the slope ε _q (ε _l ), where ε _q and ε _l are the transverse and longitudinal strains. From these engineering properties, the components of the compliance tensor are calculated by means of

$$ \begin{array}{ccc}\hfill {S}_{11}^{\left(\alpha \right)}=\frac{1}{E^{\left(\alpha \right)}}\hfill & \hfill \mathrm{and}\hfill & \hfill {S}_{12}^{\left(\alpha \right)}=\frac{v^{\left(\alpha \right)}}{E^{\left(\alpha \right)}}\hfill \end{array} $$

(15.32)

For q experimental tests on specimens with different angles α _i (i = 1, … q) of textile orientation, these results can be related to the components of the compliance tensor S _xx, S _yy , and S _ss in the main axis system x-y, where Sss designates the shear compliance. Assuming orthotropic material behavior, the following system of equations results:

$$ \left[\begin{array}{llll}{m}_1^4\hfill & {n}_1^4\hfill & 2{m}_1^2{n}_1^2\hfill & {m}_1^2{n}_1^2\hfill \\ {}{m}_2^4\hfill & {n}_2^4\hfill & 2{m}_2^2{n}_2^2\hfill & {m}_2^2{n}_2^2\hfill \\ {}\vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {}{m}_q^4\hfill & {n}_q^4\hfill & 2{m}_q^2{n}_q^2\hfill & {m}_q^2{n}_q^2\hfill \\ {}{m}_1^2{n}_1^2\hfill & {m}_1^2{n}_1^2\hfill & {m}_1^4+{n}_1^4\hfill & -{m}_1^2{n}_1^2\hfill \\ {}\vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {}{m}_q^2{n}_q^2\hfill & {m}_q^2{n}_q^2\hfill & {m}_q^4+{n}_q^4\hfill & -{m}_q^2{n}_q^2\hfill \end{array}\right]\left(\begin{array}{l}{S}_{xx}\hfill \\ {}{S}_{yy}\hfill \\ {}{S}_{xy}\hfill \\ {}{S}_{ss}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {S}_{11}^{\left({\alpha}_1\right)}\hfill \\ {}\hfill {S}_{11}^{\left({\alpha}_2\right)}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {S}_{11}^{\left({\alpha}_q\right)}\hfill \\ {}\hfill {S}_{12}^{\left({\alpha}_1\right)}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {S}_{12}^{\left({\alpha}_q\right)}\hfill \end{array}\right), $$

(15.33)

Here, m _i := cos(α _i ) and n _i := sin(α _i ). If the number of tests and therefore of results to be analyzed is more than four, the equation system (15.33) is overdetermined, and the solution of the unknown components of the compliance tensor can be determined by means of a regression calculation, for instance in MATLAB.

15.5.1.2 Flexural Tests

The behavior of composite materials under flexural loads can deviate significantly from tensile or compressive loads. This is due to the structural design of the composite in thickness direction [50]. Therefore, an experimental examination of the flexural stiffness is necessary, especially for thinner composite plates.

A great number of different construction methods are available for the flexural test device. In addition to the deliberation regarding tests based on standards in Sect. 14.6.2.3, a distinction can be drawn between devices with horizontal or vertical specimen arrangement and devices with the possibility to apply alternating flexural loads. To examine the behavior of materials under alternative flexural loads, the Institute of Solid Mechanics at TU Dresden developed a horizontal device with four-point bearing. As shown in Fig. 15.38, the specimen is mounted between two fixed and two mobile rollers.

Fig. 15.38

Horizontal alternating flexural load device

The carriers of the roller pairs have an internal distance l _b , and are pivoted in order to avoid a prevention of flexural deformation. Mobile rollers, which are fixed to the shafts with bearing pins at a distance L _b  > l _b , expose the specimen to the load. The construction of this device allows a variable adjustment of the geometry values l _b and L _b .

Suitable sensors on the test station record data of the path and force measurement from the control computer. Additionally, the spatial displacement of the specimen surface is determined by the ARAMIS measuring system. Using the displacement field shown for 0° and 45° directions in Fig. 15.39, the lateral contraction of the composite material can be determined [50].

Fig. 15.39

Color-coded representation of the displacement u _z of the specimen surface of a composite with MLG reinforcement, (a) textile orientation 0°, (b) textile orientation 45°

Assuming a linear stress plot across the thickness of the composite (regarded as homogeneous), the measured strains ε_b on the surface allow a determination of the plots σ _b (ε _b ) of the flexural stress. The slope of the initially linear curve is referred to as flexural Young’s modulus E ^(α) _b for the textile orientation α. A comparison of the tensile and flexural Young’s modulus in the composite plane of an MLG composite is shown in the polar diagram of Fig. 15.40.

Fig. 15.40

Young’s modulus in the composite plane, from tensile and flexural test on a MLG composite

An excellent match of the results in 45° direction is evident. In comparison, the Young’s modulus at 0° is higher (and lower at 90°, respectively) than the values from the tensile tests. This effect is caused by an inhomogeneous loading under flexure, and by the construction of the reinforcement structure. For instance, the specimens with a 90° orientation are exposed to a flexural load around 0°. Here, the absolute flexural stress increases towards the specimen surface starting at the mid-surface plane. In this direction, there is no reinforcement in the sections close to the surface. By contrast, the weft yarns situated on the outer edges of the layer construction cause a higher resistance against the deformation when bent by 90°. The location of the reinforcement yarns in thickness direction is irrelevant for stiffness under pure tensile loads.

15.5.1.3 Shear Tests

A variety of different testing and loading devices for an experimental examination of the composite behavior under pure shear loads are available (see Sect. 14.6.2.4). As described in [75], testing with a shear frame is distinguished by a number of advantages over alternative methods. Figure 15.41 shows one such device, dimensioned based on DIN 53399-2. By means of applied cap strips, a homogeneous load introduction is ensured. Analogous to the tensile tests, the laser extensometer or ARAMIS can be used for measuring the deformation on the respectively opposite side of the specimen.

Fig. 15.41

Test setup and measuring devices of the shear test

The macroscopic shear stress τ is calculated with the equation

$$ \tau =\frac{\sqrt{2}}{2ld}F, $$

(15.34)

where l is the edge length of the measured surface, and F designates the outer tensile force on the test device. The result of the ARAMS measurements is determining the strain plots in the diagonal directions of the square measured surface. Due to the parallel determination of the vertical strain by means of the laser extensometer, a possible flexure of the specimen can be determined.

The test setup in Fig. 15.41 correlates to the vertical strain of the major strain ε₁ and the horizontal strain of the minor strain ε₂. With due regard to an anisotropic deformation, the shear strain γ results from [76]

$$ \upgamma =\frac{\varepsilon_1-{\varepsilon}_2}{1+{\varepsilon}_1+{\varepsilon}_2}. $$

(15.35)

Figure 15.42 shows the distribution of the major strain determined by ARAMIS. Except for local inhomogeneities, the homogeneous strain distribution is not disturbed by boundary effects caused by the load transmission into the specimen.

Fig. 15.42

Distribution of the major strain in the shear test on a MLG composite

The plane shear modulus G _xy of the tested composite can be determined from the initial slope of the curve plot τ(γ). A comparison with the results of the tensile test allows the verification of the consistency of the results of both experiments.

15.5.2 Homogenization on the Basis of the Energy Criterion

15.5.2.1 Basics of Homogenization

For efficiency reasons, the modeling of the meso and micro structures is not a sensible option in the computer-assisted simulation of load and deformation states of macroscopic components. Therefore, the heterogeneous material for these calculations is created by a homogeneous continuum. The material parameters in the constitutive equations of the substitute continuum, which are here also referred to as effective material properties, can generally be determined by experiments. Due to the macroscopically anisotropic material behavior and the resulting multitude of specific values, this requires extensive efforts. In addition, every alteration of the reinforcement architecture or the material of the composite components makes new experiments necessary. To avoid this effort, the effective properties can be calculated using homogenization methods.

In this section, the heterogeneous micro- as well as the homogeneous macro-level are considered exemplarily for a multi-scale analysis at different length scales. On the macro-level, the characteristic length L can be defined as the maximum distance of two points in a homogeneous body Ω with

$$ L=\underset{{\mathbf{X}}_1,{\mathbf{X}}_2\in \varOmega }{ \max}\left|{\mathbf{X}}_1-{\mathbf{X}}_2\right| $$

(15.36)

Analogously, l describes a characteristic length of the micro structure. One essential basis of many homogenization methods is the concept of a representative volume element (RVE). For this, a partial area $Y=\left\{\mathbf{y}={y}^i{\mathbf{e}}_i,\left|{y}^i\right|<\frac{a}{2}\right\}$ on the micro-level is selected, which completely represents the macro-level characteristics of the material from a statistical point of view. This partial area is referred to as a representative volume element. For composite materials with a periodic micro-structure the RVE can also be defined as a unit cell, as shown in Fig. 15.43.

Fig. 15.43

Macro- and meso-level

Using the previously introduced characteristic lengths, general conditions for using homogenization methods and definitions of the RVE can be stated. If both the RVE and the substitute continuum are described within in a CAUCHY continuum, the condition

$$ L\gg a\gg l $$

(15.37)

must be met [50]. If this cannot be ensured, an extended theory, such as the COSSERAT continuum, must be used to consider the macroscopic body. Otherwise, the prerequisites for the consideration of the heterogeneous body using a homogeneous continuum are not met, making it incorrect.

In the following, it is agreed that all variables with capital letters are defined in relation with the macro-continuum, while lowercase letters refer to the micro-continuum. The basic element of homogenization within the scope of the energy criterion consists of a coupling between micro- and meso-level. The static equilibrium on micro-level, neglecting volume forces, can be stated with the equations

$$ \begin{array}{ccc}\hfill \nabla \times \sigma =0\hfill & \hfill \mathrm{and}\hfill & \hfill \sigma ={\sigma}^T\mathrm{in}Y\hfill \end{array} $$

(15.38)

where ∇ is the gradient operator, and σ is the CAUCHY-stress tensor. The constitutive equations

$$ \begin{array}{ccc}\hfill {\sigma}^n\left(\uptau \right)={\mathrm{F}}_{\sigma}^n\left(\varepsilon (t),t\in \left[0,\tau \right]\right)\hfill & \hfill \forall \hfill & \hfill n\in \left\{1\dots N\right\}\hfill \end{array} $$

(15.39)

each describe respective current stress strain relations at the time t for the material component n in a RVE with N materials. The strains ε

$$ \varepsilon \left(\mathbf{y}\right)=sym\left(\mathbf{u}\otimes \nabla \right) $$

(15.40)

are calculated from the displacement filed u(y) of the micro-level.

By means of the volume average, the specific values from micro- and macro-level are coupled, resulting in the equations

$$ \sum :=\frac{1}{\left|Y\right|}{\displaystyle {\int}_{\partial Y}\mathbf{y}\otimes \mathbf{t}\;dA}\kern1em \mathrm{with}\kern1em \mathbf{t}:{\sigma}^T\cdotp \mathbf{n} $$

(15.41)

for the macroscopic tension Σ and

$$ \mathbf{E}:\frac{1}{\left|Y\right|}{\displaystyle {\int}_{\partial Y}sym\left(\mathbf{u}\otimes \mathbf{n}\right)\;dA} $$

(15.42)

for the macroscopic strain E. Equations (15.41) and (15.42) show that macroscopic state variables are described unambiguously by the stress or strain vector t and u on the surface ∂Y of the RVE.

A calculation of effective stresses and strains based on Eqs. (15.38)–(15.42) is referred to as homogenization. The macroscopic material properties C then describe the linear transformation between these fields by

$$ \begin{array}{ccc}\hfill \left\langle \sigma \left(\mathbf{y}\right)\right\rangle =\mathbf{C}:\left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle \hfill & \hfill \mathrm{with}\hfill & \hfill \left\langle \cdots \right\rangle :=\frac{1}{\left|Y\right|}{\displaystyle {\int}_Y\left(\cdots \right)d\mathbf{y}}\hfill \end{array}. $$

(15.43)

The inverse problem, i.e. the determination of the microscopic variables with defined macroscopic variables, is referred to as localization. As there are not boundary conditions for this case, the problem is yet only incompletely formulated. The definition of these boundary conditions aims to reproduce the state of the material within the respective area as precisely as possible. Below, a summary is given of the derivation of three types of boundary conditions, based on an energy criterion.

The energy theorem according to [77], also known as HILL-MANDEL condition, requires energy equivalence of the heterogeneous micro-continuum and the homogeneous equivalent continuum. From this follow the equations

$$ \begin{array}{c}\hfill \left\langle \varepsilon \left(\mathbf{y}\right):\mathbf{c}\left(\mathbf{y}\right):\delta \varepsilon \left(\mathbf{y}\right)\right\rangle =\left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle :\mathbf{C}:\left\langle \delta \varepsilon \left(\mathbf{y}\right)\right\rangle \hfill \\ {}\hfill \frac{1}{\left|Y\right|}{\displaystyle {\int}_{\partial Y}\mathbf{t}\cdotp \delta \mathbf{u}\kern0.5em dA=}\sum :\delta \mathbf{E},\hfill \end{array} $$

(15.44)

where δ is the variation operator.

If the strain fluctuation is defined as the deviation of the field from the mean value,

$$ \overset{\check{}}{\varepsilon}\left(\mathbf{y}\right):=\varepsilon \left(\mathbf{y}\right)-\left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle . $$

applies.

The positive definition of the elasticity tensor c is ensured if

$$ \overset{\check{}}{\varepsilon}\left(\mathbf{y}\right):=\mathbf{c}\left(\mathbf{y}\right):\overset{\check{}}{\varepsilon}\left(\mathbf{y}\right)\ge 0 $$

(15.45)

applies to the quadratic form. This relationship can be combined with Eqs. (15.43) and (15.44) as

$$ \left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle :\left(\left\langle \mathbf{c}\left(\mathbf{y}\right)\right\rangle -\mathbf{C}\right):\left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle \ge 0 $$

(15.46)

The quadratic form of the average volume of c is therefore higher than that of the effective elasticity tensor C and represents an upper bound, also referred to as VOIGT bound. Analogously, these considerations, in combination with complementary energy, i.e. the quadratic form of the compliance tensor s := c ⁻¹ lead to the REUSS bound, which correlates to a bottom bound.

$$ \left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle :\left(\left\langle \mathbf{c}\left(\mathbf{y}\right)\right\rangle -\mathbf{C}\right):\left\langle \varepsilon \left(\mathbf{y}\right)\right\rangle \ge 0 $$

To determine these bounds, the microscopic strain or stress fields are constantly defined by

$$ \varepsilon \left(\mathbf{y}\right):=\left\langle \varepsilon \right\rangle /\sigma \left(\mathbf{y}\right):=\left\langle \sigma \right\rangle $$

from which follow the definitions

$$ \begin{array}{cc}\hfill {\mathbf{C}}^V:=\left\langle \mathbf{c}\right\rangle \hfill & \hfill \mathrm{and}\hfill \end{array} $$

(15.47a)

$$ {\mathbf{C}}^R:={\left\langle {\mathbf{c}}^{-1}\right\rangle}^{-1} $$

(15.47b)

as VOIGT and REUSS bounds for the effective elasticity tensor C.

By specifying a constant strain or stress field respectively, the mechanical equilibrium or the compatibility conditions is generally infringed. As the microscopic stresses and strains in Eqs. (15.41) and (15.42) are unambiguously defined by the corresponding boundary conditions, the question of boundary conditions fulfilling the HILL-MANDEL condition arises Eq. (15.44). The three following statements fulfill this condition:

1. The specification of u on the surface of the RVE by

$$ \begin{array}{ccc}\hfill \mathbf{u}\left(\mathbf{y}\right)=\mathbf{E}\cdotp \mathbf{y}\hfill & \hfill \forall \hfill & \hfill \mathbf{y}\in \partial Y\hfill \end{array} $$

(15.48)

matches displacements which are linear in y.

2. Analogously, constant surface stresses can be defined with

$$ \begin{array}{ccc}\hfill \mathbf{t}\left(\mathbf{y}\right)=\sum \cdotp \mathbf{n}\left(\mathbf{y}\right)\hfill & \hfill \forall \hfill & \hfill \mathbf{y}\in \partial Y\hfill \end{array} $$

(15.49)

3. The validity of periodic boundary displacements and anti-periodic stress vectors

$$ \mathrm{u}\left({\mathrm{y}}^{+}\right)-\mathrm{u}\left({\mathrm{y}}^{-}\right)=\mathrm{E}\cdotp \left({\mathrm{y}}^{+}-{\mathrm{y}}^{-}\right) $$

(15.50a)

$$ \mathrm{t}\left({\mathrm{y}}^{+}\right)=-\mathrm{t}\left({\mathrm{y}}^{-}\right) $$

(15.50b)

is based on a periodic microstructure in the unit cell.

y ⁺ ∈ ∂Y ⁺ and y ⁻ ∈ ∂Y ⁻ define the coordinates of two points, which are associated according to periodic geometry on the opposite surfaces ∂Y ⁻ and ∂Y ⁺ of the RVE (Fig. 15.44).

Fig. 15.44

RVE with three associated surface pairs

In a heterogeneous continuum, the three types of boundary conditions have different results. In general, and comparable to the VOIGT and REUSS approaches, the behavior of an RVE is stiffer for linear boundary displacements, and more flexible for constant boundary stresses in comparison to periodic boundary displacements. For many materials, it has been shown that periodic boundary conditions create the best results by comparison [78]. Therefore, the following considerations will be reduced to this form.

15.5.2.2 Introduction of Generalized Variables

To transfer the periodic displacement boundary conditions (15.50a) to an FE model representing the unit cell, the following generalized variables will be introduced below. They are also prerequisites for an efficient evaluation of the simulation results, e.g. for the calculation of the effective properties or tangent stiffnesses.

When considering any unit cell, for instance as shown in Fig. 15.44, the surface can be segmented into respectively associated lateral surfaces α ∈ {1, 2, 3}. These surfaces dY ^α+ and dY ^α− have to be compatible for the purpose of periodicity. Thus, the difference of the spatial coordinates in Eq. (15.50a) is constant for each surface pair α and can be expressed with the definition

$$ \begin{array}{ccc}\hfill \varDelta {\mathbf{y}}^{\alpha }:={\mathbf{y}}^{\alpha +}-{\mathbf{y}}^{\alpha -}\hfill & \hfill \forall \hfill & \hfill \alpha \in \left\{1,2,3\right\}\hfill \end{array} $$

(15.51)

With this equation and the introduction of a generalized displacement increment Δu ^α, Eq. (15.50a) can be described by

$$ \varDelta {\mathbf{u}}^{\alpha }:=\mathbf{u}\left({\mathbf{y}}^{\alpha +}\right)-\mathbf{u}\left({\mathbf{y}}^{\alpha -}\right)=\mathbf{E}:\varDelta {\mathbf{y}}^{\alpha } $$

(15.52)

The complete formulation of a spatial or plane boundary value problem (BVP) therefore requires the specification of nine or four generalized displacement increments respectively.

Analogously to the displacements, generalized forces in the form of

$$ {\mathbf{F}}^{\alpha }:={\displaystyle {\int}_{\partial {Y}^{\alpha +}}{\mathbf{t}}^{+}dA} $$

(15.53)

are added, making the homogenized stress Eq. (15.41) calculable with

$$ {\displaystyle \sum =\frac{1}{\left|Y\right|}{\displaystyle \sum_{\alpha}\varDelta {\mathbf{y}}^{\alpha }}\otimes {\mathbf{F}}^{\alpha }} $$

(15.54)

A comparison of this equation to the previous integral equation (15.41) clarifies the significantly reduced effort regarding a numerical realization made possible by the introduction of generalized variables.

To determine the effective linear-elastic stiffness tensor C, six different macroscopically homogeneous deformation states have to be considered, for which the strain tensor E is specified by

$$ {E}_{ij}={E}_{ji}=\left\{\begin{array}{ccc}\hfill 1\hfill & \hfill \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \hfill i=I,j=J\hfill \\ {}\hfill 0\hfill & \hfill \mathrm{otherwise}\hfill & \hfill \hfill \end{array}\right. $$

(15.55)

Table 15.2 contains a possible assignment for the indices I and J.

Table 15.2 Assignment for the Indices I and J in Eq. (15.55)

With the displacement boundary conditions (15.52) and the solution of the BVP, the generalized forces F ^α (E _IJ ) at averaged strain can be calculated. Thus, the macroscopic stresses in Eq. (15.54) are equivalent to the material stiffnesses induced by the deformation, and

$$ {\displaystyle {\sum}_{kl}\left({E}_{IJ}\right)}={C}_{kl IJ}{E}_{(IJ)}=\frac{1}{\left|Y\right|}{\displaystyle \sum_{\alpha}\varDelta {y}_k^{\alpha }{F}_l^{\alpha}\left({E}_{IJ}\right)} $$

(15.56)

applies, where no summation convention is applied to bracketed indices.

15.5.2.3 Homogenization in the Macroscopic In-plane or Monaxial Stress State

From a macroscopic perspective, any heterogenic materials, such as the textile composite considered here, can be regarded as shell structures within the scope of a plane stress condition (PSC), giving rise to the question of a homogenization method with which the effective mechanical properties of this structural observation can be determined directly. Due to the distinct three-dimensional architecture in the textile composite, homogenization is required to ensure the transfer from a spatially heterogeneous RVE onto a homogeneous, plane structure.

In the PSC, Σ _i3  = 0 applies, with the coordinate direction X ₃ concurs with the normal vector of the shell mid-surface. Therefore, constant surface tensions are specified on the shells surface according to the abovementioned second kind of boundary conditions. From this follows

$$ \begin{array}{ccc}\hfill \mathrm{t}\left(\mathrm{y}\right) = 0\hfill & \hfill \forall \hfill & \hfill \mathrm{y}\in \partial {Y}^3\hfill \end{array}. $$

(15.57a)

The transfer of planar macroscopic strains {E _βγ | β, γ ∈ {1, 2}} onto the RVE is then performed by the periodic displacement boundary conditions on the remaining surfaces ∂Y ¹ and ∂Y ², whose normal vectors are tangentially in the shell plane. With Eq. (15.52), these boundary conditions can be described by

$$ \begin{array}{ccc}\hfill \varDelta {\mathbf{u}}^{\alpha }=\mathbf{E}\cdot \varDelta {\mathbf{y}}^{\alpha}\hfill & \hfill \forall \hfill & \hfill \alpha \in \left\{1,2\right\}\hfill \end{array} $$

(15.57b)

As E13 = E23 = 0 applies for macroscopic strains in the context of the PSC, and the vectors Δy¹ and Δy² are located in the y₁ − y₂ plane, the displacement increments are $\varDelta u\frac{1}{3}$ and $\varDelta u\frac{2}{3}=0$.

As the result of the homogenization, the planar stresses Σ_βγ calculated with Eq. (15.54), where summation convention is applied over α ∈ {1, 2}. Additionally, the macroscopic strain E ₃₃ can be calculated with Eq. 15.42.

As a consistent continuation of the consideration regarding the PSC, the boundary conditions for a monaxial stress state can be derived. With the specification of Σ₁₁ as the macroscopic stress (different from zero), the stress vectors

$$ \begin{array}{ccc}\hfill \mathbf{t}\left(\mathbf{y}\right)=\mathbf{0}\hfill & \hfill \forall \hfill & \hfill \mathbf{y}\in \partial {Y}^2\cup {Y}^3\hfill \end{array} $$

(15.58a)

and the displacement increments are

$$ \varDelta {\mathbf{u}}^1={E}_{11}\varDelta {\mathbf{y}}^1 $$

(15.58b)

to be specified on the surface of the RVE. To ensure a completed formulation of boundary conditions in this case, it is important to prevent rigid body translation and rotation along the tensile axis.

15.5.2.4 Example for the Homogenization of a MLG Composite

In the following, an example for the application of the homogenization method applied to a composite with glass fiber MLG and epoxy resin will be considered. Here, the textile reinforcement in the composite consists of two alternatively laid knitted fabrics, whose geometry is analyzed in Sect. 15.4.2.1.

Based on the multi-scale approach, calculating the effective specific material values of a UD composite of the micro-level is the initial step. The corresponding deformation of the unit cell described Sect. 15.4.1 at unit strain E ₁₁  = 1 and unit shear stress Γ ₁₂  = 1 are shown in Fig. 15.45a, b.

Fig. 15.45

Deformation of the UD unit cell, (a) macro-deformation E ₁₁ with color-coded ε₁₁, (b) macro-deformation Γ ₁₂ with color-coded γ ₁₂

With these calculated specific effective elastic values, the constitutive equations of the binary model of the meso-level can be specified according to the description in Sect. 15.4.2.2.

The FE model of the meso-level of this composite is shown in Fig. 15.34 as a binary model. The homogenization within the scope of the plane stress state requires three simulations with specified macroscopic strain. The deformation state E _xx = 1 and Γ _xy  = 1 are shown with the calculated local strain distribution ε _xx and γ _xy respectively in Fig. 15.46.

Fig. 15.46

Deformation of the composite unit cell, (a) macrodeformation E _xx = 1 with color-coded ε _xx (x, y), (b) macrodeformation Γ _xy  = 1 with color-coded γ _xy (x, y)

The color coding of both illustrations shows that strain or shear stress = 1 for large areas of the RVE, corresponding to the macroscopically specified deformation. The local fluctuation occurs only because of the line elements.

The verification of simulation results is performed with experimental data based on engineering constants. For instance, the polar diagram of Fig. 15.47 shows the Young’s modulus of the x − y plane dependent on the angle α.

Fig. 15.47

Polar diagram with experimentally and numerically determined in-plane Young’s modulus

The lines oriented in radial direction mark the scatter ranges of the experimentally determined Young’s moduli. The curve plot of the numerically calculated Young’s moduli is very good prediction of the experimentally determined values. The little differences between simulation and experiment can often be traced to technological causes. For example, slight deformations of the textile during the consolidation process create local variations in the reinforcement architecture. This leads to a minor deviation between the modeled and the real composite geometries on the meso-level.

In summary, it can be stated that the linear-elastic effective properties of the MLG composite can be estimated very well by means of the homogenization method in combination with the binary model. Therefore, this modeling concept is much more efficient in comparison to conventional volume meshing and of equal value with regard to mechanical evaluation criteria.