Surfaces from Curves on Triangular Surfaces in Barycentric Coordinates

Abstract

Barycentric coordinates are coordinates in which a position is provided by a blending of a weighted point set where the weights sum up to 1. Bezier-triangles and ERBS-triangles are typical examples of use of Barycentric coordinates.

We look at the framework for the description of curves on surfaces that are described in Barycentric coordinates and how we define surfaces in a Coons Patch like framework with the use of these curves on surfaces. The framework also includes pre-evaluation and other optimization technics for evaluation.

The background is to construct large complex surfaces. Given a surface constructed by a connected set of non-planar triangular surfaces. If the triangular surfaces are generalized expo-rational B-spline based, constructed by blending of triangular sub-surfaces from Bezier-patches, then the surface is smooth at the vertices but only continuous over the edges between the triangular surfaces. If we introduce a second set of vertices defined by the midpoint of each triangular surface, we can introduce a new set of edges constructed by straight lines from a vertex to the midpoint in the parameter plane of the respective triangular surface. In addition we also have information about the derivatives across these edges. This gives us the data to make a connected and smooth set of surfaces that are strongly connected to the set of triangular surfaces. The triangle based surface is easy to manipulate and reshape and then the smooth dual set of squared surfaces will automatically be updated.

1 Introduction

A BezierLakså, Arne triangle is a surface parameterized with barycentric coordinates with the expression

$$ s(u,v,w) = \sum _{i=0}^{n} c_i\ b_{d,i}(u,v,w) $$

where the coordinates $c_i$ are points that describe a triangular control polygon. The basis functions $b_{d,i}(u,v,w)$ follow from expanding $(u\ v\ w)^d$ where $d$ is the polynomial degree and $n=\sum _{i=1}^{d+1} i$. Bezier triangles and in general splines on triangulation are treated by many authors, see [4, 6].

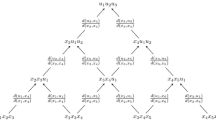
A GERBS triangle is a blending of triangular surfaces (see [2, 5]), i.e.

$$ s(u,v,w) = \sum _{i=1}^3 c_i(u,v,w)\ b_i(u,v,w), $$

where $c_i(u,v,w), i=1,2,3$ are three triangular surfaces and $b_i(u,v,w), i=1,2,3$ are GERBS blending functions for triangular patches. In Fig. 1 we can see a GERBS triangle-surface constructed by blending three Bezier triangles. In the figure the control points that define the Bezier triangles are marked. We can see 6 control points on each Bezier triangle, which indicates that the degree of the Bezier triangles are 2, although the triangles seems to be planar.

A GERBS triangle interpolates the three local triangles in their respective vertices, not only the value but also with all derivatives up to a given order, depending on the choice of blending functions.

Fig. 1.

A GERBS triangular surface, constructed by blending three Bezier triangles of degree 2 (but planar as we can see in the picture).

1.1 Surfaces over Triangular Structures

To make surfaces of all genius, it is convenient to use a set of connected triangular patches. The surface construction using GERBS-blending is as follows:

• 1. Given a point set where for each point is given surface normal and curvature.

• 2. The points must be ordered by a triangulation.

• 3. In each point we create a “local” Bezier-patch from the given surface normal and curvature. Each patch must cover the first neighborhood of points (points that are connected to the central point by an edge).

• 4. Each of these Bezier surfaces are then divided into a series of contiguous triangular faces (sub-triangles). This is done by finding closest point from each of the neighboring points.

• 5. One sub-triangle from each of three neighboring points (the one that is connected to all three points) are then blended together to form one GERBS-triangular surface.

The resulting surface, that is a connected set of triangular surfaces, is smooth on the vertices but unfortunately only continuous over the edges.

To make a smooth surface, we would, related to the set of triangular patches, introducing a dual set of (this time) square patches. First, we introduce an additional set of vertices that are in the middle of each of the triangular patches. So, with the starting point of the two vertices defining an edge and the two new internal vertices in the inner of the corresponding triangular patches, we create a square surface over each internal edge. We use a Coons patch method where we get the needed boundary curves from curves in the triangular patches, i.e. from an original vertex to one new vertex. This can be seen in Fig. 2.

Fig. 2.

The parameter plane of a surface constructed by a connected set of triangular surfaces (bold edges) and the dual set of squared patches over each internal edge.

In Fig. 3 there is an example where we approximate a sphere at six vertices, using four point around equator and one at each poles. The Bezier patches at each vertex is then moved and rotated. We now have six Bezier patches, each connected to a specific vertex. This gives eight GERBS triangular patches that are smooth at the vertices, but only continues over the totally twelve edges that connect the triangular GERBS patches. On left hand side in Fig. 3 this is shown. On right hand side we can see the dual set of twelve squared patches that are covering and smoothing the twelve edges.

Fig. 3.

On left hand side, we see a surface which consist of 8 GERBS triangular patches. The surface is made by approximating a sphere at 6 vertices. The local Bezier patches are then moved and rotated. On right hand side we see the dual set of 12 squared patches. The cubes in the figure are marking the position and orientation of the vertices.

2 Barycentric Coordinates on a Bezier Patch

The domain of a Bezier patch $S(p)$ is $U = [0,1]\times [0,1] \subset \mathbb {R}^2$, commonly using Cartesian coordinates $p=(\mu ,\nu )$.

We define a point set $p_i, i=0,1,...,n$ on $U$ describing a fan of $n$ triangles. Each triangle $\triangle _i, i=1,2,...,n$ is defined by the three points $p_0, p_i, p_{i+1}$ (where $p_{n+1} = p_1$) which is the control polygon to a first degree Bezier triangle. The formula, including the partial derivatives, for $\triangle _i$ in barycentric coordinates is

$$ \begin{aligned} \;\;\;\;\triangle _i(u,v,w)&= S(u p_0+v p_i + w p_{i+1}) , \\ D_u \triangle _i(u,v,w)&= dS_{u p_0+v p_i + w p_{i+1}}(p_0), \\ D_v \triangle _i(u,v,w)&= dS_{u p_0+v p_i + w p_{i+1}}(p_1), \\ D_w \triangle _i(u,v,w)&= dS_{u p_0+v p_i + w p_{i+1}}(p_2), \end{aligned} \quad u+v+w = 1. $$

The second order derivatives follow from that the columns of the matrix $dS$ are the partial derivatives, i.e. $dS = [S_u\ S_v]:\mathbb {R}^2\rightarrow \mathbb {R}^3$,

$$\begin{aligned} ~D_{uu} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_0)\ \ d(S_\nu )(p_0)\right] (p_0),\\ ~D_{uv} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_0)\ \ d(S_\nu )(p_0)\right] (p_i),\\ ~D_{uw} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_0)\ \ d(S_v)(p_0)\right] (p_{i+1}),\\ ~D_{vv} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_i)\ \ d(S_\nu )(p_i)\right] (p_i),\\ ~D_{vw} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_i)\ \ d(S_\nu )(p_i)\right] (p_{i+1}),\\ ~D_{ww} \triangle _i(u,v,w)&=\left[ d(S_\mu )(p_{i+1})\ \ d(S_\nu )(p_{i+1})\right] (p_{i+1}), \end{aligned}$$

where the matrices $dS_{\mu } = \left[ S_{\mu \mu }\ \ S_{\mu \nu } \right]$ and $dS_{\nu } = \left[ S_{\mu \nu }\ \ S_{\nu \nu } \right]$.

If we want more freedom in the local parameterization, we can use second degree Bezier triangles in the domain of the Bezier patches associated with the vertices.

2.1 Transferring Coordinates between Different Barycentric Coordinate System

Given two triangles, $\triangle _1(p_0,p_1,p_2)$ and $\triangle _2(p_0,p_2,p_3)$, in the domain of a Bezier patch and given a point $\bar{p}_a=(\bar{u},\bar{v},\bar{w})$ in barycentric coordinates with respect to triangle $\triangle _1$ (the situation is described in Fig. 4).

Lemma 1

The change of coordinate system to a point $p_a$ in triangle $\triangle _1$ to triangle $\triangle _2$ is: $(\bar{u},\bar{v},\bar{w}) \rightarrow (u,v,w)$, where

$$\begin{aligned} \begin{array}{ll} u &{} = \frac{(p_a-p_3)\wedge (p_2-p_3)}{(p_0-p_3)\wedge (p_2-p_3)},\\ v &{} = \frac{(p_a-p_3)\wedge (p_0-p_3)}{(p_2-p_3)\wedge (p_0-p_3)},\\ w &{} = 1-u-v, \end{array} \end{aligned}$$

(1)

and where

$$\begin{aligned} p_a = \bar{u}\ p_0 + \bar{v}\ p_1 + \bar{w}\ p_2 \end{aligned}$$

(2)

Proof

Changing coordinate system is as following using barycentric coordinates,

$$ u\ p_0 + v\ p_2 + w\ p_3 = \bar{u}\ p_0 + \bar{v}\ p_1 + \bar{w}\ p_2. $$

Reorganizing, using expression (2) and $w=1-u-v$, we get,

$$ u\ (p_0-p_3) + v\ (p_2-p_3) = p_a - p_3, $$

where we now have three vectors instead of points. Further, a wedge product of a vector with itself is zero, and therefore (1) follows.

Fig. 4.

The figure shows the parameter plane of a Bezier patch. In the parameter plane we can see 6 triangles located in a fan around point $p_0$. There is also a sketch of a squared patch $(p_0, p_b, p_2, p_a)$, covering the edge $(p_0 , p_2)$.

2.2 Points and Vectors on Triangular Surfaces

To make a squared surface over an edge, it is necessary to have the four boundary curves and four vector valued functions describing the derivatives across the boundary curves. This can be solved in the following way.

We first find the endpoints and vectors at the endpoints in the parameter plane of the two neighboring GERBS triangles. In Fig. 4 we can see the points and vectors.

• The points in triangle $\triangle _1$ and their values:

  $p_0=(1,0,0),\ p_b=(\frac{1}{3},\frac{1}{3},\frac{1}{3}),\ p_2=(0,1,0)$ and $p_a$.

• The points in triangle $\triangle _2$ and their values:

  $p_0=(1,0,0),\ p_a=(\frac{1}{3},\frac{1}{3},\frac{1}{3}),\ p_2=(0,0,1)$ and $p_b$.

The points $p_a$ in triangle $\triangle _1$ and $p_b$ in triangle $\triangle _2$ has to be computed according coordinate change formula from expression (1). The computation (initially in the parameter space to the two GERBS triangles) has to be done in the parameter space of the Bezier patch connected to the central vertex. It is important to observe that there are two Bezier patches involved, one where the central vertex is $p_0$ and one where the central vertex is $p_2$. It follows that the points and thus vectors must be computed in the parameter plane of the Bezier patch where the vectors are connected to the central vertex.

We must find all four vectors in both triangular surfaces. For vectors we thus have:

• The vectors in triangle $\triangle _1$:

  $v_1=p_a-p_2,\ v_2=p_0-p_b,\ v_3=p_b-p_2,\ v_4=p_0-p_a$,

• The vectors in triangle $\triangle _2$:

  $v_5=p_a-p_2,\ v_6=p_0-p_b,\ v_7=p_b-p_2,\ v_8=p_0-p_a$,

where $p_a$ in $v_1$ and $p_b$ in $v_3$ has to be computed in the parameter plane to the surface where $p_2$ is the central vertex, while $p_a$ in $v_2$ and $p_b$ in $v_4$ has to be computed in the parameter plane to the surface where $p_0$ is the central vertex. The reason for this is that the surface over triangulation is smooth in the vertices and not over the edges (described in more detail in [5]).

Barycentric coordinates can be made more general so that it is possible to express a vertex, in a planar triangulation, as a convex combination of its neighboring vertices. This is called mean value coordinates and can be used to calculate the coordinates in the parameter plane of a Bezier patch for barycentric coordinates, see [3].

3 Curves and Vector Valued Functions on Triangular Surfaces

The general formula for a curve or a vector valued functions is,

$$\begin{aligned} \widehat{c}(t)=\sum _{i=0}^d c_i \ b_i(t), \end{aligned}$$

where $c_i,\ i=0,1,...d$ are points or vectors, and $b_i(t),\ i=0,1,...,d$ are basis functions spanning the function space.

If the basis functions are Bernstein polynomials, they sum up to 1, and the derivatives,

$$\begin{aligned} \sum _{i=0}^j b_i^{(j)}(t) = 0, \quad j = 1,2,...,d. \end{aligned}$$

If the curve $\widehat{c}$ is in the parameter space of a surface $S$, then the formula for the space curve on the surface is,

$$\begin{aligned} c(t) = S\circ \widehat{c}(t) \end{aligned}$$

and the derivative is,

$$ c'(t) = dS(\widehat{c}'(t)). $$

If the curve is on a triangular surface using barycentric coordinates then,

$$ dS = \left[ S_u\ S_v\ S_w \right] $$

is a $3\times 3$ matrix, and it follows that the second derivative is,

$$ c''(t) = \left[ d S_u(\widehat{c}'(t))~dS_v(\widehat{c}'(t))~d S_w(\widehat{c}'(t)) \right] \left( \widehat{c}'(t)\right) + dS(\widehat{c}''(t)). $$

Now $\widehat{c}(t)$ is a point in barycentric coordinates where the sum of the coordinates is 1, and $\widehat{c}'(t)$ is a vector in barycentric coordinates where the sum of the coordinates is 0.

In the example shown in Fig. 4 the curve is linear in the parameter plane of the GERBS triangle. It follows that $\widehat{c}(t)= (1-t) p_i + t p_j$ where $i,j$ are indices of two points defining a boundary curve on the squared patch covering an edge. The derivative $\widehat{c}'(t)= p_j - p_i$.

The vectors across an edge in the parameter plane are defined by the vectors describing the direction for the derivatives across the boundary curve at each end of a boundary curve $v_i$ and $v_j$,

$$ h(t) = v_i + b(t)(v_j - v_i), $$

where $b(t)$ is a GERBS basis function, i.e. $b(0)=0, b'(0)=0, b(1)=1, b'(1)=0$ (see [2] for the properties of a GERBS function).

A vector valued function describing the derivatives across the boundary curves will be on the form:

$$ g(t) = dS(h(t)) $$

and the derivative

$$ g'(t) = \left[ d S_u(\widehat{c}'(t))~d S_v(\widehat{c}'(t))~d S_w(\widehat{c}'(t)) \right] \left( h(t)\right) + dS\left( h'(t)\right) . $$

4 Surfaces over Edges in a Triangular Structure

One way to construct the surfaces over the edges is to use a Coons patch Bicubically Blending like procedure, [1]. In Fig. 4 we have a gray area covering an edge. If we name the boundary curves $c_i(t),\ i=1,2,3,4$ we get,

$$\begin{aligned} \begin{array}{ll} c_1(t) = \triangle _1(\widehat{c}_1(t)), \quad \text{ where } &{} \quad \widehat{c}_1(t) = p_2 + t(p_b - p_2)\\ c_2(t) = \triangle _2(\widehat{c}_2(t)), \quad \text{ where } &{} \quad \widehat{c}_2(t) = p_a + t(p_0 - p_a) \\ c_3(t) = \triangle _2(\widehat{c}_3(t)), \quad \text{ where } &{} \quad \widehat{c}_3(t) = p_2 + t(p_a - p_2) \\ c_4(t) = \triangle _1(\widehat{c}_4(t)), \quad \text{ where } &{} \quad \widehat{c}_4(t) = p_b + t(p_0 - p_b), \end{array} \end{aligned}$$

(3)

where $p_a = p_b = (\frac{1}{3},\frac{1}{3},\frac{1}{3})$ and the points else are defined in Sect. 2.2. The functions for the derivatives across the edges are

$$\begin{aligned} \begin{array}{ll} g_1(t) = d\triangle _1(h_1(t)), \quad \text{ where } &{} \quad h_1(t) = v_1 + b(t)(v_2 - v_1)\\ g_2(t) = d\triangle _2(h_2(t)), \quad \text{ where } &{} \quad h_2(t) = v_5 + b(t)(v_6 - v_5) \\ g_3(t) = d\triangle _2(h_3(t)), \quad \text{ where } &{} \quad h_3(t) = v_7 + b(t)(v_8 - v_7) \\ g_4(t) = d\triangle _1(h_4(t)), \quad \text{ where } &{} \quad h_4(t) = v_3 + b(t)(v_4 - v_3) \\ \end{array} \end{aligned}$$

(4)

and the vectors $v_i$ are defined in Sect. 2.2.

The surface construction is, to make three surfaces:

$$ S_1(u,v) = \left[ c_1(u)\ c_2(u)\ g_1(u)\ g_2(u) \right] \,\left[ \begin{array}{l} H_1(v) \\ H_2(v) \\ H_3(v) \\ H_4(v) \end{array} \right] , $$

$$ S_2(u,v) = \left[ H_1(u)\ H_2(u)\ H_3(u)\ H_4(u) \right] \,\left[ \begin{array}{l} c_3(v) \\ c_4(v) \\ g_3(v) \\ g_4(v) \\ \end{array} \right] , $$

$$ S_3(u,v) = \left[ H_1(u)\ H_2(u)\ H_3(u)\ H_4(u) \right] \,\left[ \begin{array} [c]{llll} c_1(0) &{} c_1(1) &{} g_1(0) &{} g_1(1) \\ c_2(0) &{} c_2(1) &{} g_2(0) &{} g_2(1) \\ g_3(0) &{} g_3(1) &{} g_1'(0) &{} g_1'(1) \\ g_4(0) &{} g_4(1) &{} g_2'(0) &{} g_2'(1) \\ \end{array} \right] \,\left[ \begin{array} [c]{l} H_1(v) \\ H_2(v) \\ H_3(v) \\ H_4(v) \\ \end{array} \right] , $$

where $H_i(t),\ i=1,2,3,4$ are the third degree Hermite basis functions. The resulting surface is,

$$ S(u,v) = S_1(u,v) + S_2(u,v)-S_3(u,v). $$

To create surfaces covering all internal edges, as described here, will result in a composite surface that is $C^1$-smooth all over, as we can see on right hand side in Fig. 3.