Keywords

1 Introduction

Reversible logic has applications in emerging technologies such as quantum computing, quantum dot cellular automata, optical computing, etc [37, 38, 44, 47, 63]. Reversible logic based circuits satisfy the property that there is one-to-one mapping between the input and the output vectors, that is for each input vector there is a unique output vector and vice-versa. Conservative logic is a logic family which exhibit the property that there are equal number of 1s in the outputs as in the inputs. Conservative logic may or may not be in reversible in nature. Conservative logic is called reversible conservative logic when there is a one-to-one mapping between the input and the output vectors along with the property that there are equal number of 1s in the outputs as in the inputs. Conservative logic circuits are not considered reversible, if one-to-one mapping between the input and the output vectors is not preserved.

Researchers have proved that if the computation is performed in a irreversible manner each bit of information lost will produce kT ln2 Joules of heat energy [31]. From thermodynamic point of view, in order to avoid this limit, Bennett showed that kT ln2 energy dissipation would not occur, if a computation is carried out in a reversible way [5]. Thus, from thermodynamic considerations, a firm lower limit on dissipation of \(E_{diss} =kT\,\mathrm{ln}2\approx 18 \,\mathrm{{meV}}\) (in room-temperature environment) is a necessity for conventional (irreversible) logic, even if reliability issues could be ignored. Reversible logic can be useful to design non-dissipative circuits if the physical implementation of the logic is also physically reversible. CMOS cannot be considered as a practical implementation platform as CMOS is not physically reversible. In modern CMOS technology, voltage-coded logic signals have an energy of \(E_{sig} =(1/2)CV^{2}\), and whenever the node voltage is changed, it leads to dissipation of this energy and is order of magnitude higher than the kT ln2 factor. In contrast, there are emerging nanotechnologies such as Quantum Dot Cellular automata (QCA) computing, Optical Computing, and Superconductor Flux Logic (SFL) family, etc., where the energy dissipated due to information destruction will be a significant factor of the overall heat dissipation of the system [4, 13, 19, 30, 55, 56, 58]. Thus, one of the primary motivations for adopting reversible logic lies in the fact that it can provide a logic design methodology for designing ultra-low power circuits beyond kT ln2 limit for those emerging nanotechnologies in which the energy dissipated due to information destruction will be a significant factor of the overall heat dissipation. For example, in new Superconductor Flux Logic (SFL) family based on nSQUID gates, the energy dissipation in conventional logically irreversible architectures is close to few kT ln2 per logic operation. By employing reversible logic, the energy dissipation per nSQUID gate per bit measured, at 4 K temperature is below the thermodynamic threshold limit of kT ln2 [55]. Therefore, reversible logic is being investigated for its promising applications in power-efficient nanocomputing [17, 32, 35].

Further, quantum dot cellular automata (QCA) is one of the emerging field coupled nanotechnologies in which it is possible to implement reversible logic gates [19, 37, 38]. QCA makes it possible to achieve circuit densities and clock frequencies beyond the limits of existing CMOS technology [70, 71]. The logic states of 1 and 0 are represented by the position of the electrons inside the QCA cell as illustrated in Fig. 2(b). Thus, when the bit is flipped from 1 to 0 there is no actual discharging of the capacitor as in conventional CMOS. Hence, QCA does not have to dissipate all its signal energy during transition. Further, propagation of the polarization from one cell to another is because of interaction of electrons in adjacent QCA cells. As there is no movement of electrons from one QCA cell to the other, hence there is no current flow. Thus, QCA has no dissipation in signal propagation. Therefore, QCA has significant advantage compared to CMOS technology in terms of power dissipation. Further in contrast to CMOS, the cells in QCA are connected to 4 clocking zones, each lagging behind by \(90\,^{\circ }\) in phase. QCA clocking helps in the successive transfer of information from one clock zone to the next [25, 34]. Therefore, we have information flow from the input to the output in a pipelined fashion. Thus, QCA cells are inherently suitable for pipeline and systolic designs [15]. QCA computing can be implemented in semiconductor, molecular and magnetic platforms. Researchers are currently targeting magnetic and molecular QCA, several smaller circuits in magnetic and molecular QCA have been fabricated and tested [3, 7, 26, 33, 52, 53]. Theoretical studies have also shown that molecular QCA can operate at room temperature at THz of speed [36].

Several works can be found in the literature for QCA design such as adders, multipliers, shifters, memories, FPGA, synthesis etc. [9, 10, 24, 28, 45, 64, 73, 76]. Due to high error rates in nano-scale manufacturing, the major goal in QCA and other nanotechnologies is to have devices with reduced error rates [37]. In the manufacturing process for QCA, defects can occur in the synthesis and deposition phases. However, defects are more likely to occur during the deposition phase [62].

In this work, we propose the design of testable sequential circuits based on conservative logic gates. It has shown in [61] that the combinational circuits based on conservative logic gates outperform all the circuits implemented using classical gates in the area of testing. Further, any combinational circuit based on conservative logic gates can be tested for classical unidirectional stuck-at faults using only two test vectors. The two test vectors are all 1s, and all 0s [61]. This is because whenever there are unidirectional faults in combinational conservative logic circuits, the number of 1s in the inputs will differ from the number of 1s in the outputs. Thus for unidirectional stuck-at faults in conservative logic circuits, counting the number of 1s in the inputs and the outputs would be the fault detection scheme. The feedback in sequential circuits makes them untestable by all 0s and all 1s test vectors. Moreover, in reversible logic fanout is not allowed. Hence, we propose a technique that will take care of the fanout at the output of the reversible latches and can also disrupt the feedback to make them suitable for testing by only two test vectors, all 0s and all 1s. In other words, circuits will have feedback while executing in the normal mode. However, in order to detect faults in the test mode, our proposed technique will disrupt feedback to make conservative reversible latches testable as combinational circuits. The proposed technique is extended towards the design of two vectors testable master-slave flip-flops, double edge triggered flip-flops, asynchronous set/reset D latch, D flip-flop and counters. Thus, our work is significant because we are providing the design of reversible sequential circuits completely testable for any unidirectional stuck-at faults by only two test vectors. The reversible design of the double edge triggered flip-flop, ring counter and Johnson counter are proposed for the first time in literature.

Field coupled quantum dot cellular automata (QCA) computing is based on majority voting, hence the designs based on conservative logic will be completely different from those based on conventional CMOS. Single missing/additional cell defects are prominent permanent defects in QCA circuits. We implemented the Fredkin gate in the QCA technology and observed that all 0s and all 1s test vectors cannot provide 100 % fault coverage for single missing/additional cell defect in the QCA layout of the Fredkin gate. Thus, to have the 100 % fault coverage for single missing/additional cell defect by all 0s and all 1s test vectors, we identified the QCA devices in the QCA layout of the Fredkin gate that can be replaced with fault tolerant components to provide the 100 % fault coverage. Further, while designing a QCA sequential circuit, the designer may sometimes prefer to sacrifice the reversibility to save the number of QCA cells while keeping the test strategy to be the same, that is the design can still be tested by two test vectors. Thus, we also propose a new conservative logic gate called Multiplexer Conservative QCA gate (MX-cqca) which is not reversible in nature but has similar properties as the Fredkin gate of working as 2:1 multiplexer. The proposed MX-cqca gate surpasses the Fredkin gate in terms of complexity(the number of majority voter), speed and area. MX-cqca can implement the multiplexer function with 1 less majority gate than the Fredkin gate; it also requires a smaller area and fewer QCA cells in QCA layout. The design and verification of the QCA layouts were performed using the QCADesigner and HDLQ tools.

The chapter is organized as follows: Sect. 2 presents the background on conservative logic, the basics of QCA computing, such as QCA logic devices and QCA clocking, related work etc.; Sect. 3 presents design of testable reversible latches; Sect. 4 describes design of testable reversible master-slave flip-flops; Sect. 5 presents design of testable reversible double edge triggered flip-flop; Sect. 6 shows the design of testable reversible complex sequential circuits; Sect. 7 discusses the application of the proposed two vectors, all 0s and all 1s, testing approach to QCA computing; Sect. 8 presents the proposed multiplexer conservative QCA gate; Sect. 9 discusses design methodology for non-reversible testable design based on MX-cqca gate; and Sect. 10 provides some discussions and conclusions.

2 Background

A conservative logic gate is a multiple-output logic element in which the number of 1s at the inputs is equal to that of the corresponding outputs. According to [18, 61], a conservative logic circuit can be considered as a directed graph whose nodes are conservative logic gates, and the edges are wires of arbitrary lengths. The fanout at the output is not allowed in conservative logic circuits. A conservative logic network can be reversible in nature if the one-to-one mapping is maintained between the inputs and the outputs, while it will be irreversible in nature if one-to-one mapping is not preserved. Researchers in [27, 60, 61] have proved that: (i) in the event of unidirectional stuck-at-faults in a conservative logic network, either the number of 1s in its output set will differ from the number of 1s in its input set, or the output set is correct; (ii) in a conservative logic network the two vector test set, all 1s and all 0s, provide 100 % coverage for unidirectional stuck-at faults. Any stuck-at-1 fault in the conservative logic circuit can be detected by setting all inputs to 0s followed by subsequent checking of the outputs for the presence of any 1s. Any stuck-at-0 faults can be detected by setting all inputs to 1s followed by subsequent checking of outputs for the presence of any 0s. The comprehensive proofs can be referred in [27, 60, 61].

2.1 Conservative Reversible Fredkin Gate

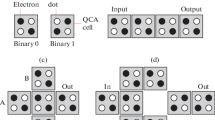
The Fredkin gate is a popularly used reversible conservative logic gate, first proposed by Fredkin and Toffoli in [18]. The Fredkin gate shown in Fig. 1(a) can be described as a mapping (c, \(i_0\), \(i_1\)) to (\(o_0 = \mathrm{c}\), \(o_1 = {\text {c}}' i_0 + \mathrm{c} i_1\),\(o_2 = \mathrm{c} i_0 + {\text {c}}' i_1\)), where c, \(i_0\), \(i_1\) are the inputs and \(o_0\), \(o_1\) and \(o_2\) are the outputs, respectively. Table 1 shows the truth table for the Fredkin gate which demonstrates that Fredkin gate is reversible and conservative in nature, that is, it has unique input and output mapping and also has the same number of 1s in the outputs as in the inputs. Fredkin gate is also called as controlled swap gate as it can swap two input bits \(i_0\), \(i_1\) when \(c_0 = 1\). The controlled swap operation of the Fredkin gate is illustrated in Fig. 1(b), (c).

Fig. 1.
figure 1

Fredkin gate and its working mode

Full size image
Table 1. Truth table for Fredkin gate
Full size table

2.2 Basics of QCA Computing

In this work, the conservative logic gates are implemented in the QCA nanotechnology, thus we are also providing the introductory material on QCA computing. A QCA cell is a coupled dot system in which four dots are at the vertices of a square. The cell has two extra electrons that occupy the diagonals within the cell due to electrostatic repulsion. The cell polarization P measures the charge distribution along diagonal axes and is given by Eq. 1 (here Pi denotes the electronic charge at dot i). When electrons are in dots 1 and 3, \(\mathrm{{P}} = -1\) (Logic ‘0’) and when electrons in dots 2 and 4, P = +1 (Logic ‘1’) [70]. Figure 2(a) and (b) illustrate the 4 quantum dots in a QCA cell, and the implementation of logic ‘0’ and logic ‘1’ in a QCA cell, respectively.

$$\begin{aligned} P=\frac{(P2+P4)-(P1+P3)}{P1+P2+P3+P4} \end{aligned}$$
(1)

The basic QCA device is the majority voter (MV) or majority gate, which is represented as \(\mathrm{Y} = X_{1}X_2 + X_{2}X_3 + X_{1}X_3\), where Y is the majority of the inputs \(X_1\), \(X_2\) and \(X_3\). Figure 3(a) shows the majority voter. The majority voter can be made to work as an AND gate or as an OR gate, by setting one of the inputs as ‘0’ and ‘1’, respectively (For example, if \(X_3 = 0\) we will get \(\mathrm{Y} = X_{1}X_2\). Similarly if \(X_3 = 1\), we will get \(\mathrm{Y} =X_1 + X_2\)). Another important gate in QCA is the inverter, which is formed when a QCA cell, say cell-1 is placed \(45\,^{\circ }\) to another QCA cell, for example cell-0, cell-1 gets the inverse value of cell-0. There can be many ways of designing the QCA inverter, one of which is shown in Fig. 3(b). In QCA computing, signal transfer is made through wires that are of two types (i) Binary wire, (ii) Inverter chain. The electrons in adjacent QCA cells interact with each other resulting in propagation of the polarization from one cell to another. Thus, a QCA wire can be formed by arranging the QCA cells in a series in which all the neighboring cells will get the polarization of the driver cell (input). The binary wire is shown in Fig. 4(a). Two wires in QCA can cross without interaction. This is because QCA provides an inverter chain of QCA cells, in which the dots in each cell are rotated by \(45\,^{\circ }\) (This is not the same as in QCA inverter). Each cell in this arrangement has opposite polarization of their neighbors as they interact inversely. The inverter chain is shown in Fig. 4(b). In QCA, when a binary wire crosses the inverter chain, there is no interaction between the two; hence the signals in the inverter chain and binary wire can pass over each other. In QCA computing, the clock helps in the synchronization of circuits and provides the power required for functionality. QCA clocking consists of four phases: switch, hold, release and relax, as shown in Fig. 5 [25, 34]. During the switch phase, the barriers are raised and the cells become polarized, depending on the state of its adjacent cell. The states of the cells are fixed during this stage. During the hold phase, the barriers are maintained at a high value. This helps the outputs to drive the inputs of the next stage, which is in the switching phase. In the release phase, the barriers are lowered and the cells are allowed to relax to an unpolarized state. During the relaxed phase, the cells remain in an unpolarized neutral state. The cells in QCA are connected to 4 clocking zones, each lagging behind by \(90\,^{\circ }\) in phase. QCA clocking helps in the successive transfer of information from one clock zone to the next. Therefore, we have information flow from the input to the output in a pipelined fashion [1].

Fig. 2.
figure 2

QCA cell and logic operation

Full size image
Fig. 3.
figure 3

QCA majority voter (MV) and inverter devices

Full size image
Fig. 4.
figure 4

QCA binary wire and inverter chain

Full size image
Fig. 5.
figure 5

QCA 4 phase clocking

Full size image
Fig. 6.
figure 6

Information flow in a QCA wire

Full size image

2.3 Related Work

The research on reversible logic is expanding towards both design and synthesis. In the synthesis of reversible logic circuits there has been several interesting attempts in the literature such as in [22, 40, 51, 59, 75]. The researchers have addressed the optimization of reversible logic circuits from the perspective of quantum cost and the number of garbage outputs. Recently, in [20, 21] interesting contributions are made towards deriving exact minimal elementary quantum gate realization of reversible combinational circuits. Any nanotechnology having applications of reversible logic such as nano-CMOS devices, NMR based quantum computing, or low power molecular QCA computing, all are susceptible to high device error rates. This attracted the attention of researchers towards testing of reversible logic circuits. In [48], it has been shown that for reversible logic circuits, the test set that detects all single stuck-at faults can also detect multiple stuck-at faults. In [50], four fault models for reversible circuits, viz., single missing gate fault, the repeated-gate fault, the multiple missing gate fault and the partial missing-gate fault are proposed based on ion-trap quantum computing at logical level. In [78], a new fault model called crosspoint fault model is proposed along with the ATPG method. In [54], a universal test set is proposed for detection of missing-gate faults in reversible circuits. In [8], a DFT methodology for detecting bridging faults in reversible logic circuits is proposed. Recently, the design of reversible finite field arithmetic circuits with error detection is also proposed [41]. An online testing methodology for reversible circuits using a combination of R1 gate along with R2 gate (a 4*4 Feynman Gate) is proposed in [72] while in [39] an automatic conversion of any given reversible circuit into an online testable circuit that can detect online the single-bit errors, including soft errors in the logic blocks is presented. The online testing methodology of reversible logic circuits is also addressed in [14]. In our recent work we addressed the concurrent testing of single missing faults in QCA circuits based on reversible logic [65, 66]. With respect to the work on design of reversible sequential circuits, various interesting contributions are made in which the designs are optimized in terms of various parameters such as the number of reversible gates, garbage outputs, quantum cost, delay etc. [11, 18, 39, 43, 57, 67, 69].

To the best of our knowledge the offline testing of faults in reversible sequential circuits is not addressed in the literature. In this work, we present the designs of reversible sequential circuits that can be tested by using only two test vectors, all 0s and all 1s for any unidirectional stuck-at-faults. Further, the approach of fault testing based on conservative logic is extended towards the design of non-reversible sequential circuits based on a new conservative logic gate called multiplexer conservative QCA gate (Mx-cqca).

Fig. 7.
figure 7

Design of testable reversible D latch using conservative Fredkin gate

Full size image

3 Design of Testable Reversible Latches

The characteristic equation of the D latch can be written as \(Q^{+} = D\cdot E + \bar{E}\cdot Q \). In the proposed work, E (Enable) refers to the clock and is used interchangeably in place of clock. When the enable signal (clock) is 1, the value of the input D is reflected at the output that is \(Q^{+} = \mathrm{D}\). While, when E = 0 the latch maintains its previous state, that is \(Q^{+} = \mathrm{Q}\). The reversible Fredkin gate has two of its outputs working as 2:1 MUxes, thus the characteristic equation of the D latch can be mapped to the Fredkin gate (F). Figure 7(a) shows the realization of the reversible D latch using the Fredkin gate. But fan-out is not allowed in conservative reversible logic. Moreover, the design cannot be tested by two input vectors all 0s and all 1s because of feedback, as the output Q would latch 1 when the inputs are toggled from all 1s to all 0s and could be misinterpreted as stuck-at-1 fault.

In this work, we propose to cascade another Fredkin gate to output Q as shown in Fig. 7(b). The design has two control signals, C1 and C2. The design can work in two modes: (a) normal mode; (b) test mode. Normal Mode: The normal mode is shown in Fig. 7(c) in which we will have C1C2 = 01 and the design will work as a D latch without any fanout problem. Test Mode (Disrupt the Feedback): In test mode , when C1C2 = 00 as shown in Fig. 7(d) the design will be testable with all 0s input vectors, as output T1 will become 0 resulting in the testable design with all 0s input vectors. Thus any stuck-at-1 fault can be detected. When C1C2 = 11 as shown in Fig. 7(e) the output T1 will become 1 and the design will become testable with all 1s input vectors for any stuck-at-0 fault. It can seen from the illustration that C1 and C2 will disrupt the feedback in test mode, and in normal mode will take care of the fan-out. Thus our proposed design works as a reversible D latch and can be tested with only two test vectors, all 0s and all 1s, for any stuck-at fault by utilizing the inherent property of conservative reversible logic.

Fig. 8.
figure 8

Design of testable negative enable D latch using conservative Fredkin gate

Full size image

3.1 Design of Testable Negative Enable Reversible D Latch

A negative enable reversible D latch will pass the input D to the output Q when E = 0; otherwise maintains the same state. The characteristic equation of the negative enable D latch is \(Q^{+} = D\cdot \bar{E} + E\cdot Q \). This characteristic equation of the negative enable reversible D latch can be mapped to the 2nd output of the Fredkin gate as shown in Fig. 8(a). The second Fredkin gate in the design take cares of the fanout. The second Fredkin gate in the design also makes the design testable by two test vectors all 0s and all 1s by breaking the feedback based on control signals C1 and C2, as illustrated above for positive enable reversible D latch. The working of the testable negative enable reversible D latch in normal mode is illustrated in Fig. 8(b). The negative enable D latch is helpful in the design of testable reversible master-slave flip-flops. This is because it can work as a slave latch in the testable reversible master-slave flip-flops in which no clock inversion is required. The details of which are discussed in the section describing reversible master-slave flip-flops.

Fig. 9.
figure 9

Design of testable reversible T Latch using conservative Fredkin gate

Full size image

3.2 Design of Testable Reversible T Latch

The characteristic equation of the T latch can be written as \(Q^{+} = (T\cdot Q)\cdot E + \bar{E}\cdot Q\). But the same result can also be obtained from \(Q^{+} = (T\cdot E)\,\oplus \, Q\). The T(toggle) latch is a complementing latch which complements its value when T = 1, that is when T = 1 and E = 1 we have \(Q^{+} = {\text {Q}}'\). When T = 0, the T latch maintains its state and we have no change in the output. Figure 9(a) shows the proposed design of reversible testable T latch with C1, C2, and C3 as control signals. The control signal C3 helps to realize the reversible AND function as we can generate \(T \cdot E\) when C3 = 0, at one of the outputs of the Fredkin gate as illustrated in Fig. 9(b). C1 and C2 are the main control signals that help in breaking the feedback to make the design testable as well as in enabling the normal mode of operation. In normal mode, as illustrated in Fig. 9(b), the values of the control signals will be C1 = 0 and C2 = 1 thus helping in realizing the function \((T\cdot E)\oplus Q\). In test mode, when C1 = 0 and C2 = 0 as shown in Fig. 9(d) it will break the feedback and test the design with all 0s test vector for any stuck-at-1 fault, while when C1 = 1 and C2 = 1 as shown in Fig. 9(c) it will break the feedback and helps in testing the design with all 1s test vector for any stuck-at-0 fault. The other types of reversible testable latches based on conservative reversible logic such as the JK latch and the SR latch can be designed similarly, thus are not discussed in this work.

Fig. 10.
figure 10

Design of testable reversible asynchronous set/reset D latch

Full size image

3.3 Design of Testable Asynchronous Set/Reset D Latch

The design of the asynchronously set/reset D latch is shown in Fig. 10(a). The design has 3 Fredkin gates. We can observe that the first Fredkin gate maps the D latch characteristic equation, while the second and the third Fredkin gates take care of the fan-out and also help in asynchronous set/reset of the output Q. The design has two control inputs C1 and C2. When C1 = 0 and C2 = 1, the design works in normal mode implementing the D latch characteristic equation. When C1 = 0 and C2 = 0, the second and third Fredkin gates will reset the output Q to 0. When C1 = 1 and C2 = 1, the design will be set to Q = 1. Thus, the control inputs help the design to work in various modes. But the design shown in Fig. 10(a) has fan-out of more than one in C1 and C2 inputs which is prohibited in reversible logic. Thus, a modified design of the D latch with asynchronous set/reset capability in which there is no fan-out is shown in Fig. 10(b). There is a special characteristic of the reversible D latch design shown in Fig. 10(b). The design shown in Fig. 10(b) has the control signals C1 and C2 which helps in disrupting the feedback. For example, the feedback is disrupted when C1C2 = 00; the feedback output Q resets to 0 which makes the reversible D latch testable with all 0s test vector for any stuck-at-1 fault. Similarly, when C1C2 = 11 the output Q sets to 1 and the design becomes testable with all 1s test vector for any stuck-at-0 fault. Thus, the proposed reversible D latch design with asynchronous set/reset significantly reduces the testing cost. Thus if we design asynchronous set/reset D latch only with Fredkin gates we can have the significant testing benefits.

4 Design of Testable Master-Slave Flip-Flops

In the existing literature, the master-slave strategy of using one latch as a master and the other latch as a slave is used to design the reversible flip-flops [11, 57, 68, 69]. In this work, we have proposed the design of testable flip-flops using the master-slave strategy that can be detected for any stuck-at faults using only two test vectors all 0s and all 1s. Figure 11(a) shows the design of the master-slave D flip-flop in which we have used positive enable Fredkin gate based testable D latch shown in Fig. 7(b) as the master latch, while the slave latch is designed from the negative enable Fredkin gate based testable D latch shown earlier in Fig. 8(a). The testable reversible D flip-flops has four control signals mC1, mC2, sC1 and sC2. mC1 and mC2 control the modes for the master latch, while sC1 and sC2 control the modes for the slave latch. In the normal mode, when the design is working as a master-slave flip-flop the values of the control signals will be mC1 = 0 and mC2 = 1, sC1 = 0 and sC2 = 1 (similar to values of the control signals C1 and C2 earlier described for the testable D latches).

Fig. 11.
figure 11

Fredkin gate based testable reversible master-slave flip-flops

Full size image
Fig. 12.
figure 12

Fredkin gate based testable reversible asynchronous set/reset master-slave D flip-flop

Full size image

In the test mode:

  1. 1.

    to make the design testable with all 0s input vectors for any stuck-at-1 fault, the values of the control signals will be mC1 = 0 and mC2 = 0, sC1 = 0 and sC2 = 0. This will produce the outputs mT1 and sT1 as 0 which results in disrupting the feedback and the design becomes testable with all 0s input vectors for any stuck-at-1 fault.

  2. 2.

    to make the design testable with all 1s input vectors for any stuck-at-0 fault, the values of the control signals will be mC1 = 1 and mC2 = 1, sC1 = 1 and sC2 = 1. This will result in outputs mT1 and st1 to have the value of 1, disrupting the feedback, and resulting in the design testable with all 1s input vectors for any stuck-at-0 fault.

The other type of master-slave flip-flops such as the testable master-slave T flip-flop, testable master-slave JK flip-flop and testable master-slave SR flip-flop can be designed similarly in which master is designed using the positive enable corresponding latch, while the slave is designed using the negative enable Fredkin gate based D latch. For example, as illustrated in Fig. 11(b), in the design of master-slave T flip-flop the master is designed using the positive enable T latch, while the slave is designed with the negative enable D latch.

The reversible design of the master-slave D flip-flop with asynchronous set/reset is shown in Fig. 12. The design contains positive enable testable D latch shown in Fig. 7(b) as the master latch and negative enable asynchronous set/reset D latch shown in Fig. 10(b) as the slave latch.

5 Design of Testable Reversible Double Edge Triggered(DET) Flip-Flops

The double edge triggered flip-flop is a computing circuit that sample and store the input data at both the edges, that is at both the rising and the falling edge of the clock. The master-slave strategy is the most popular way of designing the flip flop. In the proposed work E (Enable) refers to the clock and is used interchangeably in place of clock. In the negative edge triggered master-slave flip-flop when E = 1 (the clock is high), the master latch passes the input data while the slave latch maintains the previous state. When E = 0 (the clock is low), the master latch is in the storage state while the slave latch passes the output of the master latch to its output. Thus, the flip-flop does not sample the data at both the clock levels and waits for the next rising edge of the clock to latch the data at the master latch.

Fig. 13.
figure 13

Fredkin gate based double edge triggered (DET) flip-flop

Full size image
Fig. 14.
figure 14

Working of Fredkin gate based double edge triggered flip-flop

Full size image

In order to overcome the above problem, researchers have introduced the concept of double edge triggered (DET) flip-flops which sample the data at both the edges. Thus DET flip-flops can receive and sample two data values in a clock period thus frequency of the clock can be reduced to half of the master-slave flip flop while maintaining the same data rate. The half frequency operations make the DET flip flops very beneficial for low power computing as frequency is proportional to power consumption in a circuit. The DET flip-flop is designed by connecting the two latches, viz., the positive enable and the negative enable in parallel rather than in series. The conventional design of the DET flip-flop is illustrated in Fig. 13(a) [49]. The 2:1 MUX at the output transfer the output from one of these latches which is in the storage state (holding its previous state). The equivalent testable reversible design of the DET flip flop is proposed in this work and is shown in Fig. 13(b).

In the proposed design of testable reversible DET flip-flop, the positive enable testable reversible D latch and the negative enable testable reversible D latch are arranged in parallel. The Fredkin gates labeled as 1 and 2 form the positive enable testable D latch while the Fredkin gates labeled as 3 and 4 form the negative enable testable D latch. In reversible logic fanout is not allowed so the Fredkin gate labeled as 1 is used to copy the input signal D. The Fredkin gate labeled as 6 works as the 2:1 MUX and transfer the output from one of these testable latches (negative enable D latch or the positive enable D latch) that is in the storage state (is holding its previous state) to the output Q. In the proposed design of testable reversible DET flip-flop pC1 and pC2 are the control signals of the testable positive enable D latch, while nC1 and nC2 are the control signals of the testable negative enable D latch. Depending on the values of the pC1, pC2, nC1 and nC2 the testable DET flip-flops works either in normal mode or in the testing mode.

  1. 1.

    Normal Mode: The normal mode of the DET flip-flop is illustrated in Fig.14(a) in which the pC1 = 0, pC2 = 1, nC1 = 0 and nC2 = 1. The pC1 = 0, pC2 = 1 helps in copying the output of the positive enable D latch thus avoiding the fanout while the nC1 = 0 and nC2 = 1 helps in copying the output of the negative enable D latch thus avoiding the fanout.

  2. 2.

    Test Mode: There will be two test modes:

    1. (a)

      All 1s Test Vector: This mode is illustrated in Fig. 14(c) in which control signals will have values as pC1 = 1, pC2 = 1, nC1 = 1 and nC2 = 1. The pC1 = 1 and pC2 = 1 help in breaking the feedback of the positive enable D latch, while the nC1 = 1 and nC2 = 1 help in breaking the feedback of the negative enable D latch. This makes the design testable by all 1s test vector for any stuck-at-0 fault.

    2. (b)

      All 0s Test Vector: This mode is illustrated in Fig. 14(b) in which the control signals will have values as pC1 = 0, pC2 = 0, nC1 = 0 and nC2 = 0. The pC1 = 0 and pC2 = 0 help in breaking the feedback of the positive enable D latch while the nC1 = 0 and nC2 = 0 help in breaking the feedback of the negative enable D latch. This makes the design testable by all 0s test vector for any stuck-at-1 fault.

6 Design of Testable Reversible Complex Sequential Circuits

The set of sequential building blocks proposed in this work can be used to build complex sequential circuits that provide the capability of testing a sequential circuit using two test vectors. The proposed sequential building blocks can be used to implement various types of sequential circuits such as shifters, sequence detectors, counters and systolic circuits etc. We have illustrated the method with examples of design of reversible ring counter and reversible Johnson counter using the proposed sequential building blocks.

6.1 Design of Testable Reversible Ring Counter

A testable reversible ring counter can be designed by cascading reversible master slave D flip-flops with asynchronous set/reset capability in which the output of the last flip-flop is connected to the first flip-flop. The design of n bit testable reversible ring counter is illustrated in Fig. 15. In normal working mode, the ring counter needs to be initialized by setting the first master-slave flip flop to 1, while the remaining n-1 flip-flops need to be reset to 0. This will initialize the counter to a state \((10000\ldots 0)_n\). In Fig. 15, this is performed as follows:

$$\begin{aligned} sc1_{i}\quad and \quad sc2_{i} = {\left\{ \begin{array}{ll} 1 &{} \text{ if } i=0 \\ 0&{} \text{ if } 1\le i\le \mathrm{n}-1 \end{array}\right. } \end{aligned}$$

The above values of \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) asynchronously sets the first testable reversible flip-flop to 1, while the n-1 testable reversible D flip-flops are asynchronously reset to 0. Once the counter is initialized, the values of \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) are changed:

$$\begin{aligned} sc1_{i}\quad and \quad sc2_{i} = {\left\{ \begin{array}{ll} 0 \quad and \quad 1&\text{ if } 0\le i\le \mathrm{n}-1 \end{array}\right. } \end{aligned}$$

Thus, in the proposed reversible n bit ring counter 1 bit is circulated so the state repeats every n clock cycles. For example, in a four bit testable reversible counter, the possible states for \(Q_{0}Q_{1}Q_{2}Q_3\) will be 1000, 0100, 0010, and 0001.

The test mode of the reversible ring counter can be defined as follows:

  1. (a)

    All 1s Test Vector: In this mode, all the inputs along with \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) are set to the value of 1 to detect any stuck-at-0 fault.

  2. (b)

    All 0s Test Vector: In this mode, all the inputs along with \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) are reset to the value of 0 to detect any stuck-at-1 fault.

6.2 Design of Testable Reversible Johnson Counter

A testable reversible Johnson counter can be designed by cascading reversible master slave D flip-flops with asynchronous set/reset capability in which the Q’ output of the last flip-flop instead of Q is connected to the first flip-flop. The design of n bit testable reversible Fig. 16. In normal working mode, the Johnson counter needs to be initialized by reseting all n flip-flops. This will initialize the counter to a state \((00000\ldots 0)_n\). In Fig. 16, this is performed as follows:

$$\begin{aligned} sc1_{i}\quad and \quad sc2_{i} = {\left\{ \begin{array}{ll} 0 \quad and \quad 0&\text{ if } \quad 0\le i\le \mathrm{n}-1 \end{array}\right. } \end{aligned}$$
Fig. 15.
figure 15

Design of testable reversible ring counter

Full size image
Fig. 16.
figure 16

Design of testable reversible Johnson counter

Full size image

The above values of \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) asynchronously reset the n testable reversible D flip-flops to 0. Once the counter is initialized, the values of \(sc1_{i}\) and \(sc2_{i}\) where \(0\le i\le n-1\) are changed:

$$\begin{aligned} sc1_{i}\quad and \quad sc2_{i} = {\left\{ \begin{array}{ll} 0 \quad and \quad 1&\text{ if }\quad 0\le i\le \mathrm{n} -1 \end{array}\right. } \end{aligned}$$

Thus, the proposed reversible n bit Johnson counter produces a couting sequence so the state repeats every 2n clock cycles. For example, in a four bit testable reversible Johnson counter, the possible states for \(Q_{0}Q_{1}Q_{2}Q_{3}\) will be 0000, 1000, 1100, 1110, 1111, 0111, 0011, 0001. The test mode of the reversible Johnson counter can be designed similar to the reversible ring counter as explained in the above section.

Similar design methodologies can be proposed based on the example study shown for testable reversible latches, flip-flops and counters to design other complex sequential circuits such as shift registers, memory based on proposed testable D flip-flop and reversible data path functional units.

7 Application of Two Vectors, All 0s and All 1s, Testing Approach to QCA Computing

QCA computing provides a promising technology to implement reversible logic gates. The QCA design of Fredkin gate is shown in Fig. 17 using the four-phase clocking scheme, in which the clocking zone is shown by the number next to z (z0 means clock 0 zone, z1 means clock 1 zone and so on). It can be seen that the Fredkin gate has two level majority voter (MV) implementation, and it requires 6 MVs and 4 clocking zones for implementation. The number of clocking zones in a QCA circuit represents the delay of the circuit (delay between the inputs and the outputs). Higher the number of clocking zones, lower the operating speed of the circuit [37].

Fig. 17.
figure 17

QCA Design of Fredkin Gate using the four-phase clocking scheme, in which the clocking zone is shown by the number next to z (z0 means clock 0 zone, z1 means clock 1 zone and so on)

Full size image
Fig. 18.
figure 18

QCA Layout of Fredkin Gate. CW represents cross wire resulted from intersection of binary wire and inverter chain, MV represents majority voter

Full size image
Table 2. Fault patterns in Fredkin gate
Full size table
Fig. 19.
figure 19

Modeling of QCA Layout of Fredkin Gate. FO represents the fanout QCA device, LSW represents the L-shape wire, INV represents the QCA inverter, CW represents the crosswire and MV represents the majority voter

Full size image

In QCA manufacturing, defects can occur during the synthesis and deposition phases, although defects are most likely to take place during the deposition phase [62]. Researchers assume that QCA cells have no manufacturing defect; in metal QCA, faults occur due to cell misplacement. These defects can be characterized as cell displacement, cell misalignment and cell omission [23]. Researchers have shown that molecular QCA cells are more susceptible to missing and additional QCA cell defects [42]. The additional cell defect is because of the deposition of an additional cell on the substrate. The missing cell defect is due to the missing of a particular cell. Researchers have been addressing the design and test of QCA circuits assuming the single missing/additional cell defect model. In [37], reversible logic was proposed as a means to detect single missing/additional cell defects. It was shown that reversible 1D array is C-testable. In [6], they address the robust coplanar crossing in QCA, proving that wires having rotated cells are thermally more stable.

In this section, we discuss how the QCA implementation of the Fredkin gate can be tested by only two test vectors, all 0s and all 1s, for the offline testing of any single missing/additional cell defect. The QCA layouts of the Fredkin gate is shown in Fig. 18. In the proposed work, the QCA layout of the Fredkin gate is converted into the corresponding hardware description language notations using the HDLQ Verilog library [46]. The HDLQ design tool consists of a Verilog HDL library of QCA devices, i.e., MV, INV, fan-out, Crosswire, L-shape wire with fault injection capability. The HDLQ model of the QCA layout of the Fredkin gate is shown in Fig. 19. In the Fig. 19, FO represents the fanout QCA device, LSW represents the L-shape wire, INV represents the QCA inverter, CW represents the crosswire, MV represents the majority voter. Thus it can be seen that modeled QCA layout of the Fredkin gate has 4 FOs, 2 INVs, 5 CWs, 9 LSWs and 6 MVs. The HDLQ modeled design of the Fredkin gate is simulated for the presence of all possible single missing/additional cell defect in MVs (majority voters), INVs (Inverters), FOs (fanouts), Crosswires (CWs) and L-shape wires (LSWs). The design is simulated using the Verilog HDL simulator in the presence of faults to determine the corresponding outputs.

We conducted exhaustive testing of the HDLQ model of the Fredkin gate with 8 input patterns in the presence of all possible single missing/additional cell defect. Testing of the Fredkin gate generates 28 unique fault patterns at the output, as shown in Table 2. In the fault patterns study shown in the Table, ai is the 3 bit pattern with an equivalent decimal value of i. For example, a0 represents 000 (decimal 0) and a7 represents 111 (decimal 7). From fault tables we can see that there are 10 fault patterns 5, 6, 13, 15, 18, 23, 24, 25, 26, 27 that will produce the correct outputs for input vectors a0 (all 0s) and a7 (all 1s) even when there is a fault. Thus two test vectors a0 and a7 can only provide 64.28 % fault coverage. Thus in order to give the test vectors a0 and a7 100 % fault coverage we identified the logic devices in the HDLQ model of the Fredkin gate which can be replaced by their fault-tolerant counterpart. This will give the 100 % fault coverage for any single missing/additional cell defect to the two test vectors all 0s and all 1s. We observed that fanouts (\(F0_{2}\) and \(F0_{3}\)), inverters (\(INV_{1}\) and \(INV_{2}\)), crosswires (\(CW_{4}\) and \(CW_{2}\)) and majority voters (\(MV_{1}\), \(MV_{3}\), \(MV_{4}\), \(MV_{5}\) and \(MV_{6}\)) are devices in the QCA layout of the Fredkin gate that are making the design untestable by all 0s and all 1s test vectors. This work focuses on demonstrating the fault tolerant QCA circuits that provide ease of testability as the proposed sequential building blocks can be tested using only two test vectors. In the existing literature, several fault tolerant QCA components have been proposed such as Majority voters (MVs), Inverters (INVs), Fanouts (FOs), Crosswires (CWs) and L-shape wires (LSWs) [12, 15, 16, 74]. Thus, these devices can be replaced by their fault tolerant counterparts in the QCA layout of the Fredkin gate to have the equivalent design that gives 100 % fault coverage to test vectors all 1s and all 0s. The HDLQ model of the Fredkin gate QCA layout having 100 % coverage for any single missing/additional cell defect to test vectors all 0s and all 1s is shown in Fig. 20. In Fig. 20, the shaded devices represent their fault tolerant counterparts. Thus, conservative logic QCA circuits based on our proposed QCA layout of the Fredkin gate show in Fig. 20, can be tested by all 0s and all 1s test vectors for presence single missing/additional cell defects.

Fig. 20.
figure 20

QCA layout of the Fredkin gate testable with only all 0s and all 1s test vectors for any single missing/additional cell defect (the shaded devices represent their fault tolerant counterpart)

Full size image

8 Proposed Multiplexer Conservative QCA Gate(MX-cqca)

For many of the designs, the designer could potentially be interested in using the testing advantages of conservative logic but saving the number of QCA cells. Thus, in this work we propose a new conservative logic gate that is conservative in nature but is not reversible. The proposed conservative logic gate is called multiplexer conservative QCA gate(MX-cqca) and has 3 inputs and 3 outputs. Mx-cqca has one of its outputs working as a multiplexer that will help in mapping the sequential circuits based on it, while the other two outputs work as AND and OR gates, respectively. The mapping of the inputs to outputs of the MX-cqca is: \(o_0 = i_{0}i_1\); \(o_1 = i_{0}i_1' + i_{1}i_2\); \(o_2 = i_2 + i_3\), where \(i_o\), \(i_1\) and \(i_2\) are the inputs and \(o_o\), \(o_1\) and \(o_2\) are the outputs, respectively. Figure 21 shows the block diagram of the MX-cqca gate. Table 3 shows the truth table of the MX-cqca gate. The table verifies the gate’s conservative logic nature, i.e., the numbers of 1s in the inputs is equal to the number of 1s in the outputs. Figures 22 and 23 show the QCA design and layout of the proposed MX-cqca gate. From the QCA design, we can observe that the proposed MX-cqca gate requires 4 clocking zones and 5 majority gates for its QCA implementation. Table 4 shows the comparison between the proposed MX-cqca gate and the Fredkin gate in terms of area and number of QCA cells. The table illustrates that MX-cqca is better than the existing Fredkin gate for implementing multiplexer-based designs. The MX-cqca gate requires 5 majority voters and 218 QCA cells with an area of \(0.71\,\mathrm{{um}}^{2}\). Thus, it has 1 less majority gate, 1 less inverter, 11 % less QCA cells and 5.4 % less area compared to the Fredkin gate.

Fig. 21.
figure 21

Proposed MX-cqca gate

Full size image
Table 3. Truth table of MX-cqca gate
Full size table
Fig. 22.
figure 22

QCA design of MX-cqca gate

Full size image
Fig. 23.
figure 23

QCA layout of MX-qca gate. CW represents cross wire resulted from intersection of binary wire and inverter chain, MV represents majority voter

Full size image
Table 4. A comparison of Fredkin and MX-cqca gates
Full size table
Table 5. Fault patterns in Mx-cqca gate
Full size table
Fig. 24.
figure 24

Modeling of MX-qca gate QCA layout

Full size image
Fig. 25.
figure 25

QCA layout of Mx-cqca gate testable with only all 0s and all 1s test vectors for any single missing/additional cell defect (the shaded devices represent their fault tolerant counterpart)

Full size image
Fig. 26.
figure 26

MX-cqca gate for fanout and inversion of input B

Full size image

We also modeled the QCA layout of the MX-cqca gate using the HDLQ Verilog library for performing the fault testing. The HDLQ model of the QCA layout of the Fredkin gate is shown in Fig. 24. Thus it can be observe that modeled QCA layout have 4 FOs, 1 INV, 5 CWs, 8 LSWs and 5 MVs. We conducted exhaustive testing of the HDLQ model of the Mx-cqca gate with 8 input patterns in the presence of all possible single missing/additional cell defects. Testing of the Mx-cqca gate generates 24 unique fault patterns at the output, as shown in Table 5.

From fault tables we can see that there are 9 fault patterns 3, 7, 13, 17, 19, 20, 22, 23, 24 that will produce the correct outputs for test vectors a0 and a7 (all 0s and all 1s) even when there is fault. Thus two test vectors a0 and a7 can only provide 62.5 % fault coverage. Thus in order to give the test vectors 100 % fault coverage we identified the logic devices in the HDLQ model of the Mx-cqca gate which can be replaced by their fault-tolerant counterpart to give the 100 % fault coverage to two test vectors all 0s and all 1s, for any single missing/additional cell defect. We observed that fanout (\(F0_{3}\)), inverter (\(INV_{1}\)), crosswire (\(CW_{4}\)) and majority voters (\(MV_{1}\), \(MV_{2}\), \(MV_{3}\), \(MV_{4}\) and \(MV_{5}\)) are devices in the QCA layout of the Mx-cqca gate that are making the design untestable by all 0s and all 1s test vectors. In the existing literature, several fault tolerant QCA components have been proposed such as Majority voters (MVs), Inverters (INVs), Fanouts (FOs), Crosswires (CWs) and L-shape wires (LSWs) [12, 15, 16, 74]. Thus, these devices can be replaced by their fault tolerant counterparts to have the equivalent design that gives 100 % fault coverage to test vectors, all 1s and all 0s, for any single missing/additional cell defect. The HDLQ model of the QCA layout having 100 % coverage for single missing/additional cell defect by all 0s and all 1s test vectors is shown in Fig. 25. The shaded devices in the Fig. 25 represent their fault tolerant counterparts. Thus, conservative logic QCA circuits based on the QCA layout of the Mx-cqca gate illustrated in Fig. 25, can be tested by all 0s and all 1s test vectors for presence of single missing/additional cell defect.

9 Design Methodology for Non-reversible Testable Design Based on MX-cqca Gate

The proposed conservative logic gate ‘MX-cqca’ is useful in designing any majority logic and multiplexer logic based testable non-reversible circuits. In the existing literature 13 standard functions are proposed to represent all three-variable Boolean functions [77]. These thirteen functions are widely used in QCA and majority logic based synthesis [37, 38]. The 13 standard functions and their mapping based on MX-cqca gate is shown in Table 6. Thus based on Table 6 any three variable Boolean functions can be implemented based on MX-cqca gate. In Table 6, the complement of a input variable is used which can be easily generated using the MX-cqca as shown in Fig. 26. In order to design any complex function based on MX-cqca, the input function can be decomposed into the Boolean network in which every node has atmost three variables. Next, each node of three variables can be mapped to Mx-cqca gates based on Table 6. Finally, as fanout is not allowed in conservative logic, the nodes having fanout of more than one needs to be identified. At these identified nodes, MX-cqca gates need to be used to form the copy of the signals which have fanout of more than one. Figure 26 shows the use of the Mx-cqca gate to copy a signal (input \(i_1\) is copied to outputs \(o_0\) and \(o_2\) of the MX-cqca gate). The proposed design methodology can be summarized in the following three steps:

  • Step 1: The input function is decomposed into the Boolean network in which every node has atmost three variables. This step is similar to the design methodology proposed in [29].

  • Step 2: The three variable functions generated at every node in Step 1 are mapped to their MX-cqca based implementation based on the thirteen standard functions. The MX-cqca based implementation of thirteen standard functions is shown in Table 6.

  • Step 3: The nodes which have fanout of more than one are identified, and MX-cqca gates are used to form the copy of the signals which have fanout of more than one.

Table 6. MX-cqca based implementation of standard functions
Full size table

10 Discussion and Conclusions

This work proposes testable reversible sequential circuits based on conservative logic. Conservative logic is testable for any unidirectional stuck-at faults using only two test vectors, all 0s and all 1s. The proposed conservative reversible sequential circuits have feedback that deters their testing by only two test vectors, thus a technique is demonstrated to disrupt the feedback in test mode. Experimental simulation on a single missing/additional cell defect has verified the application of the conservative logic towards fault testing in QCA computing. A new conservative gate (Mx-cqca gate) that is not reversible is also proposed especially suiting QCA computing. There are some major challenges associated with Mx-cqca based designs. Researchers have proposed several implementation techniques for QCA devices such as semiconductor, molecular QCA and magnetic QCA. However QCA devices are difficult to fabricate due to defects such as cell displacement, cell misalignment and cell omission Thus, all the fabricated and tested QCA designs are limited to small logic gates such as majority voter, fanout, and wire design. Thus, until a complex design such as an adder, multiplier and memory components are fabricated and tested in QCA computing; research community would have to wait to practically realize the Mx-cqca based designs. Further, the current literature lacks in the research about synthesis of QCA circuits. There is no synthesis tool for mapping HDL descriptions to QCA designs and to their corresponding QCA layouts to enable simulation using the QCADesigner tool. Thus, in order to implement Mx-CQCA based designs, a synthesis tool is needed that will be equivalent of an HDL description to layout generation tool in conventional CMOS computing is needed. There is also a need of a tool that can approximate the power dissipation in proposed Mx-cqca based design.

The proposed sequential circuits based on conservative logic gates outperform the sequential circuit implemented in classical gates in terms of testability. As the sequential circuits implemented using conventional classic gates does not provide inherited support for testability. A conventional sequential circuit needs modification in the original circuitry to provide the testing capability. Also as the complexity of a sequential circuit increases the number of test vector required to test the sequential circuit increases rapidly. For example, to test a general sequential circuit more than 2000 test vectors are required to test stuck at faults of the entire circuit, while if the same sequential circuit is build using proposed reversible sequential building blocks it can be tested using only two test vectors. The main advantage of proposed conservative logic gate based reversible sequential circuits compared to the conventional sequential circuit is that, the number of test vectors required to test the reversible sequential circuit is always two test vectors and the complexity of the circuit does not impact the number of test vectors. The proposed design of reversible sequential building blocks minimizes the overhead of test time for a reversible sequential circuit. A limitation of the proposed work is that it cannot detect multiple missing/additional cell defects. In conclusion, this work advances the state of the art of testing reversible sequential circuits based on stuck-at-fault model, as well as, reversible circuits implemented in QCA circuits having single missing/additional cell defect.