Fuzzy Multiple Criteria Decision Making for Supply Chain Management

Abstract

Supply Chain Management (SCM) problem can be simply described as if an enterprise is requested to provide adequate commodities to its customers on time, it should be able to design its own appropriate purchase/production/transportation network at the lowest-cost level in time. Modeling SCM by fuzzy mathematical programming is an innovative and a popular issue, this chapter introduces fuzzy multiple attribute decision making (FMADM) and fuzzy multiple objective programming (FMOP) for the solutions of SCM.

1 Introduction

Recently, the global market schemes have generated new concepts in various economic and industrial sectors. Supply Chain Management (SCM) optimally integrates the operational networks from material suppliers to end customers, which is the most popular issue since 2000 (Chen and Tzeng 2002; Zarandi et al. 2002; Zhou et al. 2008).

Fuzzy models are also popular in the field of SCM. The advantages and disadvantages of fuzzy models are:

Advantages

• Flexibility

• Convenient user interface

• Easy computation

• Learning ability

• Quick validation

• Ambiguousness

• Combination with existed models.

Disadvantages

• Insufficient experimental evidence

• Many manual setting parameters

• Unclear options

• Dimensionality/complexity of building models for beginners.

Readers should be aware of the limitations of fuzzy models in advance. In addition, some academic fields are against the fuzzy models. This is why in the literature review most of previous models are crisp, rather than fuzzy. This chapter is dedicated to Fuzzy Multiple Criteria Decision Making (FMCDM) methods for SCM. The method of FMCDM is considering the conflicts/trade-off among multiple criteria in order to make the optimal decision (Chen and Hwang 1992).

Supply Chain Management could be simply defined as if an enterprise is requested to provide adequate commodities to its customers on time, it should be able to design its own appropriate purchase/production/transportation network at the lowest-cost level in time (Chopra and Meindl 2010; Dobrila 2001; Dobrila et al. 1998). This idea is simply illustrated in Fig. 1.

Fig. 1

Framework of supply chain

The important issues of managing supply chain summarized by Chopra and Meindl (2010) are:

• Forecasting

• Aggregate planning

• Inventory control

• Level of availability

• Network design: transportation and location

• Information technology (IT) and e-business.

Considering the published papers strongly related to FMCDM, only the topics of fuzzy multi-objective programming (FMOP) and fuzzy multi-attribute decision making (FMADM) are focused in this chapter. In such a case, not all important SCM issues above will be presented. The chapter is organized as follows: Sect. 2 is used to present the basics of fuzzy multi-objective programming and fuzzy multi-attribute decision making, i.e., a fuzzy ranking method. Section 3 gives the game model with FMOP and FMADM. Section 4 proposes the Data Envelopment Analysis (DEA) by FMOP. Finally, conclusions and recommendations are available in Sect. 5, some advanced issues are also discussed here.

Modeling SCM by fuzzy mathematical programming is an interesting, innovative and a popular issue, here the fuzzy art of modeling SC is summarized by some categories in Table 1, which includes the major studying areas of modeling SC by fuzzy sets.

Table 1 Fuzzy models for SCM

Generally speaking, it is easy to find the SCM articles of aggregate planning than the other categories, mathematical programming is the most popular technique. But the number of using FMCDM methods is comparatively less.

2 Fuzzy MCDM

The basics of FMOP and FMADM will be clearly illustrated here.

2.1 Fuzzy Multi-objective Planning

Zimmermann’s fuzzy linear programming with i linear objective functions is defined as follows (Zimmerman 1985):

$$ \begin{aligned} & {\text{Max}}\;f\left( x \right) = (f_{1} (x),f_{2} (x), \ldots ,f_{i} (x))^{T} \\ & st \\ & {\mathbf{A}}x \leq b, \; {{x}} \geq {\mathbf{0}} \\ \end{aligned} $$

(1)

f _i (x):

The objective function, $f_{i} \left( x \right) = c_{i} x, \quad i = 1, 2, \ldots ,p$;

x :

the decision variable, $\varvec{x} = \left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right)^{T}$;

b :

the Right Hand Side (RHS) value, $\varvec{b} = \left( {b_{1} ,b_{2} , \ldots ,b_{m} } \right)^{T}$;

A :

the coefficient matrix, $A = \left[ {\alpha_{i,j} } \right]_{m \times n.}$.

The advantages and disadvantages of FMOP are:

• Advantages

  • Multiple objectives are considered at one time

  • Easy computation.

• Disadvantages

  • Membership functions should be set first: each objective has an individual setting

  • Many computations for one problem.

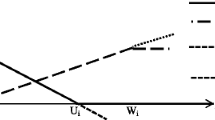
For each of the objective function $f_{i} \left( x \right), \; i = 1,2,\ldots,p$; of this problem, assuming that the decision maker has a fuzzy goal, e.g., maximizing the profit; thus, the corresponding linear membership function $\mu_{i}^{L} \left( f_{i} \left( x \right) \right)$ is defined as:

$$ \mu_{i}^{L} \left( {f_{i} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}c} 0 & ; & {f_{i} \left( x \right) \le f_{i} \left( x \right)^{ - } } \\ {\frac{{f_{i} \left( x \right) - f_{i} \left( x \right)^{ - } }}{{f_{i} \left( x \right)^{ + } - f_{i} \left( x \right)^{ - } }}} & ; & {f_{i} \left( x \right)^{ - } \le f_{i} \left( x \right) \le f_{i} \left( x \right)^{ + } } \\ 1 & ; & {f\left( x \right) \ge f_{i} \left( x \right)^{ + } } \\ \end{array} } \right. $$

(2)

$f_{i} \left( x \right)^{ - }$ denotes the objective value of pessimistic expectation by a decision maker, and $f_{i} \left( x \right)^{ + }$ denotes the objective value of optimistic expectation by a decision maker. His membership function is shown in Fig. 2 (Zimmerman 1985).

Fig. 2

Achievement level/aspiration degree for each fuzzy goal

Using such a linear membership function $\mu_{i}^{L} \left( {f_{i} \left( x \right)} \right), \; i = 1,2,\ldots,p$; and apply the min operator, the original problem can be changed as in Eq. (3) by interpreting the auxiliary variable $\lambda$:

$$ \begin{aligned} & {\text{Max}} \;\lambda \\ & st \\ & \lambda \leq \mu_{i}^{L} \left( {f_{i} \left( x \right)} \right) ,\quad i = 1,2, \ldots ,p \\ & {\mathbf{A}}x \le \varvec{b},\;\varvec{x} \ge 0 \\ \end{aligned} $$

(3)

Equation (1.3) is the fuzzy transformation for general uses. A supply chain game to show the aggregate planning is available in Sect. 3.

• (1) Fuzzy Multi-Attribute Decision Making

Here two MADM techniques: Fuzzy Analytical Hierarchy Process (FAHP) and FMADM game are presented.

FAHP

Thomas L. Saaty, professor in Pittsburgh University in U.S.A., developed AHP method in 1971 and it is applied popularly recently among economics, society, management field, etc. to dealing with complicated policy decision (Chen and Hwang 1992). The advantages and disadvantages of AHP are:

• Advantages

  • Easy understanding for users

  • Easy computation.

• Disadvantages

  • Consistency test is complicated

  • Questionnaire consumes much time because of the pair-wise comparison.

However, in real situation, the recognition of the interviewee is often fuzzy, thus “capital” criteria “much” more important than “secure sanitary management, and If the evaluation scale which Saaty offered was expressed, the definition of “much more” maybe just 1/7, 1/8, 1/9, in other words, there exits some differences between the pair comparative values and the real recognition cognition of the interviewees. For expressing the feeling of the interviewees more accurately, the following adopts fuzzy theory to handling the linguistic scale problems.

• (i) Triangular Fuzzy Number

A triangular fuzzy number ${{\tilde{A}}}$ whose value point is $(a_{1} ,a_{2} ,a_{3})$ (Fig. 3), and the membership function will be defined as Eq. (4):

$$ \mu_{{\tilde{A}}} (x) = \left\{ \begin{array}{ll} 0,\qquad x < a_{1}\\ \frac{{x - a_{1} }}{{a_{2} - a_{1} }},\qquad a_{1} \le x \le a_{2} \\ \frac{{a_{3} - x}}{{a_{3} - a_{2} }},\qquad a_{2} \le x\le a_{3} \\ 0,\qquad x > a_{3} \\ \end{array}\right.$$

(4)

Fig. 3

Triangular fuzzy number $\tilde{A}$

• (ii) Fuzzy Number Calculating

Now there are two fuzzy numbers

$$ \tilde{A} = (a_{1} ,a_{2} ,a_{3} ),\tilde{B} = (b_{1} ,b_{2} ,b_{3} ), $$

then

$$ \begin{aligned} (a_{1} ,a_{2} ,a_{3} ) \oplus (b_{1} ,b_{2} ,b_{3} ) &= (a_{1} + b_{1} ,a_{2} + b_{2} ,a_{3} + b_{3} ) \hfill \\ (a_{1} ,a_{2} ,a_{3} ) \otimes (b_{1} ,b_{2} ,b_{3} ) &= (a_{1} b_{1} ,a_{2} b_{2} ,a_{3} b_{3} ) \hfill \\ \tilde{A}^{ - 1} &= (a_{1} ,a_{2} ,a_{3} )^{ - 1} \cong (\frac{1}{{a_{3} }},\frac{1}{{a_{2} }},\frac{1}{{a_{1} }}) \hfill \\ \end{aligned} $$

(5)

• (iii) α-Cut (Fig. 4)

  Fig. 4

  

  α - cut

$$ \begin{aligned} & \forall \alpha \in \left[ {0,1} \right],\tilde{A}\;{\text{of}}\;\alpha {-} cut\;{\text{shows}}\;{}^{\alpha }\tilde{A},\;{\text{and}} \hfill \\ & {}^{\alpha }\tilde{A} = \left[ {(a_{2} - a_{1} )\alpha + a_{1} , -\, (a_{3} - a_{2} )\alpha + a_{3} } \right] = [{}^{\alpha }a_{l} ,{}^{\alpha }a_{r} ] \hfill \\ \end{aligned} $$

(6)

• (iv) Fuzzy AHP

FAHP (Fuzzy Analytic Hierarchy Process) is offered by Buckley in 1985. The method makes the pair comparative value in AHP offered by Saaty, and calculates the fuzzy weight with Geometric Mean Method. The theory and methodology are as follow. Consider a fuzzy orthogonal matrix $\tilde{A} = [\tilde{a}_{ij} ]$, and $\tilde{a}_{ij} = (\alpha_{ij} ,\beta_{ij} ,\gamma_{ij} ,\delta_{ij} )$ is a trapezium fuzzy number. Taking Saaty’s max-λ method as base and considering:

$$ \tilde{A} \otimes \tilde{w} = \tilde{\lambda } \otimes \tilde{w} $$

(7)

In which $\tilde{w}^{T} = (\tilde{w}_{1} , \cdot \cdot \cdot ,\tilde{w}_{m} ),\;\tilde{w}_{i} = (\tilde{\varepsilon }_{i} ,\tilde{\xi }_{i} ,\tilde{\eta }_{i} ,\tilde{\theta }_{i} ),\quad \tilde{\lambda } = (\tilde{\lambda }_{1} ,\tilde{\lambda }_{2} ,\tilde{\lambda }_{3} ,\tilde{\lambda }_{4} )$ are all fuzzy numbers. Where $A = [\alpha_{ij} ],B = [\beta_{ij} ],\,\,C = [\gamma_{ij} ],D = [\delta_{ij} ]$.

Let $A = [\alpha_{ij} ],B = [\beta_{ij} ],\,\,C = [\gamma_{ij} ],D = [\delta_{ij} ]$, then

${\mathbf{x}}^{1} = (\varepsilon_{1} ,\cdot \cdot \cdot ,\varepsilon_{m} )^{T} ,{\mathbf{x}}^{2} = (\xi_{1} ,\cdot \cdot \cdot ,\xi_{m} )^{T} , { } {\mathbf{x}}^{3} = (\eta_{1} ,\cdot \cdot \cdot ,\eta_{m} )^{T} , { }{\mathbf{x}}^{4} = (\theta_{1} ,\cdot \cdot \cdot ,\theta_{m} )^{T}$ Then Eq. (7) will be adapted as

$$ A{\mathbf{x}}^{1} = \lambda_{1} {\mathbf{x}}^{1} , { }B{\mathbf{x}}^{2} = \lambda_{2} {\mathbf{x}}^{2} , { }C{\mathbf{x}}^{3} = \lambda_{3} {\mathbf{x}}^{3} , { }D{\mathbf{x}}^{4} = \lambda_{4} {\mathbf{x}}^{4} , $$

In such a case, there will be four sets of max-λ and eigenvalues, so they cannot be coped with the problem with Saaty’s max-λ. Therefore Buckley led in one method for calculating fuzzy weight and fuzzy utilities.

• (v) Fuzzy Weight

Hypothesizing $A = [a_{ij} ]$ as a positive reciprocal matrix, and listing the geometric mean value

$$ r_{i} = \left( {\prod\limits_{j = 1}^{m} {a_{ij} } } \right)^{1/m} ,w_{i} = r{}_{i}/(r_{1} + r_{2} + \ldots + r_{m} ) $$

If m = 3, the result is the same as Saaty’s max-λ, If m > 3, the two results of both methods are pretty close.

Now if assuming $\tilde{A} = [\tilde{a}_{ij} ]$, $\tilde{a}_{ij} = (\alpha_{ij} ,\beta_{ij} ,\gamma_{ij} ,\delta_{ij} )$ as the attribute (j = 1,2,…, m) of pair comparison matrix, then the fuzzy weight of the i-th attribute is:

$$ \tilde{r}_{i} = (\tilde{a}_{i1} \otimes \cdots \otimes \tilde{a}_{im} )^{1/m} , \; \tilde{w}_{i} = \tilde{r}_{i} \otimes (\tilde{r}_{1} \oplus \cdots \oplus \tilde{r}_{m} )^{ - 1} $$

(8)

Fuzzy MADM Game

Multiple Attribute Decision Making (MADM) is a management science technique, popularly used to rank the priority of alternatives with respect to their competing attributes in a crisp or a fuzzy environment (Chen and Hwang 1992; Chen and Larbani 2006).

$$ \tilde{D} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} } & {C_{2} } & \ldots & {C_{n} } \\ \end{array} } \\ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \ldots \\ {A_{m} } \\ \end{array} } & {\left[ {\begin{array}{*{20}c} {\tilde{a}_{11} } & {\tilde{a}_{12} } & \ldots & {\tilde{a}_{1n} } \\ {\tilde{a}_{21} } & {\tilde{a}_{22} } & \ldots & {\tilde{a}_{2n} } \\ \ldots & & & \\ {\tilde{a}_{m1} } & {\tilde{a}_{m2} } & \ldots & {\tilde{a}_{mn} } \\ \end{array} } \right]} \\ \end{array} $$

(9)

The advantages and disadvantages of FMADM game are:

• Advantages

  • No pair-wise comparison is needed: data collection and data input are simple

  • Friendly user interface: only a decision matrix is required.

• Disadvantages

  • Computation is complicated

  • Users are encouraged to understand the game theory.

The FMADM game is shown as follows: considering a fuzzy MADM problem with the fuzzy decision matrix (9)

FMADM game is a two-person zero-sum game. Here a DM is player A, who has m alternatives ($A_{i} ,i = 1,2, \ldots ,m$) with respect to n attributes ($C{}_{j},j = 1,2, \ldots ,n$); the normalized weight of $A_{i}$ is x _i , the normalized weight of C _j is y _j , $\tilde{a}_{ij}$ represents the evaluation of alternative i with respect to attribute j, i = 1,2,…, m and $\tilde{a}_{ij} \ge 0$; j = 1,2,…, n. Nature is player B, who gives the fuzzy decision matrix (9). This fuzzy MADM problem defined as the DM chooses the best alternative according to the available $\tilde{D}$ as a fuzzy matrix with triangular membership function, i.e. $\tilde{D} = (D^{L} ,\;D^{C} ,\;D^{U} )$. The membership function of $\tilde{D}$ is assumed in Fig. 5 and Eq. (10).

Fig. 5

Triangular fuzzy decision matrix ${\tilde{D}}$

$$ \begin{gathered} \mu_{{\tilde{D}}} (D) = \mu_{{\tilde{D}}} (\lambda D^{U} + (1 - \lambda )D^{L} ) = \mu (\lambda ) = \left\{ {\begin{array}{*{20}l} {0,} & {\lambda \le 0} \\ {\frac{\lambda - 0}{{\bar{\lambda } - 0}},} & {0 < \lambda < \bar{\lambda }} \\ {1,} & {\lambda = \bar{\lambda }} \\ {\frac{1 - \lambda }{{1 - \bar{\lambda }}},} & {\bar{\lambda } < \lambda < 1} \\ {0,} & {\lambda \ge 1} \\ \end{array} } \right. \hfill \\ \, \hfill \\ \end{gathered} $$

(10)

Thus, the $\tilde{D}$’s behavior can be described by various α-cuts:

$$ \tilde{D}_{\alpha } = [D_{\alpha }^{U} ,D_{\alpha }^{L} ] = \{D_{\alpha }^{U} + ( 1- )D_{\alpha }^{L} , [0,1]\} $$

(11)

A vector x in $IR^{m}$ is a mixed strategy of player A if it satisfies the following probability condition:

$$ x^{t} e_{m} = 1 $$

(12)

where the components of $x = [x_{1} ,x_{2} , \ldots ,x_{m} ]^{t}$ are greater than or equal to zero; e _m is an m × 1 vector, where each component is equal to 1. Similarly, a mixed strategy of player B is defined by $y = [y_{1} ,y_{2} , \ldots ,y_{n} ]^{t}$ and $y^{t} e_{n} = 1$. If the mixed strategies x and y, are proposed by players A (decision maker) and B (Nature) respectively, then the fuzzy expected payoff of player A is defined by

$$ x^{t} \tilde{D}y = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\tilde{a}_{ij} x_{i} y_{j} } } $$

(13)

The Eq. (13) is player A’s objective and should be maximized. Considering the two-person zero-sum game (9), x ^* and y ^* are optimal strategies under the Nash equilibrium: if $x^{t} \tilde{D}y^{*} \le \, x{}^{*t}\tilde{D}y^{*} \,$ and $x^{t*} \tilde{D}y \ge \, x{}^{*t}\tilde{D}y^{*}$, for any mixed strategies x and y. Player A’s objective is to maximize his pay-off over all possible x when player B chooses his best strategy y ^*. Player B’s objective is to minimize his pay-off over all possible y when player A chooses his best strategy x ^*.

The solution for the two-person zero-sum game is (9) a given α-cut derives from the optimal solutions of the following pair of optimization problems (14)–(15):

$$ \begin{aligned} {\mathop {\text{Max}}\limits_{x} } \; & {v_{A} } \\ st \quad & x^{t} D_{\alpha }^{U} \ge v_{A} \, e_{n}^{t} \\ & x^{t} D_{\alpha }^{L} \ge v_{A} \, e_{n}^{t} \\ & x^{t} e_{m} = 1,\;x \ge 0 \\ \end{aligned} $$

(14)

$$ \begin{aligned} {\mathop {Min}\limits_{y} } \; & {v_{B} } \\ st \quad & D_{\alpha }^{U} y \le v_{B} e_{m} \\ & D_{\alpha }^{L} y \le v_{B} e_{m} \\ & y^{t} e_{n} = 1, \; y \ge 0. \\ \end{aligned} $$

(15)

Moreover, the fuzzy score of each alternative is computed by the following interval:

$$ ES(A_{i} ) = [ \, x_{i,\alpha }^{*} \sum\limits_{j = 1}^{n} {a_{\alpha \, ij}^{L} y_{j,\alpha }^{*} } , \, x_{i,\alpha }^{*} \sum\limits_{j = 1}^{n} {a_{\alpha \, ij}^{U} y_{j,\alpha }^{*} \, ]} $$

(16)

The alternative with higher score is more preferred. Any de-fuzzy method can be used to decide the final rank of these alternatives.

Example 1

Experienced experts from various vendors and customers of this logistics company are invited to rank eleven candidate warehouse locations in Fig. 6 for Taipei. Multiple attributes for appropriately ranking the location of warehouse are collected—these attributes are land cost (C ₁), labor cost (C ₂), traffic congestion (C ₃), accessibility to the metropolitan (C ₄), accessibility to the industrial park (C ₅), accessibility to the international airport (C ₆) and accessibility to the international harbor (C ₇). These experienced logistics managers are asked to provide their evaluations of the locations with respect to attributes. These fuzzy values are ranged within the quality interval from 1 to 10 from the beneficial side, where “1” means the lowest degree and “10” means the highest degree.

Fig. 6

Candidate locations around the taipei metropolitan (yellow district)

An Excel interface with Visual Basic Application (VBA) is proposed to facilitate the use of fuzzy MADM game. The ranking results are available in Fig. 7. In addition, the fuzzy decision matrix is available in Table 2. According to the computational results and defuzzification by choosing the median between the lower bound and the upper bound for each alternative, the top three (most preferred) alternatives are: A ₄ > A ₉ > A ₁₀. Readers should recognize that only one fuzzy decision matrix: Table 2 is needed for the computation of Example 1, this is much simpler than the pair-wise comparison in FAHP. The ranking method provides here is appropriate to solve any priority problem in SCM.

Fig. 7

Ranking results by excel

Table 2 Fuzzy decision matrix for location decision

3 Supply Chain Game by FMOP

This section is designed to illustrate using FMOP on Supply Chain Game. The SC game will be deduced step by step so that readers are able to use or develop some advanced fuzzy games of their own.

3.1 Supply Chain Game

Game theory is concerned with the actions (strategies) of decision makers, who are aware that their actions affect each other (Rasmusen 1989). In addition to the Table 1 of literature review in Sect. 2, Nagarajan and Sošić (2008) mentioned about the cooperation analysis in SC game; in addition, Huang and Li (2001), and Li et al. (2002) also analyzed the SC performance from the game aspect. Interested readers may find the literature above for further reading. However, their formulations are crisp rather than using FMOP.

The advantages and disadvantages of game models are:

• Advantages

  • Rigid deduction process

  • Strong proofs in mathematics

  • Extension with existed models.

• Disadvantages

  • Users are encouraged to have sufficient background in mathematics

  • Complicated symbols for beginners because of formulations and extensions are very various and abstract.

A two-person zero-sum game is the simplest case of game theory with only two players. Such a game is resolved by assuming that both players propose pure (discrete), mixed (probability) or continuous strategies. The strategies proposed here for each partner will be its capacity to meet the maximal satisfaction: both from the micro scope and macro scope.

The degree of cooperation (or non-cooperation) between players is assumed to be vague in this study: the cooperation degree won’t be measured in this study; actually, it is an abstract idea. Let us consider the following n-person non-cooperative game in normal form (Rasmusen 1989):

$$ \left\langle {I, \, X, \, f\left( x \right)} \right\rangle $$

(17)

$I = \left\{ { 1,2, \ldots ,n } \right\}$ is the set of players, X is the set of situations of the game, X _i is the set of strategies of the i-th player, i = 1, 2, …, n; $f = \left( {f_{1} ,f_{2} , \ldots ,f_{n} } \right)$, f _i is the objective function of the i-th player; $x = \left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right) \in X$ is a situation of the game, $x_{i} \in X_{i}$ is the strategy of the i-th player, $i = 1,2, \ldots ,n$.

Definition 1

The game (17) is in the normal form if it is played one time.

Definition 2

The game (17) is non-cooperative if players cannot make enforceable agreements.

Definition 3

$x^{0} \in X$ is called Nash equilibrium of the game (17) if $\begin{array}{*{20}l} {\forall i \in I,} & {\forall x_{i} \in X_{i} ,} & {f_{i} \left( {x^{0} //x_{i} } \right)} \\ \end{array} \le f_{i} \left( {x^{0} } \right)$.

$\left( {x^{0} //x_{i} } \right)$ is the issue obtained from the issue x ⁰ by substituting the i-th component of the vector x ⁰ for x _i .

Definition 4

Suppose that in the game (17) there are n players, the pay-off function of each player is f _i and I = {1, 2, …, n}. Here the game is not necessarily non-cooperative. The relation between players is represented by the following n × n matrix:

$$ {\mathbf{C}} = \left[ {\begin{array}{*{20}c} {\alpha_{1,1} } & {\alpha_{1,2} } & \ldots & {\alpha_{1,n} } \\ {\alpha_{2,1} } & {\alpha_{2,2} } & \ldots & {\alpha_{2,n} } \\ \ldots & \ldots & \ldots & \ldots \\ {\alpha {}_{n,1}} & {\alpha_{n,2} } & \ldots & {\alpha_{n,n} } \\ \end{array} } \right]_{n \times n} $$

(18)

Thus, the Nash equilibrium of the game: $\left\langle {I, \, X, \, g\left( x \right) = {\text{C}} \times [f_{i} ]_{n \times 1} } \right\rangle$ is defined as A-Nash equilibrium (Aliged Nash equilibrium). Here $\alpha_{i,j} \in \left[ {\begin{array}{*{20}c} { - 1,} & 1 \\ \end{array} } \right]$, which represents the degree of cooperation between player i and player j or more precisely between two players. C is named as the “alliance matrix”.

Remark 1

If a coefficient α _i,j is positive, it is easy to show that there is cooperation between player i and player j because their pay-offs are united. If α _i,j is negative then it means that the player i is in competition with player j resulting from their interests are antagonistic. If α _i,j  = 0 then the player i is neutral according to player j. It is easy to formulate the Definition 4 for the general case of n-person game. Let us briefly illustrate our ideas of alliance matrix of a SC as follows:

• (1) each partner in a SC is playing the cooperative or non-cooperation game;

• (2) the cooperation degree α _i,j between partners can be regarded as their various alliances, e.g., $\alpha_{i,j} \in \left[ { - 1,\;1} \right]$;

• (3) such alliances among partners can be described by alliance matrix: A. Thus, consider n players in a SC, each partner’s objective is, e.g., $f_{1} ,f_{2} , \ldots ,f_{n}$, etc., their integrated objectives from the micro level can be expressed by the following equation:

$$ A \times f(x) = \left[ {\begin{array}{*{20}c} {\alpha_{11} } & {\alpha_{12} } & \ldots & {\alpha_{1n} } \\ {\alpha_{21} } & {\alpha_{22} } & \ldots & {\alpha_{2n} } \\ \ldots & \ldots & \ldots & \ldots \\ {\alpha {}_{n1}} & {\alpha_{n2} } & \ldots & {\alpha_{nn} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \ldots \\ {f_{n} } \\ \end{array} } \right] $$

(19)

where α _i,j represents the cooperation degree between partner i and partner j; α _i,j  = 1 if i = j and $\alpha_{i,j} \in \left[ { - 1,\;1} \right]$. The cooperation degree is arbitrarily decided in this study; however, exploring the measurement of α _i,j would be an interesting issue for readers.

3.2 Formulation and Resolution

In this section, a simple example is illustrated for SC game. Now Fig. 1 in Sect. 2 is used as the model formulation. The objective and constraints of each partner in the SC will be established. The symbols are shown in Table 3.

Table 3 Symbol notations

• (1) Supplier partner’s objective and constraints

The supplier partner’s objective is assumed to maximize its own net profits. And constraints are available storage space and working time.

$$ \begin{aligned} & {\text{Max}}\quad f_{s,t} = \mathop \sum\limits_{m \in M} \mathop \sum\limits_{e \in E} p_{s}^{e} x_{sm,t}^{e} - \mathop \sum\limits_{m \in M} \mathop \sum\limits_{e \in E} c_{s}^{e} x_{sm,t}^{e} , \forall s \in S,\forall t \in T \\ & st \\ & \mathop \sum\limits_{m \in M} x_{sm,t}^{e} \le {space_{s} }, {\forall s \in S,\forall t \in T} , \\ & \mathop \sum\limits_{m \in M} \mathop \sum\limits_{e \in E} wt_{s}^{e} x_{sm,t}^{e} \le {awt_{s} }, {\forall s \in } S, \forall t \in T, \\ \end{aligned} $$

(20)

• (2) Manufacturing partner’s objective and constraints

The Mfg. partner’s objective is similarly assumed to maximize its own net profits. And constraints are available storage space and working time. In addition, the manufacturing ability of each Mfg. partner is assumed various in the last constraint.

$$ \begin{aligned} & {\text{Max}}\quad f_{m,t} = \mathop \sum\limits_{l \in L} p_{m}^{{}} x_{ml,t}^{{}} - \mathop \sum\limits_{l \in L} c_{m}^{{}} x_{ml,t}^{{}} , \forall m \in M,\forall t \in T \\ & st \\ & \mathop \sum\limits_{l \in L} x_{ml,t}^{{}} \le {space_{m} }, {\forall m \in M,\forall t \in T} , \\ & \mathop \sum\limits_{l \in L} wt_{m}^{{}} x_{ml,t} \le {awt_{m} }, {\forall m \in } M,\forall t \in T, \\ & x_{ml,t} = \mathop \sum\limits_{e \in E} \mathop \sum\limits_{s \in S} p\,a_{m}^{e} {x_{sm,t}^{e} } , {\forall m \in } M,\forall t \in T, \\ \end{aligned} $$

(21)

• (3) Logistics partner’s objective and constraints

The logistics partner also achieves to maximize its own net profits. And constraints are available storage (the first one) space and constant flow (the last one).

$$ \begin{aligned} & {\text{Max}}\;f_{l,t} = \mathop \sum\limits_{v \in V} p_{lv} x_{lv,t} - \mathop \sum\limits_{v \in V} c_{lv} x_{lv,t} , \forall l \in L,\forall t \in T \\ & st \\ & \mathop \sum\limits_{l \in L} x_{lv,t} \le {space_{l} } , {\forall v \in V,\forall t \in T} , \\ & \mathop \sum\limits_{l \in L} wt_{m} x_{ml,t} \le {awt_{m} } , {\forall m \in } M,\forall t \in T, \\ & \mathop \sum\limits_{v \in V} x_{lv,t} = d_{v,t} ,\forall l \in L,\forall t \in T, \\ \end{aligned} $$

(22)

Finally, the following constraints of globally constant flow should be satisfied:

$$ \begin{aligned} \mathop \sum\limits_{m \in M} \mathop \sum\limits_{l \in L} x_{ml,t} & = \mathop \sum\limits_{l \in L} \mathop \sum\limits_{v \in V} x_{lv,t} = \mathop \sum\limits_{v \in V} d_{v,t} \quad {\forall t \in T} \\ \mathop \sum\limits_{m \in M} x_{ml,t} & = \mathop \sum\limits_{v \in V} x_{lv,t} , \quad \forall l \in L, \; \forall t \in T, \\ \end{aligned} $$

(23)

Therefore, the micro objective of SC game is presented as follows:

$$ {\text{Max}}\;A \times f\left( x \right) \equiv \left[ {\begin{array}{*{20}c} {\alpha_{11} } & \cdots & {\alpha_{17} } \\ \vdots & \ddots & \vdots \\ {\alpha_{71} } & \cdots & {\alpha_{77} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {f_{s = 1} } \\ \vdots \\ {f_{l = 2} } \\ \end{array} } \right] $$

(24)

And the macro objective is

$$ \begin{aligned} & {\text{Min}}\;\mathop \sum\limits_{s \in S} \mathop \sum\limits_{m \in M} tc_{sm,t} x_{sm,t} + \mathop \sum\limits_{m \in M} \mathop \sum\limits_{l \in L} tc_{ml,t} x_{ml,t} + \mathop \sum\limits_{l \in L} \mathop \sum\limits_{v \in V} tc_{lv,t} x_{lv,t} , \quad \forall t \in T \\ \end{aligned} $$

(25)

The optimization problem above is a vector optimization problem by considering the constraints of each partner simultaneously: i.e., this is a multi-objective optimization problem. And it is resolved by the fuzzy multi-objective approach (3) of Sect. 2.

Example 2

The model parameters of partners are arbitrarily set as follows.

• (1) Supplier Partner 1 (s = 1)

$$ \begin{aligned} & {\text{Max}}\quad f_{s = 1,t} = 3x + 4y - x - y,\forall t \in T, \\ & st\quad x + y \le 400,\forall t \in T \\ & \quad 2x + y \le 600,\forall t \in T, \\ \end{aligned} $$

(26)

• (2) Supplier Partner 2 (s = 2)

$$ \begin{aligned} & {\text{Max}}\quad f_{s = 2,t} = 4x + 3y - 2x - y,\forall t \in T, \\ & {\text{st}}\quad x + y \le 600,\forall t \in T \\ & \quad x + 2y \le 500,\forall t \in T, \\ \end{aligned} $$

(27)

• (3) Mfg. Partner 1 (m = 1)

$$ \begin{aligned} & {\text{Max}}\quad f_{m = 1,t} = 2z - z,\forall t \in T \\ & {\text{st}}\quad {\text{z}} = 2x + y,\forall t \in T \\ & \quad z \,\le\, 200,\forall t \in T, \\ & \quad 5z \,\le\, 900,\forall t \in T, \\ \end{aligned} $$

(28)

• (4) Mfg. Partner 2 (m = 2)

$$ \begin{aligned} & {\text{Max}}\quad f_{m = 2,t} = 4z - 2z,\forall t \in T \\ & {\text{st}}\quad {\text{z}} = x + 2y,\forall t \in T \\ & \quad z \,\le\, 600,\forall t \in T, \\ & \quad 2z \,\le\, 600,\forall t \in T, \\ \end{aligned} $$

(29)

• (5) Mfg. Partner 3 (m = 3)

$$ \begin{aligned} & {\text{Max}}\quad f_{m = 3,t} = 3z - 2z,\forall t \in T \\ & {\text{st}}\;{\text{z}} = x + y,\forall t \in T \\ & \quad z \,\le\, 300,\forall t \in T, \\ & \quad 3z \,\le\, 1000,\forall t \in T, \\ \end{aligned} $$

(30)

• (6) Logistics Partner 1 (l = 1)

$$ \begin{aligned} & {\text{Max}} \; f_{l = 1,t} = 6 x_{l = 1,v = 1} + 7x_{l = 1,v = 2} + 9x_{l = 1,v = 3} - x_{l = 1,v = 1} - x_{l = 1,v = 2} - 2x_{l = 1,v = 3} ,\forall t \in T \\ & {\text{st}} \\ & \quad x_{l = 1,v = 1} + x_{l = 1,v = 2} + x_{l = 1,v = 3} \le 500 \\ \end{aligned} $$

(31)

• (7) Logistics Partner 2(l = 2)

$$ \begin{aligned} & {\text{Max}}\quad f_{l = 2,t} = 7x_{l = 2,v = 1} + 6x_{l = 2,v = 2} + 7x_{l = 2,v = 3} - 3x_{l = 2,v = 1} - x_{l = 2,v = 2} - x_{l = 2,v = 3} ,\forall t \in T \\ & {\text{st}} \\ & \quad x_{l = 2,v = 1} + x_{l = 2,v = 2} + x_{l = 2,v = 3} \le 1000 \\ \end{aligned} $$

(32)

• (8) Transportation Cost (Table 4).

  Table 4 Transportation cost

3.3 Results and Discussions

Three scenarios: ideal cooperation (all partner are joined as a big union with only one objective), Stackberg competition (every partner maximizes its own pay-off by ignoring the pay-offs of others) and extreme competition (every partner maximizes its own pay-off by minimizing the pay-offs of others) are simulated for Example 2. Discussions are also presented in the end of this section.

The vendors’ demands are given first for each planning period, after that the problem is resolved by the fuzzy multi-objective approach (3) of Sect. 2. The first alliance matrix is the ideal cooperation case, the elements of are assumed as all ones. The second alliance matrix is the extreme competition case, the elements in A are all negative ones except the diagonal elements are positive ones. The third case is stackelberg competition case, the elements in A are all zeros, except the diagonal elements are ones. The global profit is defined as the sum of each partner’s profit. The computational results are summarized in Table 5.

Table 5 Computational results of various alliances

According to the computational results above, discussions are proposed as follows:

According to the simulation results, it is clear that the global achievement level: $\lambda$ value is Ideal cooperation > Extreme competition > Stackberg competition Extreme competition. This is beyond our previous imagination that: Stackberg competition > Extreme competition. Thus, from the macro scope, cooperation seems to add the global achievement level because the ideal cooperation case has the largest $\lambda$.

However, ideal cooperation doesn’t guarantee the maximal profit of each partner: especially satisfying the individual objective optimum of partner from the micro scope. This hints satisfying the allocation of global profit to each partner would be a challenging problem in the ideal cooperation case. If a partner feels unsatisfied for its individual objectives, then this partner may not be willing to join this supply chain. In short, globally maximal satisfaction doesn’t guarantee locally maximal satisfaction, and vice versa.

According to the simulation results, using the fuzzy multi-objective game theory for modeling SC is an interesting idea. A new and simple concept of alliance matrix is introduced, which is designed to describe the cooperation degree between partners. Simulation results reflect greater realities and show that ideal cooperation is the best from the macro scope; however, extreme competition could have better individual performance of partner from the micro scope. Because of these conflicts and selfishness of partners, ideal cooperation is not easy to survive in practices. About the future studies, our new model could be used to explore the real alliance between partners. This means, readers are encouraged to extend and modify the SC model proposed here in order to meet their customized needs. A more complicated and advanced game via FMOP is available in the paper of Chen et al. (2010).

4 Fuzzy Data Envelopment Analysis for Supply Chain Management

This section is designed to illustrate the basic concepts of DEA by using FMOP. The extension from basic form will be deduced step by step so that readers are able to use or develop some advanced DEA by FMOP.

4.1 Basic DEA

Data envelopment analysis (DEA) defines mathematical programming of the outputs/inputs ratio as the index of production efficiency, developed by Charnes, et al. (1978), and followed by many others (Chen et al. 2009; Karsak and Ahiska 2007; Seiford 1996). The advantages and disadvantages of DEA are:

Advantages

• Ratio concept is easy for users

• Easy computation.

Disadvantages

• Not all inputs and outputs can be quantified

• Many decision making units (DMUs) could have the same and the highest scores, i.e., one (low discrimination power)

• Dual form of DEA is complicated.

The DEA model, developed by Charnes, et al. (1978), is changing the fractional programming problem to a linear mathematical programming model, which is able to handle several inputs and outputs. This model assumes n decision-making units (DMUs), with m inputs and p outputs, where the efficiency evaluation model of the k-th DMU can be defined as in Eq. (33).

$$ \begin{aligned} {\text{Max}}\quad f_{k} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rk} } }}{{\sum\limits_{i = 1}^{m} {v_{i} } x_{ik} }} \\ \text{{s}.{t}}.\quad \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rl} } }}{{\sum\limits_{i = 1}^{m} {v_{i} } x_{il} }} \le 1,\;l = 1, 2, \ldots ,n; \\ \qquad u_{r} \ge \varepsilon ,\;r = 1,2, \ldots ,p; \\ \qquad v_{i} \ge \varepsilon ,\;i = 1,2, \ldots ,m. \\ \end{aligned} $$

(33)

where

x _il :

the i-th input value for l-th DMU;

y _rl :

the r-th output value for the l-th DMU;

u _r :

the weight values of the r-th output;

v _i :

the weight values of the i-th input i,

ɛ :

a very small positive value.

Obtaining the solution from Eq. (33) is difficult because it is a nonlinear programming problem. Charnes et al. transformed Eq. (33) into a linear programming problem by assuming $\sum\limits_{i = 1}^{m} {v_{i} } x_{ik} = 1$.

4.2 DEA with Fuzzy Inputs and Outputs

There are many available models for fuzzy DEA, which are based on various assumptions and deductions. The idea with fuzzy inputs and outputs here (Chen 2002) is modified from the model of Nagano et al. (1995).

First, considering the firm n as the reference point in a DEA model, i.e.,$\sum\limits_{r} {v_{i} } x_{in}^{M} = 1$. Let $\tilde{\theta }_{n} = (\theta_{n}^{L} ,\theta_{n}^{M} ,\theta_{n}^{U} ) = \left (\sum\limits_{r} {u_{r} } y_{rn}^{L} ,\sum\limits_{r} {u_{r} } y_{rn}^{M} ,\sum\limits_{r} {u_{r} } y_{rn}^{U} \right)$. Thus, there are two desired objectives for this DEA model with fuzzy data:

• (1) the fuzzy width of $\tilde{\theta }_{n}$ should be minimized—this situation is shown in Fig. 8,

  Fig. 8

  

  Fuzzy inputs and outputs

• (2) the overlap area in Fig. 8 should be minimized—the bounded area of triangle abc in Fig. 8 should be minimized.

The triangular fuzzy inputs and outputs are analyzed as in Fig. 8 with more details.

The first intersection type of $\mathop \sum \nolimits_{r} u_{r} \tilde{y}_{rk}$ and $\mathop \sum \nolimits_{i} v_{i} \tilde{x}_{ik}$ is analyzed as follows: considering two fuzzy numbers, the weighted sum of fuzzy outputs: $\mathop \sum \nolimits_{r} u_{r} \tilde{y}_{rk}$, which is denoted by $\tilde{Y}$; and the weighted sum of fuzzy inputs: $\mathop \sum \nolimits_{i} v_{i} \tilde{x}_{ik}$ which is denoted by $\tilde{X}$. $\tilde{X}$ and $\tilde{Y}$ may have some overlap area (intersection) in actuality—which will cause the vagueness of $\frac{{\tilde{Y}}}{{\tilde{X}}}$. Since the fuzzy efficiency score is defined by $\frac{{\tilde{Y}}}{{\tilde{X}}}$ and the unclear degree of $\frac{{\tilde{Y}}}{{\tilde{X}}}$ is the maximal $\mu_{{\frac{{\tilde{Y}}}{{\tilde{X}}}}} = \mathop {\sup }\limits_{{\frac{{\tilde{Y}}}{{\tilde{X}}}}} \hbox{min} \left( {\mu_{{\tilde{Y}}} ,\mu_{{\tilde{X}}} } \right) = h_{3t}$, the lower the $h_{3t}$ (e.g., h _3t  = 0 means the computational result of $\frac{{\tilde{Y}}}{{\tilde{X}}}$ is very clear instead of fuzzy), the more reliability level of $\frac{{\tilde{Y}}}{{\tilde{X}}}$—the maximal reliability level of $\frac{{\tilde{Y}}}{{\tilde{X}}}$ is $1 - h_{3t}$. Therefore, the following concept can be deduced: the larger the overlap area, the lower reliability level when viewing the final efficiency scores of firms. If the overlap area between the weighted sum of fuzzy inputs and outputs can be reduced as small as possible—the optimal case is no overlap area; thus, the evaluated scores of firms by a DEA will be closer to the actuality with higher reliability. Furthermore, the weighted sum of outputs has no chance to be greater than the weighted sum of outputs and resulting in: $\mathop \sum \nolimits_{r} u_{r} \tilde{y}_{rk}$ is less than or equal to $\mathop \sum \nolimits_{i} v_{i} \tilde{x}_{ik}$ in a traditional DEA model with crisp data. However, the weighted sum of outputs almost all fall down the left side of point b-except the overlap area between $\mathop \sum \nolimits_{r} u_{r} \tilde{y}_{rk}$ and $\mathop \sum \nolimits_{i} v_{i} \tilde{x}_{ik}$ (see Fig. 8) in a fuzzy condition. The overlapping degree: $h_{3t}$ can be regarded as the degree of DMUs going outside the enveloped efficiency frontier by the modified DEA model. The efficiency scores of these un-enveloped DMUs are possibly greater than 1 in the extended DEA model. Of course, this h _3t should be reduced as small as possible so as to reflect more actuality and maximize the reliability of efficiency scores—all DMUs can be enveloped within the efficiency frontier if h _3t  = 0. In addition to the first type of intersection between $\mathop \sum \nolimits_{r} u_{r} \tilde{y}_{rk}$ and $\mathop \sum \nolimits_{i} v_{i} \tilde{x}_{ik}$, the second intersection type is explained as follows: let the weighted sum of fuzzy outputs has a triangular fuzzy membership function of firm n like that in Fig. 8. Consider the fuzzy number: $\tilde{X}$ again, which is intersected with $\tilde{Y}$; moreover, $h_{1n}$ and $h_{2n}$ are created by the intersection points between $\tilde{X}$ and $\tilde{Y}$ (see Fig. 9). These two heights: $h_{1n}$ and $h_{2n}$, represent the reliability levels for the weighted sum of fuzzy outputs for the reference point: $n^{th}$ DMU, where the objective function of maximizing the fuzzy efficiency score can be obtained—because that $\mu_{{\frac{{\tilde{Y}}}{{\tilde{X}}}}} = \mathop {\sup }\limits_{{\frac{{\tilde{Y}}}{{\tilde{X}}}}} \hbox{min} \left( {\mu_{{\tilde{Y}}} ,\mu_{{\tilde{X}}} } \right) = \hbox{max} \left( {h_{1n} ,h_{2n} } \right)$ in such an intersection case of $\tilde{X}$ and $\tilde{Y}$. The concept of this objective is shown as in Fig. 9—both $h_{1n}$ and $h_{2n}$ should be maximized so as to force the $\tilde{\theta }_{n}$ within the minimal width of fuzzy interval.

Fig. 9

The first objective

Finally, an extended DEA model is proposed as follows:

$$\begin{aligned} \rm{Max}\;\;h_{1n} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{L} } }}{{1 - \left(\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{M} - } \sum\limits_{r = 1}^{p} u_{r} y_{rn}^{L} \right)} } \\ \rm{Max}\;\;h_{2n} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{U} } }}{{1 + \left(\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{U} - } \sum\limits_{r = 1}^{P} {u_{r} y_{rn}^{M}} \right)} } \\ \rm{Min}\;h_{3t} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{U} } - \sum\limits_{i = 1}^{m} {v_{i} x_{it}^{M} } }}{{\sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{U} - } \sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{M} } }}\quad (t = 1, 2, \ldots ,k;\;t \ne n; ) \\ \text{s.t}.\quad \sum\limits_{i = 1}^{m} {v_{i} x_{in}^{M} = 1;\;} \\ 0 \le h_{1n} \le 1; \\ 0 \le h_{2n} \le 1; \\ 0 \le h_{3t} \le 1,\;t = 1,2, \ldots ,k,t \ne n; \\ & u_{r} \ge \varepsilon ,\; r = 1,2, \ldots ,p; \\ & v_{i} \ge \varepsilon ,\; i = 1,2, \ldots ,m; \\ n \in \{ 1,2, \ldots ,k\} . \end{aligned}$$

(34)

Here, $h_{1n}$ and $h_{2n}$ are the reliability levels for the weighted sum of fuzzy outputs for the reference point: n ^th DMU. Furthermore, h _3t denotes the degree of some DMUs going outside the piece-wise frontier only when $t \ne n;\;\sum\limits_{i = 1}^{m} {v_{i} x_{in}^{M} = 1}$ implies that the i ^th input resource of n ^th DMU is limited. Moreover, h _1n , h _2n and h _3t must be between 0 and 1 for normalized fuzzy sets.

It is clear that Eq. (34) is a multi-objective problem; thus, this problem can be translated to a fuzzy multi-objective problem in Eq. (35) by the general λ transformation.

$$\begin{aligned} \rm{Max}\;\lambda \\ \text{{s}.{t}}.\quad h_{1n} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{L} } }}{{1 - \left(\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{M} - } \sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{L}}\right)} } \ge \lambda \\ h_{2n} = \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{U} } }}{{1 + \left (\sum\limits_{r = 1}^{p} {u_{r} y_{rn}^{U} - } \sum\limits_{r = 1}^{P} {u_{r} y_{rn}^{M}} \right )} } \ge \lambda \\ 1 - h_{3t} = 1 - \frac{{\sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{U} } - \sum\limits_{i = 1}^{m} {v_{i} x_{it}^{M} } }}{{\sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{U} - } \sum\limits_{r = 1}^{p} {u_{r} y_{rt}^{M} } }} \ge \lambda \;(t = 1, 2, \ldots ,k;\;t \ne n;) \\ \sum\limits_{i = 1}^{m} {v_{i} x_{in}^{M} = 1;\;} \\ 0 \le \lambda \le 1; \\ 0 \le h_{1n} \le 1; \\ 0 \le h_{2n} \le 1; \\ 0 \le h_{3t} \le 1,\;t = 1,2, \ldots ,k,t \ne n; \\ & u_{r} \ge \varepsilon,\; r = 1,2, \ldots ,p; \\ v_{i} \ge \varepsilon ,\;i = 1,2, \ldots ,m; \\ n \in \{ 1,2, \ldots ,k\} . \end{aligned}$$

(35)

where λ can be regarded as the global reliability level of viewing the final efficiency scores, the higher the λ value, the less vagueness in the final results. Equation (35) is a non-linear programming problem, which should be resolved by the LINGO software. The predicted efficiency score will have a lower and upper bound at a global reliability level λ:

$$ \tilde{\theta }_{n} = \left (\theta_{n}^{L} ,\theta_{n}^{M} ,\theta_{n}^{U} \right ) = \left (\sum\limits_{r} {u_{r} } y_{rn}^{L} ,\sum\limits_{r} {u_{r} } y_{rn}^{M} ,\sum\limits_{r} {u_{r} } y_{rn}^{U} \right ) $$

(36)

Example 3

A simple example will be illustrated in this section so as to validate this extended DEA model with fuzzy data. These assumed crisp/fuzzy data are shown in Table 6.

Table 6 Assumed data of Example 3

After taking the Firm 2 as the reference point and inputting all the available data in Table 6, final results are obtained by LINGO in Table 7. The approach proposed here is suitable for taking the fuzzy input/output data into account. However, the fuzzy score in Table 7 may vary when the reference point is changed. Thus, some scholars try to find the common weight for DEA: maximizing the efficiency of each DMU simultaneously.

Table 7 Computational results

4.3 DEA of FMOP

The traditional DEA model is optimized for one single objective of the referred DMU (reference point). Many scholars from MCDM seek to optimize the performance of each DMU at the same time (Golany 1988; Kao and Hung 2005; Li and Reeves 1999), which is called as the common weight approach for DEA.

Chiang and Tzeng (2000) proposed the following FMOP approach to DEA. This method provided a common weight (μ ^*, ω ^*)for all DMUs, which were evaluated on an equal standard. By employing the FMOP approach, all DMUs can be treated at the same time. Hence it is effective for large numbers of DMUs. Considering the efficiency ratio of all DMUs, it can establish the multiple objective programming model as shown in Model (37):

$$ \begin{aligned} & \rm{Max}\;z_{1} = \frac{{\sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{r1} } }}{{\sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{i1} } }} \\ & \rm{Max}\;z_{2} = \frac{{\sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{r2} } }}{{\sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{i2} } }} \\ & \quad \quad \quad \quad \quad \quad \vdots \quad \\ & \rm{Max}\;z_{n} = \frac{{\sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{rn} } }}{{\sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{in} } }} \\ {\kern 1pt} & \text{st} \\ & \quad \frac{{\sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{rk} } }}{{\sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{ik} } }} \le 1{\kern 1pt} ,\quad k = \;1,2,\, \ldots ,n \\ & \quad \mu_{r} ,\omega_{i} \ge \varepsilon > 0,\forall r,i, \\ \end{aligned} $$

(37)

where

y _rk :

the observed amount of output of the $r^{th} \;(r = 1,\,2,\, \ldots ,s)$ type for the $k^{th} \,{\text{DMU}}(\,k = 1,\, \ldots ,\,n);\,$

x _ik :

the observed amount of input of the $i^{th} (i = 1,2,\; \ldots ,m)$ type for the $k^{th} \,{\text{DMU}}(k = 1,\, \ldots ,\;n);$

ω _i :

the multiplier or weight of the $i^{th }$ input;

μ _r :

the multiplier or weight of the $r^{th}$ output;

ε :

non-Archimedean quantity.

Model (37) is a multiple objective programming (MOP). In this model, we try to solve a common weight, which makes all the DMU’s efficiency maximal at the same time. It can be solved by the FMOP approach proposed by Zimmermann in Eq. (3) of Sect. 1. The concept of FMOP utilizing the membership function transfers multi-objective function into one objective function. The membership function is as follows:

$$ \mu_{j} (z_{j} ) = \left\{ {\begin{array}{*{20}l} 0 & ; & {z_{j} \le z_{j}^{ - } } \\ {\frac{{z_{j} - z_{j}^{ - } }}{{z_{j}^{ + } - z_{j}^{ - } }}} & ; & {z_{j}^{ - } \le z_{j} \le z_{j}^{ + } } \\ 1 & ; & {z_{j} \ge z_{j}^{ + } } \\ \end{array} } \right. $$

(38)

where $z_{j}^{ - }$ and $z_{j}^{ + }$ are the negative ideal solution and the positive ideal solution respectively for the value of the objective function $z_{j}$ such that the degree of membership function is [0, 1]. The geometric view of the linear membership function is shown in Fig. 10.

Fig 10

Linear membership function of z _j

The degree of membership function of $z_{j}$ in $\mu (z_{j} )$ refers to the achievement level of the efficiency ratio for the ${\text{DMU}}_{j}$. The problem of obtaining the maximum decision is to choose $(\mu^{*} ,\omega^{*} )$ such that

$$ \begin{aligned} &\rm \mathop {Max}\limits_{\mu ,\;\omega } \rm \mathop {Min}\limits_{j} \; \left\{{\;\mu_{{_{j} }} (z_{j} )\;\left|{\,j = 1,2, \ldots } \right.,n\;}\right\} \\ & \text{st} \\& \quad \frac{{\sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{rk} }}}{{\sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{ik} } }} \le1,\quad j = 1,2, \ldots ,n \\ & \quad \mu (z_{j} ) \ge \alpha \\& \quad \mu_{r} ,\;\omega_{i} \ge \;\varepsilon > 0,\;\forall\,r,\;i \\ \end{aligned} $$

(39)

Then, the achievement level of objective functions for Model 1 should be a larger level such as:

$$ \alpha = \frac{{z_{j} - z_{j}^{ - } }}{{z_{j}^{ + } - z_{j}^{ - } }} $$

(40)

Equation (40) is variable transformation, the model has transformed $z_{j} = \alpha \cdot z_{j}^{ + } + (1 - \alpha ) \cdot z_{j}^{ - }$. Where z_j is a convex combination of $z_{j}^{ - }$ and $z_{j}^{ + }$, Eq. (38) can be rewritten as model of Eq. (40). According to the concept of multiple objective linear programming, the common weight$(\mu *, \omega *)$ should satisfy all DMUs restrictions. The weight $(\mu *, \omega *)$ from all of the DMUs is the common weight to all DMUs which are evaluated on a consist standard for ranking. We may apply LINGO for resolution to solve the model (39).

$$ \begin{aligned} & \mathop {Max}\limits_{\mu ,\omega } \alpha \\ & \text{st} \\ & \quad \sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{rk} - \sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{ik} \le 0} } ,\quad k = 1, \cdots ,n \\ & \quad \sum\limits_{r = 1}^{s} {\mu_{r} \cdot y_{rj} } - \alpha \cdot \sum\limits_{i = 1}^{m} {\omega_{i} \cdot x_{ij} } \ge 0,\quad j = 1, \cdots ,n \\ & \quad \mu_{r} , \omega_{i} \ge \varepsilon > 0 \\ \end{aligned} $$

(41)

Employing Model (41), a common weight $(\mu^{*} ,\omega^{*} )$ is determined for all DMUs and the efficiency score of each DMUj is defined as the following:

$$ e_{j} = \frac{{\sum\limits_{r = 1}^{s} {\mu_{r}^{*} \cdot y_{rj} } }}{{\sum\limits_{i = 1}^{m} {\omega_{i}^{*} \cdot x_{ij} } }} $$

(42)

Example 4

Consider three firms with two inputs and two outputs as follows (Table 8).

Table 8 Assumed Data of Example 4

Table 9 The weights of fuzzy DEA model

Using the programming problem (41); therefore, the following problem (43) is derived and resolved:

$$ \begin{aligned} & \rm \mathop {Max}\limits_{\mu ,\omega } ,\alpha \\ & \text{st} \\ & \mu_{1} \times 5 + \mu_{2} \times 1 - \omega_{1} \times 2 - \omega_{2} \times 3\, \le 0 \\ & \mu_{1} \times 4 + \mu_{2} \times 5 - \omega_{1} \times 1 - \omega_{2} \times 6\, \le 0 \\ & \mu_{1} \times 6 + \mu_{2} \times 4 - \omega_{1} \times 3 - \omega_{2} \times 3\, \le 0 \\ & \mu_{1} \times 5 + \mu_{2} \times 1 - \alpha \times (\omega_{1} \times 2 + \omega_{2} \times 3) \ge\, 0 \\ & \mu_{1} \times 4 + \mu_{2} \times 5 - \alpha \times (\omega_{1} \times 1 + \omega_{2} \times 6) \ge\, 0 \\ & \mu_{1} \times 6 + \mu_{2} \times 4 - \alpha \times (\omega_{1} \times 3 + \omega_{2} \times 3) \ge 0\, \\ & \mu_{1} ,\mu_{2} ,\omega_{1} ,\omega_{2} \ge 10^{ - 5} \\ \end{aligned} $$

(43)

Therefore the following results are computed by LINGO:

$$ \alpha = 0.61,\mu_{1} = 28.9,\mu_{2} = 10^{ - 5} ,\omega_{1} = 31.6,\omega_{2} = 26.3, $$

The efficiency score of each firm is shown as follows:

$$ e_{A} = 0. 60,e_{B} = 0.61 \; {\text{and}} \; e_{C} = 0. 9 9. $$

The model (41) is nonlinear and could result in some computational difficulties. In the next section, a linear model with FMOP is developed. Readers should distinguish the difference between model (35) and model (41). The model (41) is fuzzy multi-objective and only able to compute crisp data; however, the model (35) is also fuzzy multi-objective and is able to compute fuzzy data. Decision maker should choose the model that meets his/her requirements.

4.4 DEA of FMOP by Difference Between Inputs and Outputs

This section is presented to some readers, who are interested in advanced forms in DEA by FMOP. The presented model is based on the computation of efficiency via the difference between inputs and outputs (Chen et al. 2009) rather than the fractional model in tradition. Consider the problem (33) again. Assume that

$$ \sum\limits_{i = 1}^{m} {v_{i} } x_{il} > 0,\;l = 1, 2, \ldots ,n $$

Then the first n constraints of the problem (33) are equivalent to the following respectively

$$ \sum\limits_{r = 1}^{p} {u_{r} y_{rl} } - \sum\limits_{i = 1}^{m} {v_{i} } x_{il} \le 0,\;l = 1, 2, \ldots ,n. $$

(44)

Moreover, from the constraints of the problem (33) we deduce that

$$ 0 < f_{k} = \frac{{\sum\limits_{{r = 1}}^{p} {u_{r} y_{{rk}}}}}{{\sum\limits_{{i = 1}}^{m} {v_{i} x_{{ik}}}}} \le 1$$

Thus, the maximum value that the efficiency $f_{k}$ of a DMU k can ideally reach is 1. For DMU k, consider the function

$$ g_{k} = \sum\limits_{i = 1}^{m} {v_{i} } x_{ik} - \sum\limits_{r = 1}^{p} {u_{r} y_{rk} }, $$

From (33) we deduce that

$$ g_{k} = \sum\limits_{i = 1}^{m} {v_{i} } x_{ik} - \sum\limits_{r = 1}^{p} {u_{r} y_{rk} } \ge 0, $$

then the smallest value that $g_{k}$ can ideally reach is 0. Moreover when $g_{k}$, $\sum\nolimits_{i = 1}^{m} {v_{i} } x_{ik} = \sum\nolimits_{r = 1}^{p} {u_{r} y_{rk} }$, which means $f_{k} = 1$. Consider now the following linear programming problem. Problem (45) is formulated as a minimization problem of the $g_{k}$, for k = 1, 2, …, n as follows:

$$ \begin{aligned} & {\text{Min}}\quad g_{1} = \sum\limits_{i = 1}^{m} {v_{i} } x_{i1} - \sum\limits_{r = 1}^{p} {u_{r} y_{r1} } \\ & {\text{Min}}\;g_{2} = \sum\limits_{i = 1}^{m} {v_{i} } x_{i2} - \sum\limits_{r = 1}^{p} {u_{r} y_{r2} } \\ & \ldots \\ & {\text{Min}}\;g_{n} = \sum\limits_{i = 1}^{m} {v_{i} } x_{in} - \sum\limits_{r = 1}^{p} {u_{r} y_{rn} } \\ & st\,\sum\limits_{r = 1}^{p} {u_{r} y_{rk} } - \sum\limits_{i = 1}^{m} {v_{i} } x_{ik} \le 0,\,k = 1, 2, \ldots ,n; \\ & \quad u_{r} \ge \varepsilon ,\;r = 1,2, \ldots ,p; \\ & \quad v_{i} \ge \varepsilon ,\;i = 1,2, \ldots ,m. \\ \end{aligned} $$

(45)

Now the optimistic expectation of $g_{k}$ is assumed as zero, the pessimistic expectation of $g_{k}$ is assumed as $\xi$, the $\xi$ is a small positive value subjectively determined by the decision maker. When $g_{k}$ is zero, this also implies that the k-th DMU satisfies that: $\sum\limits_{i = 1}^{m} {v_{i} } x_{ik} = \sum\limits_{r = 1}^{p} {u_{r} y_{rk} }$. Thus, according to the fuzzy transformation in Fig. 2, the achievement level for each objective/DMU is:

$$ \mu_{k} \left( {g_{k} } \right) = \left\{ {\begin{array}{*{20}l} 0 & ; & {g_{k} \ge \xi } \\ {\frac{{\xi - g_{k} }}{\xi - 0}} & ; & {0 \le g_{k} < \xi } \\ 1 & ; & {g_{k} < 0} \\ \end{array} } \right. $$

(46)

Here $g_{k} = \sum\limits_{i = 1}^{m} {v_{i} } x_{ik} - \sum\limits_{r = 1}^{p} {u_{r} y_{rk} }$. Then resolving the problem (45) by fuzzy multi-objective approach is identical to solve the optimization problem (47):

$$ \begin{aligned} & \begin{array}{*{20}c} {\text{Max}} & \gamma \\ \end{array} \\ & st\quad \gamma \le \mu_{k} (g_{k} ),\;k = 1, 2, \ldots ,n; \\ & \sum\limits_{r = 1}^{p} {u_{r} y_{rk} } - \sum\limits_{i = 1}^{m} {v_{i} } x_{ik} \le 0,\;k = 1, 2, \ldots ,n; \\ & \quad u_{r} \ge \varepsilon ,\;r = 1,2, \ldots ,p; \\ & \quad v_{i} \ge \varepsilon ,\;i = 1,2, \ldots ,m. \\ \end{aligned} $$

(47)

Example 5

Environmental protection issues are attracting attentions from both governments and academics in the field of environmental economics. Furthermore, environmental protection performance is also becoming a major concern for green SCM (Vachon and Klassen 2008; Wu et al. 2007). The fuzzy DEA above is used to analyze the partner performance in a green supply chain. The input/output data from 23 district governments of Taiwan in 2003 are collected, district governments are encoded from “A” to “W”. The inputs are defined as: manpower of environmental protection ($v_{1}$), budget of environmental protection ($v_{2}$) and advertisement of environmental protection ($v_{3}$); in addition, the outputs are defined as: the reduced amount of harmful emission (${\textit{u}}_{1}$), the reduced number of noise event (${\textit{u}}_{2}$), ratio of qualified water (${\textit{u}}_{3}$), recycle quantity from wastes (${\textit{u}}_{4}$) and the reduced number of malodorous air event (${\textit{u}}_{5}$). These data are normalized in Table 10.

Table 10 Normalized Input/Output data 2003

Here $\varepsilon$ is assumed as 10⁻⁵ and $\xi$ is set to 0.1 in this study, the computed results for are available in Tables 9 and 11.

Table 11 Efficiency Score

According to the computational results, the district K is the most efficient DMU (less inputs and more outputs); on the contrary, the district A is the least efficient DMU (more inputs and less outputs). These reports are valuable to push the district government competing for further improvements of environmental protection. The model (47) is linear, fuzzy multi-objective and appropriate for crisp data.

5 Conclusions and Future Studies

According to the simulation results and examples in previous sections, readers are encouraged to use fuzzy MCDM: FMOP and FMADM for solving problems of SCM and develop/extend the fuzzy model in this chapter further. These two methods: FMOP and FMADM are valuable for developing new and advanced approaches in the near future. In addition, FMOP validates its general use for various optimization models of SC. For example, it could be useful in network design, aggregate planning, vehicle routing problem, production scheduling problem, …, etc.

In Sect. 2, the simple framework of SC is proposed; furthermore, FMOP and FMADM are both presented. A new and simple game of alliance matrix for simulating SC performance is illustrated in Sect. 3, which is designed to describe the cooperation degree between partners. Simulation results reflect greater realities and show that ideal cooperation is the best from the macro scope; however, extreme competition could have better individual performance of partner from the micro scope. In Sect. 4, the fuzzy DEA model and its extensions are presented by FMOP. In this section, some possible studies for future are provided. Readers are encouraged to develop their own applications and advanced models from this beginning.

About the future studies, all these fuzzy models presented in this chapter could be integrated with IT technologies nowadays. This means: all optimization models should be computed on line or accept transmitted data by internet for real-time decision making. These efforts will extend the ability of fuzzy models for SCM. The basic idea of cloud computing is simply introduced here, the implementation of IT framework, issues of green supply chain and other trends are summarized as follows:

• (1) Cloud Computing

Cloud computing is the delivery of computing as a service, whereby shared resources, software, and information over an internet (Buyya et al. 2008). Today, the latest paradigm to emerge is that of Cloud computing which promises reliable services delivered through next-generation data centers that are built on compute and storage virtualization technologies. Consumers will be able to access applications and data from a “Cloud” anywhere in the world on demand. Cloud computing is simply shown as follows in Fig. 11 for better understanding. Actually, some scholars are starting to study SCM issues by setting a cloud. The articles of Lindner et al. (2010), and Celesti et al. (2010) provide visions for integrating Information Technology (IT) and SCM in the very near future.

Fig. 11

Simple model of cloud computing. Source Wikimedia commons by Johnston S

Enterprises currently are eager to employ cloud services in order to improve the scalability of their services and to deal with bursts in resource demands. With the cloud service, consumers are able to use the services by internet anytime and anywhere. Although there are many papers to talk about the cloud framework from the theoretical view, the number of practical implementations/applications for SCM are still less in academic papers.

• (2) IT Framework

The model concept to integrate SCM and the optimization module is simple; eventually, a Decision Support System (DSS) should be developed. The data from the demand side and the supply side are considered simultaneously to make the best decision for resource allocation. For example, ranking the suppliers by FMADM approach via collecting the attribute data on line is an interesting idea. For example, Chen et al. use the fuzzy MADM for selecting the appropriate hospital to transfer patients (Chen et al. 2012), the fuzzy resolution approach for any SCM problem could be implemented by a cloud service by the IT framework of Fig. 12.

Fig. 12

IT framework

In addition to the IT platform of C#, SQL and Flash, the Java + MySQL platform is also popular. Once the IT framework is set up, decision maker can make mobile decisions by smart devices: e.g., phones, computers, anytime and anywhere. Readers interested in real applications are encouraged to refer the research as follows: Yong and Zhang (2008) propose fuzzy evaluating method for channel selection (IT platform), Balan et al. (2007) reduce the Bullwhip effect in a supply chain with fuzzy logic, Harnisch and Buxmann (2013) use FAHP to evaluate cloud services. Fang et al. (2002) propose the DSS for SCM in textile industry, and Radio Frequency Identification (RFID) is used to integrate the multi-objective model for dispatching patients to hospitals for emergency by Chen et al. (2011). DSS usually has three elements: graphical user interface, model and database. Fuzzy MCDM could play important roles in the model construction.

• (3) Green Supply Chain Management

Green SCM focuses influence and relationships between supply-chain management and environmental thinking into supply-chain management, including product design (concept), material sourcing and selection, manufacturing processes, delivery of the final product to the consumers as well as end-of-life management of the product after its useful life (Srivastava 2007), which is illustrated in Fig. 13.

Fig. 13

Green supply chain management. Source www.dlinkgreen.com

The literature here is simply classified following categories:

• (i) Green Design

Understanding of how design decisions affect a product’s environmental compatibility is concerned in this field; for example, Madu et al. (2002) present a very useful hierarchic framework for environmentally conscious design. Interested readers can also find the literature existing on design for material and product recovery (He et al. 2004; Krikke et al. 2003).

• (ii) Green Operations

Three main streams are popularly discussed here. The first stream is recycling. Remanufacturing is defined as recycling-integrated manufacturing. Industries that apply remanufacturing typically include automobiles, electronics (Hsu and Hu 2008) and tires (Hoshino et al. 1995). Product recovery refers to the broad set of activities designed to reclaim value from a product at the end of its useful life. A model for evaluating recovery strategies for the product without violating the physical and economical feasibility constraints is proposed by Krikke et al. (2003). The second stream is reverse logistics and network design. Reverse logistics networks have some generic characteristics related to the coordination requirement of two markets, supply uncertainty, returns disposition decisions, postponement and speculation (Yalabik et al. 2005). As a result, they extend the traditional network design to a more wide consideration. The final stream is waste management: disposal has always been a compelling problem and has led to green consciousness. Teunter and Vlachos (Teunter and Vlachos 2002) focus on the necessity of a disposal option for remanufacturable items.

Some scholars mentioned the use of MOP/MADM on green SCM (Wu et al. 2007). Paksoy et al. (2012) use fuzzy multi-objective model by including environmental hazards. Chen et al. (2008) proposed the route planning for transportation of nuclear waste by Geographical Information System (GIS). Lin (2013) uses the fuzzy DEMATEL to evaluate the management practices. In addition, fuzzy and crisp AHP models are also popular here (Peng 2012; Wang et al. 2011). It is important to note that many issues of green supply chain often include social justice inside, e.g., the issues of handling environmental hazards, nuclear waste, toxic material,… etc. Interested readers may study further by these aforementioned articles.

• (iii) Others

The concept of SCM is not only useful in manufacturing industries, but also valuable in service industries. Readers are encouraged to explore more SCM applications by FMOP/FMADM in addition to the traditional applications. Especially when considering the service industries, Pramod and Banwet (2013) use fuzzy ISM on the SCM issues of telecom service, Cho et al. (2012) use FAHP on catering enterprises and Chen et al. (2012) employ FMOP on dispatching patients to hospitals for Emergency Medicine (EM). The service industry is an interesting, developing and attractive area for SCM models with IT, FMOP and FMADM in the very near future.