Mixing Monte-Carlo and Partial Differential Equations for Pricing Options

Abstract

There is a need for very fast option pricers when the financial objects are modeled by complex systems of stochastic differential equations. Here the authors investigate option pricers based on mixed Monte-Carlo partial differential solvers for stochastic volatility models such as Heston’s. It is found that orders of magnitude in speed are gained on full Monte-Carlo algorithms by solving all equations but one by a Monte-Carlo method, and pricing the underlying asset by a partial differential equation with random coefficients, derived by Itô calculus. This strategy is investigated for vanilla options, barrier options and American options with stochastic volatilities and jumps optionally.

1 Introduction

Since the pioneering work has been achieved by Phelim Boyle [6], Monte-Carlo (or MC for short) methods introduced and shaped financial mathematics as barely any other method can compare. They are often appreciated for their flexibility and applicability in high dimensions, although they bear as well a number of drawbacks: error terms are probabilistic and a high level of accuracy can be computationally burdensome to achieve. In low dimensions, deterministic methods as quadrature and quadrature based methods are strong competitors. They allow deterministic error estimations and give precise results.

We propose several methods for pricing basket options in a Black-Scholes framework. The methods are based on a combination of Monte-Carlo, quadrature and partial differential equations (or PDE for short) methods. The key idea was studied by two of the authors a few years ago in [14], and it tries to uncouple the underlying system of stochastic differential equations (or SDE for short), and then applies the last-mentioned methods appropriately.

In Sect. 2, we begin with a numerical assessment on the use of Monte-Carlo methods to generate boundary conditions for stochastic volatility models, but this is a side remark independent of what follows.

The way of mixing MC and PDE for stochastic volatility models is formulated in Sect. 3. A numerical evaluation of the method is made by using closed form solutions to the PDE. In Sects. 6 and 4, the method is extended to the case of American options and to the case where the underlying asset is modeled with jump-diffusion processes.

In Sect. 5, a method reducing the number of samples is given based on the smooth dependence of the option price on the volatility.

Finally, in Sect. 7, the strategy is extended to multidimensional problems like basket options, and numerical results are also given.

Moreover, some related results can be found in [5, 8, 9, 16–18].

2 Monte-Carlo Algorithm to Generate Boundary Conditions for the PDE

The diffusion process that we have chosen for our examples is the Heston stochastic volatility model (see [12]). Under a risk neutral probability, the risky asset S _t and the volatility σ _t follow the diffusion process

$$\begin{aligned} \mathrm{d}S_t & = S_t\bigl(r \mathrm{d}t + \sigma_t \mathrm{d}W^1_t\bigr), \end{aligned}$$

(2.1)

$$\begin{aligned} \mathrm{d}v_t & = k(\theta- v_t)\mathrm{d}t + \delta \sqrt{v_t} \mathrm{d} W^2_t, \end{aligned}$$

(2.2)

and the put option price is given by

$$\begin{aligned} P_t=\mathrm{e}^{-r(T-t)}\mathbb{E}\bigl[(K-S_T)^+|S_t,v_t \bigr], \end{aligned}$$

(2.3)

where $v_{t} = \sigma_{t}^{2}$, $\mathbb{E}(\mathrm{d}W^{1}_{t} \cdot\mathrm {d}W^{2}_{t}) = \rho\mathrm{d}t$, $\mathbb{E}( \cdot)$ is the expectation with respect to the risk neutral measure, and r is the interest rate on a risk less commodity.

The pair (W ¹,W ²) is a two-dimensional correlated Brownian motion, with the correlation between the two components being equal to ρ. As it is usually observed in equity option markets, options with low strikes have an implied volatility higher than that of options at the money or with high strikes, and it is known as the smile. This phenomenon can be reproduced in the model by choosing a negative value of ρ.

The time is discretized into N steps of length δt. Denoting by T the maturity of the option, we have T=Nδt. Full Monte-Carlo simulation (see [10]) consists in a time loop starting at $S_{0},v_{0}=\sigma_{0}^{2}$ of

$$\begin{aligned} & v_{i+1} = v_i + k(\theta- v_i)\delta t + \sigma_i\sqrt{\delta t}N^2_{0,1}\delta\quad \hbox{with }\sigma_i=\sqrt{v_i}, \end{aligned}$$

(2.4)

$$\begin{aligned} & S_{i+1}=S_i \bigl(1+r\delta t + \sigma_i \sqrt{\delta t}\bigl(N^1_{0,1}\rho+N^2_{0,1} \sqrt{1-\rho^2}\bigr)\bigr), \end{aligned}$$

(2.5)

where $N^{j}_{0,1}\ (j=1,2)$ are realizations of two independent normal Gaussian variables. Then set $P_{0}=\frac{\mathrm{e}^{-rT}}{M}\sum(K-S^{m}_{N})^{+}$, where $\{S^{m}_{N}\}_{m=1}^{M}$ are M realizations of S _N .

The method is slow, and at least 300000 samples are necessary for a precision of 0.1 %. Of course acceleration methods exist (quasi-Monte-Carlo, multi-level Monte-Carlo etc.), but alternatively, we can use the PDE derived by Itô calculus for u below and set P ₀=u(S ₀,v ₀,T).

If the return to volatility is 0 (i.e., zero risk premium on the volatility (see [1])), then u(S,y,τ) is given by

$$\begin{aligned} \begin{aligned} & \partial_\tau u - \frac{y S^2}{2} \partial_{SS}u - \rho\lambda S y\partial_{Sy}u -\frac{\lambda^2y}{2} \partial_{yy}u - r S \partial_S u - k(\theta-y)\partial_y u + r u=0, \\ & u(S,y,0) = (K-S)^+. \end{aligned} \end{aligned}$$

(2.6)

Now instead of integrating (2.6) on $\mathbb{R}^{+}\times\mathbb{R}^{+}\times (0,T)$, let us integrate it on Ω×(0,T), $\varOmega\subset\mathbb {R}^{+}\times\mathbb{R}^{+}$, and add Dirichlet conditions on ∂Ω computed with MC by solving (2.4)–(2.5).

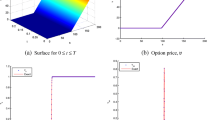
Notice that this domain reduction does not change the numerical complexity of the problem. Indeed to reach a precision ε with the PDE, one needs at least O(ε ⁻³) operations to compute the option at all points of a grid of size ε with a time step of size ε. Monte-Carlo needs O(ε ⁻²) per point S ₀,v ₀, and there are O(ε ⁻¹) points on the artificial boundary, when the number of discretization points in the full domain is O(ε ⁻²). However, the computation shown in Fig. 1 validates the methodology, and it may be attractive to use it to obtain more precision on a small domain.

Fig. 1

Put option with Heston’s model computed by solving the PDE by implicit Euler + FEM using the public domain package freefem++ (see [11])

3 Monte-Carlo Mixed with a 1-Dimensional PDE

Let us rewrite (2.1) as

$$\begin{aligned} \mathrm{d}S_t & = S_t \bigl[r \mathrm{d}t + \sigma_t \sqrt{1-\rho^2}\mathrm{d}\widetilde{W}^{(1)}_t+ {\sigma_t\rho\mathrm{d}\widetilde{W}^{(2)}_t}\bigr], \end{aligned}$$

(3.1)

where ${\widetilde{W}}^{1}_{t},{\widetilde{W}}^{2}_{t}$ are now independent Brownian motions.

Drawing a trajectory of v _t by (2.4), with the same δt and the same discrete trajectory $W_{i+1}^{(2)}=W_{i}^{(2)} +N_{0,1}^{2}\sqrt{\delta t}$, we consider

$$\begin{aligned} \mathrm{d}S_t & = S_t \bigl[ \mu_t \mathrm{d}t + \sigma_t\sqrt{1-\rho^2} \mathrm{d}\widetilde{W}^{(1)}_t\bigr], \end{aligned}$$

(3.2)

$$\begin{aligned} {\mu_t} & = r+ \rho\sigma_t\frac{W^{(2)}_{i+1} - W^{(2)}_i}{\delta t} - \frac{1}{2} \rho^2 \sigma_t^2,\quad t \in[t_i,t_{i+1}[. \end{aligned}$$

(3.3)

Proposition 3.1

As δt→0, S _t given by (2.4) and (3.2)–(3.3) converges to the solution to Heston’s model (2.1)–(2.2). Moreover, the put $P=\mathrm{e}^{-rT}\mathbb{E}(K-S_{T})^{+}$ is also the expected value of u(S ₀,0), with u given by

$$\begin{aligned} \partial_t u + \frac{1}{2} \bigl(1-\rho^2 \bigr)\sigma_t^2 S^2 \partial_{SS} u + S\mu_t \partial_S u - ru = 0, \quad u(S,T)=(K-S)^+ \end{aligned}$$

(3.4)

with σ _t given by (2.4) and μ _t given by (3.3).

Proof

By Itô’s formula, we have

$$\begin{aligned} \mathrm{d}\log(S_t) & = \frac{\mathrm{d}S_t}{S_t}+\frac{1}{2}(\log S)''\bigl(S_t^2 \sigma_t^2\bigl(1-\rho^2\bigr)\mathrm{d}t \bigr)= \frac{\mathrm{d}S_t}{S_t}- \frac{\sigma_t^2}{2}\bigl(1-\rho ^2\bigr) \mathrm{d}t \\ & = \mu_t \mathrm{d}t + \sqrt{1-\rho^2} \sigma_t \mathrm{d}\widetilde{W}^{(1)}_t - \bigl(1-\rho^2\bigr)\frac{\sigma^2_t}{2} \mathrm{d}t \\ & \approx r \delta t + \rho\sigma_t \delta W^{(2)}_t -{\frac{\rho^2\sigma_t^2}{2} }\delta t + \sqrt{1-\rho^2}\sigma_t \delta\widetilde{W}^{(1)}_t - \bigl(1-{\rho^2} \bigr)\frac{\sigma^2_t}{2} \delta t \\ & \approx r \mathrm{d}t + \rho\sigma_t \mathrm{d}W^{(2)}_t + \sqrt{1-\rho^2}\sigma_t \mathrm{d}\widetilde{W}^{(1)}_t - \frac {\sigma^2_t}{2} \mathrm{d}t . \end{aligned}$$

(3.5)

Consequently,

$$\begin{aligned} S_t=S_0\exp\biggl(\int _0^t\mu_t\mathrm{d}t+ \int _0^t \sqrt{1-\rho^2} \sigma_t \mathrm{d} W^{(1)}_t -\int _0^t\frac{1}{2}\bigl(1-\rho^2\bigr) \sigma_t^2\mathrm{d}t \biggr). \end{aligned}$$

(3.6)

 □

Proposition 3.2

If we restrict the MC samples to those that give 0<σ _m ≤σ _t ≤σ _M , for some given σ _m ,σ _M , then equations (2.4) and (3.3)–(3.4) are well-posed.

Proof

Let

$$\begin{aligned} \varLambda_\tau=\int_{T-\tau}^T \mu_\xi\mathrm{d}\xi,\quad y=\frac{S}{K} \mathrm{e}^{\varLambda(\tau)}. \end{aligned}$$

(3.7)

Then $u(t,S) = v(T-t,\frac{S}{K} \mathrm{e}^{\varLambda(\tau)})$, where v is the solution to

$$\begin{aligned} \partial_\tau v -\frac{1}{2}\bigl(1-\rho^2\bigr) \sigma^2_{T-\tau}y^2\partial_{yy} v = 0,\quad v(0,y)=(1-y)^+. \end{aligned}$$

(3.8)

If 0<σ _m ≤σ _t ≤σ _M almost surely and for all t, then the solution exists in the sense of Barth et al. [3]. □

Remark 3.1

Note that (3.6) is also

$$\begin{aligned} \overline{\sigma}^2 =& \frac{{1-\rho^2}}{T}\int_0^T \sigma_t^2 \mathrm{d} t,\quad\quad m = r-\frac{\overline{\sigma}^2}{2} + \frac{\rho}{T} \sum_i \sigma_{t_i} \bigl(W^{(2)}_{t_{i+1}} - W^{(2)}_{t_i}\bigr), \end{aligned}$$

(3.9)

$$\begin{aligned} S_T(x) =& S_0 \exp(m T + \overline{\sigma}T x). \end{aligned}$$

(3.10)

Therefore,

$$\begin{aligned} \mathbb{E}\bigl[u(S_0,0)\bigr] & = \mathrm{e}^{-rT}\int _{\mathbb{R}^+}\bigl(K-S_0 \mathrm{e}^{m T + \overline{\sigma}T x} \bigr)^+\frac{\mathrm{e}^{-\frac{x^2}{2T}}}{\sqrt{2\pi T}}\mathrm{d}x. \end{aligned}$$

(3.11)

There is a closed form for this integral, namely the Black-Scholes (or BS for short) formula with the interest rate r, the dividend m+r and the volatility $\overline{\sigma}$.

3.1 Numerical Tests

In the simulations, the parameters are S ₀=100, K=90, r=0.05, σ ₀=0.6, θ=0.36, k=5, λ=0.2, T=0.5. We compared a full MC solution with M samples to the new algorithm with M′ samples for μ _t and σ _t given by (2.4). The Black-Scholes formula is used as indicated in Remark 3.1.

To observe the precision with respect to ρ (see Table 1), we have taken a large number of Monte-Carlo samples, i.e., M=3×10⁵ and M′=10⁴. Similarly, the number of time steps is 300 with 400 mesh points and S _max=600 (i.e., δS=1.5).

Table 1 Precision versus ρ

To study the precision, we let M and M′ vary. Table 2 shows the results for 5 realizations of both algorithms and the corresponding mean value for P _N and variance.

Table 2 Precision study with respect to M and M′. Five realizations of pure MC and MC+PDE for various M′ and M

Note that one needs many more samples for pure MC than those for the mixed strategy MC+BS. This variance reduction explains why MC+BS is much faster.

4 Lévy Processes

Consider Bates model (see [4]), i.e., an asset modeled with stochastic volatility and a jump process,

$$\begin{aligned} \mathrm{d} v_t& = k(\theta- v_t)\mathrm{d}t + \xi \sqrt{v_t}\mathrm{d} W^{(2)}_t, \quad \sigma_t=\sqrt{v_t}, \end{aligned}$$

(4.1)

$$\begin{aligned} \mathrm{d}X_t& = \biggl(r-\frac{\sigma_t^2}{2} \biggr)\mathrm{d}t + \sigma_t \bigl(\sqrt{1-\rho^2}\mathrm{d}\widetilde{W}^{(1)}_t+\rho\mathrm{d}\widetilde{W}^{(2)}_t \bigr) + \eta\mathrm{d}N_t, \end{aligned}$$

(4.2)

where X _t =lnS _t and N _t is a Poisson process. As before, this is

$$\begin{aligned} &\mathrm{d}X_t = \widetilde{\mu}_t \mathrm{d}t + \sigma_t \sqrt{1-\rho^2}\ \mathrm{d} \widetilde{W}^{(1)}_t + \eta\mathrm{d}N_t, \end{aligned}$$

(4.3)

$$\begin{aligned} & {\widetilde{\mu}_t = r- \frac{\sigma_t^2}{2} +\rho\sigma_t \frac {\delta W^{(2)}}{\delta t}} . \end{aligned}$$

(4.4)

By Itô, a put on S _t with u(T)=(K−e^x)⁺ satisfies

$$\begin{aligned} & {\partial_t u -r u }+\frac{1}{2}\bigl(1-\rho^2 \bigr)\sigma_t^2\partial_{xx} u +\widetilde{\mu}_t \partial_x u \\ & \quad = - \int_\mathbb{R}\bigl[\bigl(u(x+z)-u(x)\bigr)J(z) - \partial_x u(x) \bigl(\mathrm{e} ^z-1\bigr)J(z)\bigr] \mathrm{d}z. \end{aligned}$$

(4.5)

Let us apply a change of variables τ=T−t, $y= x-\int_{T-\tau}^{T}\overline{\mu}_{t} \mathrm{d} t$ with $\overline{\mu}_{t}=\widetilde{\mu}_{t}-\int_{\mathbb{R}}(\mathrm {e}^{z}-1)J(z)\mathrm {d}z$, and use

$$\begin{aligned} v(y,\tau) = \mathrm{e}^{(r+\int_\mathbb{R}J(z)\mathrm{d} z)\tau}u \biggl(y+ \int _{T-\tau}^T\overline{\mu}_t \mathrm{d} t,T-\tau \biggr). \end{aligned}$$

(4.6)

Proposition 4.1

$$\begin{aligned} \partial_\tau v -\frac{1}{2}\bigl(1-\rho^2\bigr) \sigma_{T-\tau}^2\partial_{yy}v - \int _\mathbb{R} v(y+z) J(z)\mathrm{d}z=0,\quad v(y,0)=\bigl(K- \mathrm{e}^y\bigr)^+. \end{aligned}$$

(4.7)

Proof

Let $\overline{r} = r+\int_{\mathbb{R}}J(z)\mathrm{d} z$. Then

$$\begin{aligned} &\partial_\tau v = \mathrm{e}^{\overline{r}\tau} \biggl[- \biggl(r+\int _\mathbb{R}J(z)\mathrm{d} z \biggr)u + \overline{\mu}_{T-\tau} \partial_x u -\partial_t u \biggr], \\&\quad\partial_y v = \mathrm{e}^{\overline{r}\tau}\partial_x u,\quad\partial_{yy}v = \mathrm{e}^{\overline{r}\tau }\partial_{xx}u. \end{aligned}$$

(4.8)

Therefore,

$$\begin{aligned} & \mathrm{e}^{-\overline{r}\tau} \biggl[ \partial_\tau v -\frac{1}{2}\bigl(1- \rho^2\bigr) \sigma_\tau^2\partial_{yy}v - \int_\mathbb{R}v(y+z) J(z)\mathrm{d}z \biggr] \\ &\quad = \biggl(r +\int_\mathbb{R}J(z)\mathrm{d} z \biggr) u + \overline{\mu}_t\partial_x u -\partial_t u-\bigl(1- \rho^2\bigr) \frac{\sigma_t^2}{2} \partial_{xx}u - \int _\mathbb{R}u(x+z) J(z)\mathrm{d}z, \end{aligned}$$

which is zero by (4.5). □

Remark 4.1

Once more, we notice that the PDE depends on time integrals of $\widetilde{\mu}_{t}$ and σ _t , and integrals damp the randomness and make the partial integro-differential equation (or PIDE for short) (4.7) easier to solve. Table 3 displays 9 realizations of $\sqrt{\frac{1}{T}\int_{0}^{T}\sigma^{2}_{t}\mathrm{d} t}$ for M′=100 and 500.

Table 3 9 realizations of $(\frac{1}{T}\int_{0}^{T}\sigma^{2}_{t}\mathrm{d} t)^{\frac{1}{2}}$ for M′=100 and 500

Remark 4.2

Let $\overline{f}_{\tau}=\frac{1}{\tau}\int _{T-\tau}^{T} f(t)\mathrm{d}t$. From (4.6), we see that the option price is recovered by

$$\begin{aligned} u(S,t) & = \mathrm{e}^{-(r+\int_\mathbb{R}J(z)\mathrm{d} z)(T-t)} v \biggl(\ln S - \biggl(r- \frac{\overline{\sigma_t^2}|_{t}}{2}-\int_\mathbb{R}\bigl(\mathrm{e} ^z-1\bigr)J(z)\mathrm{d}z \\ &\quad{}+\rho\overline{\sigma_t\frac{\delta W^{(2)}}{\delta t}} \bigg|_{t} \biggr) (T-t),T-t \biggr), \end{aligned}$$

where v is the solution to (4.7). For a European put option, with the standard diffusion-Lévy process model and the dividend q, the formula is

$$\begin{aligned} \begin{aligned} & u(S,t) = \mathrm{e}^{-(r+\int_\mathbb{R}J(z)\mathrm{d} z)(T-t)}v \biggl(\ln S - \biggl(r-q- \frac{\sigma^2}{2} \\&\quad\quad\quad\quad\ \ {}-\int_\mathbb{R}\bigl( \mathrm{e}^z-1\bigr)J(z)\mathrm{d} z \biggr) (T-t),T-t \biggr), \\ & \partial_\tau v -\frac{1}{2}\sigma^2\partial_{yy}v - \int _\mathbb{R}v(y+z) J(z)\mathrm{d} z=0,\quad v(y,0)=\bigl(K- \mathrm{e}^y\bigr)^+. \end{aligned} \end{aligned}$$

(4.9)

It means that any solver for the European put option, with the standard diffusion-Lévy process model and the dividend q, can be used provided that the following modifications are made:

• (1) In the solver, change σ ² into $(1-\rho^{2})\overline{\sigma_{t}^{2}}|_{t}$.

• (2) Change q into $q+\rho^{2}\overline{\sigma_{t}^{2}}|_{t} - \rho \overline{\sigma_{t}\frac{\delta W^{(2)}}{\delta t}}|_{t}$.

4.1 The Numerical Solution to the PIDE by the Spectral Method

Let the Fourier transform operators be

$$\begin{aligned} \mathbb{F}(u)=\int_\mathbb{R} \mathrm{e}^{-{\rm i}\omega x}u(x) \mathrm{d}x\quad\hbox{and}\quad\mathbb{F}^{-1}(\widehat{u})=\frac{1}{2\pi} \int_\mathbb{R}\mathrm{e}^{{\rm i}\omega x}\widehat{u}(\omega)\mathrm{d} \omega. \end{aligned}$$

(4.10)

Applying the operator $\mathbb{F}$ to the PIDE (4.7) for a call option gives

$$\begin{aligned} \partial_\tau\widehat{v} -\varPsi\widehat{v} = 0\quad\hbox{in }\mathbb {R},\quad\widehat{v}( \omega,0) =\mathbb{F}\bigl(\mathrm{e}^x-K\bigr)^+ , \end{aligned}$$

(4.11)

where Ψ is

$$\begin{aligned} \varPsi(\omega) = -\bigl(1-\rho^2\bigr)\frac{\sigma_t^2}{2} \omega^2 -\varphi(\omega),\quad\varphi(\omega)=\int _\mathbb{R}\mathrm{e}^{{\rm i}\omega y}J(y)\mathrm{d}y. \end{aligned}$$

(4.12)

So, with m indicating a realization, the solution is

$$\begin{aligned} & u \biggl(x-\int_{T-\tau}^T\overline{\mu}_t \mathrm{d} t \biggr) \\&\quad = \frac{1}{M'}\sum _m \mathrm{e}^{-rT}\bigl(K-\mathbb{F}^{-1} \bigl[\bigl\{ \mathbb{F} v^0\bigr\} (\omega)\mathrm{e}^{-\varphi (w)\tau-\omega^2\frac{1-\rho^2}{2}\int _{T-\tau}^T{\sigma^m_t}^2 \mathrm{d} t} \bigr]\bigr)^+ \end{aligned}$$

(4.13)

with $\widetilde{\mu}_{t}$ given by (3.3) and $\overline{\mu}_{t}=\widetilde{\mu}_{t}+\int_{\mathbb{R}}(\mathrm {e}^{z}-1)J(z)\mathrm{d}z$.

Remark 4.3

The Car-Madan trick in [7] must be used, and v ⁰ must be replaced by e^−ηS(S−K)⁺, which has a Fourier transform, in the case of a call option. Then in (4.13) $\mathbb{F}^{-1}\widehat{\chi}$ must be changed into

$$\frac{K^\eta}{\pi}\int_0^\infty\Re\bigl( \mathrm{e}^{-\mathrm{i}\omega S}\widehat{\chi}(\xi+{\rm i}\eta)\bigr)\mathrm{d}\xi. $$

Remark 4.4

As an alternative to the fast Fourier transform (or FFT for short) methods, following Lewis [13], for a call option, when ℑω>1,

$$ \mathbb{F}v^0=\mathbb{F}\bigl(\mathrm{e}^y-K\bigr)^+=- \frac{\mathrm{e}^{\ln K({\rm i}\omega +1)}}{\omega^2-{\rm i}\omega}. $$

(4.14)

Using such extended calculus in the complex plane, Lewis obtained for the call option,

$$ u(S,T) = S - \frac{\sqrt{KS}}{\pi}\int_0^\infty \Re\biggl[\mathrm{e} ^{{\rm i}u k}\phi_T \biggl(u- \frac{\rm i}{2} \biggr) \biggr]\frac{\mathrm {d}u}{u^2+\frac{1}{4}} $$

(4.15)

with $k=\ln\frac{S}{K}$, where ϕ _t is the characteristic function of the process, which, in the case of (4.7) with Merton Kernel (see [15])

$$J(x)= \lambda\frac{\mathrm{e}^{-\frac{(x-\mu)^2}{\delta ^2}}}{\sqrt{2\pi\delta^2}}, $$

is

$$\phi_T(u) = \exp\biggl({\rm i}u w T -\frac{1}{2} u^2 \varSigma^2 T + T \lambda\bigl(\mathrm{e}^{-\frac{\delta^2 u^2}{2} +{\rm i}\mu u }-1\bigr) \biggr) $$

with $\varSigma^{2}=\frac{1}{T}\int_{0}^{T}\sigma^{2}_{\tau}\mathrm{d}\tau$ and $w = \frac{1}{2}\varSigma^{2} -\lambda(\mathrm{e}^{\frac{\delta^{2}}{2}+\mu}-1)$. The method has been tested with the following parameters:

$$\begin{aligned} \begin{aligned} & T=1,\quad\mu= -0.5, \quad\lambda=0.1, \quad\delta=0.4, \quad K=1, \quad r=0.03, \quad \sigma_0=0.4, \\ & \theta=0.4, \quad\kappa=2,\quad \rho= -0.5, \quad\xi=0.25, \quad M'=10000,\quad \delta t=0.001. \end{aligned} \end{aligned}$$

(4.16)

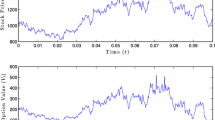
Results for a put are reported in Fig. 2. The method is not precise out of the money, i.e., S>K. The central processing unit (or CPU for short) is 0.8″ per point on the curve.

Fig. 2

Put calculated with Bates’ model by mixing MC with Lewis’ formula (see (4.15))

4.2 Numerical Results

The method has been tested numerically. The coefficients for the Heston+Merton-Lévy are T=1, r=0, ξ=0.3, v ₀=0.1, θ=0.1, k=2, λ=0.3, ρ=0.5. This gives an average volatility 0.27. For the Heston and the pure Black-Scholes for comparison, T=1, r=0, σ=0.3, λ=5, m=−0.01, v=0.01.

The results are shown in Fig. 3.

Fig. 3

Call calculated by a Heston+Merton-Lévy by mixed MC-Fourier (see the blue curve), and compared with the solution to the 2-dimensional PIDE Black-Scholes+Lévy (see the red curve), and a pure Black-Scholes (see the green curve)

5 Conditional Expectation with Spot and Volatility

If the full surface σ ₀,S ₀→u(σ ₀,S ₀,0) is required, MC+PDE becomes prohibitively expensive, much like MC is too expensive if S ₀→u(S ₀,0) is required for all S.

However, notice that after some time t ₁ the stochastic differential equation (or SDE for short) for σ _t will generate a large number of sample values σ ₁. Let us take advantage of this to compute u(σ ₁,S ₁,t ₁).

5.1 Polynomial Fits

Let τ=T−t ₁ for some fixed t ₁.

Instead of gathering all u(⋅,τ) corresponding to the samples $\sigma^{m}_{\tau}$ with the same initial value σ ₀ at t=0, we focus on the time interval (t ₁,T), consider that $\sigma^{m}_{t}$ is a stochastic volatility initiated by $\sigma^{(m)}_{t_{1}}$, then search for the best polynomial fit in terms of σ for u, i.e., a projection on the basis ϕ _k (σ) of $\mathbb{R}$, and solve

$$\min_\alpha J({\bf\alpha}):=\frac{1}{M}\sum _m\frac{1}{L}\int_0^L \bigg\| \sum _k\alpha_k(S)\phi^k \bigl(\sigma^{(m)}_\tau\bigr)-u^{(m)}(S,\tau) \bigg\| ^2\mathrm{d} S. $$

It leads to solving, for each S _i =iδS,

$$\begin{aligned} \biggl(\frac{1}{M}\sum_m \phi_k\bigl(\sigma^{(m)}_\tau\bigr) \phi_l\bigl(\sigma^{(m)}_\tau\bigr) \biggr) \alpha_{k}^i =\frac{1}{M} \sum_m u^{(m)}(S_i,\tau)\phi_l\bigl( \sigma^{(m)}_\tau\bigr). \end{aligned}$$

(5.1)

5.2 Piecewise Constant Approximation on Intervals

We begin with a local basis of polynomials, namely, ϕ _k (σ)=1 if σ∈(σ _k ,σ _k+1) and ϕ _k (σ)=0 otherwise.

Algorithm 5.1

• (1) Choose σ _m ,σ _M ,δσ,σ ₀.

• (2) Initialize an array $n[j]=0, j=0,\ldots, J:=\frac{\sigma_{M}-\sigma_{m}}{\delta\sigma}$.

• (3) Compute M realizations $\{\sigma^{(m)}_{t_{i}}\}$ by MC on the volatility equation.

• (4) For each realization, compute u(⋅,τ) by solving the PDE.

• (5) Set $j=\frac{\sigma^{(m)}_{\tau}-\sigma_{m}}{\delta\sigma}$ and n[j]+=1, and store u(⋅,τ) in w(⋅)[j].

• (6) The answer is $u(\sigma;S,\tau)= \frac{w(S)[j]}{n[j]}$ with $j=\frac{\sigma-\sigma_{m}}{\delta\sigma}$.

5.3 Polynomial Projection

Now we choose ϕ _k (σ)=σ ^k.

Algorithm 5.2

• (1) Choose σ _m ,σ _M ,δσ,σ ₀.

• (2) Set A[⋅][⋅]=0, b[⋅][⋅]=0.

• (3) Compute M realizations $\{\sigma^{(m)}_{t_{i}}\}$ by MC on the volatility equation and for each realization.

  • (i) Compute u(⋅,τ) by solving the PDE.

  • (ii) Do $A[j][k]+=\frac{1}{M} \sum_{m}(\sigma^{(m)}_{\tau})^{j+k}, j,k=1,\ldots,K$.

  • (iii) Do $b[i][k]+=\frac{1}{M} u(i\delta S,\tau)(\sigma^{(m)}_{\tau})^{k}, k=1,\ldots,K$.

• (4) The answer is found by solving (5.1) for each i=1,…,N.

5.4 The Numerical Test

A Vanilla put with the same characteristics as in Sect. 3.1 has been computed by Algorithm 5.2 for a maturity of 3 years. The surface $S_{t_{1}},\sigma_{t_{1}}\to u$ is shown after t ₁=1.5 years in Fig. 4. The implied volatility is also shown.

Fig. 4

Both surfaces (a) and (b) are on top of each other, indistinguishable

6 American and Bermudan Options

For American options, we must proceed step by step backward in time as in the dynamic programming for binary trees (see [2]).

Consider M′ realizations $[\{\sigma^{m}_{t}\}_{t\in(0,T)}]_{ m=1}^{M'}$, giving $[\{\mu_{t}^{m}\}_{t\in(0,T)}]_{ m=1}^{M'}$ by (3.3). At time t _n =T, the price of the contract is (K−S)⁺. At time t _n−1=T−δt, it is given by the maximum of the European contract, knowing S and σ at t _n−1 and (K−S)⁺, i.e.,

$$\begin{aligned} u_{n-1}(S)=\max\biggl\{ \frac{1}{|M_\sigma|}\sum _{m\in M_\sigma} u^m_{n-1}(S),(K-S)^+ \biggr\} , \end{aligned}$$

(6.1)

where $u^{m}_{n-1}$ is the solution at t _n−1 to

$$\begin{aligned} \begin{aligned}& \partial_t u + \bigl(1-\rho^2 \bigr)\frac{(S\sigma^m_t)^2}{2} \partial_{SS} u + S\mu^m_t \partial_S u - ru =0,\quad t \in(t_{n-1},t_n), \\ &u_n:= u(S,t_n), \end{aligned} \end{aligned}$$

(6.2)

where u _n is known, and M _σ is the set of trajectories which give a volatility equal to σ at time t.

Here we have used the piecewise constant approximation intervals to compute the European premium. Alternatively, one could use any projection method, and the backward algorithm follows the same lines.

As with American options with binary trees, convergence with optimal order will hold only if δt is small enough. M _σ is built as in the previous section.

To prove the concept, we computed a Bermudan contract at $\frac{1}{2} T$ by the above method, using the polynomial basis for the projection. The parameters are the same as above except K=100. The results are displayed in Fig. 5. To obtain the price of the option at time zero, the surface of Fig. 5, i.e., (6.1), must be used as time-boundary conditions for the MC-PDE mixed solver for $t\in(0,\frac{1}{2} T)$, while for Americans, this strategy is applied at every time step, but here it is done once only at $\frac{1}{2} T$.

Fig. 5

A Bermuda option at $\frac{1}{2} T$ with Heston’s model compared with (K−S)⁺

7 Systems of Dimension Greater than 2

Stochastic volatility models with several SDEs for the volatilities are now in use. However, in order to assess the mixed MC-PDE method, we need to work on a systems for which an exact or precise solution is easily available. Therefore, we will investigate basket options instead.

7.1 Problem Formulation

We consider an option P on three assets whose dynamics are determined by the following system of stochastic differential equations:

$$\begin{aligned} \mathrm{d} S_{i,t} = S_{i,t} ( r \mathrm{d} t + \mathrm{d} W_{i,t} ), \quad t>0,\ i=1,2,3 \end{aligned}$$

(7.1)

with initial conditions S _i,t=0=S _i,0, $S_{i,0}\in\mathbb {R}^{+}$. The parameter $r\ (r\in\mathbb{R}_{\ge0})$ is constant, and $W_{i} := \sum_{j=1}^{3} a_{ij} B_{j}$ are linear combinations of standard Brownian motions B _j , such that

$$\begin{aligned} \operatorname{Cov}[W_{i,t},W_{j,t}]=\rho_{ij} \sigma_i \sigma_j t, \quad t>0. \end{aligned}$$

We further assume that $\varXi:= ( \rho_{ij} \sigma_{i} \sigma_{j} )_{i,j=1}^{3}$ is symmetric positive definite with

$$\begin{aligned} \rho_{ij}=1 \quad (i=j) \quad\text{or} \quad\rho_{ij} \in(-1,1)\quad \text{otherwise}. \end{aligned}$$

The coefficients $a_{ij}\ (a_{ij}\in\mathbb{R})$ have to be chosen, such that

$$\begin{aligned} \operatorname{Cov}[W_{i,t},W_{j,t}] & = E[ W_{i,t} W_{j,t}] \\ & = E\bigl[( a_{i1} B_{1,t} + a_{i2} B_{2,t} + a_{i3} B_{3,t} ) ( a_{j1} B_{1,t} + a_{j2} B_{2,t} + a_{j3} B_{3,t} )\bigr] \\ & = a_{i1} a_{j1} E\bigl[ B_{1,t}^2 \bigr] + a_{i2} a_{j2} E\bigl[ B_{2,t}^2 \bigr] + a_{i3} a_{j3} E\bigl[ B_{3,t}^2 \bigr] \\ & = ( a_{i1} a_{j1} + a_{i2} a_{j2} + a_{i3} a_{j3} ) t, \quad t>0, \end{aligned}$$

or equivalently,

$$\begin{aligned} A A^{\rm T} = \varXi, \end{aligned}$$

where $A := (a_{ij})_{i,j=1}^{3}$. Without loss of generality, we may set the strict upper triangular components of A to zero and find

$$\begin{aligned} A = \left ( \begin{array}{c@{\quad}c@{\quad}c} \sigma_1 & 0 & 0 \\ \sigma_2 \rho_{21} & \sigma_2 \sqrt{1-\rho_{12}^2} & 0 \\ \sigma_3 \rho_{31} & \sigma_3 \frac{\rho_{32}-\rho_{21}\rho _{31}}{\sqrt{1-\rho_{12}^2}} & \sigma_3 \sqrt{1-\rho_{31}^2- (\frac{\rho_{32}-\rho_{21}\rho_{31}}{\sqrt{1-\rho_{12}^2}} )^2} \end{array} \right ). \end{aligned}$$

The option P has the maturity $T \ (T\in\mathbb{R}^{+})$, the strike $K\ (K\in\mathbb{R}^{+})$ and the payoff function $\varphi:{\mathbb {R}^{+}}^{3}\to\mathbb{R}$,

$$\begin{aligned} \varphi(x) = \Biggl( K - \sum _{i=1}^3 x_i \Biggr)^+, \quad x=(x_1,x_2,x_3)^{\rm T} \in{\mathbb{R}^+}^3. \end{aligned}$$

The Black-Scholes price of P at time 0 is

$$\begin{aligned} P_0 = \mathrm{e}^{-r{T}} E^* \Biggl[ \Biggl( K - \sum _{i=1}^3 S_{i,T} \Biggr)^+ \Biggr], \end{aligned}$$

(7.2)

where E ^∗ denotes the expectation with respect to the risk-neutral measure.

7.2 The Uncoupled System

In order to combine different types of methods (Monte-Carlo, quadrature and/or PDE methods), we will uncouple the SDE in (7.1), we start with a change of variable to logarithmic prices. Let s _i,t :=log(S _i,t ), i=1,2,3, and then Itô’s lemma shows that

$$\begin{aligned} \mathrm{d} s_{i,t} = r_i \mathrm{d} t + \mathrm{d} W_{i,t}, \quad t>0 \end{aligned}$$

(7.3)

with initial conditions s _i,t=0=s _i,0:=log(S _i,0). The parameters r _i (i=1,2,3) have been defined as $r_{i} = r - \frac{a_{i1}^{2}}{2} - \frac{a_{i2}^{2}}{2} - \frac{a_{i3}^{2}}{2} = r - \frac{\sigma_{i}^{2}}{2}$. In the rest of the section, the time index of any object is omitted to simplify the notation.

We note that (7.3) can be written as

$$\begin{aligned} \left ( \begin{array}{c} \mathrm{d} s_1 - r_1 \mathrm{d} t \\ \mathrm{d} s_2 - r_2 \mathrm{d} t \\ \mathrm{d} s_3 - r_3 \mathrm{d} t \end{array} \right ) = \left ( \begin{array}{c@{\quad}c@{\quad}c} a_{11} & 0 & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & a_{33} \end{array} \right ) \left ( \begin{array}{c} \mathrm{d} B_1 \\ \mathrm{d} B_2 \\ \mathrm{d} B_3 \end{array} \right ). \end{aligned}$$

Then, uncoupling reduces to Gaussian elimination. Using the Frobenius matrices

$$\begin{aligned} F_1 := \left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ -\frac{a_{21}}{a_{11}} & 1 & 0 \\ -\frac{a_{31}}{a_{11}} & 0 & 1 \end{array} \right ),\quad \quad F_2 := \left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{a_{32}}{a_{22}} & 1 \end{array} \right ), \end{aligned}$$

we write

$$\begin{aligned} F_2 F_1 ( \mathrm{d} s + r \mathrm{d} t ) = \operatorname{Diag}(a_{11},a_{22},a_{33}) \mathrm{d} B, \end{aligned}$$

where $s=(s_{1},s_{2},s_{3})^{\rm T}$, $r=(r_{1},r_{2},r_{3})^{\rm T}$ and $B=(B_{1},B_{2},B_{3})^{\rm T}$. We set L ⁻¹:=F ₂ F ₁, and define

$$\begin{aligned} \widetilde{s}:= L^{-1}s\quad\text{and}\quad\widetilde{S}:= \mathrm{e}^{ L^{-1}s}. \end{aligned}$$

Remark 7.1

(i) The processes $\widetilde{s}_{1}$, $\widetilde{s}_{2}$ and $\widetilde{s}_{3}$ are independent of each other, and are analogous with $\widetilde{S}_{1}$, $\widetilde{S}_{2}$ and $\widetilde{S}_{3}$, respectively.

(ii) Let $\widetilde{r} := L^{-1} r$. Then

$$\begin{aligned} \mathrm{d}\widetilde{s}= \widetilde{r}\mathrm{d} t + \operatorname{Diag}(a_{11},a_{22},a_{33}) \mathrm{d} B. \end{aligned}$$

(iii) The coupled system expressed in terms of the uncoupled system is $s=L \widetilde{s}$.

(iv) In the next section, we will make use of the triangular structure of $L=(L_{ij})_{i,j=1}^{3}$ and $L^{-1}=((L^{-1})_{ij})_{i,j=1}^{3}$,

$$\begin{aligned} L= \left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ \frac{a_{21}}{a_{11}} & 1 & 0 \\ \frac{a_{31}}{a_{11}} & \frac{a_{32}}{a_{22}} & 1 \end{array} \right )\quad \text{and}\quad L^{-1} = \left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ -\frac{a_{21}}{a_{11}} & 1 & 0 \\ \frac{a_{21}a_{32}}{a_{11}a_{22}}-\frac{a_{31}}{a_{11}} & \frac {a_{32}}{a_{22}} & 1 \end{array} \right ). \end{aligned}$$

(v) The notation has been symbolic and the derivation heuristic.

7.3 Mixed Methods

We describe nine combinations of Monte-Carlo, quadrature (or QUAD for short) and/or PDE methods.

Convention

If Z is a stochastic process, we denote by Z ^m a realization of the process. Let M′ stand for a fixed number of Monte-Carlo samples.

Basic Methods

(i) MC3 method

Simulate M′ trajectories of (S ₁,S ₂,S ₃). An approximation of the option price P ₀ is

$$\begin{aligned} P_0^a := \mathrm{e}^{-rT} \frac{1}{M'}\sum _{m=1}^{M'} \varphi \bigl(S_{1,T}^m,S_{2,T}^m,S_{3,T}^m \bigr). \end{aligned}$$

(ii) QUAD3 method

In order to use a quadrature formula, we replace the risk neutral measure in

$$\begin{aligned} P_0 = \mathrm{e}^{-rT} E^*\bigl[\bigl( K - \mathrm{e}^{ ( L {\widetilde{s}_T})_1 } - \mathrm{e}^{ ( L {\widetilde{s}_T})_2 } - \mathrm{e}^{ ( L {\widetilde{s}_T})_3 } \bigr)^+ \bigr] \end{aligned}$$

by the Lebesgue-measure. Note

$$\begin{aligned} \widetilde{s}_{i,t} \sim N\bigl( \mu_{i,t} , a_{ii}^2 t \bigr), \quad1\le i\le3, \end{aligned}$$

where $\mu_{i,t}=\widetilde{s}_{i,0}+\widetilde{r}_{i} t$. Let f _i,t be the density of $\widetilde{s}_{i,t}$, i.e.,

$$\begin{aligned} f_{i,t}(x_i) = \frac{1}{ \sqrt{ 2\pi} a_{ii} \sqrt{t} } \mathrm{e}^{ -\frac{1}{2}( \frac{x_i-\mu_{i,t}}{a_{ii}\sqrt{t}})^2 } ,\quad x_i\in\mathbb{R}, \ 1\le i \le3. \end{aligned}$$

Due to the independence of $\widetilde{s}_{1,t}$, $\widetilde{s}_{2,t}$ and $\widetilde{s}_{3,t}$, the density of

$$\begin{aligned} \bigl( K - \mathrm{e}^{ ( L {\widetilde{s}_T})_1 } - \mathrm{e}^{ ( L {\widetilde{s}_T})_2 } - \mathrm{e}^{ ( L {\widetilde{s}_T})_3 }\bigr)^+ \end{aligned}$$

is

$$\begin{aligned} (x_1,x_2,x_3)\mapsto f_{1,T}(x_1) f_{2,T}(x_2) f_{3,T}(x_3),\quad (x_1,x_2,x_3)\in\mathbb{R}^3. \end{aligned}$$

The formula for the option price becomes

$$\begin{aligned} P_0 = \mathrm{e}^{-rT} \int_{\mathbb{R}^3} \bigl( K - \mathrm{e}^{ (Lx)_1 } - \mathrm{e} ^{ (Lx)_2 } - \mathrm{e}^{ (Lx)_3 }\bigr)^+ f_{1,T}(x_1) f_{2,T}(x_2) f_{3,T}(x_3)\mathrm{d} x. \end{aligned}$$

Now, a quadrature formula can be used to compute the integral.

The methods, which are based on a combination of quadrature and some other methods, will be presented for the case, where the trapezoidal rule is used. Next we show how the trapezoidal rule can be used to compute the integral. This allows us to introduce the notation for the description of methods, which are combinations of quadrature and some other methods.

To compute the integral, we truncate the domain of integration to κ standard deviations around the means μ _1,T , μ _2,T and μ _3,T . Let

$$\begin{aligned} x_{i,0} &= \mu_{i,T}-\kappa a_{ii}^2, \\ x_{i,n} &= x_{i,0} + n \delta x_i,\quad n=1, \ldots,{N_{\rm Q}}, \end{aligned}$$

1≤i≤3, where $\delta x_{i}=\frac{2\kappa}{N_{\rm Q}}$, ${N_{\rm Q}}$.

The option price P ₀ is then approximated by

$$\begin{aligned} P_0^a:= \mathrm{e}^{-rT} \sum _{n_1,n_2,n_3=1}^N \Biggl(\prod _{i=1}^3 \chi_{n_i}\delta x_i f_{i,T}(x_{i,n_i}) \Biggr) \bigl( K - \mathrm{e}^{(Lx_n)_1} - \mathrm{e}^{(Lx_n)_2} - \mathrm{e}^{(Lx_n)_3} \bigr)^+, \end{aligned}$$

where $x_{n}:=(x_{1,n_{1}},x_{2,n_{2}},x_{3,n_{3}})^{\rm T}$ and

$$\begin{aligned} \chi_n = \begin{cases} 0.5, & \text{if}\ n=0\ \text{or}\ n={N_{\rm Q}},\\ 1, & \text{otherwise}. \end{cases} \end{aligned}$$

(iii) MC2-PDE1 method (combination of two methods)

Note

$$\begin{aligned} P_0 &= \mathrm{e}^{-rT} E^* \bigl[ \bigl( K - S_{1,T} - S_{2,T} - S_{1,T}^{-2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}} \widetilde{S}_{3,T}\bigr)^+\bigr] \\ &= \mathrm{e}^{-rT} E^* \bigl[( \overline{K} - \widetilde{\widetilde{S}}_{3,T})^+\bigr], \end{aligned}$$

where

$$\begin{aligned} \overline{K} := K - S_{1,T} - S_{2,T}, \end{aligned}$$

and $\widetilde{\widetilde{S}}_{3}$ is the solution to the stochastic initial value problem

$$\begin{aligned} \mathrm{d}\widetilde{\widetilde{S}}_{3,t} &= \widetilde{\widetilde{S}}_{3,t} ( \widetilde{\widetilde{r}}_3 \mathrm{d} t + a_{33}\mathrm{d} B_{3,t} ), \\ \widetilde{\widetilde{S}}_{3,t=0} &= \alpha\widetilde{S}_{3,0} \end{aligned}$$

with parameters $\widetilde{\widetilde{r}}_{3} := \widetilde{r}_{3} + \frac{a_{33}^{2}}{2}$ and $\alpha=S_{1,T}^{-2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}}$.

The method is then as follows. Simulate M′ realizations of (S ₁,S ₂) and set $\overline{K}^{m}=K - S_{1,T}^{m} - S_{2,T}^{m}$ and $\alpha^{m}={S_{1,T}^{m}}^{-2(L^{-1})_{31}} {S_{2,T}^{m}}^{-(L^{-1})_{32}}$. Compute an approximation of P ₀ by

$$\begin{aligned} P_0^a:= \frac{1}{M'}\sum _{m=1}^{M'} u\bigl(x_3,t;\overline{K}^m\bigr)\big|_{ x_3=\alpha^m\widetilde{S}_{3,0},t=T} , \end{aligned}$$

where u is the solution to the initial value problem for the one-dimensional Black-Scholes PDE with the parametrized (β) initial condition

$$\begin{aligned} \frac{\partial u}{\partial t} - \frac{ (a_{33} x_3)^2 }{2} \frac {\partial^2 u}{\partial x_3^2} - \widetilde{ \widetilde{r}}_3 x_3 \frac{\partial u}{\partial x_3} + \widetilde{ \widetilde{r}}_3 u &= 0\quad \text{in}\ \varOmega \times(0,T), \end{aligned}$$

(7.4a)

$$\begin{aligned} u(t=0) &= u_0\quad\mbox{in}\ \varOmega, \end{aligned}$$

(7.4b)

where $\varOmega=\mathbb{R}^{+}$ and

$$\begin{aligned} u_0(x_3;\beta):= ( \beta- x_3 )^+,\quad x_3>0. \end{aligned}$$

(iv) QUAD2-PDE1 method

Note

$$\begin{aligned} P_0 &= \mathrm{e}^{-rT} \int_{\mathbb{R}^2} E^* \bigl[\bigl( K - \mathrm{e}^{L_{11}x_1} - \mathrm{e}^{L_{21}x_1+L_{22}x_2} \\ &\quad{}- \mathrm{e}^{L_{31}x_1+L_{32}x_2} \mathrm {e}^{L_{33}\widetilde{s}_{3,T}} \bigr)^+\bigr] f_{1,T}(x_1) f_{2,T}(x_2)\mathrm{d} x_1 \mathrm{d} x_2. \end{aligned}$$

The option price P ₀ is approximated by

$$ P_0^a:= \sum _{n_1,n_2=1}^{N_{\rm Q}} \Biggl(\prod_{i=1}^2 \chi_{n_i} \delta x_i f_{i,T}(x_{i,n_i}) \Biggr) u(x_3,t;\overline{K}_{n_1n_2})|_{ x_3=\alpha_{n_1n_2}\widetilde{S}_{3,0},t=T}, $$

where

$$\begin{aligned} \overline{K}_{n_1n_2} &:= K - \mathrm{e}^{L_{11}x_{1,n_1}} - \mathrm {e}^{L_{21}x_{1,n_1}+L_{22}x_{2,n_2}}, \\ \alpha_{n_1n_2} &:= \mathrm{e}^{L_{31}x_{1,n_1}+L_{32}x_{2,n_2}}, \end{aligned}$$

and u denotes the solution to (7.4a)–(7.4b).

(v) MC1-PDE2 method

Note

$$ P_0 = \mathrm{e}^{-rT} E^* \bigl[\bigl( K - S_{1,T} - S_{2,T} - S_{1,T}^{-2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}} \widetilde{S}_{3,T}\bigr)^+\bigr]. $$

Simulate M′ realizations of $\widetilde{S}_{3}$. The option price P ₀ is then approximated by

$$ P_0^a:= \frac{1}{M'}\sum _{m=1}^{M'} u\bigl(x_1,x_2,t;\widetilde{S}_{3,T}^m \bigr)\big|_{ x_1=S_{1,0},x_2=S_{2,0},t=T}, $$

where u denotes the solution to the initial value problem for the 2-dimensional Black-Scholes PDE with the parameterized (β) initial condition

$$ u_0(x_1,x_2,0;\beta) =\bigl( K - x_1 - x_2 - x_1^{ - 2(L^{-1})_{31} } x_2^{ - (L^{-1})_{32} } \beta\bigr)^+,\quad x_1,x_2>0. $$

The problem is

$$\begin{aligned} \frac{\partial u}{\partial t} - \sum _{i,j=1}^2 x_i x_j \varrho_{ij} \frac{\partial u}{\partial x_i} \frac{\partial u}{\partial x_j} - r \sum _{i=1}^2 x_i \frac{\partial u}{\partial x_i} + r u &= 0\quad\text{in}\ \varOmega\times(0,T), \end{aligned}$$

(7.5a)

$$\begin{aligned} u(t=0) &= u_0\quad\text{in}\ \varOmega, \end{aligned}$$

(7.5b)

where $\varOmega=\mathbb{R}^{+}\times\mathbb{R}^{+}$ and

$$\begin{aligned} \varrho= ( \varrho_{ij} )_{i,j=1,\ldots,3} = \frac{1}{2} \left ( \begin{array}{c@{\quad}c} a_{11}^2 & a_{11} a_{21} \\ a_{11} a_{21} & a_{21}^2 + a_{22}^2 \end{array} \right ). \end{aligned}$$

(7.6)

(vi) QUAD1-PDE2 method

Note

$$ P_0 = \mathrm{e}^{-rT} \int_{\mathbb{R}} E^* \bigl[\bigl( K - S_{1,T} - S_{2,T} - S_{1,T}^{-2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}} \mathrm{e}^{x_3}\bigr)^+\bigr] f_{3,T}(x_3)\mathrm{d} x_3. $$

With the notation above, another approximation of the option price P ₀ is

$$\begin{aligned} P_0^a &: = \sum _{n=1}^{N_{\rm Q}} \delta x_3 f_{3,T}( x_{3,n} ) \mathrm{e}^{-rT} E^*\bigl[\bigl( K - S_{1,T} - S_{2,T} - S_{1,T}^{2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}} \mathrm{e}^{ x_{3,n} }\bigr)^+\bigr] \\ &= \sum _{n=1}^{N_{\rm Q}}\delta x_3 f_{3,T}( x_{3,n} ) u(x_1,x_2,t;x_{3,n})|_{ x_1=S_{1,0},x_2=S_{2,0},t=T}, \end{aligned}$$

where u is the solution to the initial value problem (7.5a)–(7.5b).

(vii) MC1-QUAD2 method

Reformulating (7.2), we deduce

$$\begin{aligned} P_0 &= \mathrm{e}^{-rT} E^* \int_{\mathbb{R}^2} \bigl( K - \mathrm{e}^{ (Lx)_1 } - \mathrm{e}^{ (Lx)_2 } - \mathrm{e}^{ L_{31}x_1 + L_{32}x_2 + \widetilde{s}_{3,T} } \bigr)^+ \\ &\quad{}\times f_{1,T}(x_1) f_{2,T}(x_2)\mathrm{d} x_1 \mathrm{d} x_2, \end{aligned}$$

and obtain the following method.

Compute M′ realizations of $\widetilde{s}_{3,T}$, and approximate P ₀ by

$$\begin{aligned} P_0^a&:= \mathrm{e}^{-rT} \frac{1}{M'} \sum _{n_1,n_2=1}^{N_{\rm Q}} \sum _{m=1}^{M'} \Biggl(\prod _{i=1}^2 \chi_{n_i}\delta x_i f_{i,T}(x_{i,n_i}) \Biggr) \\ &\ \quad{}\cdot\bigl( K - \mathrm{e}^{ x_{1,n_1} } - \mathrm{e}^{ L_{21}x_{1,n_1} + x_{2,n_2} } - \mathrm{e}^{ L_{31} x_{1,n_1} + L_{32} x_{2,n_2} + \widetilde{s}_{3,T}^{\,m} }\bigr)^+. \end{aligned}$$

(viii) MC2-QUAD1 method

Note

$$ P_0 = \mathrm{e}^{-rT} \int_{\mathbb{R}} E^* \bigl[\bigl( K - S_{1,T} - S_{2,T} - S_{1,T}^{-2(L^{-1})_{31}} S_{2,T}^{-(L^{-1})_{32}} \mathrm{e}^{x_3}\bigr)^+ \bigr] f_{3,T}(x_3)\mathrm{d} x_3. $$

The method is as follows. Simulate M′ realizations of (S ₁,S ₂), and compute

$$\begin{aligned} P_0^a &:= \mathrm{e}^{-rT} \frac{1}{M'} \sum _{m=1}^{M'} \sum _{n=1}^{N_{\rm Q}} \chi_n \delta x_3 f_{3,T}( x_{3,n} ) \bigl( K - S_{1,T}^m - S_{2,T}^m \\ &\ \quad{}- {S_{1,T}^m}^{-2(L^{-1})_{31}} {S_{2,T}^m}^{-(L^{-1})_{32}} \mathrm{e}^{x_{3,n}}\bigr)^+. \end{aligned}$$

(ix) MC1-QUAD1-PDE1 method (combination of three methods)

Note

$$\begin{aligned} P_0& = \int_\mathbb{R}f_{2,T}(x_2) \mathrm{e}^{-rT} E^*\bigl[\bigl( K - \mathrm{e}^{ \widetilde{s}_{1,T} } - \mathrm{e}^{ L_{21} \widetilde{s}_{1,T} + x_2 } \\ &\quad{}- \mathrm{e}^{ (-2(L^{-1})_{31}-(L^{-1})_{32}L_{21})\widetilde{s}_{1,T} -(L^{-1})_{32} x_2 } \widetilde{S}_{3,T}\bigr)^+\bigr] \mathrm{d} x_2. \end{aligned}$$

Then an approximation to P ₀ is

$$\begin{aligned} P_0^a:= \frac{1}{M'} \sum _{m=1}^{M'} \sum_{n=1}^{N_{\rm Q}} \chi_2\delta x_2 f_{2,T}(x_{2,n}) u \bigl(x_3,t;\overline{K}_n^m\bigr)\big|_{ x_3=\alpha_n^m\widetilde{S}_{3,0},t=T} , \end{aligned}$$

where

$$\begin{aligned} \overline{K}_n^m &:= K - \mathrm{e}^{ \widetilde{s}_{1,T}^m } - \mathrm{e}^{ L_{21} \widetilde{s}_{1,T}^{\,m} + x_{2,n_2} }, \\ \alpha_n^m &:= \mathrm{e}^{ (-2(L^{-1})_{31}-(L^{-1})_{32}L_{21})\widetilde{s}_{1,T}^{\,m} -(L^{-1})_{32} x_{2,n} }, \end{aligned}$$

and u denotes the solution to (7.4a)–(7.4b).

7.4 Numerical Results

This section provides a documentation of numerical results. We have considered European put options on baskets of three and five assets, and used mixed methods to compute their prices. If the method is stochastic, i.e., if a part of it is Monte-Carlo simulation, then we have run the method with different seed values several times (N _S ) and computed mean (m) and standard deviation (s) of the price estimates. If the method is deterministic, we have chosen the discretization parameters, such that the first three digits of $P_{0}^{a}$ remained fix, while the discretization parameters have been further refined. Instead of solving the 1-dimensional Black-Scholes PDE, we have used the Black-Scholes formula.

(i) European put on three assets

The problem is to compute the price of a European put option on a basket of three assets in the framework outlined in Sect. 7.1.

We have chosen the parameters as follows: K=150, T=1, r=0.05, S ₀=(55,50,45),

$$\begin{aligned} \rho= \left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & -0.1 & -0.2 \\ -0.1 & 1 & -0.3 \\ -0.2 & -0.3 & 1 \end{array} \right ),\quad \quad \sigma= \left ( \begin{array}{c@{\quad}c@{\quad}c} 0.3 & 0.2 & 0.25 \end{array} \right )^{\rm T}. \end{aligned}$$

We have used various (mixed) methods to compute approximations to P ₀ (see (7.2)).

We have used freefem++, and the rest is programmed in C++. The implementation in freefem++ requires a localization and the weak formulation of the Black-Scholes PDE. The triangulation of the computational domain and the discretization of the Black-Scholes PDE by conforming P1 finite elements are done by freefem++.

A reference result for P ₀ has been computed by using the Monte-Carlo method with 10⁷ samples.

The numerical results are displayed in Table 4. One can see that the computational load for the PDE2 methods (i.e., MC1-PDE2, QUAD1-PDE2) is much larger than that for the other methods. Furthermore, the results seem to be less precise than those in the other cases. The results have been obtained very fast if just quadrature (i.e., QUAD3) or quadrature in combination with the Black-Scholes formula (i.e., QUAD2-PDE1) was used. In these cases, the results seem to be very precise although the discretization has been coarse (${N_{\rm Q}}=12$). Comparison of the results obtained by the MC3 method with the results obtained by the MC2-PDE1 method shows that the last mentioned seems to be superior. The computing time is about equal, but the standard deviation for MC2-PDE1 is much less than that for MC3.

Table 4 Pricing a European put option on a basket of three assets, i.e., estimates of the option price at time 0. Columns 1–3: the method used to approximate P ₀. Columns 4–6: the discretization parameters. M′ is the number of Monte-Carlo samples, ${N_{\rm Q}}$ is the number of quadrature points, $N_{\rm S}$ is the number of samples used to compute the mean (m) and the standard deviation (s). Column 9: the computing time

(ii) European put on five assets

Let P be a European put option on a basket of five assets, with payoff

$$\begin{aligned} \varphi(x) = \Biggl( K - \sum _{i=1}^5 x_i \Biggr)^+. \end{aligned}$$

The system of stochastic differential equations, which describes the dynamics of the underlying assets, has the usual form. We have set K=250, T=1, r=0.05,

$$\begin{aligned} S_0& = (40 , 45 , 50 , 55 , 60)^{\rm T}, \\ \sigma&=(0.3, 0.275, 0.25, 0.225, 0.2)^{\rm T}, \\ \rho&= \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & -0.37 & -0.40 & -0.44 & -0.50 \\ -0.37 & 1 & -0.50 & -0.46 & -0.05 \\ -0.40 & -0.50 & 1 & 0.51 & 0.29 \\ -0.44 & -0.46 & 0.51 & 1 & 0.20 \\ -0.50 & -0.05 & 0.29 & 0.20 & 1 \end{array} \right ). \end{aligned}$$

We approximated the price of P at time 0 by various (mixed) methods. The results are displayed in Table 5. One can see that for all tested methods the (mean) price has been close (±0.003) to the reference price (1.159). Since ${N_{\rm Q}}=10$ turned out to be enough, the computational effort has been very low for QUAD5 and QUAD4-PDE1. In the case, the method is stochastic, and deterministic methods allow to reduce the variance, such as in MC4-QUAD1 and MC4-PDE1-QUAD1.

Table 5 Pricing a European put option on a basket of five assets, i.e., estimates of the option price at time 0. Columns 1–3: the method used to approximate P ₀. Columns 4–6: the discretization parameters. M′ is the number of Monte-Carlo samples, ${N_{\rm Q}}$ is the number of quadrature points, $N_{\rm S}$ is the number of samples used to compute the mean (m) and the standard deviation (s). Columns 7–9: the numerical results. Column 7: the mean of P ₀. Column 8: the standard deviation of P ₀. Column 9: the computing time

8 Conclusion

Mixing Monte-Carlo methods with partial differential equations allows the use of closed formula on problems which do not have any otherwise. In these cases, the numerical methods are much faster than full MC or full PDE. The method works also for nonconstant coefficient models with and without jump processes and also for American contracts, although proofs of convergence have not been given here.

For multi-dimensional problems, we tested all possibilities of mixing MC and PDE and also quadrature on semi-analytic formula, and we found that the best is to apply PDE methods to one equation only.

The speed-up technique by polynomial fit has been discussed also, but we plan to elaborate on such ideas in the future particularly in the context of reduced basis, such as POD (proper orthogonal decomposition), ideally suited to the subproblems arising from MC+PDE, because the same PDE has to be solved many times for different time dependent coefficients.