Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Various kinds of instabilities that can influence the propagation of reaction fronts can be encountered in several physical problems, including the thermo-diffusional instability, the hydrodynamical instability as well as the convective instability. For instance, the thermo-diffusional instability appears as a result of competition between the heat production in the reaction zone and heat transfer to the cold reactants. To investigate this type of instability, the density of the medium can be taken as constant to remove the influence of hydrodynamics and to simplify the model. The stability conditions in this case were studied in [1–5]. In hydrodynamic instability of reaction fronts, the density of the medium is variable and usually considered as a given function of the temperature. In this case, the instability is caused by heat expansion of the gas or liquid in a neighborhood of the reaction zone [6–10]. Due to the fact that instabilities of reaction fronts are undesirable phenomena, several works have been devoted to studying the effect of a periodic vibration on the convective instability of these reaction fronts. For instance, it was shown that high-frequency vibrations can influence stability of various convective flows, namely periodic modulations can have a stabilizing effect for low frequencies and a destabilizing effect for high ones [11].

It is worth noticing that the case of reaction fronts with liquid reactant and solid product was considered in [12], while the case where the reactant and the product are liquids was analyzed in [13, 14]. It was concluded in these cases that a periodic vibration can affect the onset of convection. Specifically, it was indicated that the case where the polymerization front in liquids is different from the case when the polymer is solid. The difference is that in liquids, the convective instability may exist also in descending fronts [15].

The case of reaction fronts in porous media has also been tackled and the influence of periodic vibration on convective instability has been investigated. The linear stability analysis and direct numerical simulations were performed and the effect of vibration on the onset of convection was examined. In addition, in the case of a porous medium saturated by a fluid, the effect of vertical vibrations on thermal stability of a conductive solution was examined in [16]; for other directions of vibration, depending on the vibrational parameter and the angle of vibration, stabilizing and destabilizing effects were discussed [17].

Mechanical and thermal vibrations have also been studied in connection with the Rayleigh–Bénard convection [18, 19], directional solidification [20, 21], and doubly diffusive convection [22]. In spite of numerous results on the influence of vibrations on convective instability, some questions still remain open. In particular, normal vibrations cannot stabilize the conductive state in an unbounded domain [23], while tangential vibration is only effective for vibration frequencies that are not too large [24].

It is worth noticing that the problem of convective instability under the influence of periodic gravity or periodic heating of a liquid layer or the effect of periodic magnetic field on magnetic liquid layer has been widely analyzed during the last decades; see for instance [18, 25–34] and references therein.

While the influence of a periodic modulation on the convective instability was extensively studied in various physical problems and using different types of modulation, only few works have been devoted to study the effect of a quasi-periodic (QP) vibration on such a convective instability. To the best of our knowledge, Boulal et al. [35] were the first who investigated the effect of a QP gravitational modulation with two incommensurate frequencies on convective instability from analytical view point. They considered the problem of stability of a heated fluid layer. The threshold of convective instability was determined in the case of heating from below or from above, and it was shown that the frequencies ratio of QP vibration strongly affects the convective instability threshold. Motivated by the successful treatment in studying QP convective instability in the later problem, similar studies were performed. The influence of QP gravitational modulation on convective instability in Hele-Shaw cell was examined in [36], and its influence on thermal instability in a horizontal Newtonian magnetic liquid layer with non-magnetic rigid boundaries (in the presence of a vertical magnetic field) was analyzed in [37]. It was shown that in the case of a heating from below, a QP modulation produces a stabilizing or a destabilizing effect depending on the frequencies ratio.

In these works [35–37], the original QP partial differential equations modeling the problem are reduced to a QP Mathieu equation using Galerkin method truncated to the first order. Due to the fact that the Floquet theory cannot be applied in the QP forcing case, the approach used to obtain the marginal stability curves was based on the application of the harmonic balance method and Hill’s determinants [38, 39].

Recently, the effect of QP gravitational modulation on convective instability of reaction fronts in porous media was studied in [40]. The QP modulation has been chosen as a sum of two modulations having two incommensurate frequencies. It was concluded that in a certain regions corresponding to small values of the amplitude vibration, a stabilizing effect can be achieved, whereas large amplitudes of vibration induce a destabilizing effect. The results also shown that for a given value of the critical Rayleigh number and for large frequencies, the front can undergo abrupt change of stability by varying the amplitude of vibration.

The aim of this chapter is to give an overview on the effect of different gravitational modulations on the convective instability of reaction front. We first consider the case where the amplitude of the periodic vibration is modulated. In this situation, two cases are considered. In the first case, the frequency of the modulation is assumed to be twice the frequency of the vibration itself, while in the second case, the frequency of the modulation is supposed to be half that of the vibration. In a second case, we discuss the effect of QP gravitational modulation on the convective instability of reaction front. These studies are motivated by applications arising in some physical problems, as for instance, frontal polymerization [41] or problem related to environmental pollution [42]. The QP vibration may eventually result from a simultaneous existence of a basic vibration applied to the system with a frequency ν 1 and of an additional residual vibration having a frequency ν 2, such that ν 1 and ν 2 are incommensurate. Indeed, this residual vibration may come from various sources as machinery, friction or just a modulation phenomenon leading to the modulation of the amplitude of the basic vibration.

It what follows we consider a periodic vibration and QP one with two incommensurate frequencies in the vertical direction upon the system containing a reaction reactant and a reaction product. This excitation causes the acceleration, b, perpendicular to the reactant–product interface. In order to investigate the influence of different vibration (periodic, QP and with modulation of amplitude), we consider the time dependence of the instantaneous acceleration acting on the fluids given by g + b(t), where g is the gravity acceleration and b(t) can be a periodic, modulated periodic or QP force. In other words, wa shall consider the following three cases: b(t) = λsin(νt), \(b(t) =\lambda _{1}sin(\nu _{1}t) +\lambda _{2}sin(\nu _{2}t)\) and \(b(t) =\lambda cos(\nu _{2}t)sin(\nu _{1}t)\) where λ, λ 1, λ 2 and ν, ν 1, ν 2 are respectively, the amplitudes and the frequencies of the considered vibration. Here, we consider reaction fronts in a porous medium with the fluid motion described by the Darcy law and the Boussinesq approximation, which takes into account the temperature dependence of the density only in the volumetric forces.

It is worthy to notice that the problem of reducing the original Navier–Stokes equations to a standard QP Mathieu equation using Galerkin method, harmonic balance method and Hill’s determinants [35–37] cannot be exploited here due to the coupling of the concentration and the heat equations (reaction-diffusion problem coupled with the Darcy equation). Therefore, to obtain the convective stability boundary, we first reduce the original reaction-diffusion problem to a singular perturbation one using the so-called matched asymptotic expansion (see Appendix), we perform a linear stability analysis, and then solve the reduced interface problem using numerical simulations.

This chapter is organized as follow. Section 2 is devoted to state the problems and to perform the linear stability analysis. In Sect. 3, we analyze the influence of different gravitational modulation on the convective instability of reaction front, and we conclude in the last section.

2 Governing Equations and Linear Stability Analysis

2.1 The Model

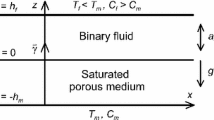
We consider an upward propagating reaction front in a porous medium filled by an incompressible reacting fluid submitted to a periodic or QP gravitational vibration, as shown in Fig. 1. The model of a such process can be described by a reaction-diffusion system coupled with the hydrodynamic equations under the Darcy law:

Fig. 1
figure 1

Sketch of the reaction front propagation

Full size image
$$\displaystyle{ \frac{\partial T} {\partial t} + \mathbf{v}.\nabla T =\kappa \Delta T + qK(T)\phi (\alpha ), }$$
(1)
$$\displaystyle{ \frac{\partial \alpha } {\partial t} + \mathbf{v}.\nabla \alpha = d\Delta \alpha + K(T)\phi (\alpha ), }$$
(2)
$$\displaystyle{ \mathbf{v} + \frac{K} {\mu } \nabla p = \frac{g\beta K} {\mu } \rho (T - T_{0})(1 + b(t))\boldsymbol{\gamma }, }$$
(3)
$$\displaystyle{ \nabla.\mathbf{v} = 0. }$$
(4)

with the following boundary conditions:

$$\displaystyle\begin{array}{rcl} T& =& T_{i}\text{ , }\alpha = 1\text{ and }v = 0\text{ when }y \rightarrow +\infty ,\end{array}$$
(5)
$$\displaystyle\begin{array}{rcl} T& =& T_{b}\text{ , }\alpha = 0\text{ and }v = 0\text{ when }y \rightarrow -\infty.\end{array}$$
(6)

Here T is the temperature, α the depth of conversion, v = (v x , v y ) the fluid velocity, p the pressure, κ the coefficient of thermal diffusivity, d the diffusion, q the adiabatic heat release, g the gravity acceleration, ρ the density, β the coefficient of thermal expansion, μ the viscosity and γ is the unit vector in the upward direction. In addition, T 0 is the mean value of temperature, T i is an initial temperature while T b is the temperature of the burned mixture given by \(T_{b} = T_{i} + q\). The function K(T)ϕ(α) is the reaction rate where the temperature dependence is given by the Arrhenius law [10]:

$$\displaystyle{ K(T) = k_{0}\exp {\Bigl ( - \frac{E} {R_{0}T}\Bigr )} }$$
(7)

where E is the activation energy, R 0 the universal gas constant and k 0 is the pre-exponential factor. For the asymptotic analysis of this problem we assume that the activation energy is large and we consider zero order reaction for which

$$\displaystyle{ \phi (\alpha ) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\text{ if}\ \alpha < 1\quad \\ 0\text{ if} \ \alpha = 1\quad \end{array} \right.. }$$
(8)

The gravitational modulation force b(t) is given depending of the nature of modulation. If it is periodic, b(t) = λsin(νt), and if it is QP, \(b(t) =\lambda _{1}\mathit{sin}(\nu _{1}t) +\lambda _{2}\mathit{sin}(\nu _{2}t)\).

2.2 The Dimensionless Model

In order to write down the dimensionless model, we now introduce the spatial variables \(x\prime = \frac{xc_{1}} {\kappa }\), \(y\prime = \frac{yc_{1}} {\kappa }\), time \(t\prime = \frac{tc_{1}^{2}} {\kappa d}\), velocity \(\frac{\mathbf{v}} {c_{1}}\), pressure \(\frac{p\kappa \mu } {K}\) with \(c_{1} = c/\sqrt{2}\) and frequency \(\sigma = \frac{\kappa } {c_{1}^{2}}\nu\). Denoting \(\theta = \frac{T - T_{b}} {q}\) and keeping for convenience the same notation for the other variables, we obtain the system

$$\displaystyle{ \frac{\partial \theta } {\partial t} + v\nabla \theta = \Delta \theta + W_{Z}\left (\theta \right )\phi \left (\alpha \right ), }$$
(9)
$$\displaystyle{ \frac{\partial \alpha } {\partial t} + v\nabla \alpha = \Lambda \Delta \alpha + W_{Z}\left (\theta \right )\phi \left (\alpha \right ), }$$
(10)
$$\displaystyle{ v + \nabla p = R_{p}\left (\theta +\theta _{0}\right )\left({0\atop 1}\right)(1 + b_{d}(t)), }$$
(11)
$$\displaystyle{ \mathit{div}\left (v\right ) = 0 }$$
(12)

with the following conditions at infinity:

$$\displaystyle\begin{array}{rcl} \theta & =& -1\text{ , }\alpha = 0\text{ and }v = 0\text{ when }y \rightarrow +\infty ,\end{array}$$
(13)
$$\displaystyle\begin{array}{rcl} \theta & =& 0\text{ , }\alpha = 1\text{ and }v = 0\text{ when }y \rightarrow -\infty.\end{array}$$
(14)

Here \(\Lambda = d/\kappa\) is the inverse of the Lewis number, \(R_{p} ={ \frac{Kc_{1}^{2}{P}^{2}R} {\mu }^{2}}\), where R is the Rayleigh number and P the Prandtl number that are defined by \(R = \frac{g\beta {q\kappa }^{2}} {\mu c_{1}^{3}}\) and \(P = \frac{\mu } {\kappa }\). In addition, we use the parameters \(\delta = \frac{R_{0}T_{b}} {E}\) and \(\theta _{0} = \frac{T_{b} - T_{0}} {q}\). The reaction rate is given by:

$$\displaystyle{ W_{Z}(\theta ) = Z\exp {\Bigl ( \frac{\theta } {{Z}^{-1}+\delta \theta }\Bigr )}, }$$
(15)

where \(Z = \frac{qE} {R_{0}T_{b}^{2}}\) stands for Zeldovich number. The dimensionless modulation force is given by \(b_{d}(t) =\lambda \mathit{sin}(\sigma t)\) in the periodic modulation case, or \(b_{d}(t) =\lambda _{1}\mathit{sin}(\sigma _{1}t) +\lambda _{2}\mathit{sin}(\sigma _{2}t)\) in the QP modulation case.

2.3 Linear Stability Analysis

2.4 Approximation of Infinitely Narrow Reaction Zone

To study the problem analytically, we reduce it to a singular perturbation problem where the reaction zone is supposed to be infinitely narrow and the reaction term is neglected outside the reaction zone. This method, called Zeldovich–Frank-Kamenetskii approximation, is a well-known approach for combustion problems [10, 43]. We will carry out a formal asymptotic analysis with \(\epsilon = \frac{1} {Z}\) taken as a small parameter to obtain a closed interface problem. Let us denote by ζ(t, x) the location of the reaction zone in the laboratory frame reference. The new independent variable in the direction of the front propagation is written as

$$\displaystyle{ y_{1} = y -\zeta (t,x). }$$
(16)

We introduce new functions θ 1, α 1, v 1, p 1 as follows

$$\displaystyle{ \begin{array}{l} \theta (t,x,y) =\theta _{1}(t,x,y_{1}),\;\;\alpha (t,x,y) =\alpha _{1}(t,x,y_{1}), \\ \mathbf{v}(t,x,y) = \mathbf{v}_{1}(t,x,y_{1}),\;\;p(t,x,y) = p_{1}(t,x,y_{1}) \end{array} }$$
(17)

and we re-write the equations in the form (the index 1 for the new functions is omitted):

$$\displaystyle{ \frac{\partial \theta } {\partial t} - \frac{\partial \theta } {\partial y_{1}} \frac{\partial \zeta } {\partial t} + \mathbf{v}.\widetilde{\nabla }\theta =\widetilde{ \Delta }\theta + W_{Z}(\theta )\phi (\alpha ), }$$
(18)
$$\displaystyle{ \frac{\partial \alpha } {\partial t} - \frac{\partial \alpha } {\partial y_{1}} \frac{\partial \zeta } {\partial t} + \mathbf{v}.\widetilde{\nabla }\alpha = W_{Z}(\theta )\phi (\alpha ), }$$
(19)
$$\displaystyle{ \mathbf{v} +\widetilde{ \nabla }p = R_{p}(\theta +\theta _{0})(1 + b_{d}(t))\boldsymbol{\gamma }, }$$
(20)
$$\displaystyle{ \frac{\partial v_{x}} {\partial x} -\frac{\partial v_{x}} {\partial y_{1}} \frac{\partial \zeta } {\partial x} + \frac{\partial v_{y}} {\partial y_{1}} = 0, }$$
(21)

where we have set

$$\displaystyle{ \widetilde{\Delta } = \frac{{\partial }^{2}} {\partial {x}^{2}} + \frac{{\partial }^{2}} {\partial y_{1}^{2}} - 2 \frac{\partial \zeta } {\partial x} \frac{{\partial }^{2}} {\partial x\partial y_{1}} +{\Bigl ({ \frac{\partial \zeta } {\partial x}\Bigr )}}^{2} \frac{{\partial }^{2}} {\partial y_{1}^{2}} - \frac{{\partial }^{2}\zeta } {\partial {x}^{2}} \frac{\partial } {\partial y_{1}}, }$$
(22)
$$\displaystyle{ \widetilde{\nabla } ={\Bigl ( \frac{\partial } {\partial x} - \frac{\partial \zeta } {\partial x} \frac{\partial } {\partial y_{1}}, \frac{\partial } {\partial y_{1}}\Bigr )}. }$$
(23)

We use the method of matched asymptotic expansions. To do so, we assume that the outer solution of the problem can be written in the form

$$\displaystyle{ \begin{array}{l} \theta {=\theta }^{0} {+\epsilon \theta }^{1}+\ldots ,\;\;\;\alpha {=\alpha }^{0} {+\epsilon \alpha }^{1}+\ldots , \\ \mathbf{v} ={ \mathbf{v}}^{0} +\epsilon { \mathbf{v}}^{1}+\ldots ,\;\;\;p = {p}^{0} +\epsilon {p}^{1} +\ldots.\end{array} }$$
(24)

Here \({(\theta }^{0}{,\alpha }^{0},{\mathbf{v}}^{0})\) is a dimensionless form of the basic solution.

In order to obtain jump conditions in the reaction zone, we consider the inner problem and we introduce the stretching coordinate \(\eta = y_{1}/\epsilon\), with \(\epsilon = 1/Z\). On the other hand, the inner solution is sought in the form

$$\displaystyle{ \begin{array}{ll} &\theta {=\epsilon \tilde{\theta } }^{1}+\ldots ,\;\;\;\alpha {=\tilde{\alpha } }^{0} {+\epsilon \tilde{\alpha } }^{1}+\ldots , \\ &\mathbf{v} =\tilde{{ \mathbf{v}}}^{0} +\epsilon \tilde{{ \mathbf{v}}}^{1}+\ldots ,\;\;\;p =\tilde{ {p}}^{0} +\epsilon \tilde{ {p}}^{1}+\ldots ,\;\;\;\zeta {=\tilde{\zeta } }^{0} {+\epsilon \tilde{\zeta } }^{1} +\ldots.\end{array} }$$
(25)

Substituting these expansions into (18)–(21), we obtain the first-order inner problem:

$$\displaystyle{ \Big(1 +\Big( \frac{{\partial \tilde{\zeta }}^{0}} {\partial x}\Big)^{2}\Big)\frac{{\partial {}^{2}\tilde{\theta }}^{1}} {\partial \eta^{2}} +\exp \Big( \frac{\tilde{\theta }^{1}} {1 +\delta \tilde{\theta}^{1}}\Big)\phi(\tilde{\alpha}^{0}) = 0, }$$
(26)
$$\displaystyle{ -\frac{\partial \tilde{\alpha}^{0}} {\partial \eta } \frac{{\partial \tilde{\zeta }}^{0}} {\partial \eta } -\frac{{\partial \tilde{\alpha }}^{0}} {\partial \eta } \Big(\tilde{v}_{x}^{0} \frac{{\partial \tilde{\zeta }}^{0}} {\partial x} -\tilde{ v}_{y}^{0}\Big) =\exp \Big( \frac{\tilde{\theta}^{1}} {1 +\delta \tilde{\theta}^{1}}\Big)\phi(\tilde{\alpha}^{0}), }$$
(27)
$$\displaystyle{ \frac{\partial \tilde{{p}}^{0}} {\partial \eta } = 0, }$$
(28)
$$\displaystyle{ \tilde{v}_{x}^{0} + \frac{\partial \tilde{{p}}^{0}} {\partial x} -\frac{{\partial \tilde{\zeta }}^{0}} {\partial t} \frac{\partial \tilde{{p}}^{1}} {\partial \eta } = 0, }$$
(29)
$$\displaystyle{ \tilde{v}_{y}^{0} + \frac{\partial \tilde{{p}}^{1}} {\partial \eta } = -R_{p}\theta _{0}(1 + b_{d}(t)), }$$
(30)
$$\displaystyle{ -\frac{\partial \tilde{v}_{x}^{0}} {\partial \eta } \frac{{\partial \tilde{\zeta }}^{0}} {\partial x} + \frac{\partial \tilde{v}_{y}^{0}} {\partial \eta } = 0. }$$
(31)

Then, the matching conditions are

$$\displaystyle{ \eta \rightarrow +\infty {:\;\;\tilde{\theta } }^{1} {\sim \theta }^{1}\vert _{ y_{1}=0+} +\eta \frac{{\partial \theta }^{0}} {\partial y_{1}}\vert _{y_{1}=0+}{,\;\;\tilde{\alpha }}^{0} \rightarrow 0,\;\;\tilde{{\mathbf{v}}}^{0} \rightarrow {\mathbf{v}}^{0}\vert _{ y_{1}=0+}, }$$
(32)
$$\displaystyle{ \eta \rightarrow -\infty {:\;\;\tilde{\theta } }^{1} {\rightarrow \theta }^{1}\vert _{ y_{1}=0-}{,\;\;\tilde{\alpha }}^{0} \rightarrow 1,\;\;\tilde{{\mathbf{v}}}^{0} \rightarrow {\mathbf{v}}^{0}\vert _{ y_{1}=0-}. }$$
(33)

From (28) we obtain that \(\tilde{{p}}^{0}\) does not depend on η, which implies that the pressure is continuous through the interface. Next, denoting by s the quantity

$$\displaystyle{ s =\tilde{ v}_{x}^{0} \frac{{\partial \tilde{\zeta }}^{0}} {\partial x} -\tilde{ v}_{y}^{0}, }$$
(34)

we obtain from (31) that s does not depend on η. Finally from (29), (30) and (34) we easily obtain that \(\tilde{v}_{x}^{0}\) and \(\tilde{v}_{y}^{0}\) do not depend on η, which provides the continuity of the velocity through the interface.

We next derive the jump conditions for the temperature from (26), in the same way as it is usually done for combustion problems. From (27) it follows that \(\tilde{\alpha}^{0}\) is a monotone function and \(0 {<\tilde{\alpha } }^{0} < 1\). Since we consider zero-order reaction, we have \(\phi {(\tilde{\alpha }}^{0}) \equiv 1\). We conclude from (26) that \(\tilde{\theta}^{1}\) is also a monotone function. Thus, multiplying (26) by \(\frac{{\partial \tilde{\theta }}^{1}} {\partial \eta }\) and integrating, we obtain

$$\displaystyle{ \Bigl(\frac{\partial \tilde{\theta}^{1}} {\partial \eta } \Bigr)^{2}\Bigl|_{ \eta =+\infty }-\Bigl(\frac{\partial \tilde{\theta}^{1}} {\partial \eta } \Bigr)^{2}\Bigl|_{ \eta =-\infty } = -\frac{2} {A}\int _{-\infty }^{{\theta }^{1} }\exp ( \frac{\tau } {1+\delta \tau })d\!\tau , }$$
(35)

where we have set

$$\displaystyle{ A = 1 +{\Bigl ({ \frac{{\partial \tilde{\zeta }}^{0}} {\partial x}\Bigr )}}^{2}. }$$
(36)

Next, subtracting (26) from (27) and integrating, we obtain

$$\displaystyle{ \frac{{\partial \tilde{\theta }}^{1}} {\partial \eta } \Bigl |_{\eta =+\infty }-\frac{{\partial \tilde{\theta }}^{1}} {\partial \eta } \Bigl |_{\eta =-\infty } = -\frac{1} {A}\Bigl (\frac{{\partial \tilde{\zeta }}^{0}} {\partial t} + s\Bigr ). }$$
(37)

Using now the matching conditions and truncating the expansion as:

$$\displaystyle{{ \theta }^{0} \approx \theta {,\;\;\theta }^{1}\vert _{ y_{1}=0-}\approx Z\theta \vert {_{y_{1}=0}\;\;\zeta }^{0} \approx \zeta ,\;\;\mathbf{v} \approx {\mathbf{v}}^{0}, }$$
(38)

we obtain the jump conditions

$$\displaystyle\begin{array}{rcl}\Bigl (\frac{\partial \theta } {\partial y_{1}}\Bigr )^{2}\Bigl |_{ y_{1}=0+} -\Bigl ( \frac{\partial \theta } {\partial y_{1}}\Bigr )^{2}\Bigl |_{ y_{1}=0-} = 2Z\Bigl (1 +\Bigl ( \frac{\partial \zeta } {\partial x}\Bigr ){}^{2}\Bigr )^{-1}& & \\ \int _{-\infty }^{\theta \vert _{y_{1}=0} }\exp ( \frac{\tau } {{Z}^{-1}+\delta \tau })d\!\tau ,& & \\ \end{array}$$
(39)
$$\displaystyle{ \frac{\partial \theta } {\partial y_{1}}\Bigl |_{y_{1}=0+} - \frac{\partial \theta } {\partial y_{1}}\Bigl |_{y_{1}=0-} = -\Bigl (1 +\Bigl (\frac{\partial \zeta } {\partial x}\Bigr ){}^{2}\Bigr )^{-1}\Bigl ( \frac{\partial \zeta } {\partial t} + (v_{x} \frac{\partial \zeta } {\partial x} - v_{y})\Bigr |_{y_{1}=0}\Bigr ). }$$
(40)

2.5 Formulation of the Interface Problem

Let us summarize the interface problem. We have for y > ζ (in the unburnt medium)

$$\displaystyle{ \frac{\partial \theta } {\partial t} + \mathbf{v}.\nabla \theta = \Delta \theta , }$$
(41)
$$\displaystyle{ \alpha \equiv 0, }$$
(42)
$$\displaystyle{ \mathbf{v} + \nabla p = R_{p}(\theta +\theta _{0})(1 + b_{d}(t))\boldsymbol{\gamma }, }$$
(43)
$$\displaystyle{ \nabla.\mathbf{v} = 0. }$$
(44)

The equations in the burnt medium (y < ζ) lead to the following system:

$$\displaystyle{ \frac{\partial \theta } {\partial t} + \mathbf{v}.\nabla \theta = \Delta \theta , }$$
(45)
$$\displaystyle{ \alpha \equiv 1, }$$
(46)
$$\displaystyle{ \mathbf{v} + \nabla p = R_{p}(\theta +\theta _{0})(1 + b_{d}(t))\boldsymbol{\gamma }, }$$
(47)
$$\displaystyle{ \nabla.\mathbf{v} = 0. }$$
(48)

We finally complete this system by the following jump conditions at the interface y = ζ:

$$\displaystyle{ [\theta ] = 0,\;\;{\Bigl [ \frac{\partial \theta } {\partial y}\Bigr ]} = \frac{ \frac{\partial \zeta } {\partial t}} {1 +{\Bigl ({ \frac{\partial \zeta } {\partial x}\Bigr )}}^{2}}, }$$
(49)
$$\displaystyle{ {\Bigl [{\Bigl ({ \frac{\partial \theta } {\partial y}\Bigr )}}^{2}\Bigr ]} = - \frac{2Z} {1 + {( \frac{\partial \zeta } {\partial x})}^{2}}\int _{-\infty }^{\theta (\zeta )}\exp {\Bigl ( \frac{s} {1/Z +\delta s}\Bigr )}ds, }$$
(50)
$$\displaystyle{ [\mathbf{v}] = 0. }$$
(51)

Here we denote by [  ] the quantity

$$\displaystyle{ [f] = f\vert _{\zeta -0} - f\vert _{\zeta +0}. }$$
(52)

The above free boundary problem is completed with the conditions at infinity:

$$\displaystyle{ y \rightarrow +\infty ,\;\;\theta = -1\text{ and }\mathbf{v} = 0, }$$
(53)
$$\displaystyle{ y \rightarrow -\infty ,\;\;\theta = 0\text{ and }\mathbf{v} = 0. }$$
(54)

2.6 Travelling Wave Solution

In this subsection we perform the linear analysis of the steady-state solution for the interface problem. This problem has a travelling wave solution:

$$\displaystyle{ \theta (t,x,y) =\theta _{s}(y - ut),\;\;\alpha (t,x,y) =\alpha _{s}(y - ut)\text{ and }\mathbf{v} = 0, }$$
(55)

where

$$\displaystyle{ \theta _{s}(t,y) = \left \{\begin{array}{@{}l@{\quad }l@{}} 0 \quad &\text{ if}\ y < 0\\ {e}^{-uy } - 1\quad &\text{ if} \ y > 0 \end{array} \right., }$$
(56)

and

$$\displaystyle{ \alpha _{s}(t,y) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\;\;\;\quad &\text{ if}\ y < 0\\ 0\quad &\text{ if} \ y > 0 \end{array} \right.. }$$
(57)

where the number u stands for the wave speed. It can easily be computed using the jump conditions of the free boundary problem.

We now introduce the coordinates in the moving frame defined by \(y_{1} = y - ut\). In this referential, the above travelling wave is a stationary solution of the problem

$$\displaystyle{ \frac{\partial \theta } {\partial t} + u \frac{\partial \theta } {\partial y} + \mathbf{v}.\nabla \theta = \Delta \theta , }$$
(58)
$$\displaystyle{ \mathbf{v} + \nabla p = R_{p}(\theta +\theta _{0})(1 + b_{d}(t))\boldsymbol{\gamma }, }$$
(59)
$$\displaystyle{ \nabla.\mathbf{v} = 0, }$$
(60)

together with the jump condition found in the previous subsection.

We now consider a small perturbation of this stationary solution. For that purpose we consider a perturbation of the reaction front of the form

$$\displaystyle{ \zeta (t,x) = ut +\xi (t,x),\text{ with }\xi (t,x) =\epsilon _{1}(t){e}^{ikx}. }$$
(61)

To study the stability of the solution of our problem, we look for a solution of the problem in the form of the perturbed stationary solution:

$$\displaystyle{ \theta =\theta _{s}+\tilde{\theta },\ \ v = v_{s} +\tilde{ v}, }$$
(62)

where

$$\displaystyle{ \begin{array}{ll} &\tilde{\theta }(t,x,y) =\theta _{j}(y,t){e}^{ikx},\text{ for}\ j = 1,2, \\ &\tilde{v}(t,x,y) = v_{j}(y,t){e}^{ikx},\text{ for}\ j = 1,2. \end{array} }$$
(63)

Here the index j = 1 corresponds to functions for z < 0 and j = 2 for z > 0.

We exclude the pressure p and the component v x of the velocity from the interface problem applying two times the operator curl. Thus, we obtain the following problem:

For the burnt media (y < 0 ):

$$\displaystyle{ v_{1}\prime\prime - {k}^{2}v_{ 1} = -R_{p}{k}^{2}(1 + b_{ d}(t))\theta _{1}, }$$
(64)
$$\displaystyle{ \frac{\partial \theta _{1}} {\partial t} -\theta _{1}\prime\prime - u\theta _{1}\prime + {k}^{2}\theta _{ 1} = 0. }$$
(65)

For the unburnt media (y > 0 ):

$$\displaystyle{ v_{2}\prime\prime - {k}^{2}v_{ 2} = -R_{p}{k}^{2}\theta _{ 2}(1 + b_{d}(t)), }$$
(66)
$$\displaystyle{ \frac{\partial \theta _{2}} {\partial t} -\theta _{2}\prime\prime - u\theta _{2}\prime + {k}^{2}\theta _{ 2} = u\exp (-uy)v_{2}, }$$
(67)

go back to the margin where u stands for the stationary front velocity. Taking into account that

$$\displaystyle{ \theta \left \vert _{\xi =\pm 0}\right. =\theta _{s}(\pm 0) +\xi \theta \prime_{s}(\pm 0) +\tilde{\theta } (\pm 0), }$$
(68)

and

$$\displaystyle{ \frac{\partial \theta } {\partial y}\left \vert _{\xi =\pm 0}\right. =\theta \prime_{s}(\pm 0) +\xi \theta _{ s}^{\prime\prime}(\pm 0) + \frac{\partial \tilde{\theta }} {\partial y}(\pm 0), }$$
(69)

we obtain the following jump conditions:

$$\displaystyle{ \theta _{2}(0,t) -\theta _{1}(0,t) = u\epsilon _{1}(t), }$$
(70)
$$\displaystyle{ \theta \prime_{2}(0,t) -\theta \prime_{1}(0,t) = -\epsilon _{1}(t){u}^{2} -\epsilon _{ 1}^{{\prime}}(t) + v_{ 1}(0,t), }$$
(71)
$$\displaystyle{ \epsilon _{1}(t){u}^{2} +\theta \prime_{ 2}(0,t) = -\frac{Z} {u} \theta _{1}(0,t), }$$
(72)
$$\displaystyle{ v_{2}^{(i)}(0,t) = v_{ 1}^{(i)}(0,t)\quad i = 0,1. }$$
(73)

3 Numerical Results and Discussion

3.1 Case of Periodic Vibration

In this case, b d (t) = λcos(σt). To find the convective instability boundary, we solve numerically the problem (64)–(67) with the jump conditions (70)–(73). The numerical accuracy is controlled by decreasing the time and space steps.

For fixed Z and k we vary R p . If the Rayleigh number R p is less than a critical value R c , the solution is decreasing in time. If R p  > R c , the solution increases, and for R p  = R c it is periodic in time (Fig. 2, bottom). Similar behavior is observed in the case without vibrations (Fig. 2, top). When the Rayleigh number exceed the critical value the perturbation grows in time and when the Rayleigh number is bellow the critical value the perturbation decays. There are no oscillations because the amplitude of vibrations is equal to zero.

Fig. 2
figure 2

Temperature maximum as a function of time for k = 3. 14, Z = 8, u = 1. 4142, λ = 0 (top) and for k = 3. 14, Z = 8, u = 1. 4142, λ = 5, σ = 50 (bottom)

Full size image

Figure 3 shows the critical value of the Rayleigh number as a function of the amplitude of vibrations for different frequencies. If λ = 0, we obtain the same value R c  = 26 as in the absence of vibrations [44]. For small positive λ, vibrations stabilize the solution: R c is an increasing function. For larger values of λ, vibrations destabilize the solution: R c is a decreasing function. When we increase the frequency σ, the front becomes more stable.

Fig. 3
figure 3

Convective instability boundary: critical Rayleigh number as a function of the amplitude of vibrations for k = 3. 14, Z = 8 and u = 1. 4142 and for different values of the frequency σ

Full size image

Figure 4 shows the critical value of the Rayleigh number as a function of the frequency of vibrations for different amplitudes. If λ = 0, the curve takes a constant value R c  = 26 corresponding to the absence of vibration. If λ≠0, all curves are increasing functions, i.e. when the frequency increases the front become more stable. It can be seen that all curves have a asymptotic behavior when the frequency is sufficiently large, which means that high-frequency vibration can stabilize the front.

Fig. 4
figure 4

Convective instability boundary: critical Rayleigh number as a function of the frequency of vibrations for k = 3. 14, Z = 8 and u = 1. 4142 and for different values of the amplitude λ

Full size image

3.2 Case of Periodic Vibration with Modulation of Amplitude

In this case, \(b_{d}(t) =\lambda cos(\sigma _{2}t)sin(\sigma _{1}t)\) where now the amplitude of the vibration is modulated and is written as λcos(σ 2 t). The interface problem is solved numerically leading to the critical Rayleigh number. Figure 5 shows the critical Rayleigh number as function of the amplitude for some different choice of the frequencies ratio. It is worth noticing that in the absence of vibration modulation (σ 2 = 0), we find the same result as in [16] which is consistent with the current analysis. Results in Fig. 5 indicate that for relatively small values of the modulation amplitude λ and for a value of the frequency modulation equal to half the frequency of the vibration (\(\sigma _{2} =\sigma _{1}/2\)), the reaction front undergoes a destabilizing effect. In contrast, a stabilizing effect is gained when the frequency modulation is twice that of the vibration (σ 2 = 2σ 1). In other words, the front is less stable when (\(\sigma _{2} =\sigma _{1}/2\)) and it is more stable when (σ 2 = 2σ 1).

Fig. 5
figure 5

Critical Rayleigh number as function of the amplitude λ for different values of frequencies ratio and for σ 1 = 100

Full size image

Figure 6 depicts the critical Rayleigh number as function of the frequency of the vibration, σ 1, in the case where (σ 2 = 2σ 1). This figure shows that when σ 2 = 2σ 1, increasing the frequency of the vibration, σ 1, causes the critical Rayleigh number to increase stepwise leading the reaction front to substantially gain stability.

Fig. 6
figure 6

Critical Rayleigh number as function of the frequency σ 1 for λ = 10 and for σ 2 = 2σ 1

Full size image

3.3 Case of Quasi-periodic Modulation

In this case, the form of the QP gravitational modulation is written as \(b_{d}(t) =\lambda _{1}sin(\sigma _{1}t) +\lambda _{2}sin(\sigma _{2}t)\), where λ 1, λ 2 and σ 1, σ 2 are the amplitudes and the frequencies, respectively. Figure 7 depicts the variation of the maximum of temperature as function of time. It can be seen from these plots that if the Rayleigh number R p is less than a critical value R c , the solution is decreasing in time which corresponds to a stable (bounded) variation of the maximum of temperature. For values of R p larger than R c , the maximum of temperature presents unbounded oscillations which corresponds to unstable solutions. To detect this instability, we start our computations with small Rayleigh numbers and then we increase it slowly until the critical value of the Rayleigh number is captured. The figure shows that the maximum of temperature variation is decreasing for R p  = 26 and increasing for R p  = 28 indicating that the critical Rayleigh number is approximatively located between, i.e. R c ≈ 27.

Fig. 7
figure 7

Maximum of temperature as function of time for λ 1 = 2, λ 2 = 2, σ 1 = 100 and \(\sigma _{2} = \sqrt{2}\sigma _{1}\)

Full size image

Figure 8 shows, for λ 1 = 5 and σ 1 = 500, the variation of the critical Rayleigh number as function of the amplitude λ 2. The plots indicate that for small values of the frequencies ratio \(\sigma = \sigma _{2}/\sigma _{1}\), as the amplitude λ 2 increases, the critical Rayleigh number decreases from a certain value of R p ( ≈ 325). If σ is increased substantially, a stabilizing effect appears in a region corresponding to small values of λ 2. In this zone, one can expect a regaining of stability of reaction fronts. For higher values of λ 2 the critical Rayleigh number decreases for different σ indicating that large values of λ 2 induce a destabilizing effect. Figure 9 illustrates similar results for σ 1 = 250. It is seen in this figure that for higher values of σ, a stabilizing effect appears in two successive regions corresponding, respectively, to small and moderate values of the amplitude λ 2. This result means that increasing σ, stability may be gained in certain specific intervals of λ 2.

Fig. 8
figure 8

Critical Rayleigh number as function of the amplitude λ 2 for λ 1 = 5 and σ 1 = 500

Full size image
Fig. 9
figure 9

Critical Rayleigh number as function of the amplitude λ 2 for λ 1 = 5 and σ 1 = 250

Full size image

Finally, Fig. 10 shows, for given amplitudes and for different values of the frequencies ratio σ, the critical Rayleigh number as function of σ 1. This figure indicates clearly that in the absence of QP vibration (\(\sigma _{1} = 0,\sigma _{2} = 0\)), the curves start at the value R c  = 26 corresponding to the unmodulated case, which is in good agreement with the previous works [16, 44] and hence validating the numerical simulations. This figure also depicts an interesting phenomenon, that is, in a certain interval of σ 1, the value of the critical Rayleigh number increases from the unmodulated case R c  = 26 with oscillatory variation. Increasing σ, the oscillating variation of the critical Rayleigh number increases creating a repeated alternating zones where stability is gained. At a certain value of σ 1 ≈ 700, the critical Rayleigh number suddenly drops to meet the unmodulated case, R c  = 26. Above σ 1 ≈ 700, the frequencies ratio has no effect on the critical Rayleigh number and the problem becomes equivalent to the unmodulated case.

Fig. 10
figure 10

Critical Rayleigh number as function of frequency σ 1 for \(\lambda _{1} =\lambda _{2} = 5\)

Full size image

We have shown that in the presence of a QP vibration, the convection instability of reaction fronts in porous media can be controlled and the reaction fronts may remain stable in certain regions, and for certain combinations of the amplitudes and the frequencies ratio of the QP vibration.

4 Summary

In this chapter we have presented an overview on the effect of a vertical periodic and QP gravitational modulation on the convective instability of reaction fronts in porous media. Attention was focused on two cases. The case where the gravitational vibration is periodic and its amplitude is modulated, and the case where the vibration is QP having two incommensurate frequencies. In both cases the heating is acted from below such that the sense of reaction is opposite to the gravity sense. To approximate the convective instability threshold, the original reaction-diffusion problem is first reduced to a singular perturbation one using the matched asymptotic expansion. Then, the linear stability analysis of the steady-state solution for the interface problem is performed. The obtained reduced problem is solved numerically.

In the case where the modulation of the vibration is periodic, it was shown that for relatively small values of the modulation amplitude and for a value of the frequency modulation equal to half the frequency of the vibration (\(\sigma _{2} = \frac{\sigma _{1}} {2}\)), the reaction front undergoes a destabilizing effect. In contrast, a stabilizing effect is gained when the frequency modulation is twice that of the vibration (σ 2 = 2σ 1). It was also shown that increasing the frequency of the vibration, σ 1, causes the critical Rayleigh number to increase stepwise leading the reaction front to substantially gain stability.

In the case of QP gravitational modulation, it was shown that for relatively small values of the amplitudes λ 1 and λ 2 of the QP vibration, an increase of the frequencies ratio \(\sigma = \frac{\sigma _{2}} {\sigma _{1}}\) has a stabilizing effect. The results also revealed that for given values of λ 1 and λ 2 and below a critical value of the frequency σ 1, an increase of the frequencies ratio σ produces a stabilizing effect. In this interval of σ 1, the convection threshold grows from the critical Rayleigh number of the unmodulated case, R c  = 26, with oscillating variation. This alternating variation of the critical Rayleigh number indicates that for appropriate values of parameters, a more pronounced stabilizing effect can be gained. At a certain critical value of σ 1, the critical Rayleigh number drops to the unmodulated case. Above the critical value of σ 1, the frequencies ratio has no effect on the critical Rayleigh number showing that for higher values of the frequency σ 1, the QP vibration has no effect and the problem tends to the unmodulated case. The results of this work shown that in the presence of a QP vibration, the convection instability of reaction fronts in porous media can be controlled and the reaction fronts may be sustained in stability regions for appropriate values of the amplitudes and frequencies of the vibration.

5 Appendix

5.1 The Method of Matched Asymptotic Expansions

In a large class of singular perturbed problems, the domain may be divided into two subdomains. On one of these, the solution is accurately approximated by an asymptotic series found by treating the problem as a regular perturbation. The other subdomain consists of one or more small areas in which that approximation is inaccurate, generally because the perturbation terms in the problem are not negligible there. These areas are referred to as transition layers, or boundary or interior layers depending on whether they occur at the domain boundary (as is the usual case in applications) or inside the domain.

An approximation in the form of an asymptotic series is obtained in the transition layer(s) by treating that part of the domain as a separate perturbation problem. This approximation is called the “inner solution,” and the other is the “outer solution,” named for their relationship to the transition layer(s). The outer and inner solutions are then combined through a process called “matching” in such a way that an approximate solution for the whole domain is obtained. More details can be found in [45, 46].

5.2 Simple Example

Consider the equation

$$\displaystyle{\epsilon y\prime\prime + (1+\epsilon )y\prime + y = 0,}$$

where y is a function of t, y(0) = 0, y(1) = 1 and 0 < ε ≪ 1.

5.2.1 Outer and Inner Solutions

Since ε is very small, the first approach is to find the solution to the problem

$$\displaystyle{y\prime + y = 0,\,}$$

which is

$$\displaystyle{y = A{e}^{-t}\,}$$

for some constant A. Applying the boundary condition y(0) = 0, we would have A = 0; applying the boundary condition y(1) = 1, we would have A = e. At least one of the boundary conditions cannot be satisfied. From this we infer that there must be a boundary layer at one of the endpoints of the domain.

Suppose the boundary layer is at t = 0. If we rescal \(\tau = t/\epsilon\), the problem becomes

$$\displaystyle{\frac{1} {\epsilon } y\prime\prime(\tau ) + \left (1+\epsilon \right )\frac{1} {\epsilon } y\prime(\tau ) + y(\tau ) = 0,\,}$$

which, after multiplying by ε and taking ε = 0, is

$$\displaystyle{y\prime\prime + y\prime = 0\,}$$

with the solution

$$\displaystyle{y = B - C{e}^{-\tau }\,}$$

for some constants B and C. Since y(0) = 0, we have C = B, so the inner solution is

$$\displaystyle{y_{I} = B\left (1 - {e}^{-\tau }\right ) = B\left (1 - {e}^{-t/\epsilon }\right ).\,}$$

5.2.2 Matching

Notice that we have assumed the outer solution to be

$$\displaystyle{y_{O} = {e}^{1-t}.\,}$$

The idea of matching is for the inner and outer solutions to agree at some value of t near the boundary layer as ε decreases. For example, if we fix \(t = \sqrt{\epsilon }\), we have the matching condition

$$\displaystyle{\lim _{\epsilon \rightarrow 0}y_{I}\left (\sqrt{\epsilon }\right ) =\lim _{\epsilon \rightarrow 0}y_{O}\left (\sqrt{\epsilon }\right ),\,}$$

thereby B = e. Note that instead of \(t = \sqrt{\epsilon }\), we could have chosen any other power law t = ε k with 0 < k < 1. To obtain our final matched solution, valid on the whole domain, one popular method is the uniform method. In this method, we add the inner and outer approximations and subtract their overlapping value, y overlap . In the boundary layer, we expect the outer solution to be approximate to the overlap, y O   ∼ y overlap . Far from the boundary layer, the inner solution should approximate it, y I   ∼ y overlap . Hence, we want to eliminate this value from the final solution. In our example, y overlap   ∼ e. Therefore, the final solution is,

$$\displaystyle{y(t) = y_{I} + y_{O} - e = e\left (1 - {e}^{-t/\epsilon }\right ) + {e}^{1-t} - e = e\left ({e}^{-t} - {e}^{-t/\epsilon }\right ).\,}$$

5.2.3 Accuracy

Substituting the matched solution in the differential equation yields

$$\displaystyle{\epsilon y\prime\prime + \left (1+\epsilon \right )y\prime + y = 0,\,}$$

which implies, due to the uniqueness of the solution, that the matched asymptotic solution is identical to the exact solution up to a constant multiple, as it satisfies the original differential equation. This is not necessarily always the case, any remaining terms should go to zero uniformly as ε → 0. As to the boundary conditions, y(0) = 0 and \(y(1) = 1 - {e}^{1-1/\epsilon }\), which quickly converges to the value given in the problem.

Not only does our solution approximately solve the problem at hand; it closely approximates the exact solution. It happens that this particular problem is easily found to have exact solution

$$\displaystyle{y(t) = \frac{{e}^{-t} - {e}^{-t/\varepsilon }} {{e}^{-1} - {e}^{-1/\varepsilon }},\,}$$

which, as previously noted, has the same form as the approximate solution. Note also that the approximate solution is the first term in a binomial expansion of the exact solution in powers of \(y(1) = {e}^{1-1/\epsilon }\).

Figure 11 shows convergence of the exact solution for various ε and the outer solution. Note that since the boundary layer becomes narrower with decreasing ε, the approximations converge to the outer solution pointwise, but not uniformly.

Fig. 11
figure 11

Convergence approximation

Full size image

5.2.4 Location of Boundary Layer

Conveniently, we can see that the boundary layer, where y′ and y′ are large, is near t = 0, as supposed earlier. If we had supposed it to be at the other endpoint and proceeded by making the rescaling \(\tau = (1 - t)/\epsilon\), we would have found it impossible to satisfy the resulting matching condition. For many problems, this kind of trial and error is the only way to determine the true location of the boundary layer.