Keywords

1 Introduction

In 2010, the small body explorer Hayabusa of JAXA completed its journey and returned to the Earth, and its success drew increasing worldwide attention to small body exploration, which requires long period observations to obtain detailed information. However, it is very difficult for an explorer to orbit a low-mass and irregularly shaped small body. In this case, fly-by and formation flying are two alternatives to explore small bodies.

This paper studies the dynamics and technology of formation flying with small bodies in the solar system. For the motions of an explorer in the solar system, the two most frequently used dynamic models are the perturbed two-body problem and the perturbed circular restricted three-body problem. The first one is usually used for circling orbits in the gravity field of a central body such as the sun or other planets while the second is more applicable for interplanetary cruise in deep space explorations.

Generally speaking, most small bodies in the solar system are small and light weighted. To solve the problem of formation flying with this kind of celestial bodies, different strategies should be adopted under different conditions: if the gravity of the small body can be neglected, C–W equation used in formation flying is applicable; if its gravity cannot be ignored, the problem can be solved based on the dynamics of motions around libration points in the CRTBP.

This paper mainly studies the dynamics and station keeping strategies of collinear libration point L1 of CRTBP with small \( \mu \), which is applicable in the case of formation flying with small bodies, and figures out the features of the halo orbits. Orbit control for station keeping of the spacecraft is also discussed and the relationship between energy consumption and the parameter \( \mu \) is presented. Our work shows that formation flying with a small body on the basis of halo orbit around libration point is feasible in small body explorations. This strategy, in some cases, consumes less energy for orbit control than that of the strategy based on C–W equations. However, if the influence of solar radiation pressure on the C–W equation type of formation flying is taken into consideration, we will find its great influence on the orbit configuration of C–W equation and in this case the C–W equation type of formation flying does not have any advantage.

2 Dynamic Model of CRTBP

In the dynamic model of circular restricted three-body problem of the sun, a small body and a spacecraft, assuming that the mass of two primaries are \( m_{1} \) and \( m_{2} \) (\( m_{1} > m_{2} \)), the following normalized unit can be used:

$$ [M] = m_{1} + m_{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [L] = d,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [T] = \left( {d^{3} /\mu } \right)^{\frac{1}{2}} = \frac{1}{n} $$
(39.1)

where \( d \) is the distance between the sun and the small body, \( n \) is the angular velocity of the relative motion of the two primaries, \( \mu = \frac{{m{}_{2}}}{{m_{1} + m_{2} }} \). In the rotating frame, the two major bodies lie on two points on the x-axis at \( ( - \mu ,0) \) and \( (1 - \mu ,0) \) respectively. Assuming that the mass of the spacecraft is \( m \) and its position is \( \vec{r} = (x,y,z)^{T} \), the equation of motion can be written as [1–3]:

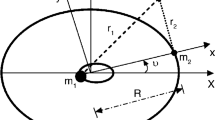
$$ \left\{ \begin{array}{l} \ddot{\vec{r}} + 2\left( { - \dot{y},\dot{x},0} \right)^{T} = \left( {{{\partial \Upomega } \mathord{\left/ {\vphantom {{\partial \Upomega } {\partial \vec{r}}}} \right. \kern-0pt} {\partial \vec{r}}}} \right)^{T} \hfill \\ \Upomega \left( {x,y,z} \right) = {{\left( {\mu \left( {1 - \mu } \right) + x^{2} + y^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu \left( {1 - \mu } \right) + x^{2} + y^{2} } \right)} 2}} \right. \kern-0pt} 2} + {{\left( {1 - \mu } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \mu } \right)} {r_{1} }}} \right. \kern-0pt} {r_{1} }} + {\mu \mathord{\left/ {\vphantom {\mu {r_{2} }}} \right. \kern-0pt} {r_{2} }} \hfill \\ \end{array} \right. $$
(39.2)

where \( \mu = m_{2} /(m_{1} + m_{2} ) \), \( r_{1} ,r_{2} \) are respectively the distances between the spacecraft and the two primaries. There are five stationary positions in this dynamic system, namely, libration points \( L_{i} \) including three collinear points on the x-axis and two triangular points in the x–y plan, all of which are depicted in Fig. 39.1.

Fig. 39.1
figure 1

Rotating frame and five libration points

Full size image

Taking collinear libration point \( L_{1} \) as an example, the position of \( L_{1} \) can be denoted as \( \vec{r}_{1} = (1 - \mu + \gamma_{1} ,0,0)^{T} \), and the relative position of the small body is \( \vec{r} = (\xi ,\eta ,\zeta )^{T} \). From the conversion \( \vec{R} = \vec{r}_{1} + \vec{r} \), the linear equation of motion obtained from Eq. (39.2) is:

$$ \left\{ \begin{array}{l} \ddot{\xi } - 2\dot{\eta } - \left( {1 + 2c_{2} } \right)\xi = 0 \hfill \\ \ddot{\eta } + 2\dot{\xi } - \left( {1 - c_{2} } \right)\eta = 0 \hfill \\ \ddot{\zeta } + c_{2} \zeta = 0 \hfill \\ \end{array} \right. $$
(39.3)

Where \( c_{2} = {\mu \mathord{\left/ {\vphantom {\mu {r_{11}^{3} }}} \right. \kern-0pt} {r_{11}^{3} }} + {{\left( {1 - \mu } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \mu } \right)} {r_{12}^{3} }}} \right. \kern-0pt} {r_{12}^{3} }} \),\( r_{11} ,r_{12} \) are respectively the distances between \( L_{1} \) and the two primaries. In the sense of linear approximation, the equation of motion can be depicted as:

$$ \left\{ \begin{array}{l} \xi = C_{1} e^{{d_{1} t}} + C_{2} e^{{ - d_{1} t}} + C_{3} \cos d_{2} t + C_{4} \sin d_{2} t \hfill \\ \eta = \alpha_{1} C_{1} e^{{d_{1} t}} - \alpha_{1} C_{2} e^{{ - d_{1} t}} - \alpha_{2} C_{3} \sin d_{2} t + \alpha_{2} C_{4} \cos d_{2} t \hfill \\ \zeta = C_{5} \cos d_{3} t + C_{6} \sin d_{3} t \hfill \\ \end{array} \right. $$
(39.4)

The solution to this equation is unstable through an exponential type defocusing while it’s conditionally stable when \( C_{1} = C_{2} = 0 \). Therefore, the initial conditions for the conditionally stable solution are [1–3]:

$$ \dot{\xi }_{0} = \left( {\frac{{d_{2}^{2} }}{{\alpha_{2} d_{2} }}} \right)\eta_{0} \begin{array}{*{20}c} , & {\dot{\eta }_{0} = - \left( {\alpha_{2} d_{2} } \right)\xi_{0} } \\ \end{array} $$
(39.5)

Then the solution can be written as:

$$ \left\{ \begin{array}{l} \xi = \xi_{0} \cos d_{2} t + {{\eta_{0} \sin d_{2} t} \mathord{\left/ {\vphantom {{\eta_{0} \sin d_{2} t} {\alpha_{2} }}} \right. \kern-0pt} {\alpha_{2} }} \hfill \\ \eta = - \alpha_{2} \xi_{0} \sin d_{2} t + \eta_{0} \cos d_{2} t \hfill \\ \zeta = C_{5} \cos d_{3} t + C_{6} \sin d_{3} t \hfill \\ \end{array} \right. $$
(39.6)

In the real dynamic model there exist various kinds of perturbations, which have a significant effect on the orbit. Meanwhile, the neglected higher order terms of Eq. (39.4) also weaken the stability of the periodic orbits. In this case, a more stable nominal orbit under a more accurate dynamic model is required.

Richardson worked out the third-order approximation solutions to the kinetic equations for halo orbits, providing a more accurate orbit in the real dynamic model. An accurate quasi-halo orbit of CRTBP can also be worked out using numerical methods based on multiple shooting algorithm.

3 C–W Equation

For most small bodies in the solar system, the parameter \( \mu \) of the three-body problem is very small. Under this circumstance, the dynamic model of the restricted two-body problem (\( \mu = 0 \)) may be a better choice. In the latter model, the origin of the rotating frame in Fig. 39.1 moves to the center of the Sun, and the positions of \( L_{1} \) and \( L_{2} \) coincide. Therefore, the position of \( L_{1} \) becomes \( \vec{r}_{1} = (1,0,0)^{T} \), and the linear equation of the motion can be written as:

$$ \left\{ \begin{array}{l} \ddot{\xi } - 2\dot{\eta } = 3\xi \hfill \\ \ddot{\eta } + 2\dot{\xi } = 0 \hfill \\ \ddot{\zeta } + \zeta = 0 \hfill \\ \end{array} \right. $$
(39.7)

This equation is called C–W equation. The solution to this equation is [4]:

$$ \left\{ \begin{array}{l} \xi = - \frac{3}{2}C_{2} + \frac{1}{2}C_{3} \sin t - \frac{1}{2}C_{4} \cos t \hfill \\ \dot{\xi } = \frac{1}{2}C_{3} \cos t + \frac{1}{2}C_{4} \sin t \hfill \\ \eta = C_{1} + C_{2} t + C_{3} \cos t + C_{4} \sin t \hfill \\ \dot{\eta } = C_{2} - C_{3} \sin t + C_{4} \cos t \hfill \\ \end{array} \right. $$
(39.8)

The initial conditions for the periodic solution are:

$$ \dot{\xi }_{0} = \eta_{0} /2\begin{array}{*{20}c} , & {\dot{\eta }_{0} = - 2\xi_{0} } \\ \end{array} $$
(39.9)

This is the mechanism of formation flying of satellites of the earth, and it may also be used in formation flying with very small bodies in the solar system. This is the mechanism of formation flying of satellites of the earth, and it may also be used in formation flying with very small bodies in the solar system.

4 Numerical Simulation and Results

In this part, we adopt the theta-D control method [5–7] to solve the problem of station keeping in formation flying with the small body based on respectively the two different dynamic models.

4.1 Results Based on Halo Orbit Control

For near-earth small bodies, assuming that the semi major axis of their revolution 1AU, the energy consumption for station keeping can be worked out using the control strategies mentioned above (taking the halo orbit around \( L_{1} \) point of the CRTBP composed of the sun, the small body and the spacecraft as an example). Assuming that the amplitude of halo orbit in z-direction is \( 0.155\gamma_{1} \), differential correction method and numerical simulations are used to calculate the nominal orbits for different \( \mu \) see Fig. 39.2. The variation of amplitude in x-direction due to \( \mu \) is shown in Fig. 39.3a. The approximate 10 years’ energy consumption for station keeping in these orbits is shown in Fig. 39.3b.

Fig. 39.2
figure 2

Projection of halo orbits

Full size image
Fig. 39.3
figure 3

a Variation of amplitude in X-direction of halo orbits due to μ; b variation of energy increment due to μ

Full size image

As \( \mu \) decreases, both the amplitude of halo orbits and the energy consumption for orbit control will decrease. If the ratio of the amplitude in x-direction to \( \gamma_{1} \) keeps unchanged (=0.155), the periods of halo orbits are almost the same (about 190 days). As a result of the stability of CRTBP and the dynamics of halo orbit formation, nominal halo orbits do not exist if the ratio is too large or too small. Therefore, different amplitude should be considered for different \( \mu \) in nominal orbit design.

4.2 Comparison of the Results of Different Strategies

Taking the near-earth small body 2005TF49 as an example, the formation flying orbits for an explorer with this small body are designed using respectively halo orbit calculated in numerical ways and C–W equation. This small body has a semi major axis of 155866014.57599 km and a gravity of about \( 10^{ - 19} \) to the sun. The amplitude in x-direction of the halo orbit around \( L_{1} \) is about 7.78 km, while the distance between \( L_{1} \) and the small body is about 50.16 km, which is also taken as the amplitude on x and y direction in orbit design with C–W equation. The amplitudes in z direction of both the halo orbit and the nominal orbit with C–W equation are all set at about 14 km. Figure 39.4 shows the nominal orbits resulted respectively from the two dynamic models. The variation of orbit control due to time is depicted in Fig. 39.5.

Fig. 39.4
figure 4

a Nominal halo orbit; b nominal orbit resulted from C–W equation

Full size image
Fig. 39.5
figure 5

a Variation of orbit control for nominal halo orbit due to time; b variation of orbit control for nominal orbit computed by C–W equation

Full size image

Given an initial error of 1 × 10−6 in the computation, the total cost in the former model is 0.277 m/s while it is more than 6 m/s using C–W equation. Comparison shows that it costs less for station keeping when the nominal orbit is computed in CRTBP.

5 The Effect of Solar Radiation Pressure

Simulation results above have not taken into consideration the effect of solar radiation pressure perturbation. The aim of the omission is to show the effect of the small body’s gravity on the dynamics. However, solar radiation pressure perturbation is not negligible when the explorer formation flies with a small body in a real dynamic model. Solar radiation pressure is a kind of surface force. Since the area-to-mass ratio of the small solar system body is usually far less than that of the spacecraft, the effect of solar radiation pressure perturbation on the small body can be ignored while it has to be considered for that of the spacecraft. It is this differentiation that leads to the failure of the C–W equation configuration. This situation is quite different from that of the formation flying of two earth satellites, which have similar area-to-mass ratio and thus have similar effects by solar radiation pressure. The discussion above explains the different situations when applying C–W equation to formation flying of two earth satellites and to that of a spacecraft in formation flight with a small solar system body.

Considering the solar radiation pressure perturbation, the equation of motion of the explorer in the rotating frame can be depicted as:

$$ \left\{ \begin{array}{l} \ddot{\vec{r}} + 2\left( { - \dot{y},\dot{x},0} \right)^{T} = \left( {{{\partial \Upomega } \mathord{\left/ {\vphantom {{\partial \Upomega } {\partial \vec{r}}}} \right. \kern-0pt} {\partial \vec{r}}}} \right)^{T} + \varepsilon_{lt} {\varvec{\alpha}} \hfill \\ \Upomega \left( {x,y,z} \right) = {{\left( {\mu \left( {1 - \mu } \right) + x^{2} + y^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu \left( {1 - \mu } \right) + x^{2} + y^{2} } \right)} 2}} \right. \kern-0pt} 2} + {{\left( {1 - \mu } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \mu } \right)} {r_{1} }}} \right. \kern-0pt} {r_{1} }} + {\mu \mathord{\left/ {\vphantom {\mu {r_{2} }}} \right. \kern-0pt} {r_{2} }} \hfill \\ \end{array} \right. $$
(39.10)

where \( {\varvec{\alpha}} \) is the nominal direction of solar radiation pressure perturbation, \( \varepsilon_{lt} = \frac{(1 + \eta )S}{m}\frac{{\rho_{AU} \Updelta_{S}^{2} }}{{r^{2} }} \), \( \eta \) is the reflection factor of the explorer and \( 0 \le \eta \le 1 \), \( S/m \) is the area to mass ratio. \( \rho_{AU} = 4.5605\; \times \;10^{ - 6} \,{\text{N}}/{\text{m}}^{2} \) is the solar radiation pressure at 1 AU. In this case, the form of Eq. (39.7) can be written as:

$$ \left\{ \begin{array}{l} \ddot{\xi } - 2\dot{\eta } = 3\xi + \varepsilon_{lt} \alpha_{x} \hfill \\ \ddot{\eta } + 2\dot{\xi } = \varepsilon_{lt} \alpha_{y} \hfill \\ \ddot{\zeta } + \zeta = \varepsilon_{lt} \alpha_{z} \hfill \\ \end{array} \right. $$
(39.11)

Assuming that the area and the mass of the explorer are respectively 18 m2 and 1500 kg, \( \varepsilon_{lt} \sim 10^{ - 5} \) can be obtained when the normalized units in (39.1) are used. The condition to apply C–W equation is \( \varepsilon_{lt} << \sqrt {\xi^{2} + \eta^{2} + \zeta^{2} } < < 1 \), that is, \( \sqrt {\xi^{2} + \eta^{2} + \zeta^{2} } >> 10^{3} \;{\text{km}} \). However, for formation flying, the distance between the explorer and the target body is generally not allowed to be large for scientific purposes. A distance of 10–100 km is acceptable, but the effect of solar radiation pressure, in this case, will destroy the configuration of C–W equation (as illustrated in Fig. 39.6). Therefore, the application of C–W equation in formation flying problems is not preferable when solar radiation pressure is taken into consideration.

Fig. 39.6
figure 6

The effect of solar radiation pressure on nominal orbit based on C–W equation

Full size image

6 Conclusions

This paper studies formation flying with small bodies in the solar system. Both CRTBP and perturbed two-body problem are considered. Halo orbits around \( L_{1} \) and orbits based on C–W equation are respectively applied to form nominal orbits. As \( \mu \) decreases, the amplitude of halo orbits energy consumption for orbit control decreases. Because of the higher accuracy of its dynamic models, energy consumption for station keeping for halo orbits is less than that of the formation flying orbits using C–W equation. A dynamic model considering the solar radiation pressure is also studied while simulation results show that it has no significant advantage to use C–W equation in this case.