Chip Formation

Abstract

In cutting and abrasive processes, the cutting edge penetrates into the workpiece material, which is thus plastically deformed and slides off along the rake face of the cutting edge.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

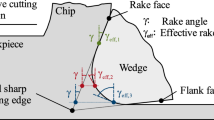
In cutting and abrasive processes, the cutting edge penetrates into the workpiece material, which is thus plastically deformed and slides off along the rake face of the cutting edge. This is called chip formation. The processes in chip formation can be examined within the orthogonal plane (Fig. 1.9), because essential parts of the material flow take place within this plane (Fig. 2.1). We can assume that the deformation is two-dimensional. The two-dimensional deformation is only disturbed at the edges of the cross section of the undeformed chip, at the free surface and in front of the cutting edge corner, as there is material flow at an angle towards the orthogonal plane, which is caused by linkage to the undeformed material by the free surface respectively.

Fig. 2.1

Undeformed chip cross section and the cutting edge

Depending on the deformation behavior of the workpiece material, there are different mechanisms of chip formation with either continuous or discontinuous chip flow.

2.1 Mechanisms of Chip Formation

Depending on the workpiece material and the cutting conditions, the following mechanisms of chip formation can be distinguished (Fig. 2.2):

Fig. 2.2

Mechanisms of chip formation

• continuous chip formation

• lamellar chip formation

• segmented chip formation

• discontinuous chip formation.

In continuous chip formation the chip slides off along the rake face at a constant speed in a stationary flow. Continuous chip formation is promoted by a uniform, fine-grained structure and high ductility of the workpiece material, by high cutting speeds and low friction on the rake face, by positive rake angles and a low undeformed chip thickness (Fig 2.3).

Fig. 2.3

Scanning electron micrographs of chip forms

Lamellar chip formation is a continuous, periodic chip formation process similar to pure continuous chip formation. However, there are variations in the deformation process that cause more or less significant cleavages or even concentrated shear bands. The lamellae are produced due to thermal or elastomechanical processes with a high formation frequency within the kHz range. Lamellar chips occur with highly ductile workpiece materials with an increased strength, especially at high cutting speeds (q. v. high speed cutting).

Segmented chip formation is the discontinuous formation of a chip with still more or less connected elements, yet with significant variations in the degree of deformation along the flow path. It primarily occurs with negative rake angles, lower cutting speeds and a higher chip thickness.

Discontinuous chip formation occurs if the plastic ductility of the workpiece material is very low or if predefined slide paths are formed due to high inhomogeneities (e. g. if cast iron with lamellar graphite is machined). Parts of the workpiece material are ripped out of the compound material without significant deformation. The workpiece surface is then rather produced by the ripping out process in the chip formation than by the tool traces.

With continuous chip formation, built-up edges can occur (Fig. 2.4). They are formed by particles of the workpiece material, which adhere to the rake face and to the cutting edge. These particles have been subject to high deformation and have been strain-hardened. They are much harder than the base workpiece material. Built-up edges only occur if

Fig. 2.4

Formation of built-up edges

• the workpiece material promotes strain-hardening,

• the chip formation is stable and largely stationary,

• there is a stagnant zone in the material flow in front of the cutting edge,

• the temperatures in the chip formation zone are sufficiently low and do not allow for recrystallization.

Built-up edges influence the cutting edge geometry. They generally facilitate chip formation (lower forces). When they move off, they can drag along workpiece particles (adhesive wear). Sometimes strain-hardened parts of the built-up edges are integrated into the newly formed workpiece surface. Therefore, the formation of built-up edges is generally undesirable. However, it does not occur at higher cutting speeds and resulting higher temperatures in the chip formation zone, because there is no strain-hardening if the recrystallization temperature is exceeded during the deformation process.

The process for continuous chip formation can be described using a model of five deformation zones (Fig. 2.5). The main part of the plastic deformation takes place in the primary shear zone in the form of shear deformation. In the secondary shear zones in front of the rake face and the flank face, the workpiece material is additionally deformed under the influence of high friction forces. A stagnant zone (zone with high pressure from all sides) develops in front of the cutting edge. The actual separation of workpiece material also takes place in this zone. Furthermore, minor plastic deformations occur in the preliminary deformation zone. This zone has an essential influence on the penetration depth of plastic deformations in the workpiece and so on the external workpiece zone.

Fig. 2.5

Chip formation zones [WAR74]

2.2 Chip Root Analysis

Several methods have been developed to visualize the deformation process in front of the cutting edge and to analyze the chip formation process and the material behavior in the working zone. The most important methods are

• interrupted cut

• micro-cinematography

• the finite element method (FEM).

The analyses provide information on the mechanisms of chip formation, the plastic deformations in the chip formation zone and the position of the shear plane. They provide the basis for a calculation of the kinematic, mechanical and thermal conditions in the chip formation zone.

The basic principle of the interrupted cut is an abrupt separation of the tool from the workpiece. The current status in the deformation process is thus “frozen”, can be subject to metallographic preparation and analyzed under the microscope. Although the process is interrupted in an abrupt manner (quick–stop), the process has to be slowed down from the initial deformation speed until it actually comes to zero. Therefore, the cutting process is not frozen at the normal, stationary cutting speed, but at an unsteady phase while slowing down. In spite of this, the interrupted cut method is widely accepted. It should however be considered problematic for highly time-dependent processes, like thermally dominated processes or processes with fast, unsteady deformation.

The cutting speed at which the chip root is to be frozen determines the design of the devices used for the interrupted cut. Especially with high cutting speeds, the process has to be interrupted within a minimum time interval t_o.

Figure 2.6 is a highly simplified illustration of the speed ratios for the interrupted cut method. We assume that the constant acceleration a is negative (deceleration), thus

$$ v_{rel} = v_{c} - a_{T} \cdot t $$

(2.1)

With v_rel = 0 m/min after t₀, the necessary braking distance Δx is

$$ \Updelta x = \frac{1}{2}v_{c} t_{0} $$

(2.2)

These equations can be used to determine the necessary deceleration a for the maximum permitted braking distance:

$$ a_{T} = \;\;\frac{{v_{c}^{2} }}{2\Updelta x} $$

(2.3)

This shows that the deceleration value has to be very high, even with low cutting speeds and a maximum permitted braking distance of up to 10 % of the undeformed chip thickness. Please note that the second order value of the cutting speed is used in Eq. 2.3. In order to keep the necessary deceleration forces within acceptable limits, especially with high cutting speeds, it is important to keep the decelerated masses at a minimum (Fig 2.6).

Fig. 2.6

Speed ratios for the interrupted cut method

Different methods can be used to interrupt the cut (Abb. 2.7). Generally, either the tool or the workpiece can be accelerated or decelerated.

Part (a) of Fig. 2.7 illustrates the principle of interrupting the cut by accelerating the tool [KLO93]. Usually, the whole tool unit is accelerated via the tool holder. The necessary potential energy which has initially been stored is transferred into kinetic energy within a few milliseconds. The energy is stored using springs, compressed air or explosive materials. The tool can also be accelerated by means of mechanical cut-off devices [BAI88]. For this purpose, a mechanical barrier initially rotates with the tool and is then within one revolution, brought to a position where it accelerates the tool out of the workpiece.

Fig. 2.7

Methods used for the interrupted cut

In part (b), the tool (a double-sided cutting insert) is fixed on a low-mass slide. For example, the slide is accelerated using compressed air and hits the workpiece. A short length of material is cut (by planing), and the tool on the slide is decelerated by the workpiece, which works as an impact ring.

The method illustrated in part (c) relates to a set-up for high cutting speeds developed by Ben Amor [BEN03] based on an approach by Buda [BUD68]. This method can only be used for very low masses. Some details of this method are illustrated in Fig. 2.8. A predetermined breaking point is introduced into a bar, which is then cut by radial grooving. The remaining cross section at the predetermined breaking point is finally reduced to an extent where the break stress is exceeded and the segment breaks off from the workpiece. This segment including adhesive chips, is then accelerated away from the workpiece by means of the cutting force and is used as a chip root for the analysis of the chip formation process. The following exemplary values demonstrate that this method is very effective. The given parameters are as follows:

$$ {\text{h}}\cdot{\text{b}} = 0. 2\cdot 3\, {\text{mm}}^{ 2} ,{\text{ v}}_{\text{c}} = 300 \,{\text{m}}/{ \hbox{min} },{\text{ C45 steel}},{\text{ F}}_{\text{c}} = 1 800 \,{\text{N}},{\text{ m}} = 3\, {\text{g}}. $$

Fig. 2.8

Interrupted cut method according to Ben Amor

We assume that the initial accelerating force is applied throughout the whole separation process and that accordingly, the acceleration is constant. As a result,

$$ a_{T} = F_{c} /m $$

(2.4)

According to Eq. 2.3, the corresponding acceleration distance is 21 μm.

Figure 2.9 shows a chip root obtained by this method at a high cutting speed. Although the accelerating distance is higher than 10 % of the undeformed chip thickness, the image is well-suited for analyzing the deformation mechanisms in front of the cutting edge.

Fig. 2.9

C15 steel chip root obtained at a high cutting speed [TÖN05]

Part (d) of Fig. 2.7 illustrates the method of accelerating a low-mass workpiece in a slideway by means of compressed air and then, after a short length of material has been cut, rapidly decelerating it by making it hit an impact plate. The chip roots in Fig. 2.10 have been obtained using a similar method with an initial cutting speed of 2,400 m/min and a braking distance of less than 20 μm [HOW05].

Fig. 2.10

TiAl6V4 chip roots [HOW05]

In contrast to the interrupted cut method, micro-cinematography allows for examining the chip formation while the process is still running [WAR74]. For this purpose, a polished and etched specimen (black-and-white structure) is pressed against a fused quartz glass plate (Fig. 2.11) and cut by orthogonal turning. The process can be observed through the fused quartz glass plate and magnified using a microscope. However, the image of the process is only an approximation because of the free surface of the workpiece. Images without motion blur can only be taken at cutting speeds of up to 1 m/min.

Fig. 2.11

Test stand for micro-machining processes [WAR74]

2.3 Shear Plane Model

Several theories for the calculation of parameters in cutting and abrasive processes make use of a shear plane model, assuming that all plastic deformations take place within the shear plane. Depending on the deformation behavior of the workpiece material and on the process conditions, this model can be adequately true to reality. If we assume that the shear plane model (Fig. 2.12) is applicable and that the deformation is two-dimensional (orthogonal cut), the shear velocity v_ϕ can be calculated as

$$ {\text{v}}_{\upphi } = {\text{v}}_{c} \frac{{\sin \,(90^{^\circ } - \gamma )}}{{\sin \,(90^{^\circ } + \gamma - \upphi )}} = {\text{v}}_{c} \frac{\cos \gamma }{\cos \,(\upphi - \gamma )}$$

(2.5)

Fig. 2.12

Shear plane model and shear velocity

As major plastic deformations take place, the volume can be regarded as constant, thus¹

$$ \frac{b' }{b}\; \cdot \;\frac{h'}{h}\; \cdot \;\frac{w' }{w}\; = \;1\;oder\;\lambda_{b} \; \cdot \;\lambda_{h} \; \cdot \;\lambda_{w} \; = \;1, $$

(2.6)

for the compressions λ. As we assume that the deformation is two-dimensional, the compression of the chip width (chip width ratio) is λ_b = 1; thus,

$$ \lambda_{\text{h}} \cdot \lambda_{\text{w}} = 1. $$

(2.7)

Furthermore,

$$ \lambda_{w} = \frac{{w^{\prime}}}{w} = \frac{vch}{{v_{c} }} $$

(2.8)

And consequently,

$$ \lambda_{h} \; = \;\frac{{v_{c} }}{{v_{ch} }} = \frac{1}{{\lambda_{w} }}. $$

(2.9)

From the velocity triangle (Fig. 2.12) follows

$$ \lambda_{h} \; = \;\frac{\cos \;(\phi \; - \;\gamma )}{\sin\phi }$$

(2.10)

The compression of the chip thickness λ_h (chip thickness ratio) can be determined by measuring the chip thickness or the chip length (with an interrupted cut) and by means of the manipulated variables, so that the shear angle ϕ can be determined experimentally.

In plastomechanics (the mechanics of plastic deformations), deformations are treated as relative parameters. Figure 2.13 shows the mechanisms of compression, tension and shearing.

Fig. 2.13

Deformations

In literature, two different notations are used for the numerical description of plastic deformations of the overall shape. The notation used in English-speaking countries and in material science in general is based on the relative dimensional change  or strain ε, with ε_C for compression and ε_T for tension.

$$ \varepsilon_{C} = \frac{{h_{0} - h}}{{h_{0} }} = 1 - \frac{h}{{h_{0} }} $$

(2.11)

and

$$ \varepsilon_{T} = \frac{{h - h_{0} }}{{h_{0} }} = \frac{h}{{h_{0} }} - 1 $$

(2.12)

In the field of forming technology and in German-speaking countries, the logarithmic deformation φ is used²:

$$ \varphi = ln\frac{h}{{h_{0} }} $$

(2.13)

Please note that B.A. Behrens gives good reasons for using the notation of logarithmic deformation [DOB07, p. 56 et seq.]. It is easy to transform one notation into the other:

$$ \varphi = \ln \left( {1 - \varepsilon_{C} } \right) $$

(2.14)

and

$$ \varphi = ln (\varepsilon_{T} - 1) $$

(2.15)

For small deformations below φ = 0.1, the calculated values are practically identical.

The notations for the deformation rate (compression and tension) are:

$$ \varepsilon_{C} = 1 - e^{\varphi } $$

(2.14a)

and

$$ \varepsilon_{T} = e^{\varphi } - 1 $$

(2.15a)

$$ \dot{\varepsilon }_{C} = \frac{d}{d\varphi }\left( {1 - e^{\varphi } } \right) \cdot \frac{d\varphi }{dt} $$

(2.16)

and

$$ \dot{\varepsilon }_{T} = \frac{d}{d\varphi }\left( {e^{\varphi } - 1} \right)\frac{d\varphi }{dt} $$

(2.17)

$$ \dot{\varphi } = \frac{1}{{1 - \varepsilon_{C} }} \dot{\varepsilon }_{C} $$

(2.16a)

and

$$ \dot{\varphi } = \frac{1}{{\varepsilon_{T} - 1}} \dot{\varepsilon }_{T} $$

(2.17a)

In plastomechanical calculations for cutting and abrasive processes, the focus is on the extent of the deformations within the workpiece material. If the following assumptions are valid, the shear γ_S can be calculated as the tangent of the deformation angle χ³ (Fig. 2.14):

Fig. 2.14

Geometry of the deformations in an orthogonal cutting process

• shear plane model

• constant volume

• homogeneous workpiece material

• isotropic workpiece material

• two-dimensional deformation.

The deformation angle χ is measured at the normal to the shear plane. Thus

$$ \tan \chi \; = \;\tan \;(\upphi \; - \;\gamma )\; + \;\frac{1}{\tan \upphi } $$

(2.18)

The volume segment in Fig. 2.14 is parallel to the shear plane, so that the shear deformation tan χ is directly visible. To relate the deformation process to a reference deformation, we have to determine the relative deformations, the maximum tension ε_T and the maximum compression ε_C of the workpiece material after it has passed through the shear plane. For this purpose, we use an unsigned volume element, i. e. a circular element, which is deformed into an ellipse behind the shear plane (Fig. 2.15).

Fig. 2.15

Changes in the overall shape in cutting processes

The ratios of the long axis (2a) and the short axis (2b) to the diameter (2r) of the circular element correspond to the maximum tension and compression respectively. Thus, the tension and compression are

$$ \varepsilon_{T} = \frac{2a}{d} - 1 $$

(2.19)

and

$$ \varepsilon_{C} = 1 - \frac{2b}{d} $$

(2.20)

$$ \varepsilon_{T} = \frac{1}{2}\,\left[ {\tan \left( {\phi - \gamma } \right) + \frac{1}{\tan \phi }} \right] - 1 + \sqrt {\left[ {\tan \left( {\phi - \gamma } \right) + \frac{1}{\tan \phi }} \right]^{2} + 1} $$

(2.19a)

$$ \varepsilon_{C} = \frac{1}{2}\,\left[ {\tan \left( {\upphi - \gamma } \right) + \frac{1}{\tan \upphi }} \right] + 1 + \sqrt {\left[ {\tan \left( {\upphi - \gamma } \right) + \frac{1}{\tan \upphi }} \right]^{2} + 1} $$

(2.20b)

We can conclude that

$$ \varepsilon_{T} + \varepsilon_{C} = \tan \chi = \gamma_{\text{s}} $$

(2.21)

Figure 2.16 shows the progression of the tension ε_T and the shear γ_S across the shear angle ϕ for a rake angle of γ = 0°. The shear angle, the tension and the shear decrease with higher rake angles.

Fig. 2.16

Deformations and shear angles [KÖH68]

The calculations of deformations and their conversion are only based on geometrical relations. Forming technology usually uses comparative hypotheses to convert multiaxial deformations and strains into uniaxial reference values [DOB07, S.153 f]. Tresca uses the shear stress hypothesis for his calculation, while von Mises uses the strain energy hypothesis. We can also deduce the reference deformations using an energy approach.

The shear γ_S in Eq. 2.21 can be converted into the uniaxial reference deformation φ. We obtain

$$ \varphi = \frac{1}{2}\gamma_{s} \quad \quad {\text{according to Tresca}} $$

(2.22)

$$ \varphi = \frac{1}{\sqrt 3 }\gamma_{s} \quad \quad {\text{according to v}}.{\text{ Mises}} $$

(2.23)

2.4 Questions

• 1. What is “two-dimensional deformation” and what is “plane strain”?

• 2. Which processes can be used for orthogonal cutting?

• 3. How can we describe uniaxial deformations? Please give both notations.

• 4. How can the strain velocity be derived?

• 5. Which parameters must be known to determine the angle with which a segment in the shear plane is deformed by shear if the shear plane model is applicable?

• 6. How can these parameters be measured?

• 7. Which methods can be used to examine the chip root? These methods only provide an approximated image of the deformation process. Which restrictions apply?

• 8. Which are the different zones of deformation in chip formation processes?

• 9. Define the different types of chip formation. How are they distinct from the chip forms?

• 10. What is a lamellar chip? How can we determine the corresponding degree of uniformity?

• 11. Under which conditions might a shear cleavage be produced?

• 12. What are built-up edges?

• 13. Why do built-up edges only occur with continuous chips?

• 14. Which effect does a built-up edge have on the workpiece quality and on the tool?

• 15. Determine the shear velocity by means of the shear plane model.

• 16. Using Poisson’s ratio (which is usually applied for metallic materials), explain why the volume is not constant with elastic (non-plastic) deformations.

• 17. How can the shear angle be determined by means of the chip compression ratio?

• 18. How can the deformation angle χ be calculated?