Computational Methods for the Assignment of Vibrational Modes in Crystalline Materials

Abstract

In this chapter we provide a description of the computational tools used for the calculation of the terahertz absorption spectrum of a crystalline material, with a particular focus on molecular crystals. We explain using examples why it is not correct to use the normal modes of vibration of an isolated molecule to understand the vibrational spectrum of a material in the terahertz range, but that the features in this spectral region are largely related to intermolecular interactions. It is, therefore, necessary to use methods that consider the periodicity of the crystal structure. We describe the two main methods used for the calculation of the vibrational frequencies and their absorption intensities of a crystal: lattice dynamics and molecular dynamics, providing examples showing the benefits and limitations of each method.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

The vibrational spectrum of a material is directly related to its internal properties: a vibration is probed when the material absorbs energy from incoming radiation, and the energies at which the material absorbs reflect the interactions between atoms in the material. In classical infrared spectroscopy, it is often possible to directly connect an observed absorption to the distortion (e.g. stretch or bend) of a bond in a molecule, usually without the need of calculation. This is because the vibrational normal modes are often localized in nature and because their associated vibrational frequencies are usually only slightly shifted by their chemical environment. Therefore, certain vibrational frequency ranges are characteristic of known distortions of covalent bonds.

However, the vibrational normal modes become increasingly more complex at lower frequencies; in the terahertz region, it is not generally possible to associate an absorption feature to a simple motion such as the stretching of a bond. Instead, absorption features generally result from collective motions of all the atoms in the material. To correctly assign the nature of molecular motions associated with a particular absorption, it is thus necessary to rely on simulations. If a simulation is theoretically well-founded and can reproduce the positions and intensities of features in an observed spectrum, the results can also be trusted to provide a faithful description of the vibrational motions that give rise to these features. In this chapter, we discuss the methods that are applied to the simulation of lattice modes in crystalline molecular materials and can, therefore, be applied to characterise the features observed in measured terahertz spectra.

7.1.1 Single Molecule Versus Periodic Crystal Structure Calculations

A tempting approach to calculating the absorption spectrum of a molecular material is to calculate the normal modes of vibration of an isolated molecule, as such single-molecule calculations are generally much cheaper (in computing time and required computing resources) than calculations that include the entire periodic crystal structure. However, the vibrational features observed in the gas phase and in a solid can be radically different: in the gas phase, the interaction between molecules can be neglected, while in solids this is not true, especially when considering low frequency vibrations. Furthermore, pure rotational modes of molecules are allowed in the gas phase (as can be seen in the absorption spectrum of water vapour [1]), while molecular rotations are hindered in the solid phase by molecular close-packing and by the interactions between molecules.

Fig. 7.1

Molecular structures of naphthalene, 2,2$^\prime$-bithiophene and MDMA

Consider the case of naphthalene (Fig. 7.1), whose lowest frequency infrared active vibrational frequencies are listed in Table 7.1. The terahertz spectrum of the gas phase and the calculation of the isolated molecular vibrational frequencies [2] agree in finding no absorption below 175 cm$^{-1}$, while the experimental [3] spectrum of crystalline naphthalene shows several features below 100 cm$^{-1}$. These additional features only appear for the crystalline sample, so must be related to the intermolecular interactions within the crystal. Indeed, simulations that include the periodic structure of the crystal [4, 5] reproduce the observed frequencies and indicate that the corresponding vibrations relate to whole-molecule motions about the equilibrium crystallographic positions. Another example is the terahertz spectrum of 2,2$^\prime$-bithiophene, shown in Fig. 7.2. Again, there are clear differences between the vibrational modes of the isolated molecule and those of the crystal: in this case, the isolated molecule does have low-energy vibrational modes near and below 100 cm$^{-1}$. However, this region of the spectrum becomes much more detailed in the crystal and the number and position of these features can only be reproduced in a calculation that includes the entire crystal structure.

Table 7.1 Comparison of the three lowest energy infrared/terahertz active absorption frequencies (cm$^{-1}$) for naphthalene, in crystal and gas phase

Fig. 7.2

Experimental terahertz spectrum of crystalline 2,2$^\prime$bithiophene (a, upper spectrum) compared with a solid state calculation (a, lower spectrum) and a molecular calculation (b). The strongest experimental features are indicated with letters. Reprinted with permission from [6]. Copyright 2005 Americal Chemical Society

A trickier example is represented by calculations on the drug molecule 3,4-methylenedioxymethamphetamine (MDMA or ecstasy, Fig. 7.1). In this case, calculations on the isolated molecule [7] seem to provide excellent agreement with the experimental spectrum (Table 7.2), so that features of the terahertz spectrum were assigned to intramolecular vibrations. However, a series of calculations [8, 9] based on the dynamics of the known crystal structure, showed that the intramolecular vibrations are shifted out of the terahertz region by coupling to the crystal environment (see Sect. 7.2.2). Moreover, the calculations produce a series of intermolecular vibrational modes at the frequencies seen in the experimental spectrum. Here, it seems that the agreement of the frequencies found in the isolated molecule calculation with the experimental spectrum was a result of fortuitous coincidence.

Table 7.2 Experimental [7] and calculated [7, 8] frequencies of the terahertz absorption of MDMA (cm$^{-1}$), from isolated molecule and from lattice dynamics of the crystal, and corresponding assignment to vibrational features

In conclusion, to correctly calculate the terahertz spectrum and the corresponding vibrational modes of a crystalline material it is necessary to employ methods that consider the molecular arrangement in the periodic structure and the associated intermolecular interactions present in a crystal. Two computational approaches are available: lattice dynamics and molecular dynamics (MD).

Lattice dynamics, described in Sect. 7.2, relies on calculating the forces acting on the atoms in the crystal as a periodic system in static equilibrium. A harmonic analysis of the forces leads to the normal modes of the system. MD, on the other hand (Sect. 7.3), is a more general computational approach to investigating the dynamics in chemical systems, where Newton’s laws of motion are applied to follow the dynamics of molecules in a crystal around its equilibrium structure. The vibrational modes can then be extracted from an analysis of the trajectories of atoms through time.

There are, of course, different types of systems: ionic crystals, covalent crystals, semiconductors, and molecular crystals to name a few. Each of these has its own peculiarity, and methods may need to be carefully tailored to address the differences in their behaviour. In the proceeding sections, we will try to consider these different aspects, but we will focus mainly on molecular organic crystals; for other types of systems, we refer whenever possible to the relevant literature.

7.2 Theory of Crystal Phonons

All the vibrational motions of atoms in a crystal can be described as a superposition of the normal modes of vibration; the quanta of vibrations in a periodic system are called phonons. The normal modes are characterised by the property that each atom of the crystal oscillates with the same frequency $\omega$, and that these oscillations can interact with light of the corresponding frequency, producing absorption signals detectable in vibrational spectroscopy. In the following section, we will introduce how it is possible to calculate these normal mode frequencies for different types of periodic systems.

7.2.1 Phonon in a 1-Dimensional Crystal

We start with the simplest model system: a 1-dimensional (1D) infinite chain of equally spaced atoms, in which first neighbours interact via a harmonic interaction. The instantaneous position $x_n$ of the $n$th atom can be written as

$$\begin{aligned} x_n = nd_0 + u_n, \end{aligned}$$

(7.1)

where $d_0$ is the equilibrium separation between neighbouring atoms, and $u_{n}$ the displacement from the equilibrium position. Defining the force constant of the harmonic nearest-neighbour interaction as $C$, and the atomic mass $m$, leads to the following system of equations:

$$\begin{aligned} m \frac{\mathrm{d}^2 {u}_n}{\mathrm{d} t^2} = C \left( u_{n+1}-2u_{n} + u_{n-1}\right), \end{aligned}$$

(7.2)

From the periodicity of the system we expect the solution to be in the form of a travelling wave:

$$\begin{aligned} u_n(t) = A \exp \,({\text{ i}} kd_0n - {\text{ i}} \omega t), \end{aligned}$$

(7.3)

where $A$ is the amplitude of motion of an atom, i.e. the maximum displacement from the equilibrium position. Using this form of the solution we have simplified the initial problem to a simpler parametric equation. We can find the so-called dispersion relation between $\omega$ and $k$:

$$\begin{aligned} \omega = \sqrt{\frac{4C}{m}} \left| \sin \frac{1}{2}k d_{0} \right| \end{aligned}$$

(7.4)

The wavevector k is an important parameter in a crystal and is associated with a crystal momentum $\hbar k$. Quantum transitions within the crystal require that the crystal momentum is conserved,¹ which has an important consequence in spectroscopy: because of the low momentum of a photon, interaction of a phonon with light is possible only if $k \approx 0$.

Another important rule for allowed transitions in vibrational terahertz and infrared spectroscopy is that the phonon vibration must generate a vibrating electrical dipole to interact with light; we must explore a less simple model to investigate the consequences of this selection rule.

We now consider a linear chain of alternating atoms, of mass $m_1$ and $m_2$, respectively, each of equal distance $\frac{1}{2}d_0$ from each other. If we call $u_n$ and $v_n$ (see Fig. 7.3) the displacement of the atoms from their equilibrium positions, we obtain the system of equations:

$$\begin{aligned} \begin{array}{rl} m_1 \frac{\mathrm{d}^2 {u}_n}{\mathrm{d} t^2}&= C \left( v_{n-1} + v_{n} - 2u_n\right) \\ [6pt] m_2 \frac{\mathrm{d}^2 {v}_n}{\mathrm{d} t^2}&= C \left( u_{n} + u_{n+1} - 2v_n\right), \end{array} \end{aligned}$$

(7.5)

Fig. 7.3

Infinite linear chain of two alternating types of atom separated by a distance $\frac{1}{2}d_0$. The atoms are displayed in their equilibrium position, and the displacement $u$ and $v$ are indicated

As with the first monoatomic chain model, the solution we look for will still be in the form of a travelling wave, but now with two amplitudes, $A_1$ and $A_2$, for the two atom types:

$$\begin{aligned} \begin{array}{rl} u_n&= A_1 \exp \left({ \mathrm{i} kd_0n- \mathrm{i} \omega t} \right) \\ [6pt] v_n&= A_2 \exp \left({ \mathrm{i} kd_0n- \mathrm{i} \omega t} \right) \end{array} \end{aligned}$$

(7.6)

Substituting into Eq. 7.5 leads to the following matrix relation:

$$\begin{aligned} \left(\begin{array}{ll} \dfrac{1}{C}\omega ^2 m_{1}-2&1 + \exp \left( -\mathrm{i} k d_0 \right) \\ 1 + \exp \left( \mathrm{i} k d_0 \right)&\dfrac{1}{C}\omega ^2 m_{2}-2 \end{array} \right) \left( \begin{array}{l} A_1 \\ A_2 \end{array} \right) = 0 \end{aligned}$$

(7.7)

Non-trivial solutions exist only if the determinant of the matrix is 0. We can solve the equations to obtain two dispersion relations between $\omega$ and $k$:

$$\begin{aligned} \omega _{\pm }^2 = C\left( \frac{1}{m_1} + \frac{1}{m_2}\right) \pm C \sqrt{\left( \frac{1}{m_1} + \frac{1}{m_2}\right)^2 - \frac{4\sin ^2 \left(\frac{1}{2}kd_0 \right) }{m_1m_2}} \end{aligned}$$

(7.8)

Fig. 7.4

Phonon dispersion (left) for a diatomic linear chain with the mass ratio $m2/m1 = 2$ and relative motion (right) of the atoms at $k = 0$

In the spectroscopically interesting region near $k = 0$ we can write the approximate solutions as

$$\begin{aligned} \begin{array}{rl} \omega _{-}^2&= \frac{C}{2 (m_1 +m_2)}k^2 d_0^2 \\ [6pt] \omega _{+}^2&= 2C\left( \frac{1}{m_1}+ \frac{1}{m_2} \right) \end{array} \end{aligned}$$

(7.9)

The $\omega _+$ solution has a finite frequency at $k = 0$ and, since this vibrational frequency can then be observed by optical spectroscopy, it is therefore known as an optical phonon. The solution $\omega _-$, which tends to $\omega =0$ at $k=0$ is called an acoustic phonon.

To examine the associated atomic displacements we substitute $\omega _+$ back into Eq. 7.7 to obtain a relation between the amplitudes of the two types of atom:

$$\begin{aligned} \frac{A_1}{A_2} = -\frac{m_2}{m_1} \end{aligned}$$

(7.10)

The two neighbouring atoms move with opposing directions (Fig. 7.4), their centre of mass being fixed: if the atoms have opposite charges, the motion creates a vibrating dipole, which can interact with electromagnetic radiation.

Conversely, for the frequency $\omega _-$, we find that $A_1 = A_2$ and all the atoms move coherently together: no dipole variation is possible.

7.2.2 Normal Modes in Vacuum and in Condensed State

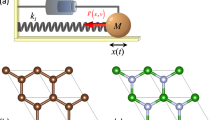
When it comes to molecular solids, it is useful to consider the coupling between the strong bonding within a molecule and the relatively weak intermolecular interactions. As an illustration, consider a model of a homonuclear diatomic molecule: two atoms of mass $m$ connected by a spring of elastic constant $k$ (Fig. 7.5). In a simple model of this molecule in the condensed phase, the atoms also interact with their surroundings (here, a pair of fixed walls) via additional bonds of spring constant $k_1$. This second system is equivalent to the isolated molecule when $k_1=0$.

Fig. 7.5

Simple system of a diatomic molecule. In the upper picture, two equal masses connected with a spring of elastic constant $k$. In the lower the same molecule interacts with fixed walls through springs of elastic constant $k_1$. The displacements $x_1$ and $x_2$ are indicated

The normal modes can be calculated by considering the system of equations

$$\begin{aligned} \begin{array}{rl} m \frac{\mathrm{d}^2 {x}_1}{\mathrm{d} t^2}&= k_1 x_1 + k \left( x_2 - x_1\right) \\ [6pt] m \frac{\mathrm{d}^2 {x}_2}{\mathrm{d} t^2}&= k_1 x_2 + k \left( x_1 - x_2 \right) \end{array} \end{aligned}$$

(7.11)

and looking for an oscillatory solution for the displacements:

$$\begin{aligned} \begin{array}{rl} {x}_1&= A_1 \exp {\left( \mathrm{i} \omega t \right)} \\ [6pt] {x}_2&= A_2 \exp {\left( \mathrm{i} \omega t \right)} \end{array} \end{aligned}$$

(7.12)

Substitution into Eq. 7.11, in matrix representation:

$$\begin{aligned} \left(\begin{array}{cc} k + k_1 - \omega ^2 m&k \\ k&k + k_1 - \omega ^2 m \end{array} \right) \left( \begin{array}{l} A_1 \\ A_2 \end{array} \right) = 0, \end{aligned}$$

(7.13)

which has non-trivial solution only if the matrix is singular. The solutions are:

$$\begin{aligned} \begin{array}{rl} \omega _1^2&= k_1 /m\\ [6pt] \omega _2^2&= \left(2k + k_1 \right)/m \end{array} \end{aligned}$$

(7.14)

In the case of a molecule in isolation ($k_1=0$) there is only one mode of vibration: stretching of the bond with frequency $\omega _2^2 = 2k/m$. For the constrained molecule interacting with the two walls, there is the same stretching mode, but at increased frequency $\omega _2^2 = (2k+k_1)/m$, and a second vibration at frequency $\omega _1^2 = k_1/m$ corresponding to translation of the whole molecule.

Depending on the strength of the intermolecular interactions, the absorption frequencies of intramolecular vibrations are always shifted to higher frequencies. This is sometimes enough for them to be shifted outside of the terahertz region. The new vibrational modes that are introduced as a consequence of interactions of a molecule with its surroundings correspond to whole-molecule motions. In two- or three-dimensional systems, these can involve molecular rotation as well as the translation seen in this simple 1D example.

7.2.3 Phonons in a 3D Crystal

The procedure to calculate the vibrational spectrum for a 3D crystal is a generalisation of what has been described in the previous sections: one main difference is that atomic displacements are now vectors. Furthermore, for real systems we must usually consider the interactions between all atoms, rather than the simplified nearest neighbour interactions that we used in the model systems.

To derive the equations of motion, we start from the potential energy of the crystal, $\phi$.

For small displacements we can expand the potential energy $\phi$ in a Taylor series up to second order in the displacement $u_\alpha ^{nl}$, the subscript $\alpha$ representing one of the Cartesian coordinates (x, y, z) of atom $n$ within the unit cell $l$:

$$\begin{aligned} \phi =\phi _0 +\frac{1}{2}\sum _{\alpha nl}\sum _{\alpha ^\prime n^\prime l^\prime } \left( \frac{\partial ^2 \phi }{\partial u_\alpha ^{nl} \partial u_{\alpha ^\prime }^{n^\prime l^\prime } } \right)_0 u_\alpha ^{nl} u_{\alpha ^\prime }^{n^\prime l^\prime }. \end{aligned}$$

(7.15)

where the subscript 0 indicates that the potential has been expanded about the equilibrium position. In the equilibrium configuration there are no net forces acting on the atoms, hence there is no linear term; $\phi _0$ is the equilibrium potential energy.

From here, we can write the equations of motion:

$$\begin{aligned} m_n \frac{\mathrm{d}^2 u_\alpha ^{nl}}{\mathrm{d} t^2} = - \sum _{\alpha ^\prime n^\prime l^\prime } \left( \frac{\partial ^2 \phi }{\partial u_\alpha ^{nl} \partial u_{\alpha ^\prime }^{n^\prime l^\prime } } \right) _0 u_{\alpha ^\prime }^{n^\prime l^\prime } = - \sum _{\alpha ^\prime n^\prime l^\prime }\phi _{\alpha \alpha ^\prime }^{nn^\prime (l-l^\prime )} u_{\alpha ^\prime }^{n^\prime l^\prime } \end{aligned}$$

(7.16)

Due to the translational invariance within a crystal, the force $\phi _{\alpha \alpha ^\prime }^{nn^\prime (l-l^\prime )}$ depends only on the distance between the unit cells $l$ and $l^\prime$, so we can drop the $l$ dependence and consider $l^\prime$ as the distance to a reference cell.

As in the previous section, we look for wave-like solutions of the form

$$\begin{aligned} u_\alpha ^{nl^\prime }= \frac{A_\alpha ^{n}(\mathbf k )}{\sqrt{m_n}} \exp \left( \mathrm{i} \mathbf k \cdot \mathbf r ^{l^\prime } -\mathrm{i} \omega (\mathbf k ) t \right), \end{aligned}$$

(7.17)

where the frequency depends on $\mathbf k$, which is now a vector (called the wavevector). Substitution into Eq. 7.16 gives

$$\begin{aligned} -\omega ^2(\mathbf k ) A_\alpha ^n(\mathbf k )&= \sum _{\alpha ^\prime n^\prime l^\prime } \frac{\phi _{\alpha \alpha ^\prime }^{nn^\prime l^\prime }}{\sqrt{m_n m_{n^{\prime }}}} A_{\alpha ^\prime }^{n^\prime }(\mathbf k ) \exp \left( -\mathrm{i} \mathbf k \cdot \mathbf r ^{l^\prime } \right) \nonumber \\&= \sum _{\alpha ^\prime n^\prime l^\prime } D_{\alpha \alpha ^\prime }^{nn^\prime l^\prime }(\mathbf k ) A_{\alpha ^\prime }^{n^\prime }(\mathbf k ) \end{aligned}$$

(7.18)

that are now a set of algebraic equations. $D(\mathbf k )$ is called the dynamical matrix, and is the mass weighted Fourier transform of the force matrix.

The equations are simplified if we consider only the phonons involved in the absorption of light ($\mathbf k = 0$): we can thus drop the exponential dependence in 7.18, leading to:

$$\begin{aligned} \omega ^2(\mathbf 0 ) A_\alpha ^n(\mathbf 0 ) = \sum _{\alpha ^\prime n^\prime l^\prime } D_{\alpha \alpha ^\prime }^{nn^\prime l^\prime }(\mathbf 0 ) A_{\alpha ^\prime }^{n^\prime }(\mathbf 0 ) \end{aligned}$$

(7.19)

This is an eigenvalue problem, composed of $3n_b$ equations, where $n_b$ is the number of atoms in the unit cell. It is possible to obtain both the eigenvectors $u_\alpha ^n(\mathbf k )$ and their associated frequencies $\omega (\mathbf k )$ by standard linear algebra techniques. Three (acoustic) phonons have a frequency $\omega =0$ at $\mathbf k = 0$: these correspond to bulk translation of all the atoms in the unit cell. The remaining $3n_b -3$ phonons are optical: they have non-zero frequencies and can interact with an electric field.

From the resulting eigenvectors $A_\alpha ^n(\mathbf 0 )$ it is possible to return to the atomic displacements $u_\alpha ^{nl}$ using the relation 7.17.

Terahertz intensities $I_N$ are directly correlated with the change in electric dipole moment $\mu$ of the system with respect to all of the atomic motions under excitation of a phonon mode $Q_N$:

$$\begin{aligned} I_N \propto \left| \frac{\mu }{Q_N} \right|^2 \end{aligned}$$

(7.20)

The calculation of how the cell dipole varies along each eigenvector depends on the computational method employed. If the electronic part of the system is not treated quantum mechanically (as in force field calculations and classical MD, see Sects. 7.2.4 and 7.3), the dipole variation is most simply evaluated from the rigid displacement of the atomic partial charges or multipoles.

In quantum mechanical methods (Sect. 7.2.5) the dipole has to be related to the perturbation of the electronic distribution by the normal mode displacement; to do so, the contribution of each of the $n$ atoms to the cell dipole variation is expressed using the Born effective charge tensor $\mathbf Z _n$, which is defined as the first derivative of the polarisation $\mathbf P$ per unit cell with respect to the atomic displacements $\mathbf u ^{nl}$:

$$\begin{aligned} Z_{n,\alpha \beta } \propto \frac{\mathrm{d} P_\alpha }{\mathrm{d} u_\beta ^{nl}} \end{aligned}$$

(7.21)

where $\alpha$ and $\beta$ indicate the Cartesian coordinates.

Once the lattice frequencies and associated absorption intensities are known, the spectrum can be simulated by assuming a peak shape for each absorption feature; it is common to express the spectrum as a sum of Lorentzian functions

$$\begin{aligned} f(x) = \sum _N{\frac{I_N}{\pi } \left( { \frac{\gamma }{(x - x_N)^2} + \gamma ^2 } \right)}, \end{aligned}$$

(7.22)

centred at the absorption frequencies $x_N$, whose relative intensity $I_N$ equals the area under the curve. The parameter $\gamma$ simulates the signal broadening of the experimental spectrum. Examples of this treatment are reported in Figs. 7.7 and 7.10.

7.2.3.1 Simple Parameterisation for Ionic Systems

It should be clear from the previous sections that, in order to perform a phonon calculation, we need a model for the forces acting between atoms within the system of interest. Various computational methods, with different degrees of approximation, have been applied to evaluate the required forces to model the vibrations in crystals.

One of the earliest calculations of the phonon spectrum of an ionic crystal was attempted by Kellermann [11] in 1940 for the simple cubic salt structure NaCl. This is a simple cubic crystal: each atom is located at the corner of a cube, and each Na$^+$ ion is surrounded by 6 Cl$^-$ neighbours (and vice versa). The system was treated as a field of interacting classical point charges held apart by a repulsive potential, $v_0$, between nearest neighbour atoms, which is necessary to keep the atoms at their equilibrium positions. It is not necessary to know the exact form of this potential, but only its behaviour near to the equilibrium position: the first derivative was calculated from the equilibration of forces within the crystal, knowing that the forces on all atoms in the crystal must vanish at the equilibrium structure. The second derivative of the interatomic potential was determined from experimental data on compressibility of the crystal.

From this model for the interatomic forces, a 6D (3D for each atom in the unit cell) dynamical matrix was then constructed and diagonalised. One of the two measurable frequencies of NaCl (two coinciding longitudinal optical phonons, LO) is in remarkable agreement with experimental data (Table 7.3), especially considering the simplicity of the model potential; the other (the transverse optical phonon, TO) is more dependent on the effects of charge displacements (polarisation), which were not included in this first model.

This method is simple enough to be performed on a simple system without the need for a computer (Kellermann produced a phonon spectrum for $\mathbf k \ne 0$ as well!), and has been repeated for a number of structurally equivalent alkali halides and oxides [12, 13].

Table 7.3 Phonon frequencies (THz) of the optical phonons of NaCl for $\mathbf k = 0$ by Kellermann compared with experimental values [14] and a calculation that includes charge displacement [15]

Unfortunately the model for the interactions between atoms here is too simplified to be generalisable to more complex solids. More sophisticated models have been addressed in a number of studies, considering models to account for polarisation of atomic charges [15, 16] and extended interactions beyond nearest neighbours [17]. Many more adjustable parameters must be introduced to the model of interatomic forces to account for these interactions, and the simplicity of the model is lost. Interesting systems usually consist of more than two atoms in the unit cell, so that many different atom–atom interactions must be considered. Furthermore, for crystals of electrically neutral molecules, the interactions between atomic charges are usually not the dominant attractive intermolecular interactions. Instead, a more realistic model of the van der Waals forces is necessary. Overall, it is generally necessary to calculate the phonon spectrum with the aid of a computer, by numerically evaluating the matrix of second derivatives from a detailed description of the forces acting within a crystal.

The quality of a molecular simulation depends on how well the interactions between atoms in the system are represented. Two types of approach have been applied to calculate the necessary forces:

• The atom–atom method: this is a generalisation of the approach used in the NaCl example given above. A functional form is assumed for the important interatomic interactions and these functions are parameterised to provide a description of the energy and forces within the crystal. The combination of functional form and parameters is often referred to as a force field. Electrostatic interactions in the atom–atom method are treated classically, usually by atomic partial charges, and sometimes with higher order atomic or molecular multipole expansions.

• Quantum mechanical electronic structure calculations: from the quantum mechanical point of view, all of the relevant forces ultimately arise from the electrostatic interactions between the electrons and nuclei. The electronic problem can be solved by separating the nuclear and electronic wavefunctions (the Born–Oppenheimer approximation) so that the energy and forces acting within a crystal can be calculated for any configuration of its constituent atoms. The most commonly applied electronic structure method in recent years is density functional theory (DFT) for which several software packages (see Sect. 7.2.5) are available to perform this type of calculation.

Electronic structure calculations on periodic systems are orders of magnitude more computationally expensive than those based on the atom–atom force field approach. The techniques necessary for DFT-based phonon calculations (density functional perturbation theory [18]), along with the necessary computational power, have only been available since the 1990s. While large-scale computing is nowadays common in research facilities, the cost of such calculations still limits their application to the crystal structures of fairly small molecules. For large systems, such as the crystal structures of pharmaceutical molecules with hundreds of atoms within the unit cell, the the atom–atom approach is still often the only practical solution. In the next two sections we describe these two approaches in more detail.

7.2.4 The Atom–Atom Potential (Force Field) Method

The quality of a molecular simulation depends on how well the interactions between atoms in the system are represented. The atom–atom potential method has been very successfully applied to modelling a wide range of materials, and some of the early development and applications are described by Pertsin and Kitaĭgorodskiĭ [19].

In most atom–atom calculations, there are three types of terms in the force field used to describe the interactions between atoms [19]: repulsion–dispersion; electrostatics and intramolecular terms.

• The repulsion–dispersion terms consist of a short-range repulsion, which arises due to unfavourable overlap of electron density as the internuclear separation between non-bonded atoms is decreased, and a longer range attractive term to model London dispersion forces. The two commonly used forms of the repulsion term are an $AR^{-n}$ term ($R$ being the interatomic separation), where $n$ is usually in the range from 9 to 14, or a theoretically better founded exponential, $A\exp {(-BR)}$. The attractive dispersion interaction between atoms arises from correlated fluctuations in the electron charge distribution around the atoms, the leading term of which corresponds to fluctuating dipole–dipole interactions and has an $R^{-6}$ dependence. $R^{-8}$ and higher terms arise from higher order correlated electron density fluctuations, but are less important and usually omitted. Thus, two common forms of atom–atom repulsion–dispersion terms are:

  $$\begin{aligned} \begin{array}{rl} U_{ik, \mathrm {repulsion-dispersion} }&= A^{\iota \kappa } R^{-n}_{ik} - C^{\iota \kappa } R^{-6}_{ik} \\ [6pt] U_{ik, \mathrm {repulsion-dispersion} }&= A^{\iota \kappa } \exp {\left(-B^{\iota \kappa } R_{ik}\right)} - C^{\iota \kappa } R^{-6}_{ik} \end{array} \end{aligned}$$

  (7.23)

  where $R_{ik}$ is the separation between atoms $i$ and $k$. These interactions are determined by the parameters $A$, $B$ and $C$, whose values depend on the types ($i$ and $\kappa$) of atoms involved.

• The electrostatic interactions arise because electronic charge is not spread uniformly within a molecule: its distribution can most simply be modelled by assigning fractional point charges to each atom in the molecule. The electrostatic interaction between point charges has the usual long range $R^{-1}$ dependence on interatomic separation and does not depend on the mutual orientation of the interacting atoms. However, some features of the electrostatic potential around molecules cannot be adequately modelled using such a simple spherical atom model. For example, localised lone pairs and aromatic $\pi$-electron density introduce important anisotropy in the electron charge distribution around atoms. Therefore, some atom–atom models include higher order multipoles (dipole, quadrupole, etc.) on each atom.

• Intramolecular potentials. While the repulsion–dispersion and electrostatic terms are used to model the interactions between non-bonded atoms, covalent bonding is treated by a separate set of terms. At its most basic, an intramolecular force field consists of bond stretching functions, usually modelled either as harmonic in the bond length or using a more realistic Morse potential form, 3-atom angle bending terms and 4-atom terms to model the torsional potential within four neighbouring atoms.

Force fields differ in which of the above terms are included, their exact functional form and how the parameters in each term are determined. These parameters depend on the types of atoms that are interacting and are often developed to be transferable between systems with similar chemical functionality, e.g. the parameters describing repulsion-dispersion interactions between carbon atoms might be fitted to model any carbon atoms in organic molecules. More elaborate parameter sets might include separate sets of parameters for carbon atoms in different chemical environments, such as different parameters for aromatic and aliphatic carbon atoms. The advantage of such transferable parameter sets is that there is no need to develop a new force field for each new system that is to be studied.

An example of this approach is the set of repulsion-dispersion parameters developed by Williams for hydrocarbons [20], oxygen [21], nitrogen [22] and fluorine containing [23] hydrocarbons. The parameters in such transferable force fields were fitted to reproduce structural parameters and heats of sublimation of a large set of molecular organic crystal structures and can therefore be used to describe a wide class of organic molecules.

An alternative approach to these transferable parameters is to develop and optimise specific force fields for a single molecule or small family of molecules [5, 24, 25], sometimes without the need to fit to experimental data. While such molecule-specific models involve much more work, the advantage is that the functional form and parameters can be fine-tuned to very accurately describe a particular molecule.

7.2.4.1 All-Atom Versus Rigid-Molecule Calculations

Having chosen a suitable force field, the construction of the dynamical matrix is performed by considering the forces generated by a series of perturbations about the equilibrium structure. In the all-atom approach, this involves evaluating the 2nd derivatives of the lattice energy with respect to translations of each atom in the unit cell in each of three orthogonal directions: the x, y and z directions in a globally defined axis frame. The resulting dynamical matrix will provide the entire vibrational spectrum of the crystal, including both the intramolecular vibrational modes (bond stretching, angle bending, etc.) and the lattice modes, which are dominated by overall translation and rotation of molecules about their equilibrium positions. It is the latter types of modes that dominate the terahertz region (from 0 to 5 THz). Indeed, despite the number of studies calculating the vibrational spectra of molecular crystals, the interest has often been on the intramolecular frequencies that are more easily accessible by infrared and Raman spectroscopy, with the calculation of the vibrational frequencies in the terahertz range arising as a “by-product” of the calculations.

Developments allowing better experimental access to high quality spectra in the terahertz frequency range has prompted more interest in calculations aimed at characterising the vibrational modes in this region. One commonly employed simplification in these calculations has been the rigid-molecule approach, which takes advantage of the fact that intermolecular and intramolecular interactions often act on very different strength scales; the geometry of small molecules in their crystal structures is often unchanged from their gas phase geometry, indicating that the intermolecular forces in the crystal are much weaker than the intramolecular forces that dictate the molecular geometry. The rigid-molecule approximation assumes that inter- and intramolecular interactions are completely uncoupled, so that all of the intramolecular force field terms can be ignored when calculating the lattice mode region of the vibrational spectrum. Furthermore, the relative positions of atoms within a molecule can be kept fixed, so that the only relevant perturbations from the equilibrium structure are overall molecular translations and rotations.

Thus, in the rigid-molecule approximation, the lattice dynamical equations are reformulated such that the dynamical matrix (Eq. 7.18) refers to molecular centre-of-mass displacements and rotations about molecular moments of inertia rather than atomic displacements. Rigid-molecule lattice dynamics is fully described by Walmsley [26] and Califano [5]. This approach can dramatically reduce the dimensionality of the dynamical matrix and lowers the computational cost of the calculation; for a crystal structure with $Z$ molecules in the unit cell, rigid-molecule lattice dynamics leads to $6Z$ vibrational modes at $\mathbf k = 0$, three of which are the acoustic translational modes with $\omega = 0$ at $\mathbf k = 0$.

The rigid-molecule approximation is clearly most appropriate when there is a large separation between the lowest energy intramolecular vibrational frequency and the highest energy of these $6Z$ intermolecular vibrational modes, which are typically found in the range from just under 1 THz to about 5 THz (or from approximately 30 to 160 cm$^{-1}$). If the separation in frequency is large, then coupling of the two types of motion should be small.

7.2.5 Quantum Mechanical Electronic Structure Calculations

The basic requirement to be able to perform a calculation of the electronic structure is the separation of the nuclear coordinates from the electronic coordinates, using the Born–Oppenheimer approximation. Under this assumption the calculation of the electronic wavefunction of a crystal can be viewed as a system of interacting electrons in a field of nuclei. The equilibrium geometry of the crystal is the configuration where there is no net force acting on each nucleus, and can be found by performing a minimisation of the energy of the crystal with respect to the coordinates of the nuclei.

The forces necessary to build the dynamical matrix can be obtained by distortion of the nuclear equilibrium structure: moving an atom away from the equilibrium position generates a restoring force that does not depend only on the equilibrium electronic distribution, but on its variation as well [27], due to the parametric dependence of the electron wavefunction on the nuclear perturbation. The generation of the dynamical matrix thus needs the calculation of the electronic density (a computationally expensive task) for a high number of nuclear configurations, and this contributes to the significant computational cost of such a calculation. The calculation of the electronic charge distribution is usually performed using density functional theory (DFT). Hohenberg and Kohn [28] proved that only the electron density (rather than the wavefunction) is necessary to describe the ground state of a system. Furthermore, for a system of interacting electrons in an external potential $V$ (such as the potential generated by the atomic nuclei in the crystal) there exists a universal functional $F$ of the electron density $n$, independent of the external potential, such that the energy $E$ is defined as

$$\begin{aligned} E[n] = F[n] + \int V[\mathbf r ] n[\mathbf r ] \mathrm{d}\mathbf r \end{aligned}$$

(7.24)

Unfortunately, the theorem proves only the existence of the functional, not its exact form. A practical approach, suggested by Kohn and Sham [29], is to express the functional as a sum of physically recognisable contributions: it is the exchange–correlation potential that is unknown, but possible to approximate. Therefore, many functionals have been suggested and tested for their ability to reproduce the geometries, energies and properties of molecules and crystals. The simplest form, the local density approximation (LDA), relates the energy to the value of the electron density at each point in space. This approach is exact in the limit of a slowly varying electron density, so correctly describes weakly correlated systems such as semiconductors, but fails to describe complex systems where the potential varies more drastically. More elaborate functional forms have been developed through the years, containing dependence on the gradient of the electron density (generalised gradient approximations) and by including the exact exchange energy from Hartree–Fock wavefunction calculations (hybrid functionals, such as the very popular B3LYP functional). The main limitation in current functionals is their unsatisfactory description of the dispersion attraction between molecules, which is often the dominant contribution to the stability of organic molecular solids. DFT-based lattice energy minimisation of molecular organic crystals usually leads to unrealistic unit cell dimensions because, although the intramolecular bonds are treated correctly, intermolecular interactions are typically underestimated. As an example, the unit cell volume of the explosive material RDX, modelled with the PBE functional [30, 31] gives an energy-converged unit cell with a 20 % larger volume than the experimentally determined unit cell. As this structural distortion relates to large changes in intermolecular contact distances, calculated frequencies of vibrational modes in the terahertz region cannot be accurately modelled in such an energy-minimised structure. A common workaround when applying DFT to organic solids where the dispersion attraction is dominant is to avoid the optimisation of the unit cell, constraining the lattice vectors to their experimentally determined values (see column a in Table 7.6). A more satisfactory solution to the dispersion problem in DFT is to supplement the functional by a set of parameterised atom–atom $\rm R ^{-6}$ terms of the same form as those included in force fields, leading to methods known as DFT-D [32]. These added terms add very little to the computational cost over pure DFT [31]. However, as with force fields, the parameterisation of these terms is not unique and different parameters are required to correct different functionals.

7.2.5.1 Basis Set and Implementation

In practice, the electronic density in a DFT calculation is expanded as a linear combinations of basis functions, with the expansion coefficients to be determined as a part of the calculation. While an infinite number of basis functions might be necessary for mathematical completeness, the number of basis functions that can be included in a calculation is finite. In order to control the resulting finite basis set errors, the choice of basis functions is crucial.

There are two classes of functions commonly employed, each with advantages and drawbacks; we briefly describe them here, along with some of the software packages that employ them²:

• Localised basis set: basis functions are centred at points in space, usually around the nuclei of each atom, and the functions vanish as the distance $\mathbf r$ to the nucleus tends to infinity. Thus, the number of basis functions required for a calculation scales linearly with the number of atoms in the unit cell. The two frequently implemented choices of localised basis functions are the atomic-like, Slater-type, orbitals and Gaussian-type orbitals. Atomic-like orbitals, with a $\exp (-\zeta \mathbf r )$ radial dependence, represent the best approximation of a real wavefunction in the long range limit: only few functions are necessary to achieve a good description of an atomic orbital. The packages DMol$^3$ [33] and SIESTA [34] use numerically fitted atomic orbitals obtained from solutions of the single atom problem, so that the functions represent the correct radial dependence. The main advantage of this method is its fast convergence with the number of basis functions; on the other hand dealing with this kind of wavefunctions is numerically complex, and there are difficulties in the assessments of how the convergence behaves with larger basis sets [35]. The advantage of Gaussian wavefunctions, used for example in the CRYSTAL package [36], lies in their mathematical properties: the solutions of integrals involving two or more Gaussian functions (one of the main computational tasks to be performed in electronic structure calculations) are easily expressed as combinations of other Gaussian functions centred at a different point. The ease in the manipulation in these functions comes at a cost: the difference in the behaviour of these function from true atomic orbitals both in the short range, with a smooth behaviour at $\mathbf r =0$ instead of a cusp, and in the long range, where they behave as $\exp (-\xi \mathbf r ^{-2})$ instead of the correct $\exp (-\zeta \mathbf r )$, means that linear combinations of large numbers of Gaussian basis functions are needed in order to achieve a good representation of the true electron density.

• Plane wave basis sets: each basis function is a plane wave function $\exp (\mathrm{i} \mathbf k \cdot \mathbf r )$, whose periodicity makes them natural solutions for periodic systems. Furthermore, the simple mathematical form and the relation between $\mathbf k$ and the kinetic energy provides a straightforward approach to systematically improving the basis set completeness, by including higher kinetic energy plane waves until the calculated properties of interest converge to the required level. Among the disadvantages of plane waves are their poor description of localised states (it is necessary to introduce pseudopotentials for the description of tightly bound core electrons) and the dependence of the basis functions on the dimensions of the unit cell. The latter means that large changes in the unit cell volume on energy minimisation will change the kinetic energy cutoff and therefore the consistency of the calculation. The plane wave approach is implemented in codes CASTEP [37] and VASP [38].

Fig. 7.6

Molecular structures of benzene, pyrazine, imidazole, carbamazepine and benzoic acid

7.2.6 Example Calculations

7.2.6.1 Atom–Atom Potential Results

First, we examine the influence of the rigid-molecule approximation, as described in Sect. 7.2.4. Benzene, C$_6$H$_6$ (Fig. 7.6), is a prototypical example of a rigid molecule for which the rigid-molecule approach should be appropriate; there is nearly a 300 cm$^{-1}$ gap between the highest frequency lattice modes at around 130 cm$^{-1}$ and the lowest frequency intramolecular vibrations at around 400 cm$^{-1}$. Taddei et al. [39] examined the influence of the rigid molecule approach on the calculated lattice dynamics of crystalline benzene (Table 7.4). Their study found that coupling of intramolecular modes to the lattice vibrations has a negligible effect on the calculated displacement coordinates associated with the lattice modes, and the effect of allowing coupling of intramolecular vibrations is to lower the frequencies of the lattice modes by 1–3 cm$^{-1}$. This effect is small compared to differences in calculated frequencies with different parameter sets for the interatomic potentials. Errors resulting from the rigid-molecule approach become more significant with increasing molecular size. Naphthalene, C$_{10}$H$_8$, has a significantly smaller gap of approximately 50 cm$^{-1}$ between the lowest intramolecular mode and highest lattice mode frequencies. Pawley and Cyvin [40] calculated differences between all-atom and rigid-molecule phonon frequencies for crystalline naphthalene, finding that coupling to intramolecular modes typically lowers the lattice mode frequencies by about 5 cm$^{-1}$, and by up to 10 cm$^{-1}$ for some lattice modes. These errors are now significant in comparison to errors in the experimental measurements and variations that are found between atom–atom parameter sets. The errors resulting from the rigid-molecule simplification become more severe for molecules with rotatable single bonds, where vibrational frequencies of the free molecule are likely to overlap with the frequency range of the lattice modes. The coupling might not influence all calculated lattice modes equally. For example, Li et al. [41] found that the torsional intramolecular vibration about the exocyclic C–C bond in benzoic acid strongly influences the lattice modes corresponding to molecular rotations about that molecular axis. However, the remaining molecular rotations and translations are satisfactorily modelled in the rigid-molecule approximation.

Table 7.4 Comparison of observed low temperature infrared [42] and Raman [43] with calculated $\mathbf k = 0$ lattice mode frequencies of crystalline benzene ( cm$^{-1}$)

Next, we examine the sensitivity of the calculated lattice mode frequencies to the form and parameterisation of the intermolecular atom–atom potential. Taddei [39] found that the calculated lattice mode frequencies of benzene are very sensitive to the parameters of the $\exp -6$ atom–atom potential; changing from Williams’ [20] parameters, which were fitted to the crystal structures of aromatic hydrocarbons, to Williams’ [44] parameters, which were fitted to both aliphatic and aromatic hydrocarbon crystal structures, resulted in a mean absolute change of 8 cm$^{-1}$ in the lattice mode frequencies, with individual frequencies shifting by up to 17 cm$^{-1}$. Even for such a simple molecule, the choice and validation of the force field parameters is very important. For crystalline benzene, the results shown in Table 7.4 demonstrate that adequate lattice dynamics results can be obtained using a repulsion–dispersion model with no model of intermolecular electrostatic interactions. However, many molecules of interest contain polar functional groups, leading to a greater importance of electrostatic contributions to intermolecular interactions.

Table 7.5 Sensitivity of calculated lattice mode frequencies (in cm$^{-1}$) of crystalline imidazole to the intermolecular model potential, using the lattice dynamics method

Take imidazole (Fig. 7.6) as an example, where the rigid molecule approach should again be appropriate: imidazole molecules are aligned in the crystal structure so as to form infinite chains of N–H$\cdots$N hydrogen bonds. Neighbouring chains are antiparallel aligned and interact via C–H$\cdots$N contacts, which could also be described as weak hydrogen bonds. Hydrogen bonds are largely electrostatic in nature and, as a result of their prevalence in this crystal structure, the electrostatic contribution to atom–atom interactions contributes approximately 60 % of the total lattice energy of the crystal [52]. Calculated rigid-molecule lattice mode frequencies using a range of atom–atom potentials are given in Table 7.5, along with low temperature observed frequencies from Raman and far-infrared spectroscopy. The UNI, FIT and W99 are different parameterisations of the $\exp -6$ functional form for repulsion-dispersion interactions. The UNI model was developed so that electrostatic effects are absorbed into the parameters of the $\exp -6$ terms, so was used without an explicit electrostatic model. FIT and W99 were each paired with atomic partial charge and atomic multipole (DMA) electrostatic models. The UNI model performs remarkably well, given its simplified functional form; the largest errors are a result of underestimating the frequencies of vibrational modes that bend the N–H$\cdots$N hydrogen bonds, and those that twist the molecules about the hydrogen bond axis. Frequencies of hydrogen bond bending and twisting vibrations are also underestimated using the atomic point charge electrostatic models, but these motions are significantly stiffened when atomic charges are replaced by multipole expansions. Indeed, with the multipole models, vibrational frequencies of the bending modes are largely overestimated. The vibrational modes that lead to minimal distortion of the strong N–H$\cdots$N hydrogen bonds are relatively insensitive to the potential used in the calculations.

Results reported using the same set of atom–atom potentials for crystalline pyrazine demonstrate that the electrostatic model can have even more dramatic effects on the lattice dynamics of polar molecules that lack strong hydrogen bonds [52]. Pyrazine molecules interact via weak C–H$\cdots$N hydrogen bonds in the crystal structure and the electrostatic contribution is less dominant than in imidazole (contributing about 35–40 % of the lattice energy). However, the electrostatic model is found to be even more important in determining the lattice dynamics of the crystal: the restoring force for motions that bend the weak C–H$\cdots$N hydrogen bonds is almost entirely due to dipole–dipole and higher order electrostatic interactions [52, 54]. In fact, with the simplest atomic charge electrostatic model, the crystal structure is unstable to such molecular motions, resulting in non-physical negative values for the eigenvalues ($\omega ^2$) of the dynamical matrix.

Using the most successful atom–atom potentials, the absolute errors in calculated frequencies are not large: for imidazole, most are predicted to within 10–15 cm$^{-1}$. However, the low symmetry of most molecular crystals leads to many distinct $\mathbf k = 0$ lattice modes and the frequency range in which these are found is fairly narrow. Therefore, a one-to-one assignment of calculated and observed frequencies will often not be possible based on the absorption frequencies alone. In attempting to assign spectral features to calculated vibrational modes, it can be helpful to consider the absorption intensities from the dipole transition along each calculated vibrational mode (Eq. 7.20). These intensities can vary greatly between modes, as shown in the terahertz spectra of two of the polymorphs of carbamazepine (Fig. 7.7). In the case of the thermodynamically stable polymorph (form III, a and b in Fig. 7.7), the calculated intensities reproduce the observed relative peak intensities very well, giving confidence in assigning specific calculated normal modes to the observed features. In this case, the features could then be characterised in terms of the type of distortion of the hydrogen bonding in the crystal [55]. In the case of carbamazepine form I (c and d in Fig. 7.7), the crystal is of a particularly low symmetry, leading to a very crowded terahertz spectrum; in this case, even with calculated absorption intensities, it would not be possible to make a confident one-to-one assignment of calculated lattice modes and observed features. Nevertheless, the calculations are still useful for describing the types of molecular vibrations associated with each region of the spectrum.

Fig. 7.7

Comparison of calculated (a, c) and observed (b, d) terahertz spectra of two crystal forms of carbamazepine (Fig. 7.6). (a) and (c) show the lattice dynamics calculated spectra of polymorphic forms III and I, respectively, using the FIT–DMA atom–atom potential described in the text. Vertical lines indicate the normal mode frequencies, with heights scaled by the calculated absorption intensities. The dashed lines represent the simulated spectrum, assuming a Lorentzian line shape with a line width of 2 cm$^{-1}$. (b) and (d) show the $\text{ T}=7\text{ K}$ observed terahertz spectra for forms III and I, respectively. (oop = out-of-plane). Adapted with permission from [55]. Copyright 2006 American Chemical Society

Fig. 7.8

Molecular structures of RDX, ketamine and naproxen

Fig. 7.9

Phonon dispersion relation of MgO calculated with a CASTEP calculation on a 2$\times$2$\times$2 supercell, compared with neutron diffraction data (open symbols) and infrared reflectivity data (stars). Reproduced from [56] with permission from Elsevier

Fig. 7.10

Comparison of DFT lattice dynamics calculated (black lines) terahertz spectra of MDMA$\cdot$HCl (see Fig. 7.1) using different exchange–correlation functionals with the experimentally observed absorption from a powdered sample of the crystal (blue lines). All calculations were performed within a unit cell fixed at the experimentally determined T $=$ 161K dimensions. The calculated plots are generated by fitting the absorption frequency using a 7 cm$^{-1}$ Lorentzian line shape. Adapted with permission from [57]. Copyright 2010 American Chemical Society

7.2.6.2 Density Functional Theory Results

Density functional theory calculations have been applied to model the phonon modes of several classes of material such as salts, semiconductors, oxides and molecular organic crystal: general considerations and systems are reported in Baroni’s review on density functional theory [58]. For simple systems (such as—see Fig. 7.9), it is possible to routinely achieve nearly perfect agreement between calculated and observed phonon spectra. The same excellent agreement is found for minerals such as forsterite (Mg$_{2}$SiO$_{4}$), for which the calculated vibrational frequencies differ from measured absorption frequencies by at most 4 cm$^{-1}$ [59]. For more complex materials, when the dispersion forces become relevant, the agreement between calculated and measured frequencies is less reliable. Recent articles directly calculating terahertz spectra of organic molecular crystals have mainly been inspired by applications of terahertz technology for monitoring polymorphism in pharmaceuticals and detection of explosives.

There are a number of studies where it is possible to see the difference in calculated spectra associated with different exchange correlation functionals and basis set types. For example, the explosive material RDX (Fig. 7.8) has been studied using different DFT methods: Allis [60] and Ciezak [61] with atom-centred basis sets using DMol$^3$; Miao [62] studied the same material using plane-wave basis set calculations using VASP and Shimojo [31] applied dispersion corrected functionals. Some of these results are summarised in Table 7.6; the lattice dynamics calculations provide good agreement with the observed spectrum, while variations in calculated frequencies associated with different choices of functional, basis set and the inclusion of dispersion-correction terms to the DFT are mostly on the order of about 5–10 cm$^{-1}$. These differences between methods range up to 20cm$^{-1}$ or more for some of the higher frequency vibrations. Overall, these variations are similar in magnitude to the differences between parameter sets and electrostatic models seen with force field based calculations.

Korter et al. have also performed studies to investigate the dependence of lattice dynamics results on the exchange–correlation functionals, considering the drugs MDMA hydrochloride [9] and ketamine [57]. These studies have provided insight into the subtle dependences of calculated spectra on the DFT methods employed. One of the most important observations from their study of MDMA hydrochloride was that the number of normal modes calculated within the 0–100 cm$^{-1}$ range (counting both terahertz active and inactive modes) is not constant, varying from as few as 18 modes in this range using the RPBE functional to as many as 23 using the BLYP functional. Furthermore, it can be seen from a visual inspection of Fig. 7.10 that the calculated intensity of absorptions of similar frequency have high variability with choice of DFT functional, which is a warning sign that the calculated eigenvectors, which describe the atomic displacements associated with each mode, differ significantly from one calculation to another. These two factors lead to significant differences between the predicted spectra from different functionals; in this case, the BP and BOP functionals provided the best agreement with experimental data. This example shows that, even using a potentially very accurate electronic structure method to calculate the lattice dynamics, a poor choice of DFT functional can have dramatic effects on the quality of the simulated spectrum.

Table 7.6 Terahertz calculated absorption frequencies ( cm$^{-1}$) for RDX with various methods

The use of a dispersion correction removes the need to constrain the unit cell to experimentally determined dimensions during the structural minimisation task of a DFT calculation, since effective dispersion correction terms should maintain a realistic unit cell during an unconstrained lattice energy minimisation. For RDX (Fig. 7.8) the effect of the dispersion correction to DFT is to provide agreement of the unit cell volume to within 1 %, without significant increase of the computational cost over pure DFT [31]. The resulting absorption frequencies calculated at the minimised structure are shown in Table 7.6 and show overall excellent agreement with experimentally determined frequencies. It is to be noticed that the choice of the dispersion correction parameters is not unique and can have a dramatic effect on the final results. For example, King [63] performed a series of calculations on naproxen (see Fig. 7.8) showing that, for this system, the dispersion correction implemented in the CRYSTAL09 code [36] generates a 10 % contraction in the unit cell when used with the PBE functional, an error which is almost equal in magnitude to the uncorrected PBE calculation, which results in +12 % volume expansion. It was demonstrated that a fine-tuning of the coefficients is capable of providing agreement within 2.23 % of the experimental low temperature unit cell parameters and excellent agreement with the experimental spectrum (see Fig. 7.11). This result was obtained by rescaling of the dispersion coefficients by a factor 0.52.

More results are shown in the next section, together with MD calculations.

Fig. 7.11

Naproxen simulated spectrum with optimised dispersion parameters (A) compared with low temperature terahertz measurement. From [63]. Reproduced by permission of the PCCP Owner Societies

7.3 Molecular Dynamics

MD is a computational technique that can be used to model the evolution of a system through time. This is performed through the numerical integration of the Newtonian equation of motion arising from the interactions between the particles, starting from an initial configuration: the final result is a collection of snapshots of the atomic configuration, taken at discrete time steps. According to statistical mechanics, physical quantities are obtained through an average over a high number of configurations of the atoms in the system, and the effectiveness of a MD simulation lies in the number (and the completeness) of configurations sampled in the trajectory. The main advantage over lattice dynamics is that anharmonicity and the temperature-dependence of vibrational frequencies is automatically included, while MD suffers from much longer computational times and more complex analysis required to extract vibrational frequencies from the atomic trajectories.

For the calculation of the absorption spectrum of a crystal, it is sufficient to follow its vibrational dynamics around an equilibrium structure. The properties of a crystal can be calculated by assigning random velocities to the atoms near their equilibrium lattice positions, to wait for the equilibration of the system, after which the configuration of the system will evolve, oscillating through time. Initial velocities need not be so high as to break equilibrium conditions, or to introduce interactions that cause instability of the system, and are chosen to provide the final temperature (related to the total kinetic energy) of interest. MD can be performed with controls placed on a number of other macroscopic properties such as pressure, volume and total energy of the system. Apart from thermodynamic controls, the time step chosen to evolve the system is crucially important: the time scale needs to be smaller than the characteristic time associated with vibrations, which is typically in the range of femtoseconds, and the number of steps has to be big enough to sample all of the vibrations on the system.

It is customary to make use of the periodicity of the crystal within MD calculations by use of periodic boundary conditions: the motion of all atoms within a supercell of the unit cell of the crystal structure are treated explicitly. The positions and displacements within this supercell are replicated in all directions, so that each translational copy of an atom has the same velocity as that in the reference cell. Periodic boundary conditions can generate artefacts in the MD calculation if an atom interacts with a copy of itself; for this reason it is generally suggested to consider a supercell large enough that no atom interacts with its image via short range interactions.

As with the lattice dynamics method, a correct description of the dynamics of a system cannot be achieved without a proper handling of the forces acting between atoms. The interactions within a crystal can be computed using electronic structure methods such as DFT, or force fields, as discussed in Sect. 7.2.3.1. However, electronic structure MD methods, developed by Car and Parrinello [64] are so demanding on computational time that, at the moment, they can be used only for crystals with small unit cells (see [65] for an example); furthermore smaller time-steps are needed to account for the dynamics and the rearrangement of the electron density, which is much faster than that of the ions, and requires even smaller time steps, adding to the computation cost.

Fig. 7.12

CASTEP ab initio molecular dynamics simulations of the terahertz absorption of an ammonia crystal at 160 K. The effect of the length of the simulation (Blackman window in the graph) is considered. Reprinted with permission from [65]. Copyright 2008 American Chemical Society

We refer to Sect. 7.2.4 for details on force fields; we can add here that there are a huge number of force fields that have been applied in MD studies of organic molecules, mostly relating to studies performed in the protein and macromolecule community: as a non-comprehensive list we can mention, among others MM2 [66] and CFF [67] force fields, used for small organic molecules; CHARMM [68] and GROMACS [69], for biomolecules and macromolecules; and UFF [70], with parameters for elements up to the actinoids. Furthermore, as mentioned previously, it is possible to generate and fine-tune a force field specifically designed to apply to a specific system, either where a well-developed force field does not exist or to improve the accuracy of an older force field [71]. Once the trajectory of atoms or molecules in a structure has been generated over a long enough time scale, the information about the vibrational motion of the molecules is contained in the autocorrelation functions: mathematical tools to determine patterns of a function that repeat in time. For a property $v$, the autocorrelation function, is defined as the time average of the product of that property’s value at a particular time with the value at a time origin, $t_0$:

$$\begin{aligned} A(t) = \left\langle v(t_0)v(t_0+t)\right\rangle , \end{aligned}$$

(7.25)

The brackets indicate an average over all configurations separated by a time interval  $t$.

The autocorrelation function is easy to understand if we consider an example with atoms within a crystal all oscillating with an oscillatory movement of period $\tau$. If the time $t$ is not an integer multiple of $\tau$ the average over all configurations will be zero, while when t is a multiple of the vibrational period, $\tau$, the function $v$ will take on the same value at all pairs t and $(t + \tau )$ and the autocorrelation function will be non-zero. For a complex trajectory, the autocorrelation function extracts only the periodic part of the whole movement, with a weight proportional to its contribution. The Fourier transform of the autocorrelation function gives the frequency spectrum: an example showing calculations on crystalline ammonia is shown in Fig. 7.12. Again, to have a faithful representation of the slowest vibrations, the total simulation time needs to be long enough, while the time steps used in the MD simulation must be short enough to reproduce the fast vibrations. The absorption spectrum is obtained from the electrostatic dipole autocorrelation function.

Information about the eigenvectors can be extracted from the velocity autocorrelation function, noting that (since the simulation tries to sample all microscopic states) the Fourier transform produces the spectrum of all phonon states ($\mathbf k \ne 0$ as well). The number of $k$ points sampled in a calculation depends on the size of the supercell used: larger cells provide a denser sampling of $k$ points, as well as a better description of the dynamics of the system. It is possible to separate $k$ points by considering the different phase of velocity for equivalent atoms in different cells: for atoms at positions $r_1$ and $r_2$, separated by a distance $\mathbf R$, the relation between the velocities $v$ is

$$\begin{aligned} v_2 = v_1 \exp {\left(\mathrm{i}\mathbf k \cdot \mathbf R \right)} \end{aligned}$$

(7.26)

As a result, by a summation over all equivalent atoms with constraints dictated by the relation in their velocities, it is possible to sort out the $\mathbf k = 0$ phonons we are interested in for optical spectroscopy (see [72] or [53] for details of the procedure). Once the frequencies and their dispersion with $\mathbf k$ are known, it is possible to extract the associated atomic displacements associated with each vibrational mode from the trajectory.

Table 7.7 Calculated NH$_3$ absorption frequencies ( cm$^{-1}$) from Car Parrinello molecular dynamics and DFT lattice dynamics

Where direct comparisons have been made between the results of lattice dynamics calculations and phonon frequencies extracted from MD, the agreement between the two methods is generally very good. Table 7.7 shows DFT-based results for crystalline ammonia. MD frequencies are in fairly good agreement with those from lattice dynamics calculations, although calculations using the same DFT functional (PW91) find that frequencies from lattice dynamics are shifted to higher frequencies by 15–30 cm$^{-1}$ compared to those from MD; this frequency shift could be attributed to the harmonic approximation applied in the lattice dynamics approach, while also possibly being influenced by differences in the basis sets used in the two calculations.

Rigid-molecule force field based results for imidazole (Table 7.5) also show good agreement between the MD and lattice dynamics approaches: frequencies calculated using the exact same force field (FIT–DMA) agree to within about 5 cm$^{-1}$ and molecular displacements determined from the MD analysis were also reported to be in very good agreement with the eigenvectors calculated from lattice dynamics [53]. Here, the frequency shifts can be directly related to the influence of anharmonicity and we find that the frequencies extracted from MD trajectories are mostly shifted to lower frequency. Interestingly, this shift was found to relate to the influence of the vibration on the hydrogen bonds in the crystal structure: hydrogen bond stretching modes are shifted to lower frequency by anharmonicity, while hydrogen bond bending modes are either unaffected or, surprisingly, shifted to higher frequencies in the MD simulation.

7.4 Conclusions, Summary and Limitations of the Methods

The phonon modes in crystals correspond to collective oscillations of the atoms in the structure. For molecular crystals, the vibrational modes in the terahertz region are largely due to whole molecule motions about their equilibrium positions, including both translational and rotational oscillations of the molecules. Therefore, these modes are very sensitive to the interactions between molecules, making terahertz spectroscopy a powerful probe of the intermolecular forces in crystals. However, the origin of the features observed in experimentally determined spectra are difficult to interpret without the aid of modelling methods. The methods available for simulating the vibrational spectra of crystals are lattice dynamics and MD, either of which can be based on atom–atom (force field) or electronic structure methods, whose main limitations and strengths are summarised below.

7.4.1 Force Fields Versus Electronic Structure (DFT) Calculations

The lattice dynamics approach performed within a force field framework was historically the first to be implemented, thanks to the lesser computational requirements compared with a DFT calculation, allowing the fast calculation of the lattice modes of systems with hundreds of atoms within the unit cell. For example, force fields have been used to the calculate the spectrum of a chain of the protein ricin, with a molecular mass in excess of 20,000 Dalton and with more than 300 vibrational modes in the narrow frequency range from 2 to 50 cm$^{-1}$ [73]. Such a system is currently intractable using electronic structure-based methods. The same holds for MD: force field MD has been used to calculate the terahertz spectrum of opsins (proteins responsible for the absorption of light in the eye), weighing around 40,000 Dalton, where it has even been possible to consider the effect of a hydration shell around the molecule [74].

The most important limitation in force field methods is often in the accuracy of the description of the electronic interactions, which is necessarily approximate and usually limited to fixed atomic partial charges. Furthermore, the effectiveness of a general force field is often related to the similarity of the system under study with the systems to which the force field has been parameterised. Ad hoc, non-empirically derived force fields, while potentially more precise, can take considerable time to be developed and are typically limited to small molecules. On the other hand, DFT results are also sensitive to the choice of functional. DFT calculations are potentially very accurate and should provide a better description of the covalent, intramolecular interactions within a molecule. However, current functionals poorly describe the intermolecular van der Waals interactions between neutral organic molecules. Therefore, such calculations need to be corrected by an atom–atom dispersion correction term.

7.4.2 Lattice Dynamics Versus Molecular Dynamics

Of the two, lattice dynamics is by far the simpler and less computationally demanding method for simulating the lattice modes in crystals. The main advantage of a MD calculation is the flexibility of the method: it is possible to perform calculations at different temperatures, considering the effect on the spectrum explicitly. Furthermore, through the treatment of the vibrations at finite temperature it is possible to include the anharmonicity of the crystal in a natural way. In contrast, lattice dynamics calculations are often limited to a harmonic treatment where the results of the calculation formally relate to zero kelvin.

MD methods may also be applied to non-periodic systems, allowing predictions of the spectra liquids [75] or disordered materials. A related disadvantage of the MD method is that the crystal symmetry cannot be enforced in the simulation, so that it might therefore be difficult to assign the correct symmetry of the normal modes of vibration; in lattice dynamics, symmetry analysis of the lattice modes is straightforward. Lattice dynamics can also be more readily extended to include the effect of long range electrostatic forces, while are known to break the degeneracy (and therefore change the frequency) of some of the normal modes in polar crystals: this effect is known as LO-TO splitting [76].

7.4.3 General Problems to Address

The examples included in this chapter show that the lattice dynamics and MD approaches can give good agreement with the observed frequencies of lattice vibrational modes, and are thus powerful methods for understanding the underlying molecular vibrations that lead to observed features in terahertz spectra. A large focus of work for improving these methods is the development and fine-tuning of the methods used to calculate the interactions in the structures. Apart from further improvements to our force field or electronic structure-based energy models, we also highlight several further effects that should be considered when simulating the spectrum of a crystal using the methods described in the previous sections. These relate to the fact that the computational methods are generally applied to infinite, perfect crystal structures, while real measurements are affected by imperfections and the finite size of the crystals being studied. Among others, we can mention:

• Surface effects, resulting from the finite size of the sample;

• the microcrystalline nature of samples;

• and disorder or impurities in crystal.

7.4.3.1 Surface Effects

It is currently not possible to account accurately for the finite size of the crystal on a measured spectrum: lattice dynamics methods assume an infinite, periodic structure, while MD methods cannot deal with a large enough number of atoms to form a macroscopic crystal. The most significant deviations from the infinite crystal theory occur when the dimension of the crystal are comparable to the wavelength of light.

It is possible to consider finite size effects for very simple crystals. Similarly to what we described in Sect. 7.2.3.1, Ruppin and Englman [77] considered the case of a cubic crystal of finite size and simple structure, introducing the conditions imposed by Maxwell’s equations for travelling light into the lattice equations. The results of this treatment are polariton modes: mixed modes with both phonon and photon contributions, that describe the propagation of radiation inside the crystal. These polariton modes may be either non-radiative (where the intensity decays outside the crystal) or radiative (where the intensity does not decay, and can therefore be detected).

The vibrational modes can be further classified according to their behaviour inside the crystal: in bulk modes, the vibration occurs across the entire crystal, while the motions associated with surface modes decrease exponentially away from the surface of the sample into the bulk. The bulk frequencies calculated for finite crystallites are not necessarily coincident with the frequencies arising from the treatment of an infinite crystal, but tend towards the bulk frequencies as the dimension of the crystal is increased. For example, for a finite NaCl crystal there is not one vibrational mode, but a set of modes centred around the transverse and longitudinal frequencies of the infinite crystal, $\omega _T$ and $\omega _L$ (Fig. 7.13).

Fig. 7.13

Calculated absorption for slab particles of NaCl. In the top figure the particle height is 10 $\upmu$m. In the lower figure, it is 1 $\upmu$m. The absorption frequencies from the infinite crystal, $\omega _T$ and $\omega _L$, are indicated. Adapted from [77] with permission from the Institute of Physics

The surface modes are intermediate in frequency between $\omega _T$ and $\omega _L$, and are characterised by motions that can be sustained at the interface of the crystal (see Fig. 7.14). These modes are therefore strongly dependent on the geometry of the crystallite. Analytic solutions for the modes can be found for simple structures in the case of spherical crystallites, cylinders and rectangular slabs.

Fig. 7.14

Experimental absorption of small parallelepipeds of KCl of different sizes. The sizes are (in $\upmu$m) 2 $\times$ 4.5 $\times$ 4.5 for the full curve, 2.5 $\times$ 9 $\times$ 9 for the dashed curve (adapted from [77] with permission from the Institute of Physics). The infinite crystal calculated frequencies are indicated as $\omega _T$ and $\omega _L$

7.4.3.2 Powder Spectra

Measured absorption spectra often relate to microcrystalline samples, composed of a myriad of randomly oriented microcrystals, often embedded in a binder that displays limited absorption in the terahertz region. Such measurements are affected by the issues exposed in the previous section: the presence of surface modes on crystals of different sizes and with different orientations are also found to depend on the dimension of the sample and on the dielectric constant of the medium in which they are embedded (i.e. the measured frequency would be different for spherical crystallites in air or in a binder).

Fig. 7.15

Experimental and calculated infrared spectrum of kaolinite (reproduced from [78] with permission from Elsevier). The frequency eigenvalues are indicated by vertical lines at the bottom of the spectra

Balan [78] has calculated the IR powder spectrum of a sedimentary natural clay (kaolinite, Al$_2$Si$_2$O$_5$(OH)$_4$) taking into account the experimental set-up (Fig. 7.15). The geometry of the microcrystals is experimentally known to be thin plates; these are diluted in KBr powder binder, and compressed into a pellet. In a simple treatment, the binder is theoretically approximated as a uniform dielectric medium, and its influence on the microcrystal consists of a charge polarisation effect on the surface and in the bulk crystal. This effect is averaged over the randomly oriented microcrystals, and the effect was calculated on the normal modes calculated using DFT-based lattice dynamics. The result is that some of the absorption frequencies are shifted with respect to the normal modes of the crystal (see Fig. 7.15) and the absorption of some of the modes is found to be strongly dependent on the dielectric constant of the binder. This calculation resolved some of the issues related to shifted absorption bands that could not be correctly assigned from previous calculations. It is to be noted that this treatment required a detailed knowledge of the microcrystal geometry that might not be possible for many systems, where distributions in size and shape of crystallites are likely to exist.

Fig. 7.16

Possible configuration of the benzoic acid dimer, and the position inside a crystallographic unit cell ($a$ and $c$ axes shown). The hydrogen bond within the molecule is indicated with a dotted line. Adapted from [79]

7.4.3.3 Disorder and Impurities

The periodicity within a crystal can be broken by impurities and defects, whose presence modifies the local environment of molecules inside the crystal and will therefore affect the local intermolecular forces and, consequently, the lattice mode spectrum of a crystal. An example is crystalline benzoic acid, in which molecules are arranged as hydrogen bonded dimers. In this crystal structure, there are two possible configurations for a benzoic acid dimer, differing only in the positions of the protons within the hydrogen bond dimers (see Fig. 7.16). The relative populations of the two types of dimer are temperature-dependent, with  87 % of dimers being found in the lower energy configuration at $\text{ T}=4\text{ K}$, while the ratio is as high as 1:2 [79] at higher temperatures.

Fig. 7.17

Experimental and calculated terahertz spectra of crystalline benzoic acid (From [41]. Reproduced by permission of the PCCP Owner Societies). a The experimental spectrum, measured at T = 110 K, b the calculated spectrum averaged over several supercell models of the disordered structure, c the calculated spectrum with all hydrogen bond dimers in the lower energy configuration, d the calculated spectrum with all dimers in the higher energy configuration

The influence of this disorder on the terahertz spectrum was recently investigated by Li et al. [41], who modelled the disorder by considering several crystalline supercells of the known crystal structure in which the benzoic acid dimers were randomly assigned one of the two configurations in the observed 1:2 ratio. These supercells were then treated using force field-based lattice dynamics calculations and compared to the results of calculations on completely ordered structures. While the frequencies of all vibrational modes are overestimated by the force field method used, it is clear (see Fig. 7.17) that the disorder in the proton positions has a noticeable effect on the simulated spectrum. Furthermore, the effect of the disorder is different from what would be predicted from an average of the spectra from the two ordered models: additional weak features are introduced and the splitting between the stronger features is affected by the disorder.

The treatment of disorder here is only approximate, as a periodic unit cell is still needed for the lattice dynamics approach. However, the results do demonstrate how the spectrum is strongly influenced by the subtle effect of changing the position of a single atom within a molecule. It is easy to imagine that the disorder in other structures may have an even greater influence on the terahertz spectrum and may be necessary to consider in fully understanding the details in observed spectra. Again, for this kind of treatment it is necessary to have a detailed knowledge of the subtleties of a crystal structure.

Overall, computational methods have an integral role to play in interpreting the terahertz spectra of molecular crystals. While the subtleties of observed spectra may require further development of models to account for the influences of finite crystalline size and imperfections, existing methods can already help understand the molecular motions corresponding to observed features. These methods are thus enabling a chemical interpretation of spectra in terms of the interactions between molecules.