The vibrational frequencies of forsterite Mg₂SiO₄: an all-electron ab initio study with the CRYSTAL code

Abstract

The vibrational spectrum of Mg₂SiO₄ olivine was calculated at the Γ point by using the periodic ab initio CRYSTAL program. An all electron localized Gaussian-type basis set and the B3LYP Hamiltonian were employed. The full set of frequencies (35 IR active, 36 Raman active, 10 “silent” modes) was computed and compared to experimental data from different sources (four for IR and four for Raman). A generally good agreement is observed with experiment (the mean absolute difference ranging from 7 to 10 cm⁻¹ for the various sets), when some of the experimental frequencies, whose attribution is uncertain or appears to be affected by large errors, are not taken into account. A small number of observed peaks are not consistent with calculated frequencies, and a few theoretical peaks do not correspond to measured values. The implications are discussed in detail. The full set of modes are characterized using different tools, namely isotopic substitution, direct inspection of the eigenvectors and graphical representation, so as to obtain a consistent mode assignment.

Introduction

Olivines are important rock-forming silicates, as they belong to the most abundant phases of the Earth’s crust and upper mantle. In particular, the pure Mg-end member forsterite (Mg₂SiO₄) has been the subject of many experimental studies on crystallographic, thermodynamic and spectroscopic properties. First-principles investigations have concentrated on the elastic and structural behavior at high pressure (Jochym et al. 2004; Brodholt et al. 1996; Da Silva et al. 1997), whereas no ab initio simulations of vibrational spectra of forsterite have been performed yet, to our knowledge. On the other hand, a large number of infrared (IR) (Servoin and Piriou 1973; Hohler and Funck 1973; Iishi 1978; Hofmeister 1987; Hofmeister et al. 1989; Reynard 1991) and Raman (Servoin and Piriou 1973; Iishi 1978; Chopelas 1991; Kolesov and Geiger 2004) measurements are reported in the literature. Yet, not all vibrational bands allowed by symmetry have been observed in such studies, and the frequencies of some observed bands are not perfectly established (see Hofmeister 2001, introduction section). Most of the allowed Raman peaks have been assigned in a very recent paper (Kolesov and Geiger 2004), although some doubts still remain concerning their attribution to internal and external motions of atomic subunits, namely Si–O stretching and O–Si–O bending within the SiO₄ tetrahedra, SiO₄ rotations and translations, and Mg cation translations. In most cases, the assignments have been supported by force-field lattice dynamical calculations based on semiempirical interatomic potentials (Devarajan and Funck 1975; Pilati et al. 1995), as usual in solid-state vibrational spectroscopy. However, an accurate first-principles calculation of the Brillouin-zone centre lattice dynamical frequencies would be very helpful to definitely clarify all the open points referred to above.

It should be also pointed out that reliable calculations of the vibrational properties by a quantum-mechanical approach can open the way to full ab initio thermodynamics of the crystalline phases, within the frame of the quasi-harmonic approximation. Results obtained at the Γ point are the first step towards this final goal, which appears to be particularly attractive for important geological materials such as forsterite (Rao et al. 1988). In this respect theoretical calculations are important, as they provide also frequencies of the IR and Raman inactive modes, whose contribution to the thermodynamic functions has to be taken into account. CRYSTAL, an ab initio periodic all-electron computer program that uses a gaussian type basis set for representing the electronic crystalline orbitals (Saunders et al. 2003), was chosen as computational tool for this work. The method here adopted is based on the calculation of the Hessian matrix by numerical differentiation, starting from the analytical energy gradients with respect to nuclear positions.

In a previous paper (Pascale et al. 2004), devoted to illustrating the methodological aspects, the effects of the computational parameters controlling the accuracy of the calculated vibrational frequencies are discussed at length with reference to α-quartz. A subsequent study (Zicovich-Wilson et al. 2004) also analyzes how different basis sets and Hamiltonians affect the accuracy of calculated frequencies, again with application to α-quartz. In particular, excellent results are proved to be obtained by use of the B3LYP (Becke 1993) Hamiltonian, with a mean absolute difference of 6–7 cm⁻¹ with respect to experiment for the quartz frequencies. The aim of the present paper is to show that we can now calculate the full vibrational spectrum of forsterite at the Γ point with the superior accuracy afforded by the quantum-mechanical B3LYP functional. This will be also exploited to assess the several spectroscopic data available in the literature.

The nesosilicate forsterite, Mg₂SiO₄, is orthorhombic (space group Pbnm, non-conventional setting of Pnma, n. 62). There are six symmetry-independent atoms and 28 atoms (four formula units) in the unit-cell, giving rise to 84 vibrational modes. Their symmetry decomposition corresponds to:

$$\Gamma_{\rm total} = 11A_{g} + 11B_{1g} + 7B_{2g} + 7B_{3g} + 10A_{u} + 10B_{1u} + 14B_{2u} + 14B_{3u}.$$

A total of 35 IR active modes of type B _1u ,B _2u and B _3u and 36 Raman active modes (11A _g  + 11B _1g  + 7B _2g  + 7B _3g ) is then expected, plus 10 A _u inactive modes. The three B _1u , B _2u and B _3u modes left correspond to rigid translations.

The structure of the paper is as follows. We first summarize briefly the method employed for the calculation of vibrational spectra. The Results section presents our calculated data, analyzes the vibrational modes and compares the present results with experiment, separately for IR and Raman spectroscopic frequencies. Dielectric properties and isotope effects are also discussed, together with a statistical analysis of different sets of measurements versus theoretically predicted quantities.

Computational methods

For the present calculations we have used a development version of the CRYSTAL program (Saunders et al. 2003), which is a periodic quantum-mechanical ab initio code for calculating the total-energy-dependent and wave-function-dependent properties of crystalline solids. A localized gaussian-type basis set for the expansion of one-electron wave functions is therein employed.

The B3LYP Hamiltonian (Becke 1993), containing a hybrid Hartree-Fock/Density-Functional-Theory exchange-correlation term, has been adopted. This Hamiltonian is widely and successfully used in molecular quantum chemistry (Kochand Holthausen 2000) as well as in solid state calculations, where it has been shown to provide excellent results for geometries and vibrational frequencies, (Zicovich-Wilson et al. 2004; Prencipe et al. 2004) which are superior to the ones obtainable with LDA or GGA type functionals (Zicovich-Wilson et al. 2004; Tosoni et al. 2005).

The level of accuracy in evaluating the Coulomb and Hartree-Fock exchange series is controlled by five parameters, (Saunders et al. 2003) for which standard values have been used (6 6 6 6 12).

The DFT exchange-correlation contribution is evaluated by numerical integration over the cell volume (Pascale et al. 2004). Radial and angular points of the atomic grid are generated through Gauss-Legendre and Lebedev quadrature schemes. A grid pruning is usually adopted, as discussed in ref (Pascale et al. 2004). The impact of the grid size on both the accuracy and cost of the calculation has been discussed at length in previous papers (Pascale et al. 2004, 2005b; Tosoni et al. 2005; Prencipe et al. 2004). For the present calculations a (75,974)p grid has been used, where the notation (n _r ,n _Ω)p is used to indicate a pruned grid with n _r radial points and n _Ω points on the Lebedev surface in the most accurate integration region (see the ANGULAR keyword in the CRYSTAL user’s manual; Saunders et al. 2003). This grid corresponds to 632036 integration points in the unit cell; the accuracy in the integration can be measured by quoting the error in the integrated electronic charge in the unit cell (Δ _e =−3.10⁻⁶ |e| for a total of 280 electrons). It provides essentially the same frequencies as larger grids (Pascale et al. 2005b), whereas smaller grids such as (55,434)p give frequencies that can differ by as much as 30 cm⁻¹ from the present ones (165572 points; Δ _e =8880.10⁻⁶|e|).

The reciprocal space was sampled according to a regular sublattice with a shrinking factor IS equal to 4, corresponding to 27 independent k vectors in the irreducible Brillouin zone. The gradient with respect to the atomic coordinates is evaluated analytically (Doll et al. 2001; Doll 2001); equilibrium atomic positions are determined (Civalleri et al. 2001) by using a modified conjugate gradient algorithm as proposed by Schlegel (1982).

An all-electron basis set has been used. This basis set has been indicated as basis set B in ref (Pascale et al. 2005b); it is a 8-511G(d), 8-6311G(d) and 8-411G(d) contraction for Mg, Si and O, respectively; the exponent (in bohr⁻² units) of the most diffuse sp shells are 0.68 and 0.22 (Mg), 0.32 and 0.13 (Si) and 0.59 and 0.25 (O). The exponent of the single gaussian d shell is 0.5 (Mg), 0.6 (Si) and 0.5 (O).

As regards the calculation of frequencies, we refer to a previous paper (Pascale et al. 2004) for a more explicit formulation of the method; here we simply remind that, within the harmonic approximation, frequencies at the Γ point have been obtained by diagonalizing the mass weighted Hessian matrix W, whose (i,j) element is defined as $W_{ij}=H_{ij}/\sqrt{M_iM_j},$ where M _i and M _j are the masses of the atoms associated with the i and j coordinates, respectively.

By the way, once the Hessian matrix H is calculated, frequency shifts due to isotopic substitutions can readily be calculated, at no cost, by changing the masses M _i , in the above formula. In the present case, isotopic effects have been estimated for the substitution of ²⁶Mg for ²⁴Mg, ³⁰Si for ²⁸Si and ¹⁸O for ¹⁶O.

Energy first derivatives with respect to the atomic positions, v _j  = ∂V/∂u _j , are calculated analytically for all u _j coordinates (u _j is the displacement coordinate with respect to equilibrium), whereas second derivatives at u = 0 are calculated numerically using a single displacement:

$$ \left [\frac{{v_j}}{{u_i}}\right ]_0 \approx \frac{{v_j(0,\cdots,u_i,\cdots)}}{ {u_i}} $$

u _i =0.001 Å has been used for the present calculations (see Pascale et al. (2004, 2005b) for the discussion of the numerical aspects concerning the calculation of the hessian matrix). Since the energy variations for the displacements here considered can be as small as 10⁻⁶–10⁻⁸ hartree, the tolerance on the convergence of the SCF cycles has been set to 10⁻¹⁰ hartree.

The non-analytical correction to the Hessian, that must be added in the case of ionic compounds to take long range Coulomb effects due to coherent displacement of the crystal nuclei into account [see Born and Huang (1954) Sects. 5, 10, 34, 35, and Umari et al. (2001) Equs. 3 and 6], depends essentially on the electronic (clamped nuclei) dielectric tensor ɛ^∞ and on the Born effective charge tensor associated with every atom. The former is evaluated by applying a saw-tooth finite field along the direction of interest (Darrigan et al. 2003), and the latter through the use of well localized Wannier functions (Noel et al. 2002; Baranek et al. 2001; Zicovich-Wilson et al. 2001, 2002).

The IR intensity of the ith mode is defined as:

$$ A_i \propto d_i {\left| \frac{{\partial \mu}}{ {\partial Q_i}} \right|}^2 $$

i.e. they are proportional to the square of the first derivative of the dipole moment with respect to the normal mode coordinate Q _i times the d _i degeneracy of the ith mode. The dipole moment derivative is evaluated numerically by using the unit cell localized Wannier functions (Zicovich-Wilson et al. 2001, 2002).

Results and discussion

Structure and elasticity

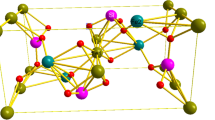
The crystal structure of forsterite is built up by SiO₄ and MgO₆ distorted tetrahedra and octahedra, respectively. Si polyhedra share vertices with the Mg ones, but not with one another. There are two symmetry-independent Mg atoms, named Mg1 (on the inversion centre at 0,0,0) and Mg2 (Hazen 1976). The Mg1 octahedra share edges forming rods parallel to the crystallographic c axis, and the Mg2 octahedra are linked laterally to such rods by edge-sharing, too (Fig. 1). Si tetrahedra are stuffed within the [001] channels.

Fig. 1

View of the crystal structure of forsterite, Mg₂SiO₄, along the crystallographic z axis. SiO₄ tetrahedra and MgO₆ octahedra (corresponding to the two independent Mg1 and Mg2 atoms) are emphasized. Oxygen atoms are shown as spheres

The calculated equilibrium geometry, given in Table 1, is in good agreement with experiment. Cell parameters are slightly overestimated (largest deviation: 0.8% for a), as usual for B3LYP (Becke 1993). The experimental Si–O and Mg–O distances are very well reproduced (the largest difference is smaller than 0.025 Å). The Si tetrahedron and the Mg1 octahedron turn out to be almost regular, according also to experimental data, whereas a larger distortion is shown by the Mg2 octahedron (e.g., the Mg2–O distances vary from 2.06 to 2.22 and from 2.07 to 2.21 Å in the calculated and experimental geometry, respectively).

Table 1 Calculated and experimental geometry of forsterite (Pbnm space group)

In Table 2 the measured (Isaak et al. 1989) and calculated elastic constants are reported; experimental data have been extrapolated to 0 K by using the temperature dependence data provided by the authors of the experimental paper. A very good agreement is observed for the diagonal components c ₁₁, c ₂₂ and c ₃₃, with differences smaller than 2%; deviations are larger for some of the other constants, but they never exceed 7%, confirming the high quality of the structural and elastic properties obtained with the present hamiltonian and basis set.

Table 2 Calculated and experimental elastic constants of fosterite (GPa)

Dielectric properties

The calculated Born effective charge and dielectric tensors are given in Tables 3 and 4, respectively. Born tensors are essentially diagonal and relatively little anisotropic, but for O1, for which anisotropy reaches 0.9|e|. The average value of the diagonal elements of the Mg and O atoms are close to their formal charges (±2|e|). For Si, the value is slightly smaller than +3|e|.

Table 3 Atomic Born effective charge tensors

Table 4 Calculated and experimental high frequency and static dielectric tensor components of forsterite

ε⁰ _ij is obtained by adding to ε^∞ _ij the ionic contribution obtained from the frequency eigenvalues, ω _m , eigenvectors, u _(A,i),m , and atomic Born tensors Z ^* _A,ij :

$$\epsilon^{0}_{ij}(\omega)=\epsilon^{\infty}_{ij}+\frac{{4\pi}}{ {\Omega_0}}\sum_m\frac{{\bar{Z}_{m,i}\;\bar{Z}_{m,j}}}{ {\omega_m^2-\omega^2}},$$

where

$$\bar{Z}_{m,j}=\sum_{(B,k)}\bar{u}_{(A,i)(B,k)}\;Z^*_{(B,k)j}$$

Ω₀ is the cell volume, ω is the electric field frequency, ω _m is the frequency of mode m, A labels the N atoms of the unit cell and i and j indicate the three x, y and z components [then m and (A,i) span the same set of 3N values].

ε^∞ is nearly symmetric and its components are about 1/3 of those of ε⁰. ε⁰ _xx and ε⁰ _zz are quite similar, whereas ε⁰ _yy is larger by about 10%. The components calculated at T = 0 K are about 3–7% smaller than the experimental ones (Cygan and Lasaga 1986; Shannon and Subramanian 1989) measured at room temperature. However, when corrected for the temperature effects by using the T dependence reported by Cygan and Lasaga (1986) (see third column of Table 4), they become very similar to the experimental data.

Infrared and Raman modes, and comparison with experiment

The reducible representation based on the cartesian coordinates of the atoms in the unit-cell is decomposed according to the scheme reported in the Introduction section and derived automatically by the CRYSTAL code.

We begin our analysis from the 35 IR active modes; the present theoretical results are compared to experiment. Four sets of measured data (Reynard 1991; Hofmeister 1987; Iishi 1978; Servoin and Piriou 1973) collected in the 1973–1991 period (we are not aware of more recent papers) and reported in Table 5, have been considered. Hofmeister provides the full set of 35 peaks, both for TO and LO; the other sets are incomplete (27 peaks are reported by Iishi, 28 by Servoin et al., 31 by Reynard). There is a quite general good agreement between the present results and the various experiments; however in a few cases definite discrepancies exist, that can be classified in three groups:

• 1. Lines are observed in experiments that do not have any calculated counterpart. In Table 5, 40 lines are reported (instead of 35, corresponding to the 35 IR frequencies) because 5 additional entries have been added for the “extra experimental peaks” not observed in the calculation. Two of them are reported by Hofmeister only (line 15 and line 29), one is observed by Hofmeister and Servoin et al. (line 10), and two are observed in three experiments (line 5, by Hofmeister, Reynard and Iishi, and line 33, by Hofmeister, Reynard and Servoin et al.). In the calculated spectrum there are no peaks in a relatively large window around these “extra” peaks, that are probably artefacts resulting from the numerical elaboration of the observed spectrum. This relatively sharp statement can be formulated on the basis of the observation that in the calculated spectrum, at variance with experiment, there is no reason for errors for the individual frequencies varying by large amount, as all the frequencies are generated by the same algorithm and are then affected, roughly speaking, by the same error (due to the selected hamiltonian, limitations in the basis set, numerical errors). In the experiment, on the contrary, many different features can affect the attribution of a given frequency: low intensity, peak superposition, background, overtones.

• 2. Calculated peaks not observed in any of the experimental spectra; this is the case of lines 1, 22, 34 and 36. The calculated TO intensity for the four cases is very small (0, 0, 18 and 9 in a scale that reaches 2,600), and this could explain why they are not observed. The intensity of the LO modes is however larger (at least for lines 34 and 36), so that, in principle, the LO components should have been detected.

• 3. There are two LO frequencies (lines 11 and 40) for which good agreement is observed between our calculated data and Reynard and Iishi (and Servoin et al. for line 40). Hofmeister’s data for both and Servoin’s for line 11 are however affected by a very large error (Δν = 95 and 45 cm⁻¹ respectively); for this reason these data are not considered in the statistics given in Table 6.

Table 5 Calculated wavenumbers ν (cm⁻¹) and intensities (arbitrary units) of the IR-active TO and LO modes of forsterite

Table 6 Statistical analysis of the differences Δν (cf. the previous table) between the experimental and calculated TO and LO sets of IR wavenumbers (cm⁻¹)

Table 6 provides statistical indices that permit to estimate the differences between the various sets of experimental data (Δν _e ) and between calculation and experiment (Δν). The $\overline{|\Delta \nu_{e}|}$ value among experimental sets ranges from 4.0 to 7.2 cm⁻¹; $\overline{\Delta \nu_{e}}$ shows that in some cases (Reynard vs Iishi and Servoin et al.) differences are systematic. |Δν _e |_max is as large as 38 cm⁻¹ (remember that data in parentheses in Table 5 are not taken into account in the statistical analysis, otherwise the largest discrepancy would have been as large as 95 cm⁻¹).

When compared to these differences among experimental data, the calculated vs experimental indices are very satisfactory: $\overline{|\Delta \nu|}$ ranges from 5.7 to 9.4 cm⁻¹ and only in the comparison with Hofmeister |Δν|_max exceeds 20 cm⁻¹.

On the whole the present results can be considered to be very satisfactory, because (a) they agree well with experiment for most of the modes; (b) the full set of modes is generated, also the ones not available experimentally, due to intensity problems; (c) ambiguous cases, where double peaks are erroneously reported in experiments, are clarified.

Similarly to the IR case, there are various sets of experimental Raman data available in the literature, ranging from the very old ones by Servoin and Piriou (1973) and Iishi (1978) (both papers have already been quoted with reference to the IR spectrum), to the very recent paper by Kolesov and Geiger (2004). In Table 7 these three sets, the set collected by Chopelas (1991) and the present calculated data are reported, whereas in Table 8 statistical indices comparing the various sets are given, as already done for the IR experimental and calculated data. As for the IR case, we had to add lines in Table 7 for including “extra” experimental peaks with no correspondence to theoretical results: there are however only three such cases, all due to Servoin and Piriou (1973) (see lines 27, 36 and 37; a peak that does not have any calculated counterpart is also reported by Chopelas, and is included at line 36 of our table). Kolesov and Geiger report only 25 out of 36 modes; the agreement with the other experiments on this reduced set is very high, as shown by the “Kolesov and Geiger” horizontal entry in Table 8: the mean absolute and largest wavenumber differences are 1.8 and 7 cm⁻¹, respectively. The disagreement is slightly larger when considering the 32 frequencies common to Iishi and Servoin et al. ( $\overline{|\Delta \nu_{e}|}= 2.1; |\Delta \nu_{e}|_{\rm max}=27\,{\rm cm}^{-1}$) and even larger when the comparison is performed with the set proposed by Chopelas ( $\overline{|\Delta \nu_{e}|}=3.9;|\Delta \nu_{e}|_{\rm max}=35\,{\rm cm}^{-1}$), indicating that there are difficulties in identifying and locating some of the peaks not included in the “safe” set of Kolesov and Geiger. In summary, the four experimental sets provide very consistent results for a common set of 25 modes, with quite small differences; for the other modes, differences among experiments can be much larger, and reach nearly 40 cm⁻¹.

Table 7 Calculated and observed wavenumbers ν (cm⁻¹) of the RAMAN-active modes of forsterite

Table 8 Statistics of RAMAN-active modes of forsterite

Let us consider now the comparison between calculated and experimental data. Large discrepancies are often observed for low frequency modes: This is the case of the first B _1g (Servoin et al.), B _2g (Iishi) and B _3g (Iishi, Kolesov and Geiger) modes, probably because of experimental limitations. In other cases (for example lines 29 and 38, where calculated wavenumbers are larger by about 20 cm⁻¹ with respect to all experiments), the differences might reflect limitations of the present theoretical model, possibly related to the variational basis set that is not sufficiently flexible. It is however interesting to notice that these two modes, for which the largest differences with respect to experiment are observed (apart from the low frequency modes mentioned above and given in parentheses in Table 7), fall at exactly the same frequency; we wonder whether the superposition of the two peaks might give interpretation problems on the experimental side. When the few data in parentheses are excluded, the agreement between our data and experiment is quite satisfactory, with $\overline{|\Delta \nu|}$ ranging from 7 to 8 cm⁻¹, and |Δν|_max never larger than 31 cm⁻¹. The interesting point about simulation, however, is that the full set of frequencies is generated, with roughly the same accuracy, so that interpretation problems of the experimental spectra can easily be solved.

The results obtained can also be usefully compared to those of a pioneering study based on semi-empirical force-fields (Price et al. 1987). By using the same statistical indicators as in Tables 6 and 8, the force-field frequencies give their best performance against experimental ones with respect to Iishi’s data ( $\overline{|\Delta \nu|}=18.8,$ 18.1, 17.9 and |Δν|_max = 56, 42, 45 cm⁻¹ for TO, LO and Raman frequencies, respectively). These deviations are about double those given by our first-principles results, so that the improvement achieved by quantum-mechanical simulations can be clearly appreciated.

Concerning the A _u inactive modes, the only measured data come from a single-crystal inelastic neutron scattering experiment limited to the low energy range (Rao et al. 1988), where just one inactive zone-center phonon frequency is reported (104 cm⁻¹). This result compares favorably with 101.5 cm⁻¹, the smallest of our computed A _u values.

Mode assignment

Vibrational modes in silicates are usually classified in two main categories, namely “internal modes” (I), and “external modes” (E). The former ones include the stretching and bending vibrations of the SiO₄ tetrahedra, that represent the covalent part of the system. E modes include rotations and translations of the tetrahedra, and translations of the cations. The site group to factor group analysis applied to forsterite (Hohler and Funck 1973; Stidham et al. 1976) leads to 36 internal (16 stretching and 20 bending) modes and 45 external (12 tetrahedral rotations, 9 tetrahedral translations and 24 Mg translations) modes. This classification obviously simplifies the reality, because large mixing can occur when modes with the same symmetry are at about the same frequency. This point was stressed by many authors in the past.

In previous work (Servoin and Piriou 1973; Iishi 1978; Hofmeister 1987; Reynard 1991; Chopelas 1991; Kolesov and Geiger 2004) the problem of mode assignment in forsterite was discussed at length, and the classifications of the various authors agree to a large extent.

Ab initio simulations provide many tools for establishing the nature of the atomic motion in a given mode. These tools have already been used successfully in our previous studies of pyrope (Pascale et al. 2005b), andradite (Pascale et al. 2005a) and katoite (Orlando et al. 2006), and consist essentially in:

• direct inspection of the eigenvectors of the dynamical matrix;

• isotopic substitution of the various species present in the unit cell; the larger the frequency shift, the larger the participation of the substituted atom to the movement; viceversa, zero frequency shift indicates that the substituted atom is not participating to the mode;

• graphical representation of the eigenvectors; as for our previous studies, animation of all the modes are available at CRYSTAL web-site (web). In order to make the animation as clear as possible, manipulations such as rotations of the frame, different perspective points of view and polyhedra representations are possible.

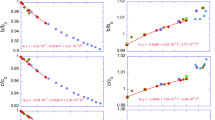
In Table 9 the full set of calculated wavenumbers is reported, together with the isotopic shifts when one of the four kinds of atoms (Mg1, Mg2, Si and O) is substituted by its most abundant isotope. Figure 2a–d give a more direct evidence of the isotopic shift effects. Consider for example the case of Mg1 and Mg2, shown in Figs. 2a, b. Mg1 presents large isotopic shifts (say larger than 3.5 cm⁻¹, in bold in Table 9) in a wide wavenumber range from 187 to 540 cm⁻¹, with a smaller and a larger peak in the 206–293 and 403–513 cm⁻¹ intervals, respectively. For Mg2, shifts are smaller, and they are spread in a range (260–392 cm⁻¹) which lies at lower frequencies than in the previous case. This result is consistent with the Mg1 octahedra being tightly linked to one another by edge sharing, so as to form rigid [001] chains (cf. Fig. 1), whereas the Mg2 octahedra are more loosely connected to the sides of such chains.

Fig. 2

Isotopic shift versus wavenumber ν (cm⁻¹) for all vibrational modes of forsterite

Figure 2c shows that silicon is mainly involved in the high-frequency stretching modes and in the bending modes around 600 cm⁻¹, although shifts of the order of 3 cm⁻¹ are also observed down to 200 cm⁻¹. Oxygen (Fig. 2), as expected, is involved in all modes, with an isotopic shift which is roughly proportional to the mode frequency.

The analysis based on the isotopic shifts and, even better, on the animations available on the CRYSTAL web-site (web), allows us to propose the schematic classification of modes given in Fig. 3.

Fig. 3

Assignment of forsterite vibrational modes (infrared, Raman and inactive) by using the eigenvectors and the isotopic substitutional analysis (see Table 9). According to the literature, modes are classified in five groups, namely SiO₄ stretching and bending (internal modes), Mg translations, tetrahedra rotations and translations (external modes). Each mode is represented, on the wavenumber (cm⁻¹) scale, by a vertical bar in the group to which it belongs. Mixed modes are attributed to various groups. Groups are vertically spaced for clarity reasons

The stretching band, ranging from 819 to 989 cm⁻¹ and including 16 modes (No. 66–81), is separated by a 174 cm⁻¹ wide gap from the lowest part of the spectrum.The various combinations of the four symmetric stretchings (coming from four tetrahedra in the unit cell) are at the low side of the band (modes 68–71); for all stretching modes the Mg isotopic shift is extremely small (maximum value: 0.7  cm⁻¹). In principle, the 20 bending modes of the tetrahedra are expected to follow (modes 46–65, from 442 to 645  cm⁻¹). In practice, only a few of them can be interpreted as pure bending modes of the tetrahedra, according to the animation (web) and isotopic substitution. For example, a large Mg shift is observed for modes 57, 54, 52, 49 and 48; the latter, in particular, presents the largest Mg isotopic shift among the full set, confirming that mixing is quite important for frequencies lower than 500 cm⁻¹. For this reason we will avoid to enter too much into details in this analysis, performed by using Table 9 and the full set of animations (web), and whose conclusions are summarized in Fig. 3. In short, the SiO₄ rotation modes range from 183 to 432 cm⁻¹; Mg translation modes are mainly localized below 300 cm⁻¹; however, as already mentioned, they give very important contributions to modes up to 540 cm⁻¹. The very low frequency modes can be mostly interpreted as SiO₄ translations; this set of modes (always quite mixed with other kinds of motions) can be found up to about 300 cm⁻¹.

Table 9 Effect of the ²⁶Mg, ³⁰Si and ¹⁸O isotopic substitutions on the calculated wavenumbers ν (cm⁻¹) of all modes