Keywords

1 Introduction

Rotordynamic study became prominent in the second half of 19th century, when the inclusion of rotation speed in the analysis of the dynamic behavior of rotating machines was made necessary. Since then, the search for higher power, lower weight, higher speeds and greater reliability in this kind of machinery has driven the pursuit for solutions that are economically feasible.

However, for a detailed analysis it is necessary take into account several parameters, i.e., besides the rotor dynamics, other system components, as the bearings, must be considered. Although these elements are usually linearly approximated by stiffness and damping coefficients [1, 2] they can have a strong nonlinear behavior. This characteristic is still studied for many researchers [3,4,5,6], which emphasize the use of hydrodynamic bearing model for the real understanding of rotating machines, especially when it presents high vibration amplitudes.

The solution of nonlinear rotor-bearing dynamic problems is highly time consuming, because the Reynolds equations, that gives the nonlinear hydrodynamic forces, must be simultaneously solved with the equation of motion for each time step. Thus, ways to simplify the hydrodynamic forces in order to reduce computational time, with minimum loss of the nonlinear characteristics, are still subject of research until the present time.

Initially, some works [7,8,9] utilized the analytical short bearing model proposed by Capone [10, 11], since this simplification generates good results for bearings with small L/D ratio. Nevertheless, due to this limitation new alternatives were evaluated to improve the solution effectiveness for finite length bearings.

Besides analytical solutions, other alternatives were proposed to model the hydrodynamic forces and reduce processing time of the nonlinear dynamic solutions. The Taylor series expansion of the force, trough perturbations in displacement and velocity around the equilibrium position, is one of the most promising. Unlike linear model, the truncation happens for high order terms, generating nonlinear coefficients.

Using least square method and experimental time series for the hydrodynamic forces, Zhao et al. [12] proposed the identification of dynamic coefficients for three different models (24, 28 and 36 coefficients). For all analyzed cases, the nonlinear models were able to represent the bearing force, while the linear model presented discrepancies. In addition, it was observed that the linearized solution presented hydrodynamic force results comparable to the nonlinear model only for excitations lower than 2.5% of the radial clearance.

Asgharifard-Sharabiani and Ahmadian [13] used a subset selection technique to retain the 40 most influent coefficients from a 13th order Taylor series expansion, for a rigid rotor supported by tilting-pad bearings. The system degrees of freedom do not consider the angular movement of the pads and the model was valid only for weak nonlinearities. This made possible the use of the same linear coefficients obtained by small perturbation method for the linear part of the new expansion. Therefore, the obtained dynamic results were compared with simulations taking into account the Reynolds model showing good agreement.

The research found in literature for adjustment of nonlinear forces by Taylor series expansion, usually employs simplified rotors for the analysis, not considering basics characteristics found in real situations, as for instance rotor flexibility. Additionally, the analysis were also restricted for situations of weak nonlinearities. Hence, the present work aims to analyze the use of nonlinear force approximation by high order Taylor series expansion, through ridge regression method, in the context of strong nonlinearities. The adjusted forces are obtained from the simulation of a flexible rotor modeled by finite elements and supported by hydrodynamic journal bearings.

2 Methodology

Typical elements of rotating systems are rotors, shafts, bearings and foundation, the last one considered rigid for this paper, being a largely employed configuration the Laval/Jeffcott rotor, showed in Fig. 1. Modeling the system through the finite element method [14, 15], with Timoshenko beam, it is possible to represent a continuous system in a finite number of elements, each node having four degrees of freedom, two of translation (y and z) and two of rotation (ϴy and ϴz). Therefore, using the Lagrange formulation it is possible to find the equation of motion [16]:

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + \left( {\left[ C \right] +\Omega \left[ G \right]} \right)\left\{ {\dot{q}} \right\} + \left[ K \right]\left\{ q \right\} = \left\{ {F_{U} } \right\} + \left\{ {F_{W} } \right\} + \left\{ {F_{H} } \right\} $$
(1)

where, [M], [C], [G], [K] are respectively the global mass, damping, gyroscopic and stiffness matrices, Ω is the rotor’s rotation speed, {q} is the vector with the degrees of freedom, {FU} is the unbalance force vector, {FW} is the weight force vector and {FH} is the hydrodynamic force vector.

Fig. 1.
figure 1

Typical rotor model: (a) x-z view; (b) y-z view.

Full size image

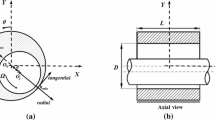
The hydrodynamic force is obtained through the pressure distribution generated by the journal motion inside the bearing, which is calculated by the Reynolds equation. This equation derives from the equations of momentum conservation and mass conservation for a viscous fluid, under certain hypothesis. For the bearing scheme seen in Fig. 2, the isoviscous Reynolds equation can be mathematically written as [17]:

$$ \frac{\partial }{\partial \theta }\left( {h^{3} \frac{\partial p}{\partial \theta }} \right) + \frac{\partial }{\partial x}\left( {h^{3} \frac{\partial p}{\partial x}} \right) = 6\mu \left( {U\frac{\partial h}{\partial \theta }} \right) - 12\mu \frac{\partial h}{\partial t} $$
(2)

being, p the pressure, ϴ and x the circumferential and axial coordinates, µ the oil film viscosity, U the tangential journal velocity, t the time and h the lubricant film thickness:

$$ h = CR + y\sin \theta - z\cos \theta $$
(3)

CR is the bearing radial clearance, and y and z, respectively the horizontal and vertical coordinates of the journal center.

Fig. 2.
figure 2

Radial journal bearing scheme: (a) lateral view; (b) axial view

Full size image

With the estimated pressure field, it is possible to evaluate the resultant forces in the oil film. For this, the pressure distribution should be integrated over the bearing area generating the horizontal and vertical force components:

$$ \left\{ {\begin{array}{*{20}c} {F_{Hy} } \\ {F_{Hz} } \\ \end{array} } \right\} = \int_{{ - \frac{L}{2}}}^{{\frac{L}{2}}} {\int_{{\theta_{1} }}^{{\theta_{2} }} {p\;\left\{ {\begin{array}{*{20}c} {\sin \theta } \\ { - \cos \theta } \\ \end{array} } \right\}} } \;d\theta {\kern 1pt} dx $$
(4)

Thus, the hydrodynamic forces are dependent on the shaft rotational speed as well as position and velocity of the journal center inside the bearing:

$$ F_{H} = F_{H} \left( {\Omega ,y,z,\dot{y},\dot{z}} \right) $$
(5)

So, for displacements around the equilibrium position, a Taylor series expansion [18], depending on the previously described variables, can be performed to create an analytical expression that represents the force generated by the oil film:

$$ F_{Hi} = \sum\limits_{j = o}^{n} {\frac{{\left( {\left\{ x \right\} - \left\{ a \right\}} \right)^{j} }}{{j\,{\kern 1pt} !}}\,\left. {\frac{{\partial^{j} f\left( {\left\{ x \right\}} \right)}}{{\partial \left\{ x \right\}^{j} }}} \right|}_{{\left\{ a \right\}}} $$
(6)

in which, j represents y or z, {x} is the vector with the function variables, {a} is the vector with the bearing equilibrium position for a given rotation and n is the expansion order.

For the first order expansion, one have the classical hydrodynamic force linearization proposed by Lund [1, 2]. In this case, the force is described by eight dynamic coefficients of stiffness (Kmn) and damping (Cmn):

$$ \begin{array}{*{20}c} {F_{y} = F_{y0} + K_{yy} \cdot \Delta y + K_{yz} \cdot \Delta z + C_{yy} \cdot \Delta \dot{y} + C_{yz} \cdot \Delta \dot{z}} \\ {F_{z} = F_{z0} + K_{zy} \cdot \Delta y + K_{zz} \cdot \Delta z + C_{zy} \cdot \Delta \dot{y} + C_{zz} \cdot \Delta \dot{z}} \\ \end{array} $$
(7)

being the coefficients determined by the partial derivative of the force evaluated in the journal equilibrium position:

$$ \begin{array}{*{20}c} {K_{yz} = \left. {\frac{{\partial F_{y} }}{\partial z}} \right|_{0} ;} & {C_{yz} = \left. {\frac{{\partial F_{y} }}{{\partial \dot{z}}}} \right|_{0} } \\ \end{array} $$
(8)

However, it is known that the bearing nature can be highly nonlinear and that the linearization is only valid for small vibrations amplitudes. So, for a more accurate analysis of rotating machines, the nonlinear model must be adopted. Nevertheless, the use of nonlinear hydrodynamic forces, by means of simultaneous solution of the Reynolds equation and the equation of motion, is very time consuming. To minimize this problem, it is possible to use an analytical expression based on high order Taylor series expansion as proposed by Zhao et al. [12].

Obtaining \( y\left( t \right) \), \( z\left( t \right) \), \( \dot{y}\left( t \right) \), \( \dot{z}\left( t \right) \), \( \bar{F}_{Hy} \left( t \right) \) and \( \bar{F}_{Hz} \left( t \right) \) from a time series analysis, the ridge regression method [19] can be used to minimize the squared difference between the adjusted force (\( F_{i} \left( k \right) \)) and the force calculated through the Reynolds equation solution (\( \bar{F}_{Hi} \left( k \right) \)). The minimization results in the expansion nonlinear coefficients:

$$ \left\{ K \right\}_{i} = \mathop {\arg \hbox{min} }\limits_{{K \in \Re^{N} }} \sum\limits_{k = 1}^{M} {\left[ {\bar{F}_{Hi} \left( k \right) - F_{i} \left( k \right)} \right]^{2} } + \lambda \sum\limits_{j = 1}^{N} {K_{{i_{J} }}^{2} } $$
(9)

or in matrix form:

$$ \left\{ K \right\}_{i} = \mathop {\arg \hbox{min} \;}\limits_{{K \in \Re^{N} }} \left\| {\left\{ {F_{H} } \right\}_{i} - \left[ X \right]_{i} \left\{ K \right\}_{i} } \right\|_{2}^{2} + \lambda \,\left\| {\left\{ K \right\}_{i} } \right\|_{2}^{2} $$
(10)

where, {K}i is the nonlinear coefficients vector, N is the coefficient number generated by the Taylor expansion, M is the number of time steps used to obtain the hydrodynamic forces, [X] is the predictor matrix and \( \lambda \ge 0 \) is the adjustment parameter.

The optimization problem described in Eq. 10 has analytical solution, since it is enough to derive the objective function with respect to the coefficients K:

$$ \left\{ K \right\}_{i}\,=\,\left( {\left[ X \right]_{i}^{T} \left[ X \right]_{i} + \lambda \,\left[ I \right]} \right)^{ - 1} \left[ X \right]_{i}^{T} \left\{ {F_{H} } \right\}_{i} $$
(11)

Therefore, for each bearing, and for each direction of the hydrodynamic force, there is a minimization problem, which can generate N coefficients defined by the order of the Taylor series expansion.

The λ parameter defines the amount of penalization applied to the original least square. When \( \lambda \to 0 \) the same solution generated by the least square method is found. When \( \lambda \to \infty \) the solution is null. A shrinkage of the coefficients happens for intermediate values, causing a reduction in variance but an increase in bias. Moreover, the penalty introduction improves the conditioning of [X] Ti [X]i matrix. To calculate λ an one-dimensional minimization process (line search) is used to generate the smallest value for the objective function (Eq. 10).

3 Discussion and Results

The rotor used in the simulations was a Laval/Jeffcott rotor, discretized by finite elements as previously mentioned. Ten Timoshenko beam elements and a central rigid disk element, placed at node 6, were used to compose the system. Two identical hydrodynamic bearings are located at nodes 3 and 9. Figure 3 shows the rotor finite element model, Table 1 the detailed discretization, and Table 2 shows the bearing parameters. The excitation force adopted comes from unbalance and was inserted at disk position. The damping matrix [C] is proportional to the stiffness matrix [K], and the proportional coefficient is \( \beta = 1.5 \times 10^{ - 5} \). Moreover, shaft and disk are made of steel with elastic modulus of 200 GPa and density of 7850 kg/m3.

Fig. 3.
figure 3

Finite element model

Full size image
Table 1. Finite elements details.
Full size table
Table 2. Bearings Parameters.
Full size table

Because Reynolds equation is a second order differential equation, it does not have a closed solution. Therefore, numerical methods are necessary to find the pressure distribution inside the bearing. The finite volume method, that transform partial differential equations in a set of algebraic equations, was adopted for the simulations [20]. The first critical speed is 22 Hz and, consequently, at 44 Hz the system is subjected to fluid-induced instability.

Furthermore, when considering nonlinearities in a machine simulation, its dynamical behavior is completely changed, and a robust integration method must be employed. So, in this work, the nonlinear implicit iterative Newmark integrator is used. Hence, for each time step, a variable prediction is calculated by Newmark equations and updated by Newton-Raphson method until the equation of motion is satisfied [21]. The Reynolds equation should be solved for each bearing and at each iteration of the procedure, resulting in elevated computational time.

To overcome this problem the hydrodynamic force approximation described in Sect. 2 is utilized. The amount of time needed for a good force adjustment depends on the machine operation condition. However, the transitory part of the movement is of great interest, because it is the path followed by the rotor under this situation and expands the region covered by the adjustment. Despite the initial cost to obtain and adjust the hydrodynamic force given by the Reynolds equation, the simulation time drops from hours to minutes. For this work, it was used a Taylor series expansion up to the fifth order, since this was the lowest order able to fit the case under fluid induced instability.

The simulation cases analyzed take into account situations with strong nonlinear bearing behavior. So, critical rotation speeds, as the first natural frequency (22 Hz) and the fluid induced instability (44 Hz), are selected. Additionally, high unbalance level contributes to increase nonlinearities, and for the situations previously mentioned a 8.5 g mass placed at 37 mm from the center of the disk is used (Balance Quality Grade G12,8 [22]). Because the rotor is symmetrical, the bearings have the same response. So, only the first bearing is used in the analysis. Notice that results for Reynolds and Nonlinear coefficients are coincident for most of the cases. Those results are shown in Figs. 4 and 5.

Fig. 4.
figure 4

Simulation results for rotational speed equal to 22 Hz: (a) Horizontal hydrodynamic force; (b) Vertical hydrodynamic force; (c) Bearing orbit; (d) Disk orbit.

Full size image
Fig. 5.
figure 5

Simulation results for rotational speed equal to 44 Hz: (a) Horizontal hydrodynamic force; (b) Vertical hydrodynamic force; (c) Bearing orbit; (d) Disk orbit; (e) Horizontal bearing displacement; (f) Vertical bearing displacement.

Full size image

Figure 4a, b show the hydrodynamic forces for horizontal and vertical direction obtained by Reynolds equation, high order Taylor expansion and linear coefficients for 22 Hz. As can be seen, in the beginning of the transitory motion, all hydrodynamic forces are comparable. However, when the displacement amplitude increases, the linear force can no longer represent the original hydrodynamic forces obtained by Reynolds equation. On the other hand, the force calculated by nonlinear coefficients is in good agreement during all period. The same behavior can be seen for the fluid induced instability in Fig. 5a, b, e, f.

Furthermore, observing the orbits presented in Fig. 4c, d, it is clear that the nonlinear coefficients can represent the rotor orbits with higher accuracy while the linear forces violates the bearing clearance and have different shape and size for the disk orbit.

For the fluid induced instability, the nonlinear coefficients can well reproduce the limit circle described by the journal inside the bearing (Fig. 5c) and the whirling movement of the disk (Fig. 5d). Moreover, small discrepancies can be observed in the orbits.

Three special cases, with high eccentricity and extreme unbalance level are also analyzed. Concentrated vertical forces were applied at both bearing nodes in order to keep bearing eccentricity ratio value equal to 0.9. The unbalanced mass was changed to 1.7 kg (Balance Quality Grade G1170). Those hypothetical cases should not occur in reality but are simulated to verify the efficiency of the adjustment under extreme nonlinear situations. For the results in Fig. 6, the concentrated force was set to 500 N and the rotation speed to 10 Hz. In order to make the vibration amplitude of bearing 1 higher, two approaches were followed: (1) the unbalance force was changed from node 6 to node 1 (results in Fig. 7) and (2) preserving unbalance at node 6, at rotational speed of 20 Hz (Balance Quality Grade G2338) (Fig. 8).

Fig. 6.
figure 6

Simulation results for rotational speed equal to 10 Hz and 500 N applied load: (a) Horizontal hydrodynamic force; (b) Vertical hydrodynamic force; (c) Bearing orbit; (d) Disk orbit.

Full size image
Fig. 7.
figure 7

Simulation results for rotational speed equal to 10 Hz, 500 N applied load and unbalance at node 1: (a) Horizontal hydrodynamic force; (b) Vertical hydrodynamic force; (c) Bearing orbit; (d) Disk orbit.

Full size image
Fig. 8.
figure 8

Simulation results for rotational speed equal to 20 Hz and 800 N applied load: (a) Horizontal hydrodynamic force; (b) Vertical hydrodynamic force; (c) Bearing orbit; (d) Disk orbit.

Full size image

Observing Figs. 6, 7 and 8, it is clear that as the bearing vibration amplitude increases higher is the difference between linear and nonlinear models. However, in all cases of linear approximation, the orbits touch or violate the bearing wall, while the nonlinear coefficients model follows the Reynolds orbits.

The most critical case is the one shown in Fig. 8, where high eccentricity is combined with a rotational speed close to the first natural frequency. In this situation, despite a good force adjustment, there are some discrepancies in the journal motion comparing Reynolds and nonlinear coefficients solution. Nevertheless, nonlinear coefficients can perform the overall bearing behavior while linear approximation totally fails.

This difference comes from the amount of penalization used in the adjustment. The desirable value for the penalization parameter is the one that minimizes the objective function, as can be seen in Fig. 9. However, Fig. 9d shows that all λ values give objective functions higher than the original least square (λ = 0). In this situations, the tradeoff between variance and bias, that traduces the model accuracy, should be analyzed in order to define a suitable value for λ, since for the original least square method the solution is unbiased but can have high variance. Therefore, for some situations under extremely high nonlinearities, lower variance can be desirable, but this will cause loss in accuracy. Observing Fig. 10 it is possible to obtain λ.

Fig. 9.
figure 9

Objective function behavior: (a) For horizontal force adjustment; (b) Zoom in for horizontal force adjustment; (c) For vertical force adjustment; (d) Zoom in for vertical force adjustment.

Full size image
Fig. 10.
figure 10

Tradeoff between variance and bias: (a) For the horizontal force adjustment; (b) For the vertical force adjustment.

Full size image

Nevertheless, for these simulations, it is possible to note that linear and nonlinear hydrodynamic forces are close, but the bearing orbits associated to them are not. In high eccentricities, the wedge term associated to the Reynolds equation is dominant for the pressure generation and consequently for the force calculation. Therefore, shape and behavior of the movement does not affect considerably the force value. However, the linear solution cannot reproduce high order harmonics making linear orbits elliptical, while nonlinear coefficients can satisfactorily reproduce the orbits.

4 Conclusions

The paper presented the use of high order Taylor series expansion, by means of nonlinear coefficients, to approximate bearings’ hydrodynamic forces. The simulations were accomplished for rotors submitted to high nonlinear bearing behavior, as critical speeds, fluid induced instability and cases with high eccentricities.

The results showed that nonlinear coefficients model can satisfactorily reproduce hydrodynamic forces and rotor dynamics, greatly reducing the simulation time. Moreover, for situations with extremely high nonlinearities the penalty parameter λ of the ridge regression should promote variance reduction to favor convergence of the dynamic problem. Additionally, when the rotor experiences high eccentricity the linear and nonlinear hydrodynamic forces have close behavior. However, the response with linear force cannot reproduce high order harmonics changing the bearing orbit shape, what does not happen when nonlinear coefficients are used.