Keywords

1 Introduction

The hydrodynamic bearings are critical components of rotating machines, especially those that require high fatigue life. The forces generated in the fluid film acts on the rotor in radial and tangential directions, which can lead it to an undesirable auto-excited behavior, known as fluid induced instability (oil whirl/whip).

The first phenomenon, oil whirl, is easily identified, because its amplitude is related to the precession movement of the shaft and its frequency is approximately 0.5 times the rotational speed. The second phenomenon, oil whip, occurs at a rotation velocity associated to the vibration frequency of the first bending mode of the rotor. In this case, the rotor movement suddenly becomes unstable, generating high precession amplitudes, which no longer depend on the rotation speed of the shaft.

The phenomenon of fluid-induced instability in rotating machinery was firstly observed by Newkirk [1]. Afterwards, many authors directed their efforts to study this problem, especially for obtaining the threshold of instability, since it may give the operation limit for the rotating systems supported by hydrodynamic bearings.

Lund [2] proposed a method to evaluate the dynamic coefficients of the fluid film in the bearings, including direct and cross-coupled coefficients, still in use for the most of the rotor dynamic problems. Later, Lund [3] also presented a formal way to obtain the threshold of stability developing the critical mass theory. In the 70’s, the same author used the damped critical speed concept to find the instability threshold in flexible rotors supported by fluid-film bearings [4], and this method is still used as can be seen in the works of Cloud [5] and Pettinato [6].  

However, the lubrication problem is usually solved by the classical Reynolds’ equation, basically considering isothermal condition in the bearings. On the other hand, is well known that the viscosity is highly dependent on the temperature, which in turn can significantly change with the rotation velocity of the rotor shaft and along the bearing wall. Hence, a thermodynamic model of the fluid-film can affect the equivalent coefficients of stiffness and damping and, consequently, the threshold of instability. Dowson [7] introduced a generalized Reynolds’ equation to model the variation of relevant quantities, not only viscosity but density, both through and along the oil film. This equation was derived from hydrodynamic’s fundamental equations with minimal restrictive assumptions. Thereafter, Dowson and March [8] accomplished a series of experimental analysis as well as Lund and Hansen [9], and later Khonsari et al. [10] accomplished many simulations and experiments to create charts for rapid screening of the temperature influence on the behavior of the bearing.

Hence, this paper aims to apply both methods of critical mass and logarithm decrement to identify of the fluid induced instability threshold, comparing the HD and THD models for the bearings with focus on the impact on the rotor stability prediction.

2 Methodology

The hydrodynamic lubrication depends on the pressure distribution in the lubricant film to create the hydrodynamic forces able to support the load of the rotor. The equation that describes the dynamics of the oil film is the Reynolds Equation to incompressible fluid. When the Reynolds’ Equation is applied in a thermohydrodynamic analyses (THD), its general form is given by Eq. (1):

$$\frac{\partial }{\partial x}\left[ {F_{2}^{\prime } \cdot \frac{\partial p}{\partial x}} \right] + \frac{\partial }{\partial z}\left[ {F_{2}^{\prime } \cdot \frac{\partial p}{\partial z}} \right] = U \cdot \frac{\partial }{\partial x}\left[ {h - \frac{{F_{1} }}{{F_{0} }}} \right] \, - \frac{\partial h}{\partial t}$$
(1)

where \(x = r \cdot \theta\) is the circumferential coordinate, z is the axial coordinate, y is the radial coordinate, h is the thickness of the oil film, p is the pressure in the oil film, U is tangential velocity of the fluid, and the viscosity integrals \(F_{0} = \int_{0}^{h} {\frac{dy}{\mu }} ,\,F_{1} = \int_{0}^{h} {\frac{y}{\mu }dy} ,\,F_{2}^{'} = \int_{0}^{h} {\frac{y}{\mu } \cdot \left( {y - \frac{{F_{1} }}{{F_{0} }}} \right)dy}\).

The solution of the thermohydrodynamic lubrication problem requires the simultaneous solution of the the Energy Equation to evaluate the viscosity dependence with the temperature, as presented in Eq. (2):

$$\rho \cdot Cp \cdot \left( {u \cdot \frac{\partial T}{\partial x} + v \cdot \frac{\partial T}{\partial y}} \right) = k \cdot \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \mu \cdot\Phi$$
(2)

where \(\Phi = \left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial w}{\partial y}} \right)^{2}\) is the viscous dissipation term, ρ is the fluid density, \(C_{p}\) is specific heat, T is the temperature and u, v and z are the circumferential, radial and axial velocities, respectively.

The viscosity is the common term in Reynolds Equation and Energy Equation. The viscosity dependence with temperature is given by Petroff expression in Eq. (3):

$$\mu \left( T \right) = \frac{0.2023}{{1 - 0.0468 \cdot T + 0.0029 \cdot T^{2} }}$$
(3)

As described by Lund [2, 3], the hydrodynamic forces can be expanded in Taylor Series of first order and linearized as in Eq. (4):

$$\begin{aligned} F_{x} & = F_{x0} + K_{xx} \cdot\Delta x + K_{xy} \cdot\Delta y + B_{xx} \cdot\Delta \dot{x} + B_{xy} \cdot\Delta \dot{y} \\ F_{y} & = F_{y0} + K_{yx} \cdot\Delta x + K_{yy} \cdot\Delta y + B_{yx} \cdot\Delta \dot{x} + B_{yy} \cdot\Delta \dot{y} \\ \end{aligned}$$
(4)

The stiffness and damping coefficients are the partial derivatives evaluated at the equilibrium position:

$$K_{xy} = \left( {\frac{{\partial F_{x} }}{\partial y}} \right)_{0} \;\;\;B_{xy} = \left( {\frac{{\partial F_{x} }}{\partial y}} \right)_{0}$$
(5)

The terms \(K_{xx}\) and \(K_{yy}\), just as \(B_{xx}\) and \(B_{yy}\), are direct coefficients of stiffness and damping respectively, while the terms \(K_{xy}\) and \(K_{yx} ,\,B_{xy}\) and \(B_{yx}\), are the cross coupled coefficients of stiffness and damping respectively.

According to Lund [4], the stability analysis can be obtained from the equation of motion of the bearing, considering a generic mass M:

$$\left\{ {\begin{array}{*{20}c} {M \cdot\Delta \mathop x\limits^{..} +\, B_{xx} \cdot\Delta \dot{x} + K_{xx} \cdot\Delta x + B_{xy} \cdot\Delta \dot{y} + K_{xy} \cdot\Delta y = 0} \\ {M \cdot\Delta \mathop y\limits^{..} +\, B_{yy} \cdot\Delta \dot{y} + K_{yy} \cdot\Delta y + B_{yx} \cdot\Delta \dot{x} + K_{yx} \cdot\Delta x = 0} \\ \end{array} } \right.$$
(6)

Assuming a solution in the form \(e^{st}\) to \(\Delta x\) and \(\Delta y\), being \(s = \lambda + i \cdot \omega\), and bearing in mind that if the real part of the solution is positive the system is stable, and if the real part is negative the solution is instable, the threshold of instability occurs when \(\lambda = 0\). In this case, Eq. (6) can be written in matrix form and the solution of the eigenvalue problem gives both following expressions:

$$M \cdot \omega^{2} = \frac{{K_{xx} \cdot B_{yy} + K_{yy} \cdot B_{xx} - K_{xy} \cdot B_{yx} - K_{yx} \cdot B_{xy} }}{{B_{xx} + B_{yy} }} = k_{0}$$
(7)
$$\omega^{2} = \frac{{\left( {K_{xx} - k_{0} } \right) \cdot \left( {K_{yy} - k_{0} } \right) - K_{xy} \cdot K_{yx} }}{{B_{xx} \cdot B_{yy} - B_{xy} \cdot B_{yx} }}$$
(8)

Equations (7) and (8) give critical mass \(M_{crit}\) and the precession frequency of the fluid film \(\omega_{0}\). Solving Eq. (6), instead, considering the portion of the rotor mass applied on the bearing, the eigenvalue problem gives a total impedance of the rotor-bearing system:

$$Z = \frac{{Z_{xx} + Z_{yy} }}{2} \pm \sqrt {\frac{1}{4} \cdot \left( {Z_{xx} - Z_{yy} } \right)^{2} +\, Z_{xy} \cdot Z_{yx} }$$
(9)

where: \(Z_{xx} = K_{xx} + i \cdot \omega \cdot B_{xx}\) is the mechanical impedance of the bearing for the direct coefficients in the x direction, and analogously for y and cross-coupled directions. From Eq. (9), the maximum and minimum bearing impedance can be obtained.

$$\left\{ {\begin{array}{*{20}c} {Z_{\hbox{max} } = K_{\hbox{max} } + j \cdot \omega \cdot B_{\hbox{max} } } \\ {Z_{\hbox{min} } = K_{\hbox{min} } + j \cdot \omega \cdot B_{\hbox{min} } } \\ \end{array} } \right.$$
(10)

If \(B_{\hbox{min} }\) is positive the bearing is stable. However, there is a frequency \(\omega_{0}\) in which \(B_{\hbox{min} } = 0\) and \(K_{\hbox{min} } = k_{0}\), namely, the threshold of instability. The previous condition happens when the precession frequency \(\omega_{0}\) reaches the natural frequency of the mass-spring system ω and, consequently, the rotor-bearing system becomes instable.

Another method to analyze the rotor-bearing stability is the logarithm decrement. This analysis depends on the overall dynamic behavior of the rotating system since it is derived from the modal damping factor. In this case, according to Cloud [5], the stability analysis considers the rate of decay of the free oscillation to determine the amount of damping present in the system. Hence, the free vibration can be written as:

$$x\left( t \right) = \left| x \right| \cdot e^{\lambda t} \cdot \cos \left( {\omega_{d} t + \phi } \right) = \text{Re} \left\{ {\left( {x_{1} + j \cdot x_{2} } \right)e^{st} } \right\}$$
(11)

Being \(\left| x \right|\) the vibration amplitude, \(\phi\) the phase angle, \(\omega_{d}\) the damped frequency, \(\xi\) the damping factor and s the complex eigenvalue, given by:

$$s = \lambda \pm j \cdot \omega_{d} = - \xi \cdot \omega \pm j \cdot \omega \cdot \sqrt {1 - \xi^{2} }$$
(12)

In this case, if \(\lambda\) is negative the system is damped and the free vibration vanishes with time, i.e., the system is stable. However, if \(\lambda\) is positive the amplitude increases with time turning the system unstable. However, it is usual to observe the logarithm decrement instead of the magnitude of \(\lambda\), as given in Eq. (13):

$$\delta = \ln \left( {\frac{x\left( t \right)}{{x\left( {t + \tau } \right)}}} \right) = - \frac{2 \cdot \pi \cdot \lambda }{{\omega_{d} }} = \frac{2 \cdot \pi \cdot \xi }{{\sqrt {1 - \xi^{2} } }}$$
(13)

According to Eq. (13), the threshold of instability is given when the logarithm decrement becomes negative.

3 Results

In order to obtain the dynamic behavior of the system and verify the natural frequencies and the threshold of instability, a rigid rotor (Fig. 1) was modeled by finite elements method, represented by the matrices of mass, gyroscopic effect, stiffness and damping. The model has 15 beam elements of circular cross-section and 3 rigid disk elements (Fig. 1). The dimensions of each element are given in Table 1.

Fig. 1
figure 1

Discrete model by finite elements used in the numerical simulation

Full size image
Table 1 Dimensions of the finite elements
Full size table

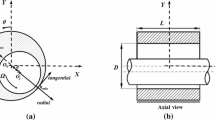
Regarding Fig. 1, the residual mass unbalance is represented by a mass of 0.0001 kg and an eccentricity of 0.001 m, located in nodes 3 and 13, respectively. Also, the hydrodynamic bearings are located in node 5 (first bearing) and node 11 (second bearing). Cylindrical radial bearings are considered in the numerical simulation. Figure 2 shows the geometric scheme of the bearings and Table 2 presents the operational conditions applied for the simulations. In the numerical model, the fluid film in contact with the shaft has the same tangential velocity, while the lubricant in contact with the bearing surface is static. In the THD model, however, the fluid shearing occurs and heats the oil, decreasing its viscosity. The viscosity drop changes the bearing behavior since the journal finds a new static equilibrium position to generate the same forces at the same rotation velocity. The new equilibrium position can influence the bearing stiffness and damping coefficients. Consequently, the HD and THD models give different results in the evaluation of the equivalent dynamic coefficients, due to different static equilibrium position found by those models at each rotational speed. As noticed in Fig. 3, the cross-coupled stiffness coefficients obtained by the THD model is lower than the one obtained by the HD model, while the direct ones are slightly higher. In the case studied here, the damping coefficients are not significantly modified by the viscosity change into the simulated frequency range. The THD model brings the cross-coupled and the direct coefficients closer than the HD model, and consequently, diminishes the bearings anisotropy, enlarging the stability range, as seen in Figs. 4 and 5.

Fig. 2
figure 2

Radial bearing geometry

Full size image
Table 2 Operational conditions
Full size table
Fig. 3
figure 3

Equivalent dynamic coefficients of the bearings: a stiffness; b damping

Full size image
Fig. 4
figure 4

Instability analyses by Lund critical mass theory: a natural and whirl frequencies. b Natural and whirl frequency detail

Full size image
Fig. 5
figure 5

System instability by logarithm decrement. a HD model. b THD model

Full size image

Lund [3] critical mass theory takes into account only bearing coefficients to predict the threshold of instability and it is formally developed for rigid and symmetrical rotors. The rotor-bearing system is considered as a mass-spring system where the spring equivalent stiffness is given by \(k_{0}\) (Eq. (7)). So, when the oil whirl frequency reaches the natural frequency of the mass-spring system (rotor-bearing system), it becomes instable.

Analyzing the system instability by this theory (Fig. 4), the different models changed the instability threshold, shifting it from 85 Hz in the HD model to 92 Hz in the THD model, making a wider stable range.

The same tendency is observed when the instability threshold is obtained by the logarithmic decrement method, i.e., the THD model makes the system more stable. In this case, the damping ratio method uses the entire rotor-bearing system to analyze the stability. In this case, the rotor is modeled by FEM to obtain the complete equation of motion of the system and the dynamic coefficients of stiffness and damping of the bearings are inserted in the matrices at the respective nodes corresponding to the bearings location. Then, the bearing anisotropy plays a fundamental role on the system stability, and since the THD model generates less anisotropic bearings, for this case, the threshold of instability occurs later than in the HD model.

Using the logarithm decrement diagram, Figs. 5, 6 and 7 show that the instability thresholds occur at 47 Hz for the HD model and 51 Hz for the THD model, since the damping ratio decay related to one of the bearings modes becomes zero. However, a second decay crossing the zero damping ratio occurs, also related to a bearing mode. However, it takes place at different rotation speeds in both models (HD: 85 Hz and THD: 92 Hz). Taking a closer look at the frequencies of the second crossing over the zero, it is possible to identify that the frequencies are the same obtained by the Critical Mass method presented by Lund. As the Critical Mass method considers the rotor-bearing as simplified mass-spring system, the only mode that can be excited is the translational (cylindrical) rigid mode, while in logarithmic decrement method the pivoted (conical) rigid mode can be excited as well. So, it’s understood that the instability, for the case studied here, is occurring for the pivoted mode and the corresponding instability threshold is lower than the translational mode (Fig. 8).

Fig. 6
figure 6

Bearing orbits for HD model: a 46 Hz. b 48 Hz

Full size image
Fig. 7
figure 7

Bearing orbits for THD model: a 50 Hz. b 52 Hz

Full size image
Fig. 8
figure 8

Operational modes: a HD model at 47 Hz; b HD model at 85 Hz; c THD model at 51 Hz; d THD model at 92 Hz

Full size image

4 Conclusion

The use of more complete lubrication models, as the THD model, for bearings analysis is sometimes necessary to better characterize the entire rotating system. Due to the changes in the fluid film viscosity, the hydrodynamic forces are modified and also the dynamic coefficients of stiffness and damping, that plays a major role on the instability analysis of rotating machines. Two different methods to analyze rotor-bearing system stability were investigated. The Critical Mass method depends only of bearing dynamic coefficients and is restricted for symmetrical and rigid rotors. The logarithmic decrement is based on the modal damping ratio of the entire system and is widely used in stability analysis. For the case studied, the Critical Mass gives a larger stability frequency range for the rotor when compared with the logarithmic decrement. The fact that Lund’s method can only predict instability for the translational rigid mode indicates that the threshold of instability pointed by the damping ratio is related to the pivoted rigid mode (HD: 47 Hz, THD: 51 Hz). Nevertheless, the threshold of instability was changed in both methods when the THD model was applied, because the anisotropy of the bearing is reduced in the THD model, indicating the importance of temperature effects mainly in high rotational speed machinery.