Modelling Water Hammer with Quasi-Steady and Unsteady Friction in Viscoelastic Pipelines

Abstract

The model of water hammer in viscoelastic pipelines was considered. Additional term describing the retarded deformation of the pipe wall was added to continuity equation. System of partial differential equations describing this type of flow was analyzed using the method of characteristics and finite difference method. To determine the unsteady wall shear stress, a new effective method of solution which corresponds to Zielke (laminar flow) and Vardy-Brown (turbulent flow) models were used. The convolution integral of local pressure history and derivative from the material creep function is found similarly to the efficient Zielke convolution solution presented by Schohl. The research was carried out with the assumption of a quasi-steady and unsteady character of resistance. The comparison of numerical simulation and experimental results was presented.

1 Introduction

An appropriate modelling of a physical phenomenon which occurs in the hydraulic transients is important for safety of a pipeline system. Well-chosen parameters of the system like pipe material, wall thickness or surge protection device can protect system from unpleasant consequences. The first common danger in hydraulic transients is associated with water hammer, which takes place after sudden valve closure. It caused unsteady flow, fast pressure and velocity pulsations, which can destroy components of the system. Polymer pipes exhibit a viscoelastic rheological behavior, that is why a prolonged delay in the mechanical response of the material is noticed during transient flow.

The study of the influence of the viscoelasticity of the conduit walls on the flow began in the 1960s. Hardung [12] described the physical phenomena which come into play in the arterial system as a consequence of heart action. He made a thorough study of the influence of internal wall friction and liquid viscosity on damping of pressure wave velocity. Also discussed were the limits of electric transmission line analogy to propagation of pulse waves in pipe systems. From the linearized dynamic equations of viscous incompressible fluid flow in visco-elastic tubes Martin [21] calculated frequency response of specific tube flow system. He concluded that realized calculations agree well with experiments made from Latex tubes. In 1970, Kokoshvili [20] derived the analytical solution for a system with low density polyethylene pipe, air chamber (as shock absorber) and a pump (designed to give an established flow rate). The milestone to modern modelling was deriving general equations of the transient flow in the viscoelastic properties by Rieutord and Blanchard [27]. Watters et al. [40] conducted water hammer experiments in PVC and PERMASTRAN (fiberglass-reinforced) plastic pipes. Their tests included buried and unburied pipes. Buried test pipes were more rigid, it lead to higher pressure wave velocities. For buried PERMASTRAN pipe measured pressure increment were 15–20% higher than calculated from Joukowski formula. Sadly, in this paper no pressure runs were presented. Fortunately, the results of the study can be found in the earlier report [39] written in Utah Water Research Laboratory which were commissioned by Johns-Manville Corporation (manufacturer of PVC pipes). Meissner [22] incorporated the complex creep compliance into the unsteady momentum and continuity equations then derived the wavespeed and damping factor for an oscillating pressure wave propagating in a thin-walled viscoelastic pipe. Rieutord and Blanchard [28] presented a theoretical study of the effect of viscoelastic properties of pipe wall material on transients. Gally et al. [9] compared the calculated (using finite difference method) pressure runs, with waterhammer laboratory test data in polyethylene pipes, showing a good agreement between numerical and experimental results. Güney [11] later proposed a modified model that took into account the effects of time-varying: diameter, pipe thickness, parameter representing pipe constraints. Also, Güneys model simulated cavitation effects and used Zielke frequency-dependent friction (valid only for laminar flow). Hirschmann [13] studied the resonating conditions in viscoelastic pipes with a modified impedance method, later Franke and Seyler [8] utilized an impulse response method to calculate water hammer. This method was later further extended and modified by Sou and Wylie [32, 33]. Horlacher [14] presented pressure transients results from real HDPE water supply pipes (1625 and 2314 m long) buried in ground near Halle and Oschatz (Germany).

Waterhammer in viscoelastic pipes has been experimentally investigated at the beginning of XXI century by Covas et al. [4, 5], who conducted tests on a 277 m high density polyethylene (HDPE) pipeline which where a part of test stand build in Imperial College London. In this work, the authors presented also the new simplified model that allowed a fast calculation of pressure runs in viscoelastic conduit. Weinerowska-Bords [41] concluded that application of a viscoelastic model is connected with many problems of different natures, of which very important is parameter estimation. Soares et al. [31] and Duan et al. [6] argued that the combination of unsteady friction and pipe wall viscoelasticity have similar effects on the transient pressures and that this two mechanisms must contribute to an accurate calculation of the damping of pressure waves. Brunone and Berni [3] studied the significance of the unsteady pipe friction effect and its interaction with viscoelasticity. Bergant et al. [1] investigated transients accompanying waterhammer experiments in a large-scale pipeline apparatus made of polyvinyl chloride (PVC). The authors of [2] conclude that the incorporation of both unsteady skin friction and viscoelastic pipe wall behaviour in the hydraulic transient model contributed to a more favourable fitting between numerical results and observed data. Keramat et al. [17] investigated cavitated flows in viscoelastic pipes using method of characteristics, and concluded that column separation can hardly result in pressures higher than the Joukowsky pressure (even for fast closure of an upstream valve). Another conclusion was that the simplest model (DVCM) of column separation provided acceptable results for cavitating flow in viscoelastic pipes. Later [18] these authors have extended their model so it could simulate the FSI (fluid structure interaction) effects. In conclusion to their paper they state that damping in transient flow may come from (unsteady) friction, (unsteady) valve resistance, small amounts of air, wall viscoelasticity, fluid structure interaction, rubbing, ratcheting and other non-elastic behaviour of supports, radiation to surrounding soil and water, pipe lining, etc. (many of these effects are unknown). When these effects are not (properly) included in the transient solver, the Kelvin-Voigt model will not only represent viscoelasticity, but all the rest too. In 2013 Keramat [16] proposed to use a time-dependent Poisson’s ratio in standard Covas viscoelastic model, next year in a collaboration with Haghighi [15] showed a straightforward transient-based approach for the creep function determination.

Recently many authors [7, 23, 42] concluded that one element Kelvin-Voigt model is sufficiently good to obtain the satisfactory solution. Kodura [19] showed that, the characteristic of butterfly valve closure has a significant influence on water hammer in PE pipes for closure times higher than 25% of the return time of the reflected pressure wave. For shorter closures the maximum pressure could be calculated with Joukowsky’s formula. Ferrante and Capponi [7] introduced generalized viscoelastic Maxwell model, based on fractional derivatives. After several water hammer tests for HDPE and PVC-O they conclude that this model performs slightly better than the well-known generalized Kelvin-Voigt model. The optimization function for this new model seems to improve the calibration reliability and speed.

The goal of this paper is to determine the influence of unsteady wall shear stress on velocity and pressure pulsation. Unsteady wall shear stress plays an important role in modelling transients in pipes made from elastic materials (e.g. brass or steel) [37, 44]. The question is: what is the role of unsteady wall shear stress in modelling transients in viscoelastic pipes? The answer is not clear at this moment. The preliminary Matlab simulations showed that in particular cases quasi-steady friction gives satisfactory results.

2 Modelling Liquid Flow in a Viscoelastic Pipe

2.1 Modified Solution

Polymer pipeline do not respond according to Hook law when subjected to a certain instantaneous stress. Strain can be decomposed into a sum of instantaneous elastic strain $\varepsilon _e$ and a retarded strain $\varepsilon _r$ [5, 11, 36]:

$$\begin{aligned} \varepsilon (t)=\varepsilon _e+\varepsilon _r(t). \end{aligned}$$

(1)

The continuity equation is very similar to the one used in elastic pipeline, but does include an additional term:

$$\begin{aligned} \frac{1}{\rho c^2} \frac{\partial p}{\partial t} + \frac{\partial v}{\partial x} + 2\frac{\partial \varepsilon _r}{\partial t}=0, \end{aligned}$$

(2)

where: p – pressure [Pa], t – time [s], v – mean velocity in pipe cross section [m/s], $\rho$ – density of the fluid [${\text {kg}}/{\text {m}}^3$], c – pressure wave speed [m/s].

The retarded strain is a convolution integral of pressure and derivative of the creep function J which describes viscoelastic behavior of the pipe material:

$$\begin{aligned} \varepsilon _r(t)=\int _0^t \frac{\alpha D}{2e}\left( p(t-u)-p(0) \right) \frac{\partial J(u)}{\partial u} du, \end{aligned}$$

(3)

where: D – pipe inside diameter [m], e – pipe wall thickness [m], $\alpha$ – pipe wall constraint coefficient [−], J(u) – polymer creep function $\left[ {\text {Pa}}^{-1}\right]$.

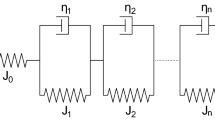
The creep function in generalized Kelvin-Voigt model is time dependent

$$\begin{aligned} J(t)=J_0+\sum _{i=1}^k J_i\left( 1-e^{-\frac{t}{T_i}} \right) , \end{aligned}$$

(4)

where: $J_0$ – creep compliance equal to the inverse modulus of elasticity ($J_0 = 1/E_0$), $T_i$ – the retardation time of the dashpot of i-element.

This function should be determined experimentally for polymer pipelines in independent mechanical tests. Because this function consists of at least a few terms

$$\begin{aligned} \varepsilon _r(t)=\sum _{i=1}^k\varepsilon _{ri}(t) and \frac{\partial \varepsilon _r(t)}{\partial t}=\sum _{i=1}^k \frac{\partial \varepsilon _{ri}(t)}{\partial t}. \end{aligned}$$

(5)

The derivative of the creep function is

$$\begin{aligned} \frac{\partial J(t)}{\partial u}=\frac{\partial }{\partial t}\left( J_0+\sum _{i=1}^k J_i\left( 1-e^{-\frac{t}{T_i}}\right) \right) =\sum _{i=1}^k \frac{J_i}{T_i}e^{-\frac{t}{T_i}}. \end{aligned}$$

(6)

So, Eq. (3) becomes

$$\begin{aligned} \varepsilon _r(t)=\int _0^t \frac{\alpha D}{2e}\left( p(t-u)-p(0) \right) \cdot \left( \sum _{i=1}^k \frac{J_i}{T_i}e^{-\frac{u}{T_i}} \right) du \end{aligned}$$

(7)

and its partial derivative with respect to time t:

$$\begin{aligned} \frac{\partial \varepsilon _r(t)}{\partial t}= \frac{\alpha D}{2e}\int _0^t \frac{\partial }{\partial t} \left( p(t-u)-p(0) \right) \cdot \left( \sum _{i=1}^k \frac{J_i}{T_i}e^{-\frac{u}{T_i}}\right) du. \end{aligned}$$

(8)

By analogy with the modeling of hydraulic resistance, where $\sum _{i=1}^k m_i e^{-n_i \frac{\nu }{R^2}u}=w(u)$, we obtain

$$\begin{aligned} \sum _{i=1}^k \frac{J_i}{T_i} e^{-\frac{u}{T_i}}=w_J(u) \end{aligned}$$

(9)

and as

$$\begin{aligned} \frac{\partial }{\partial t} \left( p(t-u)-p(0) \right) =\frac{\partial }{\partial t}p(t-u)-\frac{\partial }{\partial t}p(0)=\frac{\partial }{\partial t}p(t-u)-0, \end{aligned}$$

(10)

one obtains

$$\begin{aligned} \frac{\partial \varepsilon _r(t)}{\partial t}=\frac{\alpha D}{2e}\int _0^t \frac{\partial p(u)}{\partial t} \cdot w_J(t-u)du. \end{aligned}$$

(11)

An efficient numerical solution of this integral is presented by Schohl [30]:

$$\begin{aligned} \frac{\partial \varepsilon _r}{\partial t}(t+\varDelta t) \approx \frac{\alpha D}{2e} \sum _{i=1}^k \underbrace{\left( x_i(t) \cdot e^{- \frac{\varDelta t}{T_i}}+\frac{J_i}{\varDelta t} \left[ 1-e^{- \frac{\varDelta t}{T_i}} \right] \left( p(t+\varDelta t)-p(t) \right) \right) }_{x_i(t+\varDelta t)}, \end{aligned}$$

(12)

where: $\varDelta t$ – in method of characteristics a constant time step [s]. Writing constant as

$$\begin{aligned} A_i=\frac{J_i}{\varDelta t}\left[ 1-e^{-\frac{\varDelta t}{T_i}} \right] \text { and } B_i=e^{-\frac{\varDelta t}{T_i}}, \end{aligned}$$

(13)

one has

$$\begin{aligned} \frac{\partial \varepsilon _r}{\partial t}(t+\varDelta t)= & {} \frac{\alpha D}{2e} \sum _{i=1}^k \underbrace{\left( x_i(t) \cdot B_i +A_i \cdot p(t+\varDelta t) - A_i \cdot p(t)\right) }_{x_i(t+\varDelta t)}\end{aligned}$$

(14)

$$\begin{aligned}= & {} \frac{\alpha D}{2e} \sum _{i=1}^k A_i \cdot p(t+\varDelta t)-\frac{\alpha D}{2e} \sum _{i=1}^k \left( A_i \cdot p(t) - x_i(t)\cdot B_i \right) \end{aligned}$$

(15)

$$\begin{aligned}= & {} p(t+\varDelta t) \frac{\alpha D}{2e}\sum _{i=1}^k A_i - \frac{\alpha D}{2e} \sum _{i=1}^k \left( A_i \cdot p(t) - x_i(t) \cdot B_i \right) \end{aligned}$$

(16)

Now assuming additional constants we obtain

$$\begin{aligned} F=\frac{\alpha D}{2e}\sum _{i=1}^kA_i \text { and } G=\frac{\alpha D}{2e}\sum _{i=1}^k \left( A_i \cdot p(t)-x_i(t) \cdot B_i \right) , \end{aligned}$$

(17)

the final simplified equation that describe the derivative of retarded strain has the form

$$\begin{aligned} \frac{\partial \varepsilon _r}{\partial t}(t+\varDelta t)=p(t+\varDelta t) \cdot F-G. \end{aligned}$$

(18)

The presented solution simplifies the calculation process to analyze the transients in engineering polymer pipes.

2.2 General Final Equations

For laminar flow where Darcy-Weisbach friction factor is $\lambda =64/Re$ the complete set of equations describing this type of flow (continuity and motion) have following form:

$$\begin{aligned} \left\{ \begin{array}{rcc} \frac{1}{\rho c^2}\frac{\partial p}{\partial t}+\frac{\partial v}{\partial x}+\alpha \frac{D}{e}\int _0^t\frac{\partial p(u)}{\partial t} \cdot w_J(t-u)du&{}=&{}0,\\ {\rho }\frac{\partial v}{\partial t}+\frac{\partial p}{\partial x}+\frac{32 \mu }{D^2}v + \frac{16 \mu }{D^2}\int _0^t \frac{\partial v(u)}{\partial t} \cdot w(t-u) du&{}=&{}0, \end{array}\right. \end{aligned}$$

(19)

where: $\mu$ – dynamic viscosity of fluid [${\text {Pa}} \cdot {\text {s}}$].

There is no known analytical solution for this system of hyperbolic partial differential equations (also for a more complicated turbulent case). The initial condition is that on the length of the pipe from $x=0$ to $x=L$ the mean velocity is constant $v_0=const$, and that the linear pressure decrease in the direction of flow occurs on the pipe length. The reservoir pressure can be assumed as constant not only for the steady initial state, but also for the transient state that occurs after quick closing of the valve. On the walls of the pipe the no slip condition is generally assumed so the velocities on the walls is set to zero. At starting time $t=0$ an instantaneous valve closure is assumed on one pipe boundary (with valve) which means that the velocity changes there instantly from $v_0$ to 0. Next, the pressure oscillation of fluid occurs until the final full suppression. The final pressure on the pipe length from $x=0$ to $x=L$ is then equal to the constant reservoir pressure $p=p_R$ and the mean velocity is $v=0$ through the entire length L of pipe. The $w(t-u)$ is a weighting function with fixed shape, and the $w_J(t-u)$ function does also have a fixed shape and it describes the mechanical material properties of the pipe.

Until analytical solution is found for above formulated system, calculations must be performed using numerical methods. In this work a method of characteristics is used with classic constant rectangular grids, to avoid problems with interpolation.

3 Simulations

3.1 Experimental Setup Details

The experimental setup was composed of three main parts [9,10,11]: a constant pressure reservoir, a horizontal low density polyethylene test pipe (LDPE – with Poisson’s ratio $\nu _P = 0.38$) and a quick-closing piston valve at the downstream end of the $L=43.1$ m long pipe as shown in Fig. 1. The pipe has an inside diameter $D=0.0416$ m and a wall thickness $e=0.0042$ m. Initial steady-state flow was determined by measuring volumes of water collected in a fixed time. The experimental uncertainty was estimated to within ${\pm } 3$ kPa for pressure and ${\pm } 1$% for the initial flow velocity. Several transient tests were run for varied initial flow velocity and water temperature. Temperature strongly influences the mechanical behaviour of the pipe-wall material. The number of tests were conducted at various temperatures to determine the reliability of the values of creep function (Fig. 2) coefficient presented in Table 1. In all cases the closure time of the valve was $T_c=0.012$ s.

Fig. 1

Schematic diagram of Güney’s experimental setup

Fig. 2

Creep compliance J(t) of LDPE at different temperatures: lin-lin space (left), log-log space (right)

Table 1 Creep function coefficients (estimated by Güney)

It is not clear, as the authors of the experimental setup do not mention it [9,10,11], but according to the experimental setup schematic diagram it looks like that in all cases the liquid flow into the atmosphere. Güney in his Ph.D. work [10] presented the tank pressures values as a total dynamic heads h. The absolute reservoir pressure can be derived from the following formula:

$$\begin{aligned} p_R=p_{atm.}+hg \rho , \end{aligned}$$

(20)

where: g – acceleration due to gravity $\left[ {\text {m}}/{\text {s}}^2\right]$.

Calculated values of reservoir pressures $p_R$, and all other important parameters needed for numerical simulation are presented in Table 2.

Table 2 Case details

In Güney’s works [9,10,11] there is no details about pressure wave speed values. In Table 2 the data were calculated for theoretical values of water density, bulk modulus, viscosity and using Young modulus $E_0=1/J_0$. Unfortunately, preliminary simulations have shown that the simulated results with such values of c (and with creep function coefficients from Table 1) significantly deviated from the experimental results. The values for presented simulations where therefore calibrated accordingly (Case 1 and 4 – 425 m/s; Case 2 – 375 m/s; Case 3 and 6 – 390 m/s; Case 5 – 400 m/s). In all numerical simulations, the pipeline was divided into 64 equally long elements ($N=64$ [−], $\varDelta x \approx 0.67$ [m]). With use of Poisson’s ratio, one can determine the pipe-wall constraint coefficient $\alpha =0.97$. As in some simulations the unsteady friction were calculated, in this work a new simplified method [34, 35], and a scaling procedure [38] were needed to get proper values of weighting functions coefficients. A characteristic roughness size $k_s=1.5 \times 10^{-6}$ were assumed for LDPE pipes.

3.2 Results of Simulations

Figure 3 provides detailed comparisons between measured and calculated results corresponding to the proposed mathematical model (where: unsteady friction – UF, quasi-steady friction – no UF and no friction at all – no F), which included the viscoelastic behavior of the pipe wall material. A comparative study of these pressure runs disclosed the following:

• 1. the temperature and associated change in properties representing the conduit and liquid affect the amount of pressure amplitudes that appear in the analyzed first four second of water hammer. The smaller the temperature, the more frequent the pressure pulsation. For approximately the same initials velocities $v_0 \approx 0.55$ ${\text {m}}/{\text {s}}$ (Case 2–Case 5), in Case 2 there are five visible pressure amplitudes and in the Case 5 there is only four;

• 2. low pressures (runway valleys) was more accurately simulated with use of unsteady-friction model, while high (amplitude peaks) using a quasi-steady friction model;

• 3. surprisingly good results were obtained with complete absence of hydraulic resistance;

• 4. the most important factor in the modelling of non-stationary flows in polymeric pipes looks to be the selection of the weight function $w_J$, which is a derivative of the creep function.

Fig. 3

Comparison of computed and measured transient pressures at the downstream end of the pipe

3.3 Short Discussion

As it was noticed from completed simulations (Fig. 3), the maximal pressure in viscoelastic pipes occurs not directly after valve closing but after two time steps (Fig. 4). A formula for pressure increase can be derived using the characteristic method. According to Fig. 5 presenting the method of characteristics grid near the valve boundary the maximum pressure will occur in point M, and the final equations are:

$$\begin{aligned} p_{max}=\frac{p_S-c \rho v_0 + \frac{c \rho \varDelta t v_0 |v_0| \lambda _0}{2D}+2c^2 \rho \varDelta t G_D}{1+2c^2 \rho \varDelta t F}, \end{aligned}$$

(21)

where:

$$\begin{aligned} G_D= & {} p_D(F-H)+p_AH, \end{aligned}$$

(22)

$$\begin{aligned} H= & {} \frac{\alpha D}{2e}\sum _{i=1}^k A_i \cdot B_i. \end{aligned}$$

(23)

In Eq. (22) $p_D$ is calculated from the same formula as (21) but $G_D$ need to be replaced by the product of initial pressure and constant F ($p_AF$).

Fig. 4

Example of maximum pressures on second time steps

Fig. 5

Calculation of maximum pressures on first amplitude

From Eq. (21) one can see that the unsteady friction does not have any effect on the maximum pressure rise on the first amplitude, the opposite role fulfills the shape of assumed viscoelasticity creep function described by the generalized Kelvin-Voigt model. Also, this formula shows the weak side of the analyses fluid flow model in viscoelastic pipes. Detailed results obtained with the assumption of various time steps will be presented and discussed in an extended version of this work and during the presentation at the conference.

In the opinion of many researchers for a given temperature, the creep function depends on the stress time-history and pipe constraints, and it cannot be obtained by means of mechanical tests on pipe samples [4, 26]. So, the only way to predict the Kelvin-Voigt parameters is when transient tests can be executed on an existing pipe and evaluated as the unknowns of an inverse transient analysis (ITA) [5, 15, 31, 42, 43]. Pezzinga [25] found a decrease in the modulus of elasticity over time, and a correlation of the retardation time with the oscillation period. Moreover, some authors pointed out that the wave velocity in plastic pipes may be calculated as a function of the length of the pipeline. As an example, Mitosek with Chorzelski noticed the velocity increase when the length of the MDPE pipe decrease [24]. In a family of polyethylene pipes, one can distinguish HDPE, MDPE, LDPE, HPPE and for each type the producers give the range of the values that Young’s modulus can take [41]. If the values are taken from handbooks of polymers the range of values can also differ slightly: the modulus of elasticity for MDPE takes the values 0.6–0.8 GPa, while for HDPE one can find the values of Young’s modulus of a range 0.7–1.0 GPa [4] or even 0.6–1.4 GPa [29]. In consequence, the values of pressure wave speed calculated theoretically may differ significantly from the observed ones. However, in the perception of the authors of this paper what mainly affects the results of the simulation, is the shape of the creep function, and in particular its derivative, which occurs in the convolutional integral in the continuity equation. By changing the coefficients of the exponential terms describing this function one can “control” significantly simulated pressure run (increase-decrease the value of the successive pulsation and pressure amplitudes).

4 Conclusions

The main purpose of the presented research was to determine the influence of the applied friction model on the obtained simulation results. Studies have shown that unsteady friction affects the frequency of emerging pressure amplitudes. Omission of unsteady friction on the modeling stage increases the frequency and values of the peak pressures on following amplitudes. It follows that unsteady friction are closely related to the velocity of the pressure wave propagation.

However, to thoroughly analyze the impact of the applied friction models, new experimental studies are needed. They should be made for small Reynolds numbers ($Re <6000$) in a simple horizontal pipeline. The length of the conduit should be at least 150 m so as to minimize the effect of local resistance on the discharge from the pressure reservoir. There should be no elbows in this system that distort simulated results by introducing additional local resistance (unknown for unsteady flows).

The sub-objective goal was to study the flow model itself. The research done outlined some of the problems associated with the experimental creep function that will be solved and shown in the extended version of this work.