Numerical modeling of the fluid hammer phenomenon of viscoelastic flow in pipes

Abstract

In this study, the fluid hammer of viscoelastic flow in pipes is studied numerically. Here, the Oldroyd-B model is used as the constitutive equation. This model is suitable for dilute viscoelastic solutions and Boger liquids. The numerical solution is obtained using a two-step variant of the Lax–Friedrichs (LxF) method. The derived equations are non-dimensionalized, and the effect of Deborah and Reynolds numbers and the viscosity ratio on the behavior of viscoelastic flow during fluid hammer caused by the sudden closure of a downstream valve in a reservoir-pipe-valve system is investigated in detail. Present results show that the attenuation of the laminar fluid transient is affected by viscoelastic properties of the non-Newtonian fluid. Moreover, the results indicate that the shear stress in viscoelastic fluid hammer phenomena is significantly lower than those in Newtonian fluid with similar viscosity.

1 Introduction

“Fluid hammer” is a transitional flow caused by sudden or quick changes in flow conditions. This can harm the piping structure and therefore is a highly crucial phenomenon. The most common causes are stopping or starting the pumps or closing a valve. The problem of studying transient fluid can also be generalized for cases such as blood in veins, which is pumped by the heart and the analysis can be applied to that process [1]. Water as a typical example of fluids of Newtonian nature has been studied numerously. A detailed review of the matter has been given by Ghidaoui et al. [2]. Computational techniques for these types of fluids are built on the mass and momentum equations, which are easily solvable using the characteristics approach and generally provide an accurate prediction of the maximum pressure rise which usually occurs during the first pressure peak [3]. Streeter [4] developed a numerical model by using a constant value of the turbulent friction factor. The progress of the first group of numerical models originated in 1968 by Zielke [5]. In his study, an equation was derived which related the wall shear stress in transitional laminar pipe flow to the instantaneous mean velocity and to the weighted past velocity changes and concluded that frequency-dependent effects of viscosity can be included into the one-dimensional model of transient flow using the method of characteristics. Generally, unsteady friction models and the relevant computational methods have always been the subject of various research projects at the research centers all over the world. Multiyear effort of numerous researchers has been resulted in developing miscellaneous models of hydraulic transients with the unsteady hydraulic resistance taken into account. The most widely used models consider extra friction losses to depend on a history of weighted accelerations during unsteady phenomena or on instantaneous flow acceleration. Procedures for improving the computational efficiency of Zielke’s method [5] were proposed by Trikha [6], Suzuki et al. [7] and Schohl [8]. Moreover, Vardy et al. [9, 10] adopted an approach similar to that of Zielke [5] and developed a weighting function model to represent unsteady friction in turbulent flows. This was carried out by approximating turbulent pipe flow as a laminar annulus surrounded by a uniform core. An alternative approach was proposed by Brunone et al. [11, 12] in which the unsteady viscous effects were related to the mean local and convective acceleration terms. Vardy et al. [13] also studied frozen-viscosity models of unsteady wall shear stress. In their paper, first, detailed predictions from a validated CFD method were used to derive baseline solutions with which predictions based on approximate models can be compared. Then, alternative solutions were obtained using various prescribed frozen-viscosity distributions. Finally, they resulted that no frozen-viscosity distribution performs well for large times after the commencement of an acceleration. Shamloo et al. [14] presented a review of unsteady friction models for transient pipe flow. They considered models in which instantaneous wall shear stress is the sum of the quasi-steady value plus a term in which certain weights are given to the past velocity changes in one group and other models in another group and concluded that Zielke [5] model yields better conformance with the experimental data [15]. Urbanowicz [16] modeled hydraulic losses during transient flow of liquids in pressure lines one dimensionally. In his work, unsteady pipe wall shear stress was presented in the form of a convolution of liquid acceleration with a weighting function. The defined weighting functions depended on the dimensionless time and the Reynolds number. The results of pressure pulsation obtained when taking into account cavitating flow, or not, were surprising in the sense that the weighting function did not need to be built by a lengthy sum of exponential terms to accurately simulate the transient event. Recently Ioriatti et al. [17] proposed a new more efficient approach for evaluating the convolution integral of the unsteady wall shear stress. In this work, the authors consider the case in which instead of water, a non-Newtonian viscoelastic fluid flows in the pipe, and therefore, this phenomenon can be called “viscoelastic fluid hammer.” The term “viscoelastic fluid hammer” speaks of transients of viscoelastic fluid caused by sudden alteration in the conditions of flow. Unlike Newtonian fluid hammer, there is not a great amount of work on the non-Newtonian fluids. Papers such as [18, 19] studied flow start-up of viscoplastic fluid as well as thixotropic ones, which shows some similarities to the fluid hammer problem. In flow start-ups, a pressure step change is forced at the pipe inlet and the pipe outlet is fully opened. The main difference between these two problems is that fluid hammer involves much faster transients, as compared to the transients in waxy simple oil restart flows. The valid article related to non-Newtonian fluid hammer can be found in Wahba [20]. He studied shear-thinning and shear-thickening effects on non-Newtonian fluid hammer and concluded that the shear-thickening behavior results in more rapid attenuation of the fluid transient. In fact, in modeling of the non-Newtonian fluid hammer phenomenon, the viscoelasticity of the fluid has not been considered adequately and its effect on this process is still unknown.

Viscoelastic fluids are a common form of non-Newtonian fluid. They can exhibit a response that resembles that of an elastic solid under some conditions, or the response of a viscous liquid under other conditions. In these fluids, contrary to the Newtonian ones, a linear relation between the stress tensor and the rate of deformation tensor does not hold. Therefore, they need more complex constitutive relationships to close the system of equations that has to be solved [21]. A survey of numerical methods of viscoelastic fluids has been presented by Owens and Timothy [22]. In the field of occurrence of fluid hammer phenomenon in viscoelastic pipes, there have been some applied studies. Ramos et al. [23] discussed the importance of the implementation of a viscoelastic constitutive law for plastic pipes and also the relevance of the unsteady friction with respect to the steady one. Their results show that the pressure wave dissipation is more sensitive to the viscoelastic damping effects than to the unsteady friction losses. Furthermore, Duan et al. [24] demonstrated that the viscoelastic effects are deeply more significant when the retardation time is less than the wave travel time along the entire pipeline length. Bertaglia et al. [25] studied numerical methods for hydraulic transients in viscoelastic pipes. In his work, a wide and critical comparison of the capability of method of characteristics, explicit path-conservative (DOT solver) finite volume method and semi-implicit staggered finite volume method was presented. Covas et al. [26] studied the dynamic effect of pipe wall viscoelasticity in hydraulic transients; their major challenge was the distinction between frictional and mechanical dynamic effects. They calibrated and tested the¹ HTS considering these two effects separately. Finally, they tested the HTS using creep measured in a mechanical test, neglecting unsteady friction and obtained a good agreement. Meniconi et al. [27] investigated the analysis of the interaction between water hammer pressure waves and sudden changes of cross-sectional area in complex viscoelastic pipe systems, from both the laboratory and numerical modeling point of view. Laboratory tests concerned pipe systems in which a partial blockage was simulated by means of a small-bore pipe of different lengths.

According to the literature, the previous studies are limited to Newtonian fluid hammer or water hammer with viscoelastic pipes and a few studies have been done in the field of non-Newtonian fluids and none of them considered the effects of viscoelastic fluid properties on fluid hammer phenomenon. However, a wide range of industrial processes including most multi-phase mixtures, foods, pharmaceuticals, agricultural chemicals, synthetic propellants, and slurry fuels involve the flow of viscoelastic fluids, suggesting that the realm of viscoelastic fluid transients needs to be scrutinized. For example, in chemical and process industries, it is often required to pump fluids through a pipe from storage to various processing units and/or from one plant site to another; consideration of issues associated with sudden stopping of flow in the pipe is necessary.

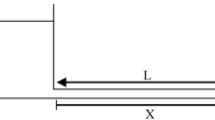
The objective of the present study is to investigate the effects of viscoelastic fluid properties on the fluid hammer phenomenon. Firstly, two equations representing the conservation of mass and momentum which govern the transitional flow for non-Newtonian fluids and the Oldroyd-B model relation are derived and then LXF numerical method is used to discretize the governing equations of viscoelastic fluid hammer. Computational results are provided in terms of the time history of pressure head at critical points of a pipe such as at the valve and the midpoint of the pipe. The results reveal that the viscoelastic fluid effects significantly contribute to attenuation time of transient flow and shear stress values. To our knowledge, this study represents the first attempt at the simulation of viscoelastic fluid hammer due to the sudden closure of a downstream valve in a simple reservoir-pipe-valve system. The schematic shape of the problem is shown in Fig. 1.

Fig. 1

Schematic of the reservoir-pipe-valve system

Figure 1 shows that the pipe system consists of a reservoir at the upstream end of the pipeline and a valve at the downstream end discharging to the atmosphere.

2 Formulation

2.1 Governing equations

The equations for fluid transients in pipes can be generally stated as the following set of continuity and axial momentum equations. The continuity equation for transient pipe flow in a cylindrical coordinate system considering axial symmetry is as follows [28]:

$$ \frac{\partial h}{\partial t} + v_{z} \frac{\partial h}{\partial z} + \frac{{c^{2} }}{g}\left( {\frac{1}{r}\frac{{\partial (rv_{r} )}}{\partial r} + \frac{{\partial v_{z} }}{\partial z}} \right) = 0 $$

(1)

where $v_{z}$ and $v_{r}$ represent the axial and radial velocity components, respectively, $c$ is the pressure wave speed, $H$ is the pressure head, and $t$ is time. The momentum equation in cylindrical coordinates in the axial direction is [28]:

$$ \rho \left[ {\frac{{\partial v_{z} }}{\partial t} + v_{r} \frac{{\partial v_{z} }}{\partial r} + v_{z} \frac{{\partial v_{z} }}{\partial z}} \right] + \frac{\partial p}{\partial z} - \left[ {\frac{1}{r}\frac{{\partial (r\tau_{rz} )}}{\partial r}} \right] = 0 $$

(2)

where $\rho$ is density,$p$ is pressure, $\tau_{rz}$ is stress shear in the liquid and:

$$ c^{2} = \frac{{\frac{{E_{f} }}{\rho }}}{{1 + k_{p} \frac{{E_{f} D}}{{eE_{p} }}}} $$

(3)

here, $E_{f}$ is the bulk modulus of compressibility for the fluid, $E_{p}$ is the Young’s modulus of elasticity for the pipe material, $e$ is the pipe thickness, $D$ is the pipe diameter, and $k_{p}$ is a function of Poisson’s ratio for the pipe material, $\upsilon_{p}$, as follows [20].

Since, in the present study elastic pipe with expansion joints in modeling was considered, according to Table 1, the value of coefficient is equal to 1 [20]. Using order of magnitude analysis, Wahba [29] and Ghidaoui et al. [2] showed that the nonlinear convective terms could be neglected from the continuity and axial momentum equations, since the pressure wave speed is several orders of magnitude larger than the flow velocity. Moreover, it should be noted that the radial velocity in the laminar flow at the pipe wall and at the centerline is zero.

Table 1 Variation of coefficient $k_{p}$ with Poisson’s ratio [20]

The problem modeling is done one dimensionally, so for fluid hammer modeling with viscoelastic fluid, using the above assumptions, Eqs. (1) and (2) can be integrated across the pipe cross section and the transitional pipe flow model takes the following form:

$$ \frac{\partial H}{\partial t} + \frac{{c^{2} }}{g}\frac{{\partial \overline{V} }}{\partial z} = 0\, $$

(4)

$$ \frac{{\partial \overline{V} }}{\partial t} + g\frac{\partial H}{\partial z} - \frac{2}{\rho R}\left. {\tau_{rz} } \right|_{r = R} = 0 $$

(5)

where $\overline{V}$ is the average cross-sectional velocity and R is the pipe radius.

$$ \begin{aligned} \overline{V} = \frac{1}{A}\int {v_{z} dA} \hfill \\ H = \frac{1}{A}\int {hdA} . \hfill \\ \end{aligned} $$

(6)

2.2 Constitutive equations

In this paper, Oldroyd-B model is used as the constitutive equation. This model is suitable for dilute polymeric solutions and especially the Boger liquids. It is usually used to investigate the effect of fluid elasticity in the absence of nonlinearity of material modulus. The general form of Oldroyd-B model is as follows [28]:

$$ {\varvec{\uptau}} + \lambda \mathop {\varvec{\uptau}}\limits^{\nabla } = \eta \left( {{\dot{\mathbf{\gamma }}} + \theta \mathop {{\dot{\mathbf{\gamma }}}}\limits^{\nabla } } \right) $$

(7)

where $\tau$ is the stress tensor, $\eta$ is viscosity, $\lambda$ is relaxation time, $\theta$ is retardation time, and $\nabla$ is the upper convected derivative which is defined as:

$$ \mathop {\mathbf{A}}\limits^{\nabla } = \frac{{{\mathbf{DA}}}}{{{\mathbf{D}}t}} - \left( {(\nabla {\mathbf{v}})^{T} \cdot {\mathbf{A}} + {\mathbf{A}} \cdot (\nabla {\mathbf{v}})} \right), $$

(8)

where A is an arbitrary tensor. In Eq. (7), the term ${\dot{\mathbf{\gamma }}}$ is shear rate, and $\mathop {{\dot{\mathbf{\gamma }}}}\limits^{\nabla }$ is an upper convected derivative of the shear rate defined as:

$$ {\dot{\mathbf{\gamma }}} = \left( {\nabla {\mathbf{v}}} \right) + (\nabla {\mathbf{v}})^{T} $$

(9a)

$$ \mathop {{\dot{\mathbf{\gamma }}}}\limits^{\nabla } = \frac{{D{\dot{\mathbf{\gamma }}}}}{Dt} - \left( {(\nabla {\mathbf{v}})^{T} \cdot {\dot{\mathbf{\gamma }}} + {\dot{\mathbf{\gamma }}} \cdot (\nabla {\mathbf{v}})} \right), $$

(9b)

where $\frac{{D{\dot{\mathbf{\gamma }}}}}{Dt}$ is complete derivative of polymer shear stress tensor, $\nabla {\mathbf{v}}$ is velocity gradient, and $T$ is transpose operator [28]. The Oldroyd-B model is usually considered for a polymeric solution in which the polymeric additives with upper-convected Maxwell model (UCM) are solved in a Newtonian solvent. Therefore, the stress of Oldroyd-B model can be expressed as

$$ {\varvec{\uptau}} = {\varvec{\uptau}}_{p} + {\varvec{\uptau}}_{s} $$

(10a)

$$ {\varvec{\uptau}}_{p} + \lambda \mathop {\varvec{\uptau}}\limits^{\nabla }_{p} = \eta_{p} {\dot{\mathbf{\gamma }}} $$

(10b)

$$ {\varvec{\uptau}}_{s} = \eta_{s} {\dot{\mathbf{\gamma }}} $$

(10c)

where subscripts s and p denote the Newtonian solvent and polymeric additives, respectively. It can easily be shown that the above statement of Oldroyd-B model [Eq. (7)] is identical with Eq. (10) by considering the following relations:

$$ \eta = \eta_{s} + \eta_{p} $$

(11a)

$$ \theta = \frac{{\eta_{s} }}{{\eta_{s} + \eta_{p} }}\lambda = (1 - \beta )\lambda $$

(11b)

where $\beta$ is viscosity ratio and defined as:

$$ \beta = \eta_{P} /\eta . $$

(12)

Regarding to Eq. (10), we have:

$$ \left. {\tau_{rz} } \right|_{r = R} = \left. {\tau_{srz} } \right|_{r = R} + \left. {\tau_{prz} } \right|_{r = R} $$

(13)

$$ \left. {\tau_{srz} } \right|_{r = R} = \eta_{s} (\nabla {\mathbf{v}} + (\nabla {\mathbf{v}})^{T} )_{rz} = \eta_{s} \left. {\left( {\frac{{\partial v_{z} }}{\partial r} + \frac{{\partial v_{r} }}{\partial z}} \right)} \right|_{r = R} $$

(14)

$$ \left. {\tau_{prz} } \right|_{r = R} + \left. {\lambda \mathop \tau \limits^{\nabla }_{prz} } \right|_{r = R} = \eta_{p} \left. {\left( {\frac{{\partial v_{z} }}{\partial r} + \frac{{\partial v_{r} }}{\partial z}} \right)} \right|_{r = R} . $$

(15)

Considering the Poiseuille velocity distribution profile equation for laminar flow in a long pipe [4] and replacing the appropriate values in Eqs. (14) and (15), the shear stress $\left. {\tau_{rz} } \right|_{r = R}$ is obtained.

So, the governing equations for viscoelastic fluid hammer are given by:

$$ \frac{\partial H}{\partial t} + \frac{{c^{2} }}{g}\frac{{\partial \overline{V} }}{\partial z} = 0\, $$

(16)

$$ \frac{{\partial \overline{V} }}{\partial t} + g\frac{\partial H}{\partial z} - \frac{2}{\rho R}(\left. {\tau_{srz} } \right|_{r = R} + \left. {\tau_{prz} } \right|_{r = R} ) = 0 $$

(17)

$$ \left. {\tau_{srz} } \right|_{r = R} = - \eta_{s} .\frac{{4\overline{V} }}{R} $$

(18)

$$ \left. {\tau_{prz} } \right|_{r = R} + \lambda \frac{{\partial \tau_{prz} }}{\partial t} = - \eta_{p} \frac{{4\overline{V} }}{R}. $$

(19)

It should be noted in the above equations that convective terms have been neglected. Replacing polymer terms in the momentum equation with zero, the classical water hammer equations are obtained.

$$ \frac{\partial H}{\partial t} + \frac{{c^{2} }}{g}\frac{\partial V}{\partial z} = 0 $$

(20)

$$ \frac{\partial V}{\partial t} + g\frac{\partial H}{\partial z} + \frac{{8\eta_{s} V}}{{\rho R^{2} }} = 0. $$

(21)

Replacing $f = \frac{{64\eta_{s} }}{\rho V2R} = \frac{64}{\text{Re}}$ in Eq. (23) for laminar fluid hammer, the conventional form of the momentum equation in classical water hammer is obtained:

$$ \frac{\partial V}{\partial t} + g\frac{\partial H}{\partial z} + \frac{fV\left| V \right|}{2D} = 0 $$

(22)

where $f$ is the Darcy–Weisbach friction factor and g is the acceleration due to gravity.

2.3 Boundary conditions

For the boundary conditions in the viscoelastic fluid hammer phenomenon, similar to the classical one, the pressure head at the upstream end is set equal to the upstream reservoir pressure, while a zero velocity boundary condition is imposed at the downstream end to simulate the abrupt closure of the valve.

2.4 Non-dimensionalization of the equations

The different variables are normalized according to the following relations:

$$ \overline{V}^{*} = \frac{{\overline{V} }}{{v_{0} }},H^{*} = \frac{H}{{{{cv_{0} } \mathord{\left/ {\vphantom {{cv_{0} } g}} \right. \kern-0pt} g}}},z^{*} = \frac{z}{D},t^{*} = \frac{t}{{{D \mathord{\left/ {\vphantom {D c}} \right. \kern-0pt} c}}},\overline{\tau }^{*} = \frac{{\overline{\tau } }}{{\rho cv_{0} }} $$

(23)

where $v_{0}$ is the velocity in steady state and non-dimensional numbers involved in this study are:

$$ De = \frac{\lambda }{{{\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D {v_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${v_{0} }$}}}},\,\,\,\,\beta = \frac{{\eta_{p} }}{{\eta_{p} + \eta_{s} }},\,\,\,\,M = \frac{{v_{0} }}{c},\,\,\,\,\text{Re} = \frac{{\rho v_{0} D}}{{\eta_{p} + \eta_{s} }} $$

(24)

where $De$ denotes the Deborah number which is attributed to an important feature of viscoelastic fluid called relaxation time constant [28], $\beta$ is the viscosity ratio to show the magnitude of polymer viscosity with respect to the total viscosity, $M$ is Mach number and is defined as the square root of the ratio of inertia force to the elastic force, and Re is the Reynolds number. Considering the above dimensionless groups, the non-dimensional equations can be expressed as follows:

$$ \frac{{\partial H^{*} }}{{\partial t^{*} }} + \frac{{\partial \overline{V}^{*} }}{{\partial z^{*} }} = 0 $$

(25)

$$ \frac{{\partial \overline{V}^{*} }}{{\partial t^{*} }} + \frac{{\partial H^{*} }}{{\partial z^{*} }} - 4(\overline{\tau }^{*}_{srz} + \overline{\tau }^{*}_{prz} ) = 0 $$

(26)

$$ \overline{\tau }^{*}_{srz} = \frac{ - 8}{\text{Re}}.M.\overline{V}^{*} .(1 - \beta ) $$

(27)

$$ \overline{\tau }^{*}_{prz} + \frac{De}{M}.\frac{{\partial \overline{\tau }_{prz}^{*} }}{{\partial t^{*} }} = - 8\beta .\frac{{\overline{V}^{*} }}{\text{Re}}.M. $$

(28)

Using $\beta = 0$, the non-dimensional equations for Newtonian fluid hammer are also achieved.

3 LXF numerical methods

The basis of LxF method is the finite difference method, and it is a good choice for solving PDE²s. The LxF method is conservative and monotone; therefore, this is a TVD (total variation diminishing) method. As for the original Godunov method, the LxF scheme is based on a piecewise constant approximation of the solution, but it does not require solving a Riemann problem for time advancing and only uses flux estimates. LxF method is available for all forms of PDEs [30]. The stability condition is $\frac{c\Delta t}{\Delta x} \le 1$ and c is pressure wave speed. In this scheme, a half step is taken with LxF on a staggered mesh. If the second half step is taken with LxF, the solution is achieved on the original mesh. Figure 2 indicates the stencil for two time steps method.

Fig. 2

Stencil for two time steps method [31]

Figure 2 shows that computational grids consist of individual cells with spatial grid size dx and time steps dt. In this paper, two-step method is used to increase the convergence and accurateness. Generally, multi-step methods uses finite difference relations at divided time levels and the function of these methods is particularly acceptable in the analysis of non-linear hyperbolic problems [30]. In this method, firstly, a half time step is taken based on LxF scheme on a staggered mesh. Then, the second half step is implemented based on LxF to arrive at the solution on the original mesh. High accuracy and convergence, low computational cost compared to other numerical methods and simple algebraic operation can be expressed as important features of this numerical method. In this one-dimensional simulation, the stability condition is considered 0.99. Table 2 lists the spatial step sizes for the three different grids used in the verification of the present numerical procedure.

Table 2 Non-dimensional spatial step sizes for the different grids

Figure 3 shows the pressure time history at the downstream valve using all three grids. As can be seen from the figure, the medium and fine grids provide nearly identical results. In order to reduce computational cost, the second grid in this paper is used which in it, the pipe is divided into 2000 parts.

Fig. 3

Grid independence for pressure time history at the valve

4 Validation of proposed numerical model

Due to the dearth of literature on experimental works about the viscoelastic fluid hammer inside the pipes, it was decided that in the first step, the result of present study is validated by a laboratory data for a Newtonian fluid in the pipe. It is important to mention that verifying the CFD simulation of non-Newtonian flows with special Newtonian cases is usual in rheology and non-Newtonian fluid mechanics which is mostly related to the lack of experimental data. In other word, the CFD code is verified at special Newtonian case by considering zero relaxation time. Holmboe and Rouleau experiment [32] is chosen as a valid laboratory sample in the field of fluid hammer phenomenon in the pipe. The properties and pipe configuration data are presented in Table 3. In this experiment, fluid transient is generated by the sudden closure of the downstream valve.

Table 3 Properties and pipe configuration data [32]

Among the numerical studies that have been modeled fluid hammer phenomenon in the pipe using different numerical methods, in the present paper, two different numerical methods of Wahba (1-D) [29] and Zielke (steady friction state) [5] for validation of proposed model are selected. Zielke [5] modeled transitional flows in the pipe in two different situations, steady and unsteady friction. He also derived an equation which relates the wall shear stress in transient laminar pipe flow to the instantaneous mean velocity and to the weighted past velocity changes. The term was applied to the method of characteristics to calculate water hammer phenomena in viscous fluids, in which effects of frequency-dependent friction cause distortion of traveling waves. Wahba [29] also studied laminar transitional flows in the pipeline in one- and two-dimensional states. In his study, Runge–Kutta schemes were used to simulate unsteady flow in elastic pipes due to sudden valve closure and the spatial derivatives were discretized using a central difference scheme. In the numerical modeling of Zielke [5] and Wahba [29], Holmboe and Rouleau experiment [32] data have been used. The comparison of modeling results of these studies shows that the results of Wahba [29] study in one-dimensional state are optimal fitting with the results of Zielke [5] modeling in steady friction state. In the present study, the modeling has been done one dimensionally, so it is expected that after ignoring the non-Newtonian terms related to the viscoelastic fluid in the equations, the results of the proposed model for Newtonian fluid using LXF method are well suited to the results of the mentioned studies. The initial conditions in Holmboe and Rouleau experiment [32] are taken according to the steady-state situation of the system. The boundary conditions describe the situation at the pipe ends, where for instance a reservoir or valve is located. The boundary condition that describing a constant head reservoir with a pipe rigidly connected to it is $H = H_{0}$ where subscript $0$ shows the value of variables in steady-state situation of the system. Figure 4 shows a comparison between the results obtained using Zielke [5] and Wahba [29] numerical modeling in mentioned states with the proposed model using LXF method and experimental results.

Fig. 4

Pressure time history

According to Fig. 4, there is a good agreement between the results of proposed model using the present method and previous numerical works in mentioned cases. It is noted that the steady-state friction in Zielke [5] method and 1-D simulation state of Wahba [29] method for validation of present method is considered. The experimental results do not match the numerical results in some points. The reason for that can be attributed to the modeling of the problem one dimensionally [29]. The 1-D model provides an excellent prediction of the magnitude of the first pressure peak. On the contrary, it underestimates the attenuation of the following pressure peaks resulting in much higher simulated pressure values than those experimentally observed. The reason for this is due to the inadequate representation of the frictional damping mechanism in the 1-D model [29]. Furthermore, comparing the solutions of the proposed model in frictionless state with exact solutions can show the accuracy of the numerical method. The exact solution of the water hammer problem is known when the convective acceleration terms are neglected [29, 33]. A comparison between the results of the present method and the exact solutions based on data in Table 3 is shown in Fig. 5.

Fig. 5

Pressure time history

Figure 5 shows a good agreement between the present results and frictionless solutions frictionless in terms of the pressure time history at the valve and midpoint of the pipe, respectively.

5 Numerical simulation

In order to obtain the results near to the physical conditions, we used the properties of a dilute polymeric solution and a real geometry to obtain the typical dimensionless groups. For this purpose, a solution of polyacrylamide (100 ppm (0.01 ${\text{wt}}\%$)) in a $80/20$ ($v/v$) glycerin/de-ionized water is considered as typical viscoelastic fluid. The molecular weight of polyacrylamide is $M_{w} = 5 \times 10^{6} {\text{g/mol}}$, and degree of purity of glycerin is 99%. The viscometric test of this solution indicates that the viscosity has a constant value of $0.08918$ Pa.s in a wide range of shear rate [34] so it could be considered as a Boger liquid and the Oldroyd-B constitutive equation is suitable to describe the mechanical behavior of this solution. The results of curve fitting of four modes generalized Maxwell model on the data of sweep frequency test at constant 10% of strain are presented in Table 4 [34]. Here, mode zero indicates the Newtonian contribution of model. Based on the data of this table, the fluid has an average relaxation time of 1.9 s [34].

Table 4 Spectrum of relaxation time and viscosity [34]

As following, the comparison between Newtonian and mentioned viscoelastic solutions with similar viscosity during fluid hammer phenomenon is done and is shown in Fig. 6. The other properties and pipe configuration data are presented in Table 5. The Reynolds number for this laminar flow case is 80, viscosity ratio is considered 0.6 and Deborah number in the mentioned viscoelastic solution according to the data of Table 3 and 4 is equal to $9.6 \approx 10$, and the fluid transient is generated by the sudden closure of the downstream valve.

Fig. 6

The comparison of pressure time history in fluid hammer with Newtonian and viscoelastic fluid. Newtonian solution: $\text{Re} = 80,\beta = 0,M = 9.66e - 5,{\text{De}} = 0$. Viscoelastic solution: $\text{Re} = 80,\beta = 0.6,M = 9.66e - 5,{\text{De}} = 10$

Table 5 Properties and pipe configuration data

Generally in fluid hammer phenomenon, after the sudden closure of the valve, the fluid’s velocity at the valve reaches to zero and at the same moment, kinetic energy is completely transformed into the potential. This imposed potential energy causes the pressure head at the valve to rise equivalent to Joukowsky head. The Joukowsky pressure rise is the maximum pressure rise that would occur during the transient when viscous effects are neglected and is equal to $\frac{{cv_{0} }}{g}$. In Fig. 6, the comparison of pressure time history is shown in Newtonian and viscoelastic fluid hammer.

In Fig. 6, two key points can be observed:

• 1. The Joukowsky pressure rise must be the maximum pressure rise that would occur during the transient at the valve when viscous effects are neglected, but in Fig. 6, the pressure rise is higher than Joukowsky’s head, from t* = 0 to t* = 2 which this point can be observed in both Newtonian and viscoelastic solutions.

• 2. The height of the transitional flow in the viscoelastic solution compared to the Newtonian solution is higher which leads to longer attenuation time.

The first point which is related to “pipeline packing” or “line packing” phenomenon is explained in Sect. 6. Shortly, in this phenomenon, the value of transient pressure continues to rise above the Joukowsky pressure value due to frictional effects. In the case of the second point, it must be referred to the viscoelastic properties of the fluid. In a Newtonian fluid, after the imposition of the potential energy caused by the sudden closure of the valve, viscous characteristic of the liquid damps the pressure wave gradually. In a viscoelastic fluid, solid and liquid properties of in it show different reactions to this sudden potential energy at the same time. In fact, a viscoelastic solution has viscous and elastic properties simultaneously. The elastic property plays an important role in storing the potential energy imposed on the fluid, while the viscous part is extremely eager to waste the imposed energy. Finally, these different actions in a viscoelastic fluid cause the damping time of the transition flow to become longer compared to Newtonian fluid.

It is interesting that if a Newtonian fluid flows into a viscoelastic pipe, what happens in the case of attenuation time of transitional flow and pressure wave damping is the opposite of the mentioned state. It means the height of the transitional flow in the elastic pipe compared to the viscoelastic pipe is higher which leads to longer attenuation time [35, 36]. The reason for this behavior is linked to the viscoelastic properties of the pipe. The viscous part of the viscoelastic pipe shows a strong tendency to waste imposed energy. As a result, the attenuation time of transitional flow in viscoelastic pipe compared to the elastic pipe is decreased [35, 36].

In Fig. 7, the comparison between shear stresses during Newtonian and viscoelastic fluid hammer at the pipe midpoint is shown.

Fig. 7

Shear stresses during fluid hammer with Newtonian and viscoelastic fluid at the pipe midpoint. Newtonian solution: $\text{Re} = 80,\beta = 0,M = 9.66e - 5,{\text{De}} = 0$. Viscoelastic solution: $\text{Re} = 80,\beta = 0.6,M = 9.66e - 5$${\text{De}} = 10$

Figure 7 shows that the shear stresses caused by fluid hammer with viscoelastic fluid are significantly reduced compared to the Newtonian state. Considering that the viscosity of the solutions is the same in both states, the reduction of shear stresses is related to viscoelastic fluid properties certainly. Storing of the potential energy in the viscoelastic solution due to the elastic properties of the solid character in it can be considered the main factor in reducing the shear stresses in a viscoelastic solution compared to the Newtonian solution. It seems that the effect of this property of viscoelastic fluid makes it possible to significantly reduce the severity of the initial shear stresses at different points of the pipe.

6 Interpretation of the non-dimensional parameter (k)

Wahba [1] used a non-dimensional parameter to provide an in-depth discussion about the phenomenon of line packing and Richardson annular effect in transient flows on Holmboe and Rouleau experiment [32]. This non-dimensional parameter is viewed as the ratio of two forces. One force is the viscous force, while the other is the force generated by the Joukowsky pressure rise. An order of magnitude analysis for the Joukowsky force $F_{J}$ and the viscous force $F_{v}$ results in:

$$ k = \frac{{F_{J} }}{{F_{v} }} = \frac{{\rho cv_{0} D^{2} }}{{D\eta lv_{0} /D}} = \frac{{\rho cD^{2} }}{\eta l} $$

(29)

where $D^{2}$ is effective area for the Joukowsky pressure force in the pipe cross-sectional area while the effective area for the viscous force is the pipe lateral area, which is $Dl$. He concluded that two issues “phenomenon of line packing” and “Richardson annular effect” are governed by the value of this parameter. Phenomenon of “line packing” that is related to the value of transient pressure continues to rise above the Joukowsky pressure value due to frictional effects, depends on the viscosity of the fluid. That is, when the viscosity of the fluid decreases, non-dimensional parameter increases and since the increase in pressure at the valve is higher than the expected Joukowsky pressure rise, line packing phenomenon occurs. Wahba [1] also indicated that with the decrease in this coefficient, the damping of the pressure transient increases. The rather surprising result is that, even though the attenuation of the transient is much more profound in this state, the values of the instantaneous wall shear stress are much smaller and the Richardson annular effect is effectively nonexistent. In order to compare the effect of k coefficient on the viscoelastic and Newtonian fluid behavior during fluid hammer, a parametric study is performed to determine the effect of varying k on the attenuation of the fluid transient in the present study. Two new cases are simulated which have the same Reynolds number as the previous case (Re = 80), but in which the value of the parameter k is varied by varying the pressure wave speed. All three simulated cases are given in Table 6. The results are shown in Fig. 8.

Table 6 Summary of simulated cases

Fig. 8

The effect of k parameter on pressure time history at the valve

Figure 8 shows that the changes of k coefficient affect the behavior of both Newtonian and viscoelastic fluid. In Newtonian solution, similar to the obtained results by Wahba [1], increasing k coefficient, the damping of the transient decreases. Moreover, since decreasing k coefficient causes an increase in viscosity, the lower the k coefficient becomes, the more “line packing phenomenon” at valve is observed. It is clear that these incidents occur in viscoelastic solution similarly. The only difference between the Newtonian and viscoelastic fluids can be observed in damping of their transition flow. Transitional flow in the Newtonian fluid hammer is sooner attenuated. The reason for this can certainly be related to special property of viscoelastic fluids such as relaxation time as explained in Fig. 8 which stores imposed energy and causes attenuation time to become longer.

7 Results and discussion

To more precisely study the pressure wave behavior, numerical modeling was also done for other polymeric solutions with lower molecular weight and a lower relaxation time constant. Also, the effect of dimensionless groups on pressure time history at the valve and midpoint was investigated. Dimensionless groups consist of Deborah, Reynolds, viscosity ratio and Mach numbers which were derived in Sect. 2. It should be noted that the Mach number in fluid hammer is so small ($M \prec \prec 1$) [2] that it is effectively negligible.

7.1 The effect of Deborah number

To investigate the effect of the Deborah number on pressure time history at the valve and midpoint, the mentioned polymer solution in Table 5 with different relaxation times which results in different Deborah numbers is simulated and the results are shown in Fig. 9.

Fig. 9

The effect of Deborah number on pressure time history $\text{Re} = 80,\beta = 0.6,M = 9.66e - 5$

Figure 9 shows that with decreasing Deborah number, pressure waves have a faster tendency to attenuation; in fact the behavior of the polymer for low Deborah numbers is similar to a Newtonian fluid. It also can be observed that in all cases at valve, “line packing” or “pipeline packing” effect increases the pressure from the Joukowsky pressure. In Fig. 10, the effect of Deborah number on shear stresses during viscoelastic fluid hammer at the pipe midpoint is shown.

Fig. 10

The effect of Deborah number on shear stresses during fluid hammer with viscoelastic fluid at the pipe midpoint $\text{Re} = 80,\beta = 0.6,M = 9.66e - 5$

As shown in Fig. 10, there is no critical point in the graph in the small Deborah (De = 0.01) and large Deborah (De = 1–10) states. In fact in these states, the graph mode follows a certain order and stability, but in the conditions between these two states (De = 0.1) that viscoelastic properties of the fluid gradually change and the fluid behavior is transferred to the viscoelastic type, the shape of the diagram also becomes slightly irregular at some points until it reaches a viscoelastic state. This is due to the gradual transition from very small Deborah numbers to large Deborah numbers and is certainly related to the increasing effect of relaxation time constant as an important feature of viscoelastic fluid. Moreover, in Fig. 10, it is clear that the higher the viscoelastic properties of the fluid, the lower the shear stresses in the pipe. In fact, this result is a confirmation of the results of Fig. 7 that the shear stresses in viscoelastic fluid hammer phenomena are significantly lower than those in Newtonian fluid with similar viscosity.

7.2 The effect of the viscosity ratio

In this section, assuming a constant viscosity for the chosen polymer solution, the viscosity of the Newtonian solvent and polymer are changed in several cases at the valve and the midpoint of the pipe and the effect of $\beta$ on pressure time history is investigated. Considering the Oldroyd-B model, the viscoelastic solution is divided into Newtonian solvent and viscoelastic polymer sections. Therefore, increasing $\beta$, the polymeric contribution of the viscoelastic solution becomes more effective. Therefore, in a viscoelastic solution, in conditions where relaxation time factor is considered constant, it is expected that with decreasing $\beta$, the polymer solution behaves more like Newtonian fluids. As mentioned, in Newtonian fluids, the attenuation time of the pressure wave is shorter and damping of transition flow happens sooner. In Fig. 11, the effect of viscosity ratio on pressure time history at valve and midpoint of the pipe is shown.

Fig. 11

The effect of viscosity ratio ($\beta$) on pressure time history $\text{Re} = 80,{\text{De}} = 10,M = 9.66e - 5$

Figure 11 shows that increasing $\beta$ causes the solution behavior to be closer to the viscoelastic polymer one and consequently the peak of the pressure wave becomes slightly higher and attenuation time will be a little longer. It also can be observed that in all cases at valve, “line packing” or “pipeline packing” effect increases the pressure from the Joukowsky pressure. In Fig. 12, the effect of viscosity ratio on shear stresses during viscoelastic fluid hammer at the pipe midpoint is shown.

Fig. 12

The effect of viscosity ratio ($\beta$) on shear stresses in fluid hammer with viscoelastic fluid at the pipe midpoint $\text{Re} = 80,M = 9.66e - 5,{\text{De}} = 10$

According to the Oldroyd-B equations, the shear stresses during fluid hammer phenomenon are calculated from the sum of Newtonian solvent and viscoelastic polymer shear stresses. Considering the relaxation time constant as a property of the viscoelastic fluid that causes the shear stresses to be significantly reduced, it can be resulted that the higher the proportion of the viscoelastic polymer section, the lower the shear stresses. In Fig. 12, it is confirmed that increasing $\beta$ makes the solution more concentrated and therefore the contribution of the viscoelastic section increases and consequently the shear stresses are reduced.

7.3 The effect of Reynolds number

The pressure wave even in the Newtonian state based on Eq. (30) is sensitive to the Reynolds number. In Figs. 13 and 14, the effect of Reynolds number on pressure time history in Newtonian and viscoelastic fluid hammer at valve and midpoint of the pipe is shown.

Fig. 13

The effect of Reynolds number on pressure time history in fluid hammer with Newtonian fluid $\beta = 0,{\text{De}} = 0,M = 9.66e - 5$

Fig. 14

The effect of Reynolds number on pressure time history in fluid hammer with viscoelastic fluid $\beta = 0.6,{\text{De}} = 10,M = 9.66e - 5$

As shown in Figs. 13 and 14, the overall pressure changes in Newtonian and viscoelastic fluids are similar but the sensitivity is higher in the Newtonian case, especially for low Reynolds numbers. It means in laminar fluid hammer phenomenon, the strength of fluid viscosity as a friction effect increases and consequently transient flow damping occurs sooner. In fact, the larger the Reynolds number, the longer the attenuation time and this general trend repeats similarly in viscoelastic fluid hammer. An important point in Figs. 13 and 14 is the intense impact of “line packing” or “pipeline packing” phenomenon at valve. As it is clear, the lower the Reynolds number, the higher the viscosity of fluid and thus “line packing” effect can be more noticeable. In Fig. 15, the comparison between shear stresses during Newtonian and viscoelastic fluid hammer with different Reynolds numbers at the pipe midpoint is done.

Fig. 15

The comparison of shear stresses during fluid hammer with different Reynolds numbers at the pipe midpoint

Figure 15 shows that the maximum shear stresses due to fluid hammer occur at low Reynolds numbers. Reynolds number is the ratio of inertial forces to viscous forces. So a low Reynolds number will be associated with viscous forces prevailing over inertial forces. The viscous forces are associated with the shear stress. Therefore, the lower the Reynolds number, the higher the shear stress.

8 Conclusions

In this paper, fluid hammer phenomenon with viscoelastic fluid in a reservoir-pipe-valve system is modeled. The fluid transient is generated by the sudden closure of the downstream valve. Equations representing the conservation of mass and momentum govern the transitional flow in the pipes, and Oldroyd-B model relations are used to calculate the viscoelastic fluid shear stresses. The numerical method used is a two-step variant of LxF method. Dimensionless groups derived at the governing equations during this phenomenon are Deborah, Reynolds, Mach and viscosity ratio numbers; Reynolds and Mach numbers also can be derived at Newtonian state. Regardless of Mach number because of the very small amount, the effect of other non-dimensional groups on pressure time history during viscoelastic solution hammer at valve and midpoint of the pipe was investigated and compared to the Newtonian solution hammer. The results show that increasing Deborah, Reynolds and viscosity ratio numbers in viscoelastic fluid hammer will make the attenuation time of transitional flow longer than the Newtonian state. Besides, the results indicate that the shear stress in viscoelastic fluid hammer is significantly lower than those in Newtonian fluid with similar viscosity.