Solving the Gene Duplication Feasibility Problem in Linear Time

Abstract

The gene duplication model, which has been pioneered by Goodman et al. nearly 40 years ago, is widely-used for resolving the discordance between the evolutionary history of a gene family (gene tree), and the species tree through which this family has evolved. This discordance is explained by reconciling the gene tree with postulated gene duplications that have occurred while the gene tree has evolved along the edges of the species tree, such that the reconciled tree can be embedded into the species tree. Today, for many gene families lower bounds on the number of gene duplications that have occurred along each edge in the species tree can be derived, for example, from known genome duplications. Here, we augment the gene duplication model by using a species tree for the reconciliation whose edges are decorated with such lower bounds, called a (duplication) scenario. A scenario is feasible for a gene family under consideration if there exists a reconciled gene tree for this family whose embedding into the species tree satisfies the lower bounds of the scenario. Non-feasibility of a credible scenario for a gene family can provide a strong indication that this family might not be well-resolved, and identifying well-resolved gene families is a challenging task in evolutionary biology. Here, we provide a linear time algorithm that decides whether a scenario is not feasible when provided a gene family.

1 Introduction

Tree reconciliation is a fundamental approach for analyzing discordant evolutionary relationships among the family histories of genes when contemplated with the histories of the species in which they have evolved. This approach has become common practice in many biological oriented research disciplines, such as molecular biology, microbiology, and biotechnology [16]. For example, gene tree reconciliation is one of the most comprehensive ways to describe the dynamics of gene family evolution [8, 15], and it is also a widely-used approach to differentiate between orthologous and paralogous genes [1, 2], an elementary task in the functional determination of genes [14]. Tree reconciliation can be performed using different biological models under which discordant relationships can be explained. Here we focus on the gene duplication model that has been pioneered by Goodman et al. nearly 40 years ago [12] and has laid the groundwork for tree reconciliation [7, 9].

The gene duplication model takes the following pair of rooted and full binary trees: (i) a gene (family) tree that represents the family history of a set of genes, and (ii) its (corresponding) species tree that is the evolutionary history of the species hosting these genes. Discordance between a gene tree and a species tree is often caused by complex histories of gene duplication events [16, 18], but can also originate from other evolutionary events like deep coalescence or lateral transfer [17]. The gene duplication model is reconciling the gene tree with its species tree under the assumption that discordance is only caused by gene duplication events. Following the parsimony principle, the reconciliation process under the gene duplication model seeks an embedding, called reconciliation, of the gene tree into the species tree that infers the minimum number of duplication events. The resulting embedding is the reconciled (gene) tree that can reveal complex histories of gene duplication events, elucidating the evolution of function and discriminating between orthologous and paralogous genes. Figure 1 depicts an example for such a reconciliation. For a more detailed treatment of the gene duplication model, the interested reader is referred to [7, 9].

Fig. 1.

An example of a gene tree - species tree reconciliation with inferred gene duplication events. The reconciliation is based on the least common ancestor mapping – it is not difficult to note that gene tree nodes x and y map to the root node of the species tree based on LCAs; hence, the duplication is at the root edge. (Color figure online)

Fig. 2.

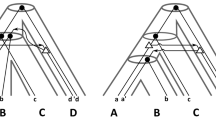
An example of a duplication scenario (in the center). The duplication lower bounds are shown as edge annotations. Observe that edges going into nodes X and Y in S have duplication lower bounds of 1, which requires that a proper gene tree reconciliation will show at least 1 duplication occurring at each of these edges. On the left hand side there are given two gene families, namely, $\{a,b,c,d\}$ and $\{a,a,b,c,d\}$, which belong to the respective capital letter species. There does not exist any gene tree for the first family that will induce the required reconciliation. On the other hand, the second gene family allows to build the gene tree $G_2$ that satisfies the given duplication scenario. (Color figure online)

A gene tree - species tree reconciliation infers a duplication scenario on the species tree, which can be characterized as the number of gene duplications that occurred along each edge of the species tree (note that we consider species trees to be planted, i.e., having an auxiliary edge connected to the root node). Formally, we define a duplication scenario as a function that maps each species tree edge to an integer that specifies the lower bound on the number duplications that occurred along that edge for the given gene family. While the exact number of duplications might be a more natural choice, the lower bounds are much easier to obtain in practice, for example, using histories of whole genome duplications [5, 19]. The phylogenetic inference of gene trees has never been subjected to known duplication scenarios, which in turn could lead to the inference of more biologically informed and accurate trees.

Here, we set out to reveal the space of feasible duplication scenarios for a specified species tree topology and a gene family. We call a duplication scenario feasible, if there exists a gene family tree and a corresponding reconciliation (under the Goodman et al. duplication model) that satisfies the provided lower bounds on the number of duplications. Figure 2 demonstrates an example of a duplication scenario. Note that satisfiability of the lower bounds depends on the gene family provided (namely, the number of gene copies for each leaf species). Consequently, we introduce the Feasibility of a Duplication Scenario (FDS) problem that decides whether a duplication scenario is feasible, and describe a linear time algorithm for this problem. In addition, the augmentation of this algorithm provides a smallest (most parsimonious) gene tree satisfying the duplication scenario. Software implementing the FDS algorithm is freely available from the web-page http://genome.cs.iastate.edu/ComBio/software.htm.

Related Work. Gene duplication is a major and frequently occurring evolutionary process that is known to cause discordance between gene trees themselves and gene trees and their corresponding species trees [18]. An efficient approach to identify such discordance is the gene duplication model from Goodman et al. [12]. This approach takes a gene tree and its corresponding species tree (both of them are rooted and full binary), and is essentially embedding the gene tree into the species tree by possibly introducing gene duplication events. The left side of Fig. 1, depicts an example of discordance between gene tree G and species tree S. To explain this discordance in the absence of phylogenetic inference error let us temporarily direct our attention only to the species tree S. The right side of the figure depicts one out of infinitely many scenarios of how a gene tree evolves within the species tree S using blue edges (solid and dashed). Initially, gene x, represented by a red circle, duplicates into two copies that are each represented by a red square. Then, each of these copies evolves along the topology of the species tree by speciation events and losses (lost gene lineages are displayed as dashed blue arrows). The resulting gene tree scenario is inferred from species tree S using exactly one duplication event. As shown in Fig. 1, gene tree G can be embedded (solid blue edges) into the gene tree scenario (solid and dashed blue edges). Thus, the gene tree scenario reconciles gene tree G by invoking one duplication, offering an explanation for the discordance between G and S. However, there can be infinitely many such scenarios, each of them invoking some number of gene duplications. Following the parsimony principle, the gene duplication model explains the incongruence with a smallest scenario, which is unique, invoking the minimum number of duplications that can be specified through a mapping that relates each gene in the gene tree to its host species [6, 9, 10].

The host species in the duplication model are defined based on the least common ancestor mapping. Formally, M is a function mapping gene tree nodes to species tree nodes, such that for each gene g that is a leaf M(g) is the leaf species from which g was sampled. Further, for an internal gene node x with children y and z, M(x) is defined as the least common ancestor (LCA) of M(y) and M(z) in the species tree; that is, the furthest from the root node s, which is the ancestor of both M(y) and M(z).

A gene in the gene tree is a gene duplication when it has a child with the same host species. Visually, we say that such gene duplication happened on the edge connecting the host species to its ancestor (see Fig. 1). The mapping and the gene duplications are linear time computable [20]. There is a rich literature of extensions and variants of the gene duplication model, which can, in most cases, be efficiently computed [7, 9]. While computationally highly complex, probabilistic models for gene/species tree reconciliation, as well as gene sequence evolution, have also been developed [1, 3].

Contribution. We present a linear time algorithm for solving the Feasibility of a Duplication Scenario (FDS) problem. The algorithm is based on dynamic programming that became possible through intrinsic properties of the gene duplication model formulated and proven in this work. In particular, a simple, but powerful property is that the caterpillar substructure of a gene tree is a minimum substructure allowing a gene tree to satisfy a lower bound on duplications in the given duplication scenario. Further, the majority of our analysis builds on the here introduced concept of gene forests that proved to be effective for establishing feasibility conditions. The algorithm utilizes the dynamic bottom-up strategy computing maximum gene forests at each step. Further, an augmentation of this algorithm can be used to produce an example gene tree that satisfies the duplication scenario. Such gene tree, as we prove, will have the property that it is smallest in size among all gene trees satisfying the duplication scenario; hence, it represents the most parsimonious way to “explain” this duplication scenario.

Applying the presented FDS algorithm, practitioners will now be able to verify the feasibility for various gene families of interest using established duplication scenarios.

2 Basics and Preliminaries

We only consider full binary rooted trees where each leaf is identified with a taxon, which we refer to as (phylogenetic) trees. Adhering to the standard notation, given a tree T, we denote its root, node set, edge set and leaf set by ${{\mathrm{\mathsf {Rt}}}}(T), V(T), E(T),$ and ${{\mathrm{\mathsf {L}}}}(T)$, respectively. The sibling and the parent of each non-root node $v \in V(T)$ are denoted by ${{\mathrm{\mathsf {Sb}}}}(v)$ and ${{\mathrm{\mathsf {Pa}}}}(v)$, respectively. If a tree is planted, then the root has a parent node as well. The set of children of each internal node $v \in V(T)$ is denoted by ${{\mathrm{\mathsf {Ch}}}}(v)$. Further, we let T(v) be a subtree of T rooted at $v \in V(T)$ . A set of leaves ${{\mathrm{\mathsf {L}}}}(T(v))$ is called a cluster of the node v and is denoted by $C_v$.

We define a partial order $\preceq _T$ on the node set V(T), such that $u \preceq v$, if v is a node on the path from u to ${{\mathrm{\mathsf {Rt}}}}(T)$. Additionally, we say $u \prec v$, if $u \preceq v$ and $u \ne v$. The least common ancestor (LCA) of a set of nodes $\{u_1, \ldots , u_k\}$, ${{\mathrm{\mathsf {lca}}}}_T(u_1, \ldots , u_k)$, is the furthest from the root node, w, such that $u_i \preceq w \; \forall i \in \{1, \ldots , k\}$. A species tree is a planted tree with leaves referring to species names. Gene tree, G, is a tree that is defined by a set of species X, such that there exists a labeling (function) $\varLambda _G :{{\mathrm{\mathsf {L}}}}(G) \rightarrow X$.

LCA Mapping. Let S be a species tree, and G be a gene tree over ${{\mathrm{\mathsf {L}}}}(S)$. An LCA mapping $M :V(G) \rightarrow V(S)$ is a function such that for each leaf node $g \in V(G)$, $M(g) := \varLambda _G(g)$, and for each internal node g with children u and w, $M(g) := {{\mathrm{\mathsf {lca}}}}_S(\{M(u), M(w)\})$. Observe that the mapping function M is monotone, implying that for $g_1 \preceq g_2$, $M(g_1) \preceq M(g_2)$.

A node g with children u and w is a duplication node if either $M(g) = M(u)$ or $M(g) = M(w)$. For a species tree node $s \in V(S)$, $\varvec{\xi (G, s)}$ denotes the number of duplication nodes $g \in V(G)$, such that $M(g) = s$.

Duplication Scenario. Given a species tree S, a duplication scenario (described in the introduction) is defined by a function $\delta :V(S) \rightarrow \mathbb {N}_{0}$. We say that a gene tree G over ${{\mathrm{\mathsf {L}}}}(S)$ satisfies a duplication scenario $\langle S, \delta \rangle$ if $\forall s \in V(S) : \xi (G, s) \ge \delta (s)$. Note that, while in the introduction the duplication scenario function was defined on edges of a species tree, here for later convenience we define it on the nodes of a species tree (which is identical, since each node uniquely defines its ancestral edge, $({{\mathrm{\mathsf {Pa}}}}(v), v)$, in planted trees).

3 Feasibility of Duplication Scenarios

In this section, we analyze the problems of the feasibility of duplication scenarios as motivated in the introduction.

3.1 General Feasibility

Given a duplication scenario and a gene family, we would like to know whether there exists a gene tree for the family whose reconciliation is satisfying the scenario, i.e., the scenario is feasible for the gene family.

A gene family is characterized by the number of gene copies for each extant species. That is, assume, we are given a species tree, S, and for each leaf-species we know the number of gene copies, given by a function $\lambda :{{\mathrm{\mathsf {L}}}}(S) \rightarrow \mathbb {N}$. We say that a gene tree G satisfies $\langle S, \delta , \lambda \rangle$ if G satisfies $\langle S, \delta \rangle$, and G contains at most $\lambda (s)$ taxa labeled with s for all $s \in {{\mathrm{\mathsf {L}}}}(S)$.

Fig. 3.

Left: an example of a species leaf s with four gene copies in the provided gene family (i.e., four genes within the family are hosted by s). ${{\mathrm{\mathcal {G}}}}'_s$ represents the maximum gene forest (consisting of each gene copy individually) if we are not taking the duplication scenario into the account. Gene forest ${{\mathrm{\mathcal {G}}}}_s$ represents a maximum gene forest, when the duplication scenario puts the lower bound $\delta (s) = 2$ on the edge incident to s. Yellow squares indicate the duplication nodes. Right: an example of a gene forest construction for an internal species node v with children u and w. ${{\mathrm{\mathcal {G}}}}_v$ is a maximum gene forest for the node v constructed using ${{\mathrm{\mathcal {G}}}}_u$ and ${{\mathrm{\mathcal {G}}}}_w$, representing maximum gene forests of nodes u and w respectively. Observe that the tree satisfying $\delta (v) = 2$ was assembled from subtrees as a caterpillar (assembly of a profile $\{G_1, T_1, G_2, T_2\}$). (Color figure online)

Problem FDS. Feasibility of a Duplication Scenario

• Instance: Duplication scenario with a gene copy function $\langle S, \delta , \lambda \rangle$

• Question: Does there exist a gene tree G over ${{\mathrm{\mathsf {L}}}}(S)$, such that G satisfies $\langle S, \delta , \lambda \rangle$

Informal Solution Description. We consider a bottom up construction of a gene tree G satisfying $\langle S, \delta , \lambda \rangle$ (if one exists). At each node of the tree S we maintain certain tree structures (parts of future tree G) that jointly satisfy all the duplication lower bounds, given by $\delta$, below that node. These structures can be treated as building blocks (subtrees) for G. The algorithm seeks to maximize the number of such building blocks at each node in order to supply them further to the parent node and so on. These building blocks are later formally defined as gene forests. The maximization is of importance, since in case that here are no available tree structures at the root of S, then G does not exist and the scenario is not feasible.

At the leaf level of species tree S the number of building blocks available is simply the number of gene copies for a species. Indeed, if a species taxon s requires $\delta (s) > 0$ duplications mapped into that node, then we need to use the available building blocks (gene copies) to generate that mapping. Similarly, for intermediate nodes. Note that maximizing the number of building blocks at each node entails minimizing the number of blocks needed to satisfy the duplications lower bound at that node. An important observation here is that if at node v the lower bound is $\delta (v) > 0$, then to create a structure (new block) satisfying that duplication count at least $\delta (v) + 1$ blocks are needed, when v is a leaf, and $\delta (v) + 2$ blocks are required otherwise. Figure 3 illustrates that observation.

Applying these ideas, Algorithm 1 below checks feasibility of a given duplication scenario.

3.2 Proof of Correctness of Algorithm 1

As was mentioned above, we introduce the concept of gene forests. We define ${{\mathrm{\mathcal {G}}}}$ to be a gene forest over $\langle S, \lambda \rangle$ if the following properties hold.

• (F1) ${{\mathrm{\mathcal {G}}}}$ is a set of phylogenetic trees over ${{\mathrm{\mathsf {L}}}}(S)$.

• (F2) Let $\varLambda ^{-1}_{G}(s)$ be a set of leaves in G labeled by s, then $\displaystyle \sum _{G \in {{\mathrm{\mathcal {G}}}}}{|\varLambda ^{-1}_{G}(s)|} \le \lambda (s)$.

• (F3) $\displaystyle \bigcup _{G \in {{\mathrm{\mathcal {G}}}}}{\varLambda _{G}({{\mathrm{\mathsf {L}}}}(G))} = {{\mathrm{\mathsf {L}}}}(S)$.

We say that a gene forest ${{\mathrm{\mathcal {G}}}}$ satisfies $\langle S, \delta , \lambda \rangle$ if ${{\mathrm{\mathcal {G}}}}$ is over $\langle S, \lambda \rangle$ and for all $s \in V(S)$ we have $\sum _{G \in {{\mathrm{\mathcal {G}}}}}{\xi (G, s)} \ge \delta (s)$. Further, given a gene forest ${{\mathrm{\mathcal {G}}}}$, we define $\overline{{{\mathrm{\mathcal {G}}}}}$ to be a gene tree obtained by assembling the trees in ${{\mathrm{\mathcal {G}}}}$ into a single tree. While there could be many ways to assemble the trees from ${{\mathrm{\mathcal {G}}}}$, we are interested in a caterpillar structure that will be used later in the analysis.

Definition 1

A gene tree $G_C$ represents a caterpillar assembly of a profile of trees $G_1, \ldots , G_k$ if it is obtained as follows. First, set $G_C := G_1$, then

Given a duplication scenario, $\langle S, \delta , \lambda \rangle$, and a node $v \in V(S)$, we say that forest ${{\mathrm{\mathcal {G}}}}_v$ satisfies $\langle S, \delta , \lambda \rangle |_{v}$ implying that ${{\mathrm{\mathcal {G}}}}_v$ satisfies the duplication-scenario restricted to subtree S(v), i.e., $\langle S(v), \delta |_{V(S(v))}, \lambda |_{C_v} \rangle$. Let $\alpha (v)$ denote the maximum size of a gene forest (in terms of a number of trees) that satisfies $\langle S, \delta , \lambda \rangle |_{v}$. The following observation then explains Line 17 of Algorithm 1.

Observation 1

(Feasibility for a given gene family). An instance $\langle S, \delta , \lambda \rangle$ of FDS is a yes-instance if and only if $\alpha ({{\mathrm{\mathsf {Rt}}}}(S)) > 0$.

Observation 2 and Lemma 1 summarize the core properties needed for the proof of correctness. Note that Observation 2 was informally described above.

Observation 2

Consider $v \in V(S)$ such that $\delta (v) > 0$.

• (I) If v is a leaf, then at least $\delta (v) + 1$ gene copies for v are required to construct a gene tree with $\delta (v)$ duplication nodes mapping into v. Note that any binary tree with $\delta (v) + 1$ leaves mapping into v will induce exactly $\delta (v)$ duplications on v (for example, a caterpillar assembly of $\delta (v) + 1$ gene copies – see Fig. 3).

• (II) If v has children u and w, then at least $\delta (v) + 2$ gene trees from maximum gene forests of u and w are required to construct a gene tree with $\delta (v)$ duplication nodes mapping into v. Further, it is always possible to use exactly $\delta (v) + 2$ gene trees via a caterpillar assembly (see Fig. 3).

Lemma 1

Let ${{\mathrm{\mathcal {G}}}}_v$ be a maximum gene forest satisfying $\langle S, \delta , \lambda \rangle |_{v}$ for some $v \in V(S)$. Then

• (MF4) If ${{\mathrm{\mathcal {G}}}}_v$ contains a tree G with a duplication vertex mapping into v, then no other tree in the forest can have a node mapping into v. That is, all duplications for a specific node are localized within the same tree.

• (MF5) For $v \not \in {{\mathrm{\mathsf {L}}}}(V)$, if $\delta (v) = 0$, then for each tree $G \in {{\mathrm{\mathcal {G}}}}_v$, the root of G maps below v. That is, $M({{\mathrm{\mathsf {Rt}}}}(G)) \prec v$.

Proof

• (MF4) Let ${{\mathrm{\mathcal {G}}}}_v$ be a maximum gene forest satisfying $\langle S, \delta , \lambda \rangle |_{v}$ and G be a tree in that forest with a duplication node mapping into v. For the purpose of contradiction, assume that ${{\mathrm{\mathcal {G}}}}_v$ also contains another tree $G'$ with a node mapping into v. Let ${{\mathrm{\mathcal {G}}}}'$ be a forest consisting of subtrees of $G'$ obtained by removing all internal nodes mapping into v from $G'$ (this will split $G'$ into at least two subtrees). If $G'$ induced k duplication nodes on v (k could be 0), then, by Observation 2, ${{\mathrm{\mathcal {G}}}}'$ will contain at least $k + 2$ subtrees (or $k+1$ if v is a leaf). Let us enumerate any $k+1$ trees in ${{\mathrm{\mathcal {G}}}}'$ as $G'_1, G'_2, \ldots , G'_k, G'_{k+1}$. Consider now an augmentation of G, tree $G_{a}$, obtained by a caterpillar assembly of a profile $(G, G'_1, G'_2, \ldots , G'_k)$. Note that $G_{a}$ induces k more duplications onto v than G. Hence, the gene forest ${{\mathrm{\mathcal {G}}}}_v - \{G\} \cup \{G_{a}, G'_{k+1}\}$ satisfies the duplication scenario $\langle S, \delta , \lambda \rangle |_{v}$ and is of size larger than ${{\mathrm{\mathcal {G}}}}_v$ – contradiction.

• (MF5) Assume (for contradiction) a maximum forest ${{\mathrm{\mathcal {G}}}}_v$ contains a tree G, such that $M({{\mathrm{\mathsf {Rt}}}}(G)) = v$. Removing the root of G will split it into two subtrees and increase the size of the gene forest by one (we denote the new gene forest by ${{\mathrm{\mathcal {G}}}}'_v$). Since $\delta (v) = 0$, this operation will maintain that ${{\mathrm{\mathcal {G}}}}'_v$ satisfies $\langle S, \delta , \lambda \rangle |_{v}$. Hence, ${{\mathrm{\mathcal {G}}}}_v$ is not maximum – contradiction.

Lemma 2 then proves the correctness of Algorithm 1 (the lemma’s proof is omitted for brevity).

Lemma 2

Function from Algorithm 1 given a node $v \in V(S)$ returns $\alpha (v)$.

3.3 Gene Trees for Feasible Scenarios

Algorithm 1 is designed to solve the feasibility problem. However, in addition, this algorithm can be modified to construct an example gene tree satisfying the given duplication scenario (if one exists). This modification would require maintaining the maximum gene forests themselves, instead of only keeping track of the number of trees in maximum gene forests. For species tree nodes v with $\delta (v) > 0$ the algorithm will need to join a subset of the available subtrees in a caterpillar that would satisfy that lower bound on duplications.

At the root of the species tree the trees in the maximum forest (if it is non-empty) should be joined together to produce an example gene tree satisfying the duplication scenario.

Time Complexity. Let m be the size of the gene family, i.e., $m = \sum _{s \in L(S)}{\lambda (s)}$. Then the complexity of constructing the gene tree as outlined above is $\varTheta (m)$. Representing gene forests as linked lists allows us to join two forests in O(1) time. Further, when assembling trees in a caterpillar, the linked lists will allow to use O(1) time per each new node created. Hence, the overall time complexity is bounded by the size of the gene tree, which is $\varTheta (m)$.

Minimum Gene Trees. Such gene tree building procedure, while of potential value on its own, can be further altered to produce a smallest gene tree satisfying the given duplication scenario. Such minimality can be achieved by not employing some of the gene copies present in the family, if it is not necessary.

For a node $v \in V(S) \setminus L(S)$ with $\delta (v) > 0$ and children u and w, let ${{\mathrm{\mathcal {G}}}}'_v$ denote the forest of available gene trees at v; that is, the union of the maximum gene forests of the children of v. We will call a gene tree trivial, if it contains exactly one node; i.e., it represents a single gene copy.

The original algorithm will proceed by assembling $\delta (v) + 2$ trees from ${{\mathrm{\mathcal {G}}}}'_v$ in a caterpillar structure. However, since we are interested in using as few gene copies as possible, we would like to use as few trivial trees for the caterpillar assembly as possible. Formally, consider all profiles of trees of the type $\{G_1, G_2, \ldots , G_{\delta (v) + 2}\}$, such that $G_1 \in {{\mathrm{\mathcal {G}}}}_u, G_2 \in {{\mathrm{\mathcal {G}}}}_w, G_3, \ldots , G_{\delta (v) + 2} \in {{\mathrm{\mathcal {G}}}}_u \cup {{\mathrm{\mathcal {G}}}}_w$ (where ${{\mathrm{\mathcal {G}}}}_u$ and ${{\mathrm{\mathcal {G}}}}_w$ are maximum forests for u and w, respectively). Let $P({{\mathrm{\mathcal {G}}}}_u, {{\mathrm{\mathcal {G}}}}_w)$ be such a profile with the minimum number of trivial trees. Then the algorithm for the minimum gene tree construction will use such a profile for the caterpillar assembly.

This constitutes a greedy strategy for the minimum gene tree construction: at each step use the minimum number of trivial trees for the caterpillar assembly. Then let ${{\mathrm{\mathcal {G}}}}_p$ be a maximum gene forest satisfying $\langle S, \delta , \lambda \rangle$ constructed that way.

Theorem 1

A minimum (most parsimonious) gene tree is obtained by removing all the trivial trees from ${{\mathrm{\mathcal {G}}}}_p$ and joining the rest together (e.g., as a caterpillar). The time complexity for constructing a minimum gene tree is O(m). That is, Algorithm 2 constructs a minimum gene tree satisfying $\langle S, \delta , \lambda \rangle$ in O(m).

Proof

The proof of correctness is omitted for brevity. Here we argue the time-complexity. The algorithm can be implemented efficiently by representing gene forests as two separate linked lists: one list for trivial trees and the other for non-trivial trees (see Algorithm 2). Then joining two forests (as needed for internal nodes v with $\delta (v) = 0$) encompasses joining two pairs of linked lists, which can be done in constant time (by maintaining a link to the last element of each list). Further, for internal nodes v with $\delta (v) > 0$ and children u and w, the algorithm has to construct a caterpillar assembly of a minimum profile $P({{\mathrm{\mathcal {G}}}}_u, {{\mathrm{\mathcal {G}}}}_w)$. Let ${{\mathrm{\mathcal {G}}}}_u^t$ and ${{\mathrm{\mathcal {G}}}}_u^{nt}$ denote the linked lists containing trivial and non-trivial trees of ${{\mathrm{\mathcal {G}}}}_u$ respectively (similarly, for w). Then $P({{\mathrm{\mathcal {G}}}}_u, {{\mathrm{\mathcal {G}}}}_w)$ can be obtained in $O(\delta (v))$ time as demonstrated in function of Algorithm 2.

The caterpillar assembly of the profile also takes $O(\delta (v))$ time and it produces $\delta (v)$ new nodes contributing to the resulting gene tree. Hence, the algorithm spends constant time per each node created. Finally, observe that for each leaf node s of the species tree the algorithm spends $O(\lambda (s))$ time. Hence, the total time spent for all leaves is O(m). Overall, the time complexity bounded by O(m).

4 Conclusion and Discussion

Gene trees play a crucial role in the inference of species trees and networks, in the systematic analysis of protein function, and other related areas [4, 13, 15]. Refining the credibility of gene trees is thereof one of the central topics in phylogenetics for many years.

Here we propose a novel framework, where the evidence of gene duplications collected throughout an abundance of biological studies can be utilized to improve on the accuracy of gene trees. In this framework we define a duplication scenario as an augmentation of the species tree with localized evidence of duplication events, and introduce a linear time algorithm for determining whether a duplication scenario is feasible for a particular gene family; that is, whether there exists an evolutionary history of the gene family whose reconciliation is in agreement with the postulated duplication events in the species tree. In addition, following the phylogenetic parsimony paradigm [11], this algorithm can construct a smallest gene tree that will satisfy the given duplication scenario.

The presented work is laying the foundation for practitioners to assess, aggregate, and study various duplication scenarios that can be inferred from the existing studies of gene families and their evolution. Our algorithm has the ability to support a much broader range of applications beyond the feasibility question, e.g., pointing out where the additional (lost) gene lineages might have existed for duplication scenarios failing the most parsimonious duplication model.