Abstract
We consider an Information-Plus-Noise type matrix where the Information matrix is a spiked matrix. When some eigenvalues of the random matrix separate from the bulk, we study how the corresponding eigenvectors project onto those of the spikes. Note that, in an Appendix, we present alternative versions of the earlier results of Bai and Silverstein (Random Matrices Theory Appl 1(1):1150004, 44, 2012) (“noeigenvalue outside the support of the deterministic equivalent measure”) and Capitaine (Indiana Univ Math J 63(6):1875–1910, 2014) (“exact separation phenomenon”) where we remove some technical assumptions that were difficult to handle.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
- Random matrices
- Spiked information-plus-noise type matrices
- Eigenvalues
- Eigenvectors
- Outliers
- Deterministic equivalent measure
- Exact separation phenomenon
4.1 Introduction
In this paper, we consider the so-called Information-Plus-Noise type model
defined as follows.
-
n = n(N), n ≤ N, c N = n∕N →N→+∞c ∈ ]0;1].
-
σ ∈ ]0;+∞[.
-
X N = [X ij]1≤i≤n;1≤j≤N where \(\{X_{ij}, i\in \mathbb {N}, j \in \mathbb {N}\}\) is an infinite set of complex random variables such that \(\{\Re (X_{ij}), \Im (X_{ij}), i\in \mathbb {N}, j \in \mathbb {N}\}\) are independent centered random variables with variance 1∕2 and satisfy
-
1.
There exists K > 0 and a random variable Z with finite fourth moment for which there exists x 0 > 0 and an integer number n 0 > 0 such that, for any x > x 0 and any integer numbers n 1, n 2 > n 0, we have
$$\displaystyle \begin{aligned}\frac{1}{n_1n_2} \sum_{i\leq n_1,j\leq n_2}P\left( \vert X_{ij}\vert >x\right) \leq KP\left(\vert Z \vert>x\right).\end{aligned} $$(4.1) -
2.
$$\displaystyle \begin{aligned}\sup_{(i,j)\in \mathbb{N}^2}\mathbb{E}(\vert X_{ij}\vert^3)<+\infty. \end{aligned} $$(4.2)
-
1.
-
Let ν be a compactly supported probability measure on \(\mathbb {R}\) whose support has a finite number of connected components. Let Θ = {θ 1;…;θ J} where θ 1 > … > θ J ≥ 0 are J fixed real numbers independent of N which are outside the support of ν. Let k 1, …, k J be fixed integer numbers independent of N and \(r=\sum _{j=1}^J k_j\). Let β j(N) ≥ 0, r + 1 ≤ j ≤ n, be such that \(\frac {1}{n} \sum _{j=r+1}^{n} \delta _{\beta _j(N)}\) weakly converges to ν and
$$\displaystyle \begin{aligned} \max _{r+1\leq j\leq n} \mathrm{dist}(\beta _j(N),\mathrm{supp}(\nu ))\mathop{\longrightarrow } _{N \rightarrow \infty } 0\end{aligned} $$(4.3)where supp(ν) denotes the support of ν.
Let α j(N), j = 1, …, J, be real nonnegative numbers such that
$$\displaystyle \begin{aligned}\lim_{N \rightarrow +\infty} \alpha_j(N)=\theta_j.\end{aligned}$$Let A N be a n × N deterministic matrix such that, for each j = 1, …, J, α j(N) is an eigenvalue of \(A_N A_N^*\) with multiplicity k j, and the other eigenvalues of \(A_N A_N^*\) are the β j(N), r + 1 ≤ j ≤ n. Note that the empirical spectral measure of \({A_N A_N^*} \) weakly converges to ν.
Remark 4.1
Note that assumption such as (4.1) appears in [14]. It obviously holds if the X ij’s are identically distributed with finite fourth moment.
For any Hermitian n × n matrix Y , denote by spect(Y ) its spectrum, by
the ordered eigenvalues of Y and by μ Y the empirical spectral measure of Y :
For a probability measure τ on \(\mathbb {R}\), denote by g τ its Stieltjes transform defined for \(z \in \mathbb {C}\setminus \mathbb {R}\) by
When the X ij’s are identically distributed, Dozier and Silverstein established in [15] that almost surely the empirical spectral measure \(\mu _{M_N}\) of M N converges weakly towards a nonrandom distribution μ σ,ν,c which is characterized in terms of its Stieltjes transform which satisfies the following equation: for any \(z \in \mathbb {C}^+\),
This result of convergence was extended to independent but non identically distributed random variables by Xie in [30]. (Note that, in [21], the authors in- vestigated the case where σ is replaced by a bounded sequence of real numbers.) In [11], the author carries on with the study of the support of the limiting spectral measure previously investigated in [16] and later in [25, 28] and obtains that there is a one-to-one relationship between the complement of the limiting support and some subset in the complement of the support of ν which is defined in (4.6) below.
Proposition 4.1
Define differentiable functions ω σ, ν, c and Φ σ, ν, c on respectively \( \mathbb {R}\setminus \mathit{\mbox{supp}}(\mu _{\sigma ,\nu ,c})\) and \( \mathbb {R}\setminus \mathit{\mbox{supp}}(\nu )\) by setting
and
Set
ω σ,ν,c is an increasing analytic diffeomorphism with positive derivative from \(\mathbb {R}\setminus \mathit{\mbox{supp}}(\mu _{\sigma ,\nu ,c})\) to \(\mathbb {E}_{\sigma ,\nu ,c}\) , with inverse Φ σ,ν,c.
Moreover, extending previous results in [25] and [8] involving the Gaussian case and finite rank perturbations, [11] establishes a one-to-one correspondence between the θ i’s that belong to the set \(\mathbb {E}_{\sigma ,\nu ,c}\) (counting multiplicity) and the outliers in the spectrum of M N. More precisely, setting
and
we have the following results.
Theorem 4.1 ([11])
For any 𝜖 > 0,
Theorem 4.2 ([11])
Let θ j be in Θ σ,ν,c and denote by n j−1 + 1, …, n j−1 + k j the descending ranks of α j(N) among the eigenvalues of \(A_NA_N^*\) . Then the k j eigenvalues \((\lambda _{n_{j-1}+i}(M_N), \, 1 \leq i \leq k_j)\) converge almost surely outside the support of μ σ,ν,c towards \(\rho _{\theta _j}:=\varPhi _{\sigma ,\nu ,c}(\theta _j)\) . Moreover, these eigenvalues asymptotically separate from the rest of the spectrum since (with the conventions that λ 0(M N) = +∞ and λ N+1(M N) = −∞) there exists δ 0 > 0 such that almost surely for all large N,
Remark 4.2
Note that Theorems 4.1 and 4.2 were established in [11] for A N as (4.14) below and with \(\mathbb {S}\cup \{0\}\) instead of \( \mathbb {S}\) but they hold true as stated above and in the more general framework of this paper. Indeed, these extensions can be obtained sticking to the proof of the corresponding results in [11] but using the new versions of [3] and of the exact separation phenomenon of [11] which are presented in the Appendix 1 of the present paper.
The aim of this paper is to study how the eigenvectors corresponding to the outliers of M N project onto those corresponding to the spikes θ i’s. Note that there are some pioneering results investigating the eigenvectors corresponding to the outliers of finite rank perturbations of classical random matricial models: [27] in the real Gaussian sample covariance matrix setting, and [7, 8] dealing with finite rank additive or multiplicative perturbations of unitarily invariant matrices. For a general perturbation, dealing with sample covariance matrices, Péché and Ledoit [23] introduced a tool to study the average behaviour of the eigenvectors but it seems that this did not allow them to focus on the eigenvectors associated with the eigenvalues that separate from the bulk. It turns out that further studies [6, 10] point out that the angle between the eigenvectors of the outliers of the deformed model and the eigenvectors associated to the corresponding original spikes is determined by Biane-Voiculescu’s subordination function. For the model investigated in this paper, such a free interpretation holds but we choose not to develop this free probabilistic point of view in this paper and we refer the reader to the paper [13]. Here is the main result of the paper.
Theorem 4.3
Let θ j be in Θ σ,ν,c (defined in (4.7)) and denote by n j−1 + 1, …, n j−1 + k j the descending ranks of α j(N) among the eigenvalues of \(A_NA_N^*\) . Let ξ(j) be a normalized eigenvector of M N relative to one of the eigenvalues \((\lambda _{n_{j-1}+q}(M_N)\) , 1 ≤ q ≤ k j). Denote by ∥⋅∥2 the Euclidean norm on \(\mathbb {C}^n\) . Then, almost surely
-
(i)
\(\displaystyle {\lim _{N\rightarrow +\infty }\left \| P_{\mathit{\mbox{Ker }}(\alpha _j(N) I_N-A_NA_N^*)}\xi (j)\right \|{ }^2_2 = \tau (\theta _j)}\)
where
$$\displaystyle \begin{aligned}\tau(\theta_j)= \frac{1-\sigma^2c g_{\mu_{\sigma,\nu,c}}(\rho_{\theta_j})}{\omega_{\sigma,\nu,c}^{\prime}(\rho_{\theta_j})}=\frac{ \varPhi_{\sigma,\nu,c}^{\prime}({\theta_j})}{1+ \sigma^2 cg_\nu(\theta_j)} \end{aligned} $$(4.10) -
(ii)
for any θ i in Θ σ,ν,c ∖{θ j},
$$\displaystyle \begin{aligned}\displaystyle{\lim_{N\rightarrow +\infty}\left\| P_{ \mathit{\mbox{Ker }}(\alpha_i(N) I_N-A_NA_N^*)}\xi(j)\right\|{}_2 = 0.}\end{aligned}$$
The sketch of the proof of Theorem 4.3 follows the analysis of [10] as explained in Sect. 4.2. In Sect. 4.3, we prove a universal result allowing to reduce the study to estimating expectations of Gaussian resolvent entries carried on Sect. 4.4. In Sect. 4.5, we explain how to deduce Theorem 4.3 from the previous Sections. In an Appendix 1, we present alternative versions on the one hand of the result in [3] about the lack of eigenvalues outside the support of the deterministic equivalent measure, and, on the other hand, of the result in [11] about the exact separation phenomenon. These new versions deal with random variables whose imaginary and real parts are independent but remove the technical assumptions ((1.10) and “b 1 > 0” in Theorem 1.1 in [3] and “ω σ,ν,c(b) > 0” in Theorem 1.2 in [11]). This allows us to claim that Theorem 4.2 holds in our context (see Remark 4.2). Finally, we present, in Appendix 2, some technical lemmas that are used throughout the paper.
4.2 Sketch of the Proof
Throughout the paper, for any m × p matrix B, \((m,p)\in {\mathbb {N}}^2\), we will denote by ∥B∥ the largest singular value of B, and by \(\Vert B\Vert _2=\{Tr (BB^*)\}^{\frac {1}{2}}\) its Hilbert-Schmidt norm.
The proof of Theorem 4.3 follows the analysis in two steps of [10].
Step A
First, we shall prove that, for any orthonormal system \((\xi _1,\cdots ,\xi _{k_j})\) of eigenvectors associated to the k j eigenvalues \(\lambda _{n_{j-1}+q}(M_N)\), 1 ≤ q ≤ k j, the following convergence holds almost surely: ∀l = 1, …, J,
Note that for any smooth functions h and f on \(\mathbb {R}\), if v 1, …, v n are eigenvectors associated to \(\lambda _1(A_NA_N^*), \ldots ,\lambda _n(A_NA_N^*)\) and w 1, …, w n are eigenvectors associated to λ 1(M N), …, λ n(M N), one can easily check that
Thus, since α l(N) on one hand and the k j eigenvalues of M N in \((\rho _{\theta _j} -\varepsilon ,\rho _{\theta _j}+\varepsilon [ )\) (for 𝜖 small enough) on the other hand, asymptotically separate from the rest of the spectrum of respectively \(A_NA_N^*\) and M N, a fit choice of h and f will allow the study of the restrictive sum \(\sum _{p=1}^{k_j}\left \| P_{\ker (\alpha _l(N) I_N-A_NA_N^*)} \xi _p \right \|{ }^2_2\). Therefore proving (4.11) is reduced to the study of the asymptotic behaviour of \(\mathrm {Tr}\left [h(M_N)f(A_NA_N^*)\right ]\) for some functions f and h respectively concentrated on a neighborhood of θ l and \(\rho _{\theta _j}\).
Step B
In the second, and final, step, we shall use a perturbation argument identical to the one used in [10] to reduce the problem to the case of a spike with multiplicity one, case that follows trivially from Step A.
Step B closely follows the lines of [10] whereas Step A requires substantial work. We first reduce the investigations to the mean Gaussian case by proving the following.
Proposition 4.2
Let X N as defined in Sect. 4.1 . Let \(\mathbb {G}_N = [\mathbb {G}_{ij}]_{1\leq i\leq n, 1\leq j\leq N}\) be a n × N random matrix with i.i.d. standard complex normal entries. Let h be a function in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with compact support, and Γ N be a n × n Hermitian matrix such that
Then almost surely,
\(\mathrm {Tr} \left (h\left (\left (\sigma \frac {X_N}{\sqrt {N}}+A_N\right )\left (\sigma \frac {X_N}{\sqrt {N}}+A_N\right )^*\right ) \varGamma _N\right )\)
The asymptotic behaviour of \(\mathbb {E}\Big (\mathrm {Tr} \Big [h\Big (\Big (\sigma \frac {\mathbb {G}_N}{\sqrt {N}}+A_N\Big )\Big (\sigma \frac {\mathbb {G}_N}{\sqrt {N}}+A_N\Big )^*\Big ) f(A_NA_N^*)\Big ] \Big )\) can be deduced, by using the bi-unitarily invariance of the distribution of \( \mathbb {G}_N\), from the following Proposition 4.3 and Lemma 4.18.
Proposition 4.3
Let \(\mathbb {G}_N = [\mathbb {G}_{ij}]_{1\leq i \leq n, 1\leq j\leq N}\) be a n × N random matrix with i.i.d. complex standard normal entries. Assume that A N is such that
where n = n(N), n ≤ N, c N = n∕N →N→+∞c ∈ ]0;1], for i = 1, …, n, \(d_i(N) \in \mathbb {C}\) , supNmaxi=1,…,n|d i(N)| < +∞ and \(\frac {1}{n} \sum _{i=1}^n \delta _{\vert d_i(N)\vert ^2}\) weakly converges to a compactly supported probability measure ν on \(\mathbb {R}\) when N goes to infinity. Define for all \(z\in \mathbb {C}\setminus \mathbb {R}\) ,
Define for any q = 1, …, n,
There is a polynomial P with nonnegative coefficients, a sequence (u N)N of nonnegative real numbers converging to zero when N goes to infinity and some nonnegative real number l, such that for any (p, q) in {1, …, n}2, for all \(z\in \mathbb {C}\setminus \mathbb {R}\) ,
with
4.3 Proof of Proposition 4.2
In the following, we will denote by o C(1) any deterministic sequence of positive real numbers depending on the parameter C and converging for each fixed C to zero when N goes to infinity. The aim of this section is to prove Proposition 4.2.
Define for any C > 0,

Set
We have

so that
Note that

so that
Similarly
Let us assume that C > 8θ ∗. Then, we have
Define for any C > 8θ ∗, \(X^C=(X^C_{ij})_{1\leq i \leq n; 1\leq j \leq N},\) where for any 1 ≤ i ≤ n, 1 ≤ j ≤ N,
Let \(\mathbb {G} = [\mathbb {G}_{ij}]_{1\leq i\leq n, 1\leq j \leq N}\) be a n × N random matrix with i.i.d. standard complex normal entries, independent from X N, and define for any α > 0,
Now, for any n × N matrix B, let us introduce the (N + n) × (N + n) matrix
Define for any \(z\in \mathbb {C}\setminus \mathbb {R}\),
and
Denote by \(\mathbb {U}(n+N)\) the set of unitary (n + N) × (n + N) matrices. We first establish the following approximation result.
Lemma 4.1
There exist some positive deterministic functions u and v on [0, +∞[ such that limC→+∞u(C) = 0 and limα→0v(α) = 0, and a polynomial P with nonnegative coefficients such that for any α and C > 8θ ∗, we have that
-
almost surely, for all large N,
$$\displaystyle \begin{aligned} &\displaystyle{ \sup_{U\in \mathbb{U}(n+N)}\sup_{(i,j)\in \{1,\ldots,n+N\}^2}\sup_{z\in \mathbb{C}\setminus \mathbb{R} } |\Im z |{}^{2} \left| (U^*\tilde{G}^{\alpha,C}(z)U)_{ij}- (U^*\tilde{{G}}(z)U)_{ij}\right|} \\ & \quad \leq u(C)+v(\alpha),{} \end{aligned} $$(4.19) -
for all large N,
$$\displaystyle \begin{aligned} & \displaystyle{ \sup_{U\in \mathbb{U}(n+N)} \sup_{(i,j)\in \{1,\ldots,n+N\}^2} \sup_{z\in \mathbb{C}\setminus \mathbb{R} } \frac{1}{ P(|\Im z |{}^{-1}) }} \\ &\quad \displaystyle{\times\left| \mathbb{E} \left( (U^*\tilde{G}^{\alpha,C}(z)U)_{ij}- (U^*\tilde{{G}}(z)U)_{ij}\right)\right|} \\ & \qquad \leq u(C)+v(\alpha)+ o_{C}(1). {} \end{aligned} $$(4.20)
Proof
Note that
Then,
It is straightforward to see, using Lemma 4.17, that for any unitary (n + N) × (n + N) matrix U,
From Bai-Yin’s theorem (Theorem 5.8 in [2]), we have
Applying Remark 4.3 to the (n + N) × (n + N) matrix \(\tilde B= \left ( \begin {array}{ll} 0_{n\times n}~~~ B\\ B^*~~~ 0_{N\times N} \end {array} \right )\) for B ∈{X N − Y C, X C − Y C, X C} (see also Appendix B of [14]), we have that almost surely
and
Then, (4.19) readily follows.
Let us introduce
Using (4.21), we have
Thus (4.20) follows.
Now, Lemmas 4.18, 4.1 and 4.19 readily yields the following approximation lemma.
Lemma 4.2
Let h be in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with compact support and \(\tilde \varGamma _N\) be a (n + N) × (n + N) Hermitian matrix such that
Then, there exist some deterministic functions on [0, +∞[, u and v, such that limC→+∞u(C) = 0 and limα→0v(α) = 0, such that for all C > 0, α > 0, we have almost surely for all large N,
and for all large N,
where
Note that the distributions of the independent random variables \(\Re (X_{ij}^{\alpha ,C})\), \(\Im (X_{ij}^{\alpha ,C})\) are all a convolution of a centred Gaussian distribution with some variance v α, with some law with bounded support in a ball of some radius R C,α; thus, according to Lemma 4.20, they satisfy a Poincaré inequality with some common constant C PI(C, α) and therefore so does their product (see Appendix 2). An important consequence of the Poincaré inequality is the following concentration result.
Lemma 4.3
Lemma 4.4.3 and Exercise 4.4.5 in [ 1 ] or Chapter 3 in [ 24 ]. There exists K 1 > 0 and K 2 > 0 such that for any probability measure \(\mathbb {P}\) on \(\mathbb {R^M}\) which satisfies a Poincaré inequality with constant C PI, and for any Lipschitz function F on \(\mathbb {R}^M\) with Lipschitz constant |F|Lip, we have
In order to apply Lemma 4.3, we need the following preliminary lemmas.
Lemma 4.4 (See Lemma 8.2 [10])
Let f be a real \(C_{\mathbb {L}}\) -Lipschitz function on \(\mathbb {R}\) . Then its extension on the N × N Hermitian matrices is \(C_{\mathbb {L}}\) -Lipschitz with respect to the Hilbert-Schmidt norm.
Lemma 4.5
Let \(\tilde \varGamma _N \) be a (n + N) × (n + N) matrix and h be a real Lipschitz function on \(\mathbb {R}\) . For any n × N matrix B,
is Lipschitz with constant bounded by \(\sqrt {2} \left \| \tilde \varGamma _N \right \|{ }_2 \Vert h \Vert _{Lip}\).
Proof
where we used Lemma 4.4 in the last line. Now,
Lemma 4.5 readily follows from (4.25) and (4.26).
Lemma 4.6
Let \(\tilde \varGamma _N \) be a (n + N) × (n + N) matrix such that \( \sup _{N,n} \left \| \tilde \varGamma _N \right \|{ }_2 \leq K\) . Let h be a real Lipschitz function on \(\mathbb {R}\). \(F_N=\mathrm {Tr} \left [ h\left ( \mathbb {M}_{N+p}\left ( \frac {X^{\alpha ,C}}{\sqrt {N}}\right ) \right ) \tilde \varGamma _N\right ]\) satisfies the following concentration inequality
for some positive real numbers K 1 and K 2(α, C).
Proof
Lemma 4.6 follows from Lemmas 4.5 and 4.3 and basic facts on Poincaré inequality recalled at the end of Appendix 2.
By Borel-Cantelli’s Lemma, we readily deduce from the above Lemma the following
Lemma 4.7
Let \(\tilde \varGamma _N \) be a (n + N) × (n + N) matrix such that \( \sup _{N,n} \left \| \tilde \varGamma _N \right \|{ }_2 \leq K\) . Let h be a real \(\mathbb {C}^1\) - function with compact support on \(\mathbb {R}\).
Now, we will establish a comparison result with the Gaussian case for the mean values by using the following lemma (which is an extension of Lemma 4.10 below to the non-Gaussian case) as initiated by Khorunzhy et al. [22] in Random Matrix Theory.
Lemma 4.8
Let ξ be a real-valued random variable such that \(\mathbb {E}(\vert \xi \vert ^{p+2}) < \infty \) . Let ϕ be a function from \(\mathbb {R}\) to \(\mathbb {C}\) such that the first p + 1 derivatives are continuous and bounded. Then,
where κ a are the cumulants of ξ, \(\vert \epsilon \vert \leq K \sup _t \vert \phi ^{(p+1)}(t)\vert \mathbb {E} (\vert \xi \vert ^{p+2})\) , K only depends on p.
Lemma 4.9
Let \(\mathbb {G}_N = [\mathbb {G}_{ij}]_{1\leq i\leq n, 1\leq j\leq N}\) be a n × N random matrix with i.i.d. complex N(0, 1) Gaussian entries. Define
for any \(z\in \mathbb {C}\setminus \mathbb {R}.\) There exists a polynomial P with nonnegative coefficients such that for all large N, for any (i, j) ∈{1, …, n + N}2, for any \(z\in \mathbb {C}\setminus \mathbb {R}\) , for any unitary (n + N) × (n + N) matrix U,
Moreover, for any (N + n) × (N + n) matrix \(\tilde \varGamma _N\) such that
and any function h in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with compact support, there exists some constant K > 0 such that, for any large N,
Proof
We follow the approach of [26] chapters 18 and 19 consisting in introducing an interpolation matrix \(X_N(\alpha )= \cos \alpha X_N + \sin \alpha \mathbb {G}_N\) for any α in \([0;\frac {\pi }{2}]\) and the corresponding resolvent matrix \(\tilde G(\alpha ,z)= \left ( zI_{N+n}- \mathbb {M}_{N+n}\left (\sigma \frac {X_N(\alpha )}{\sqrt {N}}\right ) \right )^{-1}\) for any \(z\in \mathbb {C}\setminus \mathbb {R}.\) We have, for any (s, t) ∈{1, …, n + N}2,
with
Now, for any l = 1, …, n and k = n + 1, …, n + N, using Lemma 4.8 for p = 1 and for each random variable ξ in the set \(\left \{\Re X_{l(k-n)}, \Re \mathbb {G}_{l(k-n)},\Im X_{l(k-n)}, \Im \mathbb {G}_{l(k-n)} \right \} \), and for each ϕ in the set
one can easily see that there exists some constant K > 0 such that
where \(\mathbb {H}_{n+N}(\mathbb {C})\) denotes the set of (n + N) × (n + N) Hermitian matrices and S V(Y ) is a sum of a finite number independent of N and n of terms of the form
with \(R(Y)=\left (zI_{N+n}- Y\right )^{-1}\) and {p 1, …, p 6} contains exactly three k and three l.
When (p 1, p 6) = (k, l) or (l, k), then, using Lemma 4.17,
When p 1 = p 6 = k or l, then, using Lemma 4.17,
(4.29) readily follows.
Then by Lemma 4.19, there exists some constant K > 0 such that, for any N and n, for any (i, j) ∈{1, …, n + N}2, any unitary (n + N) × (n + N) matrix U,
Thus, using (4.97) and (4.30), we can deduce (4.31) from (4.33).
The above comparison lemmas allow us to establish the following convergence result.
Proposition 4.4
Let h be a function in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with compact support and let \(\tilde \varGamma _N \) be a (n + N) × (n + N) matrix such that \( \sup _{n,N} \mathrm {rank} (\tilde \varGamma _N) <\infty \) and \( \sup _{n,N} \Vert \tilde \varGamma _N \Vert <\infty \) . Then we have that almost surely
Proof
Lemmas 4.2, 4.7 and 4.9 readily yield that there exist some positive deterministic functions u and v on [0, +∞[ with limC→+∞u(C) = 0 and limα→0v(α) = 0, such that for any C > 0 and any α > 0, almost surely
The result follows by letting α go to zero and C go to infinity.
Now, note that, for any N × n matrix B, for any continuous real function h on \(\mathbb {R}\), and any n × n Hermitian matrix Γ N, we have
where \(\tilde h(x)=h(x^2)\) and \( \tilde \varGamma _N= \begin {pmatrix} \varGamma _N & (0)\\ (0) & (0) \end {pmatrix}\). Thus, Proposition 4.4 readily yields Proposition 4.2.
4.4 Proof of Proposition 4.3
The aim of this section is to prove Proposition 4.3 which deals with Gaussian random variables.Therefore we assume here that A N is as (4.14) and set \(\gamma _q(N)=(A_N A_N^*)_{qq}\). In this section, we let X stand for \(\mathbb {G}_N\), A stands for A N, G denotes the resolvent of M N = ΣΣ ∗ where \(\varSigma =\sigma \frac {\mathbb {G}_N}{\sqrt {N}}+A_N\) and g N denotes the mean of the Stieltjes transform of the spectral measure of M N, that is
4.4.1 Matricial Master Equation
To obtain Eq. (4.35) below, we will use many ideas from [17]. The following Gaussian integration by part formula is the key tool in our approach.
Lemma 4.10 (Lemma 2.4.5 [1])
Let ξ be a real centered Gaussian random variable with variance 1. Let Φ be a differentiable function with polynomial growth of Φ and Φ′. Then,
Proposition 4.5
Let z be in \(\mathbb {C}\setminus \mathbb {R}\) . We have for any (p, q) in {1, …, n}2,

where
Proof
Using Lemma 4.10 with \(\xi =\Re X_{ij} \) or ξ = ℑX ij and \(\varPhi = G_{pi} \overline {\varSigma _{qj}}\), we obtain that for any j, q, p,
On the other hand, we have
where we applied Lemma 4.10 with \(\xi =\Re X_{qj} \) or ξ = ℑX qj and Ψ = G piA ij. Summing (4.42) and (4.44) yields
Define
From (4.46), we can deduce that
Then, summing over j, we obtain that
where Δ 1(p, q) is defined by (4.37). Applying Lemma 4.10 with \(\xi =\Re X_{ij} \) or ℑX ij and Ψ = (GA)ij, we obtain that
Thus,
where Δ 3 is defined by (4.39) and then
where Δ 2(p, q) is defined by (4.38). We can deduce from (4.47) and (4.49) that
Using the resolvent identity and (4.50), we obtain that
where ∇pq is defined by (4.36). Taking p = q in (4.51), summing over p and dividing by n, we obtain that
It readily follows that
Therefore
Proposition 4.5 follows.
4.4.2 Variance Estimates
In this section, when we state that some quantity Δ N(z), \(z \in \mathbb {C}\setminus \mathbb {R}\), is equal to \(O(\frac {1}{N^p})\), this means precisely that there exist some polynomial P with nonnegative coefficients and some positive real number l which are all independent of N such that for any \(z \in \mathbb {C}\setminus \mathbb {R}\),
We present now the different estimates on the variance. They rely on the following Gaussian Poincaré inequality (see Appendix 2). Let Z 1, …, Z q be q real independent centered Gaussian variables with variance σ 2. For any \(\mathbb {C}^1\) function \(f: \mathbb {R}^q \rightarrow \mathbb {C}\) such that f and gradf are in \(L^2(\mathbb {N}(0, \sigma ^2I_q))\), we have
denoting for any random variable a by V(a) its variance \( \mathbb {E}(\vert a-\mathbb {E}(a)\vert ^2)\). Thus, (Z 1, …, Z q) satisfies a Poincaré inequality with constant C PI = σ 2.
The following preliminary result will be useful to these estimates.
Lemma 4.11
There exists K > 0 such for all N,
Proof
According to Lemma 7.2 in [19], we have for any t ∈ ]0;N∕2],
By the Chebychev’s inequality, we have
It follows that
The result follows by optimizing in t.
Lemma 4.12
There exists C > 0 such that for all large N, for all \(z \in \mathbb {C}\setminus \mathbb {R}\) ,
Proof
Let us define \(\varPsi : \mathbb {R}^{2(n\times N)} \rightarrow { M }_{n\times N}(\mathbb {C})\) by
where e ij stands for the n × N matrix such that for any (p, q) in {1, …, n}×{1, …, N}, (e ij)pq = δ ipδ jq. Let F be a smooth complex function on \({ M }_{n\times N}(\mathbb {C})\) and define the complex function f on \(\mathbb {R}^{2(n\times N)}\) by setting f = F ∘ Ψ. Then,
Now, \(X=\varPsi (\Re (X_{ij}), \Im (X_{ij}),1\leq i\leq n,1\leq j\leq N)\) where the distribution of the random variable \((\Re (X_{ij}), \Im (X_{ij}),1\leq i\leq n,1\leq j\leq N)\) is \(\mathbb {N}(0, \frac {1}{2}I_{2nN})\).
Hence consider \(F:~H \rightarrow \frac {1}{n} \mathrm {Tr} \left (zI_n -\left (\sigma \frac { H}{\sqrt {N}} +A \right )\left (\sigma \frac {H}{\sqrt {N}} +A \right )^*\right )^{-1}\).
Let \( V\in {M }_{n\times N}(\mathbb {C})\) such that TrV V ∗ = 1.
Moreover using Cauchy-Schwartz’s inequality and Lemma 4.17, we have
We get obviously the same bound for \(\vert \frac {1}{n} \mathrm {Tr}\left (G \left (\sigma \frac {X}{\sqrt {N}} +A \right ) \sigma \frac {V^*}{\sqrt {N}} G\right )\vert \). Thus
(4.56) readily follows from (4.55), (4.59), Theorem A.8 in [2], Lemma 4.11 and the fact that ∥A N∥ is uniformly bounded. Similarly, considering
where E qp is the n × n matrix such that (E qp)ij = δ qiδ pj, we can obtain that, for any \(V\in { M }_{n\times N}(\mathbb {C})\) such that TrV V ∗ = 1,
Thus, one can get (4.57) in the same way. Finally, considering
we can obtain that, for any \(V\in { M }_{n\times N}(\mathbb {C})\) such that TrV V ∗ = 1,
Using Lemma 4.17 (i), Theorem A.8 in [2], Lemma 4.11, the identity ΣΣ ∗G = GΣΣ ∗ = −I + zG, and the fact that ∥A N∥ is uniformly bounded, the same analysis allows to prove (4.58).
Corollary 4.1
Let Δ 1(p, q), Δ 2(p, q), (p, q) ∈{1, …, n}2, and Δ 3 be as defined in Proposition 4.5 . Then there exist a polynomial P with nonnegative coefficients and a nonnegative real number l such that, for all large N, for any \(z\in \mathbb {C}\setminus \mathbb {R}\) ,
and for all (p, q) ∈{1, …, n}2,
Proof
Using the identity
(4.61) readily follows from Cauchy-Schwartz inequality, Lemma 4.17 and (4.56). (4.62) and (4.60) readily follows from Cauchy-Schwartz inequality and Lemma 4.12.
4.4.3 Estimates of Resolvent Entries
In order to deduce Proposition 4.3 from Proposition 4.5 and Corollary 4.1, we need the two following Lemmas 4.13 and 4.14.
Lemma 4.13
For all \(z\in \mathbb {C}\setminus \mathbb {R}\) ,
Proof
Since \(\mu _{M_N}\) is supported by [0, +∞[, (4.63) readily follows from
(4.64) may be proved similarly.
Corollary 4.1 and Lemma 4.13 yield that, there is a polynomial Q with nonnegative coefficients, a sequence b N of nonnegative real numbers converging to zero when N goes to infinity and some nonnegative integer number l, such that for any p, q in {1, …, n}, for all \(z\in \mathbb {C}\setminus \mathbb {R}\),
where ∇pq was defined by (4.36).
Lemma 4.14
There is a sequence v N of nonnegative real numbers converging to zero when N goes to infinity such that for all \(z\in \mathbb {C}\setminus \mathbb {R}\) ,
Proof
First note that it is sufficient to prove (4.66) for \(z\in \mathbb {C}^+:=\{z \in \mathbb {C}; \Im z >0\}\) since \( g_N(\bar z)-g_{\mu _{\sigma ,\nu ,c}} (\bar z)= \overline {g_N(z)-g_{\mu _{\sigma ,\nu ,c}}(z)}\). Fix 𝜖 > 0. According to Theorem A.8 and Theorem 5.11 in [2], and the assumption on A N, we can choose \(K> \max \{ 2/\varepsilon ; x, x \in \mathrm {supp}( \mu _{\sigma ,\nu ,c})\}\) large enough such that \(\mathbb {P}\left ( \left \|M_N\right \| >K\right )\) goes to zero as N goes to infinity. Let us write

For any \(z \in \mathbb {C}^+\) such that |z| > 2K, we have

Thus, \(\forall z \in \mathbb {C}^+,\) such that |z| > 2K, we can deduce that

Now, it is clear that  is a sequence of locally bounded holomorphic functions on \(\mathbb {C}^+\) which converges towards \(g_{\mu _{\sigma ,\nu ,c}}\). Hence, by Vitali’s Theorem,
is a sequence of locally bounded holomorphic functions on \(\mathbb {C}^+\) which converges towards \(g_{\mu _{\sigma ,\nu ,c}}\). Hence, by Vitali’s Theorem,  converges uniformly towards \(g_{\mu _{\sigma ,\nu ,c}}\) on each compact subset of \(\mathbb {C}^+\). Thus, there exists N(𝜖) > 0, such that for any N ≥ N(𝜖), for any \(z\in \mathbb {C}^+\), such that |z|≤ 2K and ℑz ≥ ε,
converges uniformly towards \(g_{\mu _{\sigma ,\nu ,c}}\) on each compact subset of \(\mathbb {C}^+\). Thus, there exists N(𝜖) > 0, such that for any N ≥ N(𝜖), for any \(z\in \mathbb {C}^+\), such that |z|≤ 2K and ℑz ≥ ε,

Finally, for any \(z\in \mathbb {C}^+\), such that ℑz ∈ ]0;ε[, we have

It readily follows from (4.68), (4.69) and (4.70) that for N ≥ N(𝜖),

Moreover, for N ≥ N′(𝜖) ≥ N(𝜖), \(\mathbb {P}\left ( \left \|M_N\right \| >K\right ) \leq \varepsilon .\) Therefore, for N ≥ N′(𝜖), we have for any \(z \in \mathbb {C}^+\),

Thus, the proof is complete by setting
Now set
and
Lemmas 4.13 and 4.14 yield that there is a polynomial R with nonnegative coefficients, a sequence w N of nonnegative real numbers converging to zero when N goes to infinity and some nonnegative real number l, such that for all \(z\in \mathbb {C}\setminus \mathbb {R}\),
Now, one can easily see that,
so that
Note that
Then, (4.16) readily follows from Proposition 4.5, (4.65), (4.73), (4.75), (4.76), and (ii) Lemma 4.17. The proof of Proposition 4.3 is complete.
4.5 Proof of Theorem 4.3
We follow the two steps presented in Sect. 4.2.
Step A
We first prove (4.11).
Let η > 0 small enough and N large enough such that for any l = 1, …, J, α l(N) ∈ [θ l − η, θ l + η] and [θ l − 2η, θ l + 2η] contains no other element of the spectrum of \(A_NA_N^*\) than α l(N). For any l = 1, …, J, choose f η,l in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with support in [θ l − 2η, θ l + 2η] such that f η,l(x) = 1 for any x ∈ [θ l − η, θ l + η] and 0 ≤ f η,l ≤ 1. Let 0 < 𝜖 < δ 0 where δ 0 is introduced in Theorem 4.2. Choose h ε,j in \(\mathbb { C}^\infty (\mathbb {R}, \mathbb {R})\) with support in \([\rho _{\theta _j} -\varepsilon ,\rho _{\theta _j}+\varepsilon ]\) such that h ε,j ≡ 1 on \([\rho _{\theta _j} -\varepsilon /2 ,\rho _{\theta _j}+\varepsilon /2 ]\) and 0 ≤ h ε,j ≤ 1.
Almost surely for all large N, M N has k j eigenvalues in \(]\rho _{\theta _j} -\varepsilon /2 ,\rho _{\theta _j}+\varepsilon /2[\). According to Theorem 4.2, denoting by \((\xi _1,\cdots ,\xi _{k_j})\) an orthonormal system of eigenvectors associated to the k j eigenvalues of M N in \(( \rho _{\theta _j} -\varepsilon /2, \rho _{\theta _j}+\varepsilon /2)\), it readily follows from (4.12) that almost surely for all large N,
Applying Proposition 4.2 with \(\varGamma _N= f_{\eta ,l}(A_NA_N^*)\) and K = k l, the problem of establishing (4.11) is reduced to prove that
Using a Singular Value Decomposition of A N and the biunitarily invariance of the distribution of \(\mathbb {G}_N\), we can assume that A N is as (4.14) and such that for any j = 1, …, J,
Now, according to Lemma 4.18,
with, for all large N,
Now, by considering
instead of dealing with \(\tilde \tau _N\) defined in (4.72) at the end of the proof of Proposition 4.3, one can prove that there is a polynomial P with nonnegative coefficients, a sequence (u N)N of nonnegative real numbers converging to zero when N goes to infinity and some nonnegative real number s, such that for any k in {k 1 + … + k l−1 + 1, …, k 1 + … + k l}, for all \(z\in \mathbb {C}\setminus \mathbb {R}\),
with
Thus,
where for all \(z \in \mathbb {C} \setminus \mathbb {R}\), \(\varDelta _N(z)= \sum _{k=k_1+\cdot +k_{l-1}+1}^{k_1+\cdot +k_{l}} \varDelta _{k,N}(z),\) and \(\left | \varDelta _{N} (z)\right | \leq k_l (1+\vert z\vert )^s P(\vert \Im z \vert ^{-1})u_N.\)
First let us compute
The function ω σ,ν,c satisfies \(\omega _{\sigma ,\nu ,c}(\overline {z})=\overline {\omega _{\sigma ,\nu ,c}(z)}\) and \(g_{\mu _{\sigma ,\nu ,c}}(\overline {z})=\overline {g_{\mu _{\sigma ,\nu ,c}}(z)}\), so that \(\Im \frac { (1-\sigma ^2 c g_{\mu _{\sigma ,\nu ,c}}(t+\mathrm{i} y))}{\theta _l-\omega _{\sigma ,\nu ,c}(t+\mathrm{i} y)}=\frac {1}{2i}[\frac { (1-\sigma ^2 c g_{\mu _{\sigma ,\nu ,c}}(t+\mathrm{i} y))}{\theta _l-\omega _{\sigma ,\nu ,c}(t+\mathrm{i} y)}- \frac { (1-\sigma ^2 c g_{\mu _{\sigma ,\nu ,c}}(t-iy))}{\theta _l-\omega _{\sigma ,\nu ,c}(t-iy)}]\). As in [10], the above integral is split into three pieces, namely \(\int _{\rho _{\theta _j}-\varepsilon }^{\rho _{\theta _j}-\varepsilon /2}+ \int _{\rho _{\theta _j}-\varepsilon /2}^{\rho _{\theta _j}+\varepsilon /2}+\int _{\rho _{\theta _j}+\varepsilon /2}^{\rho _{\theta _j}+\varepsilon }\). Each of the first and third integrals are easily seen to go to zero when y ↓ 0 by a direct application of the definition of the functions involved and of the (Riemann) integral. As h ε,j is constantly equal to one on \([\rho _{\theta _j}-\epsilon /2; \rho _{\theta _j}+\epsilon /2]\), the second (middle) term is simply the integral
Completing this to a contour integral on the rectangular with corners \(\rho _{\theta _j}\pm \varepsilon /2\pm iy\) and noting that the integrals along the vertical lines tend to zero as y ↓ 0 allows a direct application of the residue theorem for the final result, if l = j,
If we consider θ l for some l ≠ j, then \(z\mapsto (1-\sigma ^2 cg_{\mu _{\sigma ,\nu ,c}}(z))(\theta _l- \omega _{\sigma ,\nu ,c}(z))^{-1}\) is analytic around \(\rho _{\theta _j}\), so its residue at \(\rho _{\theta _j}\) is zero, and the above argument provides zero as answer.
Now, according to Lemma 4.19, we have
so that
This concludes the proof of (4.11).
Step B
In the second, and final, step, we shall use a perturbation argument identical to the one used in [10] to reduce the problem to the case of a spike with multiplicity one, case that follows trivially from Step A. A further property of eigenvectors of Hermitian matrices which are close to each other in the norm will be important in the analysis of the behaviour of the eigenvectors of our matrix models. Given a Hermitian matrix \(M\in \ M_N(\mathbb C)\) and a Borel set \(S\subseteq \mathbb R\), we denote by E M(S) the spectral projection of M associated to S. In other words, the range of E M(S) is the vector space generated by the eigenvectors of M corresponding to eigenvalues in S. The following lemma can be found in [6].
Lemma 4.15
Let M and M 0 be N × N Hermitian matrices. Assume that \(\alpha ,\beta ,\delta \in \mathbb R\) are such that α < β, δ > 0, M and M 0 has no eigenvalues in [α − δ, α] ∪ [β, β + δ]. Then,
In particular, for any unit vector \(\xi \in E_{M_0}((\alpha ,\beta ))(\mathbb C^N)\) ,
Assume that θ i is in Θ σ,ν,c defined in (4.7) and k i ≠ 1. Let us denote by \(V_1(i),\ldots , V_{k_i}(i)\), an orthonormal system of eigenvectors of \(A_NA_N^*\) associated with α i(N). Consider a Singular Value Decomposition A N = U ND NV N where V N is a N × N unitary matrix, U N is a n × n unitary matrix whose k i first columns are \( V_1(i),\ldots , V_{k_i}(i)\) and D N is as (4.14) with the first k i diagonal elements equal to \(\sqrt {\alpha _i(N)}\).
Let δ 0 be as in Theorem 4.2. Almost surely, for all N large enough, there are k i eigenvalues of M N in \((\rho _{\theta _i}- \frac {\delta _0}{4}, \rho _{\theta _i}+ \frac {\delta _0}{4})\), namely \(\lambda _{n_{i-1}+q}(M_N)\), q = 1, …, k i (where n i−1 + 1, …, n i−1 + k i are the descending ranks of α i(N) among the eigenvalues of \(A_NA_N^*\)), which are moreover the only eigenvalues of M N in \((\rho _{\theta _i}-\delta _0,\rho _{\theta _i}+\delta _0)\). Thus, the spectrum of M N is split into three pieces:
The distance between any of these components is equal to 3δ 0∕4. Let us fix 𝜖 0 such that \(0\leq \theta _i ( 2 \epsilon _0 k_i +\epsilon _0^2k_i^2) < dist(\theta _i, \mbox{supp }\nu \cup _{i\neq s}\theta _s )\) and such that \([\theta _i; \theta _i+\theta _i ( 2 \epsilon _0 k_i +\epsilon _0^2k_i^2)] \subset \mathbb {E}_{\sigma , \nu , c}\) defined by (4.6). For any 0 < 𝜖 < 𝜖 0, define the matrix A N(𝜖) as A N(𝜖) = U ND N(𝜖)V N where
and \(\left (D_N(\epsilon )\right )_{pq}=\left (D_N\right )_{pq}\) for any (p, q)∉{(m, m), m ∈{1, …, k i}}.
Set
For N large enough, for each m ∈{1, …, k i}, α i(N)[1 + 𝜖(k i − m + 1)]2 is an eigenvalue of \(A_NA_N^*(\epsilon )\) with multiplicity one. Note that, since supN∥A N∥ < +∞, it is easy to see that there exist some constant C such that for any N and for any 0 < 𝜖 < 𝜖 0,
Applying Remark 4.3 to the (n + N) × (n + N) matrix \(\tilde X_N= \left ( \begin {array}{ll} 0_{n\times n}~~~ X_N\\ X_N^*~~~ 0_{N\times N} \end {array} \right )\) (see also Appendix B of [14]), it readily follows that there exists some constant C′ such that a.s for all large N, for any 0 < 𝜖 < 𝜖 0,
Therefore, for 𝜖 sufficiently small such that C′𝜖 < δ 0∕4, by Theorem A.46 [2], there are precisely n i−1 eigenvalues of M N(𝜖) in \([0,\rho _{\theta _i}-3\delta _0/4)\), precisely k i in \((\rho _{\theta _i}-\delta _0/2,\rho _{\theta _i}+\delta _0/2)\) and precisely N − (n i−1 + k i) in \((\rho _{\theta _i}+3\delta _0/4,+ \infty [\). All these intervals are again at strictly positive distance from each other, in this case δ 0∕4.
Let ξ be a normalized eigenvector of M N relative to \(\lambda _{n_{i-1}+q}(M_N)\) for some q ∈{1, …, k i}. As proved in Lemma 4.15, if E(𝜖) denotes the subspace spanned by the eigenvectors associated to \(\{\lambda _{n_{i-1}+1}(M_N(\epsilon )),\dots ,\lambda _{n_{i-1}+k_i} (M_N(\epsilon ))\}\) in \(\mathbb C^N\), then there exists some constant C (which depends on δ 0) such that for 𝜖 small enough, almost surely for large N,
According to Theorem 4.2, for any j in {1, …, k i}, for large enough N, \(\lambda _{n_{i-1}+j}(M_N(\epsilon ))\) separates from the rest of the spectrum and belongs to a neighborhood of \(\varPhi _{\sigma ,\nu ,c} (\theta _i^{(j)}(\epsilon ))\) where
If ξ j(𝜖, i) denotes a normalized eigenvector associated to \(\lambda _{n_{i-1}+j}(M_N(\epsilon ))\), Step A above implies that almost surely for any p ∈{1, …, k i}, for any γ > 0, for all large N,
The eigenvector ξ decomposes uniquely in the orthonormal basis of eigenvectors of M N(𝜖) as \(\xi =\sum _{j=1}^{k_i}c_j(\epsilon )\xi _j(\epsilon ,i)+\xi (\epsilon )^\perp \), where c j(𝜖) = 〈ξ|ξ j(𝜖, i)〉 and \(\xi (\epsilon )^\perp =P_{ E(\epsilon )^{\bot }}\xi \); necessarily \(\sum _{j=1}^{k_i}|c_j(\epsilon )|{ }^2+\|\xi (\epsilon )^\perp \|{ }_2^2=1\). Moreover, as indicated in relation (4.81), ∥ξ(𝜖)⊥∥2 ≤ C𝜖. We have
Take in the above the scalar product with \(\xi =\sum _{j=1}^{k_i}c_j(\epsilon )\xi _j(\epsilon ,i)+\xi (\epsilon )^\perp \) to get
Relation (4.82) indicates that
where for all large N, \(\vert \varDelta _1\vert \leq \sqrt { \gamma } k_i^3\) and |Δ 2|≤ γ. Since ∥ξ(𝜖)⊥∥2 ≤ C𝜖,
Thus, we conclude that almost surely for any γ > 0, for all large N,
Since we have the identity
and the three obvious convergences \(\lim _{\epsilon \to 0}\omega _{\sigma ,\nu ,c}^{\prime }\left (\varPhi _{\sigma ,\nu ,c} (\theta _i^{(j)}(\epsilon )) \right )=\omega _{\sigma ,\nu ,c}^{\prime }(\rho _{\theta _i})\), \(\lim _{\epsilon \to 0}g_{\mu _{\sigma ,\nu ,c}}\left (\varPhi _{\sigma ,\nu ,c} (\theta _i^{(j)}(\epsilon )) \right )=g_{\mu _{\sigma ,\nu ,c}}(\rho _{\theta _i})\) and \(\lim _{\epsilon \to 0}\sum _{j=1}^{k_i}|c_j(\epsilon )|{ }^2=1\), relation (4.83) concludes Step B and the proof of Theorem 4.3. (Note that we use (2.9) of [11] which is true for any \(x\in \mathbb {C}\setminus \mathbb {R}\) to deduce that \(1-\sigma ^2 c g_{\mu _{\sigma ,\nu ,c}}(\varPhi _{\sigma ,\nu ,c}(\theta _i))= \frac { 1}{1+ \sigma ^2 cg_\nu (\theta _i)}\) by letting x goes to Φ σ,ν,c(θ i)).
References
G. Anderson, A. Guionnet, O. Zeitouni, An Introduction to Random Matrices (Cambridge University Press, Cambridge, 2009)
Z.D. Bai, J.W. Silverstein, Spectral Analysis of Large-Dimensional Random Matrices. Mathematics Monograph Series, vol. 2 (Science Press, Beijing, 2006)
Z. Bai, J.W. Silverstein, No eigenvalues outside the support of the limiting spectral distribution of information-plus-noise type matrices. Random Matrices Theory Appl. 1(1), 1150004, 44 (2012)
J.B. Bardet, N. Gozlan, F. Malrieu, P.-A. Zitt, Functional inequalities for Gaussian convolutions of compactly supported measures: explicit bounds and dimension dependence (2018). Bernoulli 24(1), 333–353 (2018)
S.T. Belinschi, M. Capitaine, Spectral properties of polynomials in independent Wigner and deterministic matrices. J. Funct. Anal. 273, 3901–3963 (2017). https://doi.org/10.1016/j.jfa.2017.07.010
S.T. Belinschi, H. Bercovici, M. Capitaine, M. Février, Outliers in the spectrum of large deformed unitarily invariant models. Ann. Probab. 45(6A), 3571–3625 (2017)
F. Benaych-Georges, R.N. Rao, The eigenvalues and eigenvectors of finite, low rank perturbations of large random matrices. Adv. Math. 227(1), 494–521 (2011)
F. Benaych-Georges, R.N. Rao, The singular values and vectors of low rank perturbations of large rectangular random matrices (2011). J. Multivar. Anal. (111), 120–135 (2012)
S.G. Bobkov, F. Götze, Exponential integrability and transportation cost related to logarithmic Sobolev inequalities. J. Funct. Anal. 163(1), 1–28 (1999)
M. Capitaine, Additive/multiplicative free subordination property and limiting eigenvectors of spiked additive deformations of Wigner matrices and spiked sample covariance matrices. J. Theor. Probab. 26(3), 595–648 (2013)
M. Capitaine, Exact separation phenomenon for the eigenvalues of large Information-Plus-Noise type matrices. Application to spiked models. Indiana Univ. Math. J. 63(6), 1875–1910 (2014)
M. Capitaine, C. Donati-Martin, Strong asymptotic freeness for Wigner and Wishart matrices. Indiana Univ. Math. J. 56(2), 767–803 (2007)
F. Benaych-Georges, C. Bordenave, M. Capitaine, C. Donati-Martin, A. Knowles, Spectrum of deformed random matrices and free probability, in Advanced Topics in Random Matrices, ed. by F. Benaych-Georges, D. Chafaï, S. Péché, B. de Tiliére. Panoramas et syntheses, vol. 53 (2018)
R. Couillet, J.W. Silverstein, Z. Bai, M. Debbah, Eigen-inference for energy estimation of multiple sources. IEEE Trans. Inf. Theory 57(4), 2420–2439 (2011)
R.B. Dozier, J.W. Silverstein, On the empirical distribution of eigenvalues of large dimensional information-plus-noise type matrices. J. Multivar. Anal. 98(4), 678–694 (2007)
R.B. Dozier, J.W. Silverstein, Analysis of the limiting spectral distribution of large dimensional information-plus-noise type matrices. J. Multivar. Anal. 98(6), 1099–1122 (2007)
J. Dumont, W. Hachem, S. Lasaulce, Ph. Loubaton, J. Najim, On the capacity achieving covariance matrix for Rician MIMO channels: an asymptotic approach. IEEE Trans. Inf. Theory 56(3), 1048–1069 (2010)
A. Guionnet, B. Zegarlinski, Lectures on logarithmic Sobolev inequalities, in Séminaire de Probabilités, XXXVI. Lecture Notes in Mathematics, vol. 1801 (Springer, Berlin, 2003)
U. Haagerup, S. Thorbjørnsen, Random matrices with complex Gaussian entries. Expo. Math. 21, 293–337 (2003)
U. Haagerup, S. Thorbjørnsen, A new application of random matrices: \(\mathrm {Ext}(C^*_{\mathrm { red}}(F_2))\) is not a group. Ann. Math. (2) 162(2), 711–775 (2005)
W. Hachem, P. Loubaton, J. Najim, Deterministic Equivalents for certain functionals of large random matrices. Ann. Appl. Probab. 17(3), 875–930 (2007)
A.M. Khorunzhy, B.A. Khoruzhenko, L.A. Pastur, Asymptotic properties of large random matrices with independent entries. J. Math. Phys. 37(10), 5033–5060 (1996)
O. Ledoit, S. Péché, Eigenvectors of some large sample covariance matrix ensembles. Probab. Theory Relat. Fields 151, 233–264 (2011)
M. Ledoux, The Concentration of Measure Phenomenon (American Mathematical Society, Providence, 2001)
P. Loubaton, P. Vallet, Almost sure localization of the eigenvalues in a Gaussian information-plus-noise model. Application to the spiked models. Electron. J. Probab. 16, 1934–1959 (2011)
L.A. Pastur, M. Shcherbina, Eigenvalue Distribution of Large Random Matrices. Mathematical Surveys and Monographs (American Mathematical Society, Providence, 2011)
D. Paul, Asymptotics of sample eigenstructure for a large dimensional spiked covariance model. Stat. Sin. 17(4), 1617–1642 (2007)
P. Vallet, P. Loubaton, X. Mestre, Improved subspace estimation for multivariate observations of high dimension: the deterministic signal case. IEEE Trans. Inf. Theory 58(2), 1043–1068 (2012)
D.V. Voiculescu, K. Dykema, A. Nica, Free Random Variables: A Noncommutative Probability Approach to Free Products with Applications to Random Matrices, Operator Algebras and Harmonic Analysis on Free Groups. CRM Monograph Series, vol. 1 (American Mathematical Society, Providence, 1992). ISBN 0-8218-6999-X
J.-s. Xie, The convergence on spectrum of sample covariance matrices for information-plus-noise type data. Appl. Math. J. Chinese Univ. Ser. B 27(2), 181191 (2012)
Acknowledgements
The author is very grateful to Charles Bordenave and Serban Belinschi for several fruitful discussions and thanks Serban Belinschi for pointing out Lemma 4.14. The author also wants to thank an anonymous referee who provided a much simpler proof of Lemma 4.13 and encouraged the author to establish the results for non diagonal perturbations, which led to an overall improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1
We present alternative versions on the one hand of the result in [3] about the lack of eigenvalues outside the support of the deterministic equivalent measure, and on the other hand of the result in [11] about the exact separation phenomenon. These new versions (Theorems 4.5 and 4.6 below) deal with random variables whose imaginary and real parts are independent, but remove the technical assumptions ((1.10) and “b 1 > 0” in Theorem 1.1 in [3] and “ω σ,ν,c(b) > 0” in Theorem 1.2 in [11]). The proof of Theorem 4.5 is based on the results of [5]. The arguments of the proof of Theorem 1.2 in [11] and Theorem 4.5 lead to the proof of Theorem 4.6.
Theorem 4.4
Consider
and assume that
-
1.
X N = [X ij]1≤i≤n,1≤j≤N is a n × N random matrix such that [X ij]i≥1,j≥1 is an infinite array of random variables which satisfy (4.1) and (4.2) and such that \( \Re (X_{ij})\) , ℑ(X ij), \((i,j)\in \mathbb {N}^2\) , are independent, centered with variance 1∕2.
-
2.
A N is an n × N nonrandom matrix such that ∥A N∥ is uniformly bounded.
-
3.
n ≤ N and, as N tends to infinity, c N = n∕N → c ∈ ]0, 1].
-
4.
[x, y], x < y, is such that there exists δ > 0 such that for all large N, \( ]x-\delta ; y+\delta [ \subset \mathbb {R}\setminus \mathrm {supp} (\mu _{\sigma ,\mu _{A_N A_N^*},c_N})\) where \(\mu _{\sigma ,\mu _{A_N A_N^*},c_N}\) is the nonrandom distribution which is characterized in terms of its Stieltjes transform which satisfies Eq.(4.4) where we replace c by c N and ν by \(\mu _{A_N A_N^*}.\)
Then, we have
Since, in the proof of Theorem 4.4, we will use tools from free probability theory, for the reader’s convenience, we recall the following basic definitions from free probability theory. For a thorough introduction to free probability theory, we refer to [29].
-
A \(\mathbb {C}^*\)-probability space is a pair \(\left (\mathbb {A}, \tau \right )\) consisting of a unital \( \mathbb {C}^*\)-algebra \(\mathbb {A}\) and a state τ on \(\mathbb {A}\) i.e. a linear map \(\tau : \mathbb {A}\rightarrow \mathbb {C}\) such that \(\tau (1_{\mathbb { A}})=1\) and τ(aa ∗) ≥ 0 for all \(a \in \mathbb {A}\). τ is a trace if it satisfies τ(ab) = τ(ba) for every \((a,b)\in \mathbb {A}^2\). A trace is said to be faithful if τ(aa ∗) > 0 whenever a ≠ 0. An element of \(\mathbb {A}\) is called a noncommutative random variable.
-
The noncommutative ⋆ -distribution of a family a = (a 1, …, a k) of noncommutative random variables in a \(\mathbb { C}^*\)-probability space \(\left (\mathbb {A}, \tau \right )\) is defined as the linear functional μ a : P↦τ(P(a, a ∗)) defined on the set of polynomials in 2k noncommutative indeterminates, where (a, a ∗) denotes the 2k-uple \((a_1,\ldots ,a_k,a_1^*,\ldots ,a_k^*)\). For any selfadjoint element a 1 in \(\mathbb {A}\), there exists a probability measure \(\nu _{a_1}\) on \(\mathbb {R}\) such that, for every polynomial P, we have
$$\displaystyle \begin{aligned}\mu_{a_1}(P)=\int P(t) \mathrm{d}\nu_{a_1}(t).\end{aligned} $$Then we identify \(\mu _{a_1}\) and \(\nu _{a_1}\). If τ is faithful then the support of \(\nu _{a_1}\) is the spectrum of a 1 and thus \(\|a_1\| = \sup \{|z|, z\in \mathrm {support} (\nu _{a_1})\}\).
-
A family of elements (a i)i ∈ I in a \(\mathbb {C}^*\)-probability space \(\left (\mathbb {A}, \tau \right )\) is free if for all \(k\in \mathbb {N}\) and all polynomials p 1, …, p k in two noncommutative indeterminates, one has
$$\displaystyle \begin{aligned} \tau(p_1(a_{i_1},a_{i_1}^*)\cdots p_k (a_{i_k},a_{i_k}^*))=0\end{aligned} $$(4.85)whenever i 1 ≠ i 2, i 2 ≠ i 3, …, i k−1 ≠ i k, (i 1, …i k) ∈ I k, and \(\tau (p_l(a_{i_l},a_{i_l}^*))=0\) for l = 1, …, k.
-
A noncommutative random variable x in a \(\mathbb {C}^*\)-probability space \(\left (\mathbb {A}, \tau \right )\) is a standard semicircular random variable if x = x ∗ and for any \(k\in \mathbb {N}\),
$$\displaystyle \begin{aligned}\tau(x^k)= \int t^k d\mu_{sc}(t)\end{aligned} $$where
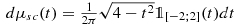 is the semicircular standard distribution.
is the semicircular standard distribution. -
Let k be a nonnull integer number. Denote by \(\mathbb {P}\) the set of polynomials in 2k noncommutative indeterminates. A sequence of families of variables (a n)n≥1 = (a 1(n), …, a k(n))n≥1 in C ∗-probability spaces \(\left (\mathbb {A}_n, \tau _n\right )\) converges in ⋆ -distribution, when n goes to infinity, to some k-tuple of noncommutative random variables a = (a 1, …, a k) in a \(\mathbb {C}^*\)-probability space \(\left (\mathbb {A}, \tau \right )\) if the map \(P\in \mathbb {P} \mapsto \tau _n( P(a_n,a_n^*))\) converges pointwise towards \(P\in \mathbb {P} \mapsto \tau ( P(a,a^*))\).
-
k noncommutative random variables a 1(n), …, a k(n), in C ∗-probability spaces \(\left (\mathbb {A}_n, \tau _n\right )\), n ≥ 1, are said asymptotically free if (a 1(n), …, a k(n)) converges in ⋆ -distribution, as n goes to infinity, to some noncommutative random variables (a 1, …, a k) in a \(\mathbb {C}^*\)-probability space \(\left (\mathbb {A}, \tau \right )\) where a 1, …, a k are free.
We will also use the following well known result on asymptotic freeness of random matrices. Let \(\mathbb {A}_n\) be the algebra of n × n matrices with complex entries and endow this algebra with the normalized trace defined for any \(M\in \mathbb {A}_n\) by \(\tau _n(M) =\frac {1}{n}\mathrm {Tr}(M)\). Let us consider a n × n so-called standard G.U.E matrix, i.e. a random Hermitian matrix \(\mathbb {G}_n = [\mathbb {G}_{jk}]_{j,k=1}^n\), where \(\mathbb {G}_{ii}\), \(\sqrt {2} \Re (\mathbb {G}_{ij})\), \(\sqrt {2} \Im (\mathbb {G}_{ij})\), i < j are independent centered Gaussian random variables with variance 1. For a fixed real number t independent from n, let \(H_n^{(1)}, \ldots , H_n^{(t)}\) be deterministic n × n Hermitian matrices such that \(\max _{i=1}^t\sup _n \Vert H_n^{(i)} \Vert < +\infty \) and \((H_n^{(1)}, \ldots , H_n^{(t)})\), as a t-tuple of noncommutative random variables in \((\mathbb {A}_n, \tau _n)\), converges in distribution when n goes to infinity. Then, according to Theorem 5.4.5 in [1], \( \frac {\mathbb {G}_n}{\sqrt {n}}\) and \((H_n^{(1)}, \ldots , H_n^{(t)})\) are almost surely asymptotically free i.e. almost surely, for any polynomial P in t+1 noncommutative indeterminates,
where h 1, …, h t and s are noncommutative random variables in some \(\mathbb {C}^*\)-probability space \((\mathbb {A}, \tau )\) such that (h 1, …, h t) and s are free, s is a standard semi-circular noncommutative random variable and the distribution of (h 1, …, h t) is the limiting distribution of \((H_n^{(1)}, \ldots , H_n^{(t)})\).
Finally, the proof of Theorem 4.4 is based on the following result which can be established by following the proof of Theorem 1.1 in [5]. First, note that the algebra of polynomials in non-commuting indeterminates X 1, …, X k, becomes a ⋆ -algebra by anti-linear extension of \((X_{i_1}X_{i_2}\ldots X_{i_m})^*=X_{i_m}\ldots X_{i_2}X_{i_1}\).
Theorem 4.5
Let us consider three independent infinite arrays of random variables, \( [W^{(1)}_{ij}]_{i\geq 1,j\geq 1}\) , \( [W^{(2)}_{ij}]_{i\geq 1,j\geq 1}\) and [X ij]i≥1,j≥1 where
-
for l = 1, 2, \(W^{(l)}_{ii}\) , \(\sqrt {2}\Re (W^{(l)}_{ij})\) , \(\sqrt {2} \Im (W^{(l)}_{ij}), i<j\) , are i.i.d centered and bounded random variables with variance 1 and \(W^{(l)}_{ji}=\overline {W^{(l)}_{ij}}\) ,
-
\(\{\Re (X_{ij}), \Im (X_{ij}), i\in \mathbb {N}, j \in \mathbb {N}\}\) are independent centered random variables with variance 1∕2 and satisfy (4.1) and (4.2).
For any \((N,n)\in \mathbb {N}^2\) , define the (n + N) × (n + N) matrix:
where \(X_N=[X_{ij}]_{ \begin {array}{ll}1\leq i\leq n{,}1 \leq j\leq N\end {array}}, \; W^{(1)}_n= [W^{(1)}_{ij}]_{1\leq i,j\leq n},\; W^{(2)}_N= [W^{(2)}_{ij}]_{1\leq i,j\leq N}\).
Assume that n = n(N) and \(\lim _{N\rightarrow +\infty }\frac {n}{N}=c \in ]0,1].\)
Let t be a fixed integer number and P be a selfadjoint polynomial in t + 1 noncommutative indeterminates.
For any \(N \in \mathbb {N}^2\) , let \((B_{n+N}^{(1)},\ldots ,B_{n+N}^{(t)})\) be a t −tuple of (n + N) × (n + N) deterministic Hermitian matrices such that for any u = 1, …, t, \( \sup _{N} \Vert B_{n+N}^{(u)} \Vert < \infty \) . Let \((\mathbb {A}, \tau )\) be a C ∗-probability space equipped with a faithful tracial state and s be a standard semi-circular noncommutative random variable in \((\mathbb {A}, \tau )\) . Let \(b_{n+N}=(b_{n+N}^{(1)},\ldots ,b_{n+N}^{(t)})\) be a t-tuple of noncommutative selfadjoint random variables which is free from s in \((\mathbb {A},\tau )\) and such that the distribution of b n+N in \((\mathbb {A},\tau )\) coincides with the distribution of \((B_{n+N}^{(1)},\ldots , B_{n+N}^{(t)})\) in \(({ M}_{n+N}(\mathbb {C}), \frac {1}{n+N}\mathrm {Tr})\).
Let [x, y] be a real interval such that there exists δ > 0 such that, for any large N, [x − δ, y + δ] lies outside the support of the distribution of the noncommutative random variable \( P\left (s, b_{n+N}^{(1)},\ldots ,b_{n+N}^{(t)}\right )\) in \((\mathbb {A},\tau )\) . Then, almost surely, for all large N,
Proof
We start by checking that a truncation and Gaussian convolution procedure as in Section 2 of [5] can be handled for such a matrix as defined by (4.87), to reduce the problem to a fit framework where,
-
(H)
for any N, (W n+N)ii, \(\sqrt {2}\Re ((W_{n+N})_{ij})\), \(\sqrt {2} \Im ((W_{n+N})_{ij}), i<j, i \leq n+N,\; j\leq n+N\), are independent, centered random variables with variance 1, which satisfy a Poincaré inequality with common fixed constant C PI.
Note that, according to Corollary 3.2 in [24], (H) implies that for any \(p\in \mathbb {N}\),
Remark 4.3
Following the proof of Lemma 2.1 in [5], one can establish that, if (V ij)i≥1,j≥1 is an infinite array of random variables such that \(\{\Re (V_{ij}), \Im (V_{ij}), i\in \mathbb {N}, j \in \mathbb {N}\}\) are independent centered random variables which satisfy (4.1) and (4.2), then almost surely we have
where
Then, following the rest of the proof of Section 2 in [5], one can prove that for any polynomial P in 1 + t noncommutative variables, there exists some constant L > 0 such that the following holds. Set \(\theta ^*=\sup _{i,j}\mathbb {E}\left (\left |X_{ij}\right |{ }^3\right )\). For any 0 < 𝜖 < 1, there exist C 𝜖 > 8θ ∗ (such that \(C_\epsilon >\max _{l=1,2} \vert W^{(l)}_{11}\vert \) a.s.) and δ 𝜖 > 0 such that almost surely for all large N,
where, for any C > 8θ ∗ such that \(C>\max _{l=1,2} \vert W^{(l)}_{11}\vert \) a.s., and for any δ > 0, \(\tilde W_{N+n}^{C,\delta }\) is a (n + N) × (n + N) matrix which is defined as follows. Let \((\mathbb {G}_{ij})_{i\geq 1, j\geq 1}\) be an infinite array which is independent of \(\{X_{ij}, W^{(1)}_{ij}, W^{(2)}_{ij}, (i,j)\in \mathbb {N}^2\}\) and such that \(\sqrt {2} \Re \mathbb {G}_{ij}\), \( \sqrt {2} \Im \mathbb {G}_{ij}\), i < j, \(\mathbb {G}_{ii}\), are independent centred standard real gaussian variables and \({\mathbb {G}}_{ij}=\overline {\mathbb {G}}_{ji}\). Set \(\mathbb {G}_{n+N}= [\mathbb {G}_{ij}]_{1\leq i,j \leq n+N }\) and define \(X_N^C=[X_{ij}^C]_{ \begin {array}{ll}1\leq i\leq n{,}1 \leq j\leq N\end {array}}\)as in (4.18) . Set
\(\tilde W_{N+n}^{C,\delta }\) satisfies (H) (see the end of Section 2 in [5]). (4.89) readily yields that it is sufficient to prove Theorem 4.5 for \(\tilde W_{N+n}^{C,\delta }\).
Therefore, assume now that W N+n satisfies (H). As explained in Section 6.2 in [5], to establish Theorem 4.5, it is sufficient to prove that for all \(m \in \mathbb {N}\), all self-adjoint matrices γ, α, β 1, …, β t of size m × m and all 𝜖 > 0, almost surely, for all large N, we have
((4.90) is the analog of Lemma 1.3 for r = 1 in [5]). Finally, one can prove (4.90) by following Section 5 in [5].
We will need the following lemma in the proof of Theorem 4.4.
Lemma 4.16
Let A N and c N be defined as in Theorem 4.4 . Define the following (n + N) × (n + N) matrices: \(P=\begin {pmatrix} I_n & (0) \\ (0) & (0) \end {pmatrix} Q=\begin {pmatrix} (0) & (0) \\ (0) & I_N\end {pmatrix}\) and \(\mathbf {A}=\begin {pmatrix} (0) & A_N \\ (0) & (0) \end {pmatrix}\) . Let s, p N, q N, a N be noncommutative random variables in some \(\mathbb {C}^*\) -probability space \(\left ( \mathbb {A}, \tau \right )\) such that s is a standard semi-circular variable which is free with (p N, q N, a N) and the ⋆ -distribution of (A, P, Q) in \(\left (M_{N+n}(\mathbb {C}),\frac {1}{N+n} \mathrm {Tr}\right )\) coincides with the ⋆ -distribution of (a N, p N, q N) in \(\left ( \mathbb {A}, \tau \right ). \) Then, for any 𝜖 ≥ 0, the distribution of \( ({\sqrt {1+c_N}}\sigma p_N s q_N+ {\sqrt {1+c_N}}\sigma q_N s p_N + {\mathbf {a}}_N+ \mathbf { a}_N^*)^2 +\epsilon p_N\) is \(\frac {n}{N+n} T_\epsilon \star \mu _{\sigma , \mu _{A_NA_N^*}, c_N} +\frac {n}{N+n} \mu _{\sigma , \mu _{A_NA_N^*}, c_N}+\frac {N-n}{N+n} \delta _{0}\) where \({T_\epsilon } {\star } \mu _{\sigma , \mu _{A_NA_N^*}, c_N}\) is the pushforward of \( \mu _{\sigma , \mu _{A_NA_N^*}, c_N}\) by the map z↦z + 𝜖.
Proof
Here N and n are fixed. Let k ≥ 1 and C k be the k × k matrix defined by

Define the k(n + N) × k(n + N) matrices
For any k ≥ 1, the ⋆ -distributions of \((\hat A_k, \hat P_k, \hat Q_k)\) in \(( M_{k(N+n)}(\mathbb {C}), \frac {1}{k(N+n)}\mathrm {Tr})\) and (A, P, Q) in \(( M_{(N+n)}(\mathbb {C}), \frac {1}{(N+n)}\mathrm {Tr})\) respectively, coincide. Indeed, let \(\mathbb {K}\) be a noncommutative monomial in \(\mathbb {C}\langle X_1,X_2,X_3,X_4\rangle \) and denote by q the total number of occurrences of X 3 and X 4 in \(\mathbb {K}\). We have
so that
Note that if q is even then \(C_k^q=I_k\) so that
Now, assume that q is odd. Note that PQ = QP = 0, A Q = A, Q A = 0, A P = 0 and P A = A (and then Q A ∗ = A ∗, A ∗Q = 0, P A ∗ = 0 and A ∗P = A ∗). Therefore, if at least one of the terms X 1X 2, X 2X 1, X 2X 3, X 3X 1, X 4X 2 or X 1X 4 appears in the noncommutative product in \(\mathbb {K}\), then \( \mathbb {K}(P,Q,\mathbf {A}, {\mathbf {A}}^*)=0,\) so that (4.91) still holds. Now, if none of the terms X 1X 2, X 2X 1, X 2X 3, X 3X 1, X 4X 2 or X 1X 4 appears in the noncommutative product in \(\mathbb {K}\), then we have \({\mathbb {K}}(P,Q,\mathbf {A}, {\mathbf {A}}^*)=\tilde {\mathbb {K}}(\mathbf {A}, {\mathbf {A}}^*)\) for some noncommutative monomial \(\tilde {\mathbb { K}}\in \mathbb {C} \langle X,Y\rangle \) with degree q. Either the noncommutative product in \(\tilde {\mathbb {K}}\) contains a term such as X p or Y p for some p ≥ 2 and then, since A 2 = (A ∗)2 = 0, we have \(\tilde {\mathbb {K}}(\mathbf {A}, {\mathbf {A}}^*)=0\), or \(\tilde {\mathbb {K}}(X,Y)\) is one of the monomials \( (XY)^{\frac {q-1}{2}}X\) or \(Y(XY)^{\frac {q-1}{2}}\). In both cases, we have \(\mathrm {Tr} \tilde {\mathbb {K}}(\mathbf {A}, {\mathbf {A}}^*)=0\) and (4.91) still holds.
Now, define the k(N + n) × k(N + n) matrices
where \(\check { A}\) is the kn × kN matrix defined by

It is clear that there exists a real orthogonal k(N + n) × k(N + n) matrix O such that \(\tilde P_k=O\hat P_k O^*\), \(\tilde Q_k=O\hat Q_k O^*\) and \(\tilde A_k=O\hat A_k O^*\). This readily yields that the noncommutative ⋆ -distributions of \((\hat A_k, \hat P_k, \hat Q_k)\) and \(({\tilde A}_k, \tilde P_k, \tilde Q_k)\) in \(( M_{k(N+n)}(\mathbb {C}), \frac {1}{k(N+n)}\mathrm {Tr})\) coincide. Hence, for any k ≥ 1, the distribution of \(({\tilde A}_k, \tilde P_k, \tilde Q_k)\) in \(( M_{k(N+n)}(\mathbb {C}), \frac {1}{k(N+n)}\mathrm {Tr})\) coincides with the distribution of (a N, p N, q N) in \(\left ( \mathbb {A}, \tau \right ). \) By Theorem 5.4.5 in [1], it readily follows that the distribution of \(({\sqrt {1+c_N}}\sigma p_N s q_N+ {\sqrt {1+c_N}}\sigma q_N s p_N + {\mathbf {a}}_N+ {\mathbf {a}}_N^*)^2 +\epsilon p_N\) is the almost sure limiting distribution, when k goes to infinity, of \(({\sqrt {1+c_N}}\sigma \tilde P_k\frac {\mathbb {G} }{\sqrt {k(N+n)}}\tilde Q_k+ {\sqrt {1+c_N}} \sigma \tilde Q_k \frac {\mathbb {G} }{\sqrt {k(N+n)}}\tilde P_k+\tilde A_k+\tilde A_k^*)^2+\epsilon \tilde P_k\) in \(( M_{k(N+n)}(\mathbb {C}), \frac {1}{k(N+n)}\mathrm {Tr})\), where \(\mathbb {G}\) is a k(N + n) × k(N + n) GUE matrix with entries with variance 1. Now, note that
where \(\mathbb {G}_{kn\times kN}\) is the upper right kn × kN corner of \( \mathbb {G}\). Thus, noticing that \(\mu _{\check { A}\check { A}^*}=\mu _{A_NA_N^*}\), the lemma follows from [15].
Proof of Theorem 4.4
Let W be a (n + N) × (n + N) matrix as defined by (4.87) in Theorem 4.5. Note that, with the notations of Lemma 4.16, for any 𝜖 ≥ 0,
Thus, for any 𝜖 ≥ 0,
Let [x, y] be such that there exists δ > 0 such that for all large N, \( ]x-\delta ; y+\delta [ \subset \mathbb {R}\setminus \mathrm {supp} (\mu _{\sigma ,\mu _{A_N A_N^*},c_N})\).
-
(i)
Assume x > 0. Then, according to Lemma 4.16 with 𝜖 = 0, there exists δ′ > 0 such that for all large n, ]x − δ′;y + δ′[ is outside the support of the distribution of \( ({\sqrt {1+c_N}}\sigma p_N s q_N+ {\sqrt {1+c_N}}\sigma q_N s p_N + {\mathbf {a}}_N+ {\mathbf {a}}_N^*)^2 \). We readily deduce that almost surely for all large N, according to Theorem 4.5, there is no eigenvalue of \(({\sqrt {1+c_N}}P\frac {\sigma W}{\sqrt {N+n}}Q+ {\sqrt {1+c_N}}Q\frac {\sigma W}{\sqrt {N+n}}P+\mathbf {A}+{\mathbf {A}}^*)^2 \) in [x, y]. Hence, by (4.92) with 𝜖 = 0, almost surely for all large N, there is no eigenvalue of M N in [x, y].
-
(ii)
Assume x = 0 and y > 0. There exists 0 < δ′ < y such that [0, 3δ′] is for all large N outside the support of \(\mu _{\sigma , \mu _{A_NA_N^*}, c_N}\). Hence, according to Lemma 4.16, [δ′∕2, 3δ′] is outside the support of the distribution of \( ({\sqrt {1+c_N}}\sigma p_N s q_N+ {\sqrt {1+c_N}}\sigma q_N s p_N + {\mathbf {a}}_N+ {\mathbf {a}}_N^*)^2 +\delta ' p_N\). Then, almost surely for all large N, according to Theorem 4.5, there is no eigenvalue of \(({\sqrt {1+c_N}}P\frac {\sigma W}{\sqrt {N+n}}Q+ {\sqrt {1+c_N}}Q\frac {\sigma W}{\sqrt {N+n}}P+\mathbf {A}+{\mathbf {A}}^*)^2 +\delta ' P \) in [δ′, 2δ′] and thus, by (4.92), no eigenvalue of \( (\sigma \frac {X}{\sqrt {N}}+A_N)(\sigma \frac {X_N}{\sqrt {N}}+A_N)^*+\delta ' I_n\) in [δ′, 2δ′]. It readily follows that, almost surely for all large N, there is no eigenvalue of \( (\sigma \frac {X_N}{\sqrt {N}}+A_N)(\sigma \frac {X_N}{\sqrt {N}}+A_N)^*\) in [0, δ′]. Since moreover, according to (i), almost surely for all large N, there is no eigenvalue of \( (\sigma \frac {X_N}{\sqrt {N}}+A_N)(\sigma \frac {X_N}{\sqrt {N}}+A_N)^*\) in [δ′, y], we can conclude that there is no eigenvalue of M N in [x, y].
The proof of Theorem 4.4 is now complete. □
We are now in a position to establish the following exact separation phenomenon.
Theorem 4.6
Let M n as in (4.84) with assumptions [1–4] of Theorem 4.4 . Assume moreover that the empirical spectral measure \(\mu _{A_NA_N^*}\) of \(A_NA_N^*\) converges weakly to some probability measure ν. Then for N large enough,
where ω σ,ν,c is defined in (4.5). With the convention that \(\lambda _0(M_N)=\lambda _0(A_NA_N^*)=+\infty \) and \(\lambda _{n+1}(M_N)=\lambda _{n+1}(A_NA_N^*)=-\infty \) , for N large enough, let i N ∈{0, …, n} be such that
Then
Remark 4.4
Since \(\mu _{\sigma ,\mu _{A_N A_N^*},c_N}\) converges weakly towards μ σ,ν,c assumption 4. implies that ∀0 < τ < δ, \([x-\tau ; y+\tau ] \subset \mathbb {R} \setminus \mathrm {supp}~ \mu _{\sigma ,\nu ,c}\).
Proof of Theorem 4.4
(4.93) is proved in Lemma 3.1 in [11].
-
If ω σ,ν,c(x) < 0, then i N = n in (4.94) and moreover we have, for all large N, \(\omega _{{\sigma ,\mu _{A_N A_N^*},c_N}}(x)<0\). According to Lemma 2.7 in [11], we can deduce that, for all large N, [x, y] is on the left hand side of the support of \(\mu _{\sigma ,\mu _{A_N A_N^*},c_N}\) so that ] −∞;y + δ] is on the left hand side of the support of \(\mu _{\sigma ,\mu _{A_N A_N^*},c_N}\). Since [−|y|− 1, y] satisfies the assumptions of Theorem 4.4, we readily deduce that almost surely, for all large N, λ n(M N) > y. Hence (4.95) holds true.
-
If ω σ,ν,c(x) ≥ 0, we first explain why it is sufficient to prove (4.95) for x such that ω σ,ν,c(x) > 0. Indeed, assume for a while that (4.95) is true whenever ω σ,ν,c(x) > 0. Let us consider any interval [x, y] satisfying condition 4. of Theorem 4.4 and such that ω σ,ν,c(x) = 0; then i N = n in (4.94). According to Proposition 4.1, \(\omega _{{\sigma ,\nu ,c}}(\frac {x+y}{2})> 0\) and then almost surely for all large N, λ n(M N) > y. Finally, sticking to the proof of Theorem 1.2 in [11] leads to (4.95) for x such that ω σ,ν,c(x) > 0.
Appendix 2
We first recall some basic properties of the resolvent (see [12, 22]).
Lemma 4.17
For a N × N Hermitian matrix M, for any \(z \in \mathbb {C}\setminus \mathrm {spect}(M)\) , we denote by G(z) := (zI N − M)−1 the resolvent of M.
Let \(z \in \mathbb {C}\setminus \mathbb {R}\) ,
-
(i)
∥G(z)∥≤|ℑz|−1.
-
(ii)
|G(z)ij|≤|ℑz|−1 for all i, j = 1, …, N.
-
(iii)
G(z)M = MG(z) = −I N + zG(z).
Moreover, for any N × N Hermitian matrices M 1 and M 2,
The following technical lemmas are fundamental in the approach of the present paper.
Lemma 4.18 (Lemma 4.4 in [6])
Let \(h: \mathbb {R}\rightarrow \mathbb {R}\) be a continuous function with compact support. Let B N be a N × N Hermitian matrix and C N be a N × N matrix. Then
Moreover, if B N is random, we also have
Lemma 4.19
Let f be an analytic function on \(\mathbb {C}\setminus \mathbb {R}\) such that there exist some polynomial P with nonnegative coefficients, and some positive real number α such that
Then, for any h in \(\mathbb {C}^\infty (\mathbb {R}, \mathbb {R})\) with compact support, there exists some constant τ depending only on h, α and P such that
We refer the reader to the Appendix of [12] where it is proved using the ideas of [20].
Finally, we recall some facts on Poincaré inequality. A probability measure μ on \(\mathbb {R}\) is said to satisfy the Poincaré inequality with constant C PI if for any \(\mathbb {C}^1\) function \(f: \mathbb {R}\rightarrow \mathbb {C}\) such that f and f′ are in L 2(μ),
with \(\mathbf {V}(f) = \int \vert f-\int f d\mu \vert ^2 d\mu \).
We refer the reader to [9] for a characterization of the measures on \(\mathbb {R}\) which satisfy a Poincaré inequality.
If the law of a random variable X satisfies the Poincaré inequality with constant C PI then, for any fixed α ≠ 0, the law of αX satisfies the Poincaré inequality with constant α 2C PI.
Assume that probability measures μ 1, …, μ M on \(\mathbb {R}\) satisfy the Poincaré inequality with constant C PI(1), …, C PI(M) respectively. Then the product measure μ 1 ⊗⋯ ⊗ μ M on \(\mathbb {R}^M\) satisfies the Poincaré inequality with constant \(\displaystyle {C_{PI}^*=\max _{i\in \{1,\ldots ,M\}}C_{PI}(i)}\) in the sense that for any differentiable function f such that f and its gradient gradf are in L 2(μ 1 ⊗⋯ ⊗ μ M),
with \(\mathbf {V}(f) = \int \vert f-\int f d\mu _1\otimes \cdots \otimes \mu _M \vert ^2 d\mu _1\otimes \cdots \otimes \mu _M\) (see Theorem 2.5 in [18]) .
Lemma 4.20 (Theorem 1.2 in [4])
Assume that the distribution of a random variable X is supported in [−C;C] for some constant C > 0. Let g be an independent standard real Gaussian random variable. Then X + δg satisfies a Poincaré inequality with constant \(C_{PI}\leq \delta ^2 \exp \left ( 4C^2/\delta ^2\right )\).
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Capitaine, M. (2018). Limiting Eigenvectors of Outliers for Spiked Information-Plus-Noise Type Matrices. In: Donati-Martin, C., Lejay, A., Rouault, A. (eds) Séminaire de Probabilités XLIX. Lecture Notes in Mathematics(), vol 2215. Springer, Cham. https://doi.org/10.1007/978-3-319-92420-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-92420-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-92419-9
Online ISBN: 978-3-319-92420-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




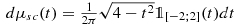 is the semicircular standard distribution.
is the semicircular standard distribution.