Passive Control of Noise Propagation in Tube Systems Using Bragg Scattering

Abstract

Noise control in acoustic tube systems is a classical problem. The use of periodic geometries and resonators is also classic in acoustic filter design. The phononic approach to the problem is much more recent. Looking at this classic problem with a novel approach may lead to innovative solutions. This work investigates the band gaps created in acoustic pipe systems using axisymmetric finite element models, wave finite element models and experiments. Periodic geometry variations are investigated. The Floquet-Bloch theorem is used on a transfer matrix of the periodic cell rearranged from a dynamic stiffness matrix to obtain the dispersion diagrams that reveal the band gaps caused by Bragg scattering. Numerical predictions of the forced response obtained with the full finite element axisymmetric model of a duct system with five cells are compared with a wave finite element model and with experimental results.

1 Introduction

The study of periodic structures began with Mead’s work in the 70s [5,6,7]. In the 80s the growing of computational power available allowed the widespread use of numerical methods and the solution of engineering problems without analytical solution. Early this century a new method, called Wave Finite Element (WFE) method was proposed to predict the behavior of a structure by applying the periodicity condition of Floquet-Bloch’s theorem [8]. This method consists in modeling a periodic cell using conventional Finite Element Method (FEM) and then using propagation models to predict the forced response of a periodic structure.

Acoustic ducts have applications in a large variety of engineering problems. The most ordinary examples are exhaust systems of combustion engines and ventilation systems [10]. The noise propagation in such systems can be controlled via the use of acoustic filters. For this purpose, the design of periodic geometries and Helmholtz resonators is a classical way to reduce noise at a specified frequency bands. Boström [1] studied the wave propagation in ducts with a periodic variation of cross-sectional area. Bradley [2] investigated acoustic wave propagation in periodic waveguides. More recently, Munday et al. [9] addressed the problem of band gaps in periodic waveguides, and Wang and Mak [11] investigated ducts with a periodic array of Helmholtz resonators.

This work investigates band gaps generated by an acoustic tube system, consisting of a five cells constructed with pipes and expansion cavities. A numerical solution by the finite element model is developed using axisymmetric triangular elements. The numerical predictions and experimental results are compared for validating the finite element model.

2 Acoustic Finite Element Formulation

The non-dissipative wave equation can be written in terms of acoustic pressure as [4]:

$$\begin{aligned} {\nabla ^2} {\varvec{p}} = {\frac{1}{c^2}} {\frac{{\partial ^2 \varvec{p}}}{\partial t ^2}} \end{aligned}$$

(1)

where c is the velocity of sound, p is acoustic pressure and t is time. The acoustic pressure field in tube systems excited by plane waves can be modeled as axisymmetric. This characteristic allows solving a three-dimensional problem using a two-dimensional model. The problem is formulated using cylindrical coordinates (radial distance r, height z, azimuth $\theta$) with no dependency of $\mathbf {\theta }$, and Eq. (1) can be rewritten as

$$\begin{aligned} \frac{1}{r} {\frac{\partial }{\partial r} \left( r \frac{\partial \varvec{p}}{\partial r} \right) + \frac{\partial ^2 \varvec{p}}{\partial z^2}} = \frac{1}{c^2} {\frac{\partial ^2 \varvec{p}}{\partial t^2}} \end{aligned}$$

(2)

To solve Eq. (2) in a specified volume, boundary conditions must be applied at its surface boundaries. Applying p = 0 on a surface implies a free surface of fluid. For a rigid boundary, the boundary condition is

$$\begin{aligned} \frac{\partial \varvec{p}}{\partial {n}}=-{\rho \ddot{\varvec{u}}_{n}} \end{aligned}$$

(3)

where $\rho$ is the mass density of the fluid, n is the outward unit surface normal vector and $\ddot{\varvec{u}}_{n}$ is the boundary acceleration in direction of n.

This boundary value problem is usually solved by finite element analysis, using Galerkin’s Method to obtain an approximated solution [3]. After discretization, the system of equations to be solved is

$$\begin{aligned} \mathbf {M_{a}}\varvec{\ddot{p}}+\mathbf {K_{a}}\varvec{p}=\varvec{f} \end{aligned}$$

(4)

where $\mathbf {K_{a}}$ is the acoustic stiffness matrix, $\mathbf {M_{a}}$ is the acoustic mass matrix, f is the acoustic excitation vector and p is the acoustic pressure nodal vector. For an axisymmetric element model, the acoustic element mass matrix, the acoustic element stiffness matrix and the acoustic load vector are given, respectively, by [3]

$$\begin{aligned} \mathbf {K^{(e)}_{a}}=2\pi \bar{r}{\int _{A} \left( \varvec{s_{r}^{T}s_{r}+s_{z}^{T}s_{z}+s_{\theta }^{T}s_{\theta }} \right) }d{A} \end{aligned}$$

(5)

$$\begin{aligned} \mathbf {M^{(e)}_{a}}=\frac{2\pi \bar{r}}{c^2}{\int _{A} \varvec{s^{T}s}} d{A} \end{aligned}$$

(6)

$$\begin{aligned} \varvec{f^{(e)}}={-\rho \varvec{s^{T}\ddot{u}_{n}}A} \end{aligned}$$

(7)

where r is the radial distance of element centroid, A is the element revolution area, s is the shape function and $\mathbf {s_{r}}$, $\mathbf {s_{z}}$ and $\mathbf {s_{\theta }}$ are its derivatives with respect to each cylindrical coordinate.

The dynamic stiffness matrix can be obtained as

$$\begin{aligned} \mathbf {D}=\mathbf {K_{a}}-\omega ^2\mathbf {M_{a}} \end{aligned}$$

(8)

which can be partitioned in terms of internal, left-sided and right-sided degrees of freedom by

$$\begin{aligned} \begin{bmatrix} \mathbf {D_{ii}}&\mathbf {D_{il}}&\mathbf {D_{ir}}\\ \mathbf {D_{li}}&\mathbf {D_{ll}}&\mathbf {D_{lr}}\\ \mathbf {D_{ri}}&\mathbf {D_{rl}}&\mathbf {D_{rr}}\\ \end{bmatrix} \begin{Bmatrix} \varvec{p}_{i}\\ \varvec{p}_{l}\\ \varvec{p}_{r}\\ \end{Bmatrix}= \begin{Bmatrix} \varvec{0}_{i}\\ \varvec{f}_{l}\\ \varvec{f}_{r}\\ \end{Bmatrix} \end{aligned}$$

(9)

From Eq. (9), the internal pressures can be obtained as

$$\begin{aligned} \varvec{p_{i}}=\mathbf {D_{ii}^{-1}}\left( \mathbf {D_{il}}\varvec{p_{l}}+\mathbf {D_{ir}}\varvec{p_{r}}\right) \end{aligned}$$

(10)

Substituting Eq. (10) into Eq. (9), the condensed acoustic stiffness matrix is obtained as

$$\begin{aligned} \begin{bmatrix} \mathbf {D_{ll}}&\mathbf {D_{lr}}\\ \mathbf {D_{rl}}&\mathbf {D_{rr}} \end{bmatrix} \begin{Bmatrix} \varvec{p_{l}}\\ \varvec{p_{r}}\\ \end{Bmatrix}= \begin{Bmatrix} \varvec{f_{l}}\\ \varvec{f_{r}}\\ \end{Bmatrix} \end{aligned}$$

(11)

where $\mathbf {D_{ll}=D_{ll}-D_{li}D_{ii}^{-1}D_{il}}$, $\mathbf {D_{rl}=D_{rl}-D_{ri}D_{ii}^{-1}D_{il}}$, $\mathbf {D_{lr}=D_{lr}-D_{li}D_{ii}^{-1}D_{ir}}$ and $\mathbf {D_{rr}=D_{rr}-D_{ri}D_{ii}^{-1}D_{ir}}$.

The periodicity condition allows predicting the behavior under harmonic disturbance of a periodic system modeling a unit-cell only. In this method the dynamic stiffness matrix of a unit-cell modeled by WFE is used to apply the periodicity condition in a harmonic disturbance propagating through the system. Using Floquet-Bloch’s theorem [8], the periodicity condition results in an eigenvalue problem. Equation (11) can be rearranged using the Transfer Matrix formulation, resulting in

(12)

where T is the transfer matrix that relates the left state vector $\varvec{q_{l}}$ with the right state vector $\varvec{q_{r}}$ of the unit-cell.

Considering now two consecutive unit-cells, m and m+1, the continuity condition of medium states that $\varvec{p_{r}}^{ (m) } =\varvec{p_{l}}^{( m +1)}$ and $\varvec{f_{r}}^{ (m) } =\varvec{-f_{l}}^{( m +1)}$, resulting in

$$\begin{aligned} \varvec{q_{l}}^{( m +1)}=\mathbf {T}\varvec{q_{l}}^{( m )} \end{aligned}$$

(13)

For wave propagation in an infinite periodic system, Floquet-Blochs theorem produces an eigenvalue problem given by

$$\begin{aligned} \mathbf {T}\varvec{q_{l}}=e^{\mu }\varvec{q_{l}} \end{aligned}$$

(14)

where $e^{\mu }$ is the eigenvalue, $\varvec{q_{l}}$ is the eigenvector, $\mu = -ikL$ is the attenuation constant, L is the unit-cell length, k is the wavenumber and i is the imaginary unit. This solution provides the behavior in terms of wave propagation.

3 Simulated Model and Experimental Setup

3.1 Simulation Description

The system that was later experimentally verified is numerically modeled with a script implemented in Matlab$^{\mathrm{{\circledR }}}$. The unit-cell is discretized with 618 triangular elements, and the whole system with five cells was simulated. Dispersion relations and Frequency Response Functions (FRFs) were obtained for each cell. The pipes and cavity walls are assumed rigid. The fluid inside the tube system is air at ambient temperature and atmospheric pressure, with 1.21 ${\mathrm {kg/m}}^{3}$ and 20 $^{\circ }$C. With these physical proprieties, FRFs and dispersion relations of the system were obtained.

Table 1 Tube system geometric parameters

Fig. 1

Schematics of the experimental setup

3.2 Experimental Setup Description

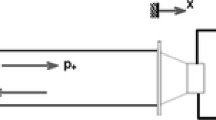
A tube system was built with five unit cells made of polyvinyl chloride (PVC), which were constructed with two pipes connected to an expansion chamber. Each pipe has 150 mm length and 37.5 mm internal diameter. The expansion chambers have 165 mm length and 145 mm internal diameter. Table 1 summarizes the geometric properties. A scheme of the experimental setup is shown in Figs. 1 and 2 illustrates the unit-cell and its dimensions.

Fig. 2

Unit-cell dimensions

The system is excited with a volume acceleration at one end. This excitation was applied using a PVC piston with circular cross section of 37 mm diameter, coupled to an electrodynamic shaker. Mounted on the piston, a piezoelectric accelerometer measures the piston acceleration, linearly proportional to the air volume acceleration. The gap between the tube wall and the piston is sealed by a rubber membrane. At the other system termination, a microphone supported on a bar measures the pressure at the system end. Each cavity is simply supported with polypropylene foam. The FRF of pressure caused by volume acceleration was measured with ten averages, a frequency band of 1125 Hz and frequency discretization of 0.625 Hz. The specifications of measurement instruments are summarized in Table 2. Figure 3 shows the experimental setup with all measurement instruments.

Table 2 Measurement instrument list

Fig. 3

Experimental setup: a system overview; b piston with accelerometer; c microphone on exit termination

4 Results and Conclusions

Figure 5 shows the dispersion diagram for the acoustic periodic cell. Two band gaps are evident, one in the 100–500 Hz range and one in the 500–900 Hz range. These are typical Bragg scattering band gaps, where the band gap is caused by interference of reflected waves. The FRF in Fig. 4 shows that at the band gaps the response is strongly attenuated. A good agreement is found between the FE and the WFE solutions and a good qualitative agreement is observed between numerical predictions and experiment.

The methodology exposed in this work may be used to design and optimize periodic duct geometries to attenuate duct noise in practical applications. The dispersion analysis of a single periodic cell is sufficient to predict the existence and frequency range of the band gaps. A similar analysis may be conducted with a different strategy consisting of introducing periodic Helmholtz resonators. This may be shown to create band gaps at lower frequencies, but band gaps caused by this local resonance effect are much narrower.

The WFE method may be used to compute the forced response of a finite periodic structure with a lower computational cost compared with a full finite element solution. The experimental results show that numerical methods may be used to predict band gaps that are reasonably robust with respect to small variations of the periodic cell, unavoidable when building the acoustic duct system.

Fig. 4

Simulated and experimental FRF’s

Fig. 5

Dispersion relation