Keywords

1 Introduction

One limitation of passive sound absorbers is the bad efficiency at low frequencies due to the required size of the material. Electrically controlled loudspeakers used as active absorbers have shown to be a way to extend the frequency bandwidth of absorption. A possible approach consists in controlling the loudspeaker dynamics in order to match the membrane impedance to the acoustic characteristic impedance of the medium, thus forcing the system to behave like an acoustic transmission line [1]. In particular, Rivet et al. [2] propose an active absorber that uses a feedback based on pressure or velocity for a current-driven boxed loudspeaker, showing broadband absorption results. The present paper restates the model and the impedance matching approach proposed in [2] and describes a new feedback law that combines (1) passive-guaranteed control based on the port-Hamiltonian systems formalism [3, 4] and (2) a (nonlinear) finite-time control law [5, 6], an alternative to asymptotic or exponential control methods. The efficiency of the proposed controller in terms of sound absorption is evaluated numerically.

2 Open-Loop Electroacoustic System

This section presents the considered models for the acoustic propagation (Sect. 2.1) and the current-driven loudspeaker (Sect. 2.2).

2.1 Plane Wave Propagation in a Tube

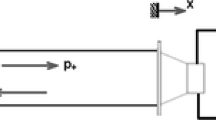
Consider a semi-infinite duct with a loudspeaker located at z = 0, with a membrane modelled as a flat piston (see Fig. 1). Acoustic plane wave propagation is assumed, therefore the pressure field can be decomposed into progressive waves p +(t − z∕c) and p −(t + z∕c), where c is the speed of sound. At z = 0, the particle velocity field equals the piston velocity, leading to the following relation between the pressure field p ac(t) at z = 0 and the piston velocity \(\dot {\xi }(t)\),

$$\displaystyle \begin{aligned} p_{\mathrm{ac}} (t) = 2p^+(t) - \rho c \ \dot{\xi}(t), {} \end{aligned} $$
(1)

where ρ is the air density.

Fig. 1
figure 1

Plane wave propagation in a semi-infinite duct. A loudspeaker, modelled as a flat piston, is located at z = 0

Full size image

2.2 Current-Driven Electrodynamic Loudspeaker Model

Physical Model

A lumped model of boxed loudspeaker is adopted, considered as a mechanical oscillator with displacement ξ(t) and momentum \(\mathfrak {p}(t) = M_{m}\dot {\xi } (t)\), where M m is the moving mass. The oscillator is excited by the Lorentz force Bl i(t) and the force due to the acoustic pressure S d p ac(t). This yields the following mechanical equation that states the force balance of the system,

$$\displaystyle \begin{aligned} K_{m} \ \xi(t) + R_{m} \ \dot{\xi}(t) + \dot{\mathfrak{p}}(t) + Bl \ i(t) = S_d \ p_{\mathrm{ac}}(t), {} \end{aligned} $$
(2)

where K m (N∕m) is the stiffness coefficient associated with the suspension and the sealed enclosure, R m (Ns∕m) is the mechanical damping coefficient, Bl (N∕A) is the electromechanical coupling factor and i is the input electric current. The current drive enables rejection of undesired electric behaviour due to induction effect of the coil, usually described by a resistance R e (Ω) and an inductance L e (H).

Port-Hamiltonian Formulation

The loudspeaker model described in (2) is restated in the port-Hamiltonian formalism [3], that relies on the expression of the system energy,

$$\displaystyle \begin{aligned} \mathcal{H}(\xi, \mathfrak{p}) = \frac{K_m \xi^2}{2} + \frac{\mathfrak{p}^2}{2 M_m}, {} \end{aligned} $$
(3)

namely the sum of the potential and kinetic energy stored by the system. Denoting the state and input of the system by, respectively,

a state-space representation of the loudspeaker dynamics can be derived:

$$\displaystyle \begin{aligned} \text{{$;\{\mathcal{S}\}$} : } \quad \begin{aligned} \dot{{\mathbf{x}}} &= \bigg( \underbrace{\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}}_{\boldsymbol{J}} - \underbrace{\begin{bmatrix} 0 & 0 \\ 0 & R_m \end{bmatrix}}_{\boldsymbol{R}} \bigg) \boldsymbol{\nabla} \mathcal{H} (\mathbf{x}) + \underbrace{\begin{bmatrix} \boldsymbol{G}_i& \boldsymbol{G}_p \end{bmatrix}}_{\boldsymbol{G}} \mathbf{u},\\ \mathbf{y} &= \underbrace{\begin{bmatrix} \boldsymbol{G}_i^\intercal \\ \boldsymbol{G}_p^\intercal \end{bmatrix}}_{\boldsymbol{G}^\intercal} \boldsymbol{\nabla} \mathcal{H}(\mathbf{x}), \end{aligned} {} \end{aligned} $$
(4)

where J is skew-symmetric, R is positive semi-definite, \(\boldsymbol {G}_i=\begin {bmatrix} 0 & -Bl \end {bmatrix}^\intercal \) and \(\boldsymbol {G}_p=\begin {bmatrix} 0 & S_d \end {bmatrix}^\intercal \). The outputs are defined as the dual quantities of the inputs u(t):

$$\displaystyle \begin{aligned} {\mathbf{y}}(t) = \begin{bmatrix} \begin{array}{rcl} e(t) & : & \mbox{back-EMF voltage} \\ v_{\text{ac}}(t) & : & \mbox{acoustic outflow} \end{array} \end{bmatrix}. \end{aligned}$$

The port-Hamiltonian formulation (4) ensures the passivity property of the physical system through its power balance

$$\displaystyle \begin{aligned} \frac{\mathrm{d}\mathcal{H} \left({\mathbf{x}}(t)\right)}{\mathrm{d} t} = \underbrace{\boldsymbol{\nabla} \mathcal{H} ({\mathbf{x}})^\intercal\dot{{\mathbf{x}}}}_{\mathcal{P}_{\mathrm{stored}}} = - \underbrace{\boldsymbol{\nabla} \mathcal{H} ({\mathbf{x}})^\intercal \boldsymbol{R} \boldsymbol{\nabla} \mathcal{H} ({\mathbf{x}})}_{\mathcal{P}_{\mathrm{diss}}} + \underbrace{{\mathbf{y}}^\intercal {\mathbf{u}}}_{\mathcal{P}_{\mathrm{ext}}}, \end{aligned} $$
(5)

where \(\mathcal {P}_{\mathrm {stored}}\), \(\mathcal {P}_{\mathrm {diss}}\) and \(\mathcal {P}_{\mathrm {ext}}\) are, respectively, the stored, dissipated and external power.

3 Closed-Loop System

This section describes the derivation of a controller that provides an input current i ⋆(t) given (1) a target membrane motion ξ ⋆(t), \(\dot {\xi }^\star (t)\) and (2) the measurement of the acoustic pressure p ac(t) and the velocity \(\dot {\xi }(t)\) at the loudspeaker membrane. The target membrane velocity can be deduced from the measured pressure

$$\displaystyle \begin{aligned} \dot{\xi}^\star(t) = \frac{p_{\mathrm{ac}} (t)}{\rho c} \end{aligned} $$
(6)

so that the acoustic impedance at the membrane equals the characteristic specific acoustic impedance ρc. First, a nonlinear control law that reaches the target \(\dot {\xi }^\star (t)\) in finite-time is presented in Sect. 3.1. Then the law is recast as a port-Hamiltonian system in order to guarantee the passivity of the controller, and thus of the closed-loop system, in Sect. 3.2.

3.1 Finite-Time Control Law

A system controlled in finite time will reach an equilibrium point in a finite time (see [7] for a formal definition). Thus, finite-time stability is a stronger property than asymptotic or exponential stability. It is useful for time-constrained and robust control. We first state the following result.

Theorem 1 (Finite-Time Control of a Double Integrator [5])

Consider the double integrator \(\dot {z}_1 = z_2\), \(\dot {z}_2 = v\). The origin is a finite-time stable equilibrium point of this system when it is controlled by the input \( v = -k_1 \lfloor z_1 \rceil ^{\frac {\alpha }{2 - \alpha }} - k_2 \lfloor z_2 \rceil ^\alpha , \) with k 1, k 2 > 0, α ∈ ]0, 1[ and \(\lfloor x \rceil ^\alpha \triangleq \mathrm {sgn} (x) |x|{ }^\alpha \).

By identification (cf. [6]), one can find a transformation between the system (4) and the double integrator controlled in finite time. We thus obtain the resulting nonlinear law on the input current that reads

$$\displaystyle \begin{aligned} i^\star(t) = \frac{S_{d} p_{\mathrm{ac}}(t) - K_m \xi(t) - R_m \dot{\xi}(t) + M_m \left(k_1 \left\lfloor \xi(t) - \xi^\star(t)\right\rceil^{\frac{\alpha}{2 - \alpha}} + k_2 \left\lfloor \dot{\xi}(t) - \dot{\xi}^\star(t) \right\rceil^\alpha\right)}{Bl}. {} \end{aligned} $$
(7)

3.2 Passive Finite-Time Control Law

Principle

The aim of this part is the derivation of a controller that guarantees (1) convergence towards specific system dynamics ξ ⋆(t) and (2) stability in case of badly tuned control parameters. In order to meet these requirements, we impose to the controller the following port-Hamiltonian structure,

$$\displaystyle \begin{aligned} \text{{$;\{\mathcal{C}\}$;} : } \quad \begin{aligned} \dot{{\mathbf{x}}}_c &= \left( \boldsymbol{J}_c - \boldsymbol{R}_c \right) \boldsymbol{\nabla} \mathcal{H}_c ({\mathbf{x}}_c) + \boldsymbol{G}_c {\mathbf{u}}_c \\{}\\ {\mathbf{y}}_c &= \boldsymbol{G}_c^\intercal \boldsymbol{\nabla} \mathcal{H}_c({\mathbf{x}}_c), \end{aligned} {}\end{aligned} $$
(8)

with J c skew-symmetric and R c positive semi-definite. The power-preserving interconnection [4] of \({\{\mathcal {C}\}}\) with \({\{\mathcal {S}\}}\) is achieved by (see Fig. 2)

$$\displaystyle \begin{aligned} \begin{bmatrix} i(t) \\ {\mathbf{u}}_c(t) \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} e(t) \\ {\mathbf{y}}_c(t) \end{bmatrix}, \end{aligned} $$
(9)

allowing the closed-loop system to be written as a port-Hamiltonian system

$$\displaystyle \begin{aligned} \text{ {$;\{\mathcal{S} {+} \mathcal{C}\}$;} : } \ \ \begin{aligned} \begin{bmatrix} \dot{{\mathbf{x}}} \\ \dot{{\mathbf{x}}_c} \end{bmatrix} &= \left( \begin{bmatrix} \boldsymbol{J} & -\boldsymbol{G}_i \boldsymbol{G}_c^\intercal \\ \boldsymbol{G}_c \boldsymbol{G}_i^\intercal & \boldsymbol{J}_c \end{bmatrix}{-}\begin{bmatrix} \boldsymbol{R} & \boldsymbol{0}_{2{\times}2} \\ \boldsymbol{0}_{2{\times}2} & \boldsymbol{R}_c \end{bmatrix} \right) \begin{bmatrix} \boldsymbol{\nabla} \mathcal{H}({\mathbf{x}}) \\ \boldsymbol{\nabla} \mathcal{H}_c({\mathbf{x}}_c) \end{bmatrix}{+}\begin{bmatrix} \boldsymbol{G}_p \\ \boldsymbol{0}_{2{\times}1} \end{bmatrix} p_{\text{ac}} \\ v_{\text{ac}} &= \begin{bmatrix} \boldsymbol{G}_p^\intercal & \boldsymbol{0}_{1{\times}2} \end{bmatrix} \begin{bmatrix} \boldsymbol{\nabla} \mathcal{H}({\mathbf{x}}) \\ \boldsymbol{\nabla} \mathcal{H}_c({\mathbf{x}}_c) \end{bmatrix}. \end{aligned} {} \end{aligned} $$
(10)

In the sequel, we choose the same states for the system and the controller: x = x c. Modifying the total energy \(\mathcal {H}_{s+c}({\mathbf {x}})\) and the interconnection matrices in (10) corresponds to an IDA-PBC control [8].

Fig. 2
figure 2

Block diagram of the proposed control architecture

Full size image

The controller \({\{\mathcal {C}\}}\) is derived by following the steps below:

  1. 1.

    Choose an energy \(\mathcal {H}_{s+c}({\mathbf {x}}) \geq 0\) for the closed-loop system that has a minimum at a desired target state x ⋆, so that it converges to x ⋆.

  2. 2.

    Deduce the energy of the controller by \(\mathcal {H}_{{c}}({\mathbf {x}}) = \mathcal {H}_{s+c}({\mathbf {x}}) - \mathcal {H}({\mathbf {x}}) \geq 0\).

  3. 3.

    The control law is provided by the second line of (8) : \({\mathbf {y}}_c = \boldsymbol {G}_c^\intercal \boldsymbol {\nabla } \mathcal {H}_{c}({\mathbf {x}})\).

Application to the Proposed Finite-Time Control Law

The closed-loop energy is chosen as

(11)

It has a minimum at ξ = ξ ⋆ and \(\mathfrak {p} = \mathfrak {p}^\star \) so that this energy expression is a good candidate to control the closed-loop system \({\{\mathcal {S}+\mathcal {C}\}}\) towards the desired targets ξ ⋆, \(\mathfrak {p}^\star \). The energy of the controller is deduced by subtracting (3) from (11), leading to

(12)

where β > K m and γ > 1 ensure that \(\mathcal {H}_{c}(\xi , \mathfrak {p})\) has a global minimum. Finally, by imposing the following port-Hamiltonian formulation:

$$\displaystyle \begin{aligned} \text{{$;\{\mathcal{C}\}$;} : } \quad \begin{aligned} \dot{{\mathbf{x}}} &= \bigg( \underbrace{\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}}_{\boldsymbol{J}_{c}} - \underbrace{\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}}_{\boldsymbol{R}_{c}} \bigg) \boldsymbol{\nabla} \mathcal{H}_c ({\mathbf{x}}) + \underbrace{\begin{bmatrix} \frac{1}{Bl} \\ \frac{R_m}{Bl} \end{bmatrix}}_{\boldsymbol{G}_{c}} {\mathbf{u}}_c \\ {\mathbf{y}}_c &= \underbrace{\begin{bmatrix} \frac{1}{Bl} & \frac{R_m}{Bl} \\ \end{bmatrix}}_{\boldsymbol{G}_{c}^\intercal} \boldsymbol{\nabla} \mathcal{H}_c({\mathbf{x}}_c), \end{aligned} {} \end{aligned} $$
(13)

the controller output yields

(14)

The proposed finite-time control law (14) is a passive version of (7) presented in Sect. 3.1, whatever its parameter values satisfying β > K m and γ > 1.

4 Numerical Results

Two control laws are assessed for an up-chirp pressure excitation p ac(t) from 20 to 300 Hz at levels 94 and 106 dB.

Law 1: passive finite-time control law (14). :

The law is evaluated through simulations of the closed-loop system \({\{\mathcal {S}+\mathcal {C}\}}\) based on a dedicated numerical scheme [9, 10] that preserves the power balance in discrete time.

Law 2: proposed in [2]. :

The law relies on a modification of the inherent electromechanical properties of the loudspeaker, taking the form of a transfer function between the measured acoustic pressure and the electric current,

$$\displaystyle \begin{aligned} I^\star(s) = \frac{S_{d} \ \rho c - s M_m (1 -\mu) - R_m - \frac{K_m}{s} (1 -\mu)}{Bl \left(\mu s\frac{M_m}{S_{d}} + \rho c + \mu \frac{K_m}{s S_{d}}\right)} P(s), {} \end{aligned} $$
(15)

where P(s) and I ⋆(s) are, respectively, the Laplace transforms of p ac(t) and i ⋆(t) and μ ∈ [0, 1] is a control parameter that adjusts the absorption bandwidth.

Simulations take the total acoustic pressure p ac(t) as input and provide electric currents generated by the control laws and the induced membrane velocities as outputs. Then the reflected pressure at the membrane is calculated as

$$\displaystyle \begin{aligned} p^-(t) = \frac{ p_{\mathrm{ac}}(t) - \rho c \ \dot{\xi}(t) }{2}. \end{aligned} $$
(16)

The control parameters are set to k 1 = 750, 000, k 2 = 50, α = 0.8, β = 1.1K m, γ = 1.1, μ = 0.15 and the loudspeaker model parameters are those used in [2]. The sampling rate is set to f s = 44, 100 Hz.

Time domain simulations of the reflected pressure p −(t) at the loudspeaker membrane for an input p ac(t) at 94 dB are depicted in Fig. 3. The weak value of the reflected pressure p −(t) compared to the total pressure p ac(t) reveals an efficient sound absorption for both control laws.

Fig. 3
figure 3

Time domain simulations of the reflected pressure p −(t) at the loudspeaker membrane for an input p ac(t) at 94 dB, for both control laws

Full size image

The absorption capabilities are also evaluated in the frequency domain by calculating the absorption coefficient as a function of the frequency f defined as

$$\displaystyle \begin{aligned} \alpha (f) = 1 - \left\lvert \frac{Z(f) - \rho c}{Z(f) + \rho c} \right\rvert ^2, \end{aligned} $$
(17)

where Z(f) = P(f)∕V (f) and P(f) and V (f) are, respectively, the Fourier transform of the pressure signal p ac(t) and the velocity signal \(\dot {\xi }(t)\).

The coefficient α(f) is depicted in Fig. 4. It can be noted that Law 2 achieves the best sound absorption (α very close to 1) around the resonance frequency of the loudspeaker (84 Hz). The proposed Law 1 is especially efficient at lower frequencies below and has a slightly broader frequency bandwidth. Note that the closed loop consisting of a linear model (4) and a nonlinear controller (14) is nonlinear. Thus its performance varies with the amplitude of the control input, as illustrated in Fig. 4 for p ac(t) at levels 94 and 106 dB.

Fig. 4
figure 4

Absorption coefficient versus frequency for both controls laws at 94 and 106 dB. The (nonlinear) Law 1 is calculated for two input pressure levels, whereas the (linear) Law 2 does not depend on the input amplitude

Full size image

5 Conclusions

This work deals with sound absorption in a duct by a current-driven loudspeaker control. A passive nonlinear control that provides an electric current from the measurements of the acoustic pressure and the membrane velocity has been presented, based on a finite-time control method. Its passivity property ensures robustness against modelling errors. Numerical evaluation of the proposed nonlinear control law shows an efficient sound absorption, especially below the resonance frequency of the loudspeaker. Further study will focus on a passive control that handles a one-sample delay between the controller input and output, towards its application on a test bench.