2D Crack Problems in Functionally Graded Magneto-Electro-Elastic Materials

Abstract

Magneto-electro-elastic composite materials have extensive applications in modern smart structures, because they possess good coupling between mechanical, electrical and magnetic fields. This new effect was reported for the first time by Van Suchtelen [1] in 1972. Due to their ceramic structure, cracks inevitably exist in these materials. If these cracks extend, the material may lose its structural integrity and/or functional properties. In this study we consider functionally graded magneto-electro-elastic materials subjected to anti-plane time-harmonic load. The purpose is to evaluate the dependence of the stress concentration near the crack tips on the frequency of the applied external load. The mathematical model is described by a boundary value problem for a system of partial differential equations. A Radon transform is used to derive fundamental solutions in a closed form. Following Wang and Zhang, for the piezoelectric case, the boundary value problem is reduced to a system of integro-differential equations along the crack. For the numerical solution, software code in FORTRAN 77 is developed and validated using available examples in literature. Simulations show the dependence of the stress intensity factors (SIF) on frequency of the incident wave for different types of load, crack dispositions and the magnitude and direction of the material gradient.

1 Introduction

Magneto-electro-elastic materials (MEEM) have drawn the interest of researchers in recent years. Their widespread application is due to their ability to convert mechanical energy into electric and magnetic energy, and vice versa. The magneto-electric property in piezoelectric/piezomagnetic composite materials was reported for the first time by Suchtelen [1] in 1972. Unlike single-phase magneto-electric materials, composite MEEM possess large magneto-electric effects at room and above, which makes them suitable for application. Owing to this, composite MEEM are potential candidates for fabricating new smart and intelligent structures. Functionally graded MEEM are the next generation of high performance multifunctional materials. Their structural integrity is becoming increasingly important as their use is extended to new frontiers. The conception of functionally graded MEEM (FGMEEM) arose for the first time in 1984 in Japan during the project SPACEPLANE. Structures consisting of several layers have been used in many products. These layered structures create stress, which can cause failures in products made of such materials. Contrary to this, FGMEEM do not have this disadvantage, because their material properties vary in a continuous way. A main disadvantage of the magneto-electro-elastic composites is their brittleness. Cracks or flaws inevitably exist in such materials. These defects provoke regions of high stress and electric/magnetic field concentrations, and may initiate fracture and damage. When MEEM with cracks are subjected to external magneto-electro-mechanical loads, the stress concentration near crack tips may increase high enough to cause crack extension and eventually lead to a serious degradation of the material. To understand the failure mechanism of these materials, an analysis of the behavior of MEEM under applied external loading is necessary. The solution of the general boundary value problem for continuously inhomogeneous MEEM requires advanced numerical tools due to the high mathematical complexity arising from the electro-magneto-elastic coupling combined with the smooth variation of material characteristics leading to the solution of partial differential equation with variable coefficients. The aim of the paper is to propose a new effective boundary integral equation method (BIEM) for solution of the problem. The proposed BIEM technique is based on a frequency dependent fundamental solution of the equation of motion derived analytically by the usage of an appropriate algebraic transformation and Radon transform. To the best of the authors’ knowledge the non-hypersingular traction BIEM for solution of the dynamic problem of an exponentially graded MEE composite with multiple cracks has not been developed.

In this paper we study the dynamic behavior of MEEM with two cracks, subjected to an incident time-harmonic anti-plane wave. The numerical results, obtained by the BIEM, show the dependence of the generalized stress intensity factor on the normalized frequency of the applied load, wave propagation direction, direction and magnitude of the material gradient and crack interaction phenomenon.

2 Statement of the Problem

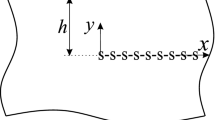
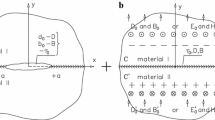
Consider an infinite transversely-isotropic functionally graded linear magneto-electro-elastic solid in a rectangular coordinate system $Ox_{1} x_{2} x_{3}$, with the symmetry axis and poling direction along the $Ox_{3}$ axis; in this case $Ox_{1} x_{2}$ is the isotropic plane. The material is subjected to antiplane shear mechanical, and inplane electric and magnetic time-harmonic load. The geometry of the considered problem in the plane $x_{3} = 0$ is shown on Fig. 1. The problem is two-dimensional, and the anti-plane time-harmonic wave motion with respect to the plane $x_{3} = 0$ is considered.

Fig. 1

A magnetoelectroelastic plane with two cracks: a general disposition of the cracks; b collinear cracks; c parallel symmetry cracks. The angle $\theta$ shows the wave propagation direction

We introduce a generalized tensor of elasticity $C_{iJKl} ,\,i,l = 1,2;\,J,K = 3,4,5$ in the following way:

$$ \begin{aligned} C_{i33l} (x) & = \left\{ {\begin{array}{*{20}l} {c_{44} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} } \right.,\;\;C_{i34l} (x) = C_{i43l} (x) = \left\{ {\begin{array}{*{20}l} {e_{15} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} } \right., \\ C_{i35l} (x) & = C_{i53l} (x) = \left\{ {\begin{array}{*{20}l} {q_{15} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} ,\;\;C_{i44l} (x) = \left\{ {\begin{array}{*{20}l} { - \varepsilon_{11} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} } \right.,} \right. \\ C_{i45l} (x) & = C_{i54l} (x) = \left\{ {\begin{array}{*{20}l} { - d_{11} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} ,} \right.\;\;C_{i55l} (x) = \left\{ {\begin{array}{*{20}l} { - \mu_{11} (x),\,i = l} \hfill \\ {0,\,i \ne l} \hfill \\ \end{array} } \right., \\ \end{aligned} $$

where $c_{44}$ is the elastic module, $e_{15}$ is the piezoelectric coefficient, $q_{15}$ is the piezomagnetic coefficient, $\varepsilon_{11}$ is the dielectric permittivity, $\mu_{11}$ is the magnetic permeability, $d_{11}$ is the magnetoelectric coefficient. We also introduce a generalized stress tensor $\sigma_{iJ} = (\sigma_{i3} ,D_{i} ,B_{i} )$, $i = 1,2$, where $\sigma_{i3}$ is the mechanical stress, $D_{i}$ and $B_{i}$ are the components of the electric displacement and magnetic induction respectively in the plane $x_{3} = 0$. The constitutive equations for this type of medium are see Sladek et al. [2], Soh and Liu [3]:

$$ \sigma_{iJ} = C_{iJKl} u_{K,l} $$

(1)

$$ div\,\vec{D} = \rho_{f} ,\quad div\,\vec{B} = 0 $$

(2)

where the density of free charges is denoted by $\rho_{f}$ and summation under repeated indexes is assumed, while comma means differentiation. The characteristic frequencies for elastic and electromagnetic processes are f_el = 10⁴ Hz and f_elm = 10⁷ Hz, respectively. Thus, if we consider dynamic loadings, with temporal changes corresponding to f_el the changes of the electromagnetic fields can be assumed to be immediate, or in other words the electromagnetic fields can be considered like quasi-static (Parton and Kudryavtsev [4]). So, the quasi-static approximation is valid, provided that the variations of the electromagnetic field with time are small enough. The frequency of the electromagnetic field is the same as the frequency of the elastic wave in the currently considered problem. The assumption is usually valid for elastic waves at MHz and below, see Sladek et al. [5], Li and Wei [6], and Dineva et al. [7]. Then, the electric and magnetic fields can be presented as gradients of scalar electric and magnetic potentials. Assuming the quasielectrostatic approximation of MEEM, the balance equations in the absence of body forces, electric charges and magnetic currents densities have the following form, see Rangelov et al. [8]:

$$ \left| {\begin{array}{*{20}l} {(c_{44} (x)u_{3,i} )_{,i} + (e_{15} (x)\varphi_{,i} )_{,i} + (q_{15} (x)\psi_{,i} )_{,i} + \rho \omega^{2} u_{3} = 0} \hfill \\ {(e_{15} (x)u_{3,i} )_{,i} - (\varepsilon_{11} (x)\varphi_{,i} )_{,i} - (d_{11} (x)\psi_{,i} )_{,i} = 0} \hfill \\ {(q_{15} (x)u_{3,i} )_{,i} - (d_{11} (x)\varphi_{,i} )_{,i} - (\mu_{11} (x)\psi_{,i} )_{,i} = 0,} \hfill \\ \end{array} } \right. $$

(3)

Here $\omega$ is the frequency of the applied load and $\rho$ is the density. In generalized notation this system can be written in the following way:

$$ (C_{iJKl} (x)u_{K,l} )_{,l} + \rho_{JK} (x)\omega^{2} u_{K} = 0, $$

(4)

where $\rho_{JK} (x) = \left\{ \begin{aligned} \rho (x),J = K = 3 \hfill \\ 0,J,K = 4\,or\,5 \hfill \\ \end{aligned} \right..$ FGM is a kind of material in which the individual material composition varies continuously along certain directions in a controllable way. The modern fabrication technology of FGM allows the possibility to manufacture graded components to meet prescribed gradients in properties. More or less, most mechanical models describing the inhomogeneous material profiles are based on the assumption that material properties vary in a similar manner, which is an idealization. This fact is connected with the available computational tools. For most of them, it is impossible to consider independent variation of the material properties. The solution of the general boundary-value problem for continuously inhomogeneous MEEM requires advanced numerical tools due to its high mathematical complexity arising from the electro-magneto-elastic coupling plus variation of material properties. In this aspect any numerical realization for any type of material gradient is useful because these results can be used as benchmark examples when validating new computational methods. We assume here that all material properties depend on $x$ in one and the same way and describe this by an inhomogeneity function $h(x)$:

$$ c_{44} (x) = h(x)c_{44} \;\;e_{15} (x) = h(x)e_{15} ,\;\;q_{15} (x) = h(x)q_{15} , $$

$$ \varepsilon_{15} (x) = h(x)\varepsilon_{15} ,\;\;d_{11} (x) = h(x)d_{11} ,\;\;\mu_{11} (x) = h(x)\mu_{11} ,\;\;\rho (x) = h(x)\rho. $$

We will consider exponentially inhomogeneous materials with the inhomogeneity function: $h(x) = e^{{2(k_{1} x_{1} + k_{2} x_{2} )}} = e^{2 < k,x > }$, where the inhomogeneity coefficient is denoted by $k = (k_{1} ,k_{2} )$.

When the incident SH-wave interacts with the cracks a scattered wave is produced. The total displacement and traction at any point of the plane can be calculated by the superposition principle:

$$ u_{J} = u_{J}^{in} + u_{J}^{sc} ,\;\;t_{J} = t_{J}^{in} + t_{J}^{sc} $$

(5)

In (5) $u_{J}^{in}$ and $t_{J}^{in}$ denote incident wave fields and $u_{J}^{sc}$ and $t_{J}^{sc}$ are the displacement and traction of scattering by the crack’s wave fields respectively. We impose the following boundary conditions:

$$ t_{J} \left| {_{{Cr_{1} \cup \,Cr_{2} }} } \right. = 0,\quad {\text{or}}\quad t_{J}^{sc} \left| {_{{Cr_{1} \cup \,Cr_{2} }} } \right. = - t_{J}^{in} \left| {_{{Cr_{1} \cup \,Cr_{2} }} } \right., $$

(6)

$$ u_{J} (x_{1} ,x_{2} ) \to 0,\quad {\text{when}}\quad (x_{1}^{2} + x_{2}^{2} )^{1/2} \to \infty . $$

(7)

The boundary condition (6) means that the cracks are free of mechanical traction and also that they are magnetoelectrically impermeable, the same as one of the extreme models available in the literature, see Sladek et al. [2]. The difference between impermeable and permeable crack models is discussed in details in Dineva et al. [7]. The boundary value problem (4), (6), together with the Sommerfeld-type radiation condition at infinity for the scattered wave field (7) is reduced to an equivalent system of integrodifferential equations along the cracks and then solved numerically.

3 Boundary Integral Equation Method

The fundamental solution of (4) is the solution of the equation:

$$ \sigma_{iJM,i}^{*} + \rho_{JK} (x)\omega^{2} u_{KM}^{*} = - \delta_{JM} \delta (x,\xi ), $$

(8)

where $i = 1,2$, i.e. the direction of the applied unit concentrate force, $\delta (x,\xi )$ is Dirac’s delta function: $< \delta (x,\xi ),\,\varphi (x) > = \varphi (\xi )$, where $\delta_{JM}$ is the Kronecker’s symbol. The solution of (8) depends on the value of $\gamma = \frac{{\rho \omega^{2} }}{{\tilde{a}}} - |k|^{2}$, where $|k|^{2}\,=\, k_{1}^{2} + k_{2}^{2}$, $\tilde{a} = \tilde{c}_{44} + \frac{{\tilde{e}_{15}^{2} }}{{\tilde{\varepsilon }_{11} }},$$\tilde{c}_{{44}} = c_{{44}} + \frac{{(q_{{15}} )^{2} }}{{\mu _{{11}}}},\,\,\tilde{e}_{{15}} = e_{{15}} - \frac{{d_{{11}} q_{{15}} }}{{\mu _{{11}} }},\,\tilde{\varepsilon }_{{11}} = \varepsilon _{{11}} - \frac{{(d_{{11}} )^{2} }}{{\mu _{{11}} }}.$ We will consider the case when $\gamma > 0$ i.e. the case of wave propagation.

Following Wang and Zhang [9] and Gross et al. [10] the following representation formulae are valid:

$$ \begin{aligned} t_{J}^{sc} (x) & = C_{iJKl} n_{i} (x)\int\limits_{{Cr_{1} \cup Cr_{2} }} {[(\sigma_{\eta JK}^{*} } (x,y,\omega )\Delta u_{J,\eta } (y,\omega ) - \rho_{QJ} \omega^{2} u_{QK}^{*} (x,y,\omega ) \\ & \quad \Delta u_{J} (y,\omega ))\delta_{\lambda l} - \sigma_{\lambda JK}^{*} (x,y,\omega )\Delta u_{J,l} (y,\omega )]n_{\lambda } (y)d\varGamma (y) \\ \end{aligned} $$

(9)

and

$$ u_{J}^{sc} (x,\omega ) = \int\limits_{{Cr_{1} \cup \,Cr_{2} }} {\sigma_{\eta MJ}^{*} (x,y,\omega )\Delta u_{M} (y,\omega )d\Gamma } (y), $$

(10)

where $\Delta u_{J} = u_{J} \left| {_{{Cr^{ + } }} } \right. - u_{J} \left| {_{{Cr^{ - } }} } \right.$, $Cr = Cr_{1} \cup Cr_{2}$, $Cr^{ + }$ and $Cr^{ - }$ are the upper and lower bound of the cracks correspondingly. $\Delta u_{J}$ are the jumps of the generalized displacement along the crack, also known as crack opening displacements (COD), $u_{QK}^{*}$ are the fundamental solutions, $\sigma_{iJM}^{*} = C_{iJK\,l} u_{KM,l}^{*}$ .

The boundary condition (7) is satisfied because of (10) and the limit $\sigma_{\eta MJ}^{*} (x,y,\omega )\mathop \to \limits_{x \to \infty } 0.$ Using boundary condition (6) and representation formula (9) we have:

$$\begin{aligned} t_{J}^{{in}} (x) & = - C_{{iJKl}} n_{i} (x)\int\limits_{{Cr_{1} \cup {\kern 1pt} Cr_{2} }} {[(\sigma _{{\eta JK}}^{*} } (x,y,\omega )\Delta u_{{J,\eta }} (y,\omega ) - \rho _{{QJ}} \omega ^{2} u_{{QK}}^{*} (x,y,\omega )\Delta u_{J} (y,\omega ))\delta _{{\lambda l}} \\ & \quad - \sigma _{{\lambda JK}}^{*} (x,y,\omega )\Delta u_{{J,l}} (y,\omega )]n_{\lambda } (y)d{\mkern 1mu} \Gamma (y),{\mkern 1mu} x \in Cr_{1} \cup Cr_{2} \\ \end{aligned} $$

(11)

Since the incident wave field $t_{J}^{in} (x)$ in (11) is known, a system of integrodifferential equations for the unknown $\Delta u_{J}$ is obtained. Once the unknown COD are found we can calculate the traction filed at any point using (9). The stress concentration field near the crack tips is computed using the following formulae:

$$ K_{III} = \mathop {\lim }\limits_{\varepsilon \to 0} t_{3} \sqrt {2\pi \varepsilon } $$

$$ K_{E} = \mathop {\lim }\limits_{\varepsilon \to 0} E_{2} \sqrt {2\pi \varepsilon } , $$

$$ K_{H} = \mathop {\lim }\limits_{\varepsilon \to 0} H_{2} \sqrt {2\pi \varepsilon } , $$

where $\varepsilon$ is the distance to the crack tip.

4 Numerical Realization and Results

The Eq. (11) is solved numerically. The cracks are discretisized using 7 boundary elements for each crack. The unknown COD are approximated by parabolic shape functions. The two-dimensional integrals are solved numerically using the Monte-Carlo method. FORTRAN 77 code is created for the numerical solution. The MEEM is the piezoelectric/piezomagnetic composite $BaTiO_{3} /CoFe_{2} O_{4}$. The half-length of the cracks is $a = 5\,{\text{mm}}$ and the material constants for this composite can be found in Song and Sih [11], Li [12]. The components of the inhomogeneity function are presented in the following way: $k_{1} = \beta \frac{\cos \alpha }{2a},$ $k_{2} = \beta \frac{\sin \alpha }{2a},$ where $\alpha$ shows the inhomogeneity direction and $\beta$ is the inhomogeneity magnitude.

4.1 Validation

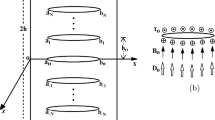
The proposed numerical scheme is validated using the solution for one crack and solutions obtained by the dual integral equation method. In the first example we consider two collinear cracks (see Fig. 1b) when the distance between them is very large. Under this condition, we expect that the result converges to the case with one crack, because crack interaction is minimal. The following normalization of the SIF is used: $K_{III}^{*} = \frac{{K_{III} }}{{t_{3}^{in} \sqrt {\pi a} }}$ and the normalized frequency is $\Omega = a\sqrt {\rho c_{44}^{ - 1} } \omega$ . The results for normalized SIF versus the normalized frequency at a fixed distance $h = 10a$ are given in Fig. 2. We see good coincidence of the results in the case of this big distance between cracks.

Fig. 2

Comparison between the results for two collinear cracks and one crack

As another example we consider two symmetric parallel cracks (see Fig. 1c) as the distance h between them increases. We expect to obtain the result for one crack, when the distance between them is large enough. The comparison shown in Fig. 3 shows the distance h between the cracks to be $h = 20a$.

Fig. 3

Comparison between the results for two symmetry parallel cracks and one crack

Our results have been validated with the results of Zhou and Wang [13], who used a dual integral equation method. The cracks are parallel as shown in Fig. 1c, and the distance h between them is increasing: $h = 0.2a, \ldots ,6.5a$. The external load is static. We present the comparison in Fig. 4. The difference is no more than 1.5%.

Fig. 4

The normalized SIF versus the ratio $\frac{{\mathbf{h}}}{{\mathbf{a}}}$

Results for the same scenario but in the case of dynamic load also show good agreement, see Fig. 5.

Fig. 5

The normalized SIF versus the ratio $\frac{{\mathbf{h}}}{{\mathbf{a}}}$, dynamic load, $\Omega = 0.4$

4.2 Parametric Studies

Our aim is to show the sensitivity of the generalized SIF to the wave propagation direction, the distance between the cracks and their geometrical configuration. The electric field intensity factor (EFIF) and magnetic field intensity factor (MFIF) are normalized as follows: $K_{E}^{*} = 10\frac{{K_{E} }}{{t_{3}^{in} \sqrt {\pi a} }}\,{\text{and}}\,K_{H}^{*} = 10^{4} \frac{{K_{H} }}{{t_{3}^{in} \sqrt {\pi a} }} .$

In Fig. 6 we present the dependence of the generalized SIF on the normalized frequency for a normal incident wave. The cracks are collinear (see Fig. 1b) and the distance between them is: $h = 0.25a,\,0.5a,\,a,\,2a$. The SIF is increasing until it reaches its peak at a normalized frequency of $\Omega \approx 0.7$, then it starts to decrease. We see increasing of the SIF when the distance between the cracks is decreasing. The EFIF and MFIF have similar behavior.

Fig. 6

Normalized SIF, EFIF and MFIF versus the normalized frequency for a normal incident wave

Results for two symmetry parallel cracks at incident angles $\theta = \frac{\pi }{2}$ and $\theta = \frac{\pi }{3}$ are given in Fig. 7a, b, where the distance between them is: $h = 6;\,9;\,12\,{\text{mm}}$. SIF increases in the frequency interval [0.7–1.6], when the distance between them increases. This is in opposite to the results shown in Fig. 6 for the case of collinear cracks. This phenomenon, called the crack shielding effect, is discussed in Ratwani [14], Zhou and Wang [13]. Results for SIFs at the right crack-tip of the left crack in the case of two collinear cracks (see Fig. 1b) in an inhomogeneous plane at a fixed distance between them $h = 0.5a$, normal incident wave $\theta = \frac{\pi }{2}$ and at different inhomogeneity magnitudes $\beta = 0.2;0.4;0.6$ are given in Fig. 7c. It can be seen that by increasing the inhomogeneity magnitude, the SIF decreases, but this effect is frequency dependent. So the conclusion is that defect driving force can be reduced by using the concept for the FGM and the idea to replace the homogeneous material with smoothly inhomogeneous one in the new smart structure technologies works.

Fig. 7

Normalized SIF: a homogeneous material, parallel cracks, normal incident wave; b homogeneous material, parallel cracks, incident wave angle $\theta = \frac{\pi }{3}$; c inhomogeneous material, collinear cracks, the distance is fixed $h = 0.5a$, $\theta = \frac{\pi }{2}$, the inhomogeneity angle $\alpha = 0$, the inhomogeneity magnitude $\beta = 0.0;0.2;0.4;0.6$

5 Conclusion

We present a numerical BIEM solution for a plane of MEEM with two cracks, subjected to incident SH waves. The numerical results show the sensitivity of SIF, EFIF and MFIF to wave propagation direction, distance between the cracks, crack disposition, crack interaction and the material inhomogeneity. The near field results can be applied in computational fracture mechanics, while the information for the scattered wave field can be used for development of new efficient non-destructive test methods for monitoring the integrity and reliability of the multifunctional materials and smart structures based on them.