Introduction to Graphs

Abstract

Graphs are used to model many applications with vertices of a graph representing the objects or nodes and the edges showing the connections between the nodes. We review notations used for graphs, basic definitions, vertex degrees, subgraphs, graph isomorphism, graph operations, directed graphs, distance, graph representations, and matrices related to graphs in this chapter.

1 Introduction

Objects and connections between them occur in a variety of applications such as roadways, computer networks, and electrical circuits. Graphs are used to model such applications with vertices of a graph representing the objects or nodes and the edges showing the connections between the nodes.

We review the basic graph theoretical concepts in a rather dense form in this chapter. This review includes notations used, basic definitions, vertex degrees, subgraphs, graph isomorphism, graph operations, directed graphs, distance, graph representations and matrices related to graphs. We leave discussion of more advanced properties of graphs such as matching, connectivity, special subgraphs, and coloring to Part II when we review sequential, parallel, and distributed algorithms for these problems. We also delay review of methods and parameters for the analysis of large graphs to Part III. These large graphs are used to model complex networks such as the Internet or biological networks, which consist of a huge number of vertices and edges. We will see there is a need for new parameters and analysis methods for the investigation of these large graphs.

2 Notations and Definitions

A graph is a set of points and a set of lines in a plane or a 3-D space. A graph can be formally defined as follows.

Definition 2.1

(graph) A graph $G=(V,E,g)$ or $G=(V(G),E(G),g)$ is a discrete structure consisting of a vertex set V and an edge set E and a relation g that associates each edge with two vertices of the set V.

The vertex set consists of vertices also called nodes, and an edge in the edge set is incident between two vertices called its endpoints. The vertex set of a graph G is shown as V(G) and the edge set as E(G). We will use V for V(G) and E for E(G) when the graph under consideration is known. A trivial graph has one vertex and no edges. A null graph has an empty vertex set and an empty edge set. A graph is called finite if both V(G) and E(G) are finite. We will consider only simple and finite graphs in this book, unless stated otherwise. The number of vertices of a graph G is called its order and we will use the literal n for this parameter. The number of edges of G is called its size and we will show this parameter by the literal m. An edge of a graph G between its vertices u and v is commonly shown as (u, v), uv or sometimes $\{u,v\}$; we will adopt the first one. The vertices at the ends of an edge are called its endpoints or end vertices or simply ends. For an edge (u, v) between vertices u and v, we say u and v are incident to the edge (u, v).

Definition 2.2

(self-loop, multiple edge) A self-loop is an edge with the same endpoints. Multiple edges have the same pair of endpoints.

An edge that is not a self-loop is called a proper edge. A simple graph does not have any self-loops or multiple edges. A graph containing multiple edges is called a multigraph. An underlying graph of a multigraph is obtained by substituting a single edge for each multiple edge. An example multigraph is depicted in Fig. 2.1.

Fig. 2.1

A graph with $V(G)=\{a,b,c,d\}$ and $E(G)=\{e_1,e_2,e_3,e_4,e_5,e_6\}$. Edge $e_2$ is a self-loop and edges $e_4$ and $e_5$ are multiple edges

Definition 2.3

(complement of a graph) The complement of a graph G(V, E) is the graph $\overline{G}(V,E')$ with the same vertex set as G and any edge $(u,v) \in E'$ if and only if $(u,v) \notin E$.

Informally, we have the same vertex set in the complement of a graph G but only have edges that do not exist in G. Complements of two graphs are shown in Fig. 2.2.

Fig. 2.2

a Complement of a sample graph, b Complement of a completely connected graph in which every vertex is connected to all other vertices

2.1 Vertex Degrees

The degree of a vertex in a graph is a useful attribute of a vertex as defined below.

Definition 2.4

(degree of a vertex) The sum of the number of proper edges and twice the number of self-loops incident on a vertex v of a graph G is called its degree and is shown by deg(v).

A vertex that has a degree of 0 is called an isolated vertex and a vertex of degree 1 is called a pendant vertex. The minimum degree of a graph G is denoted by $\delta (G)$ and the maximum degree by $\varDelta (G)$. The following relation between the degree of a vertex v in G and these parameter holds:

$$\begin{aligned} 0 \le \delta (G) \le deg(v) \le \varDelta (G) \le n-1. \end{aligned}$$

(2.1)

Since the maximum number of edges in a simple undirected graph is $n(n-1)/2$, for any such graph,

$$ 0 \le m \le \frac{n(n-1)}{2}=\left( \begin{array}{c} n \\ 2\\ \end{array}\right) $$

.

We can, therefore, conclude there are at most possible simple undirected graphs having n vertices. The first theorem of graph theory, which is commonly refered to as the handshaking lemma is as follows.

Theorem 2.1

(Euler) The sum of the degrees of a simple undirected graph $G=(V,E)$ is twice the number of its edges shown below.

$$\begin{aligned} \sum _{v \in V} deg(v)=2m \end{aligned}$$

(2.2)

Proof is trivial as each edge is counted twice to find the sum. A vertex in a graph with n vertices can have a maximum degree of $n-1$. Hence, the sum of the degrees in a complete graph where every vertex is connected to all others is $n(n-1)$. The total number of edges is $n(n-1)/2$ in such a graph. In a meeting of n people, if everyone shook hands with each other, the total number of handshakes would be $n(n-1)/2$ and hence the name of lemma. The average degree of a graph is

$$\begin{aligned} \frac{\displaystyle \sum \limits _{v \in V} deg(v)}{n}=2m/n. \end{aligned}$$

(2.3)

A vertex is called odd or even depending on whether its degree is odd or even.

Corollary 2.1

The number of odd-degree vertices of a graph is an even number.

Proof

The vertices of a graph $G=(V,E)$ may be divided into the even-degree ($v_{e}$) and odd-degree ($v_{o}$) vertices. The sum of degrees can then be stated as

$$ \sum _{v \in V}deg(v)=\sum _{v_e \in V}deg(v_e)+\sum _{v_o \in V}deg(v_o) $$

Since the sum is even by Theorem 2.1, the sum of the odd-degree vertices should also be even which means there must be an even number of odd-degree vertices.   $\square$

Theorem 2.2

Every graph with at least two vertices has at least two vertices that have the same degree.

Proof

We will prove this theorem using contradiction. Suppose there is no such graph. For a graph with n vertices, this implies the vertex degrees are unique, from 0 to $n-1$. We cannot have a vertex u with degree of $n-1$ and a vertex v with 0 degree in the same graph G as former implies u is connected to all other vertices in G and therefore a contradiction.   $\square$

This theorem can be put in practice in a gathering of people where some know each other and rest are not acquainted. If persons are represented by the vertices of a graph where an edge between two individuals, who know each other is represented by an edge we can say there are at least two persons that have the same number of acquaintances in the meeting.

2.1.1 Degree Sequences

The degree sequence of a graph is obtained when the degrees of its vertices are listed in some order.

Definition 2.5

(degree sequence) The degree sequence of a graph G is the list of the degrees of its vertices in nondecreasing or nonincreasing, more commonly in nonincreasing order. The degree sequence of a digraph is the list consisting of its in-degree, out-degree pairs.

The degree sequence of the graph in Fig. 2.1 is {2, 3, 3, 4} for vertices a, d, c, b in sequence. Given a degree sequence $D=(d_1,d_2, \ldots ,d_n)$, which consists of a finite set of nonnegative integers, D is called graphical if it represents a degree sequence of some graph G. We may need to check whether a given degree sequence is graphical. The condition that $deg(v) < n-1$, $\forall v \in V$ is the first condition and also $\sum _{v \in V} deg(v)$ should be even. However, these are necessary but not sufficient and an efficient method is proposed in the theorem first proved by Havel [7] and later by Hakimi using a more complicated method [5].

Theorem 2.3

(Havel–Hakimi) Let D be a nonincreasing sequence $d_1,d_2, \ldots ,d_n$ with $n \ge 2$. Let $D'$ be the sequence derived from D by deleting $d_1$ and subtracting 1 from each of the first $d_1$ elements of the remaining sequence. Then D is graphical if and only if $D'$ is graphical.

This means if we come across a degree sequence which is graphical during this process, the initial degree sequence is graphical. Let us see the implementation of this theorem to a degree sequence by analyzing the graph of Fig. 2.3a.

Fig. 2.3

a A sample graph to implement Havel–Hakimi theorem b A graph representing graphical sequence $\{1,1,1,1\}$ c A graph representing graphical sequence $\{0,1,1\}$

The degree sequence for this graph is $\{4,3,3,3,2,1\}$. We can now iterate as follows starting with the initial sequence. Deleting 4 and subtracting 1 from the first 4 of the remaining elements gives

$$\begin{aligned} \{2,2,2,1,1\} \end{aligned}$$

continuing similarly, we obtain

$$\begin{aligned} \{1,1,0,0\} \end{aligned}$$

The last sequence is graphical since it can be realized as shown in Fig. 2.3b. This theorem can be conveniently implemented using a recursive algorithm due to its recursive structure.

2.2 Subgraphs

In many cases, we would be interested in part of a graph rather than the graph as a whole. A subgraph $G'$ of a graph G has a subset of vertices of G and a subset of its edges. We may need to search for a subgraph of a graph that meets some condition, for example, our aim may be to find dense subgraphs which may indicate an increased relatedness or activity in that part of the network represented by the graph.

Definition 2.6

(subgraph, induced subgraph) $G'=(V',E')$ is a subgraph of $G=(V,E)$ if $V' \subseteq V$ and $E' \subseteq E$. A subgraph $G'=(V',E')$ of a graph $G=(V,E)$ is called an induced subgraph of G if $E'$ contains all edges in G that have both ends in $V'$.

When $G' \ne G$, $G'$ is called a proper subgraph of G; when $G'$ is a subgraph of G, G is called a supergraph of $G'$. A spanning subgraph $G'$ of G is its subgraph with $V(G)=V(G')$. Similarly, a spanning supergraph G of $G'$ has the same vertex set as $G'$. A spanning subgraph and an induced subgraph of a graph are shown in Fig. 2.4.

Fig. 2.4

a A sample graph G, b A spanning subgraph of G, c An induced subgraph of G

Given a vertex v of a graph G, the subgraph of G shown by $G-v$ is formed by deleting the vertex v and all of its incident edges from G. The subgraph $G-e$ is obtained by deleting the edge e from G. The induced subgraph of G by the vertex set $V'$ is shown by $G[V']$. The subgraph $G[V \setminus V']$ is denoted by $G-V'$.

Vertices in a regular graph all have the same degree. For a graph G, we can obtain a regular graph H which contains G as an induced subgraph. We simply duplicate G next to itself and join each corresponding pair of vertices by an edge if this vertex does not have a degree of $\varDelta (G)$ as shown in Fig. 2.5. If the new graph $G'$ is not $\varDelta (G)$-regular, we continue this process by duplicating $G'$ until the regular graph is obtained. This result is due to Konig who stated that for every graph of maximum degree r, there exists an r-regular graph that contains G as an induced subgraph.

Fig. 2.5

Obtaining a regular graph a The graph b The first iteration, c The 3-regular graph obtained in the second iteration shown by dashed lines

2.3 Isomorphism

Definition 2.7

(graph isomorphism) An isomorphism from a graph $G_1$ to another graph $G_2$ is a bijection $f:V(G_1) \rightarrow V(G_2)$ in which any edge $(u,v) \in E(G_1)$ if and only if $f(u)f(v) \in E(G_2)$.

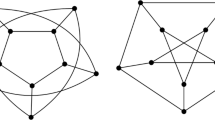
When this condition holds, $G_1$ is said to be isomorphic to $G_2$ or, $G_1$ and $G_2$ are isomorphic. Three isomorphic graphs are depicted in Fig. 2.6. Testing whether two graphs are isomorphic is a difficult problem and cannot be performed in polynomial time. An isomorphism of a graph to itself is called an automorphism. A graph invariant is a property of a graph that is equal in its isomorphic graphs. Given two isomorphic graphs $G_1$ and $G_2$, their orders and sizes are the same and their corresponding vertices have the same degrees. Thus, we can say that the number of vertices, the number of edges and the degree sequences are isomorphism invariants, that is, they do not change in isomorphic graphs.

Fig. 2.6

Three isomorphic graphs.Vertex x is mapped to vertex $x'$

3 Graph Operations

We may need to generate new graphs from a set of input graphs by using certain operations. These operations are uniting and finding intersection of two graphs and finding their product as described below.

3.1 Union and Intersection

Definition 2.8

(union and intersection of two graphs) The union of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is a graph $G_3=(V_3,E_3)$ in which $V_3=V_1 \cup V_2$ and $E_3=E_1\cup E_2$. This operation is shown as $G_3=G_1 \cup G_2$. The intersection of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is a graph $G_3=(V_3,E_3)$ in which $V_3=V_1 \cap V_2$ and $E_3=E_1 \cap E_2$. This is shown as $G_3=G_1 \cap G_2$.

Figure 2.7 depicts these concepts.

Fig. 2.7

Union and intersection of two graphs. The graph in c is the union of the graphs in a and b and the graph in d is their intersection

Definition 2.9

(join of two graphs) The join of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is a graph $G_3=(V_3,E_3)$ in which $V_3=V_1 \cup V_2$ and $E_3=E_1\cup E_2 \cup \{ (u,v): u \in V_1$ and $v \in V_2\}$. This operation is shown as $G_3=G_1 \vee G_2$.

The join operation of two graphs creates new edges between each vertex pairs, one from each of the two graphs. Figure 2.8 displays the join of two graphs. All of the union, intersection, and join operations are commutative, that is, $G_1 \cup G_2=G_2\cup G_1$, $G_1 \cap G_2=G_2\cap G_1$, and $G_1 \vee G_2=G_2 \vee G_1$.

Fig. 2.8

Join of two graphs, a Two graphs b Their join

3.2 Cartesian Product

Definition 2.10

(cartesian product) The cartesian product or simply the product of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ shown by $G_1 \square G_2$ or $G_1 \times G_2$ is a graph $G_3=(V_3,E_3)$ in which $V_3=V_1 \times V_2$ and an edge $((u_i,v_j),(u_p,j_q))$ is in $G_1 \times G_2$ if one of the following conditions holds:

• 1. $i=p$ and $(v_j,v_q) \in E_2$

• 2. $j=q$ and $(u_i,u_p) \in E_1$.

Informally, the vertices we have in the product are the cartesian product of vertices of the graphs and hence each represents two vertices, one from each graph. Figure 2.9a displays the product of complete graph $K_2$ and the path graph with 4 vertices, $P_4$. Graph product is useful in various cases, for example, the hypercube of dimension n, $Q_n$, is a special graph that is the graph product of $K_2$ by itself n times. It can be described recursively as $Q_n=K_2 \times Q_{n-1}$. A hypercube of dimension 3 is depicted in Fig. 2.9b.

Fig. 2.9

a Graph product of $K_2$ and $P_4$ b Hypercube of dimension 3

4 Types of Graphs

We review main types of graphs that have various applications in this section.

4.1 Complete Graphs

Definition 2.11

(complete graph) In a complete simple graph G(V, E), each vertex $v \in V$ is connected to all other vertices in V.

Searching for complete subgraphs of a graph G provides dense regions in G which may mean some important functionality in that region. A complete graph is denoted by $K_n$ where n is the number of vertices. Figure 2.10 depicts $K_1, \ldots ,K_5$. The complete graph with three vertices, $K_3$, is called a triangle.

Fig. 2.10

Complete graphs of sizes 1 to 5

The size of a simple undirected complete graph $K_n$ is $n(n-1)/2$ since the degree of every vertex in $K_n$ is $n-1$, there are n such vertices, and we need to divide by two as each edge is counted twice for both vertices in its endpoints.

4.2 Directed Graphs

A directed edge or an arc has an orientation from its head endpoint to its tail endpoint shown by an arrow. Directed graphs consist of directed edges.

Definition 2.12

(directed graph) A directed graph or a digraph consists of a set of vertices and a set of ordered pairs of vertices called directed edges. A partially directed graph has both directed and undirected edges.

If an edge $e=(u,v)$ is a directed edge in a directed graph G, we say e begins at u and ends at v, or u is the origin of e and v is its destination, or e is directed from u to v. The underlying graph of a directed or partially directed graph is obtained by removing the directions in all edges and replacing each multiple edge with a single edge. A directed graph is shown in Fig. 2.11. Unless stated otherwise, what we state for graphs will be valid for directed and undirected graphs. In a complete simple digraph; there is a pair of arcs, one in each direction between any two vertices.

Fig. 2.11

A directed graph with $V(G)=\{a,b,c,d,e\}$ and $E(G)=\{e_1, \ldots ,e_{10}\}$

Definition 2.13

(in-degree, out-degree) The in-degree of a vertex v in a digraph is the number of edges directed to v and the out-degree of v is the number of edges originating from it. The degree of v is the sum of its in-degree and its out-degree.

The sum of the in-degrees of the vertices in a graph is equal to the sum of the out-degrees which are both equal to the sum of the number of edges. A directed graph that has no cycles is called a directed acyclic graph (DAG).

4.3 Weighted Graphs

We have considered unweighted graphs up to this point. Weighted graphs have edges and vertices labeled with real numbers representing weights.

Definition 2.14

(edge-weighted, vertex-weighted graphs) An edge-weighted graph G(V, E, w), $w:E\rightarrow \mathbb {R}$ has weights consisting of real numbers associated with its edges. Similarly, a vertex-weighted graph G(V, E, w), $w:V\rightarrow \mathbb {R}$ has weights of real numbers associated with its vertices.

Weighted graphs find many real applications, for example, weight of an edge (u, v) may represent the cost of moving from u to v as in a roadway or cost of sending a message between two routers u and v in a computer network. The weight of a vertex v may be associated with capacity stored at v which may be used to represent a property such as the storage volume of a router in a computer network.

4.4 Bipartite Graphs

Definition 2.15

(bipartite graph) A graph $G=(V,E)$ is called a bipartite graph if the vertex set V can be partitioned into two disjoint subsets $V_1$ and $V_2$ such that any edge of G connects a vertex in $V_1$ to a vertex in $V_2$. That is, $\forall (u,v) \in E$, $u \in V_1 \wedge v \in V_2$, or $u \in V_2 \wedge v \in V_1$.

In a complete bipartite graph, each vertex of $V_1$ is connected to each vertex of $V_2$ and such a graph is denoted by $K_{m,n}$, where m is the number of vertices in $V_1$ and n is the number of vertices in $V_2$. The complete bipartite graph $K_{m,n}$ has mn edges and $m+n$ vertices. A weighted complete bipartite graph is depicted in Fig. 2.12.

Fig. 2.12

A weighted complete bipartite graph $K_{3,4}$ with $V_1=\{a,b,c\}$ and $V_2=\{d,e,f,g\}$

4.5 Regular Graphs

In a regular graph, each vertex has the same degree. Each vertex of a k-regular graph has a degree of k. Every k-complete graph is a $k-1$-regular graph but the latter does not imply the former. For example, a d-hypercube is a d-regular graph but it is not a d-complete graph. Examples of regular graphs are shown in Fig. 2.13. Any single n-cycle graph is a 2-regular graph. Any regular graph with odd-degree vertices must have an even number of such vertices to have an even number sum of vertices.

Fig. 2.13

a A 0-regular graph, b A 1-regular graph, c 2-regular graphs; d A 3-regular graph

4.6 Line Graphs

In order to construct a line graph L(G) of a simple graph G, each vertex of L representing an edge of G is formed. Then, two vertices u and v of L are connected if the edges represented by them are adjacent in G as shown in Fig. 2.14.

Fig. 2.14

a A simple graph G, b Line graph of G

5 Walks, Paths, and Cycles

We need few definitions to specify traversing the edges and vertices of a graph.

Definition 2.16

(walk) A walk W between two vertices $v_0$ and $v_n$ of a graph G is an alternating sequence of $n+1$ vertices and n edges shown as $W=(v_0,e_1,v_1,e_2, \ldots ,v_{n-1},e_n,v_n)$, where $e_i$ is incident to vertices $v_{i-1}$ and $v_i$. The vertex $v_0$ is called the initial vertex and $v_n$ is called the terminating vertex of the walk W.

In a directed graph, a directed walk can be defined similarly. The length of a walk W is the number of edges (arcs in digraphs) included in it. A walk can have repeated edges and vertices. A walk is closed if it starts and ends at the same vertex and open otherwise. A walk is shown in Fig. 2.15.

Fig. 2.15

A walk $(a,e_1,b,e_6,f,e_7,g, e_{12},b,e_9,h)$ in a sample graph shown by a dashed curve

A graph is connected if there is a walk between any pair of its vertices. Connectivity is an important concept that finds many applications in computer networks and we will review algorithms for connectivity in Chap. 8.

Definition 2.17

(trail) A trail is a walk that does not have any repeated edges.

Definition 2.18

(path) A path is a trail that does not have any repeated vertices with the exception of initial and terminal vertices.

In other words, a path does not contain any repeated edges or vertices. Paths are shown by the vertices only. For example, (i, a, b, h, g) is a path in Fig. 2.15.

Definition 2.19

(cycle) A closed path which starts and ends at the same vertex is called a cycle.

The length of a cycle can be an odd integer in which case it is called an odd cycle. Otherwise, it is called an even cycle.

Definition 2.20

(circuit) A closed trail which starts and ends at the same vertex is called a circuit.

All of these concepts are summarized in Table 2.1.

Table 2.1 Properties of simple graph traversals

A trail in Fig. 2.15 is $(h,e_9,b,e_6,f,e_5,e)$. When $e_{11}$ and h are added to this trail, it becomes a cycle. An Eulerian tour is a closed Eulerian trail and an Eulerian graph is a graph that has an Eulerian tour. The number of edges contained in a cycle is denoted its length l and the cycle is shown as $C_l$. For example, $C_3$ is a triangle.

Definition 2.21

(Hamiltonian Cycle) A cycle that includes all of the vertices in a graph is called a Hamiltonian cycle and such a graph is called Hamiltonian. A Hamiltonian path of a graph G passes through every vertex of G.

5.1 Connectivity and Distance

We would be interested to find if we can reach a vertex v from a vertex u. In a connected graph G, there is a path between every pair of vertices. Otherwise, G is disconnected. The connected subgraphs of a disconnected graph are called components. A connected graph itself is the only component it has. If the underlying graph of a digraph G is connected, G is connected. If there is a directed walk between each pair of vertices, G is strongly connected.

In a connected graph, it is of interest to find how easy it is to reach one vertex from another. The distance parameter defined below provides this information.

Definition 2.22

(distance) The distance d(u, v) between two vertices u and v in a (directed) graph G is the length of the shortest path between them.

In an unweighted (directed) graph, d(u, v) is the number of edges of the shortest path between them. In a weighted graph, this distance is the minimum sum of the weights of the edges of a path out of all paths between these vertices. The shortest path between two vertices u and v in a graph G is another term used instead of distance between the vertices u and v to have the same meaning. The shortest paths between vertices h and e are h, b, f, e and h, g, f, e both with a distance of 3 in Fig. 2.15. Similarly, shortest paths between vertices i and b are i, a, b and i, h, b both with a distance of 2. The directed distance from a vertex u to v in a digraph is the length of the shortest walk from u to v. In an undirected simple (weighted) graph G(V, E, w), the following can be stated:

• 1. $d(u,v)=d(v,u)$

• 2. $d(u,w) \le d(u,w)+d(w,v)$, $\forall w \in V$

Definition 2.23

(eccentricity) The eccentricity of a vertex v in a connected graph G is its maximum distance to any vertex in G.

The maximum eccentricity is called the diameter and the minimum value of this parameter is called the radius of the graph. The vertex v of a graph G with minimum eccentricity in a connected graph G is called the central vertex of G. Finding central vertex of a graph has practical implications, for example, we may want to place a resource center at a central location in a geographical area where cities are represented by the vertices of a graph and the roads by its edges. There may be more than one central vertex.

6 Graph Representations

We need to represent graphs in suitable forms to be able to perform computations on them. Two widely used ways of representation are the adjacency matrix and the adjacency list methods.

6.1 Adjacency Matrix

An adjacency matrix of a simple graph or a digraph is a matrix A[n, n] where each element $a_{ij}$=1 if there is an edge joining vertex i to j and $a_{ij}=0$ otherwise. For multigraphs, the entry $a_{ij}$ equals the number of edges between the vertices i and j. For a digraph, $a_{ij}$ shows the number of arcs from the vertex i to vertex j. The adjacency matrix is symmetric for an undirected graph and is asymmetric for a digraph in general. A digraph and its adjacency matrix are displayed in Fig. 2.16. An adjacency matrix requires $O(n^2)$ space.

Fig. 2.16

a A digraph, b Its adjacency matrix, c Its adjacency list. The end of the list entries are marked by a backslash

6.2 Adjacency List

An adjacency list of a simple graph (or a digraph) is an array of lists with each list representing a vertex and its (out)neighbors in a linked list. The end of the list is marked by a NULL pointer. The adjacency list of a graph is depicted in Fig. 2.16c. The adjacency matrix requires $O(n+m)$ space. For sparse graphs, adjacency list is preferred due to the space dependence on the number of vertices and edges. For dense graphs, adjacency matrix is commonly used as searching the existence of an edge in this matrix can be done in constant time. With the adjacency list of a graph, the time required for the same operation is O(n).

In a digraph $G=(V,E)$, the predecessor list $P_v \subseteq V$ of a vertex v is defined as follows.

$$ P_v=\{u \in V: (u,v) \in E\} $$

and the successor list of v, $S_v \subseteq V$ is,

$$ S_v=\{u \in V: (v,u) \in E\} $$

The predecessor and successor lists of the vertices of the graph of Fig. 2.16a are listed in Table 2.2.

Table 2.2 Predecessor lists and successor lists of vertices

6.3 Incidence Matrix

An incident matrix B[n, m] of a simple graph has elements $b_{ij}=1$ if edge j is incident to vertex i and $b_{ij}=0$ otherwise. The incidence matrix for a digraph is defined differently as below.

$$ b_{ve} = \left\{ \begin{array}{cc} -1 &{} \text {if arc}~e~\text {ends at vertex}~v \\ 1 &{} \text {if arc}~e~\text {starts at vertex}~v \\ 0 &{} \text {otherwise} \end{array}\right. $$

The incidence matrix of the graph of Fig. 2.16a is as below:

In the edge list representation of a graph, all of its edges are included in the list.

7 Trees

A graph is called a tree if it is connected and does not contain any cycles. The following statements equally define a tree T:

• 1. T is connected and has $n-1$ edges.

• 2. Any two vertices of T are connected by exactly one path.

• 3. T is connected and each edge is a cut-edge removal of which disconnects T.

In a rooted tree T, there is a special vertex r called the root and every other vertex of T has a directed path to r; the tree is unrooted otherwise. A rooted tree is depicted in Fig. 2.17. A spanning tree of a graph G is a tree that covers all vertices of G. A minimum spanning tree of a weighted graph G is a spanning tree of G with the minimum total weight among all spanning trees of G. We will be investigating tree structures and algorithms in more detail in Chap. 6.

Fig. 2.17

A general tree structure

8 Graphs and Matrices

The spectral analysis of graphs involves operations on the matrices related to graphs.

8.1 Eigenvalues

Multiplying an $n \times n$ matrix A by an $n \times 1$ vector x results in another $n \times 1$ vector y which can be written as $Ax=y$ in equation form. Instead of getting a new vector y, it would be interesting to know if the Ax product equals a vector which is a constant multiplied by the vector x as shown below.

$$\begin{aligned} Ax=\lambda x \end{aligned}$$

(2.4)

If we can find values of x and $\lambda$ for this equation to hold, $\lambda$ is called an eigenvalue of A and x as an eigenvector of A. There will be a number of eigenvalues and a set of eigenvectors corresponding to these eigenvalues in general. Rewriting Eq. 2.4,

$$\begin{aligned} Ax-\lambda x=0 \end{aligned}$$

(2.5)

$$ (A-\lambda I)x=0 $$

$$\begin{aligned} det(A-\lambda I)x=0 \end{aligned}$$

(2.6)

For A[n, n], $det(A-\lambda I)=0$ is called the characteristic polynomial which has a degree of n and therefore has n roots. Solving this polynomial provides us with eigenvalues and substituting these in Eq. 2.4 provides the eigenvectors of matrix A.

8.2 Laplacian Matrix

Definition 2.24

(degree matrix) The degree matrix D of a graph G is the diagonal matrix with elements $d_1, \ldots ,d_n$ where $d_i$ is the degree of vertex i.

Definition 2.25

(Laplacian matrix) The Laplacian matrix L of a simple graph is obtained by subtracting its adjacency matrix from its degree matrix.

The entries of the Laplacian matrix L are then as follows.

$$ l_{ij} = \left\{ \begin{array}{cll} d_i &{} \text {if}~i = j \\ -1 &{}\text {if}~i~\text {and}~j~\text {are neighbors} \\ 0 &{} \text {otherwise}. \end{array}\right. $$

The Laplacian matrix L is sometimes referred to as the combinatorial Laplacian. The set of all eigenvalues of the Laplacian matrix of a graph G is called the Laplacian spectrum of G. The normalized Laplacian matrix $\mathcal {L}$ is closely related to the combinatorial Laplacian. The relation between these two matrices is as follows:

$$\begin{aligned} \mathcal {L}=D^{-1/2}LD^{-1/2}=D^{-1/2}(D-A)D^{-1/2}=I-D^{-1/2}AD^{-1/2}. \end{aligned}$$

(2.7)

The entries of the normalized Laplacian matrix $\mathcal {L}$ can then be specified as below.

$$ \mathcal {L}_{ij} = \left\{ \begin{array}{cll} 1 &{} \text {if}~i = j \\ \frac{-1}{\sqrt{d_i d_j}} &{} \text {if}~i~\text {and}~j~\text {are neighbors} \\ 0 &{} \text {otherwise}. \end{array}\right. $$

The Laplacian matrix and adjacency matrix of a graph G are commonly used to analyze the spectral properties of G and design algebraic graph algorithm to solve various graph problems.

9 Chapter Notes

We have reviewed the basic concepts in graph theory leaving the study of some of the related background including trees, connectivity, matching, network flows and coloring to Part II when we discuss algorithms for these problems. The main graph theory background is presented in a number of books including books by Harary [6], Bondy and Murty [1], and West [8]. Graph theory with applications is studied in a book edited by Gross et al. [4]. Algorithmic graph theory focusses more on the algorithmic aspects of graph theory and books available in this topic include the books by Gibbons [2], Golumbic [3].

Exercises

• 1. Show that the relation between the size and the order of a simple graph is given by $m \le (n/2)$ and decide when the equality holds.

• 2. Find the order of a 4-regular graph that has a size of 28.

• 3. Show that the minimum and maximum degrees of a graph G are related by $\delta (G) \le 2m/n \le \varDelta (G)$ inequality.

• 4. Show that for a regular bipartite graph $G=(V1,V2,E)$, $\vert V1 \vert = \vert V2 \vert$.

• 5. Let $G=(V_1,V_2,E)$ be a bipartite graph with vertex partitions $V_1$ and $V_2$. Show that

  $$ \sum _{u \in V_1} deg(u)= \sum _{v \in V_2} deg(v) $$

• 6. A graph G has a degree sequence $D=(d_1,d_2, \ldots ,d_n)$. Find the degree sequence of the complement $\overline{G}$ of this graph.

• 7. Show that the join of the complements of a complete graph $K_p$ and another complete graph $K_q$ is a complete bipartite graph $K_{p,q}$.

• 8. Draw the line graph of $K_3$.

• 9. Let $G=(V,E)$ be a graph where $\forall v \in V$, $deg(v) \ge 2$. Show that G contains a cycle.

• 10. Show that if a simple graph G is disconnected, its complement $\overline{G}$ is connected.