Introduction to Graph Theory and Algebraic Graph Theory

Abstract

Graph theory is a branch of mathematics started by Euler [1] as early as 1736. It took a hundred years before the second important contribution of Kirchhoff [2] had been made for the analysis of electrical networks. Cayley [3] and Sylvester [4] discovered several properties of special types of graphs known as trees. Poincaré [5] defined in principle what is known nowadays as the incidence matrix of a graph. It took another century before the first book was published by König [6]. After the Second World War, further books appeared on graph theory (Ore [7], Behzad and Chartrand [8], Tutte [9], Berge [10], Harary [11], Gould [12], Wilson [13], Wilson and Watkins [14] and West [15], among many others).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

Graph theory is a branch of mathematics started by Euler [1] as early as 1736. It took a hundred years before the second important contribution of Kirchhoff [2] had been made for the analysis of electrical networks. Cayley [3] and Sylvester [4] discovered several properties of special types of graphs known as trees. Poincaré [5] defined in principle what is known nowadays as the incidence matrix of a graph. It took another century before the first book was published by König [6]. After the Second World War, further books appeared on graph theory (Ore [7], Behzad and Chartrand [8], Tutte [9], Berge [10], Harary [11], Gould [12], Wilson [13], Wilson and Watkins [14] and West [15], among many others).

Algebraic graph theory can be viewed as an extension to graph theory in which algebraic methods are applied to problems about graphs (Biggs [16]). Spectral graph theory, as the main branch of algebraic graph theory, is the study of properties of graphs in relationship to the characteristic polynomial, eigenvalues and eigenvectors of matrices associated with graphs, such as its adjacency matrix or Laplacian matrix. Spectral graph theory emerged in the 1950s and 1960s. The 1980 monograph Spectra of Graphs [17] by Cvetković, Doob and Sachs has summarised nearly all research to date in the area. In 1988 it was updated by the survey Recent Results in the Theory of Graph Spectra [18].

Graph theory has found many applications in engineering and science, such as chemical, electrical, civil and mechanical engineering, architecture, management and control, communication, operational research, sparse matrix technology, combinatorial optimisation and computer science. Therefore, many books have been published on applied graph theory such as those by Bondy and Murty [19], Chen [20], Thulasiraman and Swamy [21], Beineke and Wilson [22], Mayeda [23], Christofides [24], Gondran and Minoux [25], Deo [26], Cooke et al. [27] and Kaveh [28, 29]. In recent years, due to the extension of the concepts and applications of the graph theory, many journals such as Journal of Graph Theory, Journal of Combinatorial Theory A & B, Discrete and Applied Mathematics, SIAM Journal of Discrete Mathematics, European Journal of Combinatorics and Graphs and Combinatorics are being published to cover the advances made in this field.

In this chapter basic definitions and concepts of graph theory and algebraic graph theory are briefly presented; however, for proofs and details the reader may refer to textbooks on this subject, Refs. [11, 15, 28, 29].

2.2 Basic Concepts and Definitions of Graph Theory

There are many physical systems whose performance depends not only on the characteristics of their components but also on their relative location. As an example, in a structure, if the properties of a member are altered, the overall behaviour of the structure will be changed. This indicates that the performance of a structure depends on the characteristics of its members. On the other hand, if the location of a member is changed, the properties of the structure will again be different. Therefore, the connectivity (topology) of the structure influences the performance of the entire structure. Hence, it is important to represent a system so that its topology can clearly be understood. The graph model of a system provides a powerful means for this purpose.

In this section, basic concepts and definitions of graph theory are presented. Since some of the readers may be unfamiliar with the theory of graphs, simple examples are included to make it easier to understand the main concepts.

Some of the uses of the theory of graphs in the context of civil engineering are as follows. A graph can be a model of a structure, a hydraulic network, a traffic network, a transportation system, a construction system or a resource allocation system. These are only some of such models, and the applications of graph theory are much extensive. In this book, the theory of graphs is used as the model of a skeletal structure, and it is employed also as a means for transforming the connectivity properties of finite element meshes to those of graphs. This section will also enable the readers to develop their own ideas and methods in the light of the principles of graph theory. For further definitions and proofs, the reader may refer to Harary [11] and West [15].

2.2.1 Definition of a Graph

A graph S consists of a non-empty set N(S) of elements called nodes (vertices or points) and a set M(S) of elements called members (edges or arcs) together with a relation of incidence which associates with each member a pair of nodes (not necessarily distinct), called its ends.

Two or more members joining the same pair of nodes are known as multiple members, and a member joining a node to itself is called a loop. A graph with no loops and multiple members is called a simple graph. If N(S) and M(S) are countable sets, then the corresponding graph S is finite. In this book only finite graphs are needed, which are referred to as graphs.

The above definitions correspond to abstract graphs; however, a graph may be visualised as a set of points connected by line segments in Euclidean space; the nodes of a graph are identified with points, and its members are identified as line segments without their end points. Such a configuration is known as a topological graph. These definitions are illustrated in Fig. 2.1.

Fig. 2.1

Simple and non-simple graphs. (a) A simple graph. (b) A graph with a loop and multiple members

2.2.2 Adjacency and Incidence

Two nodes of a graph are called adjacent if these nodes are the end nodes of a member. A member is called incident with a node if this node is an end node of the member. Two members are called incident if they have a common end node. The degree (valency) of a node n_i of a graph, denoted by deg (n_i), is the number of members incident with that node. Since each member has two end nodes, the sum of node degrees of a graph is twice the number of its members.

2.2.3 Graph Operations

A subgraph S_i of S is a graph for which N(S_i) ⊆ N(S) and M(S_i) ⊆ M(S), and each member of S_i has the same ends as in S.

The union of subgraphs S₁, S₂, … , S_k of S, denoted by ${\mathrm{{S}}^\mathrm{{k}}}=\mathop{\cup}\limits_{\mathrm{{i}=1}}^\mathrm{{k}}{\mathrm{{S}}_\mathrm{{i}}} = {\mathrm{{S}}_1} \cup {\mathrm{{S}}_2} \cup \ldots \cup {\mathrm{{S}}_\mathrm{{k}}}$, is a subgraph of S with $\mathrm{N}\left( {{\mathrm{{S}}^\mathrm{{k}}}} \right) = \mathop{\cup}\limits_{\mathrm{{i}=1}}^\mathrm{{k}}\mathrm{N}\left( {{\mathrm{{S}}_\mathrm{{i}}}} \right)$ and $\mathrm{M}\left( {{\mathrm{{S}}^\mathrm{{k}}}} \right) = \mathop{\cup}\limits_{\mathrm{{i}=1}}^\mathrm{{k}}\mathrm{M}\left( {{\mathrm{{S}}_\mathrm{{i}}}} \right)$. The intersection of two subgraphs S_i and S_j is similarly defined using intersections of node sets and member sets of the two subgraphs. The ring sum of two subgraphs S_i ⊕ S_j is a subgraph which contains the nodes and members of S_i and S_j except those elements common to S_i and S_j. These definitions are illustrated in Fig. 2.2.

Fig. 2.2

A graph, two of its subgraphs, their union, intersection and ring sum. (a) S. (b) S_i. (c) S_j. (d) S_i ∪ S_j. (e) S_i ∩ S_j. (f) S_i ⊕ S_j

There are other important graph operations consisting of different graph products which will be described in detail in Chap. 3 of this book. These products and their applications in structural mechanics are the main concern of the present book.

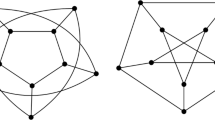
Two graphs are called isomorphic if they have the same number of nodes and the adjacency is preserved. As an example three isomorphic graphs are shown in Fig. 2.3.

Fig. 2.3

Three isomorphic graphs

2.2.4 Walks, Trails and Paths

A walk P_k of S is a finite sequence P_k = {n₀, m₁, n₁, … , m_p, n_p} whose terms are alternately nodes n_i and members m_i of S for 1 ≤ i ≤ p, and n_i−1 and n_i are the two ends of m_i. A trail in S is a walk in which no member of S appears more than once. A path is a trail in which no node appears more than once. The length of a path P_i, denoted by L(P_i), is taken as the number of its members. P_i is called the shortest path between the two nodes n₀ and n_p, if for any other path P_j between these nodes L(P_i) ≤ L(P_j). The distance between two nodes of a graph is defined as the number of the members of a shortest path between these nodes.

Two nodes n_i and n_j are said to be connected in S if there exists a path between these nodes. A graph S is called connected if all pairs of its nodes are connected. A component of a graph S is a maximal connected subgraph, that is, it is not a subgraph of any other connected subgraph of S.

2.2.5 Cycles and Cutsets

A cycle is a path (n₀, m₁, n₁, … , m_p, n_p) for which n₀ = n_p and p ≥ 1; that is, a cycle is a closed path. Similarly a closed trail (hinged cycle) and a closed walk can be defined. A cycle of a graph and a hinged cycle are shown in Fig. 2.4a, b, respectively.

Fig. 2.4

A cycle and a hinged cycle of S. (a) A cycle of S. (b) A hinged cycle of S

A disconnecting set of a connected graph S is a set of members whose removal disconnects S. As an example the removal of bold members in Fig. 2.5a will result in three disconnected subgraphs. A cutset is defined as a disconnecting set, no proper subset of which a disconnecting set. Obviously the removal of the members of a cutset will separate the remainder of the graph into two disjoint components S₁ and S₂, which are linked by each member of the cutset, Fig. 2.5b. Notice that no proper subsets of a cutset have this property. A link is a member which has its ends in S₁ and S₂. If one of S₁ or S₂ consists of a single node, the cutset is called a co-cycle (Fig. 2.5c).

Fig. 2.5

A disconnecting set, a cutset and a co-cycle of S. (a) A disconnecting set. (b) A cutset. (c) A co-cycle

2.2.6 Trees, Spanning Trees and Shortest Route Trees

A tree T of S is a connected subgraph of S which contains no cycle. A set of trees of S forms a forest. Obviously a forest with k trees contains N(S) − k members. If a tree contains all the nodes of S, it is called a spanning tree of S. Henceforth, for simplicity it will be referred to as a tree. The complement of T in S is called a cotree, denoted by T*. The members of T are known as branches and those of T* are called chords.

A shortest route tree (SRT) rooted at a specified node n₀ of S is a tree for which the distance between every node n_j of T and n₀ is minimum. An SRT of a graph can be generated by the following simple algorithm:

Label the selected root n₀ as ‘0’ and the adjacent nodes as ‘1’. Record the members incident to ‘0’ as tree members. Repeat the process of labelling with ‘2’ the unnumbered ends of all the members incident with nodes labelled as ‘1’, again recording the tree members. This process terminates when each node of S is labelled and all the tree members are recorded. This algorithm has many applications in engineering, and it is also called a breadth-first-search algorithm.

The above definitions are illustrated in Fig. 2.6.

Fig. 2.6

Different subgraphs in relation with tree of S. (a) A graph S. (b) A tree T of S. (c) A spanning tree T′ of S. (d) An SRT rooted from n_0. (e) The cotree of T′. (f) A forest with two trees

It is easy to prove that for a tree T

$$ \mathrm{M}\left( \mathrm{T} \right) = \mathrm{N}\left( \mathrm{T} \right)-1 $$

(2.1)

where M(T) and N(T) are the numbers of members and nodes of T, respectively.

For a connected graph S, the number of chords is given by

$$ \mathrm{M}\left( {{\mathrm{{T}}^{*}}} \right) = \mathrm{M}\left( \mathrm{S} \right)-\mathrm{M}\left( \mathrm{T} \right). $$

(2.2)

Since N(T) = N(S), hence,

$$ \mathrm{M}({\mathrm{{T}}^{*}}) = \mathrm{M}(\mathrm{S})-\mathrm{N}(\mathrm{S}) + 1, $$

(2.3)

where M(S) and N(S) are the numbers of members and nodes of S, respectively. Notice that for a set and its cardinality, the same notation is used and the difference should be obvious from the context.

2.2.7 Directed Graphs

A directed graph or digraph D is a set of nodes N(D), a set of members M(D), together with a relationship which associates a pair of ordered nodes with each member. The first node of an ordered pair is called the start node, and the second is known as the end node of a directed member. We say a member is directed from its start node to its end node. Naturally the underlying graph a directed graph D is a graph S with the members of D being treated as unordered pairs. A directed graph D and its underlying graphs S are shown in Fig. 2.7.

Fig. 2.7

A directed graph and its underlying graph. (a) A directed graph D. (b) The underlying graph of D

2.2.8 Different Types of Graphs

In order to simplify the study of properties of graphs, different types of graphs have been defined. Some important and relevant to our study are as follows:

A null graph is a graph which contains no members, Fig. 2.8a. Thus, N_k is a graph containing k isolated nodes.

Fig. 2.8

Three different types of graphs. (a) A null graph N_6. (b) A path graph P_4. (c) A cycle graph C₅

A path graph is a graph consisting of a single path, Fig. 2.8b. Hence, P_k is a path with k nodes and (k−1) members.

A cycle graph is a graph consisting of a single cycle, Fig. 2.8c. Therefore, C_k is a polygon with k members.

A wheel graph W_k is defined as the union of a star graph with k−1 members and a cycle graph C_k−1, connected as shown in Fig. 2.9, for k = 6. Alternatively a wheel graph W_k can be obtained from the cycle graph C_k−1 by adding a node O and members (spokes) joining O to each nodes of C_k−1.

Fig. 2.9

Two different types of graphs. (a) A wheel graph W_7. (b) A star graph

A complete graph is a graph in which every two distinct nodes are connected by exactly one member, Fig. 2.10a. A complete graph with N nodes is denoted by K_N. It can easily be proved that a complete graph with N nodes has N(N − 1)/2 members.

Fig. 2.10

Different types of graphs. (a) A complete graph K_6. (b) A bipartite graph with r = 3 and s = 4. (c) A complete bipartite graph K_3,4

A graph is called bipartite if the corresponding node set can be split into two sets N₁ and N₂ in such a way that each member of S joins a node of N₁ to a node of N₂. This graph is denoted by B(S) = (N₁, M, N₂), Fig. 2.10b. A complete bipartite graph is a bipartite graph in which each node N₁ is joined to each node of N₂ by exactly one member. If the numbers of nodes in N₁ and N₂ are denoted by r and s, respectively, then a complete bipartite graph is denoted by K_r,s, Fig. 2.10c.

A graph S is called regular if all of its nodes have the same degree. If this degree is k, then S is k-regular graph. As an example, a triangle graph is 2-regular and a cubic graph is 3-regular.

2.3 Vector Spaces Associated with a Graph

A vector space can be associated with a graph by defining a vector, the field and the binary operations as follows:

Any subset of the M(S) members of a graph S can be represented by a vector x whose M(S) components are elements of the field of integer modulo 2, where component x_i = 1 when the ith member is an element of the subset, and x_i = 0 otherwise. The sum of two subset vectors x and y, a vector z with entries defined by z_i = x_i + y_i, represents the symmetric difference of the original subsets. The scalar product of x and y defined by Σx_iy_i is 0 or 1 according as the original subsets have an even or an odd number of members in common. Although this vector space can be constructed over an arbitrary field, for simplicity the field of integer modulo 2 is considered, in which 1 + 1 = 0.

Two important subspaces of the above vector space of a graph S are the cycle subspace and cutset subspace, known as cycle space and cutset space of S.

2.3.1 Cycle Space

Let a cycle set of members of a graph be defined as a set of members which form a cycle or form several cycles having no common member, but perhaps common nodes. The null set is also defined as a cycle set. A vector representing a cycle set is called a cycle set vector. It can be shown that the sum of two cycle set vectors of a graph is also a cycle set vector. Thus, the cycle set vectors of a graph form a vector space over the field of integer modulo 2. The dimension of a cycle space is given by

$$ \mathrm{nullity}\ \left( \mathrm{S} \right) = \upnu \left( \mathrm{S} \right) = {\mathrm{{b}}_1}\left( \mathrm{S} \right) = \mathrm{M}\left( \mathrm{S} \right)-\mathrm{N}\left( \mathrm{S} \right)+{\mathrm{{b}}_0}\left( \mathrm{S} \right), $$

(2.4)

where b₁(S) and b₀(S) are the first and zero Betti numbers of S, respectively. As an example, the nullity of the graph S in Fig. 2.11a is ν(S) = 10 − 8 + 1 = 3.

Fig. 2.11

A graph S with a cycle basis and a cutset basis. (a) A graph model S. (b) A cycle basis. (c) A cutest basis

2.3.2 Cutset Space

Consider a cutset vector similar to that of a cycle vector. Let the null set be also defined as a cutset. It can be shown that the sum of two cutset vectors of a graph is also a cutset vector. Therefore, the cutset vectors of a graph form a vector space, the dimension of which is given by

$$ \mathrm{rank}\ \left( \mathrm{S} \right) = \uprho \left( \mathrm{S} \right) = \mathrm{N}\left( \mathrm{S} \right)-{\mathrm{{b}}_0}\left( \mathrm{S} \right). $$

(2.5)

As an example, the rank of S in Fig. 2.11a is ρ(S) = 8 − 1 = 7.

2.3.3 Cycle Bases Matrices

The cycle–member incidence matrix $\bar{\mathbf{C}}$ of a graph S has a row for each cycle or hinged cycle and a column for each member. An entry c_ij of $\bar{\mathbf{C}}$ is 1 if cycle C_i contains member m_j, and it is 0 otherwise. In contrast to the node adjacency and node–member incidence matrix, the cycle–member incidence matrix does not determine a graph up to isomorphism; that is, two totally different graphs may have the same cycle–member incidence matrix.

For a graph S there exist ${2^{{{\mathrm{{b}}_1}\left( \mathrm{S} \right)}}}-1$ cycles or hinged cycles. Thus, $\bar{\mathbf{C}}$ is a (${2^{{{\mathrm{{b}}_1}\left( \mathrm{S} \right)}}}-1$) × M matrix. However, one does not need all the cycles of S, and the elements of a cycle basis are sufficient. For a cycle basis, a cycle–member incidence matrix becomes a b₁(S) × M matrix, denoted by C, known as the cycle basis incidence matrix of S. As an example, matrix C for the graph shown in Fig. 2.11, for the following cycle basis,

$$ {\mathrm{{C}}_1} = \left( {{\mathrm{{m}}_1},\ {\mathrm{{m}}_4},\ {\mathrm{{m}}_5},\ {\mathrm{{m}}_8}} \right),\ {\mathrm{{C}}_2} = \left( {{\mathrm{{m}}_2},\ {\mathrm{{m}}_8},\ {\mathrm{{m}}_6},\ {\mathrm{{m}}_9}} \right),\ {\mathrm{{C}}_3} = \left( {{\mathrm{{m}}_3},\ {\mathrm{{m}}_9},\ {\mathrm{{m}}_7},\ {\mathrm{{m}}_{10 }}} \right) $$

is given by

$$ \mathbf{C}=\begin{array}{clclcllclcl}{{\mathrm{{C}}_1}} \\{{\mathrm{{C}}_2}} \\{{\mathrm{{C}}_3}} \\\end{array}\left[ {\begin{array}{clclcllclcl}1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \\0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 0 \\0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \\\end{array}} \right] $$

(2.6)

The cycle adjacency matrix D is a b₁(S) × b₁(S) matrix, each entry d_ij of which is 1 if C_i and C_j have at least one member in common, and it is 0 otherwise. This matrix is related to the cycle–member incidence matrix by the following relationship:

$$ \mathbf{C}{{\mathbf{C}}^\mathrm{{t}}} = \mathbf{D}+\mathbf{W}, $$

(2.7)

where W is diagonal matrix with w_ii being the length of the ith cycle and its trace being equal to the total length of the cycles of the basis.

2.3.4 Cutset Bases Matrices

The cutset–member incidence matrix ${{\bar{\mathbf{C}}}^{*}}$ for a graph S has a row for each cutset of S and a column for each member. An entry $\bar{{c}}_\mathrm{{ij}}^{*}$ of ${{\bar{\mathbf{C}}}^{*}}$ is 1 if cutset $\mathrm{C}_\mathrm{{i}}^{*}$ contains member m_j, and it is 0 otherwise. This matrix, like $\bar{\mathbf{C}}$, does not determine a graph completely.

Independent rows of ${{\bar{\mathbf{C}}}^{*}}$ for a cutset basis, denoted by C*, form a matrix known as a cutset basis incidence matrix, which is a η(S) × M matrix, η(S) being the rank of graph S. As an example, C* for the cutset of Fig. 2.11 with members labelled as in Fig. 2.11a is given below.

$$ {{\mathbf{C}}^{*}}=\left[ {\begin{array}{clclcllclcl}0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 \\0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 \\\end{array}} \right]. $$

(2.8)

The cutset adjacency matrix D* is a η(S) × η(S) matrix defined analogously to cycle adjacency matrix D.

2.4 Graphs Associated with Matrices

Through these matrices, many concepts from matrix algebra can be related to those of graph theory. Three types of matrices and the corresponding graphs are shown in Fig. 2.12. The sign * is used to indicate a non-zero number. M₁ is a nonsymmetric square matrix, and the corresponding graph is a directed graph with N nodes, where N is the dimension of the matrix. M₂ is a symmetric square matrix, and the corresponding graph is a nondirected graph with N nodes, where N is the dimension of the matrix. M₃ is an arbitrary rectangular matrix of dimension M × N, and the corresponding graph is a bipartite graph K_M,N. In fact M₁, M₂ and M₃ are the node adjacency matrices of these graphs.

Fig. 2.12

Matrices and the associated graphs

2.5 Planar Graphs: Euler’s Polyhedron Formula

Graph theory and properties of planar graphs were first discovered by Euler in 1736. After 190 years Kuratowski found a criterion for a graph to be planar. Whitney developed some important properties of embedding graphs in the plane. MacLane expressed the planarity of a graph in terms of its cycle basis. In this section, some of these criteria are studied, and Euler’s polyhedron formula is proved.

2.5.1 Planar Graphs

A graph S is called planar if it can be drawn (embedded) in the plane in such a way that no two members cross each other. As an example, a complete graph K₄ shown in Fig. 2.13 is planar since it can be drawn in the plane as shown.

Fig. 2.13

K₄ and two of its drawings. (a) A complete graph K₄. (b) Planar drawings of K₄

On the other hand K₅, Fig. 2.14, is not planar, since every drawing of K₅ contains at least one crossing.

Fig. 2.14

K₅ and two of its drawings. (a) A complete graph K_5. (b) Two drawings of K₅ with one crossing

Similarly K_3,3 is not planar.

A planar graph S drawn in the plane divides the plane into regions, all of which are bounded and only one is unbounded. If S is drawn on a sphere, all the regions will be bounded; however, the number of regions will not change. The cycle bounding a region is called a regional cycle. Obviously the sum of the lengths of regional cycles is twice the number of members of the graph.

Theorem

(Euler [1]): Let S be a connected planar graph. Then,

$$ \mathrm{R}\left( \mathrm{S} \right)-\mathrm{M}\left( \mathrm{S} \right)+\mathrm{N}\left( \mathrm{S} \right)=2. $$

(2.9)

Proof

For a proof, S is re-formed in two stages. In the first stage a spanning tree T of S is considered in the plane for which R(T) − M(T) + N(T) = 2. This is true since R(T) = 1 and M(T) = N(T) − 1. In the second stage chords are added one at a time. Addition of a chord increases the number of members and regions each by unity, leaving the left-hand side of Eq. 2.9 unchanged during the entire process, and the result follows.

2.6 Definitions from Algebraic Graph Theory

Spectral graph theory, as a branch of algebraic graph theory, is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix. An undirected graph has a symmetric adjacency matrix and therefore has real eigenvalues (the multiset of which is called the graph’s spectrum) and a complete set of orthonormal eigenvectors. While the adjacency matrix depends on the vertex labelling, its spectrum is a graph invariant.

2.6.1 Incidence, Adjacency and Laplacian Matrices of a Graph

A directed graph S consists of node set N(S) and member set M(S), where a member, or directed member, is an ordered pair of distinct nodes. An undirected graph can be equally viewed as a directed graph where (n_i,n_j) is a member whenever (n_j,n_i) is a member.

The incidence matrix $\mathbf{B}={{\left[ {{\mathrm{{b}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{m}}}}$ of a graph S, whose nodes are labelled as 1,2, … , n, and members as 1, 2, 3, … , m, is defined as

$$ {\mathrm{{b}}_\mathrm{{i}\mathrm{j}}} = \left\{ {\begin{array}{clclcllclcl}{1\kern0.5em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{incident}\ \mathrm{with}\ \mathrm{member}\ {\mathrm{{m}}_\mathrm{{j}}}} \\ {0\kern0.5em \mathrm{otherwise}} \\\end{array}} \right. $$

(2.10)

The adjacency matrix $\mathbf{A}={{\left[ {{\mathrm{{a}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{n}}}}$ of a graph S, whose nodes are labelled as 1,2, … , n, is defined as

$$ {\mathrm{{a}}_\mathrm{{i}\mathrm{j}}} = \left\{ {\begin{array}{clclcllclcl}{1\kern0.5em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{adjacent}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}} \\ {0\mathrm{otherwise}} \\\end{array}} \right. $$

(2.11)

The degree matrix $\mathbf{D}={{\left[ {{\mathrm{{d}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{n}}}}$ is a diagonal matrix containing node degrees. d_ij is equal to the degree of the ith node.

The Laplacian matrix $\mathbf{L} = {{\left[ {{\mathrm{{l}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{n}}}}$ is defined as

$$ \mathbf{L}=\mathbf{D}-\mathbf{A}. $$

(2.12)

Therefore, the entries of L are as follows:

$$ {\mathrm{{l}}_\mathrm{{i}\mathrm{j}}} = \left\{ \begin{array}{clclclcl}-1\mathrm{node}{\mathrm{{n}}_\mathrm{{i}}}\mathrm{i}\mathrm{s}\mathrm{adjacent}\mathrm{to}{\mathrm{{n}}_\mathrm{{j}}} \hfill \\\deg \left( {{\mathrm{{n}}_\mathrm{{i}}}} \right)\mathrm{i}\mathrm{f}\mathrm{i} = \mathrm{j} \hfill \\0\mathrm{otherwise} \hfill\end{array} \right. $$

(2.13)

As an example, the incidence, adjacency, degree and Laplacian matrices of the graph S shown in Fig. 2.15 are as follows:

Fig. 2.15

A graph S

2.6.2 Incidence and Adjacency Matrices of a Directed Graph

The incidence matrix $\mathbf{B}={{\left[ {{\mathrm{{b}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{m}}}}$ of a directed graph S, whose nodes are labelled as 1,2, … , n, and members as 1, 2, 3, … , m, is defined as

$$ {\mathrm{{b}}_\mathrm{{i}\mathrm{j}}}=\left\{ {\begin{array}{clclcllclcl}{+1\kern1em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{connected}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{and}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{the}\ \mathrm{start}\ \mathrm{node}\ \mathrm{of}\ \mathrm{member}\ {\mathrm{{m}}_\mathrm{{j}}}} \\ {-1\kern1em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{connected}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{and}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{the}\ \mathrm{end}\ \mathrm{node}\ \mathrm{of}\ \mathrm{member}\ {\mathrm{{m}}_\mathrm{{j}}}} \\ {0\kern1.8em \mathrm{otherwise}} \\\end{array}} \right. $$

(2.14)

The adjacency matrix $\mathbf{A} = {{\left[ {{\mathrm{{a}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{n}}}}$ of a directed graph D, whose nodes are labelled as 1,2, …, n, is defined as

$$ {\mathrm{{a}}_\mathrm{{i}\mathrm{j}}}=\left\{ {\begin{array}{clclcllclcl}{+1\kern1em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{connected}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{and}\ \mathrm{directed}\ \mathrm{from}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}} \\ {-1\kern1em \mathrm{if}\ \mathrm{node}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{connected}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{and}\ \mathrm{directed}\ \mathrm{from}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{i}}}} \\ {\kern.75em0\kern1em \mathrm{otherwise}} \\\end{array}} \right. $$

(2.15)

As an example, the incidence and adjacency matrices of the directed graph of Fig. 2.16 are shown in the following:

Fig. 2.16

A graph S

2.6.3 Adjacency and Laplacian Matrices of a Weighted Graph

Consider a graph with weights assigned to its nodes and edges. The nodal weight vector is

$$ \mathbf{NW} = \left[ \mathrm{{n}{\mathrm{{w}}_\mathrm{{i}}}} \right];\ \mathrm{i} = 1,2,\ldots,\mathrm{N}, $$

(2.16)

and edge weight vector is defined as follows:

$$ \mathbf{EW}=\left[ \mathrm{{e}{\mathrm{{w}}_\mathrm{{i}\mathrm{j}}}} \right];\ \left( \mathrm{{i},\mathrm{j}} \right) = 1,,\ldots,\mathrm{N}, $$

(2.17)

The adjacency matrix $\mathbf{A} = {{\left[ {{\mathrm{{a}}_\mathrm{{ij}}}} \right]}_{\mathrm{{n}\times \mathrm{n}}}}$ of a weighted graph S, containing n nodes, is defined as follows:

$$ {\mathrm{{a}}_\mathrm{{i}\mathrm{j}}} = \left\{ {\begin{array}{clclcllclcl}\mathrm{{e}{\mathrm{{w}}_\mathrm{{i}\mathrm{j}}}\kern1em \mathrm{if}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{is}\ \mathrm{adjacent}\ \mathrm{to}\ {\mathrm{{n}}_\mathrm{{j}}}} \\{0\kern6em \mathrm{otherwise}} \\\end{array}} \right. $$

(2.18)

For a non-weighted graph ew_ij should be replaced by unity.

The entries of the weighted Laplacian matrix L of a weighted graph is defined as

$$ \mathbf{L}=\mathbf{D}-\mathbf{A}, $$

(2.19)

The entries of L are as follows:

$$ {\mathrm{{l}}_\mathrm{{i}\mathrm{j}}}=\left\{ {\begin{array}{clclcllclcl}{-\mathrm{e}{\mathrm{{w}}_\mathrm{{i}\mathrm{j}}}=-\mathrm{e}{\mathrm{{w}}_\mathrm{{j}\mathrm{i}}}\kern1.5em \mathrm{i}\mathrm{f}\ \mathrm{nodes}\ {\mathrm{{n}}_\mathrm{{i}}}\ \mathrm{and}\ {\mathrm{{n}}_\mathrm{{j}}}\ \mathrm{are}\ \mathrm{adjacent}} \\ \mathrm{{e}{\mathrm{{w}}_\mathrm{{i}}}=\sum\limits_{\mathrm{{j}=1}}^{{{\mathrm{{D}}_\mathrm{{i}}}}} \mathrm{{e}{\mathrm{{w}}_\mathrm{{i}\mathrm{j}}}\kern1.5em \mathrm{for}\ \mathrm{i}=\mathrm{j}\kern9em } } \\ {0\kern7em \mathrm{otherwise}\ } \\\end{array}} \right. $$

(2.20)

For non-weighted graph this reduces to Eq. 2.13.

2.6.4 Eigenvalues and Eigenvectors of an Adjacency Matrix

Consider the eigenproblem as

$$ \mathbf{A}{\mathbf{\upphi}_i}={\upmu_i}{\mathbf{\upphi}_i} $$

(2.21)

where ${\upmu_\mathrm{{i}}}$ is the eigenvalue and ${\mathbf{\upphi}_i}$ is the corresponding eigenvector. Since A is a symmetric real matrix, all its eigenvalues are real and can be expressed as

$$ {\upmu_1}\leq {\upmu_2}\leq\ldots \leq{\upmu_{\mathrm{{n}-1}}}\leq {\upmu_\mathrm{{n}}} $$

(2.22)

The largest eigenvalue ${\upmu_\mathrm{{n}}}$ is the single root of the characteristic equation of A. The corresponding eigenvector ${\mathbf{\upphi}_\mathrm{{n}}}$ is the only eigenvector with positive entries. This vector has attractive properties employed in geography and structural mechanics. The characteristic polynomial of a matrix A is a polynomial

$$ \upphi \left( \mathbf{A,\rm\lambda } \right)=\det\ \left( {\rm\lambda \bf I-\bf A} \right). $$

(2.23)

Consider φ(A,λ) as the characteristic polynomial of A. The spectrum of a matrix is the list of its eigenvalues together with their multiplicities. The spectrum of a graph S is the spectrum of its adjacency matrix A. For two isomorphic graphs S and S′, φ(S, λ) = φ(S′, λ). However, two graphs may have the same spectrum and yet be non-isomorphic. Information such as valencies of nodes or planarity cannot be determined by the spectrum.

The following properties can easily be proved:

• 1. The number of walks with length k from n_i to n_j in a graph S is equal to (i,j)th entry of A ^k. This can be proved by induction on k.

• 2. The trace of a square matrix A is the sum of its diagonal entries, denoted by trace A. The number of closed walks with length k in a graph is equal to trace A ^k. Thus, for a graph with M members and T triangles, trace A = 0, trace A ² = 2M, and trace A ³ = 6T. Since the trace of a square matrix is also equal to the sum of its eigenvalues, therefore, the eigenvalues of A ^k are the kth power of the eigenvalues of A. Hence, trace A ^k is determined by the spectrum of A, that is, the spectrum of a graph S determines the number of nodes, members and triangles in S.

• 3. The complement $\bar{{S}}$ of a graph S has the same node set as S, where nodes n_i and n_j are adjacent in $\bar{{S}}$ if and only if they are not adjacent in S. Let $\bar{{S}}$ be the complement of S. Then the adjacency matrix of the complement S is given by

  $$ \mathbf{A}\left( {\bar{{S}}} \right) = \mathbf{J}-\mathbf{I}-\mathbf{A}\left( \mathrm{S} \right), $$

  (2.24)

  where J is all-one matrix and I is a unit matrix.

2.6.5 Eigenvalues and Eigenvectors of a Laplacian Matrix

Consider the following eigenproblem:

$$ \mathbf{L}{{\mathbf{v}}_\mathrm{{i}}}={\rm\lambda_\mathrm{{i}}}{{\mathbf{v}}_\mathrm{{i}}}, $$

(2.25)

where λ_i is the eigenvalue and v _i is the corresponding eigenvector. As for A, all the eigenvalues of L are real. It can be shown that matrix L is a positive semi-definite matrix with

$$ 0 = {\rm\lambda_1}\leq {\rm\lambda_2}\leq \ldots \leq {\rm\lambda_\mathrm{{n}}}. $$

(2.26)

And

$$ \mathbf{v}_1^\mathrm{ t}=\left\{ {1,\ 1,\ldots, 1} \right\}. $$

(2.27)

The second eigenvalue λ₂ and the corresponding eigenvector v ₂ have attractive properties. Fiedler [30] has investigated various properties of λ₂. This eigenvalue is also known as the algebraic connectivity of a graph.

2.6.6 Additional Properties of a Laplacian Matrix

Consider a graph S with an arbitrary orientation. The Laplacian of S is a matrix L(S) = BB ^t, where B is the member–node incidence matrix. Naturally the Laplacian does not depend on the orientation considered for the graph. The following results can be proved:

The rank of the Laplacian matrix L(S) of S is equal to the rank of L(S) = N–b₀(S).

• 1. If S is a graph on N nodes and 2 ≤ i ≤ N, then ${\rm\lambda_\mathrm{{i}}}\left( {\bar{{S}}} \right)=\mathrm{N}-{\rm\lambda_{\mathrm{{N}-\mathrm{i}+2}}}\left( \mathrm{S} \right)$, where $\bar{{S}}$ is the complement of S.

Proof

It can be observed that

$$ \mathbf{L}\left( \mathrm{S} \right)+\mathbf{L}\left( {\bar{{S}}} \right)=\mathrm{N}\mathbf{I}-\mathrm\mathbf{J}. $$

(2.28)

The vector I = {1 1 1 … 1}^t is an eigenvector of L(S) and $\mathbf{L}\left( {\bar{{S}}} \right)$ with the corresponding eigenvector 0. Let x be another eigenvector of L(S) with eigenvalue λ. One can assume that x is orthogonal to I. Then Jx = 0, and

$$ \mathrm{N}\mathbf{x}=\left( \mathrm{{N}\mathbf{I}-\mathbf{J}} \right)\mathbf{x}=\mathbf{L}\left( {\overline{\rm{S}}} \right)\mathbf{x}+\mathbf{L}\left( {{ \overline{ \rm S}}} \right)\mathbf{x}=\lambda \mathbf{x}+\mathbf{L}\left( {\overline{{S}}} \right)\mathbf{x}. $$

(2.29)

Therefore, $\mathbf{L}\left( {\bar{{S}}} \right)=\left( \mathrm{{N}-\rm\lambda } \right)\mathbf{x}$, and the proof follows.

• 2. Let S be a graph on N nodes with Laplacian L. Then for any vector x, we have

  $$ {{\mathbf{x}}^\mathrm{{t}}}\mathbf{Lx}=\sum\limits_{{\left( \mathrm{{i},\mathrm{j}} \right)\in \mathrm{M}\left( \mathrm{S} \right)}} {{{{\left( {{\mathrm{{x}}_\mathrm{{i}}}-{\mathrm{{x}}_\mathrm{{j}}}} \right)}}^2}} $$

  (2.30)

Proof

This follows from the observation that

$$ {{\mathbf{x}}^\mathrm{{t}}}\mathbf{Lx}={{\mathbf{x}}^\mathrm{{t}}}\mathbf{B}{{\mathbf{B}}^\mathrm{{t}}}\mathbf{x}={{\left( {{{\mathbf{B}}^\mathrm{{t}}}\mathbf{x}} \right)}^\mathrm{{t}}}\left( {{{\mathbf{B}}^\mathrm{{t}}}\mathbf{x}} \right), $$

(2.31)

and that if (i,j) ∈ M(S), then the entry of B ^t x corresponding to (i,j) is ± (x_i – x_j).

2.7 Matrix Representation of a Graph in Computer

A graph can be represented in various forms. Some of these representations are of theoretical importance; others are useful from the programming point of view when applied to realistic problems. In this section, six different representations of a graph are described.

Two important matrices, namely, incidence matrix B and the adjacency matrices A defined in Sect. 2.6.3, can be used for representing a graph to a computer. However, the storage requirements for these matrices are high and proportional to N × N and M × (N − 1), respectively. In fact large numbers of unnecessary zeros are stored in these matrices. In practice one can use different approaches to reduce the storage required, some of which are described in the following.

Member List: This type of representation is a common approach in structural mechanics. A member list consists of two rows (or columns) and M columns (or rows). Each column (or row) contains the labels of the two end nodes of each member, in which members are arranged sequentially. For example, the member list of S in Fig. 2.15 is

$$ \begin{array}{clclcllclcl}\begin{array}{clclcllclcl}{\kern5.25em {\mathrm{{m}}_1}} & {{\mathrm{{m}}_2}} & {{\mathrm{{m}}_3}} & {{\mathrm{{m}}_4}} & {{\mathrm{{m}}_5}} & {{\mathrm{{m}}_6}} & {{\mathrm{{m}}_7}} \\\end{array} \hfill \\\mathbf{ML}=\begin{array}{clclcllclcl}{{\mathrm{{n}}_\mathrm{{i}}}} \\{{\mathrm{{n}}_\mathrm{{j}}}} \\\end{array}\kern0.5em \left[ {\begin{array}{clclcllclcl}1 & {\kern0.75em 2} & {\kern0.75em 1} & {\kern0.5em 2} & {\kern0.75em 2} & {\kern0.5em 3} & {\kern0.5em 4} \\2 & {\kern0.75em 3} & {\kern0.75em 4} & {\kern0.5em 4} & {\kern0.75em 5} & {\kern0.5em 5} & {\ 5} \\\end{array}} \right]. \hfill\end{array} $$

(2.32)

It should be noted that a member list can also represent orientations on members. The storage required for this representation is 2 × M. Some engineers prefer to add a third row containing the member’s labels, for easy addressing. In this case, the storage is increased to 3 × M.

A different way of preparing a member list is to use a vector containing the end nodes of members sequentially; for example, for the previous example, this vector becomes

$$ \left( {1,2;\ 2,3;\ 1,4;\ 2,4;\ 2,5;\ 3,5;\ 4,5} \right). $$

(2.33)

This is a compact description of a graph; however, it is impractical because of the extra search required for its use in various algorithms.

Adjacency List: This list consists of N rows and D columns, where D is the maximum degree of the nodes of S. The ith row contains the labels of the nodes adjacent to node i of S. For the graph S shown in Fig. 2.15, the adjacency list is

$$ \mathbf{AL}=\begin{array}{clclcllclcl}{{\mathrm{{n}}_1}} \\{{\mathrm{{n}}_2}} \\{{\mathrm{{n}}_3}} \\{{\mathrm{{n}}_4}} \\{{\mathrm{{n}}_5}} \\\end{array}{{\left[ {\begin{array}{clclcllclcl}2 & 4 & {} & {} \\1 & 3 & 4 & 5 \\2 & 5 & {} & {} \\1 & 2 & 5 & {} \\2 & 3 & 4 & {} \\\end{array}} \right]}_{\mathrm{{N}\times \mathrm{D}}}} $$

(2.34)

The storage needed for an adjacency list is N × D.

Compact Adjacency List: In this list the rows of AL are continually arranged in a row vector R, and an additional vector of pointers P is considered. For example, the compact adjacency list of Fig. 2.15 can be written as

$$ \begin{array}{clclclcl} \mathbf{R} & = \left( {\mathbf{2},4,\mathbf{1},3,4,5,\mathbf{2},5,\mathbf{1},2,5,\mathbf{2},3,4} \right), \\\mathbf{P} & = \left( {1,3,7,9,12,15} \right).\end{array} $$

(2.35)

P is a vector (p₁, p₂, p₃, …) which helps to list the nodes adjacent to each node. For node n_i one should start reading R at entry p_i and finish at p_i+1 − 1.

An additional restriction can be put on R, by ordering the nodes adjacent to each node n_i in ascending order of their degrees. This ordering can be of some advantage, an example of which is nodal ordering for bandwidth optimisation. The storage required for this list is 2M + N + 1.

2.8 Historical Problem of Graph Theory

As mentioned before, in a topological graph the nodes are shown by points and the edges are usually identified by arcs or lines. However, an abstract graph can model a much more general set of object and relations. The following problem shows this general aspect even in the earliest application.

Euler began his paper on graphs by discussing a puzzle, the so-called Königsberg Bridge Problem. The city of Königsberg (now Kaliningrad) in East Prussia is located at the banks and on two islands of the river Pregel. The various parts of the city were connected by seven bridges. The problem arose: Is it possible to plan a tour in such a manner that starting from home, one can return there after having crossed each river bridge just once?

A schematic map of the Königsberg is reproduced in Fig. 2.17. The four parts of the city are denoted by letters A, B, C and D. Since we are interested only in the bridge crossings, we may think of A, B, C and D as the vertices of the graph with connecting edges corresponding to the bridges.

Fig. 2.17

Königsberg Bridge Problem

Euler showed that this graph cannot be traversed completely in a single circular path; in other words, no matter at which vertex one begins, one cannot cover the graph and come back to the starting point without retracing one’s steps. Such a path would have to enter each vertex as many times as it departs from it; hence, it requires an even number of edges at each vertex, and this condition is not fulfilled in the graph representing the map of Königsberg.

In this historical problem, the incidence of different parts of a city is considered with edges representing the bridges, that is, even the first graph model has been such a general one and has not been confined to points and edges as imagined by some users.

For definition on topology, the reader may refer to any textbook on topology, for example, Cooks [31].