Abstract
We explore the connection between fractional order partial differential equations in two or more spatial dimensions with boundary integral operators to develop techniques that enable one to efficiently tackle the integral fractional Laplacian. In particular, we develop techniques for the treatment of the dense stiffness matrix including the computation of the entries, the efficient assembly and storage of a sparse approximation and the efficient solution of the resulting equations. The main idea consists of generalising proven techniques for the treatment of boundary integral equations to general fractional orders. Importantly, the approximation does not make any strong assumptions on the shape of the underlying domain and does not rely on any special structure of the matrix that could be exploited by fast transforms. We demonstrate the flexibility and performance of this approach in a couple of two-dimensional numerical examples.
Dedicated to Ian H. Sloan on the occasion of his 80th birthday.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
Large scale computational solution of partial differential equations has revolutionised the way in which scientific research is performed. Historically, it was generally the case that the mathematical models, expressed in the form of partial differential equations involving operators such as the Laplacian, were impossible to solve analytically, and difficult to resolve numerically. This led to a concerted and sustained research effort into the development of efficient numerical methods for approximating the solution of partial differential equations. Indeed, many researchers who were originally interested in applications shifted research interests to the development and analysis of numerical methods. A case in point is Professor Ian H. Sloan who originally trained as physicist but went on to carry out fundamental research in a wide range of areas relating to computational mathematics. Indeed, one may struggle to find an area of computational mathematics in which Sloan has not made a contribution and the topic of the present article, fractional partial differential equations, may be one of the very few.
In recent years, there has been a burgeoning of interest in the use of non-local and fractional models. To some extent, this move reflects the fact that with present day computational resources coupled with state of the art numerical algorithms, attention is now shifting back to the fidelity of the underlying mathematical models as opposed to their approximation. Fractional equations have been used to describe phenomena in anomalous diffusion, material science, image processing, finance and electromagnetic fluids [30]. Fractional order equations arise naturally as the limit of discrete diffusion governed by stochastic processes [20].
Whilst the development of fractional derivatives dates back to essentially the same time as their integer counterparts, the computational methods available for their numerical resolution drastically lags behind the vast array of numerical techniques from which one can choose to treat integer order partial differential equations. The recent literature abounds with work on numerical methods for fractional partial differential equations in one spatial dimension and fractional order temporal derivatives. However, with most applications of interest being posed on domains in two or more spatial dimensions, the solution of fractional equations posed on complex domains is a problem of considerable practical interest.
The archetypal elliptic partial differential equation is the Poisson problem involving the standard Laplacian. By analogy, one can consider a fractional Poisson problem involving the fractional Laplacian. The first problem one encounters is that of how to define a fractional Laplacian, particularly in the case where the domain is compact, and a number of alternatives have been suggested. The integral fractional Laplacian is obtained by restriction of the Fourier definition to functions that have prescribed value outside of the domain of interest, whereas the spectral fractional Laplacian is based on the spectral decomposition of the regular Laplace operator. In general, the two operators are different [24], and only coincide when the domain of interest is the full space.
The approximation of the integral fractional Laplacian using finite elements was considered by D’Elia and Gunzburger [10]. The important work of Acosta and Borthagaray [1] gave regularity results for the analytic solution of the fractional Poisson problem and obtained convergence rates for the finite element approximation supported by numerical examples computed using techniques described in [2].
The numerical treatment of fractional partial differential equations is rather different from the integer order case owing to the fact that the fractional derivative is a non-local operator. This creates a number of issues including the fact that the resulting stiffness matrix is dense and, moreover, the entries in the matrix are given in terms of singular integrals. In turn, these features create issues in the numerical computation of the entries and the need to store the entries of a dense matrix, not to mention the fact that a solution of the resulting matrix equation has to be computed. The seasoned reader will readily appreciate that many of these issues are shared by boundary integral equations arising from classical integer order differential operators [26, 27, 31]. This similarity is not altogether surprising given that the boundary integral operators are pseudo-differential operators of fractional order.
A different, integer order operator based approach, was taken by Nochetto, Otárola and Salgado [21] for the case of the spectral Laplacian. Caffarelli and Silvestre [7] showed that the operator can be realised as a Dirichlet-to-Neumann operator of an extended problem in the half space in d + 1 dimensions.
In the present work, we explore the connection with boundary integral operators to develop techniques that enable one to efficiently tackle the integral fractional Laplacian. In particular, we develop techniques for the treatment of the stiffness matrix including the computation of the entries, the efficient storage of the resulting dense matrix and the efficient solution of the resulting equations. The main ideas consist of generalising proven techniques for the treatment of boundary integral equations to general fractional orders. Importantly, the approximation does not make any strong assumptions on the shape of the underlying domain and does not rely on any special structure of the matrix that could be exploited by fast transforms. We demonstrate the flexibility and performance of this approach in a couple of two-dimensional numerical examples.
2 The Integral Fractional Laplacian and Its Weak Formulation
The fractional Laplacian in \(\mathbb {R}^{d}\) of order s, for 0 < s < 1 and \(d\in \mathbb {N}\), of a function u can be defined by the Fourier transform \(\mathcal {F}\) as
Alternatively, this expression can be rewritten [29] in integral form as
where
is a normalisation constant and p.v. denotes the Cauchy principal value of the integral [19, Chapter 5]. In the case where s = 1 this operator coincides with the usual Laplacian. If \(\varOmega \subset \mathbb {R}^{d}\) is a bounded Lipschitz domain, we define the integral fractional Laplacian \(\left (-\varDelta \right )^{s}\) to be the restriction of the full-space operator to functions with compact support in Ω. This generalises the homogeneous Dirichlet condition applied in the case s = 1 to the case s ∈ (0, 1).
Define the usual fractional Sobolev space \(H^{s}\left (\mathbb {R}^{d}\right )\) via the Fourier transform. If Ω is a sub-domain as above, then we define the Sobolev space \(H^{s}\left (\varOmega \right )\) to be

equipped with the norm

The space
can be equipped with the energy norm

where the non-standard factor \(\sqrt {C(d,s)/2}\) is included for convenience. For s > 1∕2, \(\widetilde {H}^{s}\left (\varOmega \right )\) coincides with the space \(H_{0}^{s}\left (\varOmega \right )\) which is the closure of \(C_{0}^{\infty }\left (\varOmega \right )\) with respect to the \(H^{s}\left (\varOmega \right )\)-norm. For s < 1∕2, \(\widetilde {H}^{s}\left (\varOmega \right )\) is identical to \(H^{s}\left (\varOmega \right )\). In the critical case s = 1∕2, \(\widetilde {H}^{s}\left (\varOmega \right )\subset H^{s}_{0}\left (\varOmega \right )\), and the inclusion is strict. (See for example [19, Chapter 3].)
The usual approach to dealing with elliptic PDEs consists of obtaining a weak form of the operator by multiplying the equation by a test function and applying integration by parts [13]. In contrast, for equations involving the fractional Laplacian \(\left (-\varDelta \right )^{s}u\), we again multiply by a test function \(v\in \widetilde {H}^{s}\left (\varOmega \right )\) and integrate over \(\mathbb {R}^{d}\), and then, instead of integration by parts, we use the identity
Following this approach, since both u and v vanish outside of Ω, we arrive at the bilinear form
with
corresponding to \(\left (-\varDelta \right )^{s}\) on \(\widetilde {H}^{s}\left (\varOmega \right ) \times \widetilde {H}^{s}\left (\varOmega \right )\). The bilinear form \(a\left (\cdot ,\cdot \right )\) is trivially seen to be \(\widetilde {H}^{s}\left (\varOmega \right )\)-coercive and continuous and, as such, is amenable to treatment using the Lax-Milgram Lemma.
In this article we shall concern ourselves with the computational details needed to implement the finite element approximation of problems involving the fractional Laplacian. To this end, the presence of the unbounded domain Ω c in the bilinear form \(a\left (\cdot ,\cdot \right )\) is somewhat undesirable. Fortunately, we can dispense with Ω c using the following argument. The identity
enables the second integral to be rewritten using the Gauss theorem as
where n y is the inward normal to ∂Ω at y, so that the bilinear form can be expressed equivalently as
As an aside, we note that the bilinear form \(b\left (u,v\right )\) represents the so-called regional fractional Laplacian [5, 8]. The regional fractional Laplacian can be interpreted as a generalisation of the usual Laplacian with homogeneous Neumann boundary condition for s = 1 to the case of fractional orders s ∈ (0, 1). It will transpire from our work that most of the presented techniques carry over to the regional fractional Laplacian by simply omitting the boundary integral terms.
3 Finite Element Approximation of the Fractional Poisson Equation
The fractional Poisson problem
takes the variational form
Henceforth, let Ω be a polygon, and let \(\mathcal {P}_{h}\) be a family of shape-regular and globally quasi-uniform triangulations of Ω, and \(\mathcal {P}_{h,\partial }\) the induced boundary meshes [13]. Let \(\mathcal {N}_{h}\) be the set of vertices of \(\mathcal {P}_{h}\) and h K be the diameter of the element \(K\in \mathcal {P}_{h}\), and h e the diameter of \(e\in \mathcal {P}_{h,\partial }\). Moreover, let \(h:=\max _{K\in \mathcal {P}_{h}}h_{K}\). Let ϕ i be the usual piecewise linear basis function associated with a node \(\mathbf {z}_{i}\in \mathcal {N}_{h}\), satisfying \(\phi _{i}\left (\mathbf {z}_{j}\right )=\delta _{ij}\) for \(\mathbf {z}_{j}\in \mathcal {N}_{h}\), and let \(X_{h}:=\operatorname {span}\left \{\phi _{i}\mid \mathbf {z}_{i}\in \mathcal {N}_{h}\right \}\). The finite element subspace \(V_{h}\subset \widetilde {H}^{s}\left (\varOmega \right )\) is given by V h = X h when s < 1∕2 and by
when s ≥ 1∕2. The corresponding set of degrees of freedom \(\mathcal {I}_{h}\) for V h is given by \(\mathcal {I}_{h}=\mathcal {N}_{h}\) when s < 1∕2 and otherwise consists of nodes in the interior of Ω. In both cases we denote the cardinality of \(\mathcal {I}_{h}\) by n. The set of degrees of freedom on an element \(K\in \mathcal {P}_{h}\) is denoted by \(\mathcal {I}_{K}\).
The stiffness matrix associated with the fractional Laplacian is defined to be \(\boldsymbol {A}^{s}=\left \{a\left (\phi _{i}, \phi _{j}\right )\right \}_{i,j}\), where
The existence of a unique solution to the fractional Poisson problem Eq. (1) and its finite element approximation follows from the Lax-Milgram Lemma.
The rate of convergence of the finite element approximation is given by the following theorem:
Theorem 1 ([1])
If the family of triangulations \(\mathcal {P}_{h}\) is shape regular and globally quasi-uniform, and \(u\in H^{\ell }\left (\varOmega \right )\) , for 0 < s < ℓ < 1 or 1∕2 < s < 1 and 1 < ℓ < 2, then

In particular, by applying regularity estimates for u in terms of the data f, the solution satisfies

Moreover, using a standard Aubin-Nitsche argument [13, Lemma 2.31] gives estimates in \(L^{2}\left (\varOmega \right )\):
Theorem 2 ([6])
If the family of triangulations \(\mathcal {P}_{h}\) is shape regular and globally quasi-uniform, and, for 𝜖 > 0, \(u\in H^{s+1/2-\epsilon }\left (\varOmega \right )\) , then

When s = 1 classical results [13, Theorems 3.16 and 3.18] show that if \(u\in H^{\ell }\left (\varOmega \right )\), 1 < ℓ ≤ 2,

so that (2) can be seen as a generalisation to the case s ∈ (0, 1). For s = 1, \(u\in H^{2}\left (\varOmega \right )\) if the domain is of class C 2 or a convex polygon and if \(f\in L^{2}\left (\varOmega \right )\) [13, Theorems 3.10 and 3.12]. However, when s ∈ (0, 1), higher order regularity of the solution is not guaranteed under such conditions.
For example, consider the problem
with analytic solution [14]
Although the domain is C ∞ and the right-hand side is smooth, u s is only in \(H^{s+1/2-\epsilon }\left (\varOmega \right )\) for any 𝜖 > 0. Sample solutions for \(s\in \left \{0.25, 0.75\right \}\) are shown in Fig. 1.
4 Computation of Entries of the Stiffness Matrix
The computation of entries of the stiffness matrix A s in the case of the usual Laplacian (s = 1) is straightforward. However, for s ∈ (0, 1), the bilinear form contains factors \(\left |\mathbf {x}-\mathbf {y}\right |{ }^{-d-2s}\) which means that simple closed forms for the entries are no longer available and suitable quadrature rules therefore must be identified. Moreover, the presence of a repeated integral over Ω (as opposed to an integral over just Ω in the case s = 1) means that the matrix needs to be assembled in a double loop over the elements of the mesh so that the computational cost is potentially much larger than in the integer s = 1 case. Additionally, every degree of freedom is coupled to all other degrees of freedom and the stiffness matrix is therefore dense.
4.1 Reduction to Smooth Integrals
In order to compute the entries of \(\boldsymbol {A}^{s}=\left \{a\left (\phi _{i},\phi _{j}\right )\right \}_{ij}\) we decompose the expression for the entries into contributions from elements \(K,\tilde {K}\in \mathcal {P}_{h}\) and external edges \(e\in \mathcal {P}_{h,\partial }\):
where the contributions \(a^{K\times \tilde {K}}\) and a K×e are given by:
Although the following approach holds for arbitrary spatial dimension d, we restrict ourselves to d = 2 dimensions. In evaluating the contributions \(a^{K\times \tilde {K}}\) over element pairs \(K\times \tilde {K}\), several cases need to be distinguished:
-
1.
K and \(\tilde {K}\) have empty intersection,
-
2.
K and \(\tilde {K}\) are identical,
-
3.
K and \(\tilde {K}\) share an edge,
-
4.
K and \(\tilde {K}\) share a vertex.
These cases are illustrated in Fig. 2. In case 1, where the elements do not touch, the Stroud conical quadrature rule [28] (or any other suitable Gauss rule on simplices) of sufficiently high order can be used to approximate the integrals. More details as to what constitutes a sufficiently high order are given in Sect. 4.2.
Special care has to be taken in the remaining cases 2–4, in which the elements are touching, owing to the presence of a singularity in the integrand. Fortunately, the singularity is removable and can, as pointed out in [1], be treated using standard techniques from the boundary element literature [22]. More specifically, we write the integral as a sum of integrals over sub-simplices. Each sub-simplex is then mapped onto the hyper-cube [0, 1]4 using the Duffy transformation [11]. The advantage of pursuing this approach is that the singularity arising from the degenerate nature of the Duffy transformation offsets the singularity present in the integrals. For example, we obtain the following expressions
and
in which the singularity \(\left |\mathbf {x}-\mathbf {y}\right |{ }^{-d-2s}\) is no longer present. The derivations of the terms involved can be found in [2, 22] and, for completeness, are summarised in the Appendix, along with the notations used in Eqs. (5) and (6). Removing the singularity means that the integrals in Eqs. (5) and (6) are amenable to approximation using standard Gaussian quadrature rules of sufficiently high order as discussed in Sect. 4.2. The same idea is applicable in any number of space dimensions.
4.2 Determining the Order of the Quadrature Rules
The foregoing considerations show that the evaluation of the entries of the stiffness matrix boils down to the evaluation of integrals with smooth integrands, i.e. expressions Eqs. (3) and (4) for case 1 and expressions Eqs. (5) and (6) for case 2–4. As mentioned earlier, it is necessary to use a sufficiently high order quadrature rule to approximate these integrals. We now turn to the question of how high is sufficient.
The arguments used to prove the ensuing estimates follow a pattern similar to the proofs of Theorems 5.3.29, 5.3.23 and 5.3.24 in [22]. The main difference from [22] is the presence of the boundary integral term. More details on the development of this type of quadrature rules in the context of boundary element methods can be found in the work of Erichsen and Sauter [12].
Theorem 3
For d = 2, let \(\mathcal {I}_{K}\) index the degrees of freedom on \(K\in \mathcal {P}_{h}\) , and define \(\mathcal {I}_{K\times \tilde {K}}:=\mathcal {I}_{K}\cup \mathcal {I}_{\tilde {K}}\) . Let k T (respectively k T,∂ ) be the quadrature order used for touching pairs \(K\times \tilde {K}\) (respectively K × e), and let \(k_{NT}\left (K,\tilde {K}\right )\) (respectively \(k_{NT,\partial }\left (K,e\right )\) ) be the quadrature order used for pairs that have empty intersection. Denote the resulting approximation to the bilinear form \(a\left (\cdot ,\cdot \right )\) by \(a_{Q}\left (\cdot ,\cdot \right )\) . Then the consistency error due to quadrature is bounded by

where the errors are given by
\(d_{K,\tilde {K}}:=\inf _{\mathbf {x}\in K, \mathbf {y}\in \tilde {K}}\left |\mathbf {x}-\mathbf {y}\right |\) , \(d_{K,e}:=\inf _{\mathbf {x}\in K, \mathbf {y}\in e}\left |\mathbf {x}-\mathbf {y}\right |\) , and ρ j > 1, j = 1, 2, 3, 4, are constants.
The proof of the Theorem is deferred to the Appendix.
The impact of the use of quadrature rules on the accuracy of the resulting finite element approximation can be quantified using Strang’s first lemma [13, Lemma 2.27]:

where we used the Poincare inequality  in the last step. We then use the Scott-Zhang interpolation operator Π
h [9, 23] and the estimate
in the last step. We then use the Scott-Zhang interpolation operator Π
h [9, 23] and the estimate

used in the proof of Theorem 1 to bound the first term on the right-hand side:

We choose the quadrature rules in such a way that the remaining terms on the right-hand side are also of order \(\mathcal {O}\left (h^{\ell -s}\right )\), i.e.
In particular, if the pair \(K\times \tilde {K}\) (respectively K × e) is well separated, so that \(d_{K,\tilde {K}}\sim 1\) (d K,e ∼ 1), then
is sufficient.
In practice, the quadrature order for non-touching element pairs can be chosen depending on \(d_{K,\tilde {K}}\) using Eqs. (8) and (10), or an appropriate choice of cutoff distance D can be determined so that element pairs with \(d_{K,\tilde {K}}<D\) are approximated using a quadrature rule with \(\mathcal {O}\left (\left |\log h\right |\right )\) nodes, and pairs with \(d_{K,\tilde {K}}\geq D\) are computed using a constant number of nodes.
It transpires from the expressions derived in the Appendix and the fact that n ∼ h −2 that the complexity to calculate the contributions by a single pair of elements K and \(\tilde {K}\) scales like
-
\(\log n\) if the elements coincide,
-
\(\left (\log n\right )^{2}\) if the elements share only an edge,
-
\(\left (\log n\right )^{3}\) if the elements share only a vertex,
-
\(\left (\log n\right )^{4}\) if the elements have empty intersection, but are “near neighbours”, and
-
C if the elements are well separated.
Since \(n\sim \left |\mathcal {P}_{h}\right |\), we cannot expect a straightforward assembly of the stiffness matrix to scale better than \(\mathcal {O}\left (n^{2}\right )\). Similarly, its memory requirement is n 2, and a single matrix-vector product has complexity \(\mathcal {O}\left (n^{2}\right )\), which severely limits the size of problems that can be considered.
5 Solving the Linear Systems
The fractional Poisson equation leads to the linear algebraic system
whereas time-dependent problems (using implicit integration schemes) lead to systems of the form
where Δt is the time-step size. In typical examples, the time-step will be chosen so that the orders of convergence in both spatial and temporal discretisation errors are balanced.
In both cases, the matrices are dense and the condition number of A s grows as the mesh is refined (h → 0). The cost of using a direct solver is prohibitively expensive, growing as \(\mathcal {O}\left (n^{3}\right )\). An alternative is to use an iterative solver such as the conjugate gradient method but the rate of convergence will depend on the condition number. The following result quantifies how the condition number of A s depends on the fractional order s and the mesh size h:
Theorem 4 ([4])
For s < d∕2, and a family of shape regular and globally quasi-uniform triangulations \(\mathcal {P}_{h}\) with maximal element size h, the spectrum of the stiffness matrix satisfies
and hence the condition number of the stiffness matrix satisfies
The exponent of the growth of the condition number depends on the fractional order s. For small s, the matrix is better conditioned, similarly to the mass matrix in the case of integer order operators. As s → 1, the growth of the condition number approaches \(\mathcal {O}\left (h^{-2}\right )\), as for the usual Laplacian. Consequently, just as the conjugate gradient method fails to be efficient for the solution of equations arising from the discretisation of the Laplacian, CG becomes increasingly uncompetitive for the solution of equations arising from the fractional Laplacian.
In the integer order case, multigrid iterations have been used with great success for solving systems involving both the mass matrix and the stiffness matrix that arises from the discretisation of the regular Laplacian. It is therefore to be expected that the same will remain true for systems arising from the fractional Laplacian. In practice, a single multigrid iteration is much more expensive than a single iteration of conjugate gradient. The advantage of multigrid is, however, that the number of iterations is essentially independent of the number of unknowns n. Consequently, while the performance of CG degenerates as n increases, this will not be the case with multigrid making it attractive as a solver for the fractional Poisson problem.
Turning to the systems that arise from the discretisation of time-dependent problems, we first observe that an explicit scheme will lead to CFL conditions on the time-step size of the form Δt ≤ Ch 2s. On the other hand, for implicit time-stepping, the following theorem shows that if the time-step \(\varDelta t=\mathcal {O}\left (h^{2s}\right )\), we can expect the conjugate gradient method to converge rapidly, at a rate which does not degenerate as n increases, in contrast with what is observed for steady problems:
Lemma 1
For a shape regular and globally quasi-uniform family of triangulations \(\mathcal {P}_{h}\) and time-step Δt ≤ 1,
Proof
Since ch d I ≤M ≤ Ch d I, this also permits us to deduce that
and so
□
This shows that for a general time-step Δt ≥ h 2s, the number of iterations the conjugate gradient method will require for systems of the form Eq. (12) will grow as \(\sqrt {\varDelta t/h^{2s}} \sim n^{s/d}\sqrt {\varDelta t} \). Consequently, if Δt is large compared to h 2s, a multigrid solver outperforms conjugate gradient for the systems Eq. (12), but if Δt is on the same order as h 2s, conjugate gradient iterations will generally be more efficient than a multigrid method.
In this section we have concerned ourselves with the effect that the mesh and the fractional order have on the rate of convergence of iterative solvers. This, of course, ignores the cost of carrying out the iteration in which a matrix-vector multiply must be computed at each step. The complexity of both multigrid and conjugate gradient iterations depends on how efficiently the matrix-vector product A s x can be computed. By way of contrast, the mass matrix in Eq. (12) has \(\mathcal {O}\left (n\right )\) entries, so its matrix-vector product scales linearly in the number of unknowns. Since all the basis functions ϕ i interact with one another, the matrix A s is dense and the associated matrix-vector product has complexity \(\mathcal {O}\left (n^{2}\right )\). In the following section, we discuss a sparse approximation that will preserve the order of the approximation error of the fractional Laplacian, but display significantly better scaling in terms of both memory usage and operation counts for both assembly and matrix-vector product.
6 Sparse Approximation of the Matrix
The presence of a factor \(\left |\mathbf {x}-\mathbf {y}\right |{ }^{-d-2s}\) in the integrand in the expression for the entries of the stiffness matrix means that the contribution of pairs of elements that are well separated is significantly smaller than the contribution arising from pairs of elements that are close to one another. This suggests the use of the panel clustering method [17] from the boundary element literature, whereby such far field contributions are replaced by less expensive low-rank blocks rather than computing and storing all the individual entries from the original matrix. Conversely, the near-field contributions are more significant but involve only local couplings and hence the cost of storing the individual entries is a practical proposition. A full discussion of the panel clustering method is beyond the scope of the present work but can be found in [22, Chapter 7]. Here, we confine ourselves to stating only the necessary definitions and steps needed to describe our approach.
Definition 1 ([22])
A cluster is a union of one or more indices from the set of degrees of freedom \(\mathcal {I}\). The nodes of a hierarchical cluster tree \(\mathcal {T}\) are clusters. The set of all nodes is denoted by T and satisfies
-
1.
\(\mathcal {I}\) is a node of \(\mathcal {T}\).
-
2.
The set of leaves \(\text{Leaves}(\mathcal {T})\subset T\) corresponds to the degrees of freedom \(i\in \mathcal {I}\) and is given by
$$\displaystyle \begin{aligned} \text{Leaves}(\mathcal{T}) := \left\{\left\{i\right\} : i\in\mathcal{I}\right\}. \end{aligned} $$ -
3.
For every \(\sigma \in T\setminus \text{Leaves}\left (\mathcal {T}\right )\) there exists a minimal set \(\varSigma \left (\sigma \right )\) of nodes in \(T\setminus \left \{\sigma \right \}\) (i.e. of minimal cardinality) that satisfies
$$\displaystyle \begin{aligned} \sigma = \bigcup_{\tau\in\varSigma\left(\sigma\right)}\tau. \end{aligned} $$The set \(\varSigma \left (\sigma \right )\) is called the sons of σ. The edges of the cluster tree \(\mathcal {T}\) are the pairs of nodes \(\left (\sigma ,\tau \right )\in T\times T\) such that \(\tau \in \varSigma \left (\sigma \right )\).
An example of a cluster tree for a one-dimensional problem is given in Fig. 3.
Definition 2 ([22])
The cluster box Q σ of a cluster σ ∈ T is the minimal hyper-cube which contains ⋃i ∈ σsuppϕ i. The diameter of a cluster is the diameter of its cluster box \(\operatorname {diam}\left (\sigma \right ):= \sup _{\mathbf {x},\mathbf {y}\in Q_{\sigma }} \left |\mathbf {x}-\mathbf {y}\right |\). The distance of two clusters σ and τ is \(\operatorname {dist}\left (\sigma ,\tau \right ):=\inf _{\mathbf {x}\in Q_{\sigma }, \mathbf {y}\in Q_{\tau }}\left |\mathbf {x}-\mathbf {y}\right |\). The subspace V σ of V h is defined as \(V_{\sigma }:=\operatorname {span}\left \{\phi _{i}\mid i\in \sigma \right \}\).
For given η > 0, a pair of clusters \(\left (\sigma ,\tau \right )\) is called admissible, if
The admissible cluster pairs can be determined recursively. Cluster pairs that are not admissible and have no admissible sons are part of the near field and are assembled into a sparse matrix. The admissible cluster pairs for a one dimensional problem are shown in Fig. 4.
For admissible pairs of clusters σ and τ and any degrees of freedom i ∈ σ and j ∈ τ, the corresponding entry of the stiffness matrix is
with kernel \(k\left (\mathbf {x},\mathbf {y}\right )=\left |\mathbf {x}-\mathbf {y}\right |{ }^{-(d+2s)}\). The kernel can be approximated on Q σ × Q τ using Chebyshev interpolation of order m in every spatial dimension by
Here, \(\boldsymbol {\xi }_{\alpha }^{\sigma }\) are the tensor Chebyshev nodes on Q σ, and \(L_{\alpha }^{\sigma }\) are the associated Lagrange polynomials on the cluster box Q σ with \(L_{\alpha }^{\sigma }\left (\boldsymbol {\xi }_{\beta }^{\sigma }\right )=\delta _{\alpha \beta }\). This leads to the following approximation:
In fact, the expressions \(\int _{\operatorname {supp} \phi _{i}} \phi _{i}\left (\mathbf {x}\right )L_{\alpha }^{\sigma }\left (\mathbf {x}\right ) \; d \mathbf {x}\) can be computed recursively starting from the finest level of the cluster tree, since for \(\tau \in \varSigma \left (\sigma \right )\) and x ∈ Q τ
This means that for all leaves \(\sigma =\left \{i\right \}\), and all 1 ≤ α ≤ m d, the basis far-field coefficients
need to be evaluated (e.g. by m + 1-th order Gaussian quadrature). Moreover, the shift coefficients
for \(\tau \in \varSigma \left (\sigma \right )\) must be evaluated, as well as the kernel approximations
for every admissible pair of clusters \(\left (\sigma ,\tau \right )\). We refer the reader to [22] for further details.
The consistency error of this approximation is given by the following theorem:
Theorem 5 ([22], Theorems 7.3.12 and 7.3.18)
There exists γ ∈ (0, 1) such that
The consistency error between the bilinear form a(⋅, ⋅) and the bilinear form a C(⋅, ⋅) of the panel clustering method is

where
Again, by invoking Strang’s Lemma, \(\mathcal {O}\left (h^{\ell -s}\right )\) convergence is retained if the interpolation order m satisfies
By following the arguments in [22], it can be shown that the number of near field entries, i.e. the entries that need to be assembled using the quadrature rules described in Sect. 4, scales linearly in n. The same conclusion holds for the number of far field cluster pairs. Since the four dimensional integral contributions \(a^{K\times \tilde {K}}\) are evaluated using Gaussian quadrature rules with at most \(k\sim \log n\) quadrature nodes per dimension, the assembly of the near field contributions scales with \(n\log ^{2d}n\). The far field kernel approximations and the shift coefficients have size \(m^{2d}\sim \log ^{2d}n\), and are also calculated in \(\log ^{2d}n\) complexity. This means that all the kernel approximations and shift coefficients are obtained in \(n\log ^{2d}n\) time. Finally, the nm d basis far-field coefficients require the evaluation of integrals using m + 1-th order Gaussian quadrature, leading to a complexity of \(n\log ^{2d}n\) as well. The overall complexity of the panel clustering method is therefore \(\mathcal {O}\left (n\log ^{2d}n\right )\), and the sparse approximation requires \(\mathcal {O}\left (n\log ^{2d}n\right )\) memory. In practice, this means that the assembly of the near-field matrix dominates the other steps but involves only local computations.
The computation of the matrix-vector product involving upward and downward recursion in the cluster tree and multiplication by the kernel approximations can also be shown to scale with \(\mathcal {O}\left (n\log ^{2d}n\right )\).
As an aside, we note that one could also opt to use a conventional dense approximation of the discretised fractional Laplacian such as the “hybrid” scheme described in [16] which reduces the far field computation to the computation of a “Nyström-type” approximation. While the complexity of this approach still scales as \(\mathcal {O}\left (n^{2}\right )\), the constant is significantly smaller than if the dense matrix were to be used.
We illustrate the above results by assembling both the full matrix as well as its sparse approximation on the unit disk for fractional orders s = 0.25 and s = 0.75. The memory usage of the matrices are compared in Fig. 5. For low number of degrees of freedom, none of the cluster pairs are admissible, so the full matrix and its approximation have the same size. Starting with roughly 2000 degrees of freedom, the memory footprint of the sparse approximate starts to follow the \(n\log ^{4}n\) curve and therefore outperforms the full assembly. The same behaviour can be observed for the assembly times, as seen in Fig. 6.
Memory usage of the dense matrix and its sparse approximation. s = 0.25 (top), s = 0.75 (bottom). While the dense matrix uses n 2 floating-point numbers, the sparse approximation can be seen to require only \(\mathcal {O} \left (n\log ^{4}n \right )\) memory. At roughly 2000 unknowns, the memory footprint of the sparse approximation separates from the \(\mathcal {O} \left (n^{2} \right )\) curve
7 Applications
7.1 Fractional Poisson Equation
We consider the fractional Poisson problem
on the unit disk \(\varOmega = \left \{\mathbf {x}\in \mathbb {R}^{2}\mid \left |\mathbf {x}\right |\leq 1\right \}\). The discretised fractional Poisson problem then reads
where \(u_{h}=\sum _{i=1}^{n}u_{i}\phi _{i}\in V_{h}\) is the approximation to the solution u, and \(b_{i}=\left \langle \,f,\phi _{i}\right \rangle \).
Triangulations of the disc are obtained through uniform refinement of a uniform initial mesh. After each refinement, the boundary nodes are projected onto the unit circle, resulting in triangulations of the type shown in Fig. 7.
We first consider the test case introduced in Sect. 3 where f = 1 with analytic solution [14] given by
Both the full matrix and its sparse approximation are assembled for \(s\in \left \{0.25, 0.75\right \}\), and Eq. (13) is solved using LAPACK’s dgesv routine and a multigrid solver in the dense case, and multigrid and conjugate gradient methods in the sparse case. Two steps of pre- and postsmoothing by Jacobi iteration are used on every level of the multigrid solver. Recall that solutions for s = 0.25 and s = 0.75 were shown in Fig. 1. In Figs. 8 and 9, the discretisation error is plotted in \(\widetilde {H}^{s}\left (\varOmega \right )\) and in L 2-norm. It can be seen that the rates predicted by Theorems 1 and 2 of h 1∕2 and \(h^{1/2+\min (1/2,s)}\) are indeed obtained, and that the error curves for the full matrix and its sparse approximation are essentially indistinguishable.
Error \( \left | \left |u^{s}-u_{h} \right | \right |{ }_{ \widetilde {H}^{s}(\varOmega )}\) for s = 0.25 (top) and s = 0.75 (bottom) in the case of solutions with singular behaviour close to the boundary. Both the full matrix and its sparse approximation are shown to achieve the predicted rate of h 1∕2
For a second example, the right-hand side f is chosen such that \(u=1-\left |\mathbf {x}\right |{ }^{2}\in H^{2}\left (\varOmega \right )\). The action of f on v ∈ V h is approximated by
where \(I_{ \underline {h}}\) is the interpolation operator onto a highly refined mesh with \( \underline {h}<h\). The resulting consistency error in this case is

Therefore, if \( \underline {h}\) is sufficiently smaller than h, the consistency error will be negligible compared to the discretisation error.
The dependency of the error on the mesh size h can be seen in Fig. 10. The discretisation error decays as h 2−s in \(\widetilde {H}^{s}\left (\varOmega \right )\)-norm, and as h 2 in L 2-norm, which are the optimal orders that we would expect based on estimate (2).
Summarising the results of Sects. 5 and 6, we expect different solvers for the fractional Laplacian to have complexities as given in Table 1. The timings for the different combinations of dense or sparse matrix with a solver are shown in Fig. 11. It can be observed that the sparse approximation asymptotically outperforms the dense solvers. Moreover, for the larger value of s, the multigrid solver starts to outperform the conjugate gradient method for increasingly smaller numbers of unknowns as one would expect based on earlier arguments.
Solution time for the fractional Laplacian using different solvers and the full matrix and its sparse approximation for s = 0.25 (top) and s = 0.75 (bottom). The solvers using the full matrix are outperformed by the ones based on the sparse approximation. For larger fractional order s, the break-even between conjugate gradient and multigrid iteration occurs at a lower number of unknowns
7.2 Fractional Heat Equation
The fractional heat equation is given by
We propose to approximate the problem using an implicit method in time. The simplest such scheme is the backward Euler method
where \(u(\cdot , k\varDelta t)\approx \sum _{i}u_{i}^{k}\phi _i\) and \(f^{k}_{i}=\left (f(\cdot ,k\varDelta t), \phi _{i}\right )\).
More generally, let us assume that a scheme of order α is used in time. In order to obtain optimal convergence in L 2-norm, in view of Theorem 2, we shall choose \(\varDelta t^{\alpha }\sim h^{1/2+\min (1/2,s)}\), i.e.
On the other hand, if optimal \(\widetilde {H}^{s}\left (\varOmega \right )\)-convergence is desired, we need \(\varDelta t_{\,\widetilde {H}^{s}\left (\varOmega \right )}\sim h^{1/(2\alpha )}\), see Theorem 1. Consequently, if an order α scheme is used for time stepping, with optimal time step \(\varDelta t_{L^{2}}\) or \(\varDelta t_{\,\widetilde {H}^{s}\left (\varOmega \right )}\), we find by Lemma 1 that the condition numbers of the iteration matrix satisfy
In particular, in the L 2 case, this shows that the condition number will not grow at all as the mesh size decreases if \(s\in (0,1/\left (4\alpha -2\right )]\). For fractional orders s that are slightly larger than 1∕(4α − 2), the condition number only grows very slowly as the mesh size is decreased. The larger the fractional order, the faster the linear system becomes ill-conditioned. In the \(\widetilde {H}^{s}\left (\varOmega \right )\) case, the condition number of the linear system grows as the mesh size is decreased for \(s> 1/\left (4\alpha \right )\).
We illustrate the consequences of the above result in the case of a second order accurate time stepping scheme (α = 2), and for s = 0.25 and s = 0.75. In the case of s = 0.25, \(\varDelta t_{L^{2}}\sim h^{3/8}\) and \(\kappa \left (\boldsymbol {M}+\varDelta t_{L^{2}}~\boldsymbol {A}^{s}\right )\sim 1+h^{-1/8}\). This suggests that the conjugate gradient method will deliver good results for a wide range of mesh sizes h, as the number of iterations will only grow as \(\sqrt {\kappa \left (\boldsymbol {M}+\varDelta t_{L^{2}}~\boldsymbol {A}^{s}\right )}\sim h^{-1/16}\). The convergence of the multigrid method does not depend on the condition number and is essentially independent of h. This is indeed what is observed in the top part of Fig. 12. In Fig. 13, the number of iterations is shown. It can be observed that for s = 0.25 both the multigrid and the conjugate gradient solver require an essentially constant number of iterations for varying values of Δt.
Timings in seconds for CG and MG depending on Δt for s = 0.25 (top) and s = 0.75 (bottom). It can be observed that, for s = 0.25, the conjugate gradient method is essentially on par with the multigrid solver. For s = 0.75, the multigrid solver asymptotically outperforms the conjugate gradient method, since the condition number \(\kappa \left ( \boldsymbol {M}+\varDelta t_{L^{2}} \boldsymbol {A}^{s} \right )\) grows as h −1
Number of iterations for CG and MG depending on Δt for s = 0.25 (top) and s = 0.75 (bottom). For s = 0.25, the number of iterations is essentially independent of Δt. For s = 0.75, the number of iterations of the multigrid solver is independent of Δt, but the iterations count for conjugate gradient grows with h −1∕2
On the other hand, for s = 0.75, \(\varDelta t_{L^{2}}\sim h^{1/2}\) and \(\kappa \left (\boldsymbol {M}+\varDelta t_{L^{2}}~\boldsymbol {A}^{s}\right )\sim 1+h^{-1}\). Therefore, the condition number increases a lot faster as h goes to zero, and we expect that multigrid asymptotically outperforms the CG solver. This is indeed what is observed in Figs. 12 and 13.
The complexities of the different solvers for different choices of time step size are summarised in Table 2.
7.3 Fractional Reaction-Diffusion Systems
In [15], a space-fractional Brusselator model was analysed and compared to the classical integer-order case. The coupled system of equations is given by
Here, D X and D Y are diffusion coefficients, A and B are reaction parameters, and α and β determine the type of diffusion. By rewriting the solutions as deviations from the stationary solution X = A, Y = B∕A and rescaling, one obtains
with \(\eta =\sqrt {D_{Y}/D_{X}^{\beta /\alpha }}\) and Q = Aη.
In [15] the equations were augmented with periodic boundary conditions and approximated using a pseudospectral method for various different parameter combinations. Here, thanks to the foregoing developments, we have the flexibility to handle more general domains and, in particular, we consider the case where Ω corresponds to a Petri-dish, i.e. \(\varOmega =\left \{\mathbf {x}\in \mathbb {R}^{2}\mid \left |\mathbf {x}\right |\leq 1\right \}\) is the unit disk. We solve the above set of equations using a second order accurate IMEX scheme proposed by Koto [18], whose Butcher tableaux are given by Table 3. The diffusive parts are treated implicitly and therefore require the solution of several systems all of which are of the type M + cΔt A s with appropriate values of c.
In order to verify the correct convergence behaviour, we add forcing functions f and g to the system, chosen such that the analytic solution is given by
for suitable initial conditions, where u s is the solution of the fractional Poisson problem with constant right-hand side. We take α = β = 0.75, and choose Δt ∼ h 1∕2, since we already saw that the rate of the spatial approximation in L 2-norm is of order h. We measure the error as

From the error plots in Fig. 14, it can be observed that \(e_{L^{2}}\sim h\) and e V ∼ h 1∕2, as expected.
Having verified the accuracy of the method, we turn to the solution of the system Eqs. (14) and (15) augmented with exterior Neumann conditions as described in Sect. 2. Golovin et al. [15] observed that for η = 0.2, B = 1.22 and Q = 0.1, a single localised perturbation would first form a ring and then break up into spots. The radius of the ring and the number of resulting spots increases as the fractional orders are decreased. In Fig. 15, simulation results for α = β = 0.625 and α = β = 0.75 are shown. We observe that in both cases, an initially circular perturbation develops into a ring. Lower diffusion coefficients do lead to a larger ring, which breaks up later and into more spots. In the last row, we can see that the resulting spots start to replicate and spread out over the whole domain.
Localised spot solutions of the Brusselator system with α = β = 0.625 (left) and α = β = 0.75 (right). u is shown in both cases, and time progresses from top to bottom. The initial perturbation was identical in both cases. The initial perturbation in the centre of the domain forms a ring, whose radius is bigger if the fractional orders of diffusion α, β are smaller. The ring breaks up into several spots, which start to replicate and spread out over the whole domain. n ≈ 50, 000 unknowns were used in the finite element approximation
Another choice of parameters leads to stripes in the solution. For α = β = 0.75, η = 0.2, B = 6.26 and Q = 2.5, and a random initial condition, stripes without directionality form in the whole domain. This is in alignment with the theoretical considerations of Golovin et al. [15] (Fig. 16).
8 Conclusion
We have presented a reasonably complete and coherent approach for the efficient approximation of problems involving the fractional Laplacian, based on techniques from the boundary element literature. In particular, we discussed the efficient assembly and solution of the associated matrix, and demonstrated the feasibility of a sparse approximation using the panel clustering method. The potential of the approach was demonstrated in several numerical examples, and were used to reproduce some of the findings for a fractional Brusselator model. While we focused on the case of d = 2 dimensions, the generalisation to higher dimensions does not pose any fundamental difficulties. Moreover, the approach taken to obtain a sparse approximation to the dense system matrix for the fractional Laplacian does not rely strongly on the form of the interaction kernel \(k\left (\mathbf {x},\mathbf {y}\right )=\left |\mathbf {x}-\mathbf {y}\right |{ }^{-(d+2s)}\), and generalisations to different kernels such as the one used in peridynamics [25] are therefore possible. In the present work we have confined ourselves to the discussion of quasi-uniform meshes. However, solutions of problems involving the fractional Laplacian exhibit line singularities in the neighbourhood of the boundary. The efficient resolution of such problems would require locally refined meshes which form the topic of forthcoming work [3].
References
Acosta, G., Borthagaray, J.P.: A fractional Laplace equation: regularity of solutions and finite element approximations. ArXiv e-prints (2015)
Acosta, G., Bersetche, F.M., Borthagaray, J.P.: A short FE implementation for a 2d homogeneous Dirichlet problem of a Fractional Laplacian. ArXiv e-prints (2016)
Ainsworth, M., Glusa, C.: Aspects of an adaptive finite element method for the fractional Laplacian: a priori and a posteriori error estimates, efficient implementation and multigrid solver. Comput. Methods Appl. Mech. Eng. 327, 4–35 (2017). Doi: 10.1016/j.cma.2017.08.019
Ainsworth, M., McLean, W., Tran, T.: The conditioning of boundary element equations on locally refined meshes and preconditioning by diagonal scaling. SIAM J. Numer. Anal. 36(6), 1901–1932 (1999)
Bogdan, K., Burdzy, K., Chen, Z.Q.: Censored stable processes. Probab. Theory Relat. Fields 127(1), 89–152 (2003)
Borthagaray, J.P., Del Pezzo, L.M., Martinez, S.: Finite element approximation for the fractional eigenvalue problem. ArXiv e-prints (2016)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32(8), 1245–1260 (2007)
Chen, Z.Q., Kim, P.: Green function estimate for censored stable processes. Probab. Theory Relat. Fields 124(4), 595–610 (2002)
Ciarlet, P.: Analysis of the Scott–Zhang interpolation in the fractional order Sobolev spaces. J. Numer. Math. 21(3), 173–180 (2013)
D’Elia, M., Gunzburger, M.: The fractional Laplacian operator on bounded domains as a special case of the nonlocal diffusion operator. Comput. Math. Appl. 66(7), 1245–1260 (2013)
Duffy, M.G.: Quadrature over a pyramid or cube of integrands with a singularity at a vertex. SIAM J. Numer. Anal. 19(6), 1260–1262 (1982)
Erichsen, S., Sauter, S.A.: Efficient automatic quadrature in 3-d Galerkin BEM. Comput. Methods Appl. Mech. Eng. 157(3–4), 215–224 (1998)
Ern, A., Guermond, J.L.: Theory and Practice of Finite Elements. Applied Mathematical Sciences, vol. 159. Springer, New York, NY (2004)
Getoor, R.K.: First passage times for symmetric stable processes in space. Trans. Am. Math. Soc. 101(1), 75–90 (1961)
Golovin, A.A., Matkowsky, B.J., Volpert, V.A.: Turing pattern formation in the Brusselator model with superdiffusion. SIAM J. Appl. Math. 69(1), 251–272 (2008)
Graham, I.G., Hackbusch, W., Sauter, S.A.: Hybrid Galerkin boundary elements: theory and implementation. Numer. Math. 86(1), 139–172 (2000)
Hackbusch, W., Nowak, Z.P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numer. Math. 54(4), 463–491 (1989)
Koto, T.: IMEX Runge–Kutta schemes for reaction–diffusion equations. J. Comput. Appl. Math. 215(1), 182–195 (2008)
McLean, W.C.H.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge, (2000)
Meerschaert, M.M., Sikorskii, A.: Stochastic Models for Fractional Calculus, de Gruyter Studies in Mathematics, vol. 43. Walter de Gruyter & Co., Berlin (2012)
Nochetto, R.H., Otárola, E., Salgado, A.J.: A PDE approach to fractional diffusion in general domains: a priori error analysis. Found. Comput. Math. 15(3), 733–791 (2015)
Sauter, S.A., Schwab, C.: Boundary Element Methods, pp. 183–287. Springer, Berlin (2011)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54(190), 483–493 (1990)
Servadei, R., Valdinoci, E.: On the spectrum of two different fractional operators. Proc. Roy. Soc. Edinb.: Sect. A Math. 144(04), 831–855 (2014)
Silling, S.A.: Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 48(1), 175–209 (2000)
Sloan, I.H.: Error analysis of boundary integral methods. Acta Numer. 1, 287–339 (1992)
Sloan, I.H., Spence, A.: The Galerkin method for integral equations of the first kind with logarithmic kernel: theory. IMA J. Numer. Anal. 8(1), 105–122 (1988)
Stroud, A.H.: Approximate Calculation of Multiple Integrals. Prentice-Hall, Englewood Cliffs, NJ (1971)
Valdinoci, E.: From the long jump random walk to the fractional Laplacian. SeMA J.: Boletín de la Sociedad Española de Matemática Aplicada 49, 33–44 (2009)
West, B.J.: Fractional Calculus View of Complexity: Tomorrow’s Science. CRC Press, New York (2016)
Yan, Y., Sloan, I.H., et al.: On integral equations of the first kind with logarithmic kernels. J. Integral Equ. Appl. 1, 549–579 (1988)
Acknowledgements
This work was supported by the MURI/ARO on “Fractional PDEs for Conservation Laws and Beyond: Theory, Numerics and Applications” (W911NF-15-1-0562).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: Derivation of Expressions for Singular Contributions
The contributions \(a^{K\times \tilde {K}}\) and a K×e as given in Eqs. (3) and (4) for touching elements K and \(\tilde {K}\) contain removable singularities. In order to make these contributions amenable to numerical quadrature, the singularities need to be lifted. We outline the derivation for d = 2 dimensions.
The expression for \(a^{K\times \tilde {K}}\) can be transformed into integrals over the reference element \(\hat {K}\):
Similarly, by introducing the reference edge \(\hat {e}\), we obtain
for touching elements K and edges e. If K and \(\tilde {K}\) or e have c ≥ 1 common vertices, and if we designate by λ k, k = 0, …, 6 − c the barycentric coordinates of \(K\cup \tilde {K}\) or K ∪ e respectively (cf. Fig. 17), we have
where k(i) is the local index on \(K\cup \tilde {K}\) or K ∪ e of the global degree of freedom i. Moreover, we have
Here, x k, k = 0, …, 6 − c are the vertices that span \(K\cup \tilde {K}\) or K ∪ e respectively.
By setting
we can therefore write
By carefully splitting the integration domain \(\hat {K}\times \hat {K}\) into L c parts and applying a Duffy transformation to each part, the contributions can be rewritten into integrals over a unit hyper-cube, where the singularities are lifted.
The details of this approach can be found in Chapter 5 of [22] for the interactions between K and \(\tilde {K}\). We record the obtained expressions in this case.
-
K and \(\tilde {K}\) are identical, i.e. c = 3
$$\displaystyle \begin{aligned} L_{3}=3,&& \Bar J^{(1,3)}=\Bar J^{(2,3)}=\Bar J^{(3,3)}= \eta_{0}^{3-2s}\eta_{1}^{2-2s}\eta_{2}^{1-2s},\end{aligned} $$$$\displaystyle \begin{aligned} \Bar\psi_{k}^{(1,3)} &= \begin{cases} -\eta_{3} \\ \eta_{3}-1 \\ 1 \end{cases} & \Bar\psi_{k}^{(2,3)} &= \begin{cases} -1 \\ 1-\eta_{3} \\ \eta_{3} \end{cases} & \Bar\psi_{k}^{(3,3)} &= \begin{cases} \eta_{3} \\ -1 \\ 1-\eta_{3} \end{cases}\end{aligned} $$ -
K and \(\tilde {K}\) share an edge, i.e. c = 2
$$\displaystyle \begin{aligned} L_{2}=5, && \Bar J^{(1,2)}=\eta_{0}^{3-2s}\eta_{1}^{2-2s}, \\ && \Bar J^{(2,2)}=\Bar J^{(3,2)}=\Bar J^{(4,2)}=\Bar J^{(5,2)} = \eta_{0}^{3-2s}\eta_{1}^{2-2s}\eta_{2}\end{aligned} $$$$\displaystyle \begin{aligned} \Bar\psi_{k}^{(1,2)} &= \begin{cases} -\eta_{2} \\ 1-\eta_{3} \\ \eta_{3} \\ \eta_{2}-1 \end{cases} & \Bar\psi_{k}^{(2,2)} &= \begin{cases} -\eta_{2}\eta_{3} \\ \eta_{2}-1 \\ 1 \\ \eta_{2}\eta_{3}-\eta_{2} \end{cases} & \Bar\psi_{k}^{(3,2)} &= \begin{cases} \eta_{2} \\ \eta_{2}\eta_{3}-1 \\ 1-\eta_{2} \\ -\eta_{2}\eta_{3} \end{cases} \\ \Bar\psi_{k}^{(4,2)} &= \begin{cases} \eta_{2} \eta_{3} \\ 1-\eta_{2} \\ \eta_{2}-\eta_{2} \eta_{3} \\ -1 \end{cases} & \Bar\psi_{k}^{(5,2)} &= \begin{cases} \eta_{2}\eta_{3} \\ \eta_{2}-1 \\ 1-\eta_{2}\eta_{3} \\ -\eta_{2} \end{cases} \end{aligned} $$ -
K and \(\tilde {K}\) share a vertex, i.e. c = 1
$$\displaystyle \begin{aligned} L_{1}=2, && \Bar J^{(1,1)}= \Bar J^{(2,1)}= \eta_{0}^{3-2s}\eta_{2}\end{aligned} $$$$\displaystyle \begin{aligned} \Bar\psi_{k}^{(1,1)} &= \begin{cases} \eta_{2}-1 \\ 1-\eta_{1} \\ \eta_{1} \\ \eta_{2}\eta_{3}-\eta_{2} \\ -\eta_{2}\eta_{3} \end{cases} & \Bar\psi_{k}^{(2,1)} &= \begin{cases} 1-\eta_{2} \\ \eta_{2}-\eta_{2} \eta_{3} \\ \eta_{2}\eta_{3} \\ \eta_{1}-1 \\ -\eta_{1} \end{cases}\end{aligned} $$
We notice that the contributions for identical elements only depend on η 3, so that in fact only one-dimensional integrals need to be computed. Similarly, the cases of common edges or common vertices only require two and three dimensional integration.
In a similar fashion, the integration domain of a K×e can be split into several parts, so that the singularity can be lifted:
Here, \(\phi _{k}^{(\ell ,c)}\) are the expressions for the local shape functions under the Duffy transformations. The obtained expressions are
-
e is an edge of K, i.e. c = 2
$$\displaystyle \begin{aligned} L_{2}=3, && \Bar J^{(1,2)}=\Bar J^{(2,2)}=\Bar J^{(3,2)}=\eta_{0}^{-2s}\left(1-\eta_{0}\right),\end{aligned} $$$$\displaystyle \begin{aligned} \phi_{k}^{(1,2)} &= \begin{cases} 1-\eta_{0}-\eta_{2}+\eta_{0}\eta_{2} \\ \eta_{0}+\eta_{2}-\eta_{0}\eta_{1}-\eta_{0}\eta_{1} \\ \eta_{0}\eta_{1} \end{cases} & \phi_{k}^{(2,2)} &= \begin{cases} 1-\eta_{0}-\eta_{2}+\eta_{0}\eta_{2} \\ \eta_{2}-\eta_{0}\eta_{2} \\ \eta_{0} \end{cases}\\ \phi_{k}^{(3,2)} &= \begin{cases} 1-\eta_{2}+\eta_{0}\eta_{2}-\eta_{0}\eta_{1} \\ \eta_{2}-\eta_{0}\eta_{2} \\ \eta_{0}\eta_{1} \end{cases}\end{aligned} $$$$\displaystyle \begin{aligned} \Bar\psi_{k}^{(1,2)} &= \begin{cases} -1 \\ 1-\eta_{1} \\ \eta_{1} \end{cases} & \Bar\psi_{k}^{(2,2)} &= \begin{cases} -\eta_{1} \\ \eta_{1}-1 \\ 1 \end{cases} & \Bar\psi_{k}^{(3,2)} &= \begin{cases} 1-\eta_{1} \\ -1 \\ \eta_{1} \end{cases} \end{aligned} $$We notice that for s ≥ 1∕2, the integrand still contains a singularity. In this case, the finite element space V h does not include the degrees of freedom on the boundary. For the interaction of the single degree of freedom that is not on the boundary (k = 2), we obtain
$$\displaystyle \begin{aligned} \Bar J^{(1,2)}=\Bar J^{(2,2)}=\Bar J^{(3,2)}=\eta_{0}^{2-2s}\left(1-\eta_{0}\right), \end{aligned} $$$$\displaystyle \begin{aligned} \phi_{2}^{(1,2)} &= \eta_{1} & \phi_{2}^{(2,2)} &= 1 & \phi_{2}^{(3,2)} &= \eta_{1} \end{aligned} $$and \(\Bar \psi _{2}^{\ell ,c}\) as above.
-
K and e share a vertex, i.e. c = 1
$$\displaystyle \begin{aligned} L_{1}=2, && \Bar J^{(1,1)} = \eta_{0}^{1-2s}, \Bar J^{(2,1)}= \eta_{0}^{1-2s}\eta_{1} \end{aligned} $$$$\displaystyle \begin{aligned} \Bar\psi_{k}^{(1,1)} &= \begin{cases} \eta_{2}-1 \\ 1-\eta_{1} \\ \eta_{1} \\ -\eta_{2} \end{cases} & \Bar\psi_{k}^{(2,1)} &= \begin{cases} 1-\eta_{1} \\ \eta_{1}-\eta_{1} \eta_{2} \\ \eta_{1}\eta_{2} \\ -1 \end{cases} \end{aligned} $$
Appendix 2: Proof of Consistency Error Due to Quadrature
Next, we give the proof for the consistency error of the quadrature approximation first stated in Sect. 4.2.
Theorem 3
For d = 2, let \(\mathcal {I}_{K}\) index the degrees of freedom on \(K\in \mathcal {P}_{h}\) , and define \(\mathcal {I}_{K\times \tilde {K}}:=\mathcal {I}_{K}\cup \mathcal {I}_{\tilde {K}}\) . Let k T (respectively k T,∂ ) be the quadrature order used for touching pairs \(K\times \tilde {K}\) (respectively K × e), and let \(k_{NT}\left (K,\tilde {K}\right )\) (respectively \(k_{NT,\partial }\left (K,e\right )\) ) be the quadrature order used for pairs that have empty intersection. Denote the resulting approximation to the bilinear form \(a\left (\cdot ,\cdot \right )\) by \(a_{Q}\left (\cdot ,\cdot \right )\) . Then the consistency error due to quadrature is bounded by

where the errors are given by
\(d_{K,\tilde {K}}:=\inf _{\mathbf {x}\in K, \mathbf {y}\in \tilde {K}}\left |\mathbf {x}-\mathbf {y}\right |\) , \(d_{K,e}:=\inf _{\mathbf {x}\in K, \mathbf {y}\in e}\left |\mathbf {x}-\mathbf {y}\right |\) , and ρ j > 1, j = 1, 2, 3, 4, are constants.
Proof
Let the quadrature rules for the pairs \(K\times \tilde {K}\) and K × e be denoted by \(a^{K\times \tilde {K}}_{Q}\left (\cdot ,\cdot \right )\) and \(a^{K\times e}_{Q}\left (\cdot ,\cdot \right )\). Set
For u, v ∈ V h, we set
so that
Since
we find

Because

and

we obtain

For d = 2, using Theorem 6 stated below permits to conclude. □
Theorem 6 ([22], Theorems 5.3.23 and 5.3.24)
If K and \(\tilde {K}\) (K and e) are touching elements, then
where ρ 1, ρ 3 > 1 and k T , k T,∂ are the quadrature orders in every dimension of Eqs.(5) and (6).
If K and \(\tilde {K}\) (K and e) are not touching, then
where \(d_{K,\tilde {K}}:=dist(K,\tilde {K})\) , d K,e := dist(K, e), \(\tilde {\rho }_{2}(K,\tilde {K}):=\rho _{2}\max \left \{\frac {d_{K,\tilde {K}}}{h},1\right \}\) , and \(\tilde {\rho }_{4}(K,\tilde {K}):=\rho _{4}\max \left \{\frac {d_{K,e}}{h},1\right \}\) , with ρ 2, ρ 4 > 1, and k NT , k NT,∂ are the quadrature order in every dimension of Eqs.(3) and (4).
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Ainsworth, M., Glusa, C. (2018). Towards an Efficient Finite Element Method for the Integral Fractional Laplacian on Polygonal Domains. In: Dick, J., Kuo, F., Woźniakowski, H. (eds) Contemporary Computational Mathematics - A Celebration of the 80th Birthday of Ian Sloan. Springer, Cham. https://doi.org/10.1007/978-3-319-72456-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-72456-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72455-3
Online ISBN: 978-3-319-72456-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



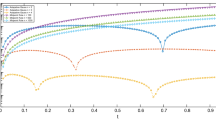










 for s = 0.25 (top) and s = 0.75 (bottom) in the case of solutions with singular behaviour close to the boundary. Both the full matrix and its sparse approximation are shown to achieve the predicted rate of
for s = 0.25 (top) and s = 0.75 (bottom) in the case of solutions with singular behaviour close to the boundary. Both the full matrix and its sparse approximation are shown to achieve the predicted rate of 
 and
and  for s = 0.25 (top) and s = 0.75 (bottom) in the case of a smooth solution
for s = 0.25 (top) and s = 0.75 (bottom) in the case of a smooth solution 





