Bifurcation Analysis and Chaotic Behaviors of Fractional-Order Singular Biological Systems

Abstract

In this chapter, singular system theory and fractional calculus are utilized to model the biological systems in the real world, some fractional-order singular (FOS) biological systems are established, and some qualitative analyses of proposed models are performed. Through the fractional calculus and economic theory, a new and more realistic model of biological systems predator-prey, logistic map and SEIR epidemic system have been extended, and besides some mathematical analysis, the numerical simulations are considered to illustrate the effectiveness of the numerical method to explore the impacts of fractional-order and economic interest on the presented systems in biological contexts. It will be demonstrated that the presence of fractional-order changes the stability of the solutions and enrich the dynamics of system. In addition, singular models exhibit more complicated dynamics rather than standard models, especially the bifurcation phenomena and chaotic behaviors, which can reveal the instability mechanism of systems. Toward this aim, some materials including several definitions and existence theorems of uniqueness of solution, stability conditions and bifurcation phenomena in FOS systems and detailed introductions to fundamental tools for discussing complex dynamical behavior, such as chaotic behavior have been added.

1 Introduction

Singular systems (differential-algebraic systems, descriptor systems, generalized state space systems, semi-state systems, singular singularly perturbed systems, degenerate systems, constrained systems, etc.), more general kind of equations which have been investigated over the past three decades, are established according to relationships among the variables (Dai 1989). As a valuable tool for system modeling and analysis, singular system theory has been widely utilized in different fields including nonlinear electric and electronic circuits, constrained mechanics, networks and economy (Lewis 1986).

This class of systems, which was introduced first by Luenberger in 1977, can be described as the following form.

$$\begin{aligned} E(t)\dot{x}(t) & = H(x(t),u(t),t), \\ y(t) & = J(x(t),u(t),t), \\ \end{aligned}$$

(1)

where $H$ and $J$ are appropriate dimensional vector functions, and the matrix $E(t)$ may be singular.

In 1954, Gordon investigated the economic theory of natural resource utilization in fishing industry and discussed the effects of harvest effort on its ecosystem (Gordon 1954). To study the economic interest of the yield of harvest effort in his theory of a common-property resource, Gordon proposed an algebraic equation to put his idea into practice. Recently, by using this theory of natural resource utilization in industry, the effects of harvest effort on biological systems were studied, and some singular model of these ecosystems were investigated to study the economic interest of the yield of harvest effort. Besides, many qualitative analyses such as stability analysis, presence of bifurcations and chaos and controller design were investigated (Zhang et al. 2010; Chakraborty et al. 2011; Zhang et al. 2012, 2014).

The majority of these works has been carried out in dynamical modeling of biological systems using integer-order differential equations which are valuable in understanding the dynamics behavior. However, the effects of long-range temporal memory and long-range space interactions in these systems are neglected. Due to its ability to provide an exact description of different nonlinear phenomena, inherent relation to various materials and processes with memory and hereditary properties and greater degrees of freedom, fractional-order modeling has recently garnered a lot of attention and gained popularity in the evaluation of dynamical systems (Podlubny 1998; Diethelm 2010; Petras 2011). According to these reasons, fractional-order modeling of many real phenomena such as biological systems has more advantages and consistency rather than classical integer-order mathematical modeling (Rivero et al. 2011).

In this chapter, singular system theory besides fractional calculus is utilized to model the biological systems in the real world which takes the general form

$$E(t)\,D^{\alpha } x(t) = F\left( {t,x(t)} \right),\quad t \ge 0,$$

(2)

where $F:{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}$ is a vector function, $0 < \alpha < 1$, $x(t) \in {\mathbb{R}}^{n}$, and $E(t) \in {\mathbb{R}}^{n \times n}$ is a singular matrix.

Based on this model, some fractional-order singular (FOS) biological systems, such as predator-prey models (Holling-II, Holling-Tanner and food web), logistic map and SEIR epidemic model are established. Then, local stability analysis is performed to investigate the complex dynamical behavior and instability of model systems around the interior equilibrium, which are beneficial to study the coexistence and interaction mechanisms of population in these systems. Furthermore, some qualitative analyses of proposed models such as bifurcation and chaos will be illustrated. These studies can be utilized to design different kinds of controllers with the purpose of stabilizing a model system around the interior equilibrium, to restore the model system to a stable state, which are also theoretical guides to formulate related measures to maintain the sustainable development of population resources in such biological systems.

The remainder of this chapter is organized as follows. Section 2 presents some preliminaries in singular systems theory, and fractional-order integral and derivative definitions will be given. Then, the FOS model will be presented, and some definitions and theorems in solvability and stability conditions will be derived. In Sect. 3, we give some theory for the local bifurcations and chaos of vector fields and maps and extend them to FOS systems. Also, we consider the proposed FOS predator–prey models, logistic map and SEIR epidemic model in Sect. 4, which are followed by some discussions of the local stability, the phenomena of bifurcations and chaos, and numerical simulations to verify the effectiveness of the obtained results. This section will be continued with interpreting of results in biological context, and finally, this chapter ends up by concluding remarks.

2 Preliminary FOS Systems Theory

This section explains the proposed FOS model, beginning with the fractional-order systems and some definitions of fractional integral and derivative operators, and also, stability theorem in Sect. 2.1. Section 2.2 explains a mathematical definition of singular systems and gives their properties, and finally, the FOS model is introduced and established, which is followed by discussion of admissibility and stability conditions.

2.1 Fractional-Order Systems

Fractional calculus as a powerful tool for mathematical modeling has been applied in different fields of sciences such as economics, engineering and biological systems. For instance, it covers the widely known classical fields such as Abel’s integral equation and viscoelastic material modeling, and also less reputed fields including feedback amplifiers, description of propagation in plane electromagnetic waves, generalized voltage divider, electro-analytical chemistry, electric conductance of biological systems, neurons modeling, etc. (Podlubny 1998). The increasing number of such applications shows that there is a significant demand for more realistic and adequate mathematical modeling of real phenomena using fractional calculus in which provides one possible approach on this way.

In this section, some basic materials on fractional calculus have been presented, and the Grunwald-Letnikov (GL), Rienlann-Liouville (RL) and Caputo definitions among many interesting definitions of fractional integral and derivatives will be defined as follows.

Definition 1

(Podlubny 1998) Relied on a generalization of classical concept in traditional calculus in which derivatives of integer order can be represented as limits of finite differences, the GL fractional derivative operator of order $\alpha \in {\mathbb{R}}^{ + }$ of a continuous function $f:{\mathbb{R}}^{ + } \to {\mathbb{R}}$ is defined by

$${}_{a}^{GL} D_{t}^{\alpha } f(t) = \mathop {\lim }\limits_{h \to 0} \frac{{\sum\limits_{r = 0}^{{\left\lfloor {\frac{t - a}{h}} \right\rfloor }} {\left( { - 1} \right)^{r} \left( {\begin{array}{*{20}c} \alpha \\ r \\ \end{array} } \right)f(t - rh)} }}{{h^{\alpha } }},$$

(3)

where ${}_{a}^{GL} D_{t}^{\alpha }$ is the GL derivative of fractional order operator, $a$ and $t$ are the lower and upper terminals, respectively.

Definition 2

(Podlubny 1998) Based on a generalization of classical concept in integral using Cauchy formula, the RL fractional integral operator of order $\alpha \in {\mathbb{R}}^{ + }$ of a continuous function $f:{\mathbb{R}}^{ + } \to {\mathbb{R}}$ is presented by

$${}_{a}^{RL} I_{t}^{\alpha } = \frac{1}{{\Gamma \left( \alpha \right)}}\int\limits_{a}^{t} {\left( {t - \tau } \right)^{\alpha - 1} f\left( \tau \right)d\tau } ,$$

(4)

in which ${}_{a}^{RL} I_{t}^{\alpha }$ is the RL integral of fractional-order operator, and $\Gamma (\, \cdot \,)$ is the Euler gamma function.

Definition 3

(Podlubny 1998) According to the Definition 2, the RL fractional derivative operator is expressed by

$${}_{a}^{RL} D_{t}^{\alpha } = \frac{{d^{n} }}{{dt^{n} }}\left\{ {{}_{a}^{RL} I_{t}^{n - \alpha } f(t)} \right\} = \frac{{d^{n} }}{{dt^{n} }}\left\{ {\frac{1}{{\Gamma \left( {n - \alpha } \right)}}\int\limits_{a}^{t} {\left( {t - \tau } \right)^{n - \alpha - 1} f\left( \tau \right)d\tau } } \right\},$$

(5)

where ${}_{a}^{RL} D_{t}^{\alpha }$ is the RL derivative of fractional order operator, and $n = \left\lceil \alpha \right\rceil = \hbox{min} \left\{ {\left. {x \in Z} \right|x \ge \alpha } \right\}$.

Practical problems require definitions of fractional derivatives allowing the utilization of physically interpretable initial conditions. Unfortunately, the RL approach leads to apply initial conditions which are practically useless, and consequently causes to conflict between the well-established and polished mathematical theory and practical needs. A certain solution to this conflict was Caputo’s definition which proposed by Michele Caputo as follows (Caputo 1966):

Definition 4

(Diethelm 2010) Based on Definition 2, the Caputo fractional derivative operator is defined by

$${}_{a}^{C} D_{t}^{\alpha } = {}_{a}^{RL} I_{t}^{n - \alpha } \left\{ {\frac{{d^{n} }}{{dt^{n} }}f(t)} \right\} = \left\{ {\frac{1}{{\Gamma \left( {n - \alpha } \right)}}\int\limits_{a}^{t} {\left( {t - \tau } \right)^{n - \alpha - 1} \frac{{d^{n} }}{{dt^{n} }}f\left( \tau \right)d\tau } } \right\},$$

(6)

where ${}_{a}^{C} D_{t}^{\alpha }$ is the Caputo derivative of fractional order operator and $n$ is defined as same as Definition 3.

All these three approaches provide an interpolation among integer-order derivatives, and their definitions must reach to the same results during steady-state dynamical processes studies.

The initial value problem of a time invariant fractional-order differential equation (FODE) model related to Definition 4 is

$$\left\{ {\begin{array}{*{20}l} {{}_{0}^{C} D_{t}^{\alpha } x(t) = F\left( {x(t)} \right),} \hfill \\ {\left. {x(t)} \right|_{{t = 0^{ + } }} = X_{0} ,} \hfill \\ \end{array} } \right.$$

(7)

in which $x(t) \in {\mathbb{R}}^{n}$ and $F:{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}$. The stability theorem on nonlinear fractional-order system (7) has been introduced below.

Theorem 1

(Petras 2011) Consider the nonlinear autonomous commensurate fractional-order system ( 7 ). The equilibrium points of this system can be calculated by solving the equation $f(x) = 0$. This system is locally asymptotically stable if all eigenvalues $\lambda_{i}$ ($i = 1, \cdots ,n$) of the Jacobian matrix $J = \partial f/\partial x$ evaluated at the equilibrium points lie in the stable regions of $R_{s}^{\alpha }$ (Fig. 1).

Fig. 1

Stability ($R_{s}^{\alpha } \,:\,\, = \left\{ {\lambda |\,\,\,|\arg (\lambda )| > \alpha \pi /2,\lambda \in {\mathbb{C}}} \right\}$) and instability ($R_{is}^{\alpha } :\,\, = \{ \lambda |\,\,\,|\arg (\lambda )| < \alpha \pi /2,\,\,\lambda \in {\mathbb{C}}\}$) regions of a fractional-order system

2.2 FOS Systems

Singular systems are general kind of equations, which have been investigated during three past decades and established according to relationships among the variables based on differential or algebraic equations that form the mathematical model of the system. As a valuable tool, the theory of these systems has been widely utilized in different fields including modeling and analysis of nonlinear electric and electronic circuits, constrained mechanics, networks and economy (Podlubny 1998).

Since the 1960s, much research has been extensively focused on analysis of a dynamical system with the state-space variable method as a core feature in modern control theory. The concept of state in a dynamic system refers to a minimum set of variables, and state-space variable method provides us with a completely new method for system analysis and offers us more understanding of systems. Using this method, state-space models of a time-varying nonlinear singular system are obtained as (1). This suitable representation can describe systems that evolve over time, especially; nonlinear singular systems which are the natural outcome of component-based modeling of complex dynamic systems.

If $H$ and $J$ are linear functions of $x(t)$ and $u(t)$, another special form of the system (1) is a time-varying linear singular system as

$$\begin{aligned} E(t)\dot{x}(t) & = A(t)x(t) + B(t)u(t), \\ y(t) & = C(t)x(t), \\ \end{aligned}$$

(8)

where $x(t) \in {\mathbb{R}}^{n}$, $y(t) \in {\mathbb{R}}^{r}$, $u(t) \in {\mathbb{R}}^{m}$, and $E(t) \in {\mathbb{R}}^{n \times n}$, $A(t) \in {\mathbb{R}}^{n \times n}$, $B(t) \in {\mathbb{R}}^{n \times m}$, and $C(t) \in {\mathbb{R}}^{r \times n}$ are time-varying matrices. Here, for singular systems mentioned above, matrix $E$ is considered to be singular, i.e., $rankE = r < n$, otherwise, the system (1) and (8) reduce to a standard (normal) system. In practical system analysis and control system design, many system models may be established in the form of (8), while they could not be described by standard forms (Campbell 1980).

Under the regularity assumption,¹ the state and output responses of singular system is derived, and it has been demonstrated that unlike standard system theory, the singular system (8) has a unique solution only for the consistent initial vector $x(0)$, and for the $h$ times piecewise continuously differentiable input function $u(t)$, where $h$ is the nilpotent index. Also, by using time domain analysis, a fair understanding of the system’s structural features and its internal properties such as reachability, controllability, observability, system decomposition, and transfer matrix were obtained (Duan 2010).

Compared with the standard systems, the price paid is that singular systems are more difficult to deal with. However, the advantage they offer over the more often used standard systems is that they are generally easier to formulate and exhibit more complicated dynamics and have been applied widely in different fields of electrical engineering (Ayasun et al. 2004; Marszalek et al. 2005; Yue and Schlueter 2004), aerospace engineering (Masoud et al. 2006), biology (Zhang et al. 2012), chemical processes (Kumar and Daoutidis 1999) and economics (Zhang 1990; Luenberger and Arbel 1997). With the help of singular model for the systems in mentioned fields, complex dynamical behaviors of them, especially the bifurcation phenomena, which can reveal the instability mechanism of systems, have been extensively studied. However, as far as the FOS system theory is concerned, the related research results are few.

Very recently, the study on FOS systems has received much attention due to the fact that the fractional order calculus has contributed great merits, particularly in non-short memory and non-local property of describing physical systems, especially in power systems and biology (Kaczorek and Rogowski 2015; Nosrati and Shafiee 2017). These complicated systems requires considering not only stability, but also regularity and impulse elimination, while the latter do not appear in fractional-order standard ones. Although a number of valuable results and great achievements in the research about FOS systems have been reported in the literature (Yao et al. 2013; N’Doye et al. 2013; Ji and Qiu 2015; Zhang and Chen 2017), there are still many challenging and unsolved problems in the field of stability analysis and controller synthesis.

An initial value problem of a time invariant nonlinear FOS model related to Definition 4 is

$$\left\{ {\begin{array}{*{20}l} {E{}_{0}^{C} D_{t}^{\alpha } x(t) = F\left( {x(t)} \right),} \hfill \\ {\left. {x(t)} \right|_{{t = 0^{ + } }} = X_{0} ,} \hfill \\ \end{array} } \right.$$

(9)

where $x \in {\mathbb{R}}^{n}$ and $F:{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}$, and $E \in {\mathbb{R}}^{n \times n}$ is a singular matrix ($rankE = r < n$), and ${}_{0}^{C} D_{t}^{\alpha }$ denotes the Caputo derivative operator. If $F$ is linear function of $x(t)$, another special form of the system (9) is a time invariant linear FOS system

$$\left\{ {\begin{array}{*{20}l} {E{}_{0}^{C} D_{t}^{\alpha } x(t) = Ax\left( t \right),} \hfill \\ {\left. {x(t)} \right|_{{t = 0^{ + } }} = X_{0} ,} \hfill \\ \end{array} } \right.$$

(10)

where $A = \partial F/\partial x \in {\mathbb{R}}^{n \times n}$ is the jacobian matrix evaluated at the equilibrium points $\left( {F(x) = 0} \right)$. Parallel to fractional-order standard systems, the concerning basic definitions and relevant facts for the FOS system (10) are given as follows (Yao et al. 2013).

Definition 5

For FOS system (8), the triplet $(E,A,\alpha )$ is called regular if there exists a constant scalar $s_{0} \in {\mathbb{C}}$ such that $\left| {s_{0}^{\alpha } E - A} \right| \ne 0$.

Similar to the proof of regularity of integer order singular systems, the triplet $(E,A,\alpha )$ in FOS system (10) is regular if and only if there exist two nonsingular matrices $Q$ and $P$ such that $QEP = diag(I_{{n_{1} }} ,N)$ and $QAP = diag(A_{1} ,I_{{n_{2} }} )$ where $n_{1} + n_{2} = n$, $A_{1} \in {\mathbb{R}}^{{n_{1} \times n_{1} }}$, $N \in {\mathbb{R}}^{{n_{2} \times n_{2} }}$ is nilpotent. Assume the triplet $(E,A,\alpha )$ in FOS system (10) is regular, then, this system can be transformed into

$$\left\{ {\begin{array}{*{20}l} {{}_{0}^{C} D_{t}^{\alpha } x_{1} (t) = A_{1} x_{1} \left( t \right),} \hfill \\ {N{}_{0}^{C} D_{t}^{\alpha } x_{2} (t) = x_{2} \left( t \right),} \hfill \\ \end{array} } \right.$$

(11)

where $\left[ {\begin{array}{*{20}c} {x_{1}^{T} \left( t \right)} & {x_{2}^{T} \left( t \right)} \\ \end{array} } \right]^{T} = P^{ - 1} x\left( t \right)$, $x_{1} \left( t \right) \in {\mathbb{R}}^{{n_{1} }}$ and $x_{2} \left( t \right) \in {\mathbb{R}}^{{n_{2} }}$. The initial state response of FOS system (11) is

$$\left[ {\begin{array}{*{20}c} {x_{1} \left( t \right)} \\ {x_{2} \left( t \right)} \\ \end{array} } \right] = P\left[ {\begin{array}{*{20}c} {E_{\alpha ,1} \left( {A_{1} t^{\alpha } } \right)x_{1} \left( 0 \right)} \\ { - \sum\limits_{k = 1}^{h - 1} {\delta^{{\left( {\left( {k - 1} \right)\alpha } \right)}} \left( t \right)N^{k} x_{2} \left( 0 \right)} } \\ \end{array} } \right],\begin{array}{*{20}c} {} & {t \ge 0} \\ \end{array}$$

where $\delta \left( t \right)$ is the impulse function, and $E_{\alpha ,\beta } \left( t \right)$ is the two-parameter Mittag-Leffler function. From the derived response, we know that the triplet $(E,A,\alpha )$ is impulse-free if $N = 0$.

Let $\sigma (E,A,\alpha ) = \{ \lambda |\,\lambda \in {\mathbb{C}},\,\lambda \,{\text{finite}},|\lambda E - A|\, = 0\}$ denotes the finite pole set for FOS system (10). It can be easily known from Theorem 1 that the system (10) is asymptotically stable, if all the finite dynamic modes lie in the domain $R_{s}^{\alpha }$.

Remark 1

Consider the nonlinear autonomous commensurate FOS system (9). This system is locally asymptotically stable if all eigenvalues $\lambda_{i}$ ($i = 1, \cdots ,n$) of the Jacobian matrix $A = \partial F/\partial x$ evaluated at the equilibrium points, satisfy the relation $\left| {\arg (\lambda_{i} )} \right|_{i = 1, \cdots ,n} > \alpha \pi /2$. Also, to assess the stability analysis of the system (9), the roots of the equation $\left| {\lambda^{\alpha } I - A} \right| = 0$ evaluated at the equilibrium points can be checked regarding the imaginary axis.

Definition 6

The generalized eigenvectors $v$ satisfying $Ev = 0$ are defined as:

• (1) The infinite eigenvector of order one satisfies $Ev_{i}^{1} = 0$.

• (2) The infinite eigenvector of order $k$ satisfies $Ev_{i}^{1} = Av_{i}^{k - 1}$, $k > 1$.

Remark 2

Suppose that $Ev^{1} = 0$, then the infinite eigenvalues associated with the generalized principal vectors $v^{k}$ satisfying $Ev^{k} = v^{k - 1}$ are impulsive modes. The triplet $(E,A,\alpha )$ is impulse-free if and only if there exists no infinite eigenvector of order two.

Definition 7

FOS system (10) is said to be admissible, if the triplet $(E,A,\alpha )$ is regular, impulse-free, and all the finite eigenvalues of triplet $(E,A,\alpha )$ lie in the stable regions of $R_{s}^{\alpha }$.

System (9) is the general or fully-implicit nonlinear time-invariant FOS system. The dynamics of a large class of physical systems, including nonlinear circuits, robotics, and biological system, can be modeled by an important especial case of the system (9), called parameter dependent semi-explicit FOS system of the form

$${}_{0}^{C} D_{t}^{\alpha } z(t)\,\, = \,\,f(z(t),y(t),p)\quad f:{\mathbb{R}}^{n + m + q} \to {\mathbb{R}}^{n} ,$$

(12a)

$$0 = g(z(t),y(t),p)\quad {\text{g}}:{\mathbb{R}}^{n + m + q} \to {\mathbb{R}}^{m} ,$$

(12b)

where $z\,\, \in \,\,Z\,\, \subset \,\,{\mathbb{R}}^{n}$, $y \in Y\,\, \subset \,\,{\mathbb{R}}^{m}$ and $p \in P\,\, \subset \,\,{\mathbb{R}}^{q}$. In the state-space $Z\,\, \times \,\,Y$, dynamic state variables $z$ and instantaneous state variable $y$ are distinguished. The dynamics of the states $z$ are directly defined by (12a) while the dynamics of the $y$ variable in such that the system satisfies the constraints (12b). The parameters $p$ define a specific system configuration and the operating condition.

As an example, for the predator-prey system, typical dynamic state variables are time dependent values of population densities of the prey and predator, and instantaneous variable is harvest effort performed by a static human population. The parameter space is composed of system parameters such as capture rate, growth rate, carrying capacity, etc., and operating parameters such as net economic profit. The interactions between prey and predator define the f equations and the constraint $g = 0$ is defined by the economic interest equation.

Lemma 1

(Nosrati and Shafiee 2017) The characteristic polynomial of system ( 12a , 12b ) can be obtained by $|\lambda^{\alpha } I - J| = 0$ , where $I$ is the identity matrix, and

$$J = \frac{\partial f}{\partial z} + \frac{\partial f}{\partial y}(\frac{\partial g}{\partial y})^{ - 1} \frac{\partial g}{\partial z}.$$

(13)

Theorem 2

The FOS system ( 12a , 12b ) is stable if and only if the fractional degree characteristic polynomial

$$D(\lambda ) = \left| {\lambda^{\alpha } I - J} \right| = a_{0} \lambda^{{\alpha_{n} }} + a_{1} \lambda^{{\alpha_{n - 1} }} + \ldots + a_{n} \lambda^{{\alpha_{0} }} ,$$

(14)

with $\alpha_{n} = \alpha = n\alpha^{\prime}$ , i.e., this polynomial has no zero in the closed right-half of the Riemann complex surface, that is

$$D(\lambda ) \ne 0,\,{\text{for}}\,\text{Re} \,\lambda \ge 0.$$

(15)

It is assumed that the fractional order is commensurate, i.e., $\alpha_{i} = i\alpha^{{\prime }}$ , for $i = 0,1, \ldots ,n - 1$ , and $\alpha \in {\mathbb{R}}$.

Proof

It can be directly derived from Theorem 9.1 in (Kaczorek 2011).

Remark 3

The commensurate degree characteristic polynomial

$$D(\lambda ) = a_{0} \lambda^{{n\alpha^{{\prime }} }} + a_{1} \lambda^{{(n - 1)\alpha^{{\prime }} }} + \ldots + a_{n}$$

(16)

is stable if and only if all zeros of this polynomial satisfy the condition (15) or, equivalently, all zeros of the associated natural degree polynomial

$$\tilde{D}(s) = a_{0} s^{n} + a_{1} s^{(n - 1)} + \ldots + a_{1} s + a_{n}$$

(17)

for $s = \lambda^{{\alpha^{\prime}}}$, lie in the domain $R_{s}^{\alpha }$.

For the system (12a, 12b), the set of all equilibrium points (AEP) and the set of all stable equilibrium points (SEP) are defined as

$$AEP = \left\{ {\left( {{\text{z}},y,p} \right) \in Z \times Y \times P;f({\text{z}},y,p) = 0,\,g({\text{z}},y,p) = 0} \right\}$$

and

$$SEP = \left\{ {\left( {{\text{z}},y,p} \right) \in AEP;{ \det }(\,\frac{\partial g}{\partial y}) \ne 0\,and\,all\,eigenvalues\,of\,matrix\,J\,lie\,in\,R_{s}^{\alpha } } \right\},$$

respectively.

Note that the full Jacobian $J$ of the functions $f$ and $g$ in the $z$ and $y$ coordinates is nonsingular for all $(z,y,p) \in SEP$, and therefore, by the implicit function theorem, the equations $f(z,y,p) = 0$ and $g(z,y,p) = 0$ can theoretically be solved uniquely for $z$ and $y$ as functions of the parameter $p$, locally near any equilibrium point in $SEP$. Hence $SEP$ is a $p$-dimensional submanifold embedded in $AEP\,\, \subset \,\,Z\,\, \times \,\,Y\,\, \times \,\,P$.

Definition 8

Given a stable equilibrium $(z_{0} ,y_{0} )$ for parameter value $p_{0}$, the connected component $F$ of $SEP$ which contain $(z_{0} ,y_{0} ,\,\,p_{0} )$ is called the feasibility region of $(z_{0} ,y_{0} ,p_{0} )$, and its boundary is named feasibility boundary.

This definition provides a convenient mathematical apparatus for analyzing the local stability properties in the nonlinear semi-explicit FOS system (12a, 12b) in light of special nonlinear phenomena that may arise near the equilibrium point. The feasibility boundary for the large system can be solved for the common zeroes (zero sets) of three different sets of functions. These three zero sets are each connected with a special nonlinear property, which are equilibrium points at the singularity, proximity of multiple equilibrium points and birth of limit cycle for the nonlinear system (12a, 12b).

Theorem 3

(Extended Feasibility Boundary Theorem) For a system defined in (12a, 12b), the feasibility boundary of a feasibility region $F$ consists of three zero sets

$$\partial F = \left( {\partial F \cap C_{sib} } \right) \cup \left( {\partial F \cap C_{sn} } \right) \cup \left( {\partial F \cap C_{H} } \right),$$

where

$$\begin{aligned} C_{sib} & = \left\{ {\left( {{\text{z}},y,p} \right) \in AEP;\,\det \left( {\frac{\partial g}{\partial y}} \right) = 0} \right\}, \\ C_{sn} & = \left\{ {\left( {{\text{z}},y,p} \right) \in AEP;\,\det \left( {\frac{\partial g}{\partial y}} \right) \ne 0,\,\det \left( A \right) = 0} \right\} \\ \end{aligned}$$

and

$$C_{H} = \left\{ {\left( {{\text{z}},y,p} \right) \in AEP;\,\det \left( {\frac{\partial g}{\partial y}} \right) \ne 0,\,\det \left( A \right) \ne 0,\,\det \left( {H_{n - 1} (J)} \right) = 0} \right\},$$

where $H_{n - 1}$ is the Hurwitz matrix as

$$H_{n - 1} = \left( {\begin{array}{*{20}c} {a_{1} } & {a_{3} } & {a_{5} } & \ldots & {a_{2n - 3} } \\ {a_{2} } & {a_{4} } & {a_{6} } & \ldots & {a_{2n - 4} } \\ 0 & {a_{1} } & {a_{3} } & \ldots & {a_{2n - 5} } \\ 0 & {a_{2} } & {a_{4} } & \ldots & {a_{2n - 6} } \\ \vdots & \vdots & \vdots & {} & \vdots \\ 0 & 0 & 0 & \cdots & {a_{n - 1} } \\ \end{array} } \right)$$

corresponding to the coefficient $a_{i}$ of the following characteristic polynomial

$$D(\lambda ) = \left| {\lambda^{\alpha } I - J} \right| = a_{0} \lambda^{{\alpha_{n} }} + a_{1} \lambda^{{\alpha_{n - 1} }} + \ldots + a_{n} \lambda^{{\alpha_{0} }} .$$

Proof

The proof is in the analogous manner with the proof of Theorem 1 in (Venkatasubramanian et al. 1995).

3 Different Bifurcations and Chaos

As we have seen from (12a, 12b), systems of physical interest typically have parameters that appear in the defining systems of equations. As these parameters are varied, changes may occur in the qualitative structure of the solutions for certain parameter values. These changes are called bifurcations and the parameter values are called bifurcation values. The bifurcation theory provides a natural platform for studying the parameter space phenomena by establishing the dynamic mechanisms that effect changes in the system structure upon parameter variations. When the system parameters are varied, the dynamics of system (12a, 12b) changes continuously; however, topologically the structure remains unchanged under small perturbations provided the system is structurally stable. Structurally unstable points then identify the parameter values where the structure of system undergoes changes.

Systems of the form (12a, 12b) typically have singular points where the implicit function theorem for solving the constraint $g = 0$ is not applicable. When the constraint (12b) is absent, it can be shown that the feasibility boundary essentially corresponds to two of three different local bifurcations, namely, the saddle-node bifurcation, transcritical bifurcation, and Hopf bifurcation. For constrained models (12a, 12b), however, the feasibility boundary typically also contains another bifurcation segment named the singularity induced bifurcation (SIB) which occurs when the system equilibrium is at the singularity. When this happens, some of the system eigenvalues may become unbounded. In what follows, we describe four bifurcations of equilibrium points and give some theory for the local bifurcations of vector fields and maps. This section will be ended by some explanations about chaos, other possible types of equilibrium behaviors, which may occur in FOS systems.

3.1 Saddle-Node Bifurcation

The saddle-node bifurcation is well understood mathematically and has been much studied in different type of systems such as power system, biology etc. A saddle-node bifurcation occurs when a system has non-hyperbolic equilibrium with a geometrically simple zero eigenvalue at the bifurcation point and additional transversality conditions are satisfied (Sotomayor 1973). By definition, the points in the set $C_{sn}$ are not singular, i.e., $\det (\partial g/\partial y) \ne 0$. Therefore, by the implicit function theorem, we can reduce the system (12a, 12b) to fractional-order system

$${}_{0}^{C} D_{t}^{\alpha } z(t) = f_{R} (z(t),p)$$

(18)

locally near $(z_{0} ,y_{0} ,p_{0} )$ for a suitable and unique function $f_{R}$.

Then points in $C_{sn}$ are saddle-node bifurcations if the following conditions are satisfied:

• (a) The matrix $\frac{{\partial f_{R} }}{\partial z} = J = \frac{\partial f}{\partial z} + \frac{\partial f}{\partial y}(\frac{\partial g}{\partial y})^{ - 1} \frac{\partial g}{\partial z}$ has a geometrically simple zero eigenvalue with right eigenvector $v$ and left eigenvector $w$ and there is no other eigenvalue on the imaginary axis.

• (b) $w^{T} \left( {\frac{{\partial f_{R} }}{\partial p}} \right) = w^{T} \left( {\frac{\partial f}{\partial p} + \frac{\partial f}{\partial y}(\frac{\partial g}{\partial y})^{ - 1} \frac{\partial g}{\partial p}} \right) \ne 0$.

• (c) $w^{T} \left( {\frac{{\partial^{2} f_{R} }}{{\partial z^{2} }}\left( {v,v} \right)} \right) \ne 0$.

At this type of bifurcations, stable and unstable equilibrium points meet and disappear in the feasibility boundary, resulting in a loss of equilibrium points locally near the bifurcation point on the wrong side of the feasibility boundary. As an example, this can be represented by the differential equation $\dot{x} = p - x^{2}$ which depends on a single parameter $p$. The bifurcation diagram for this equation is depicted in Fig. 2a.

Fig. 2

Different bifurcations; a Saddle-node bifurcation b Transcritical bifurcation c Pitchfork bifurcation (supercritical) bifurcation d Hopf bifurcation

Hypotheses (b) and (c) are the transversality conditions that control the non-degeneracy of the behavior with respect to the parameter and the dominant effect of the quadratic nonlinear term. The results obtained from the conditions above are limited in two different ways. On the one hand, it is possible that more quantitative information about the flows near bifurcation can be extracted. The second limitation is that there may be global changes in a phase portrait associated with a saddle-node bifurcation.

3.2 Transcritical and Pitchfork Bifurcation

The importance of the saddle-node bifurcation is that all bifurcations of one parameter families at an equilibrium with a zero eigenvalue can be perturbed to saddle-node bifurcations. Thus, one expects that the zero eigenvalue bifurcations encountered in applications will be saddle-nodes. If they are not, then there is probably something special about the formulation of the problem that restricts the context so as to prevent the saddle-node from occurring. The transcritical bifurcation is one example that illustrates how the setting of the problem can rule out the saddle-node bifurcation (Hartman 2002; Kielhoefer 2004).

In classical bifurcation theory, it is often assumed that there is a trivial solution from which bifurcation occurs. Thus, the reduced system (18) is assumed to satisfy $f_{R} (0,p) = 0$ for all $p$, so that $z = 0$ is an equilibrium for all parameter values. Since the saddle-node families contain parameter values for which there are no equilibria near the point of bifurcation, this situation is qualitatively different. To formulate the appropriate transversality conditions, we look at the one-parameter families that satisfy the constraint that $f_{R} (0,p) = 0$ for all $p$. This prevents hypothesis (b) from being satisfied. If we replace this condition with the requirement that $w^{T} (\partial^{2} f_{R} /\partial p\partial z)(v) \ne 0$, then the phase portraits of the family near the bifurcation will be topologically equivalent to those of Fig. 2b and we have a transcritical bifurcation or exchange of stability.

As an example, the transcritical bifurcation can be represented by the normal form $\dot{x} = px - x^{2}$, which depend on a single parameter $p$ (Fig. 2b). This kind of bifurcation can be considered as an unfolding of the saddle-node bifurcation because if we apply the transformation $\zeta = x - p/2$ in the normal form, we obtain $\dot{\zeta } = p^{2} /4 - \zeta^{2}$ is a normal form of saddle-node bifurcation parameterized by $p$.

A second setting in which the saddle-node does not occur involves systems that have a symmetry. Many physical problems are formulated so that the equations defining the system do have symmetries of some kind. The reduced fractional-order system (18) is symmetric with respect to the symmetry $z \to - z$ if $f_{R} ( - z,p) = - f_{R} ({\text{z}},p)$. Thus, the symmetric vector fields are ones for which $f_{R}$ is an odd function of $z$. In particular, all such equations have an equilibrium at zero. The transcritical bifurcation cannot occur in these systems, however, because an odd function $f_{R}$ cannot satisfy the condition $\partial^{2} f_{R} /\partial z^{2} \ne 0$ required by the transcritical bifurcation hypothesis (c). If this condition is replaced by the hypothesis $\partial^{3} f_{R} /\partial z^{3} \ne 0$, then one obtains the pitchfork bifurcation. At the point of bifurcation, the stability of the trivial equilibrium changes, and a new pair of equilibrium points appear to one side of the point of bifurcation in parameter space, as in Fig. 2c. (The pitchfork bifurcation can be represented by the normal form $\dot{x} = px - x^{3}$).

3.3 Hopf Bifurcation

A Hopf bifurcation occurs at points where the system has non-hyperbolic equilibrium connected with a pair of purely imaginary eigenvalues, but no zero eigenvalues, and additional transversality conditions are met (Guckenheimer and Holmes 1983). As an example, the Hopf bifurcation can be represented by the following normal form, which depends on a single parameter $p$ (Fig. 2d).

$$\left\{ {\begin{array}{*{20}l} {\dot{x} = - y + x(p - (x^{2} + y^{2} )),} \hfill \\ {\dot{y} = x + y(p - (x^{2} + y^{2} )).} \hfill \\ \end{array} } \right.$$

One of the basic differences between dynamical behavior of fractional-order systems and integer-order systems is that the limit set of a trajectory of integer-order system as the limit cycle of this system is a solution for this system, but in the fractional-order case, the limit set of a trajectory of fractional-order system can be, not a solution for this system (Tavazoei et al. 2009a, b). In (Tavazoei et al. 2009a, b), the authors claimed there are no periodic orbits in fractional order systems, and in (Tavazoei 2010), the authors gave an example where the solutions of the system are not periodic, but they converge to periodic signals. In (Abdelouahab et al. 2012), the authors were interested about the final state of trajectory, and it has been demonstrated that chaos, as well as the other usual nonlinear dynamic phenomena, occur in this system with mathematical order less than three. The largest Lyapunov exponents and the bifurcation diagrams show the period-doubling bifurcation and the transformation from periodic to chaotic motion through the fractional-order and confirm the justness of the proposed fractional Hopf bifurcation conditions.

Let consider the following the reduced fractional-order commensurate system (18). Suppose that $z \in {\mathbb{R}}^{3}$, and $e^{*}$ is an equilibrium point of this system. In the integer case ($\alpha = 1$), the stability of $e^{*}$ is related to the sign of $\text{Re} (\lambda_{i} )$, $i = 1,2,3$, where $\lambda_{i}$ are the eigenvalues of Jacobian matrix $A = \partial f_{R} /\partial z|_{{e^{*} }}$. The conditions of system (18) with $\alpha = 1$, to undergo a Hopf bifurcation at the equilibrium point $e^{*}$ when $p = p^{*}$, are

• (a) The Jacobian matrix has two complex-conjugate eigenvalues $\lambda_{1,2} (p)\,\, = \,\,\theta (p)\,\, \pm \,\,i\omega (p)$, and one real $\lambda_{3} (p)$ (this can be expressed by $D(P_{{e^{*} }} (p^{*} )) < 0$, where $D$ is the discriminant of characteristic equation $P(\lambda ) = |\lambda I - A|$).

• (b) $\theta (p^{*} ) = 0$, and $\lambda_{3} (p^{*} ) \ne 0$.

• (c) $\omega (p^{*} ) \ne 0$.

• (d) $d\theta /dp|_{{p = p^{*} }} \ne 0$.

But in the fractional case, the stability of $e^{*}$ is related to the sign of $m_{i} (\alpha ,p) = \alpha \pi /2 - |\arg (\lambda_{i} (p))|$, $i = 1,2,3$. If $m_{i} (\alpha ,p) < 0$ for all $i = 1,2,3$, then $e^{*}$ is locally asymptotically stable. If there exist $i$ such that $m_{i} (\alpha ,p) > 0$, then $e^{*}$ is unstable. So, the function $m_{i} (\alpha ,p)$ has a similar effect as the real part of eigenvalue in integer systems, therefore, we extend the Hopf bifurcation conditions to the fractional systems by replacing $\text{Re} (\lambda_{i} )$ with $m_{i} (\alpha ,p) < 0$ as follows:

• (a) $D(P_{{e^{*} }} (p^{*} )) < 0$.

• (b) $m_{1,2} (\alpha ,p^{*} ) = 0$, and $\lambda_{3} (p^{*} ) \ne 0$.

• (c) $dm/dp|_{{p = p^{*} }} \ne 0$.

Hopf bifurcations are especially interesting for the large system because they signal the birth or the annihilation of periodic orbits for the system (12a, 12b) which are otherwise impossible to observe by purely numerical means.

3.4 Singularity Induced Bifurcation (SIB)

SIB is a new type of bifurcation which has been characterized by a singular system and refers to a stability change of the singular system possessing some eigenvalues which diverges to infinity (Venkatasubramanian et al. 1995). The result is impulse phenomenon of the singular system which may cause to the collapse of this system.

An SIB occurs when an equilibrium point $e^{*}$ crosses the singular surface

$$S := \left\{ {\left( {z,y,p} \right) \in {\mathbb{R}}^{n + m + q} ;\,g(z,{\text{y}},{\text{p}}) = 0,\,\Delta (z,{\text{y}},{\text{p}}):= { \det }\left( {\frac{\partial g}{\partial y}} \right) = 0} \right\},$$

that is a point in the zero set $C_{sib}$, and certain additional transversality conditions are satisfied at $(z,y,p)$:

• (a) $\partial g/\partial y$ has an algebraically simple zero eigenvalue, and

  $$trace\left. {\left( {\frac{\partial f}{\partial y}adj\left( {\frac{\partial g}{\partial y}} \right)\frac{\partial g}{\partial z}} \right)} \right|_{{e^{*} }} \ne 0.$$

• (b) The following two matrices are nonsingular in $e^{*}$.

  $$\left[ {\begin{array}{*{20}c} {\frac{\partial f}{\partial z}} & {\frac{\partial f}{\partial y}} \\ {\frac{\partial g}{\partial z}} & {\frac{\partial g}{\partial y}} \\ \end{array} } \right],\quad \left[ {\begin{array}{*{20}c} {\frac{\partial f}{\partial z}} & {\frac{\partial f}{\partial y}} & {\frac{\partial f}{\partial p}} \\ {\frac{\partial g}{\partial z}} & {\frac{\partial g}{\partial y}} & {\frac{\partial g}{\partial p}} \\ {\frac{{\partial\Delta }}{\partial z}} & {\frac{{\partial\Delta }}{\partial y}} & {\frac{{\partial\Delta }}{\partial p}} \\ \end{array} } \right].$$

Suppose the above conditions are satisfied at $(0,0,p_{0} )$, then there exists a smooth curve of equilibrium points in ${\mathbb{R}}^{n + m + 1}$ that passes through this point and is transversal to the singular surface at $(0,0,p_{0} )$. When $p$ increases through $p_{0}$, one eigenvalue of the system moves from ${\mathbb{C}}^{ + }$ to ${\mathbb{C}}^{ + }$ if $B/C > 0$ (respectively, from ${\mathbb{C}}^{ + }$ to ${\mathbb{C}}^{ + }$ if $B/C < 0$) along the real axis by diverging through infinity. The other $(n - 1)$ eigenvalues remain bounded and stay away from the origin. The constants $B$ and $C$ can be computed by

$$B = - trace\left( {\frac{\partial f}{\partial y}adj\left( {\frac{\partial g}{\partial y}} \right)\frac{\partial g}{\partial z}} \right),$$

and

$$C = \left( {\frac{{\partial\Delta }}{\partial p} - \left( {\begin{array}{*{20}c} {\frac{{\partial\Delta }}{\partial z}} & {\frac{{\partial\Delta }}{\partial y}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\partial f}{\partial z}} & {\frac{\partial f}{\partial y}} \\ {\frac{\partial g}{\partial z}} & {\frac{\partial g}{\partial y}} \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {\frac{\partial f}{\partial p}} \\ {\frac{\partial g}{\partial p}} \\ \end{array} } \right)} \right).$$

3.5 Chaotic Behavior

The asymptotic behavior of an autonomous dynamical system is uniquely specified by their initial conditions. Equilibrium point, limit cycle, torus and chaos are four possible types of equilibrium behaviors. A chaotic system is a deterministic system that exhibits irregular and unpredictable behavior (Giannakopoulos et al. 2002). Chaos occurs in many nonlinear systems, and its main characteristic is that system does not repeat its past behavior. In spite of their irregularity, chaotic dynamical systems follow deterministic equations (Baker and Gollub 1990). The unique characteristic of chaotic systems is dependence on the initial conditions sensitively. Slightly different initial conditions result in very different orbits. There are various methods for detecting chaos such as Poincare maps and Lyapunov exponents.

One-dimensional bifurcation diagrams of Poincare maps present information about the dependence of the dynamics on a certain parameter to gain preliminary insight into the properties of the dynamical system. The analysis reveal the type of attractor to which the dynamics will ultimately settle down after passing the initial transient phase and within which the trajectory will then remain forever. The dynamical behavior on a Poincare surface of section can be described by a discrete map whose phase-space dimension is less than that of the original continuous flow.

Moreover, the Lyapunov exponent is another approach to detect chaos, and it is a measure of the speeds at which initially nearby trajectories of the system diverge. The Lyapunov exponent is related to the predictability of the system, and the largest Lyapunov exponent of a stable system does not exceed zero. However, a chaotic system has at least one positive Lyapunov exponent, and the more positive the largest Lyapunov exponent, the more unpredictable the system is. Consistent with the idea that the chaotic attractor is globally stable, thus the sum of all Lyapunov exponents of a chaotic system will be negative.

4 Bifurcation Analysis and Chaotic Behaviors of FOS Biological Models

As it mentioned in Sect. 1, fractional-order modeling has recently garnered a lot of attention and gained popularity in the evaluation of dynamical systems due to its ability to provide an exact description of different nonlinear phenomena and inherent relation to various materials and processes with memory and hereditary properties. It allows greater degrees of freedom in the model and is closely related to fractals which are abundant in integer-order descriptions of biological systems and describes the whole time domain for a physical process, while the integer-order derivative is related to the local properties of a certain position and indicates a variation or certain attribute at particular time. According to these reasons, fractional-order modeling of many real phenomena especially biological systems has more advantages and consistency rather than classical integer-order mathematical modeling.

In 1954, Gordon investigated the economic theory of natural resource utilization in fishing industry, and discussed the effects of harvest effort on its ecosystem (Gordon 1954). The harvest can be affected by numerous factors such as seasonality, revenue, market demand and harvest cost, and then, it’s reasonable to consider the harvest effort as a variable from the real point of view, and consequently harvest function $h(t)$ can be expressed by $h(t) = x(t)y(t)$, where $x(t)$ is the harvest effort performed by a static human population, and $y(t)$ is a harvested specious in a considered ecosystem. Finally, he proposed the following algebraic equation to study the economic interest of the yield of harvest effort in his theory of a common-property resource:

$$ph(t) - cx(t) = m$$

(19)

where $m$ represents the net economic profit, $ph(t)$ is total revenue and $cx(t)$ is total cost, where $p$ and $c$ are the price of a unit of the harvested biomass and the cost of a unit of the effort, respectively (Gordon 1954).

In line with this theory, differential-algebraic (singular) integer-order biological systems were proposed, and dynamic behaviors analysis was investigated to design some control strategies (Chakraborty et al. 2011; Zhang et al. 2012). Combining the economic theory of fishery resource with fractional calculus, some FOS biological economic models such as predator-prey models (Holling-II, Holling-Tanner and food web), logistic map and SEIR epidemic model will be introduced as follows, and their qualitative behaviors such as bifurcation and chaos will be illustrated.

4.1 Predator-Prey Models

The last few decades have been active in the development of different kinds of predator–prey model within the traditional territory of population biology. Most studies of generalists have focused on their functional response, and many authors have explored the dynamics of predator-prey systems based on type-II, Holling-Tanner and Leslie-Grower functional responses. In recent years, there was a growing interest in the research field of the predator-prey with multi-species (especially one predator and two prey) which is called food web systems, and rich dynamical behavior has been found in such a system (Gakkhar and Singh 2007; Gakkhar and Naji 2003). Here, we explain the most popular predator-prey model with Holling type-II functional response, and its FOS model will be investigated in details. We only introduce the FOS models of Holling-Tanner and food web and neglect their detail analysis which can be expressed in an analogous manner.

4.1.1 Model Formulation and Qualitative Analysis

Freedman introduced the most popular predator-prey model with the Holling type-II functional response $\beta x_{1} (t)x_{2} (t)/(1 + \sigma x_{1} (t))$, where $x_{1}$ and $x_{2}$ are the population densities of the prey and predator, respectively (Freedman 1980). $\beta$ is the feeding rate, and $\sigma$ is a positive constant that explains the effects of capture rate. The interactions between prey and predator take the form with the following ordinary differential equations:

$$\begin{aligned} \frac{{dx_{1} (t)}}{dt} & = rx_{1} (t)\left( {1 - \frac{{x_{1} (t)}}{K}} \right) - \frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}}, \\ \frac{{dx_{2} (t)}}{dt} & = \frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}} - ax_{2} (t), \\ \end{aligned}$$

(20)

where $a$ is a positive real number and the logistic growth $rx_{1} (t)(1 - x_{1} (t)/K)$ is assumed to be the prey host population with carrying capacity $K$ and a specific growth rate constant $r$.

Using the fractional calculus and the economic theory, the integer-order standard predator-prey model (20) can be extended based on the algebraic economic interest Eq. (19), and accordingly, the proposed FOS model of the predator-prey system which consists of two fractional-order differential equations and one algebraic equation can take the following form (Nosrati and Shafiee 2017):

$$\left\{ \begin{aligned} {}_{0}^{C} D_{t}^{\alpha } x_{1} (t) & = rx_{1} (t)\left( {1 - \frac{{x_{1} (t)}}{K}} \right) - \frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}}, \\ {}_{0}^{C} D_{t}^{\alpha } x_{2} (t) & = \frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}} - ax_{2} (t) - h(t), \\ 0 & = x_{3} (t)(px_{2} (t) - c) - m,\quad t \ge 0. \\ \end{aligned} \right.$$

(21)

The system (21) can also be written as the FOS system (9), where $F:{\mathbb{R}}^{3} \to {\mathbb{R}}^{3}$, $x(t) \in {\mathbb{R}}^{3}$ and the matrix $E \in {\mathbb{R}}^{3 \times 3}$ have the following forms:

$$x(t) = \left[ {\begin{array}{*{20}c} {x_{1} (t)} \\ {x_{2} (t)} \\ {x_{3} (t)} \\ \end{array} } \right],\quad E = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],\quad F = \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {rx_{1} (t)\left( {1 - \frac{{x_{1} (t)}}{K}} \right) - \frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}}} \\ {\frac{{\beta x_{1} (t)x_{2} (t)}}{{1 + \sigma x_{1} (t)}} - ax_{2} (t) - x_{3} (t)x_{2} (t)} \\ {x_{3} (t)(px_{2} (t) - c) - m} \\ \end{array} } \right].$$

As seen, the system (21) is in form of the semi-explicit FOS system (12a, 12b) in which $z(t) = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right]^{T}$, $y(t) = x_{3} (t)$, $f = \left[ {\begin{array}{*{20}c} {f_{1} } & {f_{2} } \\ \end{array} } \right]^{T}$, $g = f_{3}$.

Theorem 4

(Nosrati and Shafiee 2017) The FOS model of predator-prey system ( 21 ) is solvable if $x_{2} \ne c/p$.

The main objective is to investigate the local stability of the system (21) based on singular system, bifurcation theories and the effects of economic profit on dynamics of this system in which will be discussed in the region $R_{ + }^{3} = \{ (x_{1} ,x_{2} ,x_{3} )|x_{i} \ge 0,\,i = 1,2,3\}$ as an admissible space.

When $m = 0$ , there exist following six equilibrium points $X_{i}^{*} = (\begin{array}{*{20}c} {{}_{i}x_{1}^{*} } & {{}_{i}x_{2}^{*} } & {{}_{i}x_{3}^{*} } \\ \end{array} )^{T}$ ($i = 1,2, \ldots ,6$) for the system ( 21 ):

$$X_{1}^{*} = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right),X_{2}^{*} = \left( {\begin{array}{*{20}c} K \\ 0 \\ 0 \\ \end{array} } \right),X_{3}^{*} = \left( {\begin{array}{*{20}c} {\frac{a}{\beta - a\sigma }} \\ {\frac{ - r(a - k(\beta - a\sigma ))}{k(\beta - a\sigma )}} \\ 0 \\ \end{array} } \right),X_{4}^{*} = \left( {\begin{array}{*{20}c} 0 \\ {\frac{c}{p}} \\ { - a} \\ \end{array} } \right),X_{5}^{*} = \left( {\begin{array}{*{20}c} {{}_{5}x_{1}^{*} } \\ {\frac{c}{p}} \\ {{}_{5}x_{3}^{*} } \\ \end{array} } \right),X_{6}^{*} = \left( {\begin{array}{*{20}c} {{}_{6}x_{1}^{*} } \\ {\frac{c}{p}} \\ {{}_{6}x_{3}^{*} } \\ \end{array} } \right)$$

where ${}_{5}x_{1}^{*}$ and ${}_{6}x_{1}^{*}$ (${}_{5}x_{1}^{*} \le {}_{6}x_{1}^{*}$) are roots o f the equation $pr\sigma x_{1}^{2} + pr(1 - k\sigma )x_{1} + K(\beta c - pr) = 0$ , and also, ${}_{5}x_{3}^{*} = - a + \beta {}_{5}x_{1}^{*} /(1 + \sigma {}_{5}x_{1}^{*} )$ and ${}_{6}x_{3}^{*} = - a + \beta {}_{6}x_{1}^{*} /(1 + \sigma {}_{6}x_{1}^{*} )$.

Regarding any positive parameters and admissible space definition, all these points can be admissible except $X_{4}^{*}$ which is always negative. To assess the stability analysis of the system (21), using Remark 3 and Lemma 1, the argument eigenvalues of Jacobian matrix $J$ evaluated at the admissible equilibrium points will be checked respect to $\alpha \pi /2$.

Obviously, the equilibrium point $X_{1}^{*}$ is saddle node. The eigenvalues of system (21) at equilibrium point $X_{2}^{*}$ are $\lambda_{1} = - r$ and $\lambda_{2} = - a + \beta K/(1 + \sigma K)$. Using Remark 3, $\lambda_{1}$ is always stable, since $|\arg (\lambda_{1} )| = \pi > \alpha \pi /2$, and the stability of $\lambda_{2}$ changes under parameter variation:

$$\left| {\arg (\lambda_{2} )} \right| = \left\{ {\begin{array}{*{20}c} {0 < \frac{\alpha \pi }{2}\quad if\;\beta K > a(1 + \sigma K)\quad \Rightarrow \quad unstable} \\ {\pi > \frac{\alpha \pi }{2}\quad if\;\beta K < a(1 + \sigma K)\quad \Rightarrow \quad stable} \\ \end{array} } \right..$$

According to the analysis illustrated above, the stability of equilibrium point $X_{2}^{*}$ changes from stable to unstable when $\beta$ increases through $a(1 + \sigma K)/K$. Then, $\beta$ can be regarded as a bifurcation parameter, and the following theorem can be extracted:

Theorem 5

(Nosrati and Shafiee 2017) The system ( 21 ) undergoes transcritical bifurcation at the equilibrium point $X_{2}^{*}$ when bifurcation parameter $\mu = \beta$ is increased through $a(1 + \sigma K)/K$.

Based on the results derived in Subsect. 3.2, it is adequate to check the following statements to prove the theorem:

• (1) $\left. {\frac{{\partial f_{1,2} }}{{\partial x_{1,2} }}} \right|_{{X_{2}^{*} }} = \left[ {\begin{array}{*{20}c} { - r} & { - a} \\ 0 & 0 \\ \end{array} } \right]$, then $\left| {\lambda I - {{\partial f_{1,2} } \mathord{\left/ {\vphantom {{\partial f_{1,2} } {\partial x_{1,2} }}} \right. \kern-0pt} {\partial x_{1,2} }}} \right|_{{X_{2}^{*} }}$ has a simple zero eigenvalue with right eigenvector $v = \left( {\begin{array}{*{20}c} 1 & { - r/a} \\ \end{array} } \right)^{T}$ and left eigenvector $w = \left( {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right)$.

• (2) $w\left( {\left. {\frac{{\partial^{2} f_{1,2} }}{{\partial \mu \partial x_{1,2} }}} \right|_{{X_{2}^{*} }} } \right)v \ne 0$.

• (3) $w(\left. {\frac{{\partial^{2} f_{1,2} }}{{\partial^{2} x_{1,2} }}} \right|_{{X_{2}^{*} }} )(v,v) \ne 0$.

At the equilibrium point $X_{3}^{*}$, it is easy to check under different parameter values, this equilibrium point can be stable focus or node. The equilibrium points $X_{5}^{*}$ and $X_{6}^{*}$ are at the singularity, and after that, the matrix $J$ is not well defined because $\partial f_{3} /\partial x_{3}$ is singular. Therefore, the matrix $J$ might have some unbounded eigenvalues, and subsequently, the system (21) may show SIB behavior. Based on following theorem, the system (21) has a SIB at equilibrium points $X_{5}^{*}$ and $X_{6}^{*}$ when the bifurcation parameter $m$ is zero. If $m$ increases through zero, one eigenvalue of the system (21) evaluated at these equilibrium points will move from an open complex half plane to other open complex half plane along the real axis by diverging into infinity. The other eigenvalue remains bounded and stays away from the origin.

Theorem 6

(Nosrati and Shafiee 2017) Assume $\partial f_{1} /\partial x_{1} |_{{X_{5}^{*} ,X_{6}^{*} }} \ne 0$. The FOS model of predator-prey system ( 21 ) has an SIB at the equilibrium points $X_{5}^{*}$ and $X_{6}^{*}$ when the bifurcation parameter $m$ increases through zero. Besides, the stability of the equilibrium points varies from stable to unstable.

Suppose $\Upsilon = \partial f_{3} /\partial x_{3} = px_{2} (t) - c$. According to the results, we have

• (1) $\Upsilon |_{{X_{5}^{*} ,X_{6}^{*} }}$ has a simple zero eigenvalue, and

• (2) $\left. {\left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1,2} }}{{\partial x_{1,2} }}} & {\frac{{\partial f_{1,2} }}{{\partial x_{3} }}} \\ {\frac{{\partial f_{3} }}{{\partial x_{1,2} }}} & {\frac{{\partial f_{3} }}{{\partial x_{3} }}} \\ \end{array} } \right]} \right|_{{X_{5}^{*} ,X_{6}^{*} }} = c(r - \frac{{2r{}_{5,6}x_{1}^{*} (t)}}{K} - \frac{\beta c}{{p(1 + \sigma {}_{5,6}x_{1}^{*} (t))^{2} }}){}_{5,6}x_{3}^{*} (t)(t) \ne 0$

  and

  $$\left. {\left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1,2} }}{{\partial x_{1,2} }}} & {\frac{{\partial f_{1,2} }}{{\partial x_{3} }}} & {\frac{{\partial f_{1,2} }}{\partial \mu }} \\ {\frac{{\partial f_{3} }}{{\partial x_{1,2} }}} & {\frac{{\partial f_{3} }}{{\partial x_{3} }}} & {\frac{{\partial f_{3} }}{\partial \mu }} \\ {\frac{{\partial\Upsilon }}{{\partial x_{1,2} }}} & {\frac{{\partial\Upsilon }}{{\partial x_{3} }}} & {\frac{{\partial\Upsilon }}{\partial \mu }} \\ \end{array} } \right]} \right|_{{X_{5}^{*} ,X_{6}^{*} }} = c(r - \frac{{2r{}_{1}x_{5,6}^{*} (t)}}{K} - \frac{\beta c}{{p(1 + \sigma {}_{1}x_{5,6}^{*} (t))^{2} }}) \ne 0.$$

Therefore, there exists stability change of the equilibrium points $X_{5}^{*}$ and $X_{6}^{*}$ when $m$ increases through zero; i.e., one eigenvalue of the system (eigenvalue of Jacobian matrix $J$ evaluated along the equilibrium locus related to $X_{5}^{*}$ and $X_{6}^{*}$) moves from one half plane to other half plane. On the other hand, $B = px_{2} (t)x_{3} (t)|_{{X_{5}^{*} ,X_{6}^{*} }}$, and $C = (1/px_{3} (t))|_{{X_{5}^{*} ,X_{6}^{*} }}$. Regarding the admissibility space, $B > 0$ and $C > 0$. After that, when $\mu$ increases through zero, this eigenvalue of the system moves from left half plane to right half plane along the real axis by diverging into infinity because $B/C > 0$. The other eigenvalue maintains bounded and stays away from the origin in left half plane. Thus, the stability of system (21) changes from stable to unstable at the equilibrium points $X_{5}^{*}$ and $X_{6}^{*}$ when the economic profit increases through zero. This completes the proof. □

A complete analysis on this system under positive economic profit can be seen in (Nosrati and Shafiee 2017).

4.1.2 Numerical Simulation

In order to solve (21), the method introduced by Atanackovic and Stankovic can be used. Atanackovic and Stankovic showed that for a function $f(t)$, the Caputo fractional derivative of order $\alpha$ may be expressed as

$${}_{0}^{C} D_{t}^{\alpha } f(t) \simeq\Omega \left( {\alpha ,t,M} \right)\dot{f}(t) +\Phi \left( {\alpha ,t,M} \right)f(t) + \sum\limits_{n = 2}^{M} {A\left( {\alpha ,t,M} \right)\frac{{v_{n} \left( f \right)(t)}}{{t^{n - 1 + \alpha } }}} ,$$

(22)

where

$A\left( {\alpha ,t,M} \right) = - \frac{{\Gamma \left( {n - 1 + \alpha } \right)}}{{\Gamma \left( {2 - \alpha } \right)\Gamma \left( {\alpha - 1} \right)\left( {n - 1} \right)!}}$, $\Omega \left( {\alpha ,t,M} \right) = \frac{1}{{\Gamma \left( {2 - \alpha } \right)t^{\alpha - 1} }} + \sum\limits_{n = 1}^{M} {\frac{{A\left( {\alpha ,t,n} \right)}}{{nt^{\alpha - 1} }}}$, $\Phi \left( {\alpha ,t,M} \right) = \frac{1 - \alpha }{{t^{\alpha }\Gamma \left( {2 - \alpha } \right)}} + \sum\limits_{n = 2}^{M} {\frac{{A\left( {\alpha ,t,n} \right)}}{{t^{\alpha } }}}$ and $v_{n} \left( f \right)(t) = - \left( {n - 1} \right)\int_{o}^{t} {\tau^{n - 2} } f\left( \tau \right)d\tau$, $n = 2,3, \ldots$ (Atanackovic and Stankovic 2004). Thus, the system (21) can be expressed by

$$E^{{\prime }} \dot{x}^{{\prime }} (t,n) = F^{{\prime }} \left( {x^{{\prime }} (t,n)} \right),\quad 0 < \alpha < 1,\quad n = 2,3, \ldots ,M,\quad t \ge 0,$$

(23)

where $x^{{\prime }} (t,n) = \left[ {\begin{array}{*{20}c} {x_{1} (t)} & {w^{n} (t)} & {x_{2} (t)} & {\begin{array}{*{20}c} {u^{n} (t)} & {x_{3} (t)} \\ \end{array} } \\ \end{array} } \right]^{T}$, and also, $F^{{\prime }} :{\mathbb{R}}^{5} \to {\mathbb{R}}^{5}$ and $E^{'} \in {\mathbb{R}}^{5 \times 5}$ have the following forms:

$$E = \left[ {\begin{array}{*{20}c} {I_{4} } & 0 \\ 0 & 0 \\ \end{array} } \right],\,F^{{\prime }} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {f_{1}^{'} } \\ {f_{2}^{'} } \\ \end{array} } \\ {f_{3}^{'} } \\ {f_{4}^{'} } \\ {f_{5}^{'} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{{\Omega \left( {\alpha ,t,M} \right)}}\left[ {f_{1} -\Phi \left( {\alpha ,t,M} \right)x_{1} (t) - \sum\limits_{n = 2}^{M} {A\left( {\alpha ,t,M} \right)\frac{{w_{n} (t)}}{{t^{n - 1 + \alpha } }}} } \right]} \\ { - \left( {n - 1} \right)t^{n - 2} x_{1} \left( t \right)} \\ \end{array} } \\ {\frac{1}{{\Omega \left( {\alpha ,t,M} \right)}}\left[ {f_{2} -\Phi \left( {\alpha ,t,M} \right)x_{2} (t) - \sum\limits_{n = 2}^{M} {A\left( {\alpha ,t,M} \right)\frac{{u_{n} (t)}}{{t^{n - 1 + \alpha } }}} } \right]} \\ { - \left( {n - 1} \right)t^{n - 2} x_{2} \left( t \right)} \\ {f_{3} } \\ \end{array} } \right]$$

Now, numerical solution of the singular ordinary differential system (23) will be considered to derive orbits of the FOS predator-prey system (21) for different set of parameters. For convenience, the simulation will be implemented using the fixed parameter values $r = 0.2$, $K = 5$, $\beta = 0.2$, $\sigma = 0.01$, $a = 0.2$, $p = 1.5$, $c = 1$, $M = 10$ and $m$ will be varied.

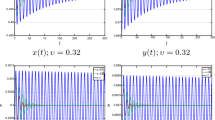
Numerical values of prey and predator, and also, phase portrait of the system (21) are presented in Figs. 3 and 4 for the set parameter values and two different values of $\beta$. As seen in Fig. 3, the trajectories of the system converge to the equilibrium point $X_{3}^{*}$ in steady state, and the equilibrium point $X_{2}^{*}$ is unstable because $\beta = 0.2 > 0.042$. In Fig. 4, the system (21) is simulated for $\beta = 0.041 < 0.042$. In this case, the equilibrium point $X_{3}^{*}$ is unstable, and the trajectories of the system converge to the equilibrium point $X_{2}^{*}$ in steady state which verifies the existence of transcritical bifurcation (Theorem 5). In all numerical runs, the solution has been approximated using the parameter values given in the captions of the figures.

Fig. 3

a Numerical value of $x_{1} (t)$ and $x_{2} (t)$ respect to time. b Phase portrait of system (21) ($\alpha = 0.8$, $\beta = 0.2$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.4$, $x_{3} (0) = 0.00025$, $m = 0$)

Fig. 4

a Numerical value of $x_{1} (t)$ and $x_{2} (t)$ respect to time. b Phase portrait of system (21) ($\alpha = 0.8$, $\beta = 0.041$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.4$, $x_{3} (0) = 0.00025$, $m = 0$)

The admissible equilibrium point $X_{5}^{*}$ is at the singularity. When economic profit $m = - 0.0001$, the eigenvalues are $\lambda_{1} = { - 193} . 8$ and $\lambda_{2} = { - 0} . 0 6 7$, and then become $\lambda_{1} = 1 9 1. 4$ and $\lambda_{2} = { - 0} . 0 6 6$ when the parameter value $m = 0.0001$. Obviously, $\lambda_{2}$ remains almost constant and $\lambda_{1}$ moves from the open complex left half plane to the open complex right half plane along the real axis by diverging through infinity. This verifies the Theorem 6 and demonstrates that the system (21) has an SIB at the equilibrium point $X_{5}^{*}$ when the bifurcation parameter $m = 0$.

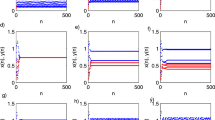
Numerical values of the system (21) are presented in Figs. 8 and 9 for two different economic profit values $m = - 0.0001$ and $m = 0.0001$. When $m = - 0.0001$, the equilibrium point $X_{5}^{*}$ is stable and the trajectories of system (21) converge to $X_{5}^{*}$ (Fig. 5). Besides the admissible equilibrium point $X_{5}^{*}$, there is another stable equilibrium point $X_{6}^{*}$ (related to $m < 0$) when the initial condition is varied. This equilibrium point is not admissible because the trajectory $x_{3} (t)$ converges to a negative point in steady state (Fig. 6). Also, when $m = 0.0001$, the stability of the equilibrium point $X_{5}^{*}$ changes to unstable, and therefore, trajectories of the system converge to $X_{6}^{*}$ (related to $m > 0$) (Fig. 7).

Fig. 5

a Numerical value of $x_{1} (t)$, $x_{2} (t)$ and $x_{3} (t)$ respect to time. b Phase portrait of system (21) ($\alpha = 0.8$, $\beta = 0.2$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.4$, $x_{3} (0) = 0.00025$, $m = - 0.0001$)

Fig. 6

a Numerical value of $x_{1} (t)$, $x_{2} (t)$ and $x_{3} (t)$ respect to time. b Phase portrait of system (21) ($\alpha = 0.8$, $\beta = 0.2$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.7$, $x_{3} (0) = - 0.002$, $m = - 0.0001$)

Fig. 7

a Numerical value of $x_{1} (t)$, $x_{2} (t)$ and $x_{3} (t)$ respect to time. b Phase portrait of system (21) ($\alpha = 0.8$, $\beta = 0.2$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.7$, $x_{3} (0) = 0.002$, $m = 0.0001$)

Furthermore, to explain the oscillation damping properties, the phase portrait of system (21) for three different values of $\alpha$ are given in Fig. 8, for two different values of $m$. The results show that, the fractional derivative damps the oscillation behavior of the model when $\alpha$ decreases, which leads to improve the stability.

Fig. 8

(Oscillation damping property). Phase portrait of system (21) respect to time a $m = 0$ b $m = 0.002$ ($\beta = 0.2$, $x_{1} (0) = 1.3$, $x_{2} (0) = 0.7$, $x_{3} (0) = 0.0025$)

It should be noted that using the fractional calculus and the economic theory, the integer-order standard predator-prey Holling-Tanner and web food models can be extended based on the algebraic economic interest Eq. (19), and accordingly, the proposed FOS model of these systems can take the (24) and (25), respectively.

$$\left\{ \begin{aligned} {}_{0}^{C} D_{t}^{\alpha } x_{1} (t) & = x_{1} (t)\left( {1 - x_{1} (t)} \right) - \frac{{x_{1} (t)x_{2} (t)}}{{\gamma + x_{1} (t)}} + \lambda (1 - cos\theta t)x_{1} (t), \\ {}_{0}^{C} D_{t}^{\alpha } x_{2} (t) & = x_{2} (t)(\delta - \beta \frac{{x_{2} (t)}}{{x_{1} (t)}}), \\ 0 & = x_{3} (t)(px_{2} (t) - c) - m,\quad t \ge 0. \\ \end{aligned} \right.$$

(24)

$$\left\{ \begin{aligned} {}_{0}^{C} D_{t}^{\alpha } x_{1} (t) & = x_{1} (t)\left( {1 - x_{1} (t) - \frac{{w_{2} x_{3} (t)}}{{1 + w_{3} x_{1} (t) + w_{4} x_{2} (t)}}} \right), \\ {}_{0}^{C} D_{t}^{\alpha } x_{2} (t) & = x_{2} (t)\left( {(1 - x_{2} (t)){\text{w}}_{5} - \frac{{w_{7} x_{3} (t)}}{{1 + w_{4} x_{2} (t) + w_{3} x_{1} (t)}}} \right), \\ {}_{0}^{C} D_{t}^{\alpha } x_{3} (t) & = x_{3} (t\left( {\frac{{w_{8} x_{1} (t) + w_{9} x_{2} (t)}}{{1 + w_{3} x_{1} (t) + w_{4} x_{2} (t)}} - {\text{w}}_{10} } \right) - {\text{w}}_{11} x_{3} (t) - x_{3} (t)x_{4} (t), \\ 0 & = x_{4} (t)x_{3} (t)(\frac{a}{{b + x_{4} (t)x_{3} (t)}} - \frac{d}{{x_{3} (t)}}) - m,\quad t \ge 0. \\ \end{aligned} \right.$$

(25)

where the parameters interpretation is mentioned in (Zhang et al. 2012). The systems (24) and (25) can also be written as the FOS system (9), and therefore, their analysis can be studied in a same analogous as the system (21) which are omitted in this study.

4.2 Logistic Map

The logistic model is widely used to investigate the growth law of various biological ecosystems such as some kind of single-cell, marine population, and birds and insects populations on continent (Clark 1990). Although many discussions have been applied on the behavior of integer-order standard logistic map (Alligood et al. 1997), fewer efforts have been contributed to the behaviors of the fractional-order and singular cases. For the famous logistic map

$$x_{k + 1} = r\,x_{k} \,(1 - \frac{{x_{k} }}{K})$$

(26)

popularized by May in (1976), the system exhibits chaotic behaviors for most values of the growth coefficient $r$. For the system (26), $x(k) > 0$ represents population density, $r > 0$ represents the intrinsic growth rate, and $K > 0$ represents the environment capacity.

In (Zhang et al. 2012), a discrete singular logistic system was proposed, and its dynamics were discussed. It was demonstrated that the model system bifurcates into periodical orbits and finally admits chaotic behavior under parameter variations. Also, in some literatures, it has been demonstrated that there is a discrete fractional logistic map which has a generalized chaos behavior (Munkhammar 2013; Wu and Baleanu 2014; Guckenheimer and Holmes 1983). These studies introduced a fractional discrete logistic map using the fractional-order difference in different senses. Compared with the one of the integer order, the fractional model has a discrete memory and a fractional difference order. When the difference order changes in the numerical results, new chaotic behaviors of the logistic map are observed. It has been demonstrated that the chaotic zones not only depends on the coefficients $r$ but the difference order. Although the chaos theory for discrete maps is well understood, how it is related to fractional calculus phenomena is perhaps less clarified and need a further investigation.

In this subsection, a discrete fractional-order singular logistic system is proposed, and the dynamics of the model system, especially chaotic behavior, are discussed.

4.2.1 Model Formulation

The growth law of various biological species is usually described by the classic logistic model (26). Compared with the continuous model, the dynamics of the discrete logistic model with one dimension are abundant. There are two fixed points for this system: $x_{1}^{*} = 0$ and $x_{2}^{*} = K$. Using these two real equilibrium points and the eigenvalues of the corresponding Jacobian matrix, the behavior of the system can be evaluated, and its rich dynamics can be derived when the parameter $r$ changes.

According to the Gordon theory and fractional calculus, the following discrete FOS system is proposed to investigate the dynamics of the logistic system and the economic interest of the harvest effort on its population:

$$E{}_{0}^{GL}\Delta _{k + 1}^{\alpha } x_{k + 1} = F(x_{k} )$$

(27)

where ${}_{0}^{GL}\Delta _{k}^{\alpha }$ denotes the GL difference operator, and $F:{\mathbb{R}}^{2} \to {\mathbb{R}}^{2}$, $x_{k} \in {\mathbb{R}}^{2}$ and the matrix $E \in {\mathbb{R}}^{2 \times 2}$ have the following forms:

$$\begin{array}{*{20}l} {x_{k} = \left[ {\begin{array}{*{20}c} {x_{1k} } \\ {x_{2k} } \\ \end{array} } \right],} \hfill & {E = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right],} \hfill & {F = \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {rx_{1k} \left( {1 - \frac{{x_{1k} }}{K}} \right) - x_{1k} x_{2k} } \\ {x_{2k} (px_{1k} - c) - m} \\ \end{array} } \right]} \hfill \\ \end{array} .$$

As seen, the system (27) is in the discrete form of the semi-explicit FOS system (12a, 12b) in which $z_{k} = \left[ {\begin{array}{*{20}c} {x_{1k} } & {x_{2k} } \\ \end{array} } \right]^{T}$, $y_{k} = x_{2k}$, $f = f_{1}$, $g = f_{2}$.

The fractional order GL difference is given by

$${}_{0}^{GL}\Delta _{k}^{\alpha } x_{k} = \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)x_{k - j} }$$

(28)

where $\alpha = diag\{ \alpha_{1} , \ldots ,\alpha_{n} \} \in {\mathbb{R}}^{n}$ is the real orders of the fractional difference, $h$ is the sampling interval, $k$ is the number of samples for which the derivative is calculated, and the coefficient

$$\left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right) = diag\left( {\left( {\begin{array}{*{20}c} {\alpha_{1} } \\ j \\ \end{array} } \right), \cdots ,\left( {\begin{array}{*{20}c} {\alpha {}_{n}} \\ j \\ \end{array} } \right)} \right)$$

is the extended form of integer-valued binomial coefficient developed by the gamma function idea, with

$$\left( {\begin{array}{*{20}c} {\alpha_{i} } \\ j \\ \end{array} } \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\,j = 0} \hfill \\ {\frac{{\Gamma \left( {\alpha_{i} + 1} \right)}}{{\Gamma \left( {\alpha_{i} + 1 - j} \right)\,.\,\Gamma \left( {j + 1} \right)}}} \hfill & {if\,j > 0} \hfill \\ \end{array} } \right.,$$

for $i = 1, \ldots ,n$. According to this definition, discrete equivalent of the fractional-order derivative and integration can be obtained when $\alpha$ is positive and negative, respectively.

For the FOS logistic system (27), $x_{1k}$, $r$ and $K$ share the same biological interpretations as in (26), and $x_{2k}$ represents the harvest effort on population, $p$ is the unit price of the harvested population, and $c$ is the united cost of the harvest effort.

4.2.2 Numerical Simulation

From (28), we can obtain the following equivalent difference equation form of the FOS logistic model (27):

$$\begin{aligned} x_{1(k + 1)} & = h^{\alpha } (rx_{1k} \left( {1 - \frac{{x_{1k} }}{K}} \right) - x_{1k} x_{2k} - \frac{1}{{h^{\alpha } }}\sum\limits_{j = 1}^{k + 1} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)x_{k + 1 - j} } ) \\ 0 & = x_{2k} (px_{1k} - c) - m\, \\ \end{aligned}$$

(29)

Compared with the map of the integer order (25), the fractionalized one (27) has a discrete kernel function. As seen from (29), the state $x_{1k}$ depends on the past information $x_{1(k - 1)} ,{\text{x}}_{1(k - 2)} , \ldots ,x_{1(0)}$. As a result, the memory effects of the discrete maps mean that their present state of evolution depends on all past states.

Assume $K = 8.05 \times 10^{7}$, $p = 5 \times 10^{ - 3}$, $c = 8.75 \times 10^{4}$, $m = 100$ and $h = 1$. We can derive the numerical solutions $x_{k}$ using the Matlab. In what follows, Figs. 9 and 10 show the numerical solutions for different $r$ and $\alpha$, for two slightly different initial conditions, one at $(0.5,0.2)$ and the other at $(0.5,0.2001)$. These graphs are nearly identical for a certain time period, but then they differ considerably. No matter how close two solutions start, they always move apart in this manner when they are close to the attractor. This is sensitive dependence on initial conditions, one of the main features of a chaotic system. In Fig. 9, for a fixed parameter $r = 2.8$, when the order $\alpha$ decreases, period doubling event occurs, and finally system undergoes to a chaotic behavior. Especially, Fig. 9c verifies the results obtained by the analysis of the integer-order singular logistic map introduced by Zhang et al. (2012) in which the proposed system showed the chaotic behavior when $r = 2.8$. Also, in Fig. 10, this simulation is repeated for a fixed parameter $r = 2.5$, and again we can see that when the order $\alpha$ decreases, period doubling event occurs, and again system undergoes to a chaotic behavior but this happens for a smaller order $\alpha$. Unlike Fig. 9c, as it can be seen from Fig. 10c, there is no chaotic behavior when $r = 2.5$ and $\alpha = 1$, which verifies the previous results obtained in literatures.

Fig. 9

The $x_{1k}$ and $x_{2k}$ graphs for two nearby initial conditions $(0.5,0.2)$ and $(0.5,0.2001)$ ($r = 2.8$)

Fig. 10

The $x_{1k}$ and $x_{2k}$ graphs for two nearby initial conditions $(0.5,0.2)$ and $(0.5,0.2001)$ ($r = 2.5$)

To discuss more precisely under parameters variations, the bifurcation diagrams of Poincare for model system (27) against variation of parameters $\alpha$ and $r$ are depicted in Figs. 11 and 12, respectively. As seen, the bifurcation diagram against variation parameter $\alpha$ moves from right to left of plane when the parameter value $r$ decreases (Fig. 11). It means that chaotic behavior happens for a smaller value of $\alpha$ when the parameter $r$ decreases. This can be seen from Fig. 13a in which the Lyaponuv exponent against variation parameter $\alpha$ gets positive for a smaller parameter value $r$. Also, the bifurcation diagram against variation parameter $r$ moves from left to right of plane when the parameter value $\alpha$ increases (Fig. 12). It means that chaotic behavior happens for a bigger value of $r$ when the parameter $\alpha$ increases. This can be seen from Fig. 13b in which the Lyaponuv exponent against variation parameter $r$ gets positive for a smaller parameter value $\alpha$.

Fig. 11

Bifurcation diagrams of Poincare for model system (27) against variation of parameter $\alpha$

Fig. 12

Bifurcation diagrams of Poincare for model system (27) against variation of parameter $r$

Fig. 13

Lyapunov Exponent diagram of the system (27) against variations of parameters a $\alpha$ and b $r$

There is a strange evolution in the bifurcation diagrams of the system (27) when the order $\alpha$ decreases (Fig. 11). This system exhibits stable equilibrium point behavior at first and undergoes to period doubling route to chaos and eventually enters to a chaotic space. When we continue the simulation while decreasing the order $\alpha$, the system (27) behaves in a reverse treatment and undergoes to inverse period doubling and is finished by stable equilibrium point. Figure 14 shows the $x_{1k}$ and $x_{2k}$ graphs for two nearby initial conditions and two parameter order values $\alpha = 0.05$ and $\alpha = 1.4$, and also, $r = 2.5$. It shows that system is stable out of a certain band of the parameter values $\alpha$, and when the order $\alpha$ increases (from left) and decreases (from right), from both sides the system undergoes to period doubling route to chaos in a reverse treatment.

Fig. 14

The $x_{1k}$ and $x_{2k}$ graphs for two nearby initial conditions ($r = 2.5$)

4.3 SEIR Epidemic System

Modeling of the population dynamics of infectious diseases has been playing an important role in better understanding epidemiological patterns, and many epidemic models have been proposed and analyzed in recent years to control of disease for a long time (Kermack and McKendrick 1927; Kot 2001; Li et al. 2001; May and Oster 1976). The primary models, which customarily called an SIR (susceptible-infectious-recovered) or SIRS (susceptible-infectious-recovered-susceptible) system, assumes that the disease incubation can be negligible that, once infected, each susceptible individual (in class S) becomes infectious instantaneously (in class I) and later recovers (in class R) with a permanent or temporary acquired immunity (Glendinning and Perry 1997; Greenhalgh et al. 2004).

To study the role of incubation in disease transmission, the systems that are more general than SIR or SIRS types need to be studied. Thus, the resulting models are of SEIR (susceptible-exposed-infectious-recovered) or SEIRS (susceptible-exposed-infectious-recovered-susceptible) types, respectively, depending on whether the acquired immunity is permanent or not, and many analysis such as the stability, bifurcation and chaos behavior of these epidemic systems have been studied (Kuznetsov and Piccardi 1994; Sun et al. 2007; Xu et al. 2005).

Although many epidemic systems were described by differential and algebraic equations (Zhang et al. 2007, Zhang and Zhang 2007), they were studied by reducing the dimension of epidemic models to differential systems, accordingly, the dynamical behaviors of the whole system were not better described. Via analysis of the whole system by singular model, one can find more complex dynamical behaviors if the SEIR epidemic system. In (Zhang et al. 2014), integer-order singular SEIR epidemic system with seasonal forcing in transmission rate was discussed, and hyper-chaotic behavior of this system and its control with the aim of elimination of the disease was illustrated.

Although a large amount of work has been done in modeling the dynamics of epidemiological diseases, it was restricted to integer-order differential equations and few works discussed an epidemics model with fractional-order case. It has been demonstrated the great properties of fractional calculus are very useful to model epidemics problems (Liu and Lu, 2014; Goufo et al. 2014; Rostamy and Mottaghi 2016). In recent years, it has turned out that SEIR system can be described very successfully by the model using fractional-order differential equations in which help us to reduce the errors arising from the neglected parameters in modeling (Ozalp and Demirci 2011; Area et al. 2015).

However, no literature discusses fractional-order singular SEIR epidemic system. To the best of our knowledge, chaotic behavior first appears in these systems based on this subsection. In what follows, the FOS model of SEIR epidemic system will be introduced, and the dynamical behaviors of the model will be analyzed.

4.3.1 Model Formulation

The Fractional-order singular SEIR epidemic model with nonlinear transmission rate is introduced as follows. At time $t$, the population of size $N(t)$ is divided into four subpopulation containing susceptible $S(t)$, exposed $E(t)$, infectious $I(t)$, and recovers $R(t)$. It is assumed that death and birth occur with the same constant rate, i.e. the population size is constant. Thus, the host total population is $N(t) = S(t) + I(t) + R(t) + E(t)$ at any time $t$. In addition, it is assumed that immunity is permanent and recovered individuals do not revert to the susceptible class, and also, all newborns are susceptible and there is a uniform birth rate.

The following fractional-order singular SEIR system is derived based on the basic assumptions:

$$\left\{ \begin{aligned} {}_{0}^{C} D_{t}^{\alpha } x_{1} (t) & = bx_{5} (t) - dx_{1} (t) - \beta \frac{{x_{1} (t)x_{3} (t)}}{{x_{5} (t)}} \\ {}_{0}^{C} D_{t}^{\alpha } x_{2} (t) & = \beta \frac{{x_{1} (t)x_{3} (t)}}{{x_{5} (t)}} - (\zeta + d)x_{2} (t) \\ {}_{0}^{C} D_{t}^{\alpha } x_{3} (t) & = \zeta x_{2} (t) - (\gamma + d)x_{3} (t) \\ {}_{0}^{C} D_{t}^{\alpha } x_{4} (t) & = \gamma x_{3} (t) - dx_{4} (t) \\ 0 & = x_{1} (t) + x_{2} (t) + x_{3} (t) + x_{4} (t) - x_{5} (t) \\ \end{aligned} \right.$$

(30)

where $x_{1} (t)$, $x_{2} (t)$, $x_{3} (t)$, $x_{4} (t)$ and $x_{5} (t)$ are the population $S(t)$, $E(t)$, $I(t)$, $R(t)$ and $N(t)$, respectively. Also, the parameter $b > 0$ is the rate for natural birth and $d > 0$ is the rate for natural death. The parameter $\zeta > 0$ is the rate at which the exposed individuals become infectious, and $\gamma > 0$ is the rate of recovery. The force of infection is $\beta x_{3} (t)/x_{4} (t)$, where $\beta > 0$ is effective per capita contact rate of infectious individuals and the incidence rate is $\beta x_{1} (t)x_{3} (t)/x_{4} (t)$.

The FOS system (30) can describe the whole behavior of certain epidemic spreads in a certain area. The first to fourth fractional-order differential equations of this system describe whole dynamical behaviors of every dynamic element and the last algebraic equation describes restriction of every dynamic element of system.

The transmission rate with seasonal forcing can be considered as $\beta = \beta_{0} (1 + \beta_{1} { \cos }(2\pi t))$, where $\beta_{0}$ is the base transmission rate, and $0 \le \beta_{1} \le 1$ measures the degree of seasonality. By utilizing some transformation as

$$x_{1}^{{\prime }} = \frac{{x_{1} }}{{x_{5} }},\,x_{2}^{{\prime }} = \frac{{x_{2} }}{{x_{5} }},\,x_{3}^{{\prime }} = \frac{{x_{3} }}{{x_{5} }},\,x_{4}^{{\prime }} = \frac{{x_{4} }}{{x_{5} }},$$

the system (30) can be attacked by studying the following subsystem:

$$\left\{ \begin{aligned} {}_{0}^{C} D_{t}^{\alpha } x_{1}^{{\prime }} (t) & = b - dx_{1}^{{\prime }} (t) - \beta x_{1}^{{\prime }} (t)x_{3}^{{\prime }} (t) \\ {}_{0}^{C} D_{t}^{\alpha } x_{2}^{{\prime }} (t) & = \beta x_{1}^{{\prime }} (t)x_{3}^{{\prime }} (t) - (\zeta + d)x_{2}^{{\prime }} (t) \\ {}_{0}^{C} D_{t}^{\alpha } x_{3}^{{\prime }} (t) & = \zeta x_{2}^{{\prime }} (t) - (\gamma + d)x_{3}^{{\prime }} (t) \\ 0 & = x_{1}^{{\prime }} (t) + x_{2}^{{\prime }} (t) + x_{3}^{{\prime }} (t) + x_{4}^{{\prime }} (t) - 1 \\ \end{aligned} \right.$$

(31)

The variable $x_{4}^{{\prime }}$ is described by the fractional-order differential equation $\gamma x_{3}^{{\prime }} (t) - dx_{4}^{{\prime }} (t)$ as well as algebraic equation $x_{4}^{{\prime }} (t) = 1 - x_{1}^{{\prime }} (t) - x_{2}^{{\prime }} (t) - x_{3}^{{\prime }} (t)$, and there is no the variable $x_{4}^{{\prime }}$ in the first to third equations of system (30). That is why the forth equation is removed.

The system (31) can also be written as the FOS system (9), where $F:{\mathbb{R}}^{4} \to {\mathbb{R}}^{4}$, $x(t) \in {\mathbb{R}}^{4}$ and the matrix $E \in {\mathbb{R}}^{4 \times 4}$ have the following forms:

$$x(t) = \left[ {\begin{array}{*{20}c} {x_{1} (t)} \\ {x_{2} (t)} \\ {x_{3} (t)} \\ {x_{4} (t)} \\ \end{array} } \right],\quad E = \left[ {\begin{array}{*{20}c} {I_{3} } & 0 \\ 0 & 0 \\ \end{array} } \right],\quad F = \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ {f_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {b - dx_{1}^{{\prime }} (t) - \beta x_{1}^{{\prime }} (t)x_{3}^{{\prime }} (t)} \\ {\beta x_{1}^{{\prime }} (t)x_{3}^{{\prime }} (t) - (\zeta + d)x_{2}^{{\prime }} (t)} \\ {\zeta x_{2}^{{\prime }} (t) - (\gamma + d)x_{3}^{{\prime }} (t)} \\ {x_{1}^{{\prime }} (t) + x_{2}^{{\prime }} (t) + x_{3}^{{\prime }} (t) + x_{4}^{{\prime }} (t) - 1} \\ \end{array} } \right].$$

As seen, the system (30) is in form of the semi-explicit FOS system (12a, 12b) in which $z(t) = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} } \right]^{T}$, $y(t) = x_{4} (t)$, $f = \left[ {\begin{array}{*{20}c} {f_{1} } & {f_{2} } & {f_{3} } \\ \end{array} } \right]^{T}$ and $g = f_{4}$.

4.3.2 Numerical Simulation

In this subsection, we consider two case of varying parameters $\beta_{1}$ and $\alpha$, and discuss the behaviors of the system (31) under these variations. In order to solve the proposed system, the method introduced by Atanackovic and Stankovic can be used similar to Sect. 4.1.2. The numerical results show that there is chaotic dynamical behavior for the FOS SEIR system (31) with $\beta_{1} = 0.28$ when the order $\alpha$ is equal to one. Also, for the case of varying parameter $\alpha$, the dynamical behaviors of system (31) are analyzed by simulation results, and it will be showed that the chaotic behavior occurs under different parameter value $\beta {}_{1}$.

Let $\beta {}_{1}$ be a varying parameter of (31), and the remaining parameters are as follows: $b = d = 0.02$, $\xi = 35.84$, $\gamma = 100$, and $\beta_{0} = 1800$, respectively (Olsen and Schaffer 1990). Figure 15 shows the $x_{1} (t)$ and $x_{2} (t)$ coordinates of two solutions that start out nearby, one at $(0.016,0.006,0.012,0.02)$ and the other at $(0.016001,0.006,0.012,0.02)$. From Fig. 15a, when $\alpha = 1$ and $\beta_{1} = 0.28$, these graphs are nearly identical for a certain time period, but then they differ considerably. No matter how close two solutions start, they always move apart in this manner when they are close to the attractor. This is sensitive dependence on initial conditions, one of the main features of a chaotic system. Also, when the order $\alpha$ decreases insignificantly, the behavior of system changes and gets periodic (Fig. 15b). Furthermore, it can be demonstrated from simulation results that the system (31) exhibit chaotic behavior at $\alpha < 1$ when the parameter $\beta {}_{1}$ increases (Fig. 16). Figure 17 depicts the phase portrait for model system (31) in the case of $\beta {}_{1} = 0.28$. As seen, the system (31) undergoes to period doubling when $\alpha$ increases and gets chaotic at $\alpha = 1$. The mathematical analysis of the system (31) will be illustrated in further investigations.

Fig. 15

The $x_{1} (t)$ and $x_{2} (t)$ graphs for two nearby initial conditions and $\beta {}_{1} = 0.28$

Fig. 16

The $x_{1} (t)$ and $x_{2} (t)$ graphs for two nearby initial conditions and different parameter values $\beta_{1}$ and $\alpha$

Fig. 17

FOS SEIR attractors in for $\beta {}_{1} = 0.28$ and different parameter values of $\alpha$

5 Conclusions and Discussions

In this chapter, some fractional-order singular (FOS) biological systems were established to investigate the impacts of economic profit and fractional derivative on the dynamic behaviors of these ecosystems. Our study extended previous models of biological systems predator-prey, logistic map and SEIR epidemic system, and proposed new and more realistic biological systems using fractional calculus and singular theory. Besides some mathematical analysis, the numerical simulations were considered to illustrate the effectiveness of the numerical method to explore the following impacts of fractional-order and singular modeling on the presented systems:

• 1. The effect of fractional derivative: It has been demonstrated that using fractional derivative can have following influences on the proposed models:

  • It reduces the errors arising from the neglected parameters in modeling of the memory-based biological systems which leads to derive the exact dynamical behavior of species interactions.

  • It acts as a time lag in ordinary differential model and causes to notably increase in the complexity of the observed behavior.

  • It takes less time for predator and prey and infectious diseases population to be settled as the fractional order decreases. Also, it will take the maximum time for the standard motion, i.e., $\alpha = 1$. In logistic map, we encountered with a strange behavior. When the order $\alpha$ decreases, this system exhibits stable equilibrium point behavior at first and undergoes to period doubling route to chaos and eventually enters to a chaotic space. Continuing this process, the system behaves in a reverse treatment and undergoes to inverse period doubling and is finished by stable equilibrium point.

  • The combination of fractional derivative and economic profit in singular form may change the stability of the system and cause the population and capture capability to be more sustainable.

  • The fractional derivative in the presented models damps the oscillation behavior and improves the stability of the solutions. In addition, the fractional order can impress the switching time from stability to instability. In recent case, the persistence and sustainable development of the ecosystem can be attained.

• 2. The effect of singular modeling: It is found that singular models exhibit more complicated dynamics rather than standard models, especially the bifurcation phenomena and chaotic behaviors, which can reveal the instability mechanism of systems. The most derived features are as follows:

  • Through the theoretical analysis and numerical simulation in predator-prey model, it has been demonstrated that there is a phenomenon of singularity induced bifurcation due to variation of economic interest of harvesting. This brings impulse phenomenon and causes a rapid growth of the species population. If this phenomenon prolongs a period of time, the species population will be out of the carrying capacity of the environment, and the collapse of the ecosystem may be happened.

  • It has been shown the predator-prey model exhibits another bifurcation phenomenon called transcritical bifurcation which varies the stability of the system and leads to extinct the predator population.

  • Using singular modeling, high dimension chaotic attractor was occurred in SEIR epidemic models. Biologic signification of these types of attractor in epidemic models is that the epidemic disease will break out suddenly and spread gradually in a region at the period of the high incidence of the epidemic disease, and accordingly, many people in the region would be infected by disease. Also, singular modeling of logistic map can affect its behavior and enrich its dynamical properties.

All results show that extinction, speciation and stability of the biological ecosystems can be affected by fractional derivative and economic interest in singular form, and with considering the constraints imposed on the ecosystem, persistence and sustainable development of the ecosystem can be attained.

The future directions of research include:

• Mathematical analysis: During FOS modeling of logistic map and SEIR epidemic system, these models exhibited equilibrium point, period doubling and chaotic behaviors. These results were derived from simulation point of view, and more detailed analysis and synthesis of these new extended models need further investigations.

• Application to medicine and engineering: Biologic signification of chaotic behavior in proposed ecosystems is that the extinction, speciation and stability of the biological ecosystems can be affected and the species population will break out suddenly. Many species would be infected by disease, for example, and some of them would even lose their lives. Nevertheless, there exists uncertain prediction for the low period of the incidence of these events. Therefore, it is important to control chaos of the biological models, which need further investigations. Further, characteristics of deterministic chaos are greatly affecting basic concepts of engineering such as prediction, control, computation, information, and optimization. New introduced chaotic models can be applied in this field of science.

• Extending to other systems: In this chapter, we proposed only three FOS models of biological systems and investigated their qualitative behaviors. This new era of modeling can be extended to other biological systems and even other systems from different fields of science such as power system, robotic, economics and so on.