Abstract
Vigelis and Cavalcante extended the Naudts’ deformed exponential families to a generic reference density. Here, the special case of Newton’s deformed logarithm is used to construct an Hilbert statistical bundle for an infinite dimensional class of probability densities.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Let \(\mathcal P\) be a family of positive probability densities on the probability space \((\mathbb X,\mathcal X,\mu )\). At each \(p \in \mathcal P\) we have the Hilbert space of square-integrable random variables \(L^2(p \cdot \mu )\) so that we can define the Hilbert bundle consisting of \(\mathcal P\) with linear fibers \(L^2(p \cdot \mu )\). Such a bundle supports most of the structure of Information Geometry, cf. [1] and the non-parametric version in [6, 7].
If \(\mathcal P\) is an exponential manifold, there exists a splitting of each fiber \(L(p \cdot \mu ) = H_p \oplus H_p^\perp \), such that \(H_p\) is equal or contains as a dense subset, the tangent space of the manifold at p. Moreover, the geometry on \(\mathcal P\) is affine and, as a consequence, there are natural transport mappings on the Hilbert bundle.
We shall study a similar set-up when the manifold is defined by charts based on mapping other than the exponential, while retaining an affine structure, see e.g. [10]. Here, we use \(p = \exp _A(v)\), where \(\exp _A\) is exponential-like function with linear growth at \(+\infty \). In such a case, the Hilbert bundle has fibers which are all sub-spaces of the same \(L^2(\mu )\) space.
The formalism of deformed exponentials by Naudts [4] is reviewed and adapted in Sect. 2. The following Sect. 3 is devoted to the adaptation of that formalism to the non-parametric case. Our construction is based on the work of Vigelis and Cavalcante [9], and we add a few more details about the infinite-dimensional case. Section 4 discusses the construction of the Hilbert statistical bundle in our case.
2 Background
We recall a special case of a nice and useful formalism introduced by Naudts [4]. Let \(A:[0,+\infty [\rightarrow [0,1[\) be an increasing, concave and differentiable function with \(A(0)=0\), \(A(+\infty )=1 \) and \(A^{\prime }(0+)=1\). We focus on the case \(A(x)=1-1/(1+x)=x/(1+x)\) that has been firstly discussed by Newton [5]. The deformed A-logarithm is the function \(\log _{A}(x)=\int _{1}^{x} A(\xi )^{-1} \ d\xi = x - 1 + \log x\), \(x\in ]0,+\infty [\). The deformed A-exponential is \(\exp _A = \log _A^{-1}\) which turns out to be the solution to the Cauchy problem \(e'(y) = A(e(y)) = 1 + 1/(1+e(y))\), \(e(0)=1\).
In the spirit of [8, 9] we consider the curve in the space of positive measures on \((\mathbb X,\mathcal X)\) given by \(t\mapsto \mu _t =\exp _{A}(tu + \log _A p) \cdot \mu \), where \(u \in L^2(\mu )\). As \(\exp _A(a+b) \le a^+ + \exp _A(b)\), each \(\mu _t\) is a finite measure, \(\mu _t(\mathbb X) \le \int (tu)^+ \ d\mu + 1\), with \(\mu _0 = p \cdot \mu \). The curve is actually continuous and differentiable because the pointwise derivative of the density \(p_t = \exp _A(tu + \log _A(p))\) is \(\dot{p}_t = A(p_t)u\) so that \(\left| \dot{p}_t\right| \le \left| u\right| \). In conclusion \(\mu _0 = p\) and \(\dot{\mu }_0 = u\).
Notice that there are two ways to normalize the density \(p_t\), either dividing by a normalizing constant Z(t) to get the statistical model \(t \mapsto \exp _A(tu - \log _A p)/Z(t)\) or, subtracting a constant \(\psi (t)\) from the argument to get the model \(t \mapsto \exp _A(tu - \psi (t) + \log _A(p))\). In the standard exponential case the two methods lead to the same result, which is not the case for deformed exponentials where \(\exp _A(\alpha +\beta ) \ne \exp _A(\alpha )\exp _A(\beta )\). We choose in the present paper the latter option.
3 Deformed Exponential Family Based on \(\exp _A\)
Here we use the ideas of [4, 8, 9] to construct deformed non-parametric exponential families. Recall that we are given: the measure space \((\mathbb X,\mathcal X,\mu )\); the set \(\mathcal P\) of probability densities; the function \(A(x)=x/(1+x)\). Throughout this section, the density \(p \in \mathcal P\) will be fixed.
Proposition 1
-
1.
The mapping \(L^{1}(\mu )\ni u \mapsto \exp _{A}(u + \log _A p) \in L^{1}(\mu )\) has full domain and is 1-Lipschitz. Consequently, the mapping
$$\begin{aligned} u \mapsto \int g\exp _{A}(u + \log _A p)\ d\mu \end{aligned}$$is \(\left\| g\right\| _{\infty }\)-Lipschitz for each bounded function g.
-
2.
For each \(u\in L^{1}(\mu )\) there exists a unique constant \(K(u)\in \mathbb {R}\) such that \(\exp _{A}(u-K(u)+\log _A p)\cdot \mu \) is a probability.
-
3.
It holds \(K(u)=u\) if, and only if, u is constant. In such a case,
$$\begin{aligned} \exp _{A}(u-K(u)+\log _A p) \cdot \mu =p \cdot \mu \ . \end{aligned}$$Otherwise, \(\exp _{A}(u-K(u)+\log _A p ) \cdot \mu \ne p \cdot \mu \).
-
4.
A density q takes the form \(q=\exp _{A}(u-K(u)+\log _A p)\), with \(u\in L^{1}(\mu )\) if, and only if, \(\log _{A}q - \log _A p \in L^1(\mu )\).
-
5.
If \(u,v\in L^{1}(\mu )\)
$$\begin{aligned} \exp _{A}(u-K(u)+\log _A p) = \exp _{A}(v-K(v) + \log _A p) \ , \end{aligned}$$then \(u-v\) is constant.
-
6.
The functional \(K :L^{1}(\mu ) \rightarrow \mathbb {R}\) is translation invariant. More specifically, \(c \in \mathbb {R}\) implies \(K(u+c) =K(u) +cK(1)\).
-
7.
The functional \(K :L^{1}(\mu ) \rightarrow \mathbb {R}\) is continuous and quasi-convex, namely all its sub-levels
 are convex.
are convex. -
8.
\(K:L^{1}(\mu )\rightarrow \mathbb {R}\) is convex.
Proof
-
1.
As \(\exp _{A}(u + \log _A p) \le u^{+} + p\) and so \(\exp _{A}(u + \log _A p)\in L^{1}(\mu )\) for all \(u \in L^{1}(\mu )\). The estimate \(\left| \exp _{A}(u+\log _A p) - \exp _{A}(v + \log _A p)\right| \le \left| u - v\right| \) leads to the desired result.
-
2.
For all \(\kappa \in \mathbb {R}\) the integral \(I(\kappa ) = \int \exp _{A}(u-\kappa + \log _A p)\ d\mu \) is bounded by \( 1 + \int (u - \kappa )^+ \ d\mu < \infty \) and the function \(\kappa \mapsto I(k)\) is continuous and strictly decreasing. Convexity of \(\exp _A\) together with the equation for its derivative imply \(\exp _{A}(u-\kappa + \log _A p) \ge \exp _{A}(u + \log _A p) - A(\exp _{A}( u + \log _A p))\kappa \), so that \(\int \exp _{A}( u-\kappa + \log _A p) \ d\mu \ge \int \exp _{A}(u + \log _A p) \ d\mu - \kappa \int A(\exp _{A}(u + \log _A p)) \ d\mu \), where the coefficient of \(\kappa \) is positive. Hence \(\lim _{\kappa \rightarrow -\infty } \int \exp _{A}(u-\kappa +\log _A p) \ d\mu = +\infty \). For each \(\kappa \ge 0\), we have \(\exp _{A}(u -\kappa + \log _A p) \le \exp _{A}( u + \log _A p) \le p + u^+\) so that by dominated convergence we get \(\lim _{\kappa \rightarrow \infty } I(\kappa ) = 0\). Therefore K(u) will be the unique value for which \(\int \exp _{A}(u-\kappa +\log _A p)\ d\mu =1\).
-
3.
If the function u is a constant, then \(\int \exp _{A}(u - u + \log _A p)\ d\mu = \int p \ d\mu = 1\) and so \(K(u) =u.\) The converse implication is trivial. The equality \(\exp _A(u-K(u)+\log _A p) = p\) holds if, and only if, \(u-K(u)=0\).
-
4.
If \(\log _{A} q = u - K(u) + \log _A p\), then \(\log _A q - \log _A p = u - K(u) \in L^1(\mu )\). Conversely, if \(\log _A q - \log _A p = v \in L^1(\mu )\), then \( q = \exp _A(v + \log _A p)\). As q is a density, then \(K(v)=0\).
-
5.
If \(u - K(u) + \log _A p = v - K(v) + \log _A p\), then \(u-v = K(u)-K(v)\).
-
6.
Clearly, \(K(c) =c=cK(1)\) and \(K(u+c) =K(u) +c\).
-
7.
Observe that \(\int \exp _{A}(u + \log _A p)\ d\mu \le 1\) if, and only if, \(K(u)\le 0\). Hence \(u_{1},u_{2}\in L_{0}\), implies \(\int \exp _{A}(u_{i} + \log _A p) \ d\mu \le 1\), \(i=1,2\). Thanks to the convexity of the function \(\exp _A\), we have \(\int \exp _{A}((1-\alpha ) u_{1}+\alpha u_{2}) + \log _A p \ d\mu \le (1-\alpha ) \int \exp _{A}(u_{1} + \log _A p) \ d\mu + \alpha \int \exp _{A}(u_{2}+\log _A p) \ d\mu \le 1\), that provides \(K((1- \alpha ) u_{1}+ \alpha u_2) \le 0\). Hence the sub-level \(L_{0}\) is convex. Notice that all the other sub-levels are convex since they are obtained by translation of \(L_{0}\). More precisely, \(L_{\alpha }=L_{0}+\alpha \). Clearly both the sets \(\left\{ \int \exp _{A}(u + \log _A p)\ d\mu \le 1\right\} \) and \(\left\{ \int \exp _{A}(u + \log _A p)\ d\mu \ge 1\right\} \) are closed in \(L^{1}(\mu )\), since the functional \(u \rightarrow \int \exp _{A}(u)\ d\mu \) is continuous. Hence \(u\rightarrow K(u)\) is continuous as well.
-
8.
A functional which is translation invariant and quasiconvex is necessarily convex. Though this property is more or less known, a proof is gathered below.
Lemma 1
A translation invariant functional on a vector space V, namely \(I :V \rightarrow \mathbb {R}\) such that for some \(v \in V\) one has \(I(x+\lambda v)=I(x)+\lambda I(v)\) for all \(x \in V\) and \(\lambda \in \mathbb {R}\), is convex if and only if I is quasiconvex, namely all level sets are convex, provided \(I(v) \ne 0\).
Proof
Let I be quasiconvex, then the sublevel \(L_{0}\left( I\right) =\left\{ x\in V:I\left( x\right) \le 0\right\} \) is nonempty and convex. Clearly, \(L_{\lambda }\left( I\right) =L_{0}\left( I\right) +(\lambda /I(v))v\) holds for every \(\lambda \in \mathbb {R}\). Hence, if \(\lambda \) and \(\mu \) are any pair of assigned real numbers and \(\alpha \in \left( 0,1\right) \), \(\bar{\alpha }=1-\alpha \), then
Therefore, if for any pair of points \(x,y\in V\), we set \(I\left( x\right) =\lambda \) and \(I\left( y\right) =\mu \), then \(x\in L_{\lambda }\left( I\right) \) and \(y\in L_{\mu }\left( I\right) \). Consequently \(\alpha x+\bar{\alpha }y\in \alpha L_{\lambda }\left( I\right) +\bar{\alpha }L_{\mu }\left( I\right) = L_{\alpha \lambda +\bar{\alpha }\mu }(I)\). That is, \(I\left( \alpha x+\bar{\alpha }y\right) \le \alpha \lambda +\bar{\alpha }\mu =\alpha I\left( x\right) +\bar{\alpha }I\left( y\right) \) that shows the convexity of I. Of course the converse holds in that a convex function is quasiconvex.
For each positive density q, define its escort density to be \(\widetilde{q} = A(q)/\int A(q) \ d\mu \), see [4]. Notice that \(0< A(q) < 1\). The next proposition provides a subgradient of the convex function K.
Proposition 2
Let \(v \in L^1(\mu )\) and \(q(v) = \exp _{A}(v - K(v) + \log _A p)\). For every \(u\in L^{1}(\mu )\), the inequality \(K(u+v)-K(v)\ge \int u \widetilde{q}(v) \ d\mu \) holds i.e., the density \(\widetilde{q}(v) \in L^{\infty }(\mu )\) is a subgradient of K at v.
Proof
Thanks to convexity of \(\exp _{A}\) and the derivation formula, we have
If we take \(\mu \)-integral of both sides,
Isolating the increment \(K(u+v)-K(v)\), the desired inequality obtains.
By Proposition 2, if the functional K were differentiable, the gradient mapping would be \(v \mapsto \widetilde{q}(v)\), whose strong continuity requires additional assumptions. We would like to show that K is differentiable by means of the Implicit Function Theorem. That too, would require specific assumptions. In fact, it is in general not true that a superposition operator such as \(L^1(\mu ) \ni u \mapsto \exp _A(u + \log _A p) \in L^1(\mu )\) is differentiable, cf. [2, Sect. 1.2]. In this perspective, we prove the following.
Proposition 3
-
1.
The superposition operator \(L^{2}(\mu )\ni v\mapsto \exp _{A}(v + \log _A p)\in L^{1}(\mu )\) is continuously Fréchet differentiable with derivative
$$\begin{aligned} d\exp _{A}(v)=(h\mapsto A(\exp _{A}(v+\log _A p))h)\in \mathcal {L}(L^{2}(\mu ),L^{1}(\mu ))\ . \end{aligned}$$ -
2.
The functional \(K:L^{2}(\mu )\rightarrow \mathbb {R}\), implicitly defined by the equation
$$\begin{aligned} \int \exp _{A}(v-K(v) + \log _A p)\ d\mu =1,\quad v\in L^{2}(\mu ) \end{aligned}$$is continuously Fréchet differentiable with derivative
$$\begin{aligned} dK(v)=(h\mapsto \int h\widetilde{q}(v)\ d\mu ), \quad q(v) = \exp _{A}(v-K(v)) \end{aligned}$$where
$$\begin{aligned} \widetilde{q}(v)=\frac{A\circ q(v)}{\int A\circ q(v)\ d\mu } \end{aligned}$$is the escort density of p.
Proof
-
1.
It is easily seen that
$$\begin{aligned} \exp _{A}(v+h+\log _A p)-\exp _{A}(v + \exp _A p) - A[\exp _{A}(v+\log _A p)]h=R_{2}(h), \end{aligned}$$with the bound \(\left| {R_{2}(h)}\right| \le (1/2)\left| {h}\right| ^{2}\). It follows
$$\begin{aligned} \frac{\int \left| {R_{2}(h)}\right| d\mu }{\left( \int \left| {h} \right| ^{2}\ d\mu \right) ^{\frac{1}{2}}}\le \frac{\frac{1}{2}\int \left| {h}\right| ^{2}\ d\mu }{\left( \int \left| {h}\right| ^{2}\ d\mu \right) ^{\frac{1}{2}}}=\frac{1}{2}\left( \int \left| {h} \right| ^{2}\ d\mu \right) ^{\frac{1}{2}}\ . \end{aligned}$$Therefore \(\left\| R_{2}(h)\right\| _{L^{1}(\mu )}=o\left( \left\| h\right\| _{L^{2}(\mu )}\right) \) and so the operator \(v\mapsto \exp _{A}(v + \log _A p)\) is Fréchet-differentiable with derivative \(h\mapsto A(\exp _{A}(v+\log _A p))h\) at v. Let us show that the F-derivative is a continuous map \(L^{2}(\mu )\rightarrow \mathcal {L}(L^{2}(\mu ),L^{1}(\mu ))\). If \(\Vert {h}\Vert _{L^{2}(\mu )}\le 1\) and \(v,w\in L^{2}(\mu )\) we have
$$\begin{aligned}&\int \left| {(A[\exp _{A}(v + \log _A p)]-A[\exp _{A}(w + \log _A p)])h}\right| \ d\mu \\&\quad \le \Vert {A[\exp _{A}(v + \log _A p)-A[\exp _{A}(w + \log _A p)]}\Vert _{L^{2}(\mu )}\le \Vert {v-w}\Vert _{L^{2}(\mu )}\ , \end{aligned}$$hence the derivative is 1-Lipschitz.
-
2.
Frechét differentiability of K is a consequence of the Implicit Function Theorem in Banach spaces, see [3], applied to the \(C^{1}\)-mapping
$$\begin{aligned} L^{2}(\mu )\times \mathbb {R}\ni (v,\kappa )\mapsto \int \exp _{A}(v-\kappa +\log _A p )\ d\mu \ . \end{aligned}$$The derivative can be easily obtained from the computation of the subgradient.
In the expression \(q(u) = \exp _A(u - K(u) + \log _A p)\), \(u \in L^1(\mu )\), the random variable u is identified up to a constant. We can choose in the class a unique representative, by assuming \(\int u\widetilde{p} \ d\mu = 0\), the expected value being well defined as the escort density is bounded. In this case we can solve for u and get
In analogy with the exponential case, we can express the functional K as a divergence associated to the N.J. Newton logarithm:
It would be interesting to proceed with the study of the convex conjugation of K and the related properties of the divergence, but do not do that here.
4 Hilbert Bundle Based on \(\exp _A\)
In this section \(A(x) = x/(1+x)\) and \(\mathcal P(\mu )\) denotes the set of all \(\mu \)-densities on the probability space \((\mathbb X,\mathcal X,\mu )\) of the form \(q = \exp _A(u - K(u))\) with \(u \in L^2(\mu )\) and \({{{\mathrm{E}}}}_{\mu }\left[ u\right] = 0\), cf. [5]. Notice that \(1\in \mathcal P(\mu )\) because we can take \(u = 0\). Equivalently, \(\mathcal P(\mu )\) is the set of all densities q such that \(\log _A q \in L^2(\mu )\) because in such a case we can take \(u = \log _A q - {{{\mathrm{E}}}}_{\mu }\left[ \log _A q\right] \). The condition for \(q \in \mathcal P(\mu )\) can be expressed by saying that both q and \(\log q\) are in \(L^2(\mu )\). In fact, as \(\exp _A\) is 1-Lipschitz, we have \(\left\| q-1\right\| _{\mu } \le \left\| u - K(u)\right\| _{\mu }\) and the other inclusion follows from \(\log q = \log _A q +1 - q\). An easy but important consequence of such a characterization is the compatibility of the class \(\mathcal P(\mu )\) with the product of measures. If \(q_i = \exp _A(u_i - K_1(u_i)) \in \mathcal P(\mu _i)\), \(i=1,2\), the product is \((q_1 \cdot \mu _1) \otimes (q_2 \cdot \mu _2) = (q_2 \otimes q_2) \cdot (\mu _1 \otimes \mu _2)\), hence \(q_2 \otimes q_2 \in \mathcal P(\mu _1 \otimes \mu _2)\) since \(\left\| q_1 \otimes q_2\right\| _{\mu _1 \otimes \mu _2} = \left\| q_1\right\| _{\mu _1} \left\| q_2\right\| _{\mu _2}\). Moreover \(\log \left( q_1 \otimes q_2\right) = \log q_1 + \log q_2\), hence \(\left\| \log \left( q_1 \otimes q_2\right) \right\| _{\mu _1 \otimes \mu _2} \le \left\| \log q_1\right\| _{\mu _1} + \left\| \log q_2\right\| _{\mu _2}\).
We proceed now to define an Hilbert bundle with base \(\mathcal P(\mu )\). For each \(p \in \mathcal P(\mu )\) consider the Hilbert spaces  with scalar product \(\left\langle u,v\right\rangle _{p} = \int uv \ d\mu \) and form the Hilbert bundle
with scalar product \(\left\langle u,v\right\rangle _{p} = \int uv \ d\mu \) and form the Hilbert bundle

For each \(p,q \in \mathcal P(\mu )\) the mapping \(\mathbb U_p^q u = u - {{{\mathrm{E}}}}_{\widetilde{q}}\left[ u\right] \) is a continuous linear mapping from \(H_p\) to \(H_q\). We have \(\mathbb U_q^r \mathbb U_p^q = \mathbb U_p^r\). In particular, \(\mathbb U_q^p \mathbb U_p^q\) is the identity on \(H_p\), hence \(\mathbb U_p^q\) is an isomorphism of \(H_p\) onto \(H_q\). In the next proposition we construct an atlas of charts for which \(\mathcal P(\mu )\) is a Riemannian manifold and \(H\mathcal P(\mu )\) is an expression of the tangent bundle.
In the following proposition we introduce an affine atlas of charts and use it to define our Hilbert bundle which is an expression of the tangent bundle. The velocity of a curve \(t \mapsto p(t) \in \mathcal P(\mu )\) is expressed in the Hilbert bundle by the so called A-score that, in our case, takes the form \(A(p(t))^{-1} \dot{p}(t)\), with \(\dot{p}(t)\) computed in \(L^1(\mu )\).
Proposition 4
-
1.
\(q \in \mathcal P(\mu )\) if, and only if, both q and \(\log q\) are in \(L^2(\mu )\).
-
2.
Fix \(p \in \mathcal P(\mu )\). Then a positive density q can be written as
$$\begin{aligned} q = \exp _A(v - K_p(v) + \log _A p), \quad with\,\, v \in L^2(\mu )\, and \,\, {{{\mathrm{E}}}}_{\widetilde{p}}\left[ v\right] = 0, \end{aligned}$$if, and only if, \(q \in \mathcal P(\mu )\).
-
3.
For each \(p \in \mathcal P(\mu )\) the mapping
$$\begin{aligned} s_p :\mathcal P(\mu ) \ni q \mapsto \log _A q - \log _A p - {{{\mathrm{E}}}}_{\widetilde{p}}\left[ \log _A q - \log _A p\right] \in H_p \end{aligned}$$is injective and surjective, with inverse \(e_p(u) = \exp _A(u - K_p(u) + \log _A p)\).
-
4.
The atlas
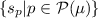 is affine with transitions $$\begin{aligned} s_q \circ e_p (u) = \mathbb U_p^q u + s_p(q) \ . \end{aligned}$$
is affine with transitions $$\begin{aligned} s_q \circ e_p (u) = \mathbb U_p^q u + s_p(q) \ . \end{aligned}$$ -
5.
The expression of the velocity of the differentiable curve \(t \mapsto p(t) \in \mathcal P(\mu )\) in the chart \(s_p\) is \(d s_p(p(t)) / dt \in H_p\). Conversely, given any \(u \in H_p\), the curve \(p :t \mapsto \exp _A(tu - K_p(tu) + \log _A p)\) has \(p(0)= p\) and has velocity at \(t=0\) expressed in the chart \(s_p\) by u. If the velocity of a curve is expressed in the chart \(s_p\) by \(t \mapsto \dot{u}(t)\), then its expression in the chart \(s_q\) is \(\mathbb U_p^q \dot{u}(t)\).
-
6.
If \(t \mapsto p(t) \in \mathcal P(\mu )\) is differentiable with respect to the atlas then it is differentiable as a mapping in \(L^1(\mu )\). It follows that the A-score is well-defined and is the expression of the velocity of the curve \(t \mapsto p(t)\) in the moving chart \(t \mapsto s_{p(t)}\).
Proof
-
1.
Assume \(q = \exp _A (u - K(u))\) with \(u \in L_0^2(\mu )\). It follows \(u - K(u) \in L^2(\mu )\) hence \(q \in L^2(\mu )\) because \(\exp _A\) is 1-Lipschitz. As moreover \(q + \log q - 1 = u - K(u) \in L^2(\mu )\), then \(\log q \in L^2(\mu )\). Conversely, \(\log _a q = q -1 + \log q = v \in L^2(\mu )\) and we can write \(q = \exp _A v = \exp _A((v - {{{\mathrm{E}}}}_{p}\left[ v\right] ) + {{{\mathrm{E}}}}_{p}\left[ v\right] )\) and we can take \(u = v - {{{\mathrm{E}}}}_{\mu }\left[ v\right] \).
-
2.
The assumption \(p,q \in \mathcal P(\mu )\) is equivalent to \(\log _A p, \log _A q \in L^2(\mu )\). Define \(u = \log _A q - \log _A p - {{{\mathrm{E}}}}_{\widetilde{p}}\left[ \log _A q - \log _A p\right] \) and \(D_A(p\Vert q) = {{{\mathrm{E}}}}_{\widetilde{p}}\left[ \log _A p - \log _A q\right] \). It follows \(u \in L^2(\mu )\), \({{{\mathrm{E}}}}_{\widetilde{p}}\left[ u\right] = 0\), and \(\exp _A(u - D_A(p\Vert q) + \log _A p) = q\). Conversely, \(\log _ Aq = u - K_p(u) + \log _A p \in L^2(\mu )\).
-
3.
This has been already proved.
-
4.
All simple computations.
-
5.
If \(p(t) = \exp _A(u(t) - K_p(u(t)) + \log _A p)\), with \(u(t) = s_p(u(t))\) then in that chart the velocity is \(\dot{u}(t) \in H_p\). When \(u(t) = tu\) the expression of the velocity will be u. The proof of the second part follows from the fact that \(\mathbb U_p^q\) is the linear part of the affine change of coordinates \(s_q \circ e_p\).
-
6.
Choose a chart \(s_p\) and express the curve as \(t \mapsto s_p(p(t)) = u(t)\) so that \(p(t) = \exp _A(u(t) - K_p(u(t)) + \log _A p)\). It follows that the derivative of \(t \mapsto p(t)\) exists in \(L^1(\mu )\) by derivation of the composite function and it is given by \(\dot{p}(t) = A(p(t)) \mathbb U_p^{p(t)} \dot{u}(t)\), hence \(A(p(t))^{-1} \dot{p}(t) = \mathbb U_p^{p(t)} \dot{u}(t)\). If the velocity at t is expressed in the chart centered at p(t), then its expression is the score.
5 Conclusions
We have constructed an Hilbert statistical bundle using an affine atlas of charts based on the A-logarithm with \(A(x) = x/(1+x)\). In particular, this entails a Riemannian manifold of densities. On the other end, our bundle structure could be useful in certain contexts. The general structure of the argument mimics the standard case of the exponential manifold. We would like to explicit some, hopefully new, features of our set-up.
The proof of the convexity and continuity of the functional K when defined on \(L^1(\mu )\) relies on the property of translation invariance. Whenever K is restricted to \(L^2(\mu )\), it is shown to be differentiable along with the deformed exponential and this, in turn, provides a rigorous construction of the A-score.
The gradient mapping of K is continuous and 1-to-1, but its inverse cannot be continuous as it takes values which are bounded functions. It would be interesting to analyze the analytic properties of the convex conjugate of \(K^*\), as both K and \(K^*\) are the coordinate expression of relevant divergences.
If F is a section of the Hilbert bundle namely, \(F :\mathcal P(\mu ) \rightarrow L^2(\mu )\) with \({{{\mathrm{E}}}}_{\widetilde{p}}\left[ F(p)\right] = 0\) for all p, differential equations take the form \(A(p(t))\dot{p}(t) = F(p(t))\) in the atlas, which in turn implies \(\dot{p}(t) = A(p(t))F(p(t))\) in \(L^1(\mu )\). This is important for some applications e.g., when the section F is the gradient with respect to the Hilbert bundle of a real function. Namely, the gradient, \({\text {grad}}\phi \), of a smooth function \(\phi :\mathcal P(\mu ) \rightarrow \mathbb {R}\) is a section of the Hilbert bundle such that
for each differentiable curve \(t \mapsto p(t) \in \mathcal P(\mu )\).
References
Amari, S.: Dual connections on the Hilbert bundles of statistical models. In: Geometrization of Statistical Theory (Lancaster, 1987), pp. 123–151. ULDM Publ., Lancaster (1987)
Ambrosetti, A., Prodi, G.: A Primer of Nonlinear Analysis, Cambridge Studies in Advanced Mathematics, vol. 34. Cambridge University Press, Cambridge (1993)
Dieudonné, J.: Foundations of Modern Analysis. Academic Press, New York (1960)
Naudts, J.: Generalised Thermostatistics. Springer, London (2011). doi:10.1007/978-0-85729-355-8
Newton, N.J.: An infinite-dimensional statistical manifold modelled on Hilbert space. J. Funct. Anal. 263(6), 1661–1681 (2012)
Pistone, G.: Nonparametric information geometry. In: Nielsen, F., Barbaresco, F. (eds.) GSI 2013. LNCS, vol. 8085, pp. 5–36. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40020-9_3
Pistone, G., Sempi, C.: An infinite-dimensional geometric structure on the space of all the probability measures equivalent to a given one. Ann. Statist. 23(5), 1543–1561 (1995)
Schwachhöfer, L., Ay, N., Jost, J., Lê, H.V.: Parametrized measure models. Bernoulli (online-to appear)
Vigelis, R.F., Cavalcante, C.C.: On \(\phi \)-families of probability distributions. J. Theor. Probab. 26, 870–884 (2013)
Zhang, J., Hästö, P.: Statistical manifold as an affine space: a functional equation approach. J. Math. Psychol. 50(1), 60–65 (2006)
Acknowledgments
L. Montrucchio acknowledges the support of Collegio Carlo Alberto Foundation. G. Pistone is a member of GNAFA-INDAM and acknowledges the support of de Castro Statistics Foundation and Collegio Carlo Alberto Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Montrucchio, L., Pistone, G. (2017). Deformed Exponential Bundle: The Linear Growth Case. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2017. Lecture Notes in Computer Science(), vol 10589. Springer, Cham. https://doi.org/10.1007/978-3-319-68445-1_28
Download citation
DOI: https://doi.org/10.1007/978-3-319-68445-1_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68444-4
Online ISBN: 978-3-319-68445-1
eBook Packages: Computer ScienceComputer Science (R0)




 are convex.
are convex.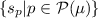 is affine with transitions
is affine with transitions