Neural Identifier-Control Scheme for Nonlinear Discrete Systems with Input Delay

Abstract

This work presents a scheme based on a discrete recurrent high order neural network identifier and a block control based on sliding modes for nonlinear discrete-time systems with input delays in real-time. The identifier is trained with an extended Kalman Filter based algorithm and the block control is used for trajectory tracking. Experimental results are included using a linear induction motor prototype with added delays to its input signals.

1 Introduction

Delays in systems are a source of instability and poor performance, also, they make system analysis a more complex task [1, 2]. Time delay systems mainly inherit delay from their components and examples can be found easily in areas like chemical industry, hydraulic systems, metallurgical processing and network systems [1, 2].

System identification is a process to obtain a mathematical model of a system from data obtained from a practical experiment with the system [3]. Among the many techniques for system identification, neural networks stand up [3, 4].

Recurrent high order neural networks (RHONNs) internal connections allow them to capture the response of complex nonlinear systems and to have characteristics like robustness against noise, on-line and off-line training, and the possibility of incorporating a priori information about the system to identified [5,6,7]. On the other hand, training of neural networks with Kalman filter algorithms has proved to be reliable and practical, also, it offers advantages for the improvement of learning convergence and computational efficiency compared to backpropagation methods [5, 6].

Neural block control is a methodology which uses a neural identifier of the block controllable form of a system, then, based on this model a discrete control law is designed combining discrete-time block-control and sliding modes technique [5].

There are a number of methodologies which work with systems with input delay [8,9,10,11]. The main disadvantages of these methodologies are that they need a lot of information about the system, in our methodology, there is not necessary to know the model of the system because it works with the model obtained in the neural identification process. Moreover, most of them work in continuous-time which could be seen as a disadvantage due to the tendency towards digital rather than analog systems [12]. In this way, we present a rather simple to work with a scheme for discrete-time systems with input delays which can be used in real time even if the model of the system is unknown or incomplete.

On the other hand, compared with some of our previous works [13,14,15] this paper differs in that none of them treat the case of input delay in the system and some do not even consider any kind of delay.

The paper outline: Sect. 2 is dedicated to neural identification using RHONNs and extended Kalman filter (EKF) training. Then, the block control is in Sect. 3, results are shown in Sect. 4. Finally, the conclusions are included in Sect. 5.

2 Neural Identification

Neural identification is a process to obtain a mathematical model of a system by selecting a neural network and an adaptation law, in a way that the neural network responds in the same way to an input as the system to be identified [3].

2.1 Recurrent High Order Neural Network Identification

In this work, we use the following RHONN series-parallel model:

$$ \widehat{x}_{i} \left( {k + 1} \right) = \omega_{i}^{T} z_{i} \left( {x\left( k \right),u\left( {k - 1} \right)} \right)i = 1, \cdots ,n $$

(1)

where $n$ is the state dimension, $\widehat{x}$ is the neural network state vector, $\omega$ is the weight vector, x is the plant state vector, and $u$ is the input vector to the neural network, $l$ is the unknown time delay and $z_{i} \left( \cdot \right)$ is defined as follows:

$$ \begin{array}{*{20}c} {z_{i} \left( {x\left( k \right),u\left( {k - l} \right)} \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {z_{{i_{1} }} } & {z_{{i_{2} }} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {z_{{i_{{L_{i} }} }} } \\ \end{array} } \\ \end{array} } \right]^{T} } \\ { = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\prod\nolimits_{{j \in I_{1} }} {\xi_{{i_{j} }}^{{d_{ij} \left( 1 \right)}} } } & {\prod\nolimits_{{j \in I_{1} }} {\xi_{{i_{j} }}^{{d_{ij} \left( 2 \right)}} } } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\prod\nolimits_{{j \in I_{{L_{i} }} }} {\xi_{{i_{j} }}^{{d_{ij} \left( {L_{i} } \right)}} } } \\ \end{array} } \\ \end{array} } \right]^{T} } \\ \end{array} $$

(2)

$$ \xi_{i} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\xi_{{i_{1} }} } & \cdots & {\xi_{{i_{n} }} } \\ \end{array} } & {\begin{array}{*{20}c} {\xi_{{i_{n + 1} }} } & \cdots & {\xi_{{i_{n + m} }} } \\ \end{array} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {S\left( {x_{1} } \right)} & \cdots & {S\left( {x_{n} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {u_{1} } & \cdots & {u_{m} } \\ \end{array} } \\ \end{array} } \right]^{T} $$

(3)

with $L_{i}$ as the respective number of high-order connections, $\left\{ {I_{1} , I_{2} , \cdots , I_{{L_{i} }} } \right\}$ is a collection of non-ordered subsets of $\left\{ {1, 2, \cdots , n + m} \right\}$, $d_{ij} \left( k \right)$ being non-negative integers and $1/\left( {1 + e^{ - \beta v} } \right)$ with $\beta > 0$ and $v$ is any real value variable.

EKF Training Algorithm.

The training goal is to find the optimal weight vector which minimizes the prediction error. In this way, the weights $\omega$ become the states to be estimated by the Kalman filter, and the identification error between $x$ and $\widehat{x}$ is considered as additive white noise [4]. The training algorithm is based on the EKF due to the nonlinearity of the neural network (1) and is defined in (4).

$$ \begin{array}{*{20}c} {\omega_{i} \left( {k + 1} \right) = \omega_{i} \left( k \right) + \eta K_{i} \left( k \right)\left( {x_{i} \left( k \right) - \widehat{x}_{i} \left( k \right)} \right)} \\ {K_{i} \left( {k + 1} \right) = P_{i} \left( k \right)H_{i} \left( k \right)\left[ {R_{i} \left( k \right) + H_{i} \left( k \right)^{T} P_{i} \left( k \right)H_{i} \left( k \right)} \right]^{ - 1} } \\ {P_{i} \left( {k + 1} \right) = P_{i} \left( k \right) - K_{i} \left( k \right)H_{i} \left( k \right)^{T} P_{i} \left( k \right) + Q_{i} \left( k \right)} \\ \end{array} $$

(4)

where $\omega_{i} \in {\mathcal{R}}^{{L_{i} }}$ is the adapted weight vector, $\eta \in {\mathcal{R}}$ is the learning rate, $\widehat{x}_{i}$ is the $i$ -th state variable of the neural network, $K_{i} \in {\mathcal{R}}^{{L_{i} }}$ is the Kalman gain vector, $R_{i} \in {\mathcal{R}}$ is the error noise covariance, $H_{i} \in {\mathcal{R}}^{{L_{i} }}$ is vector with entries $H_{ij} = \left[ {\partial \widehat{x}_{i} \left( x \right)/\partial \omega_{ij} \left( k \right)} \right]^{T}$ and $P_{i} \in {\mathcal{R}}^{{L_{i} \times L_{i} }}$ is the weight estimation error covariance matrix, $Q_{i} \in {\mathcal{R}}^{{L_{i} \times L_{i} }}$ is the estimation noise covariance matrix. $P_{i}$ and $Q_{i}$ are initialized as diagonal matrices with entries $P_{i} \left( 0 \right)$ and $Q_{i} \left( 0 \right)$, respectively.

RHONN Identification.

Consider the following Nonlinear Discrete-Time System with input delay:

$$ \begin{array}{*{20}c} {x\left( {k + 1} \right) = F\left( {x\left( k \right),u\left( {k - l} \right)} \right)} \\ {y\left( k \right) = h\left( {x\left( k \right)} \right)} \\ \end{array} $$

(5)

where $x \in {\mathcal{R}}^{n}$, $u \in {\mathcal{R}}^{m}$, $F \in {\mathcal{R}}^{n} \times {\mathcal{R}}^{m} \to {\mathcal{R}}^{n}$ is a nonlinear function and $l = 1,2, \cdots$ is the unknown delay. Then, our identification process consists of approximating the system (5) with the RHONN (1) trained online with the EKF algorithm (4).

This identification process is validated achieving a small error between the system outputs and the identifier outputs for the same inputs.

3 Neural Block Control

The model of many practical nonlinear systems can be transformed in the block controllable form [5]:

$$ \begin{array}{*{20}c} {x_{j} \left( {k + 1} \right) = f_{j} \left( {\overline{x}_{j} \left( k \right)} \right) + B_{j} \left( {\overline{x}_{j} \left( k \right)} \right)x_{j + 1} \left( k \right) + d_{j} \left( k \right)} \\ {x_{r} \left( {k + 1} \right) = f_{r} \left( {x\left( k \right)} \right) + B_{r} \left( {x\left( k \right)} \right)u\left( k \right) + d_{r} \left( k \right)} \\ {y\left( k \right) = x_{1} \left( k \right)} \\ \end{array} $$

(6)

where $j = 1, \ldots ,r - 1$, $x \in {\mathcal{R}}^{n}$ is the state variable vector with $x(k) = \left[ {x_{1} (k) \cdots x_{r} (k)^{T} } \right]$, $\bar{x}_{j} = (k)\left[ {x_{1} (k) \cdots x_{j} (k)} \right]^{T}$, $r \ge 2$ is the number of blocks, $u \in {\mathcal{R}}^{m}$, $d(k) = \left[ {d_{1} (k) \cdots d_{j} (k) \cdots d_{r} (k)^{T} } \right]$ is the bounded unknown disturbance vector and $f_{j} \left( \cdot \right)$ and $B_{j} \left( \cdot \right)$ are smooth nonlinear functions. Consider the following transformation [5]:

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\chi_{1} \left( k \right) = x_{1} \left( k \right) - x_{1}^{d} \left( k \right)} \\ {\chi_{2} \left( k \right) = x_{2} \left( k \right) - x_{2}^{d} \left( k \right)} \\ \end{array} } \\ { = x_{2} \left( k \right) - \left[ {B_{1} \left( {x_{1} \left( k \right)} \right)} \right]^{ - 1} \left( {{\rm K}_{1} z_{1} \left( k \right) - \left( {f_{1} \left( {x_{1} \left( x \right)} \right) - d_{1} } \right)} \right)} \\ {\begin{array}{*{20}c} \vdots \\ {\chi_{r} \left( k \right) = x_{r} \left( k \right) - x_{r}^{d} \left( k \right)} \\ \end{array} } \\ \end{array} $$

(7)

where $x_{1}^{d}$ is the tracking reference, $x_{i}^{d}$ is the desired value for $x_{i}$; and ${\rm K}$ is a Shur matrix. Using (7) and selecting $S_{D} \left( k \right) = \chi_{r} \left( k \right) = 0$ system (6) can be rewritten as (8):

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\chi_{1} \left( {k + 1} \right) = \,{\rm K}_{1} \chi_{1} \left( k \right) + B_{1} \chi_{2} \left( k \right)} \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\chi_{{{\text{r}} - 1}} \left( {k + 1} \right) = \,{\rm K}_{{{\text{r}} - 1}} \chi_{{{\text{r}} - 1}} \left( k \right) + B_{r - 1} \chi_{\text{r}} \left( k \right)} \\ {\chi_{\text{r}} \left( {k + 1} \right) = f_{r} \left( {x\left( k \right)} \right) + B_{r} \left( {x\left( k \right)} \right)u\left( k \right) + d_{r} \left( k \right) - x_{r}^{d} \left( {k + 1} \right)} \\ \end{array} } \\ \end{array} $$

(8)

then, $u\left( k \right)$ is defined in (9), where $u_{eq}$ is calculated from $S_{D} \left( {k + 1} \right) = 0$ and $u_{0}$ it is the control resources that bound the control.

$$ \begin{array}{*{20}c} {u\left( k \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {u_{eq} \left( k \right)} \hfill & {if} \hfill & {\left\| {u_{eq} \left( k \right)} \right\| \le u_{0} } \hfill \\ \end{array} } \\ {\begin{array}{*{20}c} {u_{0} \frac{{u_{eq} \left( k \right)}}{{\left\| {u_{eq} \left( k \right)} \right\|}}} & {if} & {\left\| {u_{eq} \left( k \right)} \right\| > u_{0} } \\ \end{array} } \\ \end{array} } \right.} \\ {U_{eq} \left( k \right) = \left[ {B_{r} \left( {x\left( k \right)} \right)} \right]^{ - 1} \left( { - f_{r} \left( {x\left( k \right)} \right) + x_{r}^{d} \left( {k + 1} \right) - d_{r} \left( k \right)} \right)} \\ \end{array} $$

(9)

Hence, the first step of the process is to design a RHONN identifier in a block controllable form for the system to be identified and then obtained the $u\left( k \right)$ as in (9).

4 Results

Test Description.

Using the Lineal Induction Motor prototype (Fig. 1) which is based in a dSPACE® board RTI1104 and a MATLAB®/Simulink® interface the neural block control is implemented in a Simulink model with communication to the prototype by the dSPACE® tools. A subsystem to induce delays in the system input is created in Simulink®. The subsystem consists of that 4 s after the prototype starting the control signal is switched to a version with random time-delay. This is achieved using the block “Variable Transport Delay” with the configuration variable time delay which receives as input at each time a random number from 0 to 10 multiplied by the sampling time set to $0.0003\,\text{s}.$

Fig. 1.

Linear induction motor prototype

Experimental Results.

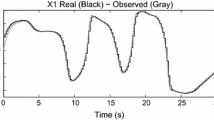
Table 1 shows the identification errors for all variable states and Fig. 2 shows two graphs the first one shows the velocity tracking, the second one shows the tracking of the flux magnitude which is defined as:

$$ flux\, magnitude = Alpha \,Flux^{2} + Beta\, Flux^{2} $$

Table 1. Root mean square errors of identification

Fig. 2.

Tracking reference real-time performance

5 Conclusions

In general, it is seen that the proposed scheme adapts itself quickly even in the presence of real-time disturbances and the added delays in the input to the system. More specifically, the errors shown in Table 1 are small for all variable states, even for alpha and beta currents considering that they real values can be as high as 30 A. Figure 2 shows the velocity tracking with a good performance and a flux magnitude which is maintained around its reference. Also, when the added time delay starts at 4 s it is noticeable that the performance changes, however, the presented RHONN identifier – control scheme is still capable of maintaining the dynamic of the desired trajectory. Moreover, it is important to note that for real-time tests a series of external parameters are involved like imperfections of the prototype components which induce noise to the lecture of the signals. We are working on improving our scheme and available equipment to test it.