Keywords

Introduction

Cerebrospinal fluid (CSF) stroke volume in the aqueduct (SVaq) is widely used to evaluate CSF dynamics disorders. In healthy population, SVaq represents around 10% of the spinal stroke volume (SVspi), while intracranial subarachnoid space (SAS) stroke volume (SVsas) represents around 90% of SVspi [1]. The amplitude of the CSF oscillations through the different compartments of the cerebrospinal system is a function of the geometry and the compliances of each compartment, but we suspect that it could also be impacted by cardiac frequency. To study the CSF distribution, a numerical model of the cerebrospinal system was developed taking into account cerebral ventricles, intracranial SASs, spinal canal, and brain tissue in fluid-structure interactions.

Numerical models of the cerebrospinal system have already been developed using fluid equations only [2] or fluid and porous media equations [3], but they are not relevant in this study, so a new numerical framework is introduced. Model geometry and parameters are detailed and numerical simulations are run. A first step of validation is done before the presentation of the results and discussion.

Materials and Methods

Numerical Framework

A numerical fluid-structure interaction model is implemented using the finite-element-method library FreeFem++ [4] to model the cerebrospinal system and its interactions with the brain. This model is based on fluid mechanics equations, Navier-Stokes equations, solid mechanics equations, and linear elasticity equations coupled in a monolithic formulation [5].

The Navier-Stokes equations that describe the fluid behavior in a moving do-

main read as follows:

$$ {\displaystyle \begin{array}{c}{\rho}^{\mathrm{F}}\frac{\partial u}{\partial t}+{\rho}^{\mathrm{F}}\left(\left(u-U\right).\nabla \right)u-2{\mu}^{\mathrm{F}}\nabla .\epsilon (u)+\nabla p={f}^{\mathrm{F}}\\ {}\nabla .u=0,\end{array}} $$

where u is velocity, p pressure, U domain velocity, f F volumetric external force (taken here to be zero, meaning gravity is neglected), ρ F density, and μ F fluid dynamic viscosity, and where

$$ \epsilon (u)=\frac{1}{2}\left(\nabla u+{\left(\nabla u\right)}^T\right). $$

The linear elasticity equations that describe solid deformations read as follows:

$$ {\rho}^{\mathrm{S}}\frac{\partial^2d}{\partial {t}^2}-\nabla .{\sigma}^{\mathrm{S}}(d)={f}^{\mathrm{S}}, $$

where d is the displacement, f S the volumetric external force (taken here to be zero, meaning gravity is neglected), and ρ S the density of the solid, and where

$$ {\sigma}^{\mathrm{S}}(d)=\lambda \left(\nabla .d\right)I+2{\mu}^{\mathrm{S}}\epsilon (d) $$

where λ and μ S are Lamé’s coefficients and I is the identity matrix.

Lamé’s coefficients are defined using the Young’s modulus and Poisson’s ratio as follows:

$$ {\displaystyle \begin{array}{c}\lambda =\frac{\nu E}{\left(1-2\nu \right)\left(1+\nu \right)}\\ {}{\mu}^{\mathrm{S}}=\frac{E}{2\left(1+\nu \right)},\end{array}} $$

where E is the Young’s modulus and ν Poisson’s ratio.

To couple these two equations, the continuity of velocity and stress is imposed at the fluid-structure interface as follows:

$$ {\displaystyle \begin{array}{c}u=\frac{\partial d}{\partial t}\\ {}{\sigma}^{\mathrm{F}}\left(u,p\right)n=-{\sigma}^{\mathrm{S}}(d)n,\end{array}} $$

where n is the normal vector and

$$ {\sigma}^{\mathrm{F}}\left(u,p\right)=- pI+2{\mu}^{\mathrm{F}}\epsilon (u). $$

The monolithic formulation of this problem leads to the following matrix form, where fluid and structure problems are strongly coupled and solved at the same time:

$$ \left(\begin{array}{ccc}A& {B}^T& 0\\ {}B& \epsilon & 0\\ {}0& 0& \epsilon \end{array}\right)\left(\begin{array}{c}U\\ {}{P}^{\mathrm{F}}\\ {}{P}^{\mathrm{S}}\end{array}\right)=\left(\begin{array}{c}L\\ {}0\\ {}0\end{array}\right), $$

where ϵ is a stabilization term, A and B are the representatives matrix of the problem, U is the fluid velocity, P F is the fluid pressure, P S is the solid pressure (equal to zero), and L represents external and coupling conditions.

Geometry

The model geometry, simplified in a first approach, is deigned in accordance to realistic volume ratios of the different compartments of the cerebrospinal system. Brain, intracranial SASs, and ventricles are designed using two-dimensional disks, and a thin tube is used to mimic the high flow resistance of the aqueduct (Fig. 1).

Fig. 1
figure 1

Model geometry

Full size image

The cranium has a radius of 10 cm, intracranial SASs have a thickness of 0.75 cm, ventricles have a radius of 3 cm, the aqueduct has a radius of 0.2 cm, and the spinal canal has a radius of 1 cm.

Parameters

Fluid and structure parameters, provided from the literature [6], are taken in accordance with the CSF and brain mechanical physiological parameters (Table 1).

Table 1 Mechanical parameters
Full size table

The model input is located on the spinal canal end where a velocity profile, close to the physiological one, is imposed:

$$ v=A\sin \left(\frac{2\pi t}{p}\right), $$

where A is the velocity amplitude and p the period of the cardiac cycle.

Remark 1

In physiological conditions, CSF oscillations come from brain expansion at each cardiac cycle. In our model, this is the inverse phenomenon: CSF oscillations cause brain deformations. This behavior has been chosen, for future use of physiological measures, because CSF flow is easily measured by phase-contrast magnetic resonance imaging (PC-MRI); contrariwise, brain deformations are hard to obtain.

Simulations are performed with different values of the heart rate period (p), keeping the same SVspi (Fig. 2). Twenty cardiac cycles are simulated and the results are extracted from the last cardiac cycle. CSF velocity and pressure and brain displacements are obtained as simulation results, and CSF flow and stroke volume are calculated on the basis of these results.

Fig. 2
figure 2

Input of model

Full size image

Remark 2

Many cardiac cycles are simulated to ensure the stabilization of the system.

Results

Validation

Model validity is successfully performed on numerical benchmarks (specific cases) to ensure the correct agreement of the algorithm. In addition, flow conservation is calculated in the used model geometry during a cardiac cycle; the net flow error is 1.4% ± 1.3 SD.

Study Case

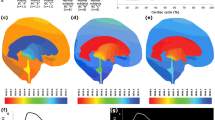
As a second validation, geometry and flow are measured in a healthy subject by MRI to design the model and impose an input velocity. Simulation results (Figs. 3 and 4) show good agreement with the PC-MRI measured data and with the physiological intracranial pressure curve shape and amplitude.

Fig. 3
figure 3

Simulation results and PC-MRI measurements of flow

Full size image
Fig. 4
figure 4

Simulation results of pressure

Full size image

Cardiac Cycle Impact

Simulation results (Figs. 5 and 6) show significant variability of SVaq and SVsas in the physiological range of cardiac frequencies; an inversion of the distribution is even observed for slow cardiac frequencies. The pressure gradient (maximum pressure minus minimum pressure during a cardiac cycle) is likewise modified by the cardiac frequency variations; it is exponentially increased with cardiac frequency growth.

Fig. 5
figure 5

Stroke volume function of cardiac frequency

Full size image
Fig. 6
figure 6

Pressure gradient function of cardiac frequency

Full size image

Discussion

Linear elasticity is justified in this application since small deformations are obtained in the simulation results. The proposed model is validated from numerical (benchmark) and physiological (flow conservation) points of view.

Numerical results in the study case are in accordance with PC-MRI measured data. In addition, the pressure curve presents a physiological amplitude and shape (peaks and valleys).

Cardiac frequency affects the CSF distribution between the two main intracranial compartments: ventricles and intracranial SASs; stroke volume distribution is in a physiological range for normal (around 60–100 bpm) and high cardiac frequencies; contrariwise, the stroke volume distribution tends to be equal in the two main compartments as cardiac frequency decreases.

Likewise, cardiac frequency affects the pressure gradient in the two compartments; the pressure gradient grows as cardiac frequency increases. Because the SVspi is conserved, a high cardiac frequency causes a rapid inflow of CSF into the intracranial compartment, which can explain this phenomenon.

Because the absolute pressure term does not appear in the Navier-Stokes formulation (only its gradient), it is impossible to obtain information about the absolute pressure of the CSF; only the gradient of the intracranial pressure is calculated.

Conclusions

A numerical model is presented taking into account the numerous fluid-structure interactions in the cerebrospinal system closed in the rigid skull. This model highlights significant variations in stroke volume distribution under cardiac frequency variations only.

In the future, spatial distribution of the intracranial pressure gradient in all the cranio spinal compartments will be studied over the time. Improvements will be introduced to the model, including with respect to arterial and venous flow. Another improvement could be the determination of the absolute intracranial pressure in connection with Marmarou’s studies and the pressure volume curve [7, 8].