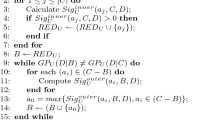Attribute Reduction on Distributed Incomplete Decision Information System

Abstract

Attribute reduction is an important issue in rough set theory. This paper mainly studies attribute reduction of distributed incomplete decision information system (DIDIS). Firstly, the definition of rough set in DIDIS is developed. Next, an algorithm for attribute reduction of DIDIS is proposed. In the end, two groups of experiments are conducted to prove the effectiveness of the proposed method. The results show that our method can remove redundant attributes of DIDIS, and does not reduce the classification capability of the system. In addition, the results indicate that the change of data missing rate has weak effect on attribute reduction with the similarity relation, but strong effect on attribute reduction with the tolerance relation.

1 Introduction

In an information system, the missing values of attributes, which we do not know, but exist actually, are ubiquitous. Generally, the data with missing values require related preprocessing for the follow-up data mining. For the processing of centralized incomplete decision information system (CIDIS), researchers carried out extensive researches, and proposed many methods, such as case deletion, imputation, model extension, etc. [1,2,3,4,5]. However, these methods cause certain degree of damage to the original information system.

In order to address the attribute reduction of CIDIS and do not change the original data distribution, many methods have been developed. Meng and Shi constructed a positive region-based attribute reduction algorithm, which is fast and efficient, and could be applied to both consistent and inconsistent incomplete decision systems [6]. Qian et al. proposed a theoretic framework based on tolerance relations, and designed a general heuristic incomplete feature selection algorithm based on this framework, and the algorithm could accelerate the process of feature selection for incomplete data [7]. Sun et al. introduced rough entropy-based uncertainty measures to evaluate the roughness and accuracy of knowledge, and proposed a heuristic feature selection algorithm with low computational complexity [8]. Dai et al. introduced another conditional entropy to measure the importance of attributes in incomplete decision system, and constructed three methods to select important attributes from incomplete decision system based on three different kinds of search strategies, but two of them are effective [9]. Zhao and Qin introduced an extended rough set model and neighborhood-tolerance conditional entropy, which can be used to reduce incomplete data with mixed categorical and numerical features [10]. Lu et al. proposed a boundary region-based feature selection algorithm, which can simplify large incomplete decision systems, and select an effective feature subset [11]. All the literatures mentioned above focus on the attribute reduction of incomplete information system which is stored in one place.

To cope with the attribute reduction of information system stored in multiple sites, researchers put forward a lot of methods. For vertically partitioned multi-decision table, Yang and Yang introduced an approximate reduction algorithm based on conditional entropy [12]. Zhou et al. developed secure sum of matrices and secure set union, and studied a privacy preserving attribute reduction algorithm based on discernible matrix for distributed datasets [13]. Ye et al. presented some SMC protocols into efficient privacy preserving attribute reduction algorithm for vertically partitioned data based on semi-trusted third party and commutative encryption [14]. Banerjee and Chakravarty proposed a privacy preserving feature selection algorithm for distributed data using virtual dimension [15]. Hu et al. defined rough set in distributed decision information system, and presented a distributed attribute reduction algorithm [16].

In summary, people have studied attribute reduction of CIDIS and distributed decision information system respectively, but rarely study attribute reduction of distributed decision information system with missing values, called distributed incomplete decision information system (DIDIS). In this paper, attribute reduction of DIDIS based on the tolerance relation and the similarity relation is studied, and the influence of different data missing rates on attribute reduction is illustrated.

This paper is structured as follows: In Sect. 2, some basic concepts of incomplete information system are reviewed. In Sect. 3, the definition of rough set in distributed incomplete decision information system is given. In Sect. 4, we propose an attribute reduction algorithm for distributed incomplete decision information system. In Sect. 5, the experimental results and analysis are presented. In Sect. 6, some conclusions are given.

2 Preliminaries

An incomplete information system refers to the absence of attribute values in an information system, as defined below [17].

Definition 1

An information system is defined as $IS = (U,A,V,f)$, U is a non-empty finite set of objects, called the universe. A is a non-empty finite set of attributes. $V = {\cup _{a \in A}}{V_a}$, where ${V_a}$ is the value of attribute a. $f:U \times A \rightarrow V$ is an information function that specifies the value of each object in universe. If there exist $a \in A$ and $x \in U$ such that $f(x,a) = *$ ($*$ indicates a missing attribute value), then the information system is incomplete, otherwise it is complete.

If the non-empty attribute set A in an incomplete information system is divided into condition attribute set C and decision attribute set D, that is, $A = C \,{\cup }\, D$, an incomplete decision table $IDT = (U,C \,{\cup }\, D,V,f)$ can be obtained. In the following, we do not consider the case where the missing values exist in the decision attribute values.

Kryszkiewicz assumed that the real value of a missing attribute value could be any one from the attribute domain, and introduced a tolerance relation to measure the similarity between objects in an incomplete information system. The tolerance relation is defined as follows [18].

Definition 2

For an incomplete decision table $IDT = (U,C \cup D,V,f)$ and a subset of condition attribute set $B \subseteq C$, the tolerance relation T is defined as

$$\begin{aligned} {\forall _{x,y \in U}}T(x,y) \Leftrightarrow {\forall _{{c_j} \in B}}({c_j}(x) = {c_j}(y) \vee {c_j}(x) = * \vee {c_j}(y) = *) \end{aligned}$$

(1)

The tolerance relation is reflexive and symmetric, but not necessarily transitive. Let $[x]_T^B$ denotes a set of individual object y that satisfy the tolerance relation T(x, y) on B, called the tolerance class of x. Given an arbitrary set $X \subseteq U$, the upper and lower approximation sets of X and the positive region of D with respect to B are defined as follows [18].

Definition 3

For an incomplete decision table $IDT = (U,C \cup D,V,f)$ and an arbitrary set $X \subseteq U$, the upper approximation $B_T^- (X)$ and the lower approximation $B_{-}^T(X)$ of X with respect to B are

$$\begin{aligned} B_T^- (X) = \{ x \in U|[x]_T^B \cap X \ne \emptyset \} \end{aligned}$$

(2)

$$\begin{aligned} B_{-}^T(X) = \{ x \in U|[x]_T^B \subseteq X\} \end{aligned}$$

(3)

Let $U/D = \{ {d_1},{d_2},...,{d_m}\}$ be the partition of the universe U defined by D. Then the positive region of D with respect to B is

$$\begin{aligned} POS_B^T(D) = \bigcup \limits _{i = 1}^m {B_{-}^T({d_i})} \end{aligned}$$

(4)

Stefanowski and Tsoukiàs assumed that the real value of a missing value is unknown and it is not allowed to compare with missing value, and introduced a similarity relation to measure the similarity between objects in an incomplete information system. The similarity relation is defined as follows [19].

Definition 4

For an incomplete decision table $IDT = (U,C \cup D,V,f)$ and a subset of condition attribute set $B \subseteq C$, the similarity relation S is defined as

$$\begin{aligned} {\forall _{x,y \in U}}S(x,y) \Leftrightarrow {\forall _{{c_j} \in B}}({c_j}(x) = {c_j}(y) \vee {c_j}(x) = *) \end{aligned}$$

(5)

The similarity relation S is reflexive and transitive, but not necessarily symmetric. Given an arbitrary object $x \in U$, one can define two sets as below [19].

Definition 5

The set of objects similar to x and the set of objects to which x is similar are defined respectively as

$$\begin{aligned} {[x]_B} = \{ y \in U|S(y,x)\} \end{aligned}$$

(6)

$$\begin{aligned}{}[x]_B^- = \{ y \in U|S(x,y)\} \end{aligned}$$

(7)

For convenience, we call $[x]_B^-$ as the similarity class of x in the following. Based on ${[x]_B}$ and $[x]_B^-$, Stefanowski and Tsoukiàs defined the upper and lower approximation sets of X and the positive region of D with respect to B [19].

Definition 6

For an incomplete decision table $IDT = (U,C \cup D,V,f)$ and an arbitrary set $X \subseteq U$, the upper approximation $B_S^- (X)$ and the lower approximation $B_{-}^S(X)$ of X with respect to B are

$$\begin{aligned} B_S^- (X) = \cup \{ {[x]_B}|x \in X\} \end{aligned}$$

(8)

$$\begin{aligned} B_{-}^S(X) = \{ x \in U|[x]_B^- \subseteq X\} \end{aligned}$$

(9)

Let $U/D = \{ {d_1},{d_2},...,{d_m}\}$ be the partition of the universe U defined by D. Then the positive region of D with respect to B is

$$\begin{aligned} POS_B^S(D) = \bigcup \limits _{i = 1}^m {B_{-}^S({d_i})} \end{aligned}$$

(10)

According to the definition above, a positive region is a set of all objects in the universe that can be classified under a given condition attribute set.

3 Rough Set in Distributed Incomplete Decision Information System

Hu et al. presented a definition of rough set in distributed decision information system and proposed an attribute reduction algorithm of distributed decision information system [16]. However, they did not discuss the absence of missing values in distributed decision information system, which will be discussed below.

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, then there is at least one incomplete decision table ${S_i} = ({U_i},{C_i} \cup D,V,f)$. There are two generic scenarios of DIDIS. One is instance-distributed, and the other is attribute-distributed. Here we mainly focus on the latter one, where ${U_1} = {U_2} = ... = {U_n}$ and ${C_i} \ne {C_j}(i \ne j)$.

Definition 7

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system. Given an arbitrary set $X \subseteq U$, an arbitrary attribute set $B \subseteq C$ where $C = \bigcup \limits _{i = 1}^n {{C_i}}$, $B = \bigcup \limits _{i = 1}^n {{B_i}}$, ${B_i} \subseteq {C_i}$, two definitions can be obtained respectively, according to the tolerance relation and the similarity relation.

Based on tolerance relation T, the upper approximation and the lower approximation of X with respect to B are

$$\begin{aligned} B_T^- (X) = \{ x \in U|{\forall _{{S_i} \in \varDelta }}([x]_T^{{B_i}} \cap X \ne \emptyset )\} \end{aligned}$$

(11)

$$\begin{aligned} B_{-}^T(X) = \{ x \in U|{\exists _{{S_i} \in \varDelta }}([x]_T^{{B_i}} \subseteq X)\} \end{aligned}$$

(12)

The positive region of $\varDelta$ with respect to B is

$$\begin{aligned} POS_B^T(D) = \{ x \in U|{\exists _{{S_i} \in \varDelta \wedge {d_j} \in U/D}}([x]_T^{{B_i}} \subseteq {d_j})\} \end{aligned}$$

(13)

where $[x]_T^{{B_i}}$ is the tolerance class of x produced by the condition attribute set ${B_i}$ of ${S_i}$.

Based on similarity relation S, the upper approximation and the lower approximation of X with respect to B are

$$\begin{aligned} B_S^- (X) = \cup \{ {[x]_{{B_i}}}|x \in X, {S_i} \in \varDelta \} \end{aligned}$$

(14)

$$\begin{aligned} B_{-}^S(X) = \{ x \in U|{\exists _{{S_i} \in \varDelta }}([x]_{{B_i}}^- \subseteq X)\} \end{aligned}$$

(15)

The positive region of $\varDelta$ with respect to B is

$$\begin{aligned} POS_B^S(D) = \{ x \in U|{\exists _{{S_i} \in \varDelta \wedge {d_j} \in U/D}}([x]_{{B_i}}^- \subseteq {d_j})\} \end{aligned}$$

(16)

where $[x]_{{B_i}}^-$ is the set of objects to which x is similar produced by the condition attribute set ${B_i}$ of ${S_i}$.

Theorem 1

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, T is the tolerance relation, the positive region of D with respect to $\varDelta$ is the union of the positive region generated by each incomplete decision table of $\varDelta$. That is, $POS_C^T(D) = \bigcup \limits _{i = 1}^n {POS_{{C_i}}^T(D)}$.

Proof

Suppose $x \in PO{S_\varDelta }(D)$, there exist ${S_i} \in \varDelta$ and ${d_j} \in U/D$, $[x]_T^{{C_i}}$ is the tolerance class of x, such that $[x]_T^{{C_i}} \subseteq {d_j}$. That means $x \in PO{S_{{C_i}}}(D)$, thus $x \in \bigcup \limits _{i = 1}^n {PO{S_{{C_i}}}(D)}$. In the contrary, if $x \in \bigcup \limits _{i = 1}^n {PO{S_{{C_i}}}(D)}$, x must belong to the positive region of an incomplete decision table of $\varDelta$. Suppose it is ${S_i}$, then there exists $[x]_T^{{C_i}} \subseteq {d_j}$. Therefore, $x \in PO{S_\varDelta }(D)$. Hence the theorem has been proved.

Theorem 2

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, S is the similarity relation, the positive region of D with respect to $\varDelta$ is the union of the positive region generated by each incomplete decision table of $\varDelta$. That is, $POS_C^S(D) = \bigcup \limits _{i = 1}^n {POS_{{C_i}}^S(D)}$.

Proof

Suppose $x \in PO{S_\varDelta }(D)$, there exist ${S_i} \in \varDelta$ and ${d_j} \in U/D$, $[x]_{{C_i}}^-$ is the similarity class of x, such that $[x]_{{C_i}}^- \subseteq {d_j}$. That means $x \in PO{S_{{C_i}}}(D)$, thus $x \in \bigcup \limits _{i = 1}^n {PO{S_{{C_i}}}(D)}$. In the contrary, if $x \in \bigcup \limits _{i = 1}^n {PO{S_{{C_i}}}(D)}$, x must belong to the positive region of an incomplete decision table of $\varDelta$. Suppose it is ${S_i}$, then there exists $[x]_{{C_i}}^- \subseteq {d_j}$. Therefore, $x \in PO{S_\varDelta }(D)$. Hence the theorem has been proved.

From above theorems, we know that the positive region of DIDIS can be calculated indirectly through the positive region of each incomplete decision table.

4 Attribute Reduction on Distributed Incomplete Decision Information System

Attribute reduction can effectively delete redundant attributes, improve data quality and speed up the subsequent data mining. In this section, we study the attribute reduction of distributed incomplete decision information system.

Theorem 3

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, $\varPhi$ and $\varPsi$ be two subsets of $\varDelta$. If $\varPhi \subseteq \varPsi$, then $PO{S_\varPhi }(D) \subseteq PO{S_\varPsi }(D)$.

Proof

The proof comes directly from Theorems 1 or 2, and hence it is omitted here.

According to Theorem 3, if we add a new incomplete decision table to a distributed incomplete decision information system $\varDelta$, then the positive region of $\varDelta$ increases or remains the same. In contrast, if we delete an incomplete decision table from $\varDelta$, then the positive region of $\varDelta$ decreases or is left unchanged.

Definition 8

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, if $PO{S_{\varDelta - \{ {S_i}\} }}(D) = PO{S_\varDelta }(D)$, then ${S_i}$ is reducible with respect to D in $\varDelta$; otherwise ${S_i}$ is irreducible with respect to D in $\varDelta$.

Theorem 4

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, if $PO{S_{{C_i}}}(D) \subseteq PO{S_{\varDelta - \{ {S_i}\} }}(D)$, then ${S_i}$ is reducible with respect to D.

Proof

The proof comes directly from Theorems 1 or 2, and hence it is omitted here.

Theorem 5

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, if and only if ${\exists _{x \in U}}(x \in PO{S_{{C_i}}}(D) \wedge x \notin PO{S_{\varDelta - \{ {S_i}\} }}(D))$, then ${S_i}$ is irreducible with respect to D.

Proof

The proof comes directly from Theorem 4, and hence it is omitted here.

Definition 9

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, ${C_i}$ is the attribute set of ${S_i}$, for any $a \in {C_i}$, if the positive region of $\varDelta$ with respect to D stays unchanged when a is deleted from ${S_i}$, that is, $POS_\varDelta ^{{S_i} - \{ a\} }(D) = PO{S_\varDelta }(D)$, then a is redundant. Otherwise a is necessary.

Theorem 6

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, a is one condition attribute of ${S_i}$. If a is reducible with respect to D in ${S_i}$, then a is reducible with respect to D in $\varDelta$.

Proof

If a is reducible with respect to D in ${S_i}$, that is, the positive region of ${S_i}$ remains the same when a is deleted from ${S_i}$. According to Theorems 1 or 2, the positive region of $\varDelta$ stays unchanged. That is, a is reducible with respect to D in $\varDelta$.

However, if a is irreducible with respect to D in ${S_i}$, it does not mean that a is irreducible with respect to D in $\varDelta$.

Definition 10

Let $\varDelta = \left\{ {{S_1},{S_2},...,{S_n}} \right\}$ be a distributed incomplete decision information system, $\varTheta = \{ {T_1},{T_2},...,{T_m}\}$ is a subsystem of $\varDelta$, for any ${T_i} \in \varTheta$, there exists ${S_j} \in \varDelta$, such that ${T_i} \subseteq {S_j}$. $\varTheta$ is a reduct of $\varDelta$ with respect to D if it satisfies the following two conditions:

• (1) $PO{S_\varTheta }(D) = PO{S_\varDelta }(D)$;

• (2) $\forall a \in {T_i},\;POS_\varTheta ^{{T_i} - \{ a\} }(D) \ne PO{S_\varTheta }(D)$.

According to the Definition 9 and Definition 10 presented above, a subsystem $\varTheta$ of a distributed incomplete decision information system $\varDelta$ has the same positive region as $\varDelta$. If any condition attribute is deleted from $\varTheta$, the positive region of $\varTheta$ decreases. The attribute reduction algorithm of distributed incomplete decision information system is developed as follows.

For a distributed incomplete decision information system, using above algorithm, one can get a reducted subsystem. The following example illustrates how to construct a reduct using ARDIDIS.

Table 1. A distributed incomplete decision information system

As shown in Table 1 is a distributed incomplete decision information system $\varDelta$ which has two incomplete decision tables, ${S_1}$ and ${S_2}$. ${S_1}$ has three condition attributes ${C_1} = \left\{ {{a_1},{a_2},{a_3}} \right\}$. ${S_2}$ has three condition attributes ${C_2} = \left\{ {{a_4},{a_5},{a_6}} \right\}$.

Based on the tolerance relation, attribute reduction for $\varDelta$ is performed using ARDIDIS, as described below.

For ${S_1}$, $[{x_0}]_T^{{C_1}} = \{ {x_0},{x_2},{x_4}\}$, $[{x_1}]_T^{{C_1}} = \{ {x_1},{x_3},{x_5}\}$, $[{x_2}]_T^{{C_1}} = \{ {x_0},{x_2},{x_3},{x_4}\}$, $[{x_3}]_T^{{C_1}} = \{ {x_1},{x_2},{x_3},{x_5}\}$, $[{x_4}]_T^{{C_1}} = \{ {x_0},{x_2},{x_4}\}$, $[{x_5}]_T^{{C_1}} = \{ {x_1},{x_3},{x_5}\}$.

$U/D = \{ \{ {x_1},{x_3},{x_5}\} ,\{ {x_0},{x_2},{x_4}\} \}$.

According to Definition 3, $POS_{{C_1}}^T(D) = \{ {x_0},{x_1},{x_4},{x_5}\}$.

For ${S_2}$, $[{x_0}]_T^{{C_2}} = \{ {x_0},{x_5}\}$, $[{x_1}]_T^{{C_2}} = \{ {x_1},{x_3},{x_5}\}$, $[{x_2}]_T^{{C_2}} = \{ {x_2}\}$, $[{x_3}]_T^{{C_2}} = \{ {x_1}, {x_3},{x_5}\}$, $[{x_4}]_T^{{C_2}} = \{ {x_4}\}$, $[{x_5}]_T^{{C_2}} = \{ {x_0},{x_1},{x_3},{x_5}\}$.

$U/D = \{ \{ {x_1},{x_3},{x_5}\}, \{ {x_0},{x_2},{x_4}\}\}$.

According to Definition 3, $POS_{{C_2}}^T(D) = \{ {x_1},{x_2},{x_3},{x_4}\}$.

According to Theorem 1, $POS_C^T(D) = POS_{{C_1}}^T(D) \cup POS_{{C_2}}^T(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4}, {x_5}\}$.

We in turn determine which attributes in each incomplete decision table are reducible.

If ${a_1}$ is deleted from ${S_1}$, then

$[{x_0}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_0},{x_2},{x_4}\}$, $[{x_1}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_1},{x_3},{x_5}\}$, $[{x_2}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_0},{x_2},{x_3},{x_4}\}$, $[{x_3}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_1},{x_2},{x_3},{x_5}\}$, $[{x_4}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_0},{x_2},{x_4}\}$, $[{x_5}]_T^{{C_1} - \{ {a_1}\} } = \{ {x_1},{x_3},{x_5}\}$. $POS_{{\mathrm{{C}}_\mathrm{{1}}} - \{ {a_\mathrm{{1}}}\} }^T(D) = \{ {x_0},{x_1},{x_4},{x_5}\}$.

$POS_C^T(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4},{x_5}\}$ stays unchanged. That is, ${a_1}$ is reducible.

Using the same method to determine the remaining attributes, we found that ${a_6}$ can also be reduced. Finally, we obtain a reduct $\{{a_2},{a_3},{a_4},{a_5}\}$.

Based on the similarity relation, attribute reduction for $\varDelta$ is performed using ARDIDIS, as described below.

For ${S_1}$, $[{x_0}]_{{C_1}}^- = \{ {x_0}\}$, $[{x_1}]_{{C_1}}^- = \{ {x_1},{x_5}\}$, $[{x_2}]_{{C_1}}^- = \{ {x_0},{x_2},{x_4}\}$, $[{x_3}]_{{C_1}}^- = \{ {x_1},{x_3},{x_5}\}$, $[{x_4}]_{{C_1}}^- = \{ {x_0},{x_4}\}$, $[{x_5}]_{{C_1}}^- = \{ {x_1},{x_5}\}$.

$U/D = \{ \{ {x_1},{x_3},{x_5}\} ,\{ {x_0},{x_2},{x_4}\} \}$.

According to Definition 6, $POS_{{C_1}}^S(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4},{x_5}\}$.

For ${S_2}$, $[{x_0}]_{{C_2}}^- = \{ {x_0}\}$, $[{x_1}]_{{C_2}}^- = \{ {x_1}\}$, $[{x_2}]_{{C_2}}^- = \{ {x_2}\}$, $[{x_3}]_{{C_2}}^- = \{ {x_1},{x_3}\}$, $[{x_4}]_{{C_2}}^- = \{ {x_4}\}$, $[{x_5}]_{{C_2}}^- = \{ {x_1},{x_5}\}$.

$U/D = \{ \{ {x_1},{x_3},{x_5}\} ,\{ {x_0},{x_2},{x_4}\} \}$.

According to Definition 6, $POS_{{C_2}}^S(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4},{x_5}\}$.

According to Theorem 2, $POS_C^S(D) = POS_{{C_1}}^S(D) \cup POS_{{C_2}}^S(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4}, {x_5}\}$.

We in turn determine which attributes are reducible in each incomplete decision table.

If ${a_1}$ is deleted from ${S_1}$, then

$[{x_0}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_0},{x_4}\}$, $[{x_1}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_1},{x_5}\}$, $[{x_2}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_0},{x_2},{x_4}\}$, $[{x_3}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_1},{x_3},{x_5}\}$, $[{x_4}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_0},{x_4}\}$, $[{x_5}]_{{C_1} - \{ {a_1}\} }^- = \{ {x_1},{x_5}\}$. $POS_{{C_\mathrm{{1}}} - \{ {a_\mathrm{{1}}}\}}^S(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4},{x_5}\}$.

$POS_C^S(D) = \{ {x_0},{x_1},{x_2},{x_3},{x_4},{x_5}\}$ stays unchanged, so ${a_1}$ can be reduced.

For the remaining attributes, we found that ${a_2}$ and ${a_3}$ can also be reduced. Finally, we obtain a reduct $\{ {a_4},{a_5},{a_6}\}$, which is different from the reduct gotten by the tolerance relation.

5 Experimental Studies

In this section, two groups of experiments were conducted. One is to prove the effectiveness of the algorithm developed in the last section, and the other is to analyze the influence of different missing rates on attribute reduction.

Fig. 1.

The experimental framework

To simulate 40 distributed incomplete decision information systems stored in two or three data sites, an incomplete dataset is divided into two or three parts, and a total of 40 splits are performed. Based on the tolerance relation and the similarity relation, all DIDISs are first reduced by ARDIDIS proposed in this paper, and then are trained to obtain the corresponding classifiers. Finally, we get the ensemble result of all classifiers. The experimental framework is shown in Fig. 1. The reason why we conducted experiments on 40 DIDISs is that we expected a static result, such as the average attribute numbers, the mean of integrated classification accuracy, which are showed in the following experimental results.

The classifiers used here are J48 and Naive Bayes (NB) that can handle missing values in weka, and all classification experiments were run in a 10-fold cross validation mode. For the sample to be classified, the integration method is to sum the probability of the same label in different data site, and the predicted label is the label with the largest probability. The calculation method is as follows.

$$\begin{aligned} \mathrm{predicted\_label} = \mathop {\arg \max }\limits _i (\sum \limits _j {{x_{ji}}}) \end{aligned}$$

(17)

where the label probability ${x_{ji}}$ represents the probability of x belonging to label i according to classifier j.

Table 2. Information of datasets

The seven datasets used in the experiments are downloaded from the UCI machine learning database, and the information of each dataset is shown in Table 2.

5.1 The Experiment Result of Group 1

• (1) Based on the tolerance relation, 40 distributed incomplete decision information systems with two data sites are reduced. The comparison of the average number of attributes and the mean of integrated classification accuracy are shown in Figs. 2 and 3, respectively.

• (2) Based on the tolerance relation, 40 distributed incomplete decision information systems with three data sites are reduced. The comparison of the average number of attributes and the mean of integrated classification accuracy are shown in Figs. 4 and 5, respectively.

• (3) Based on the similarity relation, 40 distributed incomplete decision information systems with two data sites are reduced. The comparison of the average number of attributes and the mean of integrated classification accuracy are shown in Figs. 6 and 7, respectively.

• (4) Based on the similarity relation, 40 distributed incomplete decision information systems with three data sites are reduced. The comparison of the average number of attributes and the mean of integrated classification accuracy are shown in Figs. 8 and 9, respectively.

Fig. 2.

The average attribute numbers before and after reduction

Fig. 3.

The mean of integrated classification accuracy before and after reduction

Fig. 4.

The average attribute numbers before and after reduction

Fig. 5.

The mean of integrated classification accuracy before and after reduction

Fig. 6.

The average attribute numbers before and after reduction

Fig. 7.

The mean of integrated classification accuracy before and after reduction

Fig. 8.

The average attribute numbers before and after reduction

Fig. 9.

The mean of integrated classification accuracy before and after reduction

It can be seen from Figs. 2, 4, 6 and 8 that the conditional attribute set has been reduced to varying degrees, when the tolerance relation or the similarity relation is used. From Figs. 3, 5, 7 and 9, it is found that the integration result after reduction has little or no difference as the integration result before reduction no matter which classifier is used.

5.2 The Experiment Result of Group 2

To find the influence of different random missing rates on attribute reduction, a complete dataset is randomly deleted at the rates of 5%, 10%, 15%, 20%, 25%, 30%, and then six incomplete datasets can be obtained. Each incomplete dataset is processed in the same way as before.

• (1) For all 40 distributed incomplete decision information systems with two data sites, the attribute reduction is performed based on the tolerance relation. The total number of attributes on average after reduction and the total number of attributes of original DIDISs are shown in Fig. 10. Figure 11 shows the results gotten by 40 distributed incomplete decision information systems with three data sites.

From Figs. 10 and 11, we can see that the number of reduced attributes exhibits several kinds of changes as the missing rate increases. First, when the missing rate is low, the number of attributes that can be reduced decreases gradually with the increase of the missing rate. However, when the missing rate is high, there is no obvious change on the number of attributes that can be reduced by ARDIDIS. Moreover, when the missing rate exceeds a threshold, the number of reduced attributes increases sharply.

Fig. 10.

The average attribute numbers before and after reduction

Fig. 11.

The average attribute numbers before and after reduction

The reason why we got above results is that the positive region of DIDIS varies with the increase of the missing rate. When a DIDIS is reduced using the tolerance relation, the size of tolerance class for each sample tends to monotonically increase with the missing rate increasing. When the missing rate does not reach a certain threshold, the tolerance class of each sample does not change or increase, the positive region of DIDIS remains unchanged or does not change much. That is, the classification ability of DIDIS does not change much, but the ability of each attribute to discriminate samples is decreased. Therefore, as the missing rate increases, the number of reduced attributes decreases, and DIDIS needs to retain more attributes to distinguish the samples, which is conforming to the first result. But when the missing rate exceeds a certain threshold, the positive region of DIDIS is reduced a lot due to the fact that the tolerance classes of some samples become very large. In this case, the classification ability of DIDIS is reduced, and the ability of distinguishing the samples of each attribute is also decreased. However, with the increase of the missing rate, the number of reduced attribute may increase or decrease. This analysis is consistent with the second result. If the missing rate becomes so large that the positive region of one or more incomplete decision tables become empty, the number of reduced attributes will increase sharply.

• (2) For all 40 distributed incomplete decision information systems with two data sites, the attribute reduction is performed based on the similarity relation. The total number of attributes on average after reduction and the total number of attributes of original DIDISs are shown in Fig. 12. Figure 13 shows the results gotten by 40 distributed incomplete decision information systems with three data sites.

Fig. 12.

The average attribute numbers before and after reduction

Fig. 13.

The average attribute numbers before and after reduction

From Figs. 12 and 13, there is no obvious change rule on the number of reduced attributes when the missing rate increases. That is, similarity class of each sample may increase, decrease or stay unchanged with the increase of the missing rate. As a result, the change of the positive region of DIDIS cannot be predicted. Moreover, with the increasing of the missing rate, the ability of each attribute to distinguish samples may decrease. Compared the attribute reduction using the tolerance relation with the attribute reduction using the similarity relation, the influence of the missing rate is stronger on the former.

6 Conclusions

In order to simplify a distributed incomplete decision information system and keep its classification ability, we proposed an attribute reduction method based on rough set theory. We first proposed a definition of rough set in distributed incomplete decision information system, and then developed an attribute reduction algorithm based on it. The experiment results show that our method is effective no matter the tolerance relation or the similarity relation is applied. In addition, we found that the increase of the missing rate may have larger effect on the attribute reduction when the tolerance relation is used, while less effect on the attribute reduction when the similarity relation is used.