1 Introduction

Today, micro/nanosystems have found special importance and place in many scientific and industrial sectors. With the recent advances in technology, the use of elements such as microbeams, microshells, and microsheets, etc. in modeling microstructures has increased. The most suitable tool that has been widely used in this field are microbeams. The issue of microbeam vibrations has recently received much attention due to its numerous applications in nanotechnology-related instruments such as atomic force microscopes, nanomechanical sensors, and friction force microscopes. The microbeams used in this case usually have a combined motion of bending and torsion.

Coupled bending and torsional vibration in beams can often be caused by these three conditions: (a) the distance between the center of shear and the neutral axes, (b) the gyroscopic effect, (c) the geometry of the beam. The distance between the center of mass and the center of shear can lead to a coupled bending and torsional vibration in mechanical structures, in which the presence of flexural and torsional couplings has a significant effect on the natural frequencies, the associated mode shapes, and time response [1, 2]. It should be noted that most of the researches have done so far are based on the classic beam theory of continuous media and macro scale. Therefore, at first, the activities carried out in this regard are discussed.

Banerjee [3] investigated beams with cross sections which have only one symmetry axis under the coupled bending and torsional and extracted an explicit expression for the components of the dynamic stiffness matrix without considering the axial load effect, then calculated the natural frequencies using the dynamic stiffness method for different boundary conditions. Banerjee and Williams [4] derived analytical expressions for the coupled bending–torsional dynamic stiffness matrix terms of an axially loaded uniform Timoshenko beam element in an exact sense by solving the governing differential equations of motion of the element.

Coupled bending–torsional dynamic stiffness matrix for Timoshenko beams with clamped-free type of boundary conditions by considering the effects of shear deformation and rotational inertia have also been considered.

Banerjee and Fisher [5] analyzed the coupled bending and torsional vibration of the Timoshenko beam under axial load and, obtained an explicit algorithm using the dynamic stiffness method to determine the natural frequencies and the associated mode shapes. According to the results, the axial compressive load reduces the natural frequency of the beam, and the axial tensile load increases the natural frequency [5]. For the first time, Eslimy-Isfahany et al. [6] investigated the dynamic response of a bending–torsion coupled beam to deterministic and random loads and, by comparing the behavior of the two models of Euler–Bernoulli and Timoshenko beams theory for modeling, it was found that the Euler–Bernoulli beam theory only gives us a flexural vibrational response, while the Timoshenko beam theory also can provide a torsional response.

Kaya and Ozgumus [7] studied the flexural–torsional-coupled free vibration analysis of axially loaded closed-section composite Timoshenko beam using differential variation method (DTM) and, showed that Flexural–torsional coupling has a decreasing effect on the natural frequency of the beam. Lee and Jang [8] used the spectral element model or the accurate dynamic stiffness matrix method to investigate the coupled bending-shear-torsion vibrations of the axially loaded composite Timoshenko beams and concluded that considering the material coupling causes to occur the resonance phenomenon at lower frequencies.

Daneshmehr et al. [9] studied free vibration analysis of cracked composite beams subjected to coupled bending torsion loads based on a first-order shear deformation theory. It is assumed that the composite beam had an open edge crack. The results of this study showed that bending and torsional coupling reduces the effect of crack on the natural frequency [9]. Sari et al. [10] examined the bending–torsional-coupled vibrations and buckling characteristics of single and double composite Timoshenko beams by using the Chebyshev method, and observed that that bending–torsional coupling in single composite Timoshenko beams reduces the buckling load and natural frequency, while it has an increasing or decreasing effect on the natural frequency of double composite Timoshenko beams. Soltani et al. [11] considered nonlocal analysis of the flexural–torsional stability for FG tapered thin-walled beam columns using the differential quadratures method (DQM), and showed that the nonlocal effect reduces the critical load.

As it turns out, all of the coupled bending–torsional vibration investigations done by the researchers was in the macro-dimension, and there is no work in the micro dimension. Selected works done using non-classical theories to investigate the coupled flexural–torsional vibration of beams, presented in the following.

Li and Hu [12] studied the nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. The size-dependent equations of motion and boundary conditions are derived by employing the Hamilton’s principle, and then the natural frequency of a simply supported beam obtained using Navier's solution, and showed that the nonlinear vibration frequencies can be generally increased with the increase of material length scale parameter or the decrease of nonlocal parameter [12]. Lei et al. [13] analyzed the bending and vibration of functionally graded (FG) microbeams based on the strain gradient elasticity theory, using the Navier solution and showed that the natural frequency obtained by the strain gradient theory is greater than the classic and the modified coupled stress theories.

Habibi et al. [14] discussed the free vibration of magneto-electro-elastic nanobeams based on modified couple stress theory in thermal environment. Size effects are taken into account, using the modified couple stress theory, including higher order electromechanical coupling, and the motion equations derived for Euler–Bernoulli beam model and using von-Kármán nonlinear strain. They only investigated the vibration of hinged–hinged nanobeams, and it is indicated that increasing length and decreasing thickness lead to decrease nanobeam natural frequencies [14]. Alibeigi et al. [15] analyzed the thermal buckling of magneto-electro-elastic piezoelectric nanobeams. The buckling response of nanobeams on the basis of the Euler–Bernoulli beam model with the von-Kármán geometrical nonlinearity using the modified couple stress theory is investigated under various types of thermal loading and electrical and magnetic fields. Results showed that the buckling temperature is significantly dependent on increasing the thickness and decreasing the beam length [15].

Mohtashami and Tadi [16] studied the size-dependent buckling and vibrations of piezoelectric nanobeam using finite element method, and the non-classical theory of modified coupling stress. Results showed the efficiency of the finite element method for the size effects and also the effects of the gradient of strain added in the form of non-classical matrix to the stiffness matrix [16]. Tadi et al. [17] discussed size-dependent nonlinear forced vibration of viscoelastic/piezoelectric nanobeam using compatible coupled stress theory for piezoelectric materials, and concluded with increases of size effect and piezoelectric coefficients, the hardening phenomena occurred in nanobeam.

Civalek et al. [18] investigated the free vibration behavior of carbon nanotube-reinforced composite (CNTRC) microbeams. Carbon nanotubes (CNTs) distributed in a polymeric matrix with different patterns, and governing differential equations derived by applying Hamilton's principle on the basis of couple stress theory and several beam theories. The obtained vibration equation is solved using Navier’s solution method and, the results showed that the highest frequency is related to the X-beam and O-beam has the lowest ones. It is also found that the size effect is more prominent when the thickness of the beam is close to the length scale parameter [18]. Uzun et al. [19] presented a finite element formulation to analyze the free vibration of carbon nanotube-based sensor in conjunction with modified couple stress and considering the effect of rotational inertia in calculations [19].

Akbarzadeh Khorshidi [20] examined the postbuckling of viscoelastic Euler–Bernoulli micro/nanobeams embedded in visco-Pasternak foundations based on the modified couple stress theory. The applied axial compressive load at the beam ends is considered as a function of time and they showed that the viscoelastic buckling load decreased over time, because of the fact that the strength of viscoelastic materials decreases over time [20]. Alizadeh Hamidi et al. [21] investigated the free torsional vibration of microwire with triangular cross-section based on modified couple stress theory and Hamilton's principle. They used the Galerkin method to solve the equations and showed that Poisson's ratio has an inverse effect on the natural frequency of the beam [21].

For the first time, Banerjee [22] presented the Euler–Bernoulli microbeam vibration analysis using the dynamic stiffness method. He used modified coupling stress theory to consider the size effect, and showed the efficiency of the dynamic stiffness method in comparison to the finite element method and other solution methods [22]. Pasha Zanoosi [23] investigated size-dependent thermo-mechanical free vibration analysis of functionally graded porous microbeams based on modified strain gradient theory and Hamilton. The frequency obtained from the modified strain gradient theory was higher than the classic theory and more accurate than the classic and modified coupled stress theories. Increasing thermal changes of microbeam working environment also reduces the natural microbeam natural frequency [23].

Mohammad-Abadi and Daneshmehr [24] studied the effect of length scale parameters on the buckling of Euler–Bernoulli, Timoshenko, and Reddy microbeams based on modified coupled stress theory and generalized differential quadratures method (GDQM). They showed that increasing the length scale parameter lead to increase in the critical load and the critical load obtained from the modified coupled stress theory is higher than the critical load obtained from the classic theory. Also, the Poisson ratio increases the critical load [24]. Jalali et al. [25] investigated the size-dependent vibration analysis of FG microbeams in thermal environment based on modified couple stress theory and Rayleigh ritz. The results showed that the material length scale parameter increases the natural frequency of the microbeam, and also increasing the temperature reduces the natural frequency of the beam [25].

Ma et al. [26] analyzed microstructure-dependent Timoshenko beam model using a variational formulation based on a modified couple stress theory and Hamilton's principle. Ghafarian and Ariaei [27] studied free and forced vibration analysis of a Timoshenko beam on viscoelastic Pasternak foundation featuring coupling between flapwise bending and torsional vibrations using the differential transform method (DTM). Fu and Zhang [28] established a new Timoshenko beam model is to address the size effect of microtubules (MTs) based on a modified couple stress theory and derived the bending equation and the buckling equation from the minimum total potential energy principle.

According to the above explanations, it is clear that in the modeling of beams in micro- and nanodimensions, the phenomenon of bending and torsional coupling has not been studied so far and this important issue is examined for the first time in present research. Also, according to the explanations provided in this section, during the manufacturing of micro/nanobeams, because of the low dimensions and special manufacturing methods in this dimension, the possibility of controlling precise manufacturing is very difficult, and therefore, the manufactured micro/nanobeams does not have perfect symmetry and undoubtedly, it can be expected that due to the uncertainties in the manufacturing process in the micro/nanodimensions, the micro/nanobeams will not have the coincident mass and elastic axis. Therefore, for more accurate modeling, bending and torsional coupling should be modeled simultaneously. In the present work, the coupled bending–torsional vibration analysis of microbeams based on the non-classic coupled stress theory with considering the size effect is performed.

2 The governing equations of motion of the bending–torsional coupling of the Timoshenko microbeam subjected to axial load

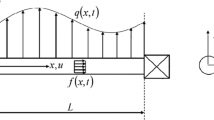
Consider a straight uniform microbeam of length L, width b, and thickness h. The shear center and centroid of the cross-section are denoted by Es and Gs, respectively, and mass axis and the elastic axis defined as the loci of the mass center and the shear center of the cross-section, which are separated by distance xα. In the right-handed Cartesian coordinate system depicted in Fig. 1, the y-axis is assumed to coincide with the elastic axis. A constant compression axial force P is assumed to act through the centroid (mass center) of the cross-section of the microbeam. P can be positive or negative, so that tension is included.

Fig. 1
figure 1

The schematic of microbeam under bending and torsional coupling

Full size image

Components of the displacement on a general point of the Timoshenko microbeam under the coupled bending–torsional may be represented according to the mid-plane characteristics such that [8]

$$\left\{ {\begin{array}{*{20}l} {u_{1} \left( {y,z,t} \right) \cong + {\text{z}}\psi \left( {y,t} \right) } \\ {u_{2} \left( {y,z,t} \right) \cong - {\text{z}}\theta \left( {y,t} \right) } \\ { u_{3} \left( {y,z,t} \right) \cong w\left( {y,t} \right) - x\psi \left( {y,t} \right)} \\ \end{array} } \right.,$$
(1)

where in the above equation, u1, u2 and u3 are the components of displacement of microbeam in the direction of x, y, z axes, respectively. Also, in the Eq. (1), the bending translation in the z-direction and the torsional rotation about the y-axis of the shear center are denoted by w(y,t) and ψ(y,t), respectively, where y and t denote distance from the origin and time, respectively. The rotation of the cross-section due to bending alone is denoted by θ(y,t).

It should be noted that, in the microdimensions, the behavior of structures is not the same as macro, and the classical continuum theories could not be proper methods to analyze the behavior of microstructures. Therefore, other methods such as experimental methods and molecular dynamics (MD) methods were used by researchers for a more accurate evaluation of the microstructures’ behaviors. Given those experimental methods in very hard to control in micro dimensions and are costly. Also, MD is costly, time-consuming, and limited to the small number of atoms in the material structure, and is not a good option in the microdimensions. Recently, non-classical elasticity methods taking into account the length scale and size parameter in scales micro are used to study the behavior of microstructures by many researchers [29,30,31,32]. Here is the modified couple stress utilized as a proper theory for modeling the coupled bending–torsional behavior of microbeams. It should also be noted that the couple stress theory has two parameters of length scales. Also, according to the research in the literature, it is very difficult to determine these parameters, therefore, in this article, the modified couple stress theory is used with a one length scale parameter.

Based on the modified coupled stress theory for linear elastic materials and infinitesimal deformations, the strain energy stored in the microbeam is expressed as [33]

$$V = \frac{1}{2}\int (\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} ){\text{d}}v,$$
(2)

where in the above relation σij, εij, mij, and xij are the components of Cauchy stress tensor, the strain tensor, coupled stress tensor, and the symmetric part of the rotation gradient tensor, respectively. According to the elastic deformation and the governing characteristic equations, the components of σij, εij, mij, and xij are presented as [33]:

$$\begin{gathered} \sigma_{ij} = {\uplambda }\varepsilon_{mm} \delta_{ij} + 2G\varepsilon_{ij} \hfill \\ \varepsilon_{ij} = \frac{1}{2}\left[ {u_{i,j} + u_{j,i} } \right] \hfill \\ m_{ij} = 2l^{2} G\chi_{ij} \hfill \\ \chi_{ij} = \frac{1}{2}\left[ {\theta_{i,j} + \theta_{j,i} } \right] \hfill \\ \theta_{i} = \frac{1}{2}\varepsilon_{ijk} u_{k,j} . \hfill \\ \end{gathered}$$
(3)

In the above relation, ui represent the displacement field, λ is the lame constant, G is the shear modulus, l is the material length scale parameter and θi is the rotation vector.

Components of strain field on an arbitrary point of the Timoshenko microbeam based on the displacement field expressed in Eq. (2), may be written as [4, 8, 33]

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{11} = \varepsilon_{33} = \gamma_{13} = 0 } \\ {\varepsilon_{22} = - z\left( {\frac{\partial \theta }{{\partial y}}} \right) } \\ {\gamma_{12} = z\left( {\frac{\partial \psi }{{\partial y}}} \right)} \\ {\gamma_{23} = \left[ {\left( {\frac{\partial w}{{\partial y}}} \right) - x\left( {\frac{\partial \psi }{{\partial y}}} \right) - \theta } \right]} \\ \end{array} } \right.,$$
(4a)
$$\left\{\begin{array}{l}{\chi }_{11}=-\frac{1}{2}\left(\frac{\partial \psi }{\partial y}\right) \\ {\chi }_{22}=\left(\frac{\partial \psi }{\partial y}\right) \\ \begin{array}{c}{\chi }_{33}=-\frac{1}{2}\left(\frac{\partial \psi }{\partial y}\right) \\ {\chi }_{12}=+\frac{1}{4}\left[\left(\frac{{\partial }^{2}w}{\partial {y}^{2}}\right)-x\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)+\left(\frac{\partial \theta }{\partial y}\right)\right]\\ \begin{array}{c}{\chi }_{23}=-\frac{1}{4}z\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)\\ {\chi }_{13}=0 \end{array}\end{array}\end{array}.\right.$$
(4b)

The virtual kinetic energy of the micro beam, T, and the virtual work done by the external force, We, express as [8]

$$\begin{aligned} & T = \frac{1}{2}\int \left( {\rho \left( {\dot{u}_{1}^{2} + \dot{u}_{2}^{2} + \dot{u}_{3}^{2} } \right)} \right){\text{d}}v \\ & W_{{\text{e}}} = \frac{1}{2}\int P\left( {w^{{\prime}{2}} - 2xw^{\prime}\psi^{\prime} + \left( {\frac{{I_{\alpha } }}{m}} \right)\psi^{{\prime}{2}} } \right){\text{d}}v. \\ \end{aligned}$$
(5)

By substituting Eqs. (3), (4) in Eq. (2) and using Eq. (5), the total energy of the beam is such that

$$\Pi =T-U-{W}_{\mathrm{e}}.$$
(6)

To measure total energy, one must substitute Eq. (4) into constitutive equations (Eq. (3)), obtain the non-zero classical and non-classical stresses (see Appendix A) and then substitute the calculated stresses into Eq. (6).

Using the Hamilton principle, it is also possible to write

$$\delta \Pi = \delta \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \mathop \int \limits_{0}^{l} \left( {T - U - W} \right){\text{d}}v{\text{d}}t = 0,$$
(7)
$$\begin{aligned} \delta \Pi & = \delta \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \mathop \int \limits_{0}^{l} \frac{1}{2}\left[ {\left\{ {m\left( {\dot{w}} \right)^{2} - 2mx_{\alpha } \dot{w}\dot{\psi } + I_{\alpha } \left( {\dot{\psi }} \right)^{2} + \rho I\left( {\dot{\theta }} \right)^{2} } \right\}} \right. \\ & \quad - \left\{ {EI(\theta^{\prime})^{2} = P(w^{\prime})^{2} + 2Px_{\alpha } w^{\prime}\psi^{\prime} - \left( {\frac{{PI_{\alpha } }}{m}} \right)(\psi^{\prime})^{2} + kAG(w^{\prime} - \theta )^{2} } \right. \\ & \quad \left. {\left. { + GJ(\psi^{\prime})^{2} } \right\} - \left\{ {3GAl^{2} \psi^{{\prime}{2}} + \frac{1}{4}GJl^{2} \left( {\psi^{\prime\prime}} \right)^{2} + \frac{1}{4}GAl^{2} \left( {w^{\prime\prime} + \theta^{\prime}} \right)^{2} } \right\}} \right]{\text{d}}y{\text{d}}t = 0. \\ \end{aligned}$$

where in the above relation, Iα is the polar mass moment of inertia and m = ρ A.

Based on the modified coupled stress theory and by applying a series of long mathematical operations, the bending–torsion coupled governing equations of motion and the associated boundary conditions for an axially loaded Timoshenko microbeam can be derived using the Hamilton principle as follows:

$$\begin{aligned} & EI\theta^{\prime\prime} + kAG\left( {w^{\prime} - \theta } \right) - \rho I\ddot{\theta } + \frac{1}{4}GAl^{2} \left( {w^{\prime\prime\prime} + \theta^{\prime\prime}} \right) - \frac{1}{4}GAl^{2} x_{\alpha } \psi^{\prime\prime\prime} = 0 \\ & \quad \left( { - EI\theta^{\prime} - \frac{1}{4}GAl^{2} \left( {w^{\prime\prime} + \theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \psi^{\prime\prime}} \right) = 0\quad {\text{or}}\quad \delta \theta = 0, \\ \end{aligned}$$
(8)
$$\begin{aligned} & kAG\left( {w^{\prime\prime} - \theta^{\prime}} \right) - P\left( {w^{\prime\prime} - x_{\alpha } \psi^{\prime\prime}} \right) - m\left( {\ddot{w} - x_{\alpha } \ddot{\psi }} \right) - \frac{1}{4}GAl^{2} \left( {w^{{\prime\prime\prime\prime}} + \theta^{\prime\prime\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \psi^{{{{\prime\prime\prime\prime}}}} = 0 \\ & \quad \left( {P\left( {w^{\prime} - x_{\alpha } \psi^{\prime}} \right) - kAG\left( {w^{\prime} - \theta } \right) + \frac{1}{4}GAl^{2} \left( {w^{\prime\prime\prime} + \theta^{\prime\prime}} \right) - \frac{1}{4}GAl^{2} x_{\alpha } \psi^{\prime\prime\prime}} \right) = 0\quad {\text{or}}\quad \delta w = 0 \\ & \quad \left( { - \frac{1}{4}GAl^{2} \left( {w^{\prime\prime} + \theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \psi^{\prime\prime}} \right) = 0\quad {\text{or}}\quad \delta w^{\prime} = 0, \\ \end{aligned}$$
(9)
$$\begin{aligned} & GJ\psi^{\prime\prime} - P\left\{ {\frac{{I_{\alpha } }}{m}\psi^{\prime\prime} - x_{\alpha } w^{\prime\prime}} \right\} - I_{\alpha } \ddot{\psi } + mx_{\alpha } \ddot{w} + 3GAl^{2} \psi^{\prime\prime} - \frac{1}{4}GJl^{2} \psi^{{{{\prime\prime\prime\prime}}}} + \frac{1}{4}GAl^{2} x_{\alpha } \theta^{\prime\prime\prime} + \frac{1}{4}GAl^{2} x_{\alpha } w^{{{{\prime\prime\prime\prime}}}} = 0 \\ & \quad \left( {P\left[ {\frac{{I_{\alpha } }}{m}\psi^{\prime} - x_{\alpha } w^{\prime}} \right] - GJ\psi^{\prime} - 3GAl^{2} \psi^{\prime} + \frac{1}{4}GJl^{2} \psi^{\prime\prime\prime} - \frac{1}{4}GAl^{2} x_{\alpha } \theta^{\prime\prime} - \frac{1}{4}GAl^{2} x_{\alpha } w^{\prime\prime\prime}} \right) = 0\quad {\text{or}}\quad \delta \psi = 0 \\ & \quad \left( {\frac{1}{4}GJl^{2} \psi^{\prime\prime} + \frac{1}{4}GAl^{2} x_{\alpha } \theta^{\prime} + \frac{1}{4}GAl^{2} x_{\alpha } w^{\prime\prime}} \right) = 0\quad {\text{or}}\quad \delta \psi^{\prime} = 0. \\ \end{aligned}$$
(10)

In special cases, these equations of motion and boundary conditions are reduced to the following equations:

By assuming l = 0, the equations obtained in this study are reduced to the equation of motion and boundary conditions in the classical continuum theory as follows [4]:

$$\begin{gathered} EI\theta^{\prime\prime} + kAG\left( {w^{\prime} - \theta } \right) - \rho I\ddot{\theta } = 0 \hfill \\ kAG\left( {w^{\prime\prime} - \theta^{\prime}} \right) - P\left( {w^{\prime\prime} - x_{\alpha } \psi^{\prime\prime}} \right) - m\left( {\ddot{w} - x_{\alpha } \ddot{\psi }} \right) = 0 \hfill \\ GJ\psi^{\prime\prime} - P\left\{ {\frac{{I_{\alpha } }}{m}\psi^{\prime\prime} - x_{\alpha } w^{\prime\prime}} \right\} - I_{\alpha } \ddot{\psi } + mx_{\alpha } \ddot{w} = 0. \hfill \\ \end{gathered}$$
(11)

The following separation of variables is compatible with the equations of motion and boundary conditions.

$$\begin{gathered} \theta \left( {y,t} \right) = e^{i\omega t} \Theta \left( y \right) \hfill \\ w\left( {y,t} \right) = e^{i\omega t} W\left( y \right) \hfill \\ \psi \left( {y,t} \right) = e^{i\omega t} \Psi \left( y \right), \hfill \\ \end{gathered}$$
(12)

where in the above relation, the Θ(y), Ψ(y), and W(y) are the bending, torsion, and transverse mode shapes of the microbeam, respectively, and i = − 1 and ω is also the natural frequencies of the microbeam. Substitution of the Eq. (12) in to the motion Eqs. (8)–(10) results into new three coupled ordinary differential equations in terms of the unknown through-the-elastic axis y functions Θ(y), Ψ(y), and W(y). The transformed equations are obtained as

$$\begin{aligned} & EI\Theta^{\prime\prime} + kAG\left( {W^{\prime} - \Theta } \right) + \rho \omega^{2} I\Theta + \frac{1}{4}GAl^{2} \left( {W^{{{{\prime\prime\prime\prime}}}} + \Theta^{\prime\prime}} \right) - \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime\prime} = 0 \\ & kAG\left( {W^{\prime\prime} - \Theta^{\prime}} \right) - P\left( {W^{\prime\prime} - x_{\alpha } \Psi^{\prime\prime}} \right) + m\omega^{2} \left( {W^{\prime\prime} - x_{\alpha } \Psi } \right) - \frac{1}{4}GAl^{2} \left( {W^{{{{\prime\prime\prime\prime}}}} + \Theta^{\prime\prime\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{{{{\prime\prime\prime\prime}}}} = 0 \\ & GJ\Psi^{\prime\prime} - P\left\{ {\frac{{I_{\alpha } }}{m}\Psi^{\prime\prime} - x_{\alpha } W^{\prime\prime}} \right\} + I_{\alpha } \omega^{2} \Psi - m\omega^{2} x_{\alpha } W + 3GAl^{2} \Psi^{\prime\prime} - \frac{1}{4}GJl^{2} \Psi^{{{{\prime\prime\prime\prime}}}} + \frac{1}{4}GAl^{2} x_{\alpha } \Theta^{\prime\prime\prime} + \frac{1}{4}GAl^{2} x_{\alpha } W^{{{{\prime\prime\prime\prime}}}} = 0. \\ \end{aligned}$$
(13)

3 Solution procedure

The motion Eq. (12) associated with the proper choice of boundary condition Eqs. (8)–(10) construct a defined boundary value problem. Various types of boundary conditions may be defined on each end of the microbaem. Each of the edges y = 0, L may be clamped (C), simply supported (S), or free (F). Mathematical expression of edge supports on the each end of the microbeam take the form as:

$$C:\Theta = W = W^{\prime} = \Psi = \Psi^{\prime} = 0,$$
$$\begin{aligned} & S:\left( { - EI\Theta^{\prime} - \frac{1}{4}GAl^{2} \left( {W^{\prime\prime} + \Theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime}} \right) = H \\ & \quad \left( { - \frac{1}{4}GAl^{2} \left( {W^{\prime\prime} + \Theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime}} \right) = \Psi \\ & \quad = \left( {\frac{1}{4}GJl^{2} \Psi^{\prime\prime} + \frac{1}{4}GAl^{2} x_{\alpha } \Theta^{\prime} + \frac{1}{4}GAl^{2} x_{\alpha } W^{\prime\prime}} \right) = 0, \\ \end{aligned}$$
$$\begin{aligned} & F:\left( { - EI\Theta^{\prime} - \frac{1}{4}GAl^{2} \left( {W^{\prime\prime} + \Theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime}} \right) \\ & \quad = \left( {P\left( {W^{\prime} - x_{\alpha } \Psi^{\prime}} \right) - kAG\left( {W^{\prime} - \Theta } \right) + \frac{1}{4}GAl^{2} \left( {W^{\prime\prime\prime} + \Theta^{\prime\prime}} \right) - \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime\prime}} \right) \\ & \quad = \left( { - \frac{1}{4}GAl^{2} \left( {W^{\prime\prime} + \Theta^{\prime}} \right) + \frac{1}{4}GAl^{2} x_{\alpha } \Psi^{\prime\prime}} \right) \\ & \quad = \left( {P\left[ {\frac{{I_{\alpha } }}{m}\Psi^{\prime} - x_{\alpha } W^{\prime}} \right] - GJ\Psi^{\prime} - 3GAl^{2} \Psi^{\prime} + \frac{1}{4}GJl^{2} \Psi^{\prime\prime\prime} - \frac{1}{4}GAl^{2} x_{\alpha } \Theta^{\prime\prime} - \frac{1}{4}GAl^{2} x_{\alpha } W^{\prime\prime\prime}} \right) \\ & \quad = \left( {\frac{1}{4}GJl^{2} \Psi^{\prime\prime} + \frac{1}{4}GAl^{2} x_{\alpha } \Theta^{\prime} + \frac{1}{4}GAl^{2} x_{\alpha } W^{\prime\prime}} \right) = 0. \\ \end{aligned}$$
(14)

To discretize Eqs. (13) and boundary conditions (14) along the length of the microbeam (along the y axis in Fig. 1), the generalised differential quadrature (GDQ) method is adopted. The basic concept of GDQ method is approximating the derivatives of a function at a sample point as the weighted linear summation of the value of the function in the whole domain. The governing differential equation are reduced to a set of algebraic equations by this approximation. The number of algebraic equations depend on the number of grid points. The nth order derivative of the function f(y) with respect to y at a sample point yi is approximated by linear sum of all the functional values at the whole grid points [34]

$$\frac{{\partial^{n} f\left( {y_{i} } \right)}}{{\partial y^{n} }} = \mathop \sum \limits_{k = 1}^{N} C_{ik}^{\left( n \right)} f\left( {y_{k} } \right),\quad i = 1, \ldots , N,\quad n = 1, \ldots , N,$$
(15)

where N is the number of grid points, yi is the location of ith grid point, f(yi) is the functional value at yi and \({C}_{ik}^{(n)}\) is the weighting coefficient corresponding to the nth order derivative in the direction y. Based on the generalized differential quadrature method, the first-order weighting coefficients are obtained as follows:

$$\begin{aligned} & C_{ij}^{\left( 1 \right)} = \frac{{M^{\left( 1 \right)} \left( {y_{i} } \right)}}{{\left( {y_{i} - y_{j} } \right)M^{\left( 1 \right)} \left( {y_{j} } \right)}}\quad i,j = 1,2, \ldots ,N\quad \left( {i \ne j} \right) \\ & C_{ii}^{\left( 1 \right)} = C_{ij}^{\left( 1 \right)} = - \mathop \sum \limits_{k = 1}^{N} C_{ik}^{\left( 1 \right)} ,\quad \left( {i.j = 1,2, \ldots ,N;\quad i \ne k;\quad i = j} \right) \\ & M^{\left( 1 \right)} \left( {y_{i} } \right) = \mathop \prod \limits_{j = 1}^{N} \left( {y_{i} - y_{j} } \right)\quad \left( {i \ne j;\quad i = 1,2, \ldots ,N} \right). \\ \end{aligned}$$
(16)

And higher order weighting coefficients may be obtained by the bellow recurrence relation recursive

$$\begin{gathered} C_{ij}^{\left( n \right)} = n \, \left( {C_{ii}^{{\left( {n - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {n - 1} \right)}} }}{{\left( {y_{i} - y_{j} } \right)}}} \right)\quad i,j = 1,2, \ldots ,N;\quad i \ne j;\quad n = 2,3, \ldots , N - 1 \hfill \\ C_{ii}^{\left( n \right)} = - \mathop \sum \limits_{j = 1}^{N} C_{ij}^{\left( n \right)} \quad \quad \quad \quad \quad \quad \quad i = 1,2, \ldots ,N;\quad i \ne j;\quad n = 1,2, \ldots ,N - 1. \hfill \\ \end{gathered}$$
(17)

Different types of grid distribution which gives an acceptable results have been introduced, meanwhile in this article the normalized Chebyshev–Gauss–Lobatto points are used.

$$y_{i} = \frac{1}{2}\left( {1 - \cos \left( {\frac{i - 1}{{N - 1}}} \right)} \right)\pi ), i = 1,2, \ldots , N.$$
(18)

Similar to the equations of motion, boundary conditions should be discretized by means of the GDQ method. Discretized equations of motion into nodal points in the microbeam domain are given in the Appendix B. Eventually, the discretized equations of motion (13) based on the GDQ method, take the following matrix form:

$$\left[{\varvec{M}}\right]\left\{\ddot{{\varvec{X}}}\right\}+\left[{\varvec{K}}\right]\left\{{\varvec{X}}\right\}=\left\{0\right\},$$
(19)

where [M] and [K] are mass and stiffness matrices, respectively. The natural frequencies of the structure may be obtained by solving the standard eigenvalue problem obtained from Eq. (19). In this research, the solution procedure by means of the GDQ method have been implemented in a MATLAB code. The SBCGE approach (method of substitution of boundary conditions into governing equations) used to apply the boundary conditions, which is an easy and powerful method for implementation of any boundary condition to the GDQ governing equations, and provides highly accurate results. For more details about GDQ method, refer to [34,35,36,37].

4 Numerical result and discussion

4.1 Comparison study

Due to the lack of results for the analysis of coupled bending–torsion vibration in microbeams using the modified coupled stress theory, in this section, the results of the present work have been validated in two special cases (three comparisons) with the results in the literature.

The first and second comparisons (Tables 1, 2) are done by considering the length scale parameter to be zero (l = 0), which shows the ability and accuracy of the formulation of this paper in the modeling of bending–torsion coupling. In this case, by assuming l = 0, the modified couple stress theory is reduced to the classical continuum theory as well as the non-classical Timoshenko beam model is reduced to the classical Timoshenko beam model.

Table 1 Natural frequencies f = ω/2π (Hz) of clamped-free thin-walled beam under axial force P = 1790 N (warping stiffness is ignored)
Full size table
Table 2 Comparison of the first five natural frequencies f = ω/2\(\pi\) (Hz) of the clamped–clamped beam under axial load P = 17900 N (warping stiffness is ignored)
Full size table

The third comparison (Table 3) is done by considering no bending and torsion coupling with modified couple stress theory, and the results are compared for the vibration analysis with bending mode to show the capability and accuracy of the formulation of this paper in the modeling of micro scales (size effect).

Table 3 Comparison between the first five natural frequencies (MHz) reported by Ke et al. [39] and present study for a simply supported Timoshenko microbeam with modified coupled stress theory (l = 17.6 µm, h/l = 1, P = 0, L = 10 h, b = 2 h, xα = 0, \(\psi\) = 0, f = ω/2π)
Full size table

A comparison study is accomplished between the results of this study and those reported by Banerjee and Williams [4] for the coupled bending–torsion vibrations of the Timoshenko beam with cross-section shown in Fig. 2, under axial load P = 1790 N using classic theory. Banerjee and Williams [4] studied the coupled bending–torsional dynamic stiffness matrix for Timoshenko beams with only clamped-free type of boundary conditions by considering the effects of shear deformation and rotational inertia. The geometric and mechanical characteristics of the beam used for comparison studies are as follow. Comparison is carried out with the results of Banerjee and Williams [4] in Table 1 at macroscale for cantilever. The excellent agreement is observed through the Natural frequency for various mode numbers.

$$\begin{gathered} EI = 6.38 \times 10^{3} \;{\text{N m}}^{2} \hfill \\ GJ = 43.46\;{\text{N}}\;{\text{m}}^{2} \hfill \\ m = \rho A = 0.835\;{\text{kg/m}} \hfill \\ \rho J = I_{\alpha } = 5.01 \times 10^{ - 4} \;{\text{kg m}} \hfill \\ x_{\alpha } = 0.0155\;{\text{m}} \hfill \\ kGA = 4.081 \times 10^{6} \;{\text{N}} \hfill \\ \rho I = 2.51 \times 10^{ - 4} \;{\text{kg m}} \hfill \\ L = 0.82\;{\text{m}}. \hfill \\ \end{gathered}$$
(20)
Fig. 2
figure 2

Cross-section of the beam used by Banerjee and Williams [4] and Li et al. [34] for comparison studies

Full size image

The next comparison study is performed by the results of Li et al. [38] for the coupled bending–torsion vibrations of the clamped–clamped Timoshenko beam with cross-section shown in Fig. 2 subjected to axial load P = 17,900 N using classic theory. Li et al. [38] considered the effects of axial force, shear deformation and rotary inertia, and derived the dynamic transfer matrix for directly solving the governing differential equations of motion for coupled bending and torsional vibration of axially loaded thin-walled Timoshenko beams. The geometric and mechanical characteristics of the beam used for comparison studies are as Eq. (20). Comparison is performed in Table 2. It is seen that, excellent agreement is observed through the Natural frequency for various mode numbers.

The third comparison study is accomplished between the results of this study and those reported by Ke et al. [39] for a simply supported Timoshenko microbeam based on modified coupled stress theory in Table 3. Excellent agreement is observed through the five natural frequencies in Table 3. In this comparison, bending and torsion coupling is ignored, and only modified couple stress theory is considered with bending analysis for microbeam.

4.2 Parametric studies

In this section, some tabulated results and illustrated graphs are provided to examine the dependency of natural frequencies of analysis of Timoshenko microbeams under coupled bending–torsion and axial load using the modified coupled stress theory to the geometric parameters and boundary conditions. In this section, a microbeam with presented mechanical properties in Table 3 is considered (Table 4).

Table 4 Mechanical properties of microbeam under coupled bending–torsion
Full size table

As seen in Table 5, the effect of the shear deformation on the natural frequency of the Timoshenko micro beam is completely significant and important. But the effect of rotary inertia seems to be insignificant. It can be seen, the natural frequencies excluding the effects of shear deformation or rotary inertia are higher than the ones including the effects of shear deformation or rotary inertia.

Table 5 First five natural frequencies f = ω/2π (MHz) of the simply supported micro-Timoshenko beam (l = 17.6 µm, h/l = 1, P = 1 µN, b = 4 h, L = 40 h, xα = 0.5 h)
Full size table

To investigate the influences of thickness to material length scale parameter ratio and type of edge supports, a parametric study is conducted and the first five natural frequencies are provided in Table 6. In this table, the symbol CF, for instance, means that the microbeam is clamped at y = 0 and free at y = L and results are given for four various combination of boundary conditions as, CC (clamped–clamped), CS (clamped-simply supported), SS (simply supported-simply supported), CF (clamped-free). For each type of mentioned edge supports, first five natural frequencies of the microbeam are reported for three different values of thickness to material length scale parameter ratios like h/l = 1, h/l = 2 and h/l = 3 in Table 6. As seen from this table, with an increase in thickness to material length scale parameter ratio, natural frequency of the microbeam decreases. A comparison among the results of Table 6 accept the fact that, fundamental frequency of CC is the highest whilst CF has the lowest fundamental natural frequency. From this table, it can be concluded that the existence of the size effect parameter, or in other words, the use of non-classic theory, predicts stiffness in the beam, and as a result, by decreasing the material length scale parameter, the natural frequency decreases.

Table 6 First five natural frequencies f = ω/2π (MHz) for various boundary conditions and different values of h/l (P = 1 µN b = 4 h L = 40 h xα = 0.5 h)
Full size table

In Fig. 3, numerical results are provided to compare the fundamental natural frequencies changes versus thickness to material length scale parameter ratio obtained by the classic and the modified coupled stress theory in terms of the ratio of thickness to the size effect parameter. It is observed that with increasing h/l, the fundamental natural frequency of the beam decreases. Also, the results found by classic theory and the modified coupled stress theory converge to each other as h/l increases. Also, the natural frequency is higher in the modified coupled stress theory than the classic theory.

Fig. 3
figure 3

Influence of thickness to material length scale parameter ratio on fundamental natural frequency of CF microbeam under a coupled bending-torsion with both classic theory and modified coupled stress theory (P = 1 µN, l = 17.6 µm, L = 40 h, b = 4 h, xα = 0.5 h, υ = 0.38)

Full size image

In Fig. 4, various boundary conditions are examined, whereas L/h and xα of the microbeam are set equal to constant values. In this plot, natural frequency of the microbeam for the different edge supports drawn in terms of thickness to the material length scale parameter. It is observed that in all boundary condition types, the natural frequency decreases with increasing h/l ratio, which alterations are more sharp for h/l < 3. It is also observed that the CC type of edge support has the highest natural frequency drop and the lowest amount of natural frequency drop is related to the CF microbeam in Fig. 4. Also, it can be concluded from this figure that reducing the material length parameter reduces the resistance and stiffness of the microbeam against coupled bending-torsion, therefore, the natural frequency decreases in all of the considered edge supports.

Fig. 4
figure 4

Fundamental natural frequency versus thickness to material length scale parameter ratio of microbeam under coupled bending–torsion obtained by modified coupled stress theory for various edge supports (P = 1 µN, l = 17.6 µm, L = 40 h, b = 4 h, xα = 0.5 h)

Full size image

In Fig. 5, the effect of compressive and tensile force and influence of the distance between the elastic and the mass axes on the fundamental natural frequency of CF microbeam are examined. As seen, with increasing distance between the elastic and the mass axes to thickness ratio xα/h, the natural frequency of the microbeam decreases. Also, the natural frequency obtained by tensile force is higher than the compressive force. Therefore, the force eccentricity reduces the stiffness and the natural frequency of the microbeam. On the other hand, applying the tensile axial load increases the stiffness of the microbeam and the applying the compressive axial load decreases the stiffness of the microbeam. As seen in Fig. 5, the alternation of fundamental natural frequency values in terms of distance between the elastic and the mass axes to thickness ratio is so slight.

Fig. 5
figure 5

Influence of the distance between the elastic and the mass axes on the fundamental natural frequency of CF microbeam under coupled bending–torsion for the compressive and tensile values of force P (h = 1 l, l = 17.6 µm, L = 40 h, b = 4 h)

Full size image

Figure 6 depicts comparison between the changes in the natural frequency of the microbeam versus the length to thickness ratio L/h and for the three values of h/l = 1, 2, 3 for the four different combinations of edge supports. It is observed that by increasing the length to thickness ratio L/h of the microbeam, the natural frequency of the beam decreases. The natural frequency drop is more keen for L/h < 40. In general, it can be concluded that as the beam becomes thinner, its stiffness against coupled bending–torsion decreases, therefore, the natural frequency decreases.

Fig. 6
figure 6

Fundamental natural frequency of microbeam under coupled bending–torsion in terms of length to thickness ratio for different h/l ratios for four different combinations of boundary condition (P = 1 µN, l = 17.6 µm, b = 4 h, xα = 0.5 h)

Full size image

Figure 7 illustrates the first three vibration mode shapes of the microbeam for various combination of edge supports and h/l = 1 and P = 1 µN. In this figure, it can be seen that the bending mode shape changes are more significant than the torsion, which can be seen better in higher modes (due to the great changes in the bending mode shapes (Θ) in comparison with torsional rotation mode shapes (ψ), the torsional rotation mode shapes are magnified with a scale of 20, in Figs. 7, 8). As seen in Fig. 7, anywhere the torsion mode shape of the beam takes their extremum values, the bending mode shape values are zero and vice versa.

Fig. 7
figure 7

First three vibration mode shapes of the microbeam under the coupled bending–torsion for various combination of edge supports (h = 1 l, l = 17.6 µm, L = 40 h, b = 4 h, xα = 0.5h)

Full size image
Fig. 8
figure 8

First three vibration mode shapes of the CF microbeam under the coupled bending–torsion for different h/l ratios (l = 17.6 µm, L = 40 h, b = 4 h, xα = 0.5 h)

Full size image

Figure 8 depicts the first three vibration mode shapes of the cantilever microbeam under axial load P = 1 µN and h/l = 1, 2, 3. As seen, the changes in the mode shapes associated with torsion are insignificant in comparison to bending mode shapes. Also, in higher modes, the changes of torsion and bending mode shapes of the microbeam observe more significant harmoniously. On the other hand, the changes of torsion and bending mode shapes along the beam are vice versa.

5 Conclusion

Coupled bending–torsional vibration analysis of axially loaded Timoshenko microbeam under arbitrary edge supports is investigated in this research. The Timoshenko microbeam is formulated within the framework of the non-classic size-dependent modified coupled stress theory. General bending–torsion coupled governing equations of motion and the complete set of boundary conditions for an axially loaded Timoshenko microbeam developed using the Hamilton principle. Two end of the microbeam assumed to be any combination of free, clamped, and simply supported. The GDQ discretization through the length of the microbeam, is developed. The set of coupled algebraic equations are solved as an eigenvalue problem to extract the natural frequencies as well as the associated mode shapes. Some comparison studies are conducted to validate the accuracy and efficiency of the present solution methodology. After that, some parametric studies are done to investigate the effects of material length scale parameter, distance between the elastic and the mass axes to thickness ratio, length to thickness ratio, axial load, and boundary conditions. It is shown that

  1. 1-

    The natural frequency of the microbeam obtained by modified coupled stress theory is higher than natural frequency calculated by the classic theory.

  2. 2-

    By increasing the thickness to material length scale parameter, the natural frequency of the beam decreases.

  3. 3-

    As the length to thickness ratio of the microbeam increases, the natural frequency decreases.

  4. 4-

    Applying the tensile axial load increases the natural frequency of the microbeam, and the compressive axial load decreases the natural frequency.

  5. 5-

    As the distance between the elastic axis and the mass axis increases, the natural frequency of the microbeam decreases.

  6. 6-

    The highest amount of natural frequency belongs to the clamped–clamped microbeam and the lowest amount of natural frequency corresponded to the clamped-free microbeam.

  7. 7-

    The natural frequencies with the effects of shear deformation or rotary inertia are less than the ones excluding the effects of shear deformation or rotary inertia.