A Physarum-Inspired Ant Colony Optimization for Community Mining

Abstract

Community mining is a powerful tool for discovering the knowledge of networks and has a wide application. The modularity is one of very popular measurements for evaluating the efficiency of community divisions. However, the modularity maximization is a NP-complete problem. As an effective optimization algorithm for solving NP-complete problems, ant colony based community detection algorithm has been proposed to deal with such task. However the low accuracy and premature still limit its performance. Aiming to overcome those shortcomings, this paper proposes a novel nature-inspired optimization for the community mining based on the Physarum, a kind of slime molds cells. In the proposed strategy, the Physarum-inspired model optimizes the heuristic factor of ant colony algorithm by endowing edges with weights. With the information of weights provided by the Physarum-inspired model, the optimized heuristic factor can improve the searching abilities of ant colony algorithms. Four real-world networks and two typical kinds of ant colony optimization algorithms are used for estimating the efficiency of proposed strategy. Experiments show that the optimized ant colony optimization algorithms can achieve a better performance in terms of robustness and accuracy with a lower computational cost.

1 Introduction

Community mining is associated with the graph clustering that is a powerful tool for knowledge discovering in many real-world complex systems [1]. Identifying the structural characteristics of a network has a wide application in knowledge discovery, such as the function prediction in the protein-protein networks [2], the real-time recommendation systems construction [3], and the information diffusion analysis [4].

Many algorithms have been proposed for mining such structures in networks, such as optimization-based algorithms [5] and stochastic model based algorithms [6]. Currently, a modularity measure Q has been proposed and widely used for estimating the qualities of community divisions [7]. Specifically, the modularity maximization is a NP-complete problem, which is intractable for traditional optimization algorithms, such as mathematical programming [8]. In the field of heuristics algorithms, ant colony optimization (ACO) algorithm is popular in dealing with the NP-complete problems [9]. But low accuracy and robustness limit its performance and application.

Recently, a kind of slime molds cell, Physarum, has shown an intelligence of network designing and path finding in biological experiments [10, 11]. Moreover, for uncovering the key mechanism of the intelligent behavior of Physarum, a mathematical model has been proposed by Tero et al. [12]. This Physarum-inspired model has been used for optimizing the heuristic algorithms [13]. Based on the characters of Physarum-inspired model, we wonder can the Physarum model optimize the ant colony optimization algorithm for community mining?

Based on the above motivation, the main contributions of this paper are as follows. Taking advantages of Physarum-inspired model, which could recognize the inter-community edges coarsely, a novel nature-inspired optimization algorithm has been proposed based on ant colony optimization. In the new algorithm, the heuristics factor of traditional ACO is optimized based on the recognition of Physarum-inspired model, which could instruct the ants to find better solutions and improve the efficiency of algorithms. Meanwhile, four real-world networks and two representative kinds of ant colony algorithms are used to demonstrate the efficiency of the proposed nature-inspired optimization algorithm, in terms of accuracy and robustness.

The remaining of this paper is organized as follows. Section 2 formulates the community mining and introduces the ant colony optimization for community mining. And then, the nature-inspired optimization is proposed based on Physarum-inspired model in Sect. 3. Section 4 reports the experiments on four real-world networks and two typical kinds of ant colony clustering algorithms. Finally, Sect. 5 concludes this paper.

2 Related Work

2.1 Formulation of Community Detection

Community mining is to divide the vertexes in a network into communities, where vertexes across communities are sparsely connected, and vertexes within a community are relatively densely connected. Based on inherent structural features, a modularity measure, denoted as Q, is proposed to evaluate the qualities of community divisions [1]. Therefore, the community mining problem can be formulated to an optimization problem, which is to maximize the modularity value. The formulation of community mining is shown as follows.

Considering a network G(V, E), where V and E stand for the sets of vertexes and edges respectively. And a community is a subset of V, where vertexes have a common certain feature. With NC indicating the number of communities, a community division is a set of communities, $C = \{ {C_1},{C_2},\ldots ,{C_{NC}}\}$, in which ${C_i} \ne \emptyset$, ${C_i} \ne {C_j}$, and ${C_i} \cap {C_j} = \emptyset$, for all i and j. After that, the mission of community mining can be represented as Eq. (1).

$$\begin{aligned} {C^*} = \arg \mathrm{{ }}\mathop {\max }\limits _C Q(G,C) \end{aligned}$$

(1)

The modularity Q is computed based on the topological structure of a network and its divisions, which is defined as Eq. (2). Specifically, $\delta (i,j)$ indicates the community relationship between vertexes i and j, while A and $d_i$ stand for the adjacent matrix of a network and degree of vertex i, respectively. $A_{i,j}$ is equal to 1, if there is an edge connecting vertexes i and j. Otherwise, $A_{i,j}$ is equal to 0. Moreover, the degree of vertex i can be expressed as ${d_i} = \sum _{j} {{A_{i,j}}}$. In details, $\delta (i,j)$ is equal to 1, if and only if vertexes i and j belong to the same community. Otherwise, $\delta (i,j)$ is equal to 0.

$$\begin{aligned} Q = \frac{1}{{2|E|}}({A_{ij}} - \frac{{{d_i}{d_j}}}{{2|E|}})\delta (i,j) \end{aligned}$$

(2)

2.2 Ant Colony Algorithms for Community Mining

Ant colony optimization is under a general category of nature-inspired algorithm, which is inspired by the collective behaviors of ants. In the ant colony optimization algorithm, each ant finds a community division based on a probability directed by the pheromone matrix and the heuristic factor. The most important parts of a ant colony algorithm are searching, mutating and updating pheromone matrix. Here, we take a typical ant colony optimization for clustering, denoted as ACOC, as an example to introduce the basic parts of an ant colony algorithm for community mining [14].

Searching Strategy: In each iteration, every ant finds a community division based on a probability matrix, which is as shown in Eq. (3). $P_{i,c_j}$ indicates the probability of vertex i belonging to community $C_j$. And $c_j$ stands for the label of community $C_j$.

$$\begin{aligned} P_{i,c_j} = \frac{{(\eta _{i,c_j})^\beta (Tau{_{i,c_j})^\alpha }}}{{\sum \limits _{k = 1}^{NC} {(\eta _{i,c_k})^\beta {(Tau_{i,c_k})^\alpha }} }} \end{aligned}$$

(3)

In Eq. (3), $\eta _{i,c_j}$ is the heuristic factor, which helps improve the search ability of ants based on the adjacent matrix of networks. For example, the heuristic factor in ACOC indicates the number of edges connecting the vertexes in community $C_j$ from vertex i. Based on the character of community structure, the more edges connecting vertexes in community $C_j$ vertex i joints, the larger probability of vertex i belonging to community $C_j$ is. And the expression of $\eta _{i,c_j}$ is shown in Eq. (4), in which $n_{i,{c_{j}}}$ indicates the number of edges connecting vertex i and vertexes in community $C_j$. Here, $C_j$ is based on the best community division found by algorithm. And Tau stands for the pheromone matrix, which is updated by the ants in each iteration based on the qualities of solutions.

$$\begin{aligned} \eta _{i,c_j} = \frac{{{n_{i,c_j}}}}{{\sum \limits _{k = 1}^{NC} {{n_{i,c_k}}} }} \end{aligned}$$

(4)

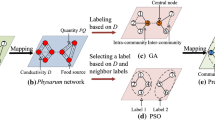
Based on the P matrix, the details in ACOC of assigning a community label to a vertex is introduced as follows. Taking the vertex i as an example, the community label $c_j$ with maximal P value (i.e., $arg~{\max }_{c_j} P_{i,c_j}$) is assigned to vertex i with a probability $p_{0}$. Meanwhile, the community label of vertex i is assigned based on the roulette way, with a probability $1- p_{0}$. As shown in Fig. 1, assigning community labels for all the vertexes in such way, a community division emerges.

Fig. 1.

The formulation of community division based on ACOC. Each community division is coded as a string of integers, which represents the community label of corresponding vertex.

Mutation Strategy: Mutation operator is a kind of random searching process, which aims to improve the diversity of solutions and protect ant colony clustering algorithms from premature. In the adopted mutation strategy of ACOC, each vertex is reassigned by a random community label with a probability $P_m$. And the mutation of a solution is accepted, if and only if the reassigning improves the modularity value of corresponding community division. Figure 2 shows an simple example of such mutation strategy.

Fig. 2.

An example of the mutation strategy in ACOC. Each mutated vertex is reassigned by a random community label. And the mutation is accepted, if and only if the reassigning improves the modularity value of corresponding community division.

Pheromone Matrix Updating Strategy: There are two phases for updating the pheromone matrix Tau. The first phase is implemented when an ant finishes its searching in an iteration. In this phase, every ant updates the pheromone matrix based on Eq. (5). Specifically, $\rho$ is the volatile coefficient of pheromone, and Q indicates the quality of community division that the ant finds. The second phase executes after all the ants finish their local searching. Based on the community divisions with the top Q values in the current iteration, Eq. (6) is implemented for enhancing the effects of better community divisions. In Eq. (6), $\phi (i,c_j)$ equals to 1, if and only if vertex i within community $C_j$ based on the corresponding community division. Otherwise, $\phi (i,c_j)$ equals to 0.

$$\begin{aligned} Tau_{i,c_j} = (1 - \rho ) \cdot Tau_{i,c_j} + 2\rho \cdot Q \cdot \phi (i,c_j) \end{aligned}$$

(5)

$$\begin{aligned} Tau_{i,c_j} = (1 - \rho ) \cdot Tau_{i,c_j} + {Q_{top} \cdot \phi (i,c_j)} \end{aligned}$$

(6)

With the local searching and updating for Tau, ants will aggregate to certain community divisions with higher Q values. And the solution with the highest Q value will be outputted as the optimal community division.

3 A Novel Nature-Inspired Optimization Algorithm for Community Mining

3.1 Edges Endowed with Weights Based on the Physarum Model

Physarum is a kind of slime with the abilities of designing networks and solving maze [10, 11]. Moreover, inspired by the bio-experiments of Physarum, a mathematical model is proposed and used for optimizing the heuristic algorithms [13]. In this paper, the Physarum model (PM) is modified to endow edges with weights, which could be used to recognize the intra-community edges in a network.

$$\begin{aligned} {PQ^t}_{i,j} = \frac{{{D^{t - 1}}_{i,j}}}{{{L_{i,j}}}}|{p^t}_i - {p^t}_j| \end{aligned}$$

(7)

The basic hypothesis of PM is a Poiseuille flow in a network. And the core mechanism of PM is the feedback system between the cytoplasmic fluxes and conductivities of tubes in the Poiseuille’s flow. This feedback system has two main processes. First, ${PQ^t}_{i,j}$, ${D^t}_{i,j}$, ${L_{i,j}}$ and ${p^t}_i$ denote the flux, the conductivity, the length of $e_{i,j}$, and the pressure of $v_i$ at time step t, respectively. Then, the relationship among the flux, conductivity, length, and pressure can be represented as Eq. (7). According to the Kirchhoff’s law, which is represented in Eq. (8), the pressures and fluxes can be obtained, by solving such equations at each iteration step. And then, ${PQ^t}_{i,j}$ feeds back to ${D^{t}}_{i,j}$ based on Eq. (9). After that, an iteration step finishes. With such feedback going on, a highly efficient network is generated.

$$\begin{aligned} \sum \limits _i {{PQ^{t - 1}}_{i,j} = \left\{ {\begin{array}{*{20}{c}} {I_0},&{}\ if ~{v_j}~is~an~inlet \\ - {I_0},&{}\ if~ v_j~is~an~ oulet\\ 0,&{}others \end{array}} \right. } \end{aligned}$$

(8)

$$\begin{aligned} {D^t}_{i,j} = \frac{{PQ_{i,j}^t + D_{i,j}^{t - 1}}}{k} \end{aligned}$$

(9)

The major modification of PM is the scheme of choosing inlets/outlets in each iteration. In such model, when a vertex is chosen as an inlet, the others are chosen as outlets. More specifically, Eq. (8) is modified as Eq. (10), in which D and L are known. With a certain inlet and outlet, we can construct a set of equations based on Eq. (10). By solving such equations, $p_{i}$ can be obtained. And, in each iteration step of PM, every vertex is chosen as the inlet once. When $v_l$ is chosen as the inlet, a local conductivity matrix, denoted as ${D^t}(v_l)$, is calculated based on the feedback system (i.e., Eqs. (7), (8) and (9)). Finally, after all the local conductivity matrixes are obtained, the global conductivity matrix is updated by the average of local conductivity matrixes based on Eq. (11). A detailed description of PM is represented in Algorithm 1.

$$\begin{aligned} \sum \limits _i {\frac{{{D^{t - 1}(v_l)}_{i,j}}}{{{L_{i,j}}}}|{p^t}_i - {p^t}_j| = \left\{ {\begin{array}{*{20}{c}} {I_0},&{}~if~v_j~is~an~inlet\\ \frac{{ - {I_0}}}{{|V| - 1}},&{}others \end{array}} \right. } \end{aligned}$$

(10)

$$\begin{aligned} {D^t} = \frac{1}{{|V|}}\sum \limits _{l = 1}^{|V|} {{D^t}(v_l)} \end{aligned}$$

(11)

Fig. 3.

Edges with top 20 percent conductivities in two networks based on the Physarum model. The different colors are used to label communities.

With such modifications, the conductivities computed by Physarum model contain the information about inter-community edges recognition. Physarum model tends to endow inter-community edges with larger conductivities, vice versa. Figure 3 shows the edges with the top 20 percent conductivities in two networks based on such Physarum model. As it reported, the most of the edges with 20 percent conductivities connect vertexes in different communities. And there is almost no edge within the communities.

3.2 Nature-Inspired Optimization for Community Mining

Utilizing the character of conductivities computed by Physarum model, a novel ant colony optimization algorithm is proposed in this section, which aims to overcome the shortcomings of the low accuracy and premature. Through endowing edges with weights based on the Physarum model, the heuristic factor of proposed ant colony algorithm is optimized for improving the computational efficiency.

$$\begin{aligned} \begin{aligned} {\eta ^*}_{i,{c_j}} = \frac{{{n^*}_{i,{c_j}}}}{{\sum \limits _{k = 1}^{NC} {{n^*}_{i,{c_k}}} }} = \frac{{\sum \limits _{h \in {C_j}} {1/{w_{i,h}}} }}{{\sum \limits _{k = 1}^{NC} {\sum \limits _{h \in {C_k}} {1/{w_{i,h}}} } }} \end{aligned} \end{aligned}$$

(12)

Taking the advantages of Physarum model, the intra-community edges tend to have larger weights. In contrast, the inter-community edges tend to have a small ones. Based on such character, we can optimize the heuristic factor of ant colony clustering algorithms in order to improve the search ability of such algorithms during the process of community detection. Takeing ACOC as an example, we can optimize heuristic factor based on Eq. (12), in which $w_{i,k}$ indicates the conductivity of $e_{i,k}$ and ${n^*}_{i,c_j} = \sum _{h \in {C_j}} {\frac{1}{{{w_{i,h}}}}}$. With such expression, ${\eta ^*}_{i,c_j}$ has a larger value when there are the same intra-community edges connecting vertex i and vertexes in community $C_j$, compared with the original ${\eta }_{i,c_j}$, vice versa. Such nature-inspired optimization exaggerates the inhomogeneity of original heuristic factor, and offers a more obvious information to ants, which leads to a higher accuracy and better robustness.

Fig. 4.

Optimizing the heuristic factor in ACOC and IACO-Net based on the conductivity matrix D returned by Physarum model. (a) A basic framework of ant colony algorithm. (b) The optimized initialization of IACO-Net. (c) The optimized probability matrix updating process of ACOC.

Although the heuristic factor is common and important in ant colony algorithms for community mining, the heuristic factor is used in different way in various ant colony algorithms. However, the Physarum based optimization strategy adapts various of ant colony algorithms easily. Here we employ two representative ant colony algorithms (i.e., ACOC [14] and IACO-Net [15]) to show the flexibility of our proposed method. Figure 4 illustrates the flowchart of optimizing the heuristic factors in ACOC and IACO.

4 Experiments

4.1 Datasets

Four real-world networks collected by Newman¹ and two ant colony clustering algorithms (i.e., ACOC [14] and IACO-Net [15]) are used to estimate the proposed algorithm. The basic topological features of those networks are shown in Table 1. For a clear expression, a prefix (i.e., $P-$) adds to the name of algorithm with the proposed strategy. And all the experiments are implemented in the same environment, which means that comparing algorithms have a same parameter setting and running environment. Moreover, the results are based on 20 repeated experiments to eliminate the fluctuation and evaluate the robustness.

Table 1. The basic topological features of the real-world networks. N and E denote the number of vertexes and edges in a network. k and C stand for the average degree and clustering coefficient of networks, respectively. NC indicates the number of communities in networks based on the background.

Table 2. Results returned by ACOC, IACO-Net and their optimized algorithms on four networks in term of Q based on 20 repeated experiments. Q1 and Q3 indicate the first and third quartiles, respectively. And AVE stands for the average of those results on four networks.

4.2 Experiment Results

Table 2 shows the box charts of modularity values returned by ACOC, IACO-Net, and their optimized algorithms on four real-world networks, which reports the distributions of results based on 20 repeated experiments. Due to the randomness of maximum and minimum, the comparison of those algorithms focuses on the first and third quartiles, and average. As is shown in such figure, the P-ACOC and P-IACO-Net have a higher average on all the four networks. And the first and third quartiles of optimized algorithms are also higher than that of original algorithms on all of four networks. Meanwhile, the distribution ranges of optimized algorithms are smaller, compared with that of original ones. It means the proposed strategy can enhance the robustness of ant colony algorithms.

Fig. 5.

The dynamic averages of Q with the increment of iteration in four networks. The results show that the proposed optimized strategy can obviously improve the search abilities of ACOs.

For further estimating the efficiency of proposed strategy, Fig. 5 reports the dynamic changes of average modularity values with the increments of iterations. As is shown in such figure, at the initial phase, the Q values of the optimized algorithms are close to those of original algorithms. However, the algorithms with the proposed strategy have a higher growth rate, compared with the original ant colony algorithms. With the growing of iterations, the difference between original and optimized algorithms emerges. There is a distinct gap between the lines of original and optimized algorithms at the end of iterations.

Other optimization and heuristic algorithms are also used to evaluate the efficiency of proposed algorithms for community mining. The compared algorithms include the evolution algorithm (i.e., GA-Net [16]), swarm intelligence algorithm (i.e., RWACO [17]), hierarchical clustering algorithm (i.e., FN [18]), and label propagation based algorithms (i.e., LPA [19]). Table 3 reports the modularity values returned by those algorithms. As shown in such table, P-IACO-Net has the highest Q values on three of four networks. Meanwhile, the Q values of P-ACOC have significant improvements, compared with that of ACOC.

Table 3. Comparison the proposed algorithms with other optimization and heuristic algorithms. The community divisions are evaluated by modularity value Q.

The cost of such Physarum-inspired optimized strategy is the computational cost. And the time complexity of Physarum model is analyzed as follows. For Physarum model, at each iterative step, every vertex should be chosen as the inlet once. When a vertex is chosen, a corresponding system of equations needs to be solved. In other words, there are N equations to solve in each iteration step. The worst computation complexity of solving a system of equations is O($N^3$). With an empirical setting (i.e., $T=1$), the total computation complexity of Physarum-inspired optimized strategy is O($N^4$). For a NP-complete problem, this computation complexity is acceptable. Moreover, Table 4 shows the running time of ACOC, IACOC-Net and their optimized algorithms in seconds, which also verifies that the proposed Physarum-inspired optimized strategy does not increase the computational complexity noticeably.

Table 4. The running time of optimization-based algorithms in seconds. From this table, we can conclude that our proposed computational framework does not bring more computational burden for original algorithms.

5 Conclusion

Inspired by the Physarum-inspired model, a novel nature-inspired optimization algorithm for community mining is proposed in this paper based on the optimized ant colony optimization. In the proposed novel algorithm, the heuristic factor is optimized by a Physarum-inspired strategy. The proposed strategy integrates the knowledge of Physarum-inspired model into the heuristic factor for exaggerating the inhomogeneity of original ones and offering more extra knowledge for ants. Experiments on four real-world networks and two typical kinds of ant colony algorithms show the improvements of optimized algorithm in terms of accuracy and robustness. Moreover, the time complexity analysis shows that the proposed strategy does not increase the computational complexity of ant colony clustering algorithm noticeably.