Keywords

1 Introduction

Many complex systems in the real world can be formulated as a complex network, such as social networks, internet and biological networks [1]. And the community structure is one of the essential topological properties of a network, where vertexes across communities are connected sparsely, and vertexes within a community are connected densely. More importantly, the community structure can provide both the sketches of a complex network and some insights into the properties of vertexes [2].

Due to the importance of community structure, many algorithms have been proposed for detecting communities [1, 3]. Generally speaking, there are two typical kinds of algorithms: optimization algorithms and model-based algorithms. Concerning the optimization algorithms, such as Genetic Algorithm (GA) [4] and Ant Colony Optimization algorithm (ACO) [5], community mining is to find a community division of network with the maximum objective function values. Currently, the most popular objective function is the modularity [6]. In term of model-based algorithms, a representative algorithm, Markov clustering algorithm (MCL), is used to highlight their mechanisms. MCL [3] is based on the flow simulation in which high-flow regions are clustered together. However, some shortcomings, such as the weaker robustness and lower accuracy, still limit their performances.

Currently, Physarum, which is a unicellular and multi-headed slime mold, shows an intelligence of path finding and network designing in biological experiments [7, 8]. Moreover, inspired by the intelligence of Physarum, a mathematic model is proposed [9], which has shown an ability to optimize some nature-inspired algorithms (e.g., GA [10] and ACO [11]) in terms of efficiency and robustness. Given the aforementioned observation and works, the following two questions are raised:

  • Does the Physarum-based mathematical model (PM) have a potential to recognize community structures in complex networks?

  • Can the intelligence of PM optimize traditional algorithms to overcome the shortcomings of community detection?

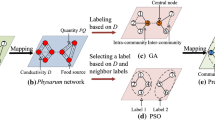
Considering the questions above mentioned, the main contributions of this paper are twofold. First, inspired by PM, a Physarum network mathematical model (PNM) is proposed, which has an ability to recognize the inter-community edges coarsely. Second, utilizing the proposed PNM, a Physarum-based general computational framework for community mining is proposed to overcome the weaker robustness and lower accuracy of traditional detection methods. And some experiments are used to estimate the efficiency of proposed framework.

The remaining parts of this paper are organized as follows: Sect. 2 formulates the community mining and introduces the basic ideas of traditional algorithms for community detection. Section 3 proposes the PNM and a Physarum-based general computational framework for community mining. Then, some typical algorithms (e.g., GA, ACO and MCL) and six classical real-world datasets are used for estimating the efficiency and scalability of proposed framework in Sect. 4. Final, Sect. 5 concludes this paper.

2 Related Works

2.1 Formulation of Community Mining

A complex network can be formulated as a graph G(V, E), where V and E stand for the sets of vertexes and edges, respectively. And, a community is denoted as c which contains a subset of V with the common certain features. A community division is denoted as \(C = \{ {c_{i}}|\mathrm{{ }}{c_i} \ne \emptyset , {c_i} \ne {c_j},{c_i} \cap {c_j} = \emptyset , 1 \le i,j \le N_c\}\), where \(N_c\) stands for the number of communities in C. The main goal of community detection is to find a community division which maximizes a particular quality metrics function f. Therefore, the formulation of community detection can be represented as Eq. (1).

$$\begin{aligned} \arg ~ \mathop {\max }\limits _C f(G,C) \end{aligned}$$
(1)

In this paper, two quality metrics, i.e., modularity and normalized mutual information (NMI), are used to provide more comprehensive comparisons. The modularity, denoted as Q, is measured by the inherent characteristics of a network, i.e., the heterogeneous relationships among edges between dense intra-community connections and sparse inter-community connections [6]. While NMI, as the object function of community detection, is widely used to quantify the similarity between detected communities and standard communities based on a certain feature in the real world [12].

2.2 Algorithms for Community Mining

Given the practical significance of community detection, many algorithms have been proposed to detect communities ranging from optimization algorithms to model-based algorithms

Concerning the perspective of optimization algorithms, a basic hypothesis for community detection is that the quality of community division can be evaluated by a network-based objective function, such as the modularity (Q). And, the object of such algorithms is to find community divisions with the maximal values of object function. In the following, we take two typical optimization algorithms (i.e., ACO and GA) as examples to describe the process of community mining of such algorithms.

  • ACO [5] is a typical optimization algorithm, which searches the optimized community division based on the cooperation of ants. Each ant first finds a community division with a value of object independently. Then, each ant informs the quality of its community division to others based on a pheromone matrix by updating local pheromone. After all ants finish the searching process, a global pheromone is updated based on the results of elitist ants. With the iteration going on, the pheromone leads ants to find better community divisions.

  • GA [4] is also an optimization algorithm, in which divisions need to be coded as integer strings, called chromosomes. And the integers in chromosomes are called genes. Every chromosome has a fitness value, which reflects the corresponding object function value. In each iteration step, some chromosomes with a higher fitness are searched by exchanging genes among chromosomes (i.e., crossover operation) and changing genes randomly (i.e., mutation operation). And only chromosomes with a higher fitness will survive with the increment of iteration steps. Final, the chromosome with the highest fitness will be output as the best community division.

In terms of the model-based algorithms, the basic hypothesis is the dynamic process taking on a network, which can be used to reveal community structures. Usually, this dynamic process is described by a model, such as the Markov chains. And communities emerge in the wake of the dynamic process. Here, we take MCL as an example to introduce the community detection of such algorithms.

  • MCL [3] is a model-based algorithm, which is based on a flow simulation. In MCL, every vertex has a quantity of fluxes, and the distribution of fluxes is represented by a matrix, called the flow matrix. Moreover, the flowing of fluxes is described by a Markov chain with a transfer probability matrix. In such situation, a positive feedback operator is emerged through the fluxes flowing based on the markov chain. With the iterations going on, fluxes of vertexes in a tightly-linked group will flow together, and those vertexes are clustered as a community.

3 Physarum Computational Framework for Community Mining

3.1 A Physarum Mathematic Network Model for Community Mining

Inspired by Physarum, a mathematical model is designed by Tero, et al. [9], which has shown the abilities of path finding [9], network designing [8] and algorithms optimizing [11]. In this paper, a Physarum-based network mathematical model (PNM) is designed to distinguish inter-community edges from intra-community ones, based on PM. The core mechanism of PNM is the feedback system between the cytoplasmic fluxes and conductivities of tubes in PM. This feedback system has two main processes. First, \({Q^t}_{i,j}\), \({D^t}_{i,j}\) and \({L_{i,j}}\) stand for the flux, conductivity and length of \(e_{i,j}\), respectively. \({p^t}_i\) indicates the pressure of \(v_i\). And the relationship among the flux, conductivity, length and pressure are formulated as Eq. (2). According to the Kirchhoff’s law as shown in Eq. (3), the pressures and fluxes can be obtained at each time step. And then, \({Q^t}_{i,j}\) feeds back to \({D^{t}}_{i,j}\) based on Eq. (4). After that, a time step finishes. In the wake of such feedback process, a high efficient network is emerged.

$$\begin{aligned} {Q^t}_{i,j} = \frac{{{D^{t - 1}}_{i,j}}}{{{L_{i,j}}}}|{p^t}_i - {p^t}_j| \end{aligned}$$
(2)
$$\begin{aligned} \sum \limits _i {{Q^{t - 1}}_{ij} = \left\{ {\begin{array}{*{20}{c}} {{I_0},~ if ~{v_j}~is ~an ~inlet }\\ { - {I_0},~ if ~ {v_j}~is ~an ~ oulet}\\ {0,~others~~~~~~~~~~~~~} \end{array}} \right. } \end{aligned}$$
(3)
$$\begin{aligned} {D^t}_{i,j} = \frac{{Q_{i,j}^t + D_{i,j}^{t - 1}}}{k} \end{aligned}$$
(4)

The major modification of PNM is the scheme of inlets/outlets choosing. In PNM, when a vertex is chosen as an inlet, the others are chosen as outlets. In other words, Eq. (3) is modified as Eq. (5). And, in each time step of PNM, every vertex is chosen as the inlet once. When \(v_i\) is chosen as the inlet, a local conductivity matrix, denoted as \({D^t}(i)\), is calculated based on the feedback system. Finally, at the end of each time step, the global conductivity matrix is updated by the average of local conductivity matrixes based on Eq. (6). As time steps increase, the inter-community edges tend to have a larger conductivity.

$$\begin{aligned} \sum \limits _i {\frac{{{D^{t - 1}}_{i,j}}}{{{L_{i,j}}}}|{p^t}_i - {p^t}_j| = \left\{ {\begin{array}{*{20}{c}} {{I_0},~if~v_j~is~an~inlet}\\ {\frac{{ - {I_0}}}{{|V| - 1}},{~others~~~~~~~~~~ }} \end{array}} \right. } \end{aligned}$$
(5)
$$\begin{aligned} {D^t} = \frac{1}{{|V|}}\sum \limits _{i = 1}^{|V|} {{D^t}(i)} \end{aligned}$$
(6)

3.2 Physarum-Based General Computational Framework for Community Mining

Utilizing the ability of PNM, a general computational framework for community mining is proposed, which aims to overcome the lower accuracy and the weaker robustness through optimizing the initialization or dynamic process of traditional algorithms. In the following, we take the optimized initialization scheme of such framework to introduce the details.

Based on PNM, the optimized initialization scheme detects communities through distinguishing inter-community edges from intra-community ones. A matrix DA is used to denote the property of \(e_{i,j}\), in which \(da_{i,j}=1\) if and only if \(e_{i,j}\) is an intra-community edges. The optimized initialization based on PNM is summarized as follows. First, a conductivity matrix D is obtained based on PNM. And then, all edges are supposed to be inter-community, i.e., \(DA=-A\). Thereafter, some vertexes are chosen randomly. Meanwhile, the edges joining those chosen vertexes are marked as intra-community edges, except for the edges with top conductivities. After that, DA could be used to denote communities.

Based on DA, the vertexes connected by intra-communities edges are identified as a community. In other works, the connected components of a network composed of intra-community edges, are identified as communities of such network. After that, a community division emerges, and the optimized initialization of community mining is completed.

4 Experiments

4.1 Datasets

Six real-world networksFootnote 1 and three typical kinds of algorithms (i.e., GA, ACO, MCL) are used for estimating the efficiency and scalability of proposed framework. The basic information of those networks is shown in Table 1.

Table 1. Basic information of used networks. The columns of clusters show the number of communities in standard community divisions, in which “-” means that standard division is nonexistent.
Full size table

For a clear expression, a prefix (i.e., PNM-) is added to the original names of optimized algorithms for distinguishing. For example, the optimized algorithm of GA is denoted as PNM-GA. All experiments are implemented with the same parameters setting and running environment. Moreover, for some random algorithms (i.e., GA and ACO), the results are averaged over 20 repeated runnings for eliminating fluctuation and evaluating the robustness of algorithms.

4.2 Accuracy Comparison

We take NGACD [4] as an example to estimate the efficiency of our proposed framework for GA. Figure 1 plots the box chart of results returned by NGACD and PNM-NGACD. Due to the randomness of maximum and minimum, efficiency comparison is mainly based on the quartiles and means. Results show that the first and third quartiles, median and means of Q returned by PNM-NGACD are higher than that of NGACD on all datasets, which means that PNM-NGACD has a stronger exploring ability. Moreover, the lengths of boxes of PNM-NGACD are shorter than that of NGACD, which verifies that the robustness of PNM-NGACD is stronger than that of NGACD.

Fig. 1.
figure 1

Box charts of results returned by PNM-NGACD and NGACD on six networks in term of Q, in which the bottom and top of box are the first and third quartiles respectively, and the band inside the box denotes the median. The ends of whiskers represent the minimum and maximum of Q. Moreover, the small quadrates in boxes stand for the means of Q.

Full size image

For ACO, we take ANCC [5] as an example to estimate the efficiency of our proposed framework. Figure 2(a) shows a comparison between ANTCC and PNM-ANTCC in term of Q. The result shows that the Q values returned by PNM-ANTCC have an obvious improvement comparing with that of ANTCC.

Because MCL is a typical model-based algorithm, and INM is a more reasonable metrics for such algorithm. The comparison on networks with standard division, between a representational MCL (i.e., R-MCL [3]) and PNM-MCL for accuracy, is based on INM. As is shown in Fig. 2(b), the NMI of PNM-MCL is higher than that of R-MCL. Meanwhile, the NMI values of PNM-MCL on karate and dolphins network are 1, which means that the communities found by PNM-MCL are same as the known communities.

Fig. 2.
figure 2

Comparison of results. (a) shows the results returned by PNM-ANTCC, ANTCC, and (b) reports the results returned by PNM-MCL, R-MCL, in term of Q.

Full size image

4.3 Computation Complexity Analysis

Using T, N to stand for the maximal iterative step and the number of nodes in network, respectively. The computation complexities of Physarum-based initialization and dynamic process are analyzed as follows.

Physarum -based initialization: For Physarum-based initialization, at every iterative step, every node should be chosen as the inlet once. When a node is chosen, a corresponding system of equations needs to be solved. In other words, N systems of equations have to be solved as every iterative step. The worst computation complexity of solving a system of equations is \(O(N^3)\). With a empirical setting (i.e., \(T=1\)), the total computation complexity of Physarum-based initialization is \(O(N^4)\).

Physarum -based dynamic process: Generally speaking, optimizing the feedback system based on the Physarum-based dynamic process, dose not change the operation sequence. For example, the computation complexity of PNM-MCL is \(O(T \times N^2)\), which is the same as that of R-MCL.

5 Conclusion

Based on PM, a modified Physarum network model with a specific scheme for community mining is proposed in this paper, which shows an ability of recognizing inter-community edges. Besides, taking the advantages of PNM, a general computing framework for community mining is proposed to overcome the shortcomings of lower accuracy and weaker robustness. Experiments with three different algorithms on six real-world datasets show that optimized algorithms with proposed framework have a higher accuracy and stronger robustness. Moreover, a computational complexity analysis verifies the scalability of our framework.