Parametric Model Checking Timed Automata Under Non-Zenoness Assumption

Abstract

Real-time systems often involve hard timing constraints and concurrency, and are notoriously hard to design or verify. Given a model of a real-time system and a property, parametric model-checking aims at synthesizing timing valuations such that the model satisfies the property. However, the counter-example returned by such a procedure may be Zeno (an infinite number of discrete actions occurring in a finite time), which is unrealistic. We show here that synthesizing parameter valuations such that at least one counterexample run is non-Zeno is undecidable for parametric timed automata (PTAs). Still, we propose a semi-algorithm based on a transformation of PTAs into Clock Upper Bound PTAs to derive all valuations whenever it terminates, and some of them otherwise.

This work is partially supported by the ANR national research program PACS (ANR-14-CE28-0002).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Timed automata (TAs) [1] are a popular formalism for real-time systems modeling and verification, providing explicit manipulation of clock variables. Real-time behavior is captured by clock constraints on system transitions, setting or resetting clocks, etc. TAs have been studied in various settings (such as planning [19]) and benefit from powerful tools such as Uppaal [21] or PAT [24].

Model checking TAs consists of checking whether there exists an accepting cycle (i. e. a cycle that visits infinitely often a given set of locations) in the automaton made of the product of the TA modeling the system with the TA representing a violation of the desired property (often the negation of a property expressed, e. g. in CTL). However, such an accepting cycle does not necessarily mean that the property is violated: indeed, a known problem of TAs is that they allow Zeno behaviors. An infinite run is non-Zeno if it takes an unbounded amount of time; otherwise it is Zeno. Zeno runs are infeasible in reality and thus must be pruned during system verification. That is, it is necessary to check whether a run is Zeno or not so as to avoid presenting Zeno runs as counterexamples. The problem of checking whether a timed automaton accepts at least one non-Zeno run, i. e. the emptiness checking problem, has been tackled previously (e. g. [11, 15, 16, 25,26,27]).

It is often desirable not to fix a priori all timing constants in a TA: either for tuning purposes, or to evaluate robustness when clock values are imprecise. For that purpose, parametric timed automata (PTAs) extend TAs with parameters [2]. Although most problems of interest are undecidable for PTAs [3], some (semi-)algorithms were proposed to tackle practical parameter synthesis (e. g. [4, 9, 18, 20]). We address here the synthesis of parameter valuations for which there exists a non-Zeno cycle in a PTA; this is highly desirable when performing parametric model-checking for which the parameter valuations violating the property should not allow only Zeno-runs. As far as the authors know, this is the first work on parametric model checking of timed automata with the non-Zenoness assumption. Just as for TAs, the parametric zone graph of PTAs (used in e. g. [4, 17, 18]) cannot be used to check whether a cycle is non-Zeno. Therefore, we propose here a technique based on clock upper bound PTAs (CUB-PTAs), a subclass of PTAs satisfying some syntactic restriction, and originating in CUB-TAs for which the non-Zeno checking problem is most efficient [27]. In contrast to regular PTAs, we show that synthesizing valuations for CUB-PTAs such that there exists an infinite non-Zeno cycle can be done based on (a light extension of) the parametric zone graph. We make the following technical contributions:

• 1. We show that the parameter synthesis problem for PTAs with non-Zenoness assumption is undecidable.

• 2. We show that any PTA can be transformed into a finite list of CUB-PTAs;

• 3. We develop a semi-algorithm to solve the non-Zeno synthesis problem using CUB-PTAs, implemented in IMITATOR and validated using benchmarks.

Outline. Section 2 recalls the necessary preliminaries. Section 3 shows the undecidability of non-Zeno-Büchi emptiness. We then present the concept of CUB-PTAs (Sect. 4), and show how to transform a PTA into a list of CUB-PTAs. Zeno-free parametric model-checking of CUB-PTA is addressed in Sect. 5, and experiments reported in Sect. 6. Finally, Sect. 7 concludes and gives perspectives for future work.

2 Preliminaries

Throughout this paper, we assume a set $X= \{ x_1, \dots , x_H\}$ of clocks, i. e. real-valued variables that evolve at the same rate. A clock valuation is a function $w: X\rightarrow {\mathbb R}_{\ge 0}$. We write $X= 0$ for $\bigwedge _{1 \le i \le H}x_i = 0$. Given $d \in {\mathbb R}_{\ge 0}$, $w+ d$ denotes the valuation such that $(w+ d)(x) = w(x) + d$, for all $x\in X$.

We assume a set $P= \{ p_1, \dots , p_M\}$ of parameters, i. e. unknown constants. A parameter valuation $v$ is a function $v: P\rightarrow {\mathbb Q}_{\ge 0}$. A strictly positive parameter valuation is a valuation $v: P\rightarrow {\mathbb Q}_{> 0}$.

In the following, we assume ${\lhd } \in \{<, \le \}$ and ${\bowtie } \in \{<, \le , \ge , >\}$. Throughout this paper, $lt$ denotes a linear term over $X\cup P$ of the form $\sum _{1 \le i \le H} \alpha _i x_i + \sum _{1 \le j \le M} \beta _j p_j + d$, with $\alpha _i, \beta _j, d \in {\mathbb N}$. Similarly, $plt$ denotes a parametric linear term over $P$, that is a linear term without clocks ($\alpha _i = 0$ for all i). A constraint $C$ (i. e. a convex polyhedron) over $X\cup P$ is a set of inequalities of the form $lt \bowtie lt '$, with $lt , lt '$ two linear terms. We denote by $true$ (resp. $false$) the constraint that corresponds to the set of all possible (resp. the empty set of) valuations. Given a parameter valuation $v$, $v(C)$ denotes the constraint over $X$ obtained by replacing each parameter $p$ in $C$ with $v(p)$. Likewise, given a clock valuation $w$, $w(v(C))$ denotes the expression obtained by replacing each clock $x$ in $v(C)$ with $w(x)$. We say that $v$ satisfies $C$, denoted by $v\models C$, if the set of clock valuations satisfying $v(C)$ is non-empty. We say that $C$ is satisfiable if $\exists w, v$ s.t. $w(v(C))$ evaluates to true. We define the time elapsing of $C$, denoted by $C^\nearrow$, as the constraint over $X$ and $P$ obtained from $C$ by delaying all clocks by an arbitrary amount of time. Given $R\subseteq X$, we define the reset of $C$, denoted by $[C]_{R}$, as the constraint obtained from $C$ by resetting the clocks in $R$, and keeping the other clocks unchanged. We denote by $C{\downarrow _{P}}$ the projection of $C$ onto $P$, i. e. obtained by eliminating the clock variables using existential quantification.

A guard $g$ is a constraint over $X\cup P$ defined by inequalities of the form $x\bowtie plt$. We assume w.l.o.g. that, in each guard, given a clock $x$, at most one inequality is in the form $x\lhd plt$, that is a clock has a single upper bound (or none). A non-parametric guard is a guard over $X$, i. e. with inequalities $x\bowtie z$, with $z \in {\mathbb N}$. A parametric zone $C$ is a constraint over $X\cup P$ defined by inequalities of the form $x_i - x_j \bowtie plt$. A parametric constraint $K$ is a constraint over $P$ defined by inequalities of the form $plt \bowtie plt '$, with $plt , plt '$ two parametric linear terms. We use the notation $v\models K$ to indicate that valuating parameters $p$ with $v(p)$ in $K$ evaluates to true. We denote by $\top$ (resp. $\bot$) the parametric constraint that corresponds to the set of all possible (resp. the empty set of) parameter valuations. Given two parametric constraints $K_1$ and $K_2$, we write $K_1 \subseteq K_2$ whenever for all $v$, $v\models K_1 \Rightarrow v\models K_2$.

Definition 1

A PTA $\mathcal {A}$ is a tuple $\mathcal {A}= (\varSigma , L, l_0, X, P, K_0, I, E)$, where: (i) $\varSigma$ is a finite set of actions, (ii) $L$ is a finite set of locations, (iii) $l_0\in L$ is the initial location, (iv) $X$ is a set of clocks, (v) $P$ is a set of parameters, (vi) $K_0$ is the initial parameter constraint, (vii) $I$ is the invariant, assigning to every $l\in L$ a guard $I(l)$, (viii) $E$ is a set of edges $e= (l,g,a,R,l')$ where $l,l'\in L$ are the source and target locations, $a\in \varSigma$, $R\subseteq X$ is a set of clocks to be reset, and $g$ is a guard.

The initial constraint $K_0$ is used to constrain some parameters (as in, e. g. [4, 17]); in other words, it defines a domain of valuation for the parameters. For example, given two parameters $p_{\min }$ and $p_{\max }$, we may want to ensure that $p_{\min } \le p_{\max }$. Given $\mathcal {A}= (\varSigma , L, l_0, X, P, K_0, I, E)$, we write $\mathcal {A}.K_0$ as a shortcut for the initial constraint of $\mathcal {A}$. In addition, given $K_0'$, we denote by $\mathcal {A}(K_0')$ the PTA where $\mathcal {A}.K_0$ is replaced with $K_0'$.

Observe that, as in [27], we do not define accepting locations. In our work, we are simply interested in computing valuations for which there is a non-Zeno cycle. A more realistic parametric model checking approach would require additionally that the cycle is accepting, i. e. it contains at least one accepting location. However, this has no specific theoretical interest, and would impact the readability of our exposé.

Given a parameter valuation $v\models \mathcal {A}.K_0$, we denote by $v(\mathcal {A})$ the non-parametric TA where all occurrences of a parameter $p_i$ have been replaced by $v(p_i)$.

Definition 2

(Concrete semantics of a TA). Given a PTA $\mathcal {A}= (\varSigma , L, l_0, X, P, K_0, I, E)$, and a parameter valuation $v$, the concrete semantics of $v(\mathcal {A})$ is given by the timed transition system $(S, s_0, {\rightarrow })$, with $S= \{ (l, w) \in L\times {\mathbb R}_{\ge 0}^H\mid w(v(I(l))) \text { is true} \}$, $s_0= (l_0, \mathbf {0})$, and ${\rightarrow }$ consists of the discrete and (continuous) delay transition relations:

• discrete transitions: $(l,w) \mathop {\rightarrow }\limits ^{e} (l',w')$, if $(l, w), (l',w') \in S$, there exists $e= (l,g,a,R,l') \in E$, $w'= [w]_{R}$, and $w(v(g))$ is true.

• delay trans.: $(l,w) \mathop {\rightarrow }\limits ^{d} (l, w+d)$, with $d \in {\mathbb R}_{\ge 0}$, if $\forall d' \in [0, d], (l, w+d') \in S$.

A (concrete) run is a sequence $r=s_0 \alpha _0 s_1 \alpha _1 \cdots s_n \alpha _n \cdots$ s.t. $\forall i, (s_i, \alpha _i,s_{i+1})\in {\rightarrow }$. We consider as usual that concrete runs strictly alternate delays $d_i$ and discrete transitions $e_i$ and we thus write concrete runs in the form $r= s_0 \mathop {\rightarrow }\limits ^{(d_0,e_0)} s_1 \mathop {\rightarrow }\limits ^{(d_1,e_1)}\cdots$. We refer to a state of a run starting from the initial state of a TA $\mathcal {A}$ as a concrete state of $\mathcal {A}$. Note that when a run is finite, it must end with a concrete state. Given a concrete state $s=(l, w)$, we say that $s$ is reachable (or that $v(\mathcal {A})$ reaches $s$) if $s$ belongs to a run of $v(\mathcal {A})$. By extension, we say that $l$ is reachable in $v(\mathcal {A})$, if there exists a concrete state $(l,w)$ that is reachable.

An infinite run is said to be Zeno if it contains an infinite number of discrete transitions within a finite delay, i. e. if the sum of all delays $d_i$ is bounded.

Symbolic Semantics. Let us recall the symbolic semantics of PTAs (as in e. g. [4, 18]). A symbolic state is a pair $\mathbf {s}= (l, C)$ where $l\in L$ is a location, and $C$ its associated parametric zone. The initial symbolic state of $\mathcal {A}$ is $\mathbf {s}_0= \big (l_0, (\{\mathbf {0}\} \wedge I(l_0))^\nearrow \wedge I(l_0) \wedge K_0\big )$. That is, the initial state corresponds to all clocks equal to 0 followed by time-elapsing, intersected with the initial invariant and the initial parameter constraint. The symbolic semantics relies on the $\mathsf {Succ}$ operation. Given a symbolic state $\mathbf {s}= (l, C)$ and an edge $e= (l,g,a,R,l')$, $\mathsf {Succ}(\mathbf {s}, e) = (l', C')$, with $C' = \big ([(C\wedge g)]_{R}\big )^\nearrow$. The $\mathsf {Succ}$ operation is effectively computable, using polyhedra operations: note that the successor of a parametric zone $C$ is a parametric zone. A symbolic run of a PTA is an alternating sequence of symbolic states and edges starting from the initial symbolic state, of the form $\mathbf {s}_0 \mathop {\Rightarrow }\limits ^{e_0} \mathbf {s}_1\mathop {\Rightarrow }\limits ^{e_1} \cdots \mathop {\Rightarrow }\limits ^{e_{m-1}} \mathbf {s}_m$, such that for all $i = 0, \dots , m-1$, we have $e_i \in E$, and $\mathbf {s}_{i+1}=\mathsf {Succ}(\mathbf {s}_i, e_i)$. The symbolic semantics is often given in the form of a parametric zone graph, i. e. symbolic states of $\mathcal {A}$ and transitions $(\mathbf {s}, e, \mathbf {s}')$ whenever $\mathbf {s}' = \mathsf {Succ}(\mathbf {s}, e)$. Given a symbolic run $(l_0, C_0) \mathop {\Rightarrow }\limits ^{e_0} (l_1, C_1) \mathop {\Rightarrow }\limits ^{e_1} \cdots \mathop {\Rightarrow }\limits ^{e_{n-1}} (l_n, C_n) \cdots$, its untimed support is the sequence $l_0 e_0 l_1 \cdots e_{n-1} l_n \cdots$. Two runs (symbolic or concrete) are equivalent if they have the same untimed support.

Let us recall a lemma relating concrete and symbolic runs.

Lemma 1

Let $\mathcal {A}$ be a PTA, and let $\mathbf {r}$ be a symbolic run of $\mathcal {A}$ reaching $(l, C)$. Let $v\models \mathcal {A}.K_0$. There exists an equivalent concrete run in $v(\mathcal {A})$ iff $v\models C{\downarrow _{P}}$.

Proof

From [17, Propositions 3.17 and 3.18].    $\blacksquare$

Given a symbolic run $\mathbf {r}$ reaching $(l, C)$, we call the concrete runs associated with $\mathbf {r}$ the concrete runs equivalent to $\mathbf {r}$ in $v(\mathcal {A})$, for all $v\models C{\downarrow _{P}}$.

Problems. In this paper, we aim at addressing the following two problems.

3 Undecidability of the Non-Zeno Emptiness Problem

As reachability is undecidable for PTAs [2], it is unsurprising that the existence of a valuation for which there exists a non-Zeno infinite run is undecidable too.

Theorem 1

The non-Zeno emptiness problem is undecidable for PTAs.

Proof

By reduction from the halting problem of a deterministic 2-counter-machine, which is undecidable [22]. We encode a 2-counter machine (2CM) using PTAs, following an encoding in [8]. This encoding is such that the location $l_{\mathtt {halt}}$ encoding the halting state of the 2CM is reachable iff the 2CM halts, and for valuations of the (unique) parameter $v$ such that $v(p)$ is larger than or equal to the maximum value of the counters along the (unique) run of the machine. Then, since this encoding is such that for any parameter valuation, the encoding stops after $v(p)$ discrete steps, the encoding has no infinite run for any valuation.

Then, from the location encoding the halting location (i. e. $l_{\mathtt {halt}}$), we add a transition resetting $x$ to a new location $l_f$. This location has a self-loop guarded with $x= 1$ and resetting $x$ (where $x$ is any of the four clocks used in the encoding in [8]). Hence whenever $l_{\mathtt {halt}}$ is reachable, there is an infinite non-Zeno run looping on $l_f$. That is, there is an infinite non-Zeno run iff the 2CM halts.

   $\blacksquare$

Since the emptiness problem is undecidable, the synthesis problem becomes intractable. In the remainder of this paper, we will devise a semi-algorithm to address non-Zeno synthesis, i. e. an algorithm that computes the exact solution if it terminates. Otherwise, we compute an under-approximation of the result.

4 CUB-Parametric Timed Automata

It has been shown (e.g. [11, 25]) that checking whether a run of TA is infeasible based on the symbolic semantics alone. In [27], the authors identified a subclass of TAs called CUB-TAs for which non-Zenoness checking based on the symbolic semantics is feasible. Furthermore, they show that an arbitrary TA can be transformed into a CUB-TA. Based on their work, we first show that arbitrary PTAs can be transformed into a parametric version of CUB-TAs, and then solve the non-Zeno synthesis problem based on parametric CUB-TAs.

As defined in [27], a clock upper bound is either $\infty$ or a pair $(n, \lhd )$ where $n\in \mathbb {Q}$ (recall that $\lhd$ is either < or $\le$). We write $(n_1, \lhd _1) = (n_2, \lhd _2)$ to denote $n_1 = n_2$ and $\lhd _1 = \lhd _2$; $(n_1, \lhd _1) \le (n_2, \lhd _2)$ to denote $n_1 < n_2$, or if $n_1 = n_2$, then either $\lhd _2$ is $\le$ or both $\lhd _1$ and $\lhd _2$ are <. Further, we write $(n, {\lhd }) > d$ where d is a constant to denote $n > d$. We define $\min ((n, {\lhd _1}), (m, {\lhd _2}))$ to be $(n, {\lhd _1})$ if $(n, {\lhd _1}) \le (m, {\lhd _2})$, and $(m,{\lhd _2})$ otherwise. Given a clock $x$ and a non-parametric guard $g$, we write $ub (g, x)$ to denote the upper bound of $x$ given $g$. Formally,

$$\begin{aligned} ub (g, x) = \left\{ \begin{array}{l l} (n, \lhd ) &{} \text {if } g\text { is } x\lhd \text {n} \\ \infty &{} \text {if } g\text { is } x> \text {n} \text { or } x\ge \text {n} \\ \infty &{} \text {if } g\text { is } x' \bowtie \text {n} \text { and } x' \ne x\\ \infty &{} \text {if } g\text { is } true \\ \min ( ub (g_1, x), ub (g_2, x)) &{} \text {if } g\text { is } g_1 \wedge g_2 \end{array} \right. \end{aligned}$$

Definition 3

A TA is a CUB-TA if for each edge $(l,g,a,R,l')$, for all clocks $x\in X$, we have (i) $ub (I(l), x) \le ub (g, x)$, and (ii) if $x\notin R$, then $ub (I(l), x) \le ub (I(l'), x)$.

Intuitively, every clock in a CUB-TA has a non-decreasing upper bound along any path until it is reset.

4.1 Parametric Clock Upper Bounds

Let us define clock upper bounds in a parametric setting. A parametric clock upper bound is either $\infty$ or a pair $( plt , \lhd )$.

Given a clock $x$ and a guard $g$, we denote by $pub (g, x)$ the parametric upper bound of $x$ given $g$. This upper bound is a parametric linear term. Formally,

$$\begin{aligned} pub (g, x) = \left\{ \begin{array}{l l} ( plt , \lhd ) &{} \text {if } g\text { is } x\lhd plt \\ \infty &{} \text {if } g\text { is } x> plt \text { or } x\ge plt \\ \infty &{} \text {if } g\text { is } x' \bowtie plt \text { and } x' \ne x\\ \infty &{} \text {if } g\text { is } true \\ \min ( pub (g_1, x), pub (g_2, x)) &{} \text {if } g\text { is } g_1 \wedge g_2 \end{array} \right. \end{aligned}$$

Recall that, in each guard, given a clock $x$, at most one inequality is in the form $x\lhd plt$. In that case, at most one of the two terms is not $\infty$ and therefore the minimum is well-defined (with the usual definition that $\min ( plt , \infty ) = plt )$.¹

We write $( plt _1, \lhd _1) \le ( plt _2, \lhd _2)$ to denote the constraint

$$\begin{aligned} \left\{ \begin{array}{l l} plt _1< plt _2 &{} \text {if }\lhd _1 = {\le } \text { and } \lhd _2 = {<} \\ plt _1 \le plt _2 &{} \text {otherwise.} \\ \end{array} \right. \end{aligned}$$

That is, we constrain the first parametric clock upper bound to be smaller than or equal to the second one, depending on the comparison operator.

Given two parametric clock upper bounds $pcub _1$ and $pcub _2$, we write $pcub _1 \le pcub _2$ to denote the constraint

$$\begin{aligned} \left\{ \begin{array}{l l} ( plt _1, \lhd _1) \le ( plt _2, \lhd _2) &{} \text {if } pcub _1 = ( plt _1, \lhd _1) \text{ and } pcub _2 = ( plt _2, \lhd _2) \\ \top &{} \text {if } pcub _2 = \infty \\ \bot &{} \text {otherwise.} \\ \end{array} \right. \end{aligned}$$

This yields an inequality constraining the first parametric clock upper bound to be smaller than or equal to the second one.

4.2 CUB Parametric Timed Automata

We extend the definition of CUB-TAs to parameters as follows:

Definition 4

A PTA is a CUB-PTA if for each edge $(l,g,a,R,l')$, for all clocks $x\in X$, the following conditions hold: (i) $\mathcal {A}.K_0\subseteq \big ( pub (I(l), x) \le pub (g, x)\big )$, and (ii) if $x\notin R$, then $\mathcal {A}.K_0\subseteq \big ( pub (I(l), x) \le pub (I(l'), x)\big )$.

Hence, a PTA is a CUB-PTA iff every clock has a non-decreasing upper bound along any path before it is reset, for all parameter valuations satisfying the initial constraint $\mathcal {A}.K_0$.

Note that, interestingly enough, the class of hardware circuits modeled using a bi-bounded inertial delay² fits into CUB-PTAs (for all parameter valuations).

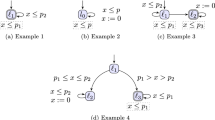
Example 1

Consider the PTA $\mathcal {A}$ in Fig. 1a s.t. $\mathcal {A}.K_0= \top$. Then $\mathcal {A}$ is not CUB: for x, the upper bound in $l_0$ is $x \le 1$ whereas that of the guard on the transition outgoing $l_0$ is $x \le p$. $(1, \le ) \le (p, \le )$ yields $1 \le p$. Then, $\top \not \subseteq \big ( 1 \le p\big )$; for example, $p= 0$ does not satisfy $1 \le p$.

Consider again the PTA $\mathcal {A}$ in Fig. 1a, this time assuming that $\mathcal {A}.K_0= (p= 1 \wedge 1 \le p' \wedge p' \le p'')$. This PTA is a CUB-PTA. (The largest constraint $K_0$ making this PTA a CUB will be computed in Example 2.)    $\square$

Lemma 2

Let $\mathcal {A}$ be a CUB-PTA. Let $v\models \mathcal {A}.K_0$. Then $v(\mathcal {A})$ is a CUB-TA.

Proof

Let $v\models \mathcal {A}.K_0$. Let $e= (l,g,a,R,l')$ be an edge. Given a clock $x\in X$, from Definition 4, we have that $v\models \big ( pub (I(l), x) \le pub (g, x)\big )$, and therefore $v( pub (I(l), x)) \le v( pub (g, x))$. This matches the first case of Definition 3. The second case ($x\notin R$) is similar.    $\blacksquare$

Fig. 1.

Examples of PTAs to illustrate the CUB concept

4.3 CUB PTA Detection

Given an arbitrary PTA, our approach works as follows. Firstly, we check whether it is a CUB-PTA for some valuations. If it is, we proceed to the synthesis problem, using the cycle detection synthesis algorithm (Sect. 5); however, the result may be partial, as it will only be valid for the valuations for which the PTA is CUB. This incompleteness may come at the benefit of a more efficient synthesis. If it is CUB for no valuation, it has to be transformed into an equivalent CUB-PTA (which will be considered in Sect. 4.4).

Our procedure to detect whether a PTA is CUB for some valuations is given in Algorithm 1. For each edge in the PTA, we enforce the CUB condition on each clock by constraining the upper bound in the invariant of the source location to be smaller than or equal to the upper bound of the edge guard (line 4). Additionally, if the clock is not reset along this edge, then the upper bound of the source location invariant should be smaller than or equal to that of the target location (line 5). If the resulting set of constraints accepts parameter valuations (i. e. is not empty), then the PTA is a CUB-PTA for these valuations.

Example 2

Consider again the PTA $\mathcal {A}$ in Fig. 1a, assuming that $\mathcal {A}.K_0= \top$. This PTA is CUB for $1 \le p \wedge 1 \le p' \wedge p' \le p''$.

Consider the PTA $\mathcal {A}$ in Fig. 1b, with $\mathcal {A}.K_0= \top$. When handling location $l_0$ and clock x, line 4 yields $\mathcal {A}.K=\top \wedge [(p,\le )\le (1,\le )]=p\le 1$ and then, from line 5, $\mathcal {A}.K= p\le 1 \wedge [(p,\le )\le (p,<)]= p\le 1 \wedge p< p= \bot$. Hence, there is no valuation for which this PTA is CUB.    $\square$

Proposition 1

Let $K= \mathsf {CUBdetect}(\mathcal {A})$. Then $\mathcal {A}(K)$ is a CUB-PTA.

Proof

From the fact that Algorithm 1 gathers constraints to match Definition 4.

   $\blacksquare$

4.4 Transforming a PTA into a Disjunctive CUB-PTA

In this section, we show that an arbitrary PTA can be transformed into an extension of CUB-PTAs (namely disjunctive CUB-PTA), while preserving the symbolic runs.

For non-parametric TAs, it is shown in [27] that any TA can be transformed into an equivalent CUB-TA. This does not lift to CUB-PTAs.

Example 3

No equivalent CUB-PTA exists for the PTA in Fig. 2b where $K_0= \top$. Indeed, the edge from $l_1$ to $l_2$ (resp. $l_3$) requires $p_1 \le p_2$ (resp. $p_1 > p_2$). It is impossible to transform this PTA into a PTA where $K_0$ (which is $\top$) is included in both $p_1 \le p_2$ and $p_1 > p_2$.    $\square$

Therefore, in order to overcome this limitation, we propose an alternative definition of disjunctive CUB-PTAs. They can be seen as a union (as defined in the timed automata patterns of, e. g. [13]) of CUB-PTAs.

Definition 5

A disjunctive CUB-PTA is a list of CUB-PTAs.

Given a disjunctive CUB-PTA $\mathcal {A}_1, \dots , \mathcal {A}_n$, with $\mathcal {A}_i = (\varSigma _i, L_i, l_0^i, X_i, P_i, K_0^i, I_i, E_i)$, the PTA associated with this disjunctive PTA is $\mathcal {A}= (\bigcup _i \varSigma _i, \bigcup _i L_i \cup \{ l_0\}, l_0, \bigcup _i X_i, \bigcup _i P_i, \bigcup _i K_0^i, \bigcup _i I_i, E)$, where $E= \bigcup _i E_i \cup E'$ with $E' = \bigcup _i (l_0, K_0^i, \epsilon , X, l_0^i)$.

Basically, the PTA associated with a disjunctive CUB-PTA is just an additional initial location that connects to each of the CUB-PTAs initial locations, with its initial constraint on the guard.³

Example 4

In Fig. 2d (without the dotted, blue elements), two CUB-PTAs are depicted, one (say $\mathcal {A}_1$) on the left with locations superscripted by 1, and one (say $\mathcal {A}_2$) on the right superscripted with 2. Assume $\mathcal {A}_1.K_0$ is $p_1 \le p_2$ and $\mathcal {A}_2.K_0$ is $p_1 > p_2$. Then the full Fig. 2d (including dotted elements) is the PTA associated with the disjunctive CUB-PTA made of $\mathcal {A}_1$ and $\mathcal {A}_2$.    $\square$

The key idea behind the transformation from a TA into a CUB-TA in [27] is as follows: whenever a location $l$ is followed by an edge $e$ and a location $l'$ for which $ub (g,x) < ub (l,x)$ or $ub (l',x) < ub (l,x)$ for some $x$ if $x\notin R$, otherwise $ub (g,x) < ub (l,x)$, location $l$ is split into two locations: one (say $l_1$) with a “decreased upper bound”, i. e. $x\lhd ub (l',x)$, that is then connected to $l'$; and one (say $l_2$) with the same invariant as in $l$, and with no transition to $l'$. Therefore, the original behavior is maintained. Note that this transformation induces some non-determinism (one must non-deterministically choose whether one enters $l_1$ or $l_2$, which will impact the future ability to enter $l'$) but this has no impact on the existence of a non-Zeno cycle.

Here, we extend this principle to CUB-PTAs. A major difference is that, in the parametric setting, comparing two clock upper bounds does not give a Boolean answer but a parametric answer. For example, in a TA, $(2, \le ) \le (3, <)$ holds (this is true), whereas in a PTA $(p_1, \le ) \le (p_2, <)$ denotes the constraint $p_1 < p_2$. Therefore, the principle of our transformation is that, whenever we have to compare two parametric clock upper bounds, we consider both cases: here either $p_1 < p_2$ (in which case the first location does not need to be split) or $p_1 \ge p_2$ (in which case the first location shall be split). This yields a finite list of CUB-PTAs: each of these CUB-PTAs consists in one particular ordering of all parametric linear terms used as upper bounds in guards and invariants. (In practice, in order to reduce the complexity, we only define an order on the parametric linear terms the comparison of which is needed during the transformation.)

Fig. 2.

Examples: detection of and transformation into CUB-PTAs

Example 5

Let us transform the PTA in Fig. 2a: if $p_1 \le p_2$ then the PTA is already CUB, and $l_1$ does not need to be split. This yields a first CUB-PTA, depicted on the left-hand side of Fig. 2d. However, if $p_1 > p_2$, then $l_1$ needs to be split into ${l_1^2}'$ (where time cannot go beyond $p_2$) and into $l_1^2$ (where time can go beyond $p_2$, until $p_1$), but the self-loop cannot be taken anymore (otherwise the associated guard makes the PTA not CUB). This yields a second CUB-PTA, depicted on the right-hand side of Fig. 2d. Both make a disjunctive CUB-PTA equivalent to Fig. 2a.

Similarly, we give the transformation of Fig. 2b in Fig. 2e.    $\square$

5 Zeno-Free Cycle Synthesis in CUB-PTAs

Taking a disjunctive CUB-PTA as input, we show in this section that synthesizing the parameter valuations for which there exists at least one non-Zeno cycle (and therefore an infinite non-Zeno run) reduces to an SCC (strongly connected component) synthesis problem.

First, we define a light extension of the parametric zone graph as follows. The extended parametric zone graph of a PTA $\mathcal {A}$ is identical to its parametric zone graph, except that any transition $(\mathbf {s}, e, \mathbf {s}')$ is replaced with $(\mathbf {s}, (e, {b}), \mathbf {s}')$, where ${b}$ is a Boolean flag which is true if time can potentially elapse between $\mathbf {s}$ and $\mathbf {s}'$. In practice, ${b}$ can be computed as follows, given $\mathbf {s}= (l, C)$ and edge $e$:

• 1. add a fresh extra clock $x_0$ to the constraint $C$, i. e. compute $C\wedge x_0= 0$

• 2. compute the successor $\mathbf {s}' = (l', C')$ of $(l, C\wedge x_0= 0)$ via edge $e$

• 3. check whether $C' \Rightarrow x_0= 0$: if so, then ${b}= \text {false}$; otherwise ${b}= \text {true}$.

Introducing such a clock is cheap: the check is not expensive, and the extra clock does not impact the size of the parametric zone graph: $x_0$ is 0 in all nodes of the zone graph and can be eliminated from the memory, therefore not requiring more space nor extra states.

In contrast to non-parametric TAs, the flag ${b}$ does not necessarily mean that time can necessarily elapse for all parameter valuations. Consider the example in Fig. 2c. After taking one loop, we have that $x_0\le p$: therefore, $x_0$ is not necessarily 0, and ${b}$ is $\text {true}$. But consider $v$ such that $v(p) = 0$: then in $l_1$ time can never elapse. However, we show in the following lemma that the flag ${b}$ does denote time elapsing for strictly positive parameters.

Lemma 3

Let $(l, C) \mathop {\Rightarrow }\limits ^{e, {b}} (l', C')$ be a transition of the extended parametric zone graph of a PTA $\mathcal {A}$. Then, for any strictly positive parameter valuation in $C'{\downarrow _{P}}$, there exists an equivalent transition in $v(\mathcal {A})$ in which time can elapse.

Proof

First note that, for any $v\models C'{\downarrow _{P}}$, an equivalent concrete transition exists in $v(\mathcal {A})$, from Lemma 1. Now, since ${b}$ is true, the extra clock $x_0$ in the state of the extended parametric zone graph corresponding to $(l, C')$ is either unbounded, or bounded by some parametric linear term $plt$. If it is unbounded, then time can elapse for any valuation, and the lemma holds trivially. Assume $x_0\le plt$ for some $plt$. As our parameters are strictly positive, then for any valuation $v$, $v( plt )$ evaluates to a strictly positive rational, and therefore time can elapse along this transition in $v(\mathcal {A})$.    $\blacksquare$

Definition 6

An infinite symbolic run $\mathbf {r}$ is non-Zeno if all its associated concrete runs are non-Zeno.

In the remainder of this section, given an edge $e= (l,g,a,R,l')$, $e.R$ denotes that the clocks in $R$ reset along $e$.

The following theorem states that an infinite symbolic run is non-Zeno iff the time can (potentially) elapse along infinitely many edges and, whenever a clock is bounded from above, then eventually either this clock is reset or it becomes unbounded.

Theorem 2

Let $\mathbf {r}= \mathbf {s}_0 \mathop {\Rightarrow }\limits ^{(e_0, {b}_0)} \mathbf {s}_1\mathop {\Rightarrow }\limits ^{(e_1, {b}_1)} \cdots$ be an infinite symbolic run of the extended parametric zone graph of a CUB-PTA $\mathcal {A}$. $\mathbf {r}$ is non-Zeno if and only if

• $*$ there exist infinitely many k such that ${b}_k = \text {true}$; and

• $\star$ for all $x\in X$, for all $i \ge 0$, given $\mathbf {s}_i = (l_i, C_i)$, if $pub (l_i, x) \ne \infty$, there exists j such that $j \ge i$ and $x\in e_j.R$ or $pub (l_j, x) = \infty$.

We now show that synthesizing parameter valuations for which there exists a non-Zeno infinite run reduces to an SCC searching problem.

First, given an SCC $scc$, we denote by $scc .K$ the parameter constraint associated with $scc$, i. e. $C{\downarrow _{P}}$, where $(l, C)$ is any state of the SCC.⁴

Theorem 3

Let $\mathcal {A}$ be a CUB-PTA of finite extended parametric zone graph $\mathcal {G}$. Let $v$ be a strictly positive parameter valuation. $v(\mathcal {A})$ contains a non-Zeno infinite run if and only if $\mathcal {G}$ contains a reachable SCC $scc$ such that $v\models scc .K$ and

• $\dagger$ $scc$ contains a transition $\mathbf {s}\mathop {\Rightarrow }\limits ^{(e, {b})} \mathbf {s}'$ such that ${b}= \text {true}$; and

• $\ddagger$ for every clock $x$ in $X$, given $\mathbf {s}= (l, C)$, if $pub (l, x) \ne \infty$ for some state $\mathbf {s}$  in $scc$, there exists a transition in $scc$ with label $(e, {b})$ such that $x\in e.R$.

Therefore, from Theorem 3, synthesizing valuations yielding an infinite symbolic run reduces to an SCC searching problem in the extended parametric zone graph. Then, we need to test each SCC against two conditions: whether it contains a transition which can be locally delayed (i. e. whether it contains a transition where ${b}= \text {true}$); and whether every clock having an upper bound other than $\infty$ at some state is reset along some transition in the SCC. Then, for all SCCs matching these two conditions, we return the associated parameter constraint.

We give in Algorithm 2 an algorithm $\mathsf {synthNZ}$ to solve the non-Zeno synthesis problem for CUB-PTAs. $\mathsf {synthNZ}$ simply iterates on the SCCs, and gathers their associated parameter constraints whenever they satisfy the conditions in Theorem 3.

If $\mathcal {G}$ is finite, then the correctness and completeness of $\mathsf {synthNZ}$ immediately follow from Theorem 3. If only an incomplete part of $\mathcal {G}$ is computed (e. g. by bounding the exploration depth, or the number of explored states, or the execution time) then only the $\Leftarrow$ direction of Theorem 3 holds: in that case, the result of $\mathsf {synthNZ}$ is correct but non-complete, i. e. it is a valid under-approximation. In the context of parametric model checking, knowing which parameter valuations violate the property is already very helpful to the designer, as it helps to discard unsafe valuations, and to refine the model.

6 Experiments

We implemented our algorithms in IMITATOR [5].⁵ The Parma Polyhedra Library (PPL) [10] is integrated inside the core of IMITATOR in order to solve mainly linear inequality system problems. Experiments were run on an Intel Core 2 Duo P8600 at 2.4 GHz and 4 GiB of memory.

We compare three approaches: (1) A cycle detection synthesis without the non-Zenoness assumption (called $\mathsf {synthCycle}$). The result may be an over-approximation of the actual result, as some of the parameters synthesized may yield only Zeno cycles. If $\mathsf {synthCycle}$ does not terminate, its result is an under-approximation of an over-approximation, therefore considered as potentially invalid; that is, there is no guarantee of correctness for the synthesized constraint. (2) Our CUB-detection (Algorithm 1) followed by synthesis (Algorithm 2): the result may be under-approximated, as only the valuations for which the PTA is CUB are considered. (3) Our CUB-transformation ($\mathsf {CUBtrans}$) followed by synthesis (Algorithm 2) on the resulting disjunctive CUB-PTA. If the algorithm terminates, then the result is exact, otherwise it may be under-approximated.

We consider various benchmarks: protocols (CSMA/CD, Fischer [2], RCP, WFAS), hardware circuits (And-Or, flip-flop), scheduling problems (Sched5), a networked automation system (simop) and various academic benchmarks.

We give from left to right in Table 1 the case study name and its number of clocks, parameters and locations. For $\mathsf {synthCycle}$, we give the computation time (TO denotes a time-out at 3600 s), the constraint type ($\bot$, $\top$ or another constraint) and the validity of the result: if $\mathsf {synthCycle}$ terminates, the result is an over-approximation, otherwise it is potentially invalid. For $\mathsf {CUBdetect}$ (resp. $\mathsf {CUBtrans}$) we give the detection (resp. transformation) time, the total time (including $\mathsf {synthNZ}$), the result, and whether it is an under-approximation or an exact result. We also mention whether $\mathsf {CUBdetect}$ outputs that all, none or some valuations make the PTA CUB; and we give the number of locations in the transformed disjunctive CUB-PTA output by $\mathsf {CUBtrans}$. The percentage is used to compare the number of valuations (comparison obtained by discretization) output by the algorithms, with $\mathsf {CUBtrans}$ as the basis (as the result is exact).

The toy benchmark CUBPTA1 is a good illustration: $\mathsf {CUBtrans}$ terminates after 0.073 s (and therefore its result is exact) with some constraint. $\mathsf {CUBdetect}$ is faster (0.015 s) but infers that only some valuations are CUB and analyzes only these valuations; the synthesized result is only 69% of the expected result. In contrast, $\mathsf {synthCycle}$ is much faster (0.006 s) but obtains too many valuations (208% of the expected result) as it infers many Zeno valuations.

Table 1. Experimental comparison of the three algorithms

Let us discuss the results. First, $\mathsf {synthCycle}$ almost always outputs a possibly invalid result (neither an under- nor an over-approximation), which justifies the need for techniques handling non-Zeno assumptions. In only one case (CUBPTA1), it outputs a non-trivial over-approximation. In two cases, it happens to give an exact answer, as the over-approximation of $\bot$ necessarily means that $\bot$ is the exact result. In contrast, $\mathsf {CUBtrans}$ gives an exact result in five cases, a non-trivial under-approximation in two cases; the five remaining cases are a disappointing result in which $\bot$ is output as an under-approximation. By studying the model manually, we realized that some non-Zeno cycles actually exist for some valuations, but our synthesis algorithm was not able to derive them. Only in one of these cases (Sched5), $\mathsf {synthCycle}$ outputs a more interesting result than $\mathsf {CUBtrans}$.

The transformation is relatively reasonable both in terms of added locations (in the worst case, there are 40 instead of 10 locations, hence four times more, for WFAS) and in terms of transformation time (the worst case is 1.2 s for Sched5). Our experiments do not allow us to fairly compare the time of $\mathsf {synthCycle}$ (without non-Zenoness) and $\mathsf {synthNZ}$ (with non-Zenoness assumption) as, without surprise due to the undecidability, most analyses do not terminate. Only two benchmarks terminate for both algorithms, but are not significant (<1 s).

Note that flip-flop is a hardware circuit modeled using a bi-bounded inertial delay, and is therefore CUB for all valuations.

An interesting benchmark is WFAS, for which our transformation procedure terminates whereas $\mathsf {synthCycle}$ does not. Therefore, we get an exact result while the traditional procedure cannot produce any valuable output.

As a conclusion, $\mathsf {CUBdetect}$ seems to be faster but less complete than $\mathsf {CUBtrans}$. As for $\mathsf {CUBtrans}$, its result is almost always more valuable than $\mathsf {synthCycle}$, and therefore is the most interesting algorithm.

7 Conclusion

We proposed a technique to synthesize valuations for which there exists a non-Zeno infinite run in a PTA. By adding accepting states, this allows for parametric model checking with non-Zenoness assumption. Our techniques rely on a transformation to a disjunctive CUB-PTA (or in some cases on a simple detection of the valuation for which the PTA is already CUB), and then on a dedicated cycle synthesis algorithm. We implemented our techniques in IMITATOR and compared our algorithms on a set of benchmarks.

Future Works. Our technique relying on CUB-PTAs extends the technique of CUB-TAs: this technique is shown in [27] to be the most efficient for performing non-Zeno model checking for TAs. However, for PTAs, other techniques (such as yet to be defined parametric extensions of strongly non-Zeno TAs [26] or guessing zone graph [16]) could turn more efficient and should be investigated.

In addition, parametric stateful timed CSP (PSTCSP) [7] is a formalism for which the CUB assumption seems to be natively verified. Therefore, studying non-Zeno parametric model checking for PSTCSP, as well as transforming PTAs into PSTCSP models, would be an interesting direction of research.

Studying the decidability of the underlying decision problem should be done for famous subclasses of PTAs constraining the use of parameters (namely L/U-PTAs, L-PTAs and U-PTAs [17]) as well as for new semantic subclasses that we recently proposed and that benefit from decidability results (namely integer-point PTAs and reset-PTAs [6]).

An interesting future will be to design a multi-core extension of our non-Zeno synthesis algorithm; this could be done by reusing parallel depth first search algorithms for finding cycles [14].

Finally, combining our synthesis algorithms with IC3 [12], as well as extending them to hybrid systems [23] is also of high practical interest.