What’s Decidable About Parametric Timed Automata?

Abstract

Parametric timed automata (PTA) are a powerful formalism to reason, simulate and formally verify critical real-time systems. After two decades of research on PTA, it is now well-understood that any non-trivial problem studied is undecidable for general PTA. We provide here a survey of decision and computation problems for PTA. On the one hand, bounding time, bounding the number of parameters or the domain of the parameters does not (in general) lead to any decidability. On the other hand, restricting the number of clocks, the use of clocks (compared or not with the parameters), and the use of parameters (e.g., used only as upper or lower bounds) leads to decidability of some problems.

This work is partially supported by the ANR national research program PACS (ANR-14-CE28-0002).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The absence of undesired behaviors in real-time critical systems is of utmost importance in order to ensure the system safety. Model checking aims at formally verifying a model of the system against a correctness property. Timed automata (TA) are a popular formalism to model and verify safety critical systems with timing constraints. TA extend finite state automata with clocks, i.e., real-valued variables increasing linearly [1]. These clocks can be compared with integer constants in guards (sets of linear inequalities that must be satisfied to take a transition) and invariants (sets of linear inequalities that must be satisfied to remain in a location). TA have been widely studied, and several state-of-the-art model checkers (such as Uppaal [28] or PAT [33]) support TA as an input language.

TA benefit from many interesting decidable properties, such as the emptiness of the accepted language, the reachability of a control state, etc. However, TA also suffer from some limitations. First, they cannot be used to specify and verify systems incompletely specified (i.e., whose timing constants are not known yet), and hence cannot be used in early design phases. Second, verifying a system for a set of timing constants usually requires to enumerate all of them one by one if they are supposed to be integer-valued; in addition, TA cannot be used anymore if these constants are rational- or real-valued, and can be taken from a dense interval. Third, robustness in TA often assumes that all guards can be enlarged or shrinked by the same small variation; considering independent variations or considering both enlarging and shrinking was not addressed, and it is actually unclear whether this can be even considered for TA.

Parametric timed automata (PTA) overcome these limitations by allowing the use of parameters (i.e., unknown constants) in guards and invariants [3]. This increased expressive power comes at the price of the undecidability of most interesting problems – at least in the general case.

Tools such as an extension of Uppaal [24], Roméo [29] or IMITATOR [5] take PTA as input formalism. Beyond the usual academic examples (such as variants of train controllers [3, 24]), PTA were also used to successfully specify and verify numerous interesting case studies such as the root contention protocol [24], Philip’s bounded retransmission protocol [24], a 4-phase handshake protocol [27], the alternating bit protocol [25], an asynchronous circuit commercialized by ST-Microelectronics [17], (non-preemptive) schedulability problems [25], a distributed prospective architecture for the flight control system of the next generation of spacecrafts designed at ASTRIUM Space Transportation [20], an unmanned aerial video system by Thales, and even analysis of music scores [19].

In this paper, we survey decision problems for PTA proposed in the past two decades. On the one hand, bounding time, bounding the number of parameters or the domain of the parameters does not (in general) lead to any decidability. On the other hand, restricting the number of clocks, the use of clocks (compared or not with the parameters), and the use of parameters (e.g., used only as upper or lower bounds) can lead to the decidability of some problems.

Related Surveys. To the best of our knowledge, no survey was dedicated specifically to decision problems for PTA. In addition, recent results in the field in the past two years (e.g., [8, 10, 16, 25, 32]) justify the need for a clear picture of these updated (un)decidability results.

Related works include a work by Henzinger et al. [21], that is not a survey, but exhibits decidable subclasses of hybrid automata, an extension of timed automata where variables can have (in general) arbitrary rates. Then, Asarin et al. proposed a work [9] acting both as a survey and as a contribution paper that studies hybrid automata with “low dimensions”, i.e., with few variables. Our survey is also concerned (in Sect. 4) with decidability results for PTA with few variables (i.e., clocks and parameters). Various problems related to the robustness in TA were also surveyed [12].

Outline. In Sect. 2, we propose a unified syntax for PTA, and we define the decision problems that we will consider throughout this manuscript. In Sect. 3, we recall general undecidability for PTA. We then study in Sect. 4 the decidability when restricting the syntax of PTA (number of variables, syntax of the constraints, etc.). We consider specifically in Sect. 5 the subclass of L/U-PTA. We conclude by emphasizing open problems in Sect. 6.

2 Parametric Timed Automata and Problems

2.1 Clocks, Parameters and Constraints

Let ${\mathbb Z}$, ${\mathbb N}$, ${{\mathbb Q}^+}$ and ${{\mathbb R}^+}$ denote the sets of (possibly negative) integer numbers, (non-negative) natural numbers, non-negative rational numbers, and non-negative real numbers, respectively. In the following, ${\mathbb T}$ denotes the domain of time, and ${\mathbb P}$ the domain of the parameters; these domains will be instantiated with ${\mathbb N}$, ${{\mathbb Q}^+}$ or ${{\mathbb R}^+}$ later on. Throughout this survey, let $d$ denote an integer constant in ${\mathbb Z}$, and $d^+$ denote a non-negative constant in ${\mathbb N}$.

Let us assume a set $X= \{ x_1, \dots , x_H\}$ of clocks, that are ${\mathbb T}$-valued variables that evolve at the same rate. Let us assume a set $P= \{ p_1, \dots , p_M\}$ of parameters, i.e., unknown constants. A parameter valuation $v$ is a function $v: P\rightarrow {\mathbb P}$. Throughout this survey, symbols $x$, $x_i$ denote clocks whereas $p$, $p_i$ denote parameters.

A parametric linear term is $\sum _{1 \le i \le M} \alpha _i p_i + d$, with $\alpha _i \in {\mathbb Z}$; in the following $plt$ will denote a parametric linear term.

A (linear) inequality is $x\sim plt$, where $x$ is a clock, $plt$ a parametric linear term, and ${\mathrel {\sim }} \in \{ <, \le , =, \ge , > \}$. We give in Table 1 the conventions used throughout this survey concerning comparison operators. A (linear) constraint is a set of linear inequalities.

A simple inequality is either $x\sim p$ or $x\sim d^+$. A simple constraint is a set of simple inequalities.

Table 1. Syntax of operators in guards

2.2 A Unified Syntax for Parametric Timed Automata

The syntax of PTA varies a lot in the literature; we give below a definition that includes any definition in the literature. That is, any definition of PTA can be obtained from the following one by adding restrictions such as removing the set of accepting locations, forbidding invariants, restricting the domain of clocks or parameters, simplifying the syntax of the guards and invariants, etc.

Definition 1

A PTA is a tuple $\mathsf{A}= (\varSigma , L, l_0, F, X, P, I, E)$, where:

• $\varSigma$ is a finite set of actions,

• $L$ is a finite set of locations,

• $l_0\in L$ is the initial location,

• $F\subseteq L$ is a set of accepting (or final) locations,

• $X$ is a set of clocks with domain ${\mathbb T}= {{\mathbb R}^+}$,

• $P$ is a set of parameters with domain ${\mathbb P}= {{\mathbb R}^+}$,

• $I$ is the invariant, assigning to every $l\in L$ a constraint $I(l)$, and

• $E$ is a set of edges $(l,g,a,R,l')$ where $l,l'\in L$ are the source and destination locations, $g$ is a constraint which is the transition guard, $a\in \varSigma$, and $R\subseteq X$ is a set of clocks to be reset.

Given a PTA $\mathsf{A}$ and a parameter valuation $v$, the valuation of $\mathsf{A}$ with $v$, denoted by $v(\mathsf{A})$, is the (non-parametric) TA where each occurrence of $p$ is replaced with $v(p)$.

We say that a PTA is deterministic if, for any $l\in L$, for any $a\in \varSigma$, there exists at most one edge $(l,g,a,R,l') \in E$, for some $g,R,l'$. (Note that it differs from a rather common definition of determinism for TA, that allows two or more outgoing transitions with the same action label provided that the corresponding guards are pairwise disjoint.)

A clock is said to be a parametric clock if it is compared with at least one parameter in at least one guard or invariant; otherwise, it is a non-parametric clock. This notion is central when studying the decidability of problems for PTA with few clocks and parameters.

Fig. 1.

A coffee machine modeled using a PTA

Example 1

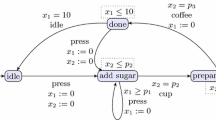
Consider the coffee machine in Fig. 1, modeled using a PTA with 4 locations, 2 clocks (${x_1}$ and ${x_2}$) and 3 parameters (${p_1}, {p_2}, {p_3}$). This PTA is deterministic; both clocks ${x_1}$ and ${x_2}$ are parametric clocks. The machine can initially idle for an arbitrarily long time. Then, whenever the user presses the (unique) button (action press), the PTA enters location “add sugar”, resetting both clocks. The machine can remain in this location as long as the invariant (${x_2} \le {p_2}$) is satisfied; there, the user can add a dose of sugar by pressing the button (action press), provided the guard (${x_1} \ge {p_1}$) is satisfied, which resets ${x_1}$. That is, the user cannot press twice the button (and hence add two doses of sugar) in a time less than ${p_1}$. Then, ${p_2}$ time units after the machine left the idle mode, a cup is delivered (action cup), and the coffee is being prepared; eventually, ${p_2}$ time units after the machine left the idle mode, the coffee (action coffee) is delivered. Then, after 10 time units, the machine returns to the idle mode – unless a user again requests a coffee by pressing the button.

Semantics. The semantics of a PTA $\mathsf{A}$ can be defined as the union over all parameter valuations $v$ of the semantics of $v(\mathsf{A})$. In the following, given $\delta \in {{\mathbb R}^+}$, $w+ \delta$ denotes the valuation such that $(w+ \delta )(x) = w(x) + \delta$, for all $x\in X$. Given $R\subseteq X$, we define the reset of a clock valuation $w$, denoted by $[w]_{R}$, as the valuation resetting the clocks in $R$, and keeping the other clocks unchanged. Given a parameter valuation $v$, $v(C)$ denotes the constraint over $X$ obtained by replacing each parameter $p$ in $C$ with $v(p)$. Likewise, given a clock valuation $w$, $w(v(C))$ denotes the expression obtained by replacing each clock $x$ in $v(C)$ with $w(x)$. We use the notation $w|v \models C$ to indicate that $w(v(C))$ evaluates to true.

Definition 2

(Semantics of a TA). Given a PTA $\mathsf{A}= (\varSigma , L, l_0, X, P, I, E)$, and a parameter valuation $v$, the semantics of $v(\mathsf{A})$ is given by the timed transition system $(Q, q_0, {\Rightarrow } )$, with

• $Q= \{ (l, w) \in L\times {{\mathbb R}^+}^H\mid v|w \models I(l) \}$,

• $q_0= (l_0, X= 0)$,

• $((l, w), e, (l', w')) \in {\Rightarrow }$ if $\exists w'' : (l,w) \mathop {\rightarrow }\limits ^{e} (l',w'') \mathop {\rightarrow }\limits ^{\delta } (l',w')$, with:

  • discrete transitions: $(l,w) \mathop {\rightarrow }\limits ^{e} (l',w')$, if $(l, w) , (l',w') \in Q$, there exists $e= (l,g,a,R,l') \in E$, $w'= [w]_{R}$, and $v|w \models g$;

  • delay transitions: $(l,w) \mathop {\rightarrow }\limits ^{\delta } (l, w+\delta )$, with $\delta \in {{\mathbb R}^+}$, if $\forall \delta ' \in [0, \delta ], (l, w+\delta ') \in Q$.

A run of a TA is an alternating sequence of states of $Q$ and edges of the form $(l_0,w_0) \mathop {\Rightarrow }\limits ^{e_0} (l_1,w_1) \mathop {\Rightarrow }\limits ^{e_1} \cdots \mathop {\Rightarrow }\limits ^{e_{m-1}} (l_m,w_m)$, such that for all $i = 0, \dots , m-1$, $e_i \in E$, and $((l_i,w_i) , e_i , (l_{i+1},w_{i+1})) \in {\Rightarrow }$.

Note that time elapsing can still be a 0-duration ($d \in {{\mathbb R}^+}$ allows $d=0$); in other words, TA allow to model Zeno behaviors, i.e., an infinite number of actions within a 0-time or, more generally, a finite time (see e.g., [34]). The accepted timed language is the set of timed words (alternating sequences of actions and time elapsing) associated with an accepting run, i.e., a run ending in a location of $F$ (or, in some works, passing infinitely often by a location in $F$). Note that some works make a difference between finite and infinite runs. The untimed language of a TA is the timed language projected onto the actions. The set of traces (or trace set) is the set of accepting runs projected onto the locations and actions, i.e., a set of alternating locations and actions.

A symbolic semantics is also defined for PTA as a parametric zone graph [4, 24, 25], where a symbolic state is made of a discrete part (the current location) and a symbolic, continuous part (a set of diagonal constraints, i.e., $x_i - x_j \sim plt$, sometimes allowing disjunctions).

Simple PTA. We defined simple PTA as the subclass of PTA where guards and invariants are simple constraints. We define this class to show that, even in this restricted situation, all non-trivial problems are undecidable (Sect. 3).

Variants of the PTA Syntax. PTA were first defined in the seminal paper [3] using a set of accepting locations. This is similar to timed automata [1]. Timed Safety Automata (TSA) were introduced later by removing the final states, but adding invariants to locations [23]; many subsequent papers then refer to timed safety automata as simply “timed automata”. In contrast, timed automata with accepting locations are often referred to as timed Büchi automata (TBA). The timed expressive power of TSA is strictly less than that of TBA [22].

The syntax of PTA differs in most of the papers in the literature. Concerning guards and invariants, in work [3] (resp. [30]), guards (resp. guards and invariants) are conjunctions of inequalities of the form $x\sim p$. In works [13, 24], guards are conjunctions of inequalities of the form $x_i - x_j \preceq plt \cup \{\infty \}$; in work [24] invariants have the same form as guards (invariants are not considered in work [13]). In work [18], guards and invariants are all open, i.e., of the form $x\mathrel {<>}p$ or $x\mathrel {<>}d^+$. In work [25], guards and invariants are conjunctions of inequalities of the form $x\sim plt$, and invariants can only bound clocks from above (i.e., $x\preceq plt$). In work [10], guards are conjunctions of inequalities of the form $x\sim p$ and invariants can only bound clocks from above (i.e., $x\preceq p$). In work [8], guards and invariants are conjunctions of inequalities of the form $x\sim p+ d$, $x\sim d^+$ or $p\sim d$ (although the proofs of undecidability only need inequalities of the form $x\sim p$ or $x\sim d^+$).

A set of accepting locations is considered in several previous works [3, 10, 13], but only one [13] is interested in infinite accepting runs, i.e., runs that pass infinitely often by an accepting location; hence this latter work considers what could be referred to as parametric timed Büchi automata. In contrast, other previous approaches [4, 8, 18, 24, 25] consider parametric timed safety automata (i.e., without accepting locations).

Expressiveness. A comparison of the expressiveness of these different syntactic models remains to be done. Whereas it is likely that allowing constraints of the form $x\sim plt$ may be simulated using constraints of the form $x\sim p$ (perhaps adding additional locations, clocks and parameters), the expressiveness may differ when adding a set of accepting locations (just as the timed expressive power of TSA is strictly less than that of TBA [22]). In fact, the expressiveness of a PTA was not even defined; we believe that shall be studied in the future.

2.3 Decision and Computation Problems

We follow here the presentation of a previous approach [25]. Given a class of decision problems $\mathcal {P}$ (reachability, unavoidability, etc.), let us define the $\mathcal {P}$-emptiness, the $\mathcal {P}$-universality and the $\mathcal {P}$-finiteness. Given a PTA A and an instance $\phi$ of $\mathcal {P}$, the $\mathcal {P}$-emptiness, $\mathcal {P}$-universality and $\mathcal {P}$-finiteness ask whether the set of parameter valuations $v$ such that $v(\mathsf{A})$ satisfies $\phi$ is empty, is equal to ${\mathbb P}^{|P|}$ and is finite, respectively.

In this survey, we mainly focus on reachability and unavoidability properties, and call them EF and AF respectively.¹ We will also mention the EG property, that checks whether there exists a maximal run along which the locations remain in a subset $G$  of the locations, and the AG property that checks whether the locations remain in $G$ for all runs.²

Additionally, we will survey the language (resp. trace) preservation (emptiness) problem [8]: given a PTA $\mathsf{A}$ and a parameter valuation $v$, does there exist another valuation $v' \ne v$ such that the untimed languages (resp. sets of traces) of $v(\mathsf{A})$ and $v'(\mathsf{A})$ are the same?

We finally define the $\mathcal {P}$-synthesis problem: Given a PTA A and an instance $\phi$ of $\mathcal {P}$, compute the parameter valuations such that $v(\mathsf{A})$ satisfies $\phi$.

Example 2

Let us exemplify some decision and computation problems for the PTA in Fig. 1. Assume the unique target location is “done”, i.e., $G=\{ \mathrm{done} \}$. EF-emptiness asks whether at least one parameter valuation can reach location “done” for some run; this is true (e.g., ${p_1} = 1$, ${p_2} = 2$, ${p_3} = 3$). EF-universality asks whether all parameter valuations can reach location “done” for some run; this is false (no parameter valuation such that ${p_2} > {p_3}$ can reach “done”). AF-emptiness asks whether at least one parameter valuation can reach location “done” for all runs; this is true (e.g., ${p_1} = 1$, ${p_2} = 2$, ${p_3} = 3$). EF-synthesis consists in synthesizing all valuations for which a run reaches location “done”; the resulting set of valuations is $0 \le {p_2} \le {p_3} \le 10 \wedge {p_1} \ge 0$.

3 Almost Everything is Undecidable for Simple PTA

In this entire section, we consider simple PTA without restriction on the number of clocks and parameters. In that situation, all non-trivial problems studied in the literature are undecidable, with the exception of the membership problem (that asks whether the language of a valuated PTA is empty) – which is rather a problem for TA. By non-trivial, we mean requiring a semantic analysis, and not, e.g., a sole analysis of the syntax of the PTA (e.g., “is the number of clocks even”, or any problem defined in Sect. 2.3 by setting $G= L$).

We also survey that bounding time (Sect. 3.3) or the parameter domain for rational-valued parameters (Sect. 3.4) preserves the undecidability. However, we will show in Sect. 4 that bounding the number of clocks and/or parameters brings decidability.

All proofs of undecidability reduce from either the halting problem, or the boundedness problem, of a 2-counter machine, known to be undecidable [31].

3.1 Decidability of the Membership

In the seminal PTA paper [3], the membership problem for PTA is defined as follows: given a PTA $\mathsf{A}$ and a parameter valuation $v$, is the language of $v(\mathsf{A})$ empty? The membership problem is not strictly speaking a problem for PTA, but rather for TA, since it considers a valuated PTA. As a consequence, the decidability of this problem only relies on known results for TA [1]: the membership problem is decidable (and PSPACE-complete) for PTA over discrete time (${\mathbb T}= {\mathbb N}$ and ${\mathbb P}= {\mathbb N}$), over dense time with integer-valued parameters (${\mathbb T}= {{\mathbb R}^+}$ and ${\mathbb P}= {\mathbb N}$), and over dense time with rational-valued parameters (${\mathbb T}= {{\mathbb R}^+}$ and ${\mathbb P}= {\mathbb Q}$). However, it becomes undecidable with real-valued (in fact irrational) parameters [30].

3.2 General Undecidable Problems

EF-, AF, EG, AG-emptiness. The seminal paper on PTA [3] showed that the EF-emptiness problem is undecidable for PTA, both for discrete time, and for dense-time (real-valued clocks and real-valued parameters). Although not explicitly stated in that paper, the proof of undecidability, that consists in reducing from the halting problem of a 2-counter machine, also works for real-valued clocks with integer-valued parameters.

It was then proved that the AF-emptiness is undecidable for L/U-PTA (a subclass of PTA, see Sect. 5), and hence for PTA as well [25]. Again, the proof of undecidability consists in reducing from the halting problem of a 2-counter machine.

AG- and EG-emptiness are also undecidable [7].

Language and trace preservation problems. Both language preservation and trace preservation problems are undecidable for simple PTA [8]. The continuous (or robust) versions of those problems additionally require that the language (resp. set of traces) is preserved under any intermediary valuation of the form $\lambda \cdot v+ (1-\lambda )\cdot v'$, for $\lambda \in [0,1]$ (with the classical definition of addition and scalar multiplication). These problems are also undecidable for simple PTA.

The language preservation problems and its continuous version are undecidable for a PTA with at least 4 parametric clocks. The trace preservation and its continuous version require either an unbounded number of non-parametric clocks and diagonal constraints (that go beyond the usual syntax of PTA), or an unbounded number of parametric clocks. This is due to the fact that the proof encodes the 2-counter machine with a fixed number of locations, which thus requires to encode each location with a different clock. It remains open whether this problem is undecidable for a bounded number of clocks.

3.3 Bounding Time

Bounded-time model checking consists in checking a property within a bounded time domain. Undecidable problems might become decidable in this situation, or be of a lower complexity. For example, time-bounded reachability becomes decidable for a special subclass of hybrid automata with monotonic rates [14].

In contrast, the EF-emptiness problem remains undecidable for (general) PTA over bounded, dense time [26, Theorem 3.4].

This said, we emphasize that (quite trivially) model checking discrete-time PTA over bounded-time would become decidable. (This remains to be shown formally though.)

3.4 Bounding the Parameter Domain

Bounding the parameter domain consists in setting a minimal and a maximal bound on the possible parameter valuations of a PTA.

For integer parameters, any problem for a PTA over a bounded parameter domain is decidable iff the corresponding problem is decidable for a TA. In fact, the $\mathcal {P}$-emptiness problem for PTA with bounded integer is PSPACE-complete for any class of problems $\mathcal {P}$ that is PSPACE-complete for TA [25]. Indeed, it suffices to enumerate all parameter valuations, of which there is a finite number. As a consequence, EF-, AF-, EG-, AG-emptiness are all decidable; and so are language and trace preservation. A symbolic method was proposed to compute EF- and AF-synthesis [25]; experiments showed that this symbolic computation is faster than an exhaustive enumeration (using Uppaal).

For rational-valued parameters, the EF-emptiness problems is undecidable for a single parameter in [1, 2] [30]. EG- and AG-emptiness [7], and language and trace preservation [8] are also undecidable for a single parameter in [0, 1].

4 Bounding the Numbers of Clocks and Parameters

4.1 EF-Emptiness

Since the seminal paper on PTA [3], the decidability of the EF-emptiness problem was studied in various settings, by bounding the number of parametric clocks, of non-parametric clocks, and of parameters. The syntax was also restrained. We summarize these results in Table 2 (partially inspired by a similar table in a previous work [18], improved by adding more dimensions, and more recent results). The open question of the syntax expressiveness requires to consider a multi-dimensional table: we need to consider not only the number of clocks and parameters, but also the syntax allowed in guards and invariants. For example, a recent paper [16] improves the complexity of the seminal PTA papers [3] (NEXPTIME-complete instead of non-elementary) over $\mathbb N$ for 1 clock, but requires non-strict inequalities, and uses invariants; it is hence unclear whether the result of the seminal paper [3] is really subsumed by that more recent paper [16].

Let us extract the most important results out of Table 2. The decidability is clearly impacted by the number of parametric clocks. First, let us consider PTA with a single parametric clock: the EF-emptiness problem is decidable over discrete time with arbitrarily many non-parametric clocks (NEXPTIME-complete when only large inequalities are used [16], and non-elementary otherwise [3]). It is NP-complete over dense time with no non-parametric clock [30]. It is open over dense time with two non-parametric clocks, and undecidable with three non-parametric clocks [30]; note that this problem is decidable over discrete time [3, 16], which exhibits a difference between dense and discrete time [30].

Second, let us consider PTA with two parametric clocks: the EF-emptiness problem is decidable over discrete time with a single parameter [16]; this result is claimed in the same paper to extend to dense time with integer-valued parameters. Any other case with two parametric clocks remains open. Third, the EF-emptiness problem is undecidable in all settings with three (or more) parametric clocks. Finally, using only strict inequalities, the EF-emptiness is undecidable over dense time for two parametric clocks, three non-parametric clocks and two parameters [18]; this situation was not considered over discrete time.

Table 2. Decidability of the EF-emptiness problem for general PTA

4.2 Language and Trace Preservation

The language- and trace-preservation problems are decidable for deterministic PTA with a single clock, and with linear parameter constraints allowed in guards and invariants, i.e., of the form $x\sim plt$ or $plt \sim 0$ [8]. A procedure to compute parameter valuations with the same trace set as a given valuation is proposed (close to the “inverse method” [4]), that is complete for deterministic PTA, and terminates in the case of a single clock [8].

4.3 Parametric Model Checking

Parametric model checking was addressed in different settings: verifying a non-parametric model against a parametric formula, or a parametric model against a non-parametric formula, or a parametric model against a parametric formula.

Non-parametric Model/Parametric Formula. An extension of LTL with parameters in the formula (“PLTL”) was studied [2]. When only parametric “always” modalities are allowed of the form “$\le p$”, checking emptiness of the valuation set is PSPACE-complete. The solution to the synthesis problem is doubly exponential in the number of parameters. However, when allowing equality in PLTL, the emptiness problem becomes undecidable [2].

Parametric Model/Non-parametric Formula. It is shown that model checking PTA with the (non-parametric) logic MTL is undecidable, even with a single clock and a single parameter, and even when the PTA is deterministic [32]. This negative result comes in contrast to the decidability of the EF-emptiness problem for one-clock PTA. Note that the proof of undecidability requires the parameters to be rational-valued (integer-valued parameters are not sufficient – and this latter case can hence be considered as open).

Parametric Model/Parametric Formula. Model checking a PTA over discrete-time with a single parametric clock against a PTCTL formula (a parametric version of TCTL) is decidable, provided the formula does not use equality constraints; otherwise the problem becomes undecidable [15].

5 The Disappointing Class of L/U-PTA

Lower-bound/upper-bound parametric timed automata (L/U-PTA) restrict the use of parameters in the model [24]. A parameter is said to be an upper-bound parameter if, whenever it is compared with a clock, it is compared as an upper bound, i.e., it only appears in inequalities of the form $x\preceq p$. Conversely, a parameter is a lower-bound parameter if it is only compared with clocks as a lower bound, i.e., of the form $p\preceq x$.

An L/U-PTA is a PTA where the set of parameters is partitioned into upper-bound parameters and lower-bound parameters. Two additional subclasses were introduced later [13]: L-PTA (resp. U-PTA) are PTA with only lower-bound (resp. upper-bound) parameters.

Example 3

Consider again the coffee machine in Fig. 1, modeled using a PTA $\mathsf{A}$. This PTA is not an L/U-PTA; indeed, the guard ${x_2} = {p_2}$ (resp. ${x_2} = {p_3}$) makes ${p_2}$ (resp. ${p_3}$) be compared with clocks both as a lower-bound and as an upper-bound. (Recall that $=$ stands for $\le$ and $\ge$.)

However, if one replaces ${x_2} = {p_2}$ with ${x_2} \le {p_2}$ and one replaces ${x_2} = {p_3}$ with ${x_2} \le {p_3}$, then $\mathsf{A}$ becomes an L/U-PTA with lower-bound parameter ${p_1}$ and upper-bound parameters $\{{p_2}, {p_3}\}$. Note that equalities are not forbidden in L/U-PTA (e.g., ${x_1} = 10$), but only equalities involving parameters.

Several case studies fit into the class of L/U-PTA: the root contention protocol, the bounded retransmission protocol and the Fischer mutual exclusion protocol are all modeled with L/U-PTA in the paper introducing L/U-PTA [24]; in two works [24, 27], both the Fischer mutual exclusion protocol and a producer-consumer are verified using L/U-PTA. Interestingly, the two case studies of the seminal paper on PTA [3] (viz., a toy railroad crossing model and a model of Fischer mutual exclusion protocol) are also L/U-PTA. In addition, most models of asynchronous circuits with bi-bounded delays (i.e., where each delay between the change of an input signal and the change of the corresponding output is a parametric interval) can be modeled using L/U-PTA.

5.1 Decidability Results

The first (and main) positive result for L/U-PTA is the decidability of the EF-emptiness problem [24]. L/U-PTA benefit from the following interesting property: increasing the value of an upper-bound parameter or decreasing the value of a lower-bound parameter necessarily relaxes the guards and invariants, and hence can only add behaviors. Hence, checking the EF-emptiness of an L/U-PTA can be achieved by replacing all lower-bound parameters with 0, and all upper-bound parameters with $\infty$; this yields a non-parametric TA, for which emptiness is PSPACE [1]. This procedure is not only sound but also complete.

Further decidability results are exhibited [13], for infinite runs acceptance properties, i.e., where a location is met infinitely often (to which we refer hereafter as BüEF). Note that, in contrast to the first paper on L/U-PTA [24] where the parameters are valued with non-negative reals, the results this later work [13] consider integer-valued parameters (though time is dense, i.e., clocks are real-valued). It is shown in this later work [13] that emptiness, universality, finiteness of the valuation set are PSPACE-complete for infinite runs acceptance properties. Remark that the decidability of the BüEF-finiteness is due to the integerness of the parameters; in short, a sufficient bound is computed on the parameters, and then valuations smaller or equal to this bound are enumerated, which would not be feasible for real-valued parameters.

A parametric extension of the dense-time linear temporal logic $\mathsf {MITL}_{0,\infty }$ (denoted “$\mathsf {PMITL}_{0,\infty }$”) is proposed [13]; when parameters are used only as lower or upper bound in the formula (to which we refer as L/U-$\mathsf {PMITL}_{0,\infty }$), satisfiability and model checking are PSPACE-complete; this is obtained by translating the formula into an L/U-automaton and checking an infinite acceptance property.

5.2 Undecidability Results

The first undecidability results for L/U-PTA are shown in works by Bozelli et al. [13]: the constrained EF-emptiness problem and constrained EF-universality problem (for infinite runs acceptance properties) are undecidable for L/U-PTA. By constrained it is meant that some parameters of the L/U-PTA can be constrained by an initial linear constraint, e.g., $p_1 \le 2 \times p_2 + p_3$. Indeed, using linear constraints, one can constrain an upper-bound parameter to be equal to a lower-bound parameter, and hence build a 2-counter machine using an L/U-PTA. However, when no upper-bound parameter is compared to a lower-bound parameter (i.e., when no initial linear inequality contains both an upper-bound and a lower-bound parameter), these two problems retrieve decidability [13].

A second negative result is shown by Jovanović et al. [25]: the AF-emptiness problem is undecidable for L/U-PTA. This is achieved by a reduction from a 2-counter machine where a lower-bound parameter is equal to an upper-bound parameter iff AF holds. This restricts again the use of L/U-PTA, as AF is essential to show that all possible runs of a system eventually reach a (good) state.

Then, it is shown that the language preservation problem is undecidable for L/U-PTA [8]. Again, this is achieved by a reduction from a 2-counter machine where a lower-bound parameter is equal to an upper-bound parameter iff the language is preserved.

We summarize in Table 3 decision problems for L/U-PTA.

Table 3. Decision problems for L/U-PTA

5.3 Intractability of the Synthesis

The most disappointing result concerning L/U-PTA is shown by Jovanović et al. [25]: if it can be computed, the solution to the EF-synthesis problem for L/U-PTA cannot be represented using a formalism for which the emptiness of the intersection with equality constraints is decidable. The proof relies on the undecidability of the constrained emptiness problem of Bozelli et al. [13]. A very annoying consequence is that such a solution cannot be represented as a finite union of polyhedra (since the emptiness of the intersection with equality constraints is decidable).

5.4 Two Open Classes: L-PTA and U-PTA

L-PTA and U-PTA (introduced by Bozelli et al. [13]) are very open classes, in the sense that to the best of our knowledge, no result known to be decidable for L-PTA (or U-PTA) was shown undecidable for L/U-PTA (and is hence either decidable or open). Conversely, and even stronger, no result known to be undecidable for L/U-PTA was shown decidable for L-PTA (or U-PTA) – and is always open.

To summarize, the AF-emptiness, the language- and trace-preservation problems, are all undecidable for L/U-PTA, but remain open for L-PTA and U-PTA.

In fact, the only result that could be described as a difference between L/U-PTA and U-PTA (resp. L-PTA) is as follows [8]: the language-preservation problem is decidable for deterministic U-PTA (resp. deterministic L-PTA) with a single integer-valued parameter, whereas this problem is proved undecidable for L/U-PTA. However, one could argue that an L/U-PTA with a single parameter is necessarily either an L-PTA (if the unique parameter is a lower-bound parameter) or a U-PTA (otherwise).

Synthesis. The synthesis for L-PTA and U-PTA was not much addressed, with the exception of integer-valued parameters: in that case, it is possible to synthesize the solution to the BüEF-synthesis problem in the form of a union of linear constraints doubly exponential in the number of parameters [13]. The authors note that it remains open whether one can construct a linear constraint with a single exponential blow-up. This result does not extend in a straightforward manner to rational-valued parameters, as the technique of Bozelli et al. [13] (for U-PTA) requires the computation of a sufficient upper bound, and then an exhaustive enumeration of parameters below this bound.

6 Open Questions

Syntax and Expressiveness. A first perspective is to compare the expressiveness of the various syntaxes of PTA defined in the literature. This implies to first agree on a definition of the expressiveness of a PTA. We propose as a perspective two possible definitions: either the union over all parameter valuations of the timed language, or the union over all parameter valuations of the untimed language. Comparing the expressiveness of the syntaxes in the literature would reduce the number of dimensions for the various decidability results of the EF-emptiness problem studied in Table 2.

Decidability Problems. A main open problem is the decidability of PTA with two clocks, that was only studied with a single parameter and over discrete time [16]. Studying further the EG-, AF- and AG-emptiness problems for few clocks and parameters (as it was quite extensively done for EF-emptiness) remains to be done too, although the theoretical or practical interest may be somehow debatable. More interesting (and promising) are the two open classes of L-PTA and U-PTA. These classes are non-trivial, and relate to the robust analysis of TA: most robustness problems (see [12]) consider an enlargement of all guards by (usually) the same constant factor, whereas U-PTA allow to enlarge or decrease some of the upper-bound guards by a possibly different parameter, which gives an orthogonal definition of robustness. The language preservation problem remains open for U-PTA [8], and the question of the synthesis is also challenging.

Also note that formalisms close to PTA (not surveyed here for lack of space) include subclasses of hybrid automata [14] and parametric interrupt timed automata [11], that benefit from promising decidability results.

Synthesis. Whereas decision problems (surveyed in this document) were much studied, little interest has been dedicated to the synthesis of parameters, which should however be a main practical challenge. Despite undecidability (in general [3]) or intractability (for L/U-PTA [25]), semi-algorithms or approximated procedures could be devised; SMT-based techniques [27], or the integer hull approximation [6, 25] can serve as a basis for future works.

Are PTA a Useless Formalism? Despite many undecidability problems, PTA were often used to model and verify various case studies (see Sect. 1). This can be seen as a paradox considering the numerous undecidability results PTA suffer from. In fact, as all of the aforementioned analyses terminate, it is challenging to understand why, and perhaps to exhibit further classes for which the problems considered in this survey become decidable.