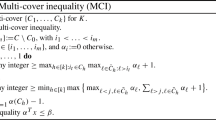Local Cuts for 0–1 Multidimensional Knapsack Problems

Abstract

This paper investigates the local cuts approach for the multidimensional knapsack problem (MKP) which has more than one knapsack constraints. The implementation of the local cuts-based cutting plane algorithm is an extension of the exact knapsack separation scheme of Vasilyev et al. (J Glob Optim 1–24, [13]). Comparisons are made with the global lifted cover inequalities (GLCI) proposed in our recent paper in Computers & Operations Research (Gu, Comput Oper Res 71:82–89, [7]). Preliminary results show that the local cuts approach may be powerful for the MKP.

1 Introduction

The multidimensional knapsack problem (MKP) is a well-known strongly NP-hard combinatorial optimization problem which has been applied to various resource allocation-related practical problems [4]. Given m knapsacks with capacities $b_i$, $i = 1, \ldots , m$, and n items contributing profits $c_j$, $j = 1, \ldots , n$, the MKP maximizes the total profits of selected items under the knapsack capacity limitations. In MKP, an item j requires simultaneous resource consumption of $a_{i,j}$ units in the ith knapsack ($i = 1, \ldots , m$, $j = 1, \ldots , n$). The MKP can be formulated as an integer linear programming (ILP):

$$\begin{aligned} \text {(MKP)}\qquad z^* = \max \{c^Tx : Ax\le b, x\in \{0,1\}^n\} \end{aligned}$$

(1)

where $c = [c_1,c_2,\ldots ,c_n]^T$ is the profit vector; $x = [x_1,x_2,\ldots ,x_n]^T$ is a vector of 0-1 decision variables; $x_i$ is equal to 1 if item i is selected, otherwise 0; $A = [a_{i,j}]$, $i = 1, 2, \ldots , m$, $j = 1, 2,\ldots , n$ is the resource consumption matrix; $b = [b_1, b_2, \ldots , b_m]^T$ is the vector of knapsack capacities. For MKP, all parameters are assumed to be nonnegative integers.

A large amount of research efforts has been committed to MKP which is closely related to the classical knapsack problem (KP) [12]. In spite of the huge theoretical and computational progress in combinatorial optimization, MKP remains a challenging problem [5, 14]. It still takes many hours on a modern computer to obtain the best-known solutions for some of the well-known benchmark problems.

In this paper, we focus on the cutting plane approach which has found tremendous success in the commercial and open-source mixed integer programming (MIP) solvers. For knapsack problem, the cover-based valid inequalities are among the best-studied classes and have been shown useful, especially for solving difficult binary integer programming problems including the MKP [8, 11]. Recently, exact knapsack separation algorithms (EKSA) were proposed in [6, 11]. Although EKSAs can produce stronger valid inequalities, they are more or less useless in the branch and cut paradigm due to much longer computation time. An efficient EKSA was implemented in [13] and was found useful for solving large instances of some classical MIP problems.

Recently, the global lifted cover inequalities (GLCI) [10] and its variants were proposed for MKP to take into account multiple knapsack constraints simultaneously when lifting the coefficients of a valid inequality. The face defined by GLCI may not be of higher dimensions than lifted cover inequalities (LCI) for MKP; however, computational results demonstrated that GLCI can be more effective in tightening the integrality gap, especially when the number of knapsack constraints increases. Furthermore, the computationally stronger GLCI can lead to improved performance of core-based heuristics [7]. This motivates the research in this paper to combine the power of exact separation and global lifting, which the authors’ believe belongs to the local cuts paradigm which is very different from the traditional template paradigm [2].

This paper is organized as follows. We first describe the cutting plane algorithm based on the local cuts approach in Sect. 2. The details of the exact separation for the reduced problem is given in Sect. 3. The global lifting procedure is described in Sect. 4. Computational results are presented in Sect. 5. The conclusion is given in Sect. 6.

2 Cutting Plane Algorithm Based on Local Cuts

The cutting plane approach [15] can be used to strengthen the linear programming (LP) relaxation of MKP which is defined as

$$\begin{aligned} \text {(MKP-LP)}\qquad \bar{z} = \max \{c^Tx : Ax\le b, x\in [0,1]^n\} \end{aligned}$$

(2)

MKP-LP is solved at each iteration of the cutting plane approach with additional constraints corresponding to the cuts generated from previous iterations. Assume that an optimal continuous solution $x^k$ is obtained at the kth iteration, an attempt will be made to generate a cut separating $x^k$ from the convex hull of the MKP polytope. If cuts are successfully generated, they are added to MKP-LP and the process is repeated until some termination criteria are met. Since the separation algorithm can be time-consuming in practice, this process has to be terminated earlier without the exact description of the convex hull of the MKP polytope. In the local cuts approach, a reduced problem of MKP (RMKP) is created at each iteration which can be efficiently separated due to much lower dimension. A valid cut for the original problem can then be induced. The cutting plane algorithm based on local cuts (CPALC) is described as follows:

The creation of the separation problem for RMKP is described in the next section. A cut for the original MKP can always be induced from a cut for RMKP through the global lifting procedure discussed in Sect. 4.

3 Exact Separation Algorithm for RMKP

Given $x^k$, the LP relation solution of MKP in CPALC, let $V^k =\{i|x^k_i = 1\}$, and $W^k = \{i|x^k_i = 0\}$. Denote $R^k = N\setminus (V^k\cup W^k) = \{r_1,r_2,\ldots ,r_p\}$, the RMKP is defined as

$$\begin{aligned} \text {RMKP}\quad \max \quad&z = \sum _{1\le j\le p}c_{r_j}y_j \\\nonumber \text {s. t. }\quad&\sum _{1\le j\le p}a_{ir_j}y_j\le \tilde{b}_i^k,\quad i=1,\ldots ,m \\\nonumber&y_j\in \{0,1\}, \quad 1\le j\le p\nonumber \end{aligned}$$

with $\tilde{b}_i^k = b_i - \sum _{j\in V^k}a_{ij}$, $i=1,\ldots ,m$.

The separation problem for RMKP is to separate $y^k$ defined as $y^k_j = x^k_{r_j}$, $1\le j\le p$. The RMKP polytope has much lower dimension than that of MKP, which may be amenable to the exact separation approach. The exact separation formulation can take many different forms. Our implementation of the exact separation for RMKP is an adaptation of the source code of [13] for single knapsack problem and is based on the formulation below [13]:

$$\begin{aligned} \text {RMKP-S}\quad \max _{\pi }\quad&z = \pi ^T y^k\\\nonumber \text {s. t. } \quad&h^T\pi \le 1,\quad \forall h\in P \\\nonumber&\pi \in \Pi \nonumber \end{aligned}$$

where $P\not = \emptyset$ is the feasible set of RMKP, and $\Pi \subset \mathscr {R}^p$ is a sufficiently large convex compact set containing the origin in its interior. Denote the optimal solution to RMKP-S by $\bar{\pi }^k$, then $y^T\bar{\pi }^k\le 1$ is a valid cut separating $y^k$ from the RMKP polytope if $y^{kT}\bar{\pi }^k > 1$. The nice property of RMKP-S is that the cut $y^T\bar{\pi }^k\le 1$ also defines a facet of RMKP.

RMKP-S can be solved by row generation. At the lth iteration, $\pi ^l$ is solved as an optimal solution to

$$\begin{aligned} \text {RMKP-S}(l)\quad \max _{\pi }\quad&z = \pi ^T y^k\\\nonumber \text {s. t. } \quad&h^T\pi \le 1,\quad \forall h\in P^l\subset P \\\nonumber&\pi \in \Pi \nonumber \end{aligned}$$

If $y^{kT}\pi ^l\le 1$, $y^k$ is an interior point of the RMKP polytope since $y^{kT}\pi ^l\ge y^T\bar{\pi }^k$. Otherwise, a new row may be obtained by solving

$$\begin{aligned} \text {Row-Gen}\quad \max _h\quad&z = h^T\pi ^l \ \\\nonumber \text {s. t. }\quad&h\in P \end{aligned}$$

which has optimal objective value $z^l$ and optimal solution $h^l$.

If $z^l\le 1$, then $\bar{\pi }^k = \pi ^l$ and $y^T\pi ^l\le 1$ is a cut for RMKP; otherwise, $h^l$ can be added to $P^l$ and a new row is generated for RMKP-S(l).

To avoid numerical errors, all coefficients in the cut need to be converted into integer. In [13], $\bar{\pi }^k$ is multiplied by a proper integer to make it an integer vector $\tilde{\pi }^k$ (within a tolerance of $10^{-5}$). The separation procedure fails if no such integer multiplier can be found within the range $[1,\ldots ,10^4]$. Then, the right-hand side can be calculated as

$$\begin{aligned} \pi _0^k = \max \{h^T\tilde{\pi }^k : h\in P\} \end{aligned}$$

(3)

$y^T\tilde{\pi }^k\le \pi _0^k$ is a valid cut for RMKP if it is violated by $y^k$.

If $y_j$ can be fixed to 0 in RMKP, i.e., $\exists i\in [1,\ldots ,m]$, $a_{i,r_j}> \tilde{b}^k_i$, we can generate a cut for RMKP in the form $y_j \le 0$ instead of solving RMKP-S which will set $\bar{\pi }^k_j$ to the largest value of $\pi _j$ in $\Pi$.

The exact separation algorithm for RMKP (ESAR) can be described as follows:

4 Global Lifting Algorithm

The valid inequality for RMKP generated by ESAR can be sequentially lifted to become valid for MKP. We apply the same idea as for GLCI in [7] by considering all the constraints in MKP when lifting a variable.

Let K be the feasible set of MKP, and $S(V,W) = K \cap \{x\in \{0,1\}^n | x_j = 0,\, \forall j\in W,\, x_j = 1, \, \forall j\in V\}$. A variable in V can be down-lifted according to the following proposition:

Proposition 1

Given $\sum _{j\in N\setminus (V\cup W)}\pi _jx_j\le \pi _0$ is valid for S(V, W). For $i\in V$, if $S(V\setminus \{i\}, W)\ne \emptyset$, then $\gamma _ix_i + \sum _{j\in N\setminus (V\cup W)}\pi _jx_j\le \pi _0 + \gamma _i$ is valid for $S(V\setminus \{i\}, W)$ for any $\gamma _i\ge \zeta - \pi _0$, where

$$\begin{aligned} \zeta = \max \{\sum _{j\in N\setminus (V\cup W)}\pi _jx_j | x_i = 0,\, x\in S(V\setminus \{i\},W)\} \end{aligned}$$

(4)

A variable in W can be up-lifted according to the following proposition:

Proposition 2

Given $\sum _{j\in N\setminus (V\cup W)}\pi _jx_j\le \pi _0$ is valid for S(V, W). For $i\in W$, if $S(V, W\setminus \{i\})\ne \emptyset$, then $\alpha _ix_i + \sum _{j\in N\setminus (V\cup W)}\pi _jx_j\le \pi _0$ is valid for $S(V, W\setminus \{i\})$ for any $\alpha _i\le \pi _0 - \zeta$, where

$$\begin{aligned} \zeta = \max \{\sum _{j\in N\setminus (V\cup W)}\pi _jx_j | x_i = 1,\, x\in S(V, W\setminus \{i\})\} \end{aligned}$$

(5)

For a cut generated by ESAR in the form of $y^T\tilde{\pi }^k \le \pi _0^k$, we can have $\sum _{1\le j\le p}x_{r_j}^T\hat{\pi }_{x_j}^k \le \pi _0^k$ with $\hat{\pi }_{x_j} = \tilde{\pi }_j^k$, which is valid for $S(V^k, W^k)$. Then, the variables in $V^k$ are down-lifted sequentially in the non-decreasing order of the reduced costs obtained when solving for $x^k$ at step 3 of Algorithm 2. Finally, the variables in $W^k$ are up-lifted sequentially in the non-increasing order of the reduced costs. To reduce computation time on lifting, we calculate the down-lifting coefficient according to $\gamma _i = \zeta _{LP} - \pi _0$, and the up-lifting coefficient according to $\alpha _i = \pi _0 - \zeta _{LP}$, where $\zeta _{LP}$ is the linear relaxation upper bound of $\zeta$ in (4) and (5).

Denote the valid inequality after lifting by $x^T\hat{\pi }^k\le \hat{\pi }^k_0$, we have

$$\begin{aligned} x^{kT}\hat{\pi }^k - \hat{\pi }^k_0 = y^{kT}\tilde{\pi }^k - \pi _0^k \end{aligned}$$

(6)

Therefore, the cut for RMKP is also a cut for MKP after the lifting.

5 Computational Results

We first compare the exact knapsack separation algorithm (EKSA) of [13] with our implementations of GLCI and its variants [7]. Then, EKSA is compared with the local cuts (LC)-based separation algorithm CPALC implemented in this paper. All experiments are carried out on the comprehensive Cho test set in [1] and the widely used Chu and Beasley MKP test set in [3]. The algorithms presented in this paper were implemented in C++ and compiled with gcc 4.4. All tests were run on a computer with 2.3 GHz AMD CPU and Red Hat 4.4 operating system. We use CPLEX 12.5 to solve the LP and IP problems in CPALC with a time limit of 60 s and a limit on the maximum number of threads to 8. The number of cuts in CPALC is limited to 100 as for GLCI, but there is no limit for the number of cuts in EKSA which typically takes no more than a few seconds. In RMKP-S(l), $\Pi$ is set to be $[-10^6,\,10^6]^p$.

The Cho test set contains classes of randomly generated instances for each combination of $n \in \{50, 100, 250\}$ items and $m \in \{5, 10, 30\}$ constraints. Each class contains 30 instances. The Cho test set represents a much larger range of correlation values than the Chu and Beasley test set under the MKP structure and was created according to a well-designed comprehensive problem generation scheme [9]. The results of GLCIs and EKSA for the Cho test set are reported in Table 1. The columns in Table 1 are explained as follows: The first column n.m represents the class of test cases where n is the number items and m is the number of knapsack constraints; the second column reports the best-known objective value $z^*$ found in the literature; the next column presents the objective value of the LP relaxation $\bar{z}$ without additional cuts; the fourth column gives the relative integrality gap $\varDelta _D = (\bar{z}-z^*)\times 100/\bar{z}\%$; the next column reports the closed integrality gap in percentage; GSA-LP and GSA-IP are the different implementations of GLCI in [7]; and the next two columns present the total number of cuts generated by the corresponding separation scheme and the total CPU time spent $T_v$ in seconds. The value of $T_v$ is replaced with “–” if it is smaller than 0.1 s. For each class of test cases, the arithmetic mean of the 30 instances of the same class is reported. It can be seen that EKSA significantly outperforms GLCIs in terms of the percentage of integrality gap closed. The computation time of EKSA is only slightly higher than that of GSA-LP. The superiority of EKSA may be due to the weak interactions of the knapsack constraints in the instances.

Table 1 Comparison of GLCI and EKSA on the Cho test set [1]

Table 2 Comparison of EKSA and CPALC on the Cho test set [1]

The results of EKSA and CPALC for the Cho test set are reported in Table 2. The time for the exact separation in Sect. 3 and the time for the global lifting in Sect. 4 are reported as $T_e$ and $T_l$ in seconds. It can be seen that CPALC significantly outperforms EKSA in terms of closed integrality gap. The computation time of CPALC is much higher than that of EKSA. The global lifting is very efficient in terms of computation time. EKSA failed to close integrity gap on many instances even without the limit on the number of cuts. CPALC can always separate the LP solution which is consistent with the theory; however, the convergence can be slow on large instances with more constraints.

The Chu and Beasley test set contains a total of 270 instances randomly generated for 27 classes which are combinations of the number of items $n \in \{100, 250, 500\}$, the number of knapsack constraints $m \in \{5, 10, 25\}$, and knapsack capacity tightness ratios $\alpha \in \{0.25, 0.5, 0.75\}$. The results for the Chu and Beasley test set are reported in Table 3 for test cases with 100 items. For each class of test cases, the arithmetic mean of the 10 instances of the same class is reported. For cases with five constraints, EKSA closed much higher integrity gaps than GLCIs with marginally longer computation time. However, GLCIs perform significantly better than EKSA when $m = 30$. The reason could be that the intersection of single knapsack polytopes is not a good approximation of the MKP polytope as the number of constraints increases. The exact separation procedure of CPALC failed on many cases when $m = 10$ and $m = 30$ due to the difficulty to make integral the cutting plane obtained from RMKP-S(l). However, CPALC achieved similar amount of closed integrity gaps with many fewer cuts when compared with GSA-IP, which demonstrated the superior strength of the exact separation procedure for MKP.

Table 3 Comparison of GLCI, EKSA, and CPALC on 100-item instances from Chu and Beasley test set [3]

6 Conclusion

The local cuts approach was implemented for the 0–1 multidimensional knapsack problem. Based on LP solution of MKP, a reduced separation problem is solved exactly with the row generation algorithm. The valid inequality for the reduced MKP problem is then globally lifted to the original MKP problem. Computational experiments are carried out on a comprehensive set of MKP instances which demonstrate the superiority of the local cuts approach in terms of closed integrity gap. Further research is needed to reduce the computation time and investigate the possibility to combine the local cuts approach with a branch and bound algorithm or other meta-heuristics.