1 Shadowing in One Variable

Begin with a one-dimensional dynamical system

$$\begin{aligned} \dot{x}=-\lambda +xb(x;\lambda ), \end{aligned}$$
(1)

where \(\lambda ={\text {sign}}(x)\) with the \({\text {sign}}\) function being \(\pm 1\) for \(x\gtrless 0\) and having the set value \((-1,+1)\) for \(x=0\). This has an attracting fixed point on the discontinuity, where \(\dot{x}=-\lambda \). Define a switch-shadowing system

$$\begin{aligned} \dot{x}=-\lambda +xb(x;\lambda ),\qquad \dot{y}=(x-y)/\gamma , \end{aligned}$$

where \(\lambda ={\text {sign}}(y)\), or a state-shadowing system

$$\begin{aligned} \dot{x}=-\lambda +yb(y;\lambda ),\qquad \dot{y}=(x-y)/\gamma , \end{aligned}$$

where \(\lambda ={\text {sign}}(x)\), \(\gamma >0\) is small, and y is an external variable representing some extra stage in the switching process, such that each shadow system relaxes to (1) as \(y\rightarrow x\). So, y tends to x like \(e^{-t/\gamma }\) (for small \(\gamma \) where we can treat x as slow varying), i.e., y shadows x.

We restrict attention to the neighbourhood of the equilibrium at \(x=y=\lambda =0\) in each system. In the switch-shadowing system, the switching surface becomes \(y=0\), and sliding no longer occurs because solutions all cross the surface (because the y component does not switch) – the surface is ‘transparent’ in some nomenclature. In the state-shadowing system the switching surface remains sliding.

We will analyze these using switching layer methods (see Glendinning–Jeffrey [2] and next section).

For the switch-shadowing system on \(y=0\) the switching layer system is

$$\begin{aligned} \dot{x}=-\lambda +xb(x;\lambda ),\qquad \varepsilon \dot{\lambda }=x/\gamma , \end{aligned}$$

for \(\lambda \in (-1,+1)\), \(\varepsilon \rightarrow 0\), and the Jacobian of the equilibrium is

$$\begin{aligned} \left( {\begin{array}{cc}\frac{\partial \dot{x}}{\partial x}&{}\frac{\partial \dot{x}}{\partial \varepsilon \lambda }\\ \frac{\partial \varepsilon \dot{\lambda }}{\partial x}&{}\frac{\partial \varepsilon \dot{\lambda }}{\partial \varepsilon \lambda }\end{array}}\right) =\left( {\begin{array}{cc}b&{}-1/\varepsilon \\ 1/\gamma &{}0\end{array}}\right) \end{aligned}$$

with eigenvalues \((b(0,0)\pm i\sqrt{4-b^2\gamma \varepsilon })/2\sqrt{\gamma \varepsilon }\rightarrow \frac{1}{2}b(0,0)\pm i\infty \) as \(\varepsilon \rightarrow 0\). Outside the switching surface the dynamics spirals in as a ‘fused focus’ towards \(x=y=0\), but once there, in the x-\(\lambda \) dynamics, the attractivity depends on the sign of b(0, 0). In particular, if \(b(0,0)>0\) then the sliding equilibrium will become unstable, and a limit cycle will be formed inside the switching layer \((x,\lambda )\in \mathbb R\times (-1,+1)\).

For the state-shadowing system on \(x=0\) the switching layer system is

$$\begin{aligned} \varepsilon \dot{\lambda }=-\lambda +yb(y;\lambda ),\qquad \dot{y}=-y/\gamma , \end{aligned}$$

where \(\lambda \in (-1,+1)\), and the Jacobian of the equilibrium is

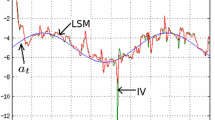
$$\begin{aligned} \frac{\partial (\varepsilon \dot{\lambda },\dot{y})}{\partial (\varepsilon \lambda ,y)} =\left( {\begin{array}{cc}-1/\varepsilon &{}b(0;0)\\ 0&{}-1/\gamma \end{array}}\right) \end{aligned}$$

with eigenvalues \(-1/\gamma \) and \(-1/\varepsilon \rightarrow -\infty \). In this case the equilibrium of the shadow system remains an attractor; see Fig.1.

Fig. 1
figure 1

The original system and its two shadow regularizations

Full size image

2 Shadowing in \({\varvec{n}}\) Variables

Now take a multivariable state \({\mathbf {x}}=(x_1,\ldots ,x_n)\), and assume there is one switch for every coordinate (this can be generalized later). So we have switching functions \(h_1,\ldots h_n\), and switching multipliers \(\varvec{\lambda }=(\lambda _1,\ldots ,\lambda _n)\) where \(\lambda _i\in [-1,+1]\), such that \(\lambda _i={\text {sign}}\,h_i\) for \(h_i\ne 0\) and \(\lambda _i\in (-1,+1)\) for \(h_i=0\). Letting \({\mathbf {f}}\) be a smooth function of \({\mathbf {x}}\) and \(\varvec{\lambda }\), the system

$$\begin{aligned} {\dot{\mathbf {x}}}={\mathbf {f}}({\mathbf {x}};\varvec{\lambda }), \end{aligned}$$
(2)

where \(\lambda _i={\text {sign}}\,h_i\), is smooth except at the thresholds \(\Sigma _i=\left\{ {\mathbf {x}}\in \mathbb R^n:h_i=0\right\} \).

In the piecewise smooth setting we assume each \(h_i\) is a regular function of \({\mathbf {x}}\), some \(h_i=h_i({\mathbf {x}})\). When \(h_i=0\) for some i, we blow up the switching surface \(h_i=0\) into a switching layer \(\lambda _i\in (-1,+1)\), with dynamics given by \(\varepsilon _i\dot{\lambda }_i={\mathbf {f}}({\mathbf {x}};\varvec{\lambda })\cdot \nabla h_i\) for \(\varepsilon _i\rightarrow 0\).

Take coordinates in which \(h_i=x_i\) for \(i=1,\ldots ,n\). When \({\mathbf {x}}\) lies on the intersection of all n switching thresholds, \(x_1=x_2=\cdots =x_n=0\), we study the dynamics in the codimension n switching layer \((\lambda _1,\ldots ,\lambda _n)\in (-1,+1)^n\) given by

$$\begin{aligned} \underline{\underline{\varepsilon }}.{\dot{\mathbf {\varvec{\lambda }}}}={\mathbf {f}}({\mathbf {0}};\varvec{\lambda }),\qquad |\underline{\underline{\varepsilon }}|\rightarrow 0, \end{aligned}$$

where \(\underline{\underline{\varepsilon }}\) denotes the diagonal matrix with entries \(\varepsilon _1,\ldots ,\varepsilon _n\) or, in components, \(\varepsilon _i\dot{\lambda }_i=f_i({\mathbf {0}};\lambda _1,\ldots ,\lambda _n)\) for \(i=1,\ldots ,n\). Sliding modes are equilibria of the fast system. We assume these lie at \({\mathbf {x}}=\varvec{\lambda }=0\), and are stable, which means that

$$\begin{aligned} \frac{\partial \underline{\underline{\varepsilon }}.{\dot{\mathbf {\varvec{\lambda }}}}}{ \partial \underline{\underline{\varepsilon }}. \varvec{\lambda }}=\underline{\underline{\varepsilon }}^{-1}. \frac{\partial {\mathbf {f}}}{\partial \varvec{\lambda }} \end{aligned}$$
(3)

has eigenvalues with negative real part at \(({\mathbf {0}};{\mathbf {0}})\).

Define a switch-shadowing system

$$\begin{aligned} {\dot{\mathbf {x}}}={\mathbf {f}}({\mathbf {x}};\varvec{\lambda }),\qquad {\dot{\mathbf {y}}}=({\mathbf {x}}-{\mathbf {y}})/\gamma , \end{aligned}$$

where \(\lambda _i={\text {sign}}(y_i)\), or a state-shadowing system

$$\begin{aligned} {\dot{\mathbf {x}}}={\mathbf {f}}({\mathbf {y}};\varvec{\lambda }),\qquad {\dot{\mathbf {y}}}=({\mathbf {x}}-{\mathbf {y}})/\gamma , \end{aligned}$$

where \(\lambda _i={\text {sign}}(x_i)\), \(\gamma >0\) is small (we could choose different \(\gamma _i\) for each component of \({\mathbf {y}}\)), and \({\mathbf {y}}\) is an n-dimensional external variable. As before, both tend to (2) as \({\mathbf {y}}\) shadows \({\mathbf {x}}\). Each has an equilibrium at \({\mathbf {x}}={\mathbf {y}}=\varvec{\lambda }=0\). For the switch-shadowing system on \({\mathbf {y}}=0\) the switching layer system is

$$\begin{aligned} {\dot{\mathbf {x}}}={\mathbf {f}}({\mathbf {x}};\varvec{\lambda }),\qquad \varepsilon {\dot{\mathbf {\varvec{\lambda }}}}={\mathbf {x}}/\gamma , \end{aligned}$$

for \(\varvec{\lambda }\in (-1,+1)^n\), and the Jacobian of the equilibrium is

$$\begin{aligned} \left( {\begin{array}{cc}\frac{\partial {\dot{\mathbf {x}}}}{\partial {\mathbf {x}}}&{}\frac{\partial {\dot{\mathbf {x}}}}{\partial \underline{\underline{\varepsilon }}.{\varvec{\lambda }}}\\ \frac{\partial \underline{\underline{\varepsilon }}.{\dot{\varvec{\lambda }}}}{\partial {\mathbf {x}}}&{}\frac{\partial \underline{\underline{\varepsilon }}.{\dot{\varvec{\lambda }}}}{\partial \underline{\underline{\varepsilon }}. {\varvec{\lambda }}}\end{array}}\right) =\left( {\begin{array}{cc}\frac{\partial {\mathbf {f}}(0;0)}{\partial {\mathbf {x}}}&{}\underline{\underline{\varepsilon }}^{-1}.\frac{\partial {\mathbf {f}}(0;0)}{\partial {\varvec{\lambda }}}\\ \underline{\underline{1}}/\gamma &{}0\end{array}}\right) , \end{aligned}$$

where \(\underline{\underline{1}}\) is the \(n\times n\) identity matrix. The stability of the term \(\underline{\underline{\varepsilon }}^{-1}.\frac{\partial {\mathbf {f}}}{\partial \varvec{\lambda }}\) from (3) does not guarantee stability of the shadow equilibrium, which will depend crucially on \(\frac{\partial {\mathbf {f}}(0;0)}{\partial {\mathbf {x}}}\).

For the state-shadowing system on \(x=0\) the switching layer system is

$$\begin{aligned} \varepsilon {\dot{\mathbf {\varvec{\lambda }}}}={\mathbf {f}}({\mathbf {y}};\varvec{\lambda }),\qquad {\dot{\mathbf {y}}}=-{\mathbf {y}}/\gamma , \end{aligned}$$

where \(\lambda \in (-1,+1)\), and the Jacobian of the equilibrium is

$$\begin{aligned} \frac{\partial (\underline{\underline{\varepsilon }}.{\dot{\varvec{\lambda }}},{\dot{\mathbf {y}}})}{\partial (\underline{\underline{\varepsilon }}.{\varvec{\lambda }},{\mathbf {y}})} =\left( {\begin{array}{cc}\underline{\underline{\varepsilon }}^{-1}.\frac{\partial {\mathbf {f}}(0;0)}{\partial {\varvec{\lambda }}}&{}\frac{\partial {\mathbf {f}}(0;0)}{\partial {\mathbf {y}}}\\ 0&{}-\underline{\underline{1}}/\gamma \end{array}}\right) . \end{aligned}$$

In this case it seems likely that the equilibrium of the shadow system remains an attractor, the stability of the term \(\underline{\underline{\varepsilon }}^{-1}.\frac{\partial {\mathbf {f}}}{\partial {\varvec{\lambda }}}\) from (3) and the term \(-\underline{\underline{1}}/\gamma \) playing the crucial role.

3 Examples

The following examples motivated the shadow regularizations proposed above.

Genetic Regulatory Networks. A typical gene network protein-only model gives the dynamics of the concentration \(x_i\) of the protein product of a gene i, for \(i=1,\ldots ,n\), as

$$\begin{aligned} \dot{x}_i=B_i(Z_1,\ldots ,Z_n)-\alpha _ix_i\;,\qquad Z_i={\text {step}}(x_i-\theta _i)\;,\qquad \qquad \qquad \;\; \end{aligned}$$

where \(\alpha _i,\theta _i>0\). In Edwards–Machina–McGregor–van-den-Driessche [1], this is extended to include the intermediary role of mRNA. Instead, we make \(x_i\) the concentration of the i-th mRNA molecule, and \(y_i\) the protein product concentration for gene i, then the proposed model is

$$\begin{aligned} \dot{x}_i=B_i(Z_1,\ldots ,Z_n)-\alpha _ix_i,\quad \dot{y}_i=\kappa _ix_i-\beta _iy_i,\quad Z_i={\text {step}}(y_i-\theta _i), \end{aligned}$$

with \(\alpha _i,\beta _i,\kappa _i,\theta _i>0\).

Time delay. Assume a system modelled by \(\dot{x}=f(x;\lambda )\) with \(\lambda ={\text {sign}}(x)\) actually switches not exactly when a solution x(t) lies at \(x(t)=0\), but when \(x(t-\tau )\) with a time delay \(\tau \). We can define a delayed variable \(y(t)=x(t-\tau )\), or let

$$\begin{aligned} \dot{x}=f(x;\lambda ),\qquad \dot{y}=(x-y)/\tau , \end{aligned}$$

where \(\lambda ={\text {sign}}(y)\).

Plankton. A predator-prey system discussed in Piltz [4] for predator population \(x_3\) and prey populations \(x_1,x_2\), is

$$\begin{aligned} \left. \begin{array}{rcl} \dot{x}_1&{}\!=\!&{}\left\{ r_1-x_3\mu \right\} x_1\\ \dot{x}_2&{}\!=\!&{}\left\{ r_2-x_3(1-\mu )\right\} x_2\\ \dot{x}_3&{}\!=\!&{}\left\{ q_1x_1\mu +q_2x_2(1-\mu )-m\right\} x_3 \end{array}\right\} , \end{aligned}$$

where \(\mu ={\text {step}}(x_1-ax_2)\), in terms of constants \(r_1\), \(r_2\), \(q_1\), \(q_2\), m, a. This assumes the consumption of prey is proportional to their population \(x_1\) or \(x_2\). If, instead, consumption is proportional to a variable \(y_1\) or \(y_2\), which tends towards the population, we have

$$\begin{aligned} \left. \begin{array}{rcl} \dot{x}_1&{}\!=\!&{}r_1x_1-x_3y_1\mu \\ \dot{x}_2&{}\!=\!&{}r_2x_2-x_3y_2(1-\mu )\\ \dot{x}_3&{}\!=\!&{}\left\{ q_1y_1\mu +q_2y_2(1-\mu )-m\right\} x_3\\ \dot{y}_1&{}\!=\!&{}(x_1-y_1)/\gamma _1\\ \dot{y}_2&{}\!=\!&{}(x_2-y_2)/\gamma _2 \end{array}\right\} , \end{aligned}$$

where \(\mu ={\text {step}}(x_1-ax_2)\).

Electronic sensors. A typical form for a piecewise affine control system is

$$\begin{aligned} {\dot{\mathbf {x}}}=\underline{\underline{A}}{\mathbf {x}}+{\mathbf {b}} u, \end{aligned}$$

where \(u={\text {step}}(x_1-\theta )\), in terms of a constant matrix A and vector \({\mathbf {b}}\) describing electronic components. In Kafanas [3] it is noted that, although a control system implements control on the state \({\mathbf {x}}\), it does so by measuring not \({\mathbf {x}}\) itself, but a sensor value \({\mathbf {y}}\), hence a more faithful model is

$$\begin{aligned} {\dot{\mathbf {x}}}=\underline{\underline{A}}{\mathbf {x}}+{\mathbf {b}}u,\qquad {\dot{\mathbf {y}}}=({\mathbf {x}}-{\mathbf {y}}).\underline{\underline{\kappa }}, \end{aligned}$$

where \(u={\text {step}}(y_1-\theta )\), for some diagonal matrix \(\underline{\underline{\kappa }}\).

4 A United Form

We can express both the switch and state shadow regularizations together by writing

$$\begin{aligned} {\dot{\mathbf {x}}}={\mathbf {f}}\left( {{\mathbf {s}}_\mu ({\mathbf {x}},{\mathbf {y}});\varvec{\lambda }}\right) ,\quad {\dot{\mathbf {y}}}=({\mathbf {x}}-{\mathbf {y}})/\gamma , \end{aligned}$$

where \(\lambda _i={\text {sign}}\left( {S_\mu (x_i,y_i)}\right) \) for vector and scalar shadow functions \({\mathbf {s}}_\mu ({\mathbf {x}},{\mathbf {y}})\) and \(S_\mu (x,y)\) which satisfy \({\mathbf {s}}_\mu ({\mathbf {x}},{\mathbf {x}})={\mathbf {x}}\) and \(S_\mu (x,x)=x\), for example \({\mathbf {s}}_\mu ({\mathbf {x}},{\mathbf {y}})=\mu {\mathbf {x}}+(1-\mu ){\mathbf {y}}\) and \(S_\mu (x,y)=\mu x+(1-\mu )y\). The switch-shadowing and state-shadowing systems are obtained at the extremes for \(\mu =1\) and \(\mu =0\) respectively. In the most general case we could consider \(\gamma \) to be a (contracting) matrix, and/or a function of \({\mathbf {x}}\) and \({\mathbf {y}}\).

In the future, it will be interesting to study how the stability of equilibria is affected under such regularizations in general, and the implications this has for the structural stability of piecewise smooth systems.

A final but important note must be made if the switching layer expression \(\varepsilon \dot{\lambda }=\cdots \) is derived as the approximation to a smooth system (as in, e.g., GRN models [1]). Then, the \(\varepsilon \) on the lefthand side of this expression is actually a function of \(\lambda \), which makes the vanishing entries of the Jacobians from \(\frac{\partial \varepsilon \dot{\lambda }}{\partial \varepsilon \lambda }\) become nonzero and, while we expect this not to qualitatively affect the result as \(\varepsilon \rightarrow 0\), further study is required.