1 Introduction

A model is a mathematical representation of any physical system (biological, electronic, mechanical). System modelling requires to consider all the relevant factors involved in its description, when the model of a plant takes into account random variations is defined as a stochastic system, these variations can be present in the parameters, measurements, inputs or disturbances, and if the inputs of the system represent functions of time determined for all instants beginning from some initial instant, like analogous systems, then the system is called continuous [1, 2]. The interest in the study of stochastic models has increased recently, due to the necessity to take into account the random effects present in physical systems. Intensified research activity in this area has been stimulated by the need to take into account random effects in complicated physical systems [3].

A fundamental task in engineering and science, is the extraction of the system information and the model from measured data. A discipline that provides tools for an efficient use of data, and the estimation of variables appearing in mathematical models is parameter estimation [4]. Parameter identification for dynamic systems has been studied for at least the last three decades, motivated by the need of designing more efficient control systems (see [5, 6]). In discrete time systems, the most common technique is the Least Squares Method (LSM) (see, [6,7,8]). This method has been very successful in theory and applications, like econometrics, robotics or mechanics.

Parameter estimation using instrumental variables has been used in problems where the regressors are correlated with the equation noise [9]. The instrumental variables can be formed as different combinations of inputs, delayed inputs and outputs, filtered inputs, etc., in [10] a general analysis of various instrumental variable methods is presented. Systems with additive-noise have the problem of errors in variable perturbations, in [11] it is presented the instrumental variable estimator in a general framework. In continuous-time the refined instrumental variable has been implemented; in [12] it is presented a study that provides the convergence property of this method.

In this paper we present the parameter estimation problem of continuous-time stochastic systems under coloured perturbations. Here it is proposed the instrumental variable method implemented in two different ways: the simple estimation algorithm (see [13]) and an extended form of the algorithm, similar to the extended LSM algorithm presented in [14]. Until now, this algorithms have been extensively applied in discrete time, but the implementation in continuous-time stochastic systems is scarce. The main idea is to compare both algorithms in order to show if the simple version is good enough to estimate coloured noise, or if it is necessary to extend the algorithm to estimate when the system presents coloured noise.

Paper structure In the second section the problem formulation is presented, as well as the assumptions needed. In the third section the extended instrumental variable algorithm is designed. Finally, the estimation technique is illustrated with two numerical examples that will show the performance of the extended IV and will compare it with the simple version of the algorithm.

2 Problem formulation

Consider the stochastic correlated continuous-time system with the dynamics states \(x_{t} \in \mathbf R ^{n}\) given by the following system of stochastic differential equations:

$$\begin{aligned} dx_{t}= & {} A_{t}\zeta (x_{t})dt+f_{t}dt+B_{t}ds_{t}\nonumber \\ ds_{t}= & {} H_{t}s_{t}dt+\sigma _{t}dW_{t} \end{aligned}$$
(1)

where the unknown time-varying matrix to be identified is \(A_{t} \in \mathbf R ^{n \times m}\), the matrix \(H_{t}:=H_{0}+\varDelta H_{t}\) has a nominal (central) matrix \(H_{0}\in \mathbf R ^{n \times n}\) that is supposed to be a priori known and \(\varDelta H_{t}\in \mathbf R ^{n\times n}\) is unknown but bounded, i.e., \(\left\| \varDelta H_{t}\right\| \le \varDelta ^{+}\), \(B_{t}\in \mathbf R ^{n\times n}\) is a known deterministic matrix , \(\sigma _{t}\in \mathbf R ^{n\times l}\) is known, \(f_{t}\) is a measurable (available at any \(t\ge 0)\) deterministic bounded excitation vector-input, \(\left( \left\| f_{t}\right\| \le f^{+}\right) \), \(\zeta : \mathbf R ^{n}\rightarrow \mathbf R ^{m}\) is a known (measurable) nonlinear Lipschitz vector function or, a regressor, and \(W_{t}\) is a standard vector Wiener process, \(s_{t}\) is the coloured perturbation defined by the deterministic matrix \(H_{t}\) and the Wiener process \(dW_{t}\).

2.1 Problem description

The main problem in this paper is to design an estimate \(\hat{A}_{t}\) of the time varying matrix \(A_{t} \in \mathbf R ^{n \times m}\) implementing an extended instrumental variable method based only on the available data up to time t that includes all information about the state dynamics \(x_{t}\) and excitation inputs. The subsystem that defines the coloured noise is formed by a nominal matrix \(H_{0}\) that is known, and the perturbation matrix \(\varDelta H_{t}\) that is unknown but bounded, and also a Wiener process. Here we will restudy the algorithm presented in [13], and extend it for the coloured noise case, and will compare both forms of the algorithm, and also compare their performance with the LSM extended algorithm presented in [14].

3 Instrumental variables algorithm for continuous-time

In [14] an algorithm for parameter estimation in stochastic systems under coloured perturbations using LSM was presented, this method represented the plant dynamic in an extended form, and it was necessary to estimate part of the structure of the noise in order to estimate \(A_{t}\). Here we will include the instrumental variable in this algorithm and will compare its performance with the simple instrumental variable algorithm in order to analyse which version is more suitable for coloured perturbations.

3.1 Estimation algorithm in the extended form

For the extended version of the IV algorithm, first let us represent the plant dynamics of Eq. (1) in the following extended form

$$\begin{aligned} dx_{t}=z_{t}C_{t}dt+f_{t}dt+B_{t}\sigma _{t}dW_{t}+B_{t}\varDelta H_{t}s_{t}dt \end{aligned}$$
(2)

where \(C_{t}\) is the vector to estimate, composed by elements \(a_{ij,t}\) from matrix \(A_{t}\) and the elements \(s_{i,t}\) from \(s_{t}\)

$$\begin{aligned}&C_{t}:=\left[ \begin{array} [c]{cccccccccc} a_{_{11,t}}&\cdots&a_{_{1m,t}}&\cdots&a_{_{n1,t}}&\cdots&a_{_{nm,t}}&s_{_{1,t}}&\cdots&s_{_{n,t}} \end{array} \right] ^{\top }\nonumber \\&\quad \in \mathbf R ^{n\times m+n} \end{aligned}$$
(3)

and the new regressor \(z_{t}\) is composed by the original regressor \(x_{t}\), and the available data \(g_{i,j}\) from \(B_{t}\) and \(H_{0}\)

$$\begin{aligned} \begin{array} [c]{c} z_{t}:=\left[ \begin{array} [c]{cccccccccc} x_{_{1,t}} &{} \cdots &{} x_{_{m,t}} &{} 0 &{} 0 &{} \cdots &{} 0 &{} g_{_{11,t}} &{} \cdots &{} g_{_{1n,t}}\\ \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} 0 &{} x_{_{1,t}} &{} \cdots &{} x_{_{m,t}} &{} g_{_{n1,t}} &{} \cdots &{} g_{_{nn,t}} \end{array} \right] \end{array} \end{aligned}$$
(4)

First, notice that, by back-integrating, for \(t\ge h\) Eq. (4) can be expressed as

$$\begin{aligned}&x_{t}-x_{t-h}- \int _{t-h}^{t} {\displaystyle \int _{t-h}^{t}} f_{s^{\prime }}ds^{\prime }= {\displaystyle \int _{t-h}^{t}} z_{s^{\prime }}C_{s^{\prime }}ds^{\prime }\nonumber \\&\quad + {\displaystyle \int _{t-h}^{t}} B_{s^{\prime }}\sigma _{s^{\prime }}dW_{s^{\prime }} + {\displaystyle \int _{t-h}^{t}} B_{s^{\prime }}\varDelta H_{s^{\prime }}s_{s^{\prime }}ds^{\prime } \end{aligned}$$
(5)

rearranging the terms of this equation in an extended output \(F_{t,t-h}\), an extended regressor \(Z_{_{t,t-h}}\), and an extended perturbation \(\xi _{t,t-h}\) in the corresponding “regression form” we get

$$\begin{aligned} F_{t,t-h}=Z_{t,t-h}C_{t}+\xi _{t,t-h} \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{array} [l]{l} F_{t,t-h}:=x_{t}-x_{t-h}-\int _{t-h}^{t}f_{s^{\prime }}ds^{\prime }\\ Z_{t,t-h}:=\int _{s^{\prime }=t-h}^{t}z_{s^{\prime }}ds^{\prime }\\ \xi _{t,t-h}:=\int _{t-h}^{t}B_{s^{\prime }}\sigma _{s^{\prime }}dW_{s^{\prime } }+\int _{t-h}^{t}z_{s^{\prime }}\left( C_{s^{\prime }}-C_{t}\right) ds^{\prime }\\ \qquad \qquad \;+\int _{t-h}^{t}B_{s^{\prime }}\varDelta H_{s^{\prime }}s_{s^{\prime }}ds^{\prime } \end{array} \end{aligned}$$
(7)

with \(h>0\) as a back-step, and \(Z_{_{t,t-h}}\) defined for \({\mathbf {\tau \ge h}}\). Here the “extended output” \(F_{t,t-h}\) and the “extended regressor” \(Z_{_{t,t-h}}\) are known at each \(t\ge 0\). Now it is necessary to define the instrumental variable as follows

$$\begin{aligned} V_{t,t-h}:=\int _{s^{\prime }=t-h}^{t}\upsilon _{s^{\prime }}ds^{\prime } \end{aligned}$$
(8)

here instead of the extended matrix \(z_{t}\) it will be used the matrix

$$\begin{aligned} \upsilon _{t}:=\left[ \begin{array} [c]{cccccccccc} v_{_{1,t}} &{} \cdots &{} v_{_{m,t}} &{} 0 &{} 0 &{} \cdots &{} 0 &{} g_{_{11,t}} &{} \cdots &{} g_{_{1n,t}}\\ \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} 0 &{} v_{_{1,t}} &{} \cdots &{} v_{_{m,t}} &{} g_{_{n1,t}} &{} \cdots &{} g_{_{nn,t}} \end{array} \right] \end{aligned}$$

that is equivalent to (1) but without the Wiener process. In this system \(x_{t}\) is replaced by the instrument \(v_{t}\), that is noise free and is based on the following system

$$\begin{aligned} \begin{array} [c]{l} dv_{t}=\tilde{A}_{t}v_{t}dt+f_{t}dt+B_{t}ds_{t}\\ \\ ds_{t}=H_{t}s_{t}dt \end{array} \end{aligned}$$
(9)

since we are trying to estimate \(A_{t}\), it is not realistic to use the exact parameter in the instrumental variable, instead we use an approximated value \(\tilde{A}_{t}\).

Multiplying (6) by the instrumental variable \(V_{_{t,t-h}}^{\top }\) and integrating back from \(t-h\) to t, we get

$$\begin{aligned}&\int _{t-h}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}d\tau =\int _{t-h} ^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}C_{\tau }d\tau \nonumber \\&\qquad + {\displaystyle \int _{t-h}^{t}} V_{\tau ,\tau -h}^{\top }\xi _{\tau ,\tau -h}d\tau \\&\quad =\left( \int _{t-h}^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}d\tau \right) C_{t}+\bar{\xi }_{t,t-h} \end{aligned}$$

where

$$\begin{aligned} \bar{\xi }_{t,t-h}=\int _{t-h}^{t}V_{\tau ,\tau -h}^{\top }\left( Z_{\tau ,\tau -h}\left[ C_{\tau }-C_{t}\right] +\xi _{\tau ,\tau -h}\right) d\tau \end{aligned}$$
(10)

If the “rate of parameter changing” \(\left\| C_{s^{\prime }} -C_{t}\right\| \) for any \(s^{\prime }\in \left[ t-h,t\right] \) is small enough (since h can be taken also small enough), one can define the current parameter estimate \(\hat{C}_{t}\) as the matrix satisfying the equalities

$$\begin{aligned} \int _{t-h}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}d\tau =\left( {\displaystyle \int _{t-h}^{t}} V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}d\tau \right) \hat{C}_{t} \end{aligned}$$
(11)

Then the “extended error-vector” \(\bar{\xi }_{t,t-h}\) will represent the current identification error corresponding to the parameter estimate \(\hat{C}_{t}\) satisfying (11). If the “persistence excitation condition” is fulfilled, i.e., if for any \(t\ge h>0\)

$$\begin{aligned} \int _{t-h}^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}d\tau >0 \end{aligned}$$
(12)

then the estimate \(\hat{C}_{t}\) can be represented by

$$\begin{aligned}&\hat{C}_{t}=\varGamma _{t}\left[ \int _{t-h}^{t}V_{\tau ,\tau -h}^{\top } F_{\tau ,\tau -h}d\tau \right] , \nonumber \\&\varGamma _{t}:=\left[ \int _{t-h} ^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}d\tau \right] ^{-1} \end{aligned}$$
(13)

that can be expressed, alternatively, as

$$\begin{aligned} \begin{array} [c]{c} \hat{C}_{t}=\varGamma _{t}\left[ \int _{0}^{t}V_{\tau ,\tau -h}^{\top } F_{\tau ,\tau -h}\chi \left( \tau \ge t-h\right) d\tau \right] \\ \varGamma _{t}:=\left[ \int _{0}^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h} \chi \left( \tau \ge t-h\right) d\tau \right] ^{-1} \end{array} \end{aligned}$$
(14)

Here, \(\chi \left( \tau \ge t-h\right) \) is the characteristic function defined by

$$\begin{aligned} \chi \left( \tau \ge t-h\right) :=\left\{ \begin{array} [c]{ccc} 1 &{} if &{} \tau \ge t-h\\ 0 &{} if &{} \tau <t-h \end{array} \right. \end{aligned}$$
(15)

In fact, this function characterizes the “window” \(\left[ t-h,t\right] \) within the integrals in (14). There, instead of \(\chi \left( \tau \ge t-h\right) \), a different kind of “windows” can be applied, for example, the “window” corresponding to the “forgetting factor” that leads to the following matrix estimate

$$\begin{aligned} \hat{C}_{t}=\varGamma _{t}Y_{t},t\ge h \end{aligned}$$
(16)

with

$$\begin{aligned}&Y_{t}=\int _{0}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}r^{t-\tau } d\tau ,\varGamma _{t}^{-1}\nonumber \\&\quad :=\int _{0}^{t}V_{\tau ,\tau -h}^{\top } Z_{\tau ,\tau -h}r^{t-\tau }d\tau \end{aligned}$$
(17)

where \(0<r<1\) is the forgetting factor. Below we will analyse differential form of the matrix estimating algorithm (16).

3.2 Differential form of the estimating algorithm

The direct derivation of (16) and (17) implies

$$\begin{aligned} \frac{d}{dt}\hat{C}_{t}=\varGamma _{t}\dot{Y}_{t}+\dot{\varGamma }_{t}Y_{t} \end{aligned}$$
(18)

where

$$\begin{aligned} \dot{Y}_{t}=V_{t,t-h}^{\top }F_{t,t-h}+\int _{0}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}\frac{d}{dt}r^{t-\tau }d\tau \end{aligned}$$
(19)

Here\(\ \frac{d}{dt}r^{t-\tau }\) \(=r^{t-\tau }\ln r\). In view of this, (19) can be rewritten as

$$\begin{aligned}&\dot{Y}_{t}=V_{t,t-h}^{\top }F_{t,t-h}+\int _{0}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}\frac{d}{dt}r^{t-\tau }d\tau \nonumber \\&\quad =V_{t,t-h}^{\top }F_{t,t-h}+\left( \int _{0}^{t}V_{\tau ,\tau -h}^{\top }F_{\tau ,\tau -h}r^{t-\tau }d\tau \right) \nonumber \\&\qquad \ln r=V_{t,t-h}^{\top } F_{t,t-h}+Y_{t}\ln r \end{aligned}$$
(20)

To calculate \(\dot{\varGamma }_{t}\), let us differentiate the identity \(\varGamma _{t}\varGamma _{t}^{-1}=I\) that leads to the following relations

$$\begin{aligned} \dot{\varGamma }_{t}\varGamma _{t}^{-1}+\varGamma _{t}\frac{d}{dt}\varGamma _{t} ^{-1}=0, \dot{\varGamma }_{t}=-\varGamma _{t}\frac{d}{dt}\varGamma _{t}^{-1} \varGamma _{t} \end{aligned}$$
(21)

The direct differentiation of (17) gives

$$\begin{aligned} \frac{d}{dt}\varGamma _{t}^{-1}= & {} V_{t,t-h}^{\top }Z_{t,t-h}+\ln r\int _{0}^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}r^{t-\tau } d\tau \nonumber \\= & {} V_{t,t-h}^{\top }Z_{t,t-h}+\ln r\varGamma _{t}^{-1} \end{aligned}$$
(22)

Replacing \(\frac{d}{dt}\varGamma _{t}^{-1}\) (22) in (21) we get

$$\begin{aligned} \dot{\varGamma }_{t}=-\varGamma _{t}V_{t,t-h}^{\top }Z_{t,t-h}\varGamma _{t}-\ln r\varGamma _{t} \end{aligned}$$
(23)

Using (23) in (18), we derive

$$\begin{aligned}&\frac{d}{dt}\hat{C}_{t}=\varGamma _{t}\dot{Y}_{t}+\dot{\varGamma }_{t}Y_{t} =\varGamma _{t}\left( V_{t,t-h}^{\top }F_{t,t-h}+Y_{t}\ln r\right) \\&\quad +\left( -\varGamma _{t}V_{t,t-h}^{\top }Z_{t,t-h}\varGamma _{t}-\ln r\varGamma _{t}\right) Y_{t}\nonumber \\&\quad =\varGamma _{t}V_{t,t-h}^{\top }\left[ F_{t,t-h} -Z_{t,t-h}\hat{C}_{t}\right] \end{aligned}$$

So, finally, the relations (23) and (20) constitute the following extended instrumental variable identification algorithm:

$$\begin{aligned}&\frac{d}{dt}\hat{C}_{t}=\varGamma _{t}V_{t,t-h}^{\top }\left[ F_{t,t-h} -Z_{t,t-h}\hat{C}_{t}\right] \nonumber \\&\dot{\varGamma }_{t}=-\varGamma _{t}V_{t,t-h}^{\top }Z_{t,t-h}\varGamma _{t}-\left( \ln r\right) \varGamma _{t}\nonumber \\&t\ge t_{0}>\inf _{t}\nonumber \\&\left\{ t\ge 0:\det \varGamma _{t}^{-1}= \det \left( \int _{0}^{t}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}r^{t-\tau }d\tau \right) {>}0\right\} \nonumber \\&\varGamma _{t_{0}}=\left[ \int _{0}^{t_{0}}V_{\tau ,\tau -h}^{\top }Z_{\tau ,\tau -h}r^{t_{0}-\tau }d\tau \right] ^{-1},\,\hat{C}_{t_{0}}=\varGamma _{t_{0}}Y_{t_{0}} \end{aligned}$$
(24)

In fact, \(t_{0}\) is any time just after the moment when the matrix \(\varGamma _{t}^{-1}\) is non-singular. This algorithm will be implemented for the coloured noise case, and compared with the simple IV algorithm shown in the following subsection.

3.3 The simple form of the IV algorithm

The IV algorithm in the simple form is based on the system

$$\begin{aligned} dx_{t}=A_{t}\zeta (x_{t})dt+f_{t}dt+\sigma _{t}dW_{t} \end{aligned}$$
(25)

where the stochastic noise is only a Wiener process. Following the same procedure presented previously we get the simple form of the IV method given by:

$$\begin{aligned} \begin{array} [c]{l} \frac{d}{dt}\hat{A}_{t}=(-\hat{A}_{t}X_{t,t-h}+F_{t,t-h})V_{t,t-h} ^{\top }\varGamma _{t}\\ \dot{\varGamma }_{t}=-\varGamma _{t}X_{t,t-h}V_{t,t-h}^{\top }\varGamma _{t}-\left( \ln r\right) \varGamma _{t}\\ \varGamma _{t_{0}}=\left[ {\displaystyle \int \limits _{0}^{t_{0}}} X_{\tau ,\tau -h}V_{\tau ,\tau -h}^{\top }r^{t_{0}-\tau }d\tau \right] ^{-1} ,\,\hat{A}_{t_{0}}=Y_{t_{0}}\varGamma _{t_{0}} \end{array} \end{aligned}$$
(26)

The error estimation analysis for both algorithms is similar to the result presented in [13, 14].

4 Numerical examples

In this section, we present two numerical examples in order to show the performance of the estimation algorithms mentioned in the previous section.

Example A. In the first example, system (1) is defined as follows

$$\begin{aligned} dx_{t}= & {} ((1.5 \sin (0.1\pi t)-5)x_{t}\nonumber \\&+\,10\sin (0.4)\pi t+5)dt+ds_{t}, \ x(0)=1.2 \end{aligned}$$
(27)
$$\begin{aligned} ds_{t}= & {} \left( -3+0.5\sin \left( .3 \pi t\right) \right) s_{t}+dW_{t}, \ s(0)=1.5 \end{aligned}$$
(28)

where \(\sigma _{t}=1\) and \(B_{t}=1\), \(h=0.0001\), and \(r=0.3\), the simulation time is \(t=100\), and the simulation method used in Matlab is ode1. The instrument \(v_{t}\) for the simple version (Eq. 25) is

$$\begin{aligned}&dv_{1t}=((1.5 \sin (0.1\pi t)-4)v_{1t}\nonumber \\&\qquad \quad +\,10\sin (0.4)\pi t+5)dt,\ x(0)=1.2 \end{aligned}$$
(29)

and for the extended version (Eq. 24)

$$\begin{aligned} dv_{2t}= & {} ((1.5 \sin (0.1\pi t)-4)v_{2t}\\&+\,10\sin (0.4)\pi t+5)dt+ds_{t}\\ ds_{t}= & {} \left( -3+0.5sin\left( .3 \pi t\right) \right) s_{t} \end{aligned}$$

In Fig. 1 it is shown the estimation algorithm using instrumental variables in the extended form, and it is compared with the least squares method, also in an extended form. Both algorithms have a similar performance, and there is not a visible benefit in the implementation of the instrumental variable.

In Fig. 2, it is presented the result of the estimation algorithm in the simple (IV2) and extended version (IV1) of the instrumental variable. Here the simple version of the algorithm shows a better performance than the extended version. This Figure shows that the simple version of the instrumental variable algorithms is strong enough to estimate even coloured noise, and is more effective than extending the estimation algorithm by adding information of the coloured noise.

The quality of the parameter estimation algorithm has been evaluated using the following performance index

$$\begin{aligned} J_{t}= \frac{1}{t+\varepsilon } \int _{0} ^{t} \left( a_{\tau } - \hat{a}_{\tau } \right) ^{2} d \tau \end{aligned}$$

with \(\varepsilon = 0.0001\) and \(t=100\), here \(\varepsilon \) is a regularizing parameter that avoids singularities in the beginning of the process (\(t=0\)). The performance index results for this example are:

$$\begin{aligned} J_{t=100}^{IV1}=2.044,\,J_{t=100}^{IV2}=1.181, \, J_{t=100}^{LSM}=2.005 \end{aligned}$$

this index shows that indeed, the simple form of the instrumental variable method is more effective for parameter estimation in systems under stochastic perturbations.

Example B. In this example the following system, from Eq. (1), is defined by

$$\begin{aligned} dx_{t}= & {} ((\sin (0.3\pi t)-1.5)x_{t}\nonumber \\&+\,0.5\sin (0.5)\pi t+12)dt+ds_{t},\ x(0)=2 \end{aligned}$$
(30)
$$\begin{aligned} ds_{t}= & {} \left( -3+0.6sin\left( .3 \pi t\right) \right) s_{t}+dW_{t}, \ s(0)=1.5\nonumber \\ \end{aligned}$$
(31)

where \(\sigma _{t}=1\), \(B_{t}=1\), \(h=0.02\) and \(r=0.2\), the simulation time is \(t=50\), and the simulation method used in Matlab is ode3, the instrument for the simple version (Eq. 25) is

$$\begin{aligned}&dv_{1t}=((\sin (0.3\pi t)-1)v_{1t}+0.5\\&\sin (0.5)\pi t+12)dt,\ x(0)=2 \end{aligned}$$

and for the extended version

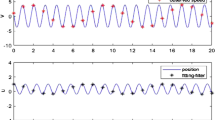
$$\begin{aligned} \begin{array}{l} dv_{2t}=((\sin (0.3\pi t)-1)v_{2t}\\ \qquad \qquad +\,0.5\sin (0.5)\pi t+12)dt+ds_{t}\\ ds_{t}=\left( -3+0.6sin\left( .3 \pi t\right) \right) s_{t} \end{array} \end{aligned}$$

The estimated parameter it is presented in Fig. 3, that displays the original parameter and the result of the estimation algorithm, this Figure shows that the simple form of the algorithm, even when some noise is present in the estimated parameter, has a good performance and is able to estimate the time varying parameter without any additional information concerning the coloured noise, and without any filtering or discretization of the system. The performance index results in this example are :

  • For the simple case \(J_{t=50}^{IV}=0.0284\)

  • For the extended case \(J_{t=50}^{IV}=0.0295\)

Fig. 1
figure 1

Parameter \(a_{t}\) and its estimated using LSM and IV

Full size image
Fig. 2
figure 2

Parameter \(a_{t}\) and its estimated using both versions if IV

Full size image
Fig. 3
figure 3

Parameter \(a_{t}\) and its estimated

Full size image

5 Conclusion

This study presented the instrumental variable (IV) technique for parameter estimation in continuous-time stochastic systems under coloured perturbations. The IV estimation algorithm was analysed in the simple form and in an extended form, that estimates part of the structure of the coloured noise. It was shown, through the performance index, that even when the extended form shows a good performance, the simple form is able to estimate coloured noise without additional information, is easier to implement and, has a better performance than the extended version.