Keywords

1.1 Introduction

Spherical friction pendulums (FP) are widely used to significantly reduce the absolute structural acceleration due to ground excitation by their effective radius that shifts the fundamental time period of the isolated structure into the region of attenuation and their friction damping that augments the damping of the structure [1]. The inherent drawback of FPs is that friction damping is nonlinear whereby the optimal friction coefficient depends on the displacement amplitude of the FP and consequently peak ground acceleration (PGA) [2]. The common approach is therefore to optimize the friction coefficient for the PGA of the design basis earthquake (DBE) and, subsequently, to check if the absolute structural acceleration due to the maximum credible earthquake (MCE) is acceptable. In addition, it must be checked if the isolation of the structure at very small PGAs is acceptable from the comfort point of view since the constant friction coefficient being optimal for the PGA of the DBE may lead to clamping effects in the FP whereby the relative motion stops in the FP and consequently the structural absolute acceleration is equal to the ground acceleration. In order to overcome these drawbacks of FPs several types of adaptive FPs have been developed: FPs with several sliding surfaces with different friction coefficients and effective radii [3] and pendulums that are extended by an external active or semi-active actuator such as hydraulic cylinders and controllable dampers on the basis of oil dampers with controlled bypass valve or magnetorheological fluids [4,5,6,7]. Controllable dampers are seen to provide a promising solution as the resulting closed-loop is unconditionally stable and their power consumption is very low compared to hydraulic actuators. This paper describes a novel approach of a semi-active isolator with the following main features:

  • controlled dynamic stiffness depending on the actual displacement amplitude of the pendulum,

  • optimum viscous damping, and

  • collocated control based on one displacement sensor.

1.2 Systems Under Consideration

1.2.1 Friction Pendulum

The common way to decouple the building/structure from the shaking ground is to support the building by FPs. The effective radius R eff  = R − h of the FP is selected to shift the time period T of the non-isolated structure from the region of amplification, i.e. T is typically in the region 0.5–2.0 s, to the region of attenuation with associated isolation time period T iso of typically 3–4 s. Subsequent to the design of the effective radius the friction coefficient μ of the sliding surface is optimized for minimum absolute structural acceleration for given T iso . As friction damping is nonlinear, the optimal value of μ depends on the bearing displacement amplitude and consequently on PGA. As a result, μ is commonly optimized for the PGA of the DBE. Finally, the structure with the designed FP is computed for the PGA due to the MCE to check if the absolute structural acceleration resulting from the MCE is acceptable and to know the displacement capacity of the FP that is required for the MCE.

1.2.2 Viscous Pendulum

In addition to the passive FP an “ideal” pendulum without friction but with linear viscous damping is considered as benchmark for passive isolators. Its effective radius is equal to that of the FP to ensure the same isolation time period T iso . Its viscous damping coefficient c is optimized for minimum absolute structural acceleration. Thanks to the linear behavior of viscous damping the optimization of c in independent of the bearing displacement amplitude and therefore independent of PGA.

1.2.3 Semi-Active Isolator

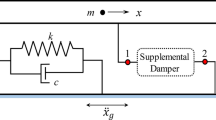
The semi-active isolator consists of a passive FP and a semi-active damper that is installed between ground and top bearing plate of the pendulum (Fig. 1.1). The design of the effective radius will be explained in the section “CONTROL LAW” as it is related to the formulation of the control law. The sliding surface of the passive FP is lubricated to minimize the passive and therefore uncontrollable friction damping of the semi-active isolator and thereby to maximize the controllability of the total isolator force. The dissipative force of the semi-active damper is controlled by the electromagnetic bypass valve. The desired control force is computed by the real-time controller based on the measured bearing displacement which is identical to the relative motion between damper cylinder and damper piston. Based on the desired control force a force tracking module computes the valve command signal such that the actual force of the semi-active damper tracks closely its desired counterpart in real-time.

Fig. 1.1
figure 1

Schematic of structure with semi-active isolator

Full size image

1.3 Modelling

Due to the large isolation time period T iso  = 3.5 s of the building with isolator the building may be modelled as a single degree-of-freedom system [1]. The according equation of motion becomes

$$ {m}_s\;{\ddot{u}}_s+{c}_s\;\left({\dot{u}}_s-\dot{u}\right)+{k}_s\;\left({u}_s-u\right)=-{m}_s\;{\ddot{u}}_g $$
(1.1)

where m s , c s , k s denote the modal mass, the viscous damping coefficient and the stiffness of the building, \( {\ddot{u}}_s \), \( {\dot{u}}_s \) and u s denote the acceleration, velocity and displacement of the structure relative to the ground, \( \dot{u} \) and u are the velocity and displacement of the top bearing plate relative to the ground and \( {\ddot{u}}_g \) is the ground acceleration given by the accelerogram of the El Centro North-South earthquake. The mass m s is determined by the typical vertical load of W = 6 MN on the isolator, \( {c}_s=2\;{\zeta}_s\;\sqrt{k_s\;{m}_s} \) is computed based on the damping ratio ζ s  = 1% and k s  = 24.15 MN/m is selected such that the natural frequency of the building without isolator is 1 Hz representing a typical value for structures that require base isolation. The equation of motion of the top plate of the isolator with mass m and with actual force \( {f}_{semi- active}^{actual} \) of the semi-active oil damper is

$$ m\;\ddot{u}+{f}_h+\frac{W}{R_{eff}}\;u={c}_s\;\left({\dot{u}}_s-\dot{u}\right)+{k}_s\;\left({u}_s-u\right)-{f}_{semi- active}^{actual}-{m}_s\;{\ddot{u}}_g $$
(1.2)

where f h is the friction force of the curved sliding surface and W/R eff is the restoring stiffness due to the effective radius R eff  = R − h of the pendulum. The force f h is modelled by the hysteretic damper modelling approach [8]

$$ {f}_h=\left\{\begin{array}{ccc}\hfill {k}_h\;u\hfill & \hfill :\hfill & \hfill pre- sliding\hfill \\ {}\hfill \mu\;W\; sign\left(\dot{u}\right)\hfill & \hfill :\hfill & \hfill sliding\hfill \end{array}\right. $$
(1.3)

where k h is the pre-sliding stiffness that is selected two orders of magnitude greater than W/R eff . In case of the passive pendulum without any friction but linear viscous damping f h in (1.2) is replaced by the term \( {c}^{opt}\;\dot{u} \) where c opt denotes the optimal viscous damping coefficient of the isolator.

1.4 Control Law

1.4.1 General Formulation

The desired active control force is formulated as follows

$$ {f}_{active}^{desired}=\left\{\begin{array}{ccc}\hfill {k}_{control}\;u+\left({c}^{opt}-{c}_{\mu}\right)\;\dot{u}\hfill & \hfill :\hfill & \hfill c-{c}_{\mu}\ge 0\hfill \\ {}\hfill {k}_{control}\;u\hfill & \hfill :\hfill & \hfill c-{c}_{\mu }<0\hfill \end{array}\right. $$
(1.4)

in order to produce:

  1. 1.

    the controlled stiffness k control that is controlled as function of the bearing displacement amplitude U to compensate for the passive stiffness of the curved surface given by W/R eff and thereby produce zero dynamic stiffness by k control  < 0 for maximum decoupling of the structure from the ground, and

  2. 2.

    the controlled damping force \( \left({c}^{opt}-{c}_{\mu}\right)\;\dot{u} \) that dissipates the same amount of damping as resulting from optimal linear viscous damping.

The desired optimal viscous damping coefficient c opt is reduced by the viscous damping coefficient c μ that is energy equivalent to the friction damping of the lubricated curved surface [2]

$$ {c}_{\mu}\approx \frac{4}{\pi}\;\frac{\mu\;W}{\omega_{iso}\;U} $$
(1.5)

in order to dissipate the cycle energy of optimal viscous damping. Since c μ is inversely proportional to the displacement amplitude U of the isolator, i.e. c μ  ∼ U −1, c μ may become greater than c opt at small U which necessitates the distinction of cases in (1.4). Notice that (1.5) represents an approximation because c μ according to Eq. (1.5) is derived based on the constant isolation radial frequency

$$ {\omega}_{iso}=\sqrt{\frac{g}{R_{eff}}} $$
(1.6)

but the actual frequency of the bearing displacement due to earthquake excitation is time-variant and therefore not detectable in real-time. However, the approximation (1.5) represents a good engineer’s solution as the actual frequency is in the vicinity of ω iso . The actual force of the semi-active oil damper can only produce the dissipative forces of the desired active control force \( {f}_{active}^{desired} \), that is

$$ {f}_{semi- active}^{actual}=\left\{\begin{array}{ccc}\hfill {f}_{active}^{desired}\hfill & \hfill :\hfill & \hfill \dot{u}\;{f}_{active}^{desired}\ge 0\hfill \\ {}\hfill 0\hfill & \hfill :\hfill & \hfill \dot{u}\;{f}_{active}^{desired}<0\hfill \end{array}\right. $$
(1.7)

The formulation (1.7) assumes that control force constraints such as minimum and maximum forces of the semi-active oil damper and control force tracking errors do not exist. Hence, the formulation (1.7) of the semi-active force represents the ideal behavior of a controllable damper.

1.4.2 Adaptive Controlled Stiffness

The maximum decoupling of the structure from the shaking ground and therefore minimum absolute structural acceleration \( {\ddot{u}}_s+{\ddot{u}}_g \) is obtained from zero dynamic stiffness of the isolator [9]. Since the passive (and positive) stiffness of the isolator is given by W/R eff , the controlled stiffness k control must be negative to reduce the total stiffness k total of the isolator to zero under dynamic operation. However, k total  = 0 for the entire bearing displacement range could not re-center the structure sufficiently. Hence, four adaptive stiffness control laws are suggested that produce zero dynamic stiffness either at U = 0 or at U ≥ U max due to the MCE:

  • Control law #1 (CL #1, Fig. 1.2a): The effective radius R eff of the curved surface is 50% of the nominal effective radius R eff − no min al generating the targeted isolation time period T iso  = 3.5 s. The controlled stiffness is formulated to produce k total  = k control  + W/R eff  = k R − eff − no min al  = W/R eff − no min al at U = 0 and zero dynamic stiffness, i.e. k total  = 0, at U ≥ U max = 0.25 m. Between U = 0 and U = U max the controlled stiffness is a linear function of U.

    Fig. 1.2
    figure 2

    Controlled stiffness and total bearing stiffness due to (a) control law #1 and (b) control law #2

    Full size image

  • Control law #2 (CL #2, Fig. 1.2b): The effective radius R eff of the curved surface is 50% of R eff − no min al . The controlled stiffness is formulated to produce zero total stiffness at U = 0 and k total  = W/R eff − no min al at U ≥ U max = 0.25 m. Between U = 0 and U = U max the controlled stiffness is a linear function of U.

  • Control law #3 (CL #3, Fig. 1.3a): The effective radius R eff of the curved surface is equal to R eff − no min al . The controlled stiffness is formulated to produce k total  = W/R eff − no min al at U = 0 and zero dynamic stiffness at U ≥ U max = 0.25 m. Between U = 0 and U = U max the controlled stiffness is a linear function of U.

    Fig. 1.3
    figure 3

    Controlled stiffness and total bearing stiffness due to (a) control law #3 and (b) control law #4

    Full size image

  • Control law #4 (CL #4, Fig. 1.3b): The effective radius R eff of the curved surface is equal to R eff − no min al . The controlled stiffness is formulated to produce zero dynamic stiffness at U = 0 and k total  = W/R eff − nom at U ≥ U max = 0.25 m. Between U = 0 and U = U max the controlled stiffness is a linear function of U.

The main difference between CL #1 and CL #3 (and between CL #2 and CL #4) is that the maximum (positive) and minimum (negative) controlled stiffness coefficients due to CL #1 (and CL #2) are only 50% of the maximum negative controlled stiffness of CL #3 (and CL #4) due to the different designs of R eff for CL #1 (and CL #2) and CL #3 (and CL #4). The control law leading to smaller controlled stiffness is more suitable for controllable dampers since the emulation of large stiffness with semi-active dampers is inherently combined with the generation of damping that is larger than the desired viscous damping given in (1.4) whereby the actual stiffness and damping of the actual semi-active force are far from their desired counterparts. Detailed information on the emulation errors of desired stiffness and damping with controllable dampers is beyond the scope of this paper but can found in [10]. The main difference between CL #1 (and CL #3) and CL #2 (and CL #4) is that CL #1 (and CL #3) results in zero dynamic stiffness at U = U max which improves the isolation of the structure at large PGAs due to earthquakes between DBE and MCE while CL #2 (and CL #4) generate zero dynamic stiffness at U = 0 which improves the isolation of the structure due to earthquakes up to DBE.

1.5 Results

1.5.1 Optimized Friction Pendulums

The effective radius of the passive FP is designed to produce the targeted isolation time period T iso  = 3.5 s. Given this effective radius the friction coefficient μ is optimized for minimum \( \max \left(|{\ddot{u}}_s+{\ddot{u}}_g|\right) \) for the PGA of the DBE that is assumed to be 5 m/s2 (Fig. 1.4b). The optimization of μ is also performed for PGA = 3.5 m/s2 and PGA = 6.5 m/s2 (Fig. 1.4a, c) to demonstrate that the best performance of the optimized FP is only obtained at the PGA value used for optimization highlighted by the green circles Fig. 1.4e.

Fig. 1.4
figure 4

Optimal friction coefficients (a–c) of passive FPs and optimal viscous coefficient (d) of passive pendulum with viscous damping; absolute structural acceleration (e) due to optimized passive FPs and pendulum with optimized viscous damping

Full size image

1.5.2 Pendulum with Optimized Linear Viscous Damping

The effective radius of the pendulum is the same as for the FP in order to guarantee equal time periods. The viscous damping coefficient is optimized for minimum \( \max \left(|{\ddot{u}}_s+{\ddot{u}}_g|\right) \) (Fig. 1.4d) which does not depend on the PGA of the ground acceleration as can be seen from the linear behavior of \( \max \left(|{\ddot{u}}_s+{\ddot{u}}_g|\right) \) as function of PGA depicted in Fig. 1.4e.

1.5.3 Semi-Active Pendulum

The isolation performance in terms of absolute structural acceleration of the semi-active pendulum with passive friction of 1.5% (lubricated) resulting from the four suggested control laws is depicted in Fig. 1.5a. The main observations are:

  • CL #1 and CL #2 perform better than CL #3 and CL #4 because the maximum controlled stiffness of CL #1 and CL #2 are only 50% of the maximum value due to CL #3 and CL #4 whereby the actual stiffness and actual damping produced by the semi-active damper are closer to their desired counterparts for CL #1 and CL #2 than for CL #3 and CL #4; further information on stiffness and damping emulations with semi-active dampers are available in [10].

  • CL #1 performs better than CL #2 at large PGAs because CL #1 is formulated to produce zero dynamic stiffness at U ≥ U max = 0.25 m whereas CL #2 outperforms CL #1 at smaller PGAs because CL #2 produces zero dynamic stiffness at U = 0.

Fig. 1.5
figure 5

Absolute structural acceleration (a) due to semi-active pendulums and (b) maximum total forces of all considered isolators

Full size image

In order to select the “best performing control law” not only the maximum reduction of the absolute structural acceleration should be considered but also the maximum force of the isolator (costs!, Fig. 1.5b), the maximum bearing displacement (costs!, Fig. 1.6a), the re-centering capability (Fig. 1.6b, re-centering error must not be larger than 50% of the bearing displacement capacity, i.e. 50% of 250 mm) and the maximum force of the semi-active damper (costs!, Figs. 1.7 and 1.8). The review of all these results reveals that CL #1 and CL #2 represent promising solutions. None of these two control laws can be denoted as superior as the project specifications alone determine if CL #1 or CL #2 is more appropriate for the isolation task, i.e. if the absolute structural acceleration should be minimized for PGAs corresponding to DBE and earthquakes beyond of DBE (CL #1) or for PGAs corresponding to DBE and earthquakes below DBE (CL #2).

Fig. 1.6
figure 6

Maximum displacements (a) and residual displacements (b) of all considered isolators

Full size image
Fig. 1.7
figure 7

Force displacement trajectories of (a) semi-active control force and (b) total force of semi-active isolator due to control law #1

Full size image
Fig. 1.8
figure 8

Force displacement trajectories of (a) semi-active control force and (b) total force of semi-active isolator due to control law #2

Full size image

1.6 Summary

This paper presents a novel semi-active base isolator based on a pendulum with uncontrollable lubricated friction of 1.5% and a semi-active oil damper in parallel. Four different control laws are formulated that target to control the total stiffness of the semi-active isolator in real-time as function of the actual bearing displacement amplitude and to produce optimal viscous damping. The numerical results demonstrate that the semi-active isolator significantly improves the isolation of the structure compared to optimized friction pendulums and a hypothetical pendulum without friction but optimal viscous damping. This result is achieved without getting larger bearing displacements and forces and the re-centering requirement is also fulfilled semi-active base isolator.