Keywords

1 Introduction

Fractional differentiation is an extension of classical integer differentiation to deal with non-integer (fractional) orders. It was defined in the 19th century by Riemann and Liouville, see for instance [13]. First applications on automatic control are cited since 1945 by Bode [9] and subsequently in [24, 34, 45].

Nowadays, fractional calculus is widely used in many engineering fields [5, 12, 16, 18, 22, 23, 32, 33, 35, 39]. It is a powerful mathematical tool for the description of long memory and hereditary properties of various materials and processes. For instance, in electrochemistry, diffusion processes of charges in acid batteries is governed by Randles models with an inherent fractional 0.5 derivatives of order [38]. Supercapacitor, which are highly energy device storage, are modeled with fractional integrator [30, 46]. In thermal diffusion, it is shown that the solution of the heat equation of a semi-infinite homogeneous medium depends on 0.5 order derivative [7]. Diffusion phenomena in semi-infinite planar, spherical and cylindrical media deals with a multiple of 0.5 differentiation order [31]. Experimental results prove that fractional models are appropriate to represent vibrations on viscoelastic materials [41]. The electromagnetic fields in dielectric media is described by a model with fractional differentiation [6, 43].

Some methods to estimate the pseudo states of fractional systems have been developed in the literature. For instance, fractional Kalman filters have been proposed for both discrete and continuous-time systems [1, 4, 21, 42]. Luenberger-based fractional observers have been also investigated in [14].

The main drawback of these techniques design is the difficulty to take into account uncertainties (unknown parameters or/and external disturbances). In the presence of uncertainty, design of conventional observers/filters, converging to the ideal value of the pseudo state is difficult to achieve. In such context, interval observers can be considered as an alternative. The latters do not permit to compute only an approximation but the set of all admissible values is characterized at each time instant. The width of the estimated domain should be proportional to the size of the uncertainties. With respect to conventional observers, the mid-value can be considered as a point estimation while the interval width is the uncertainty/deviation from such point value.

The theory of interval observers is well developed in the context of integer differentiation systems. In this chapter, such methodology is extended to fractional differentiation systems based on the theory of positive systems. It will be shown that, under some mild conditions, an interval observer can be developed for any linear fractional system subject to bounded noises and disturbances. To the best of our knowledge, it is the first time that interval observers are considered for this class of systems.

The chapter is organized as follows: some properties of fractional systems are recalled in Sect. 8.2. The main contribution is given in Sect. 8.3 where two observers are proposed for a particular case and also for general fractional linear systems. Finally, some numerical simulations are presented in Sect. 8.4 to illustrate this methodology.

2 Fractional Systems

Riemann and Liouville extended differentiation by using not only integer but also non-integer orders (fractional order). The \(\gamma \)th fractional order differentiation of a continuous real function f(t) is defined as [29]:

$$\begin{aligned} D^\gamma f(t) = \frac{1}{\varGamma \left( {1 - \gamma } \right) }\left( {\frac{d}{{dt}}} \right) ^{\left\lfloor {\gamma + 1} \right\rfloor } \int _0^t {\frac{{f\left( \tau \right) }}{{\left( {t - \tau } \right) ^\gamma }} d\tau } \end{aligned}$$
(8.1)

In the field of engineering sciences another definition of fractional differentiation has been proposed by Caputo [10]:

$$\begin{aligned} D^\gamma f(t) = \frac{1}{\varGamma ( {\left\lceil {\gamma } \right\rceil -\gamma }) } \int _0^t {\frac{{f^{(\left\lceil {\gamma } \right\rceil )} \left( \tau \right) }}{{\left( {t - \tau } \right) ^{1- \left\lceil {\gamma } \right\rceil + \gamma } }}} d\tau \end{aligned}$$
(8.2)

where \({f^{(\left\lceil {\gamma } \right\rceil )} \left( \tau \right) }\) denotes the integer derivative at \({(\left\lceil {\gamma } \right\rceil )}\) of f.

The fractional differentiation can be numerically evaluated using the Grünwald approximation [3]:

$$\begin{aligned} D^\gamma f(t) \simeq \frac{1}{h^\gamma } {\sum _{k=0}^{\infty } (-1)^k ( ^\gamma _k)} f(t-kh) \end{aligned}$$
(8.3)

where h is a small real number and

$$\begin{aligned} \left( \begin{array}{c} \gamma \\ k \end{array} \right) = \frac{\varGamma (\gamma +1)}{k!\varGamma (\gamma -k+1)} \end{aligned}$$
(8.4)

A continuous-time fractional linear system can be described with a fractional differential equation:

$$\begin{aligned} \sum _{i=0}^{n_y} a_i D^{\alpha _i} y(t) = \sum _{j=0}^{n_u} b_j D^{\beta _j} u(t) \end{aligned}$$
(8.5)

where u and y denote respectively the system input and output. The fractional differentiation orders \(\alpha _i, i=0 \ldots n_y\) and \(\beta _i, i=0 \ldots n_u\) are positive real numbers. Generally they are assumed to be rational, thus a commensurate fractional differential equation can be obtained:

$$\begin{aligned} \sum _{l=0}^{n'_y} a'_l D^{l\nu } y(t) = \sum _{k=0}^{n'_u} b'_k D^{k\nu } u(t) \end{aligned}$$
(8.6)

where the input and the output are differentiated to integer multiple of the commensurate order \(\nu \). From (8.6) the following representation can be deduced [36]:

$$\begin{aligned} \left\{ \begin{array}{rl} x^\nu (t)&{}=A x(t) + B u(t) \\ y(t)&{}= C x(t) +D u(t) \end{array} \right. \end{aligned}$$
(8.7)

where A, B, C and D are constant matrices with \(A\in \mathbb {R}^{n\times n}\), \(B\in \mathbb {R}^{n\times p}\), \(C\in \mathbb {R}^{m\times n}\) and \(D\in \mathbb {R}^{m\times p}\). For single input single output systems (\(m=p=1\)), the vector x is called a pseudo state and \( x^\nu \) denotes its fractional derivative at order \(\nu \), \(0<\nu \le 1\).

The variable x in (8.7) is not rigourously a state similar to the integer differentiation context and it has been shown in [44] that the dimension of the actual state of fractional systems is infinite. Indeed, the knowledge of x in (8.7) at t and all input values u over an arbitrary interval \([t,t+\varDelta t]\) is not sufficient to compute the state at \(t+\varDelta t\). However, the representation (8.7) is widely used when dealing with fractional systems since the pseudo state is sufficient for modelling, control and simulation purposes. Roughly speaking, in the following, (8.7) will be called fractional state space representation and x a state.

The system described by (8.7) is stable when all eigenvalues of A verify [2, 25]:

$$\begin{aligned} |arg(spec(A))|>\nu \frac{\pi }{2} \end{aligned}$$
(8.8)

In the following, a matrix M is called stable if its eigenvalues satisfy the condition (8.8).

The observability of fractional systems has been discussed in several papers [8, 17, 26, 27, 40] and a necessary and sufficient rank condition similar to the case of integer systems has been given in [17]:

$$\begin{aligned} rank\left( \begin{array}{c} C \\ CA \\ \vdots \\ CA^{n-1} \\ \end{array} \right) =n \end{aligned}$$
(8.9)

In the following and without any loss of generality, we will suppose that \(D=0\). A classical fractional observer structure for the estimation of x is given by:

$$\begin{aligned} \left\{ \begin{array}{rl} \hat{x}^\nu (t)&{}=A \hat{x}(t) + B u(t)+ L\left( y(t) - \hat{y}(t) \right) \\ \hat{y}(t)&{}= C \hat{x}(t) \end{array}\right. \end{aligned}$$
(8.10)

where \(\hat{x}\) denotes the estimated state and L is the observer gain. The estimation error is given by:

$$\begin{aligned} \tilde{x}^\nu (t)= \hat{x}^\nu (t)-{x}^\nu (t) = ( A-L C) (\hat{x}(t)-{x}(t)) \end{aligned}$$
(8.11)

To ensure the convergence of the estimation error, the system (8.11) should verify the stability condition (8.8). The observer gain L is chosen such that:

$$\begin{aligned} |arg(spec(A-L C))|>\nu \frac{\pi }{2} \end{aligned}$$
(8.12)

Note that the observer (8.10) converges asymptotically provided that the system (8.7) is not subject to noises and disturbances. Otherwise, the results can be unreliable. In the following, a robust approach is proposed to compute not only an approximation of the state but an interval which is guaranteed to enclose all the values of x consistent with the assumptions on the noises and disturbances. To the best of our knowledge, it is the first tentative to investigate this methodology for fractional systems.

A dynamical system is called internally positive if starting from any nonnegative condition and for any nonnegative input, its state remains always positive [19]. Furthermore, a matrix \(A\in \mathbb {R}^{n\times n}\) is called Metzler if all its off-diagonal entries are nonnegative, i.e. \(A = \{a_{i,j}\}, \; a_{i,j} \ge 0 ,\forall i \ne j\).

Lemma 8.1

[20] The fractional system described by (8.7) with \(\nu \le 1\) and \(x(0)\ge 0\) Footnote 1 is internally positive if and only if A is Metzler and all coefficients of the matrices B and C are nonnegative.

Lemma 8.2

[15] Given a vector \(\sigma (t)\in \mathbb {R}^{n}\) verifying \(\underline{\sigma }(t) \le \sigma \le \overline{\sigma }(t)\) for two vectors \(\underline{\sigma }(t), \overline{\sigma }(t) \in \mathbb {R}^n\). Then,

$$\begin{aligned} M^+ \underline{\sigma }(t) - M^- \overline{\sigma }(t) \le M \sigma (t) \le M^+ \overline{\sigma }(t) - M^- \, \underline{\sigma }(t) \end{aligned}$$
(8.13)

3 Main Results

Given a matrix \(M\in \mathbb {R}^{m\times n}\) and define \( M^+ = max(0,M)\) and \(M^- = M^+ -M\). \(| M |= M^+ + M^-\) is the matrix of absolute values of all elements of M.

3.1 Design of a Fractional Interval Observer

Consider the noisy fractional system

$$\begin{aligned} \left\{ \begin{array}{rl} x^\nu (t)&{}=A x(t) + B u(t)+ G w(t) \\ y(t)&{}= C x(t) + v(t) \end{array} \right. \end{aligned}$$
(8.14)

with \(\nu \le 1\). The input u(t) is known and A, B,C and G are constant matrices. w(t) and v(t) are some bounded disturbances and noises.

In the context of interval observers, the goal is to derive two trajectories \(\underline{x}(t)\) and \(\overline{x}(t)\) such that, starting from some initial conditions \(\overline{x}_0 \le x_0 \le \underline{x}_0 \), we have:

$$\overline{x}(t) \le x(t) \le \underline{x}(t), \quad \forall t \ge t_0$$

The following theorem gives a first result for the design of interval observers for (8.14).

Theorem 8.1

Given the system (8.14) with the initial condition \(x_0\) satisfying \(\underline{x}_0 \le x_0 \le \overline{x}_0\) for \(\underline{x}_0, \overline{x}_0 \in \mathbb {R}^n\). Assume that the noises and disturbances are bounded, i.e. \(|v(t)| \le V\), \(|w(t)| \le W\). If there exists a gain L such that \(A-LC\) is Metzler and \(|arg(spec(A-L C))|>\nu \frac{\pi }{2}\), then, the system (8.15) is an interval observer for (8.14):

$$\begin{aligned} \left\{ \begin{array}{ll} \underline{x}^\nu (t)= \left( A - LC \right) \underline{x}(t)+ Bu(t)+ \underline{b} (t), &{} \underline{x}(t_0)= \underline{x}_0\\ \overline{x}^\nu (t)= \left( A - LC \right) \overline{x}(t)+ Bu(t)+ \overline{b} (t) , &{} \overline{x}(t_0)= \overline{x}_0 \end{array} \right. \end{aligned}$$
(8.15)

with

$$\begin{aligned} \left\{ \begin{array}{l} \underline{b}(t) = -|G|W + Ly(t) - |L|V\\ \overline{b}(t) = |G|W + Ly(t) + |L|V \end{array}\right. \end{aligned}$$
(8.16)

Proof

Consider the observer error \(\overline{e}_x = \overline{x} - x\). Based on (8.14) and (8.15), the dynamics of \(\overline{e}_x\) is described by:

$$\begin{aligned} \begin{array}{lll} \overline{e}_x^\nu (t)&{}=&{} (A - LC)\overline{x} + Bu(t)+ |G|W + Ly + |L|V - (A x(t)+ Bu(t) + Gw(t) ) \\ &{}=&{} (A - LC)\overline{e}_x + \left( |L|V + Lv(t) \right) + \left( |G|W - Gw(t)\right) \end{array} \end{aligned}$$
(8.17)

Since the gain L is designed such that \((A-LC )\) is Metzler and by construction \(|L|V +Lv(t)\ge 0\), \(|G|W - Gw(t) \ge 0\), then the dynamics of \(\overline{e}_x\) is positive, i.e. \(\overline{e}_x = \overline{x} - x \ge 0, \forall t \ge t_0\). In addition, it is assumed that the gain L is chosen such that \(A-LC\) is stable (i.e. \(|arg(spec(A-L C))|>\nu \frac{\pi }{2}\)), thus the upper error \(\overline{e}_x\) is stable. Similarly, the same methodology can be followed to prove that \(\underline{e}_x = x - \underline{x} \ge 0, \forall t \ge t_0\) and that \(\underline{e}_x\) is stable. To conclude, it has been proven that the observation errors are stable and that:

$$\begin{aligned} \underline{x}(t) \le x(t) \le \overline{x}(t), \quad \forall t\ge t_0. \end{aligned}$$
(8.18)

\(\square \)

Note here that the observability is a sufficient condition (however, the detectability is necessary and sufficient) for the existence of a gain L ensuring the stability of both \(\underline{e}_x\) and \(\underline{e}_x\). In practice, computing a gain L satisfying both conditions of Theorem 8.1 is not obvious and may be impossible in some cases. To overcome this problem, some changes of coordinates can be used to generalize the previous result.

3.2 General Case

Usually, it is not possible to find a gain L such that \(A - LC\) is simultaneously Metzler and stable. Furthermore, the eigenvalues of the matrix \(A - LC\) are preserved under a change of coordinates. In this section, we propose a procedure to overcome this concern by computing a gain L such that \(A - LC\) is stable and a nonsingular transformation matrix \(P \in \mathbb {R}^{n\times n}\) such that, in the new coordinates \(z = Px\), the matrix \(\varGamma = P(A - LC)P^{-1}\) is Metzler. The conditions of existence of such a real transformation matrix P has been established by the following lemma.

Lemma 8.3

[37] Given the matrices \(A\in \mathbb {R}^{n\times n}\), \(R\in \mathbb {R}^{n\times n}\) and \(C\in \mathbb {R}^{p\times n}\). If there is a gain \(L\in \mathbb {R}^{n\times p}\) such that the matrices \(A-LC\) and R have the same eigenvalues, then there exists a matrix \(P\in \mathbb {R}^{n\times n}\) such that \(R=P(A-LC)P^{-1}\) provided that the pairs \((A-LC,e_{1})\) and \((R,e_{2})\) are observable for some \(e_{1}\in \mathbb {R}^{n}\), \(e_{2}\in \mathbb {R}^{n}\).

This result was used in [37] to design interval observers for integer linear time invariant systems with a Metzler matrix R.

Furthermore, based on the Jordan form, it has been shown in [28] that it is usually possible to design a transformation \(z = Px\) such that \(A - LC\) is Metzler. When the eigenvalues of \(A - LC\) are real, the matrix P is constant, otherwise, it is time-varying. A similar methodology has been developed in [11] where the complex-valued transformations are used.

In the following, given a gain L such that \(A-LC\) is stable and consider a change of coordinates \(z(t)=Px(t)\) such that \(P(A-LC)P^{-1}\) is Metzler. The matrix P can be computed using the Lemma 8.3 or the Jordan form investigated in [11, 28]. Therefore, an interval observer structure for (8.7) in the coordinated z and x is given in the following theorem.

Theorem 8.2

Given (8.14) with the initial condition \(x_0\) satisfying \(\underline{x}_0 \le x_0 \le \overline{x}_0\) for \(\underline{x}_0, \overline{x}_0 \in \mathbb {R}^n\). Assume that the noises and disturbances are bounded, i.e. \(|v(t)| \le V\), \(|w(t)| \le W\). Suppose also that P is chosen following Lemma 8.3 and L such that the stability condition (8.23) is verified. Then, the system (8.19), initialized with (8.21), is an interval observer for (8.14) in the coordinates \(z=Px\).

$$\begin{aligned} \left\{ \begin{array}{l} \underline{{z}}^\nu (t)= \varGamma \underline{{z}}(t)+ PBu(t)+ \underline{b} (t)\\ \overline{{z}}^\nu (t)= \varGamma \overline{ {z}}(t)+ PBu(t)+ \overline{b} (t) \end{array} \right. \end{aligned}$$
(8.19)

with

$$\begin{aligned} \varGamma =P\left( A - LC \right) M, \quad M=P^{-1} \end{aligned}$$
(8.20)
$$\begin{aligned} \left\{ \begin{array}{l} \underline{z}(0) = P^+ \underline{x}_0 - P^- \overline{x}_0\\ \overline{z}(0) = P^+ \overline{x}_0 - P^- \underline{x}_0 \end{array}\right. \end{aligned}$$
(8.21)
$$\begin{aligned} \left\{ \begin{array}{l} \underline{b}(t) = -|PG|W + PL y(t) - |PL| V\\ \overline{b}(t) = |PG|W + PLy(t) + |PL|V \end{array}\right. \end{aligned}$$
(8.22)
$$\begin{aligned} |arg(spec(\varGamma )|>\nu \frac{\pi }{2} \end{aligned}$$
(8.23)

In addition, an interval estimation of (8.14), in the coordinates x, is given by (8.24):

$$\begin{aligned} \left\{ \begin{array}{l} \underline{x}(t) = M^+ \underline{z}(t) - M^- \overline{z}(t)\\ \overline{x}(t) = M^+ \overline{z}(t) - M^- \underline{z}(t) \end{array}\right. \end{aligned}$$
(8.24)

Proof

The system (8.14) can be rewritten as:

$$\begin{aligned} z^\nu (t) = \varGamma z(t) + PBu(t) + PLCP^{-1}z(t) + PGw(t). \end{aligned}$$
(8.25)

Furthermore, according to (8.19) the dynamics of \(\overline{z}\) is given by:

$$\begin{aligned} \begin{array}{lll} \overline{z}^\nu (t)&{}=&{} \varGamma \overline{z}(t)+ PBu(t)+ \overline{b} (t) \\ &{}=&{} \varGamma \overline{z}(t)+ PBu(t)+ |PG|W + PLy(t) + |PL|V \\ &{}=&{} \varGamma \overline{z}(t)+ PBu(t)+ |PG|W + PLCP^{-1}z(t)\\ &{}&{}+ PLv(t) + |PL|V. \end{array} \end{aligned}$$
(8.26)

Consider now the observer error \(\overline{e}_z = \overline{z} - z\). Based on (8.25) and (8.26), the dynamics of \(\overline{e}_z\) is described by:

$$\begin{aligned} \begin{array}{lll} \overline{e}_z^\nu (t)&{}=&{} \varGamma \overline{z}_z(t)+ PBu(t)+ |PG|W + PLCP^{-1}z(t)\\ &{}&{}+ PLv(t) + |PL|V \\ &{}&{} - (\varGamma z(t)+ PBu(t) + PLCP^{-1}z + PGw(t) \\ &{}=&{} \varGamma \overline{e}_z(t)+ |PL|V +PLv(t) + |PG|W - PGw(t) \end{array} \end{aligned}$$
(8.27)

Recall that the matrix \(\varGamma = P(A-LC)P^{-1}\) is Metzler and by construction \(|PL|V +PLv(t)\ge 0\), \(|PG|W - PGw(t) \ge 0\), therefore the dynamics of \(\overline{e}_z\) is positive, i.e. \(\overline{e}_z = \overline{z} - z \ge 0, \forall t \ge t_0\).

In addition, it is assumed that the gain L is chosen such that \(A-LC\) (and consequently \(\varGamma \)) is stable, thus the upper error \(\overline{e}_z\) is stable.

Moreover, the same methodology can be followed to prove that \(\underline{e}_z = z - \underline{z} \ge 0, \forall t \ge t_0\) and that \(\underline{e}_z\) is stable.

Now, based on Lemma 8.2, it is trivial to show that:

$$ \underline{x} = M^+\underline{z} - M^-\overline{z} \le Mz = x \le M^+\overline{z} - M^-\underline{z} = \overline{x}. $$

In addition, the stability of \(x - \underline{x}\) and \(\overline{x} - x\) are deduced from that of \(\underline{e}_z\) and \(\overline{e}_z\) since such property is preserved under changes of coordinates.

4 Numerical Simulations

4.1 Example 1

Given a system described by:

$$\begin{aligned} \left\{ \begin{array}{rl} x^\nu (t)&{}=A x(t) + B u(t) \\ y(t)&{}= C x(t) + v\left( t\right) \end{array} \right. \end{aligned}$$
(8.28)

where:

$$ A= \left[ \begin{array}{cc} -5 &{} 2 \\ 6 &{} -3 \end{array} \right] , B=\left[ \begin{array}{c} 1 \\ 1 \\ \end{array} \right] , C= \left[ \begin{array}{cc} 1&1 \end{array} \right] $$

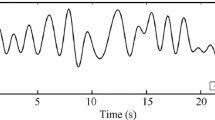
and the commensurate order is \(\nu =0.5\). v(t) is a bounded noise such that \(|v(t)| \le V = 0.1\). The initial state is arbitrarily chosen as \((5, 10)^T\) and is supposed to be affected by 50% of uncertainty. Note that uncertainty on the initial state may model the insufficient information about the past of the system. The input and the output of the system are plotted on Fig. 8.1.

Fig. 8.1
figure 1

Input, output and measurement noise for the system (8.28)

Full size image

The pair (A, C) verifies the observability condition (8.9) and there exists a gain L verifying (8.12):

$$\begin{aligned} |arg(spec(A-L C))|>0.5 \frac{\pi }{2} \end{aligned}$$
(8.29)

The gain \(L= (0.12, 0.27)^T\) is used, it allows to the eigenvalues of \(A-LC\) to be the same as those of A except the largest one which is multiplied by 4, i.e. \( spec(A-LC)= \{ -7.61 , -1.58\}\). For the chosen gain L, the matrix

$$\begin{aligned} A-LC=\left[ \begin{array}{cc} -5.36 &{} 1.64 \\ 5.17 &{} -3.83 \\ \end{array} \right] \end{aligned}$$
(8.30)

is Metzler. Therefore, the estimation error is positive and the fractional interval observer is designed according to (8.15). The actual state and its lower and upper bounds are plotted on Fig. 8.2. Clearly, the robustness is shown through this numerical example.

Fig. 8.2
figure 2

The actual states and their lower and upper bounds for the system (8.28)

Full size image
Fig. 8.3
figure 3

Fractional electrical circuit

Full size image
Fig. 8.4
figure 4

Diagonalized states and their lower and upper bounds

Full size image

4.2 Example 2

Consider an electrical circuit to illustrate the design of a fractional interval observer in the general case. The fractional electrical circuit is given on Fig. 8.3 where R is the resistance, \(C_f\) is a fractional order supercapacitor and \(L_f\) is a fractional order inductance [20]. Analysing the circuit with the Kirchhoffs laws we obtain the fractional differential equations:

$$\begin{aligned} i(t)=C_f \frac{ d^\alpha u_c(t)}{dt} \end{aligned}$$
(8.31)

and

$$\begin{aligned} u(t)= Ri(t)+ u_c(t)+ L_f \frac{ d^\beta i(t)}{dt} \end{aligned}$$
(8.32)

Assuming that \(\nu =\alpha =\beta \) and considering that only \(u_c(t)\) is measured, the following fractional state space representation can be obtained:

$$\begin{aligned} \left\{ \begin{array}{rl} \left[ \begin{array}{c} u_c(t) \\ i(t) \\ \end{array} \right] ^\nu =&{} \left[ \begin{array}{cc} 0 &{} 1/C_f \\ -1/L_f &{} -R/L_f \\ \end{array} \right] \left[ \begin{array}{c} u_c(t) \\ i(t) \\ \end{array} \right] + \left[ \begin{array}{c} 0 \\ 1/L_f \\ \end{array} \right] u(t) +w(t) \\ y(t)=&{} u_c(t)+v(t) \end{array} \right. \end{aligned}$$
(8.33)

where w(t) and v(t) are some unknown additive disturbances and noises. For simulation, the following numerical values are chosen:

$$\begin{aligned} R=20\,\Omega \quad C_f=600\,\upmu \text {F}, \end{aligned}$$
$$ L_f= 30\, \text {mH}, \nu = \alpha = \beta =0.5 $$

The observability rank condition (8.9) is verified and the gain

$$ L=\begin{bmatrix} 503.3333 \\ -29.4667 \end{bmatrix} $$

is used. Thus, the closed-loop matrix is given by:

$$\begin{aligned} A-LC=\left[ \begin{array}{rr} -0.5033 &{} 1.6667\\ -0.0039 &{} -0.6667 \end{array} \right] 10^3 \end{aligned}$$
(8.34)

Note that \((A-LC\)) is not Metzler. Therefore, the fractional interval observer of Theorem 8.1 cannot be applied. However, using a change of coordinates (a diagonalization of \( A-LC\) in this case), the interval observer of Theorem 8.2 permits to estimate the lower and the upper bounds of the state in the coordinates z and also in the initial ones (\(u_c(t)\) and i(t)).

Fig. 8.5
figure 5

\(u_c\) and i(t) and their lower and upper bounds

Full size image

Noises w(t) and v(t) are supposed to be bounded with \(|W| = |V| = 0.1\). The initial state is chosen as \((u_c(0)=2, i(0)=0.5)^T\) and is supposed to be affected by large uncertainty, i.e.:

$$\begin{aligned} \underline{u}_c(0)= 0 \quad \overline{u}_c(0)= 20 \end{aligned}$$
$$\begin{aligned} \underline{i}(0)= 0 \quad \overline{i}(0)= 5 \end{aligned}$$

Applying Theorem 8.2, the estimated bounds of the state in the coordinates z are plotted on Fig. 8.4. Those of \(u_c(t)\) and i(t) are plotted on Fig. 8.5.

5 Conclusion

The design of interval observers for fractional differentiation systems is investigated in this work. Under some mild conditions (boundedness of noises and disturbances, observability), two Luenberger-based observers allow one to compute reliable bounds for the state values consistent with the bounds of the uncertainties. A first result is given to build interval observers when it is possible to design a gain L satisfying the Metzler and stability properties of \(A-LC\). In addition, by using a change of coordinates, a general result, which can be applied to any linear fractional differentiation system, is proposed. An extension of this approach to address the case of parameter uncertainties and time-varying systems will be the subject of further works.